आणविक कक्षक: Difference between revisions

Revision as of 09:33, 11 July 2023

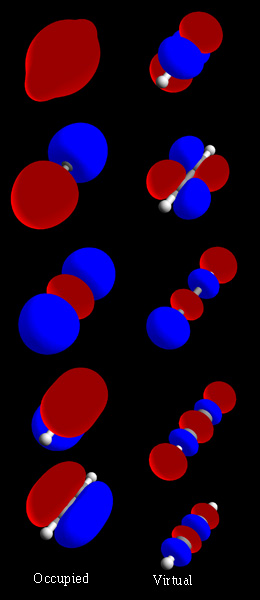
पूर्ण एसिटिलीन (H-C≡C-H) आणविक कक्षीय सेट। बायां स्तंभ एमओ को दर्शाता है जो जमीनी अवस्था में व्याप्त हैं, शीर्ष पर सबसे कम ऊर्जा कक्षीय है। कुछ MO में दिखाई देने वाली सफेद और भूरे रंग की रेखा नाभिक से गुजरने वाली आणविक धुरी है। कक्षीय तरंग कार्य लाल क्षेत्रों में सकारात्मक और नीले क्षेत्रों में नकारात्मक होते हैं। दायां कॉलम आभासी एमओ को दर्शाता है जो जमीनी अवस्था में खाली हैं, लेकिन उत्तेजित अवस्था में व्याप्त हो सकते हैं।

रसायन विज्ञान में, आणविक कक्षक (/ɒrbədl/) फ़ंक्शन (गणित) है जो अणु में इलेक्ट्रॉन के स्थान और पदार्थ तरंग | तरंग जैसे व्यवहार का वर्णन करता है। इस फ़ंक्शन का उपयोग रासायनिक और भौतिक गुणों की गणना करने के लिए किया जा सकता है जैसे कि किसी विशिष्ट क्षेत्र में इलेक्ट्रॉन खोजने की संभावना। परमाणु कक्षक और आणविक कक्षक शब्द^{[lower-alpha 1]} को 1932 में रॉबर्ट एस. मुल्लिकेन द्वारा एक-इलेक्ट्रॉन कक्षीय तरंग कार्यों के अर्थ में पेश किया गया था।^[2] प्रारंभिक स्तर पर, उनका उपयोग अंतरिक्ष के उस क्षेत्र का वर्णन करने के लिए किया जाता है जिसमें किसी फ़ंक्शन का महत्वपूर्ण आयाम होता है।

एक पृथक परमाणु में, कक्षीय इलेक्ट्रॉनों का स्थान परमाणु कक्षक नामक कार्यों द्वारा निर्धारित होता है। जब कई परमाणु रासायनिक रूप से अणु में संयोजित होते हैं, तो इलेक्ट्रॉनों का स्थान समग्र रूप से अणु द्वारा निर्धारित होता है, इसलिए परमाणु कक्षाएँ मिलकर आणविक कक्षाएँ बनाती हैं। घटक परमाणुओं से इलेक्ट्रॉन आणविक कक्षाओं पर कब्जा कर लेते हैं। गणितीय रूप से, आणविक कक्षाएँ अणु के परमाणु नाभिक के क्षेत्र में इलेक्ट्रॉनों के लिए श्रोडिंगर समीकरण का अनुमानित समाधान हैं। इनका निर्माण आम तौर पर अणु के प्रत्येक परमाणु से परमाणु ऑर्बिटल्स परमाणु ऑर्बिटल्स या संकर कक्षीय ्स या परमाणुओं के समूहों से अन्य आणविक ऑर्बिटल्स के रैखिक संयोजन द्वारा किया जाता है। उन्हें हार्ट्री-फॉक विधि | हार्ट्री-फॉक या सेल्फ-कंसिस्टेंट फील्ड (एससीएफ) विधियों का उपयोग करके मात्रात्मक रूप से गणना की जा सकती है।

आणविक कक्षाएँ तीन प्रकार की होती हैं: आबंधन आणविक कक्षाएँ जिनकी ऊर्जा उन्हें बनाने वाले परमाणु कक्षाओं की ऊर्जा से कम होती है, और इस प्रकार उन रासायनिक बंधों को बढ़ावा देती है जो अणु को साथ रखते हैं; प्रतिरक्षी आणविक ऑर्बिटल्स जिनकी ऊर्जा उनके घटक परमाणु ऑर्बिटल्स की ऊर्जा से अधिक होती है, और इसलिए अणु के बंधन का विरोध करते हैं, और गैर-बंधन ऑर्बिटल्स जिनकी ऊर्जा उनके घटक परमाणु ऑर्बिटल्स के समान होती है और इस प्रकार बॉन्डिंग पर कोई प्रभाव नहीं पड़ता है अणु.

अवलोकन

एक आणविक कक्षक (एमओ) का उपयोग अणु में उन क्षेत्रों का प्रतिनिधित्व करने के लिए किया जा सकता है जहां उस कक्षक पर कब्जा करने वाले ऋणावेशित सूक्ष्म अणु का विन्यास पाए जाने की संभावना है। आणविक कक्षाएँ अणु के परमाणु नाभिक के विद्युत क्षेत्र में इलेक्ट्रॉनों के लिए श्रोडिंगर समीकरण के अनुमानित समाधान हैं। हालाँकि इस समीकरण से सीधे ऑर्बिटल्स की गणना करना बहुत ही कठिन समस्या है। इसके बजाय वे परमाणु कक्षाओं के संयोजन से प्राप्त होते हैं, जो परमाणु में इलेक्ट्रॉन के स्थान की भविष्यवाणी करते हैं। आणविक कक्षक अणु के इलेक्ट्रॉन विन्यास को निर्दिष्ट कर सकता है: (या जोड़ी) इलेक्ट्रॉन का स्थानिक वितरण और ऊर्जा। आमतौर पर एमओ को परमाणु कक्षाओं के रैखिक संयोजन आणविक कक्षीय विधि (एलसीएओ-एमओ विधि) के रूप में दर्शाया जाता है, विशेष रूप से गुणात्मक या बहुत अनुमानित उपयोग में। वे आणविक कक्षीय सिद्धांत के माध्यम से समझे गए अणुओं में बंधन का सरल मॉडल प्रदान करने में अमूल्य हैं। कम्प्यूटेशनल रसायन विज्ञान में अधिकांश वर्तमान विधियां सिस्टम के एमओ की गणना से शुरू होती हैं। आणविक कक्षक नाभिक द्वारा उत्पन्न विद्युत क्षेत्र में इलेक्ट्रॉन के व्यवहार और अन्य इलेक्ट्रॉनों के कुछ औसत वितरण का वर्णन करता है। ही कक्षा में रहने वाले दो इलेक्ट्रॉनों के मामले में, पाउली सिद्धांत की मांग है कि उनके पास विपरीत स्पिन हो। आवश्यक रूप से यह अनुमान है, और आणविक इलेक्ट्रॉनिक तरंग फ़ंक्शन के अत्यधिक सटीक विवरण में ऑर्बिटल्स नहीं होते हैं (कॉन्फ़िगरेशन इंटरेक्शन देखें)।

सामान्य तौर पर, आणविक कक्षाएँ पूरे अणु में स्थानीयकृत होती हैं। इसके अलावा, यदि अणु में समरूपता तत्व हैं, तो इसके गैर-अपक्षयी आणविक कक्षाएँ इनमें से किसी भी समरूपता के संबंध में या तो सममित या एंटीसिमेट्रिक हैं। दूसरे शब्दों में, आणविक कक्षीय ψ में समरूपता ऑपरेशन एस (उदाहरण के लिए, प्रतिबिंब, घूर्णन, या व्युत्क्रम) के अनुप्रयोग के परिणामस्वरूप आणविक कक्षक अपरिवर्तित होता है या इसके गणितीय चिह्न को उलट देता है: Sψ = ±ψ। उदाहरण के लिए, तलीय अणुओं में, आणविक तल में परावर्तन के संबंध में आणविक कक्षाएँ या तो सममित (सिग्मा बांड) या एंटीसिमेट्रिक (पीआई बांड) होती हैं। यदि विकृत कक्षीय ऊर्जा वाले अणुओं पर भी विचार किया जाता है, तो अधिक सामान्य कथन यह है कि आणविक कक्षाएँ अणु के समरूपता समूह के अघुलनशील प्रतिनिधित्व के लिए आधार बनाती हैं।^[4] आणविक ऑर्बिटल्स के समरूपता गुणों का मतलब है कि डेलोकलाइज़ेशन आणविक ऑर्बिटल सिद्धांत की अंतर्निहित विशेषता है और इसे मूल रूप से (और पूरक) वैलेंस बॉन्ड सिद्धांत से अलग बनाता है, जिसमें बॉन्ड को स्थानीयकृत इलेक्ट्रॉन जोड़े के रूप में देखा जाता है, अनुनाद (रसायन विज्ञान) के लिए छूट के साथ स्थानीयकरण के लिए खाता.

इन समरूपता-अनुकूलित विहित आणविक कक्षाओं के विपरीत, विहित कक्षाओं में कुछ गणितीय परिवर्तन लागू करके स्थानीयकृत आणविक कक्षाएँ बनाई जा सकती हैं। इस दृष्टिकोण का लाभ यह है कि ऑर्बिटल्स अणु के बंधनों के अधिक निकट से मेल खाएंगे जैसा कि लुईस संरचना द्वारा दर्शाया गया है। नुकसान के रूप में, इन स्थानीयकृत कक्षाओं के ऊर्जा स्तर का अब भौतिक अर्थ नहीं रह गया है। (इस लेख के बाकी हिस्से में चर्चा कैनोनिकल आणविक ऑर्बिटल्स पर केंद्रित होगी। स्थानीयकृत आणविक ऑर्बिटल्स पर आगे की चर्चा के लिए, देखें: प्राकृतिक बॉन्ड ऑर्बिटल और सिग्मा-पीआई और समकक्ष-ऑर्बिटल मॉडल।)

आणविक कक्षकों का निर्माण

आणविक कक्षाएँ परमाणु कक्षाओं के बीच अनुमत अंतःक्रियाओं से उत्पन्न होती हैं, जिन्हें अनुमति दी जाती है यदि परमाणु कक्षाओं की समरूपता (समूह सिद्धांत से निर्धारित) दूसरे के साथ संगत हैं। परमाणु कक्षीय अंतःक्रियाओं की दक्षता दो परमाणु कक्षकों के बीच कक्षीय ओवरलैप (दो कक्षक दूसरे के साथ कितनी अच्छी तरह से रचनात्मक रूप से बातचीत करते हैं इसका माप) से निर्धारित की जाती है, जो महत्वपूर्ण है यदि परमाणु कक्षक ऊर्जा में करीब हैं। अंत में, बनने वाले आणविक कक्षकों की संख्या अणु बनाने के लिए संयोजित होने वाले परमाणुओं में परमाणु कक्षकों की संख्या के बराबर होनी चाहिए।

गुणात्मक चर्चा

आणविक संरचना की अस्पष्ट, लेकिन गुणात्मक रूप से उपयोगी चर्चा के लिए, आणविक कक्षकों को परमाणु कक्षकों के रैखिक संयोजन आणविक कक्षीय विधि ansatz से प्राप्त किया जा सकता है। यहां, आणविक कक्षाओं को परमाणु कक्षाओं के रैखिक संयोजन के रूप में व्यक्त किया गया है।^[5]

परमाणु कक्षकों का रैखिक संयोजन (LCAO)

आणविक कक्षाएँ पहली बार फ्रेडरिक कुत्ता द्वारा प्रस्तुत की गईं^[6]^[7] और रॉबर्ट एस. मुल्लिकेन^[8]^[9] 1927 और 1928 में.^[10]^[11] परमाणु ऑर्बिटल्स का रैखिक संयोजन या आणविक ऑर्बिटल्स के लिए एलसीएओ सन्निकटन 1929 में जॉन लेनार्ड-जोन्स|सर जॉन लेनार्ड-जोन्स द्वारा पेश किया गया था।^[12] उनके अभूतपूर्व पेपर में दिखाया गया कि क्वांटम सिद्धांतों से अधातु तत्त्व और ऑक्सीजन अणुओं की इलेक्ट्रॉनिक संरचना कैसे प्राप्त की जाए। आणविक कक्षीय सिद्धांत का यह गुणात्मक दृष्टिकोण आधुनिक क्वांटम रसायन विज्ञान की शुरुआत का हिस्सा है। परमाणु ऑर्बिटल्स (एलसीएओ) के रैखिक संयोजन का उपयोग आणविक ऑर्बिटल्स का अनुमान लगाने के लिए किया जा सकता है जो अणु के घटक परमाणुओं के बीच बंधन पर बनते हैं। परमाणु कक्षक के समान, श्रोडिंगर समीकरण, जो इलेक्ट्रॉन के व्यवहार का वर्णन करता है, आणविक कक्षक के लिए भी बनाया जा सकता है। परमाणु कक्षाओं के रैखिक संयोजन, या परमाणु तरंग कार्यों के योग और अंतर, हार्ट्री-फॉक विधि के लिए अनुमानित समाधान प्रदान करते हैं। हार्ट्री-फॉक समीकरण जो आणविक श्रोडिंगर समीकरण के स्वतंत्र-कण सन्निकटन के अनुरूप हैं। सरल द्विपरमाणुक अणुओं के लिए, प्राप्त तरंगक्रियाओं को समीकरणों द्वारा गणितीय रूप से दर्शाया जाता है

\Psi =c_{a}\psi _{a}+c_{b}\psi _{b}

\Psi ^{*}=c_{a}\psi _{a}-c_{b}\psi _{b}

कहाँ $\Psi$ और $\Psi ^{*}$ क्रमशः आबंधन और प्रतिरक्षी आण्विक कक्षकों के लिए आण्विक तरंगक्रियाएँ हैं, $\psi _{a}$ और $\psi _{b}$ क्रमशः परमाणु a और b से परमाणु तरंग फलन हैं, और $c_{a}$ और $c_{b}$ समायोज्य गुणांक हैं. ये गुणांक व्यक्तिगत परमाणु कक्षाओं की ऊर्जा और समरूपता के आधार पर सकारात्मक या नकारात्मक हो सकते हैं। जैसे-जैसे दो परमाणु एक-दूसरे के करीब आते हैं, उनके परमाणु कक्षक उच्च इलेक्ट्रॉन घनत्व के क्षेत्रों का निर्माण करने के लिए ओवरलैप होते हैं, और, परिणामस्वरूप, दोनों परमाणुओं के बीच आणविक कक्षक बनते हैं। परमाणु सकारात्मक रूप से चार्ज किए गए नाभिक और बॉन्डिंग आणविक कक्षाओं में मौजूद नकारात्मक चार्ज वाले इलेक्ट्रॉनों के बीच इलेक्ट्रोस्टैटिक आकर्षण द्वारा साथ बंधे रहते हैं।^[13]

बॉन्डिंग, एंटीबॉन्डिंग, और नॉनबॉन्डिंग एमओ

जब परमाणु ऑर्बिटल्स परस्पर क्रिया करते हैं, तो परिणामी आणविक ऑर्बिटल तीन प्रकार के हो सकते हैं: बॉन्डिंग, एंटीबॉन्डिंग, या नॉनबॉन्डिंग।

बंधन आणविक कक्षाएँ:

परमाणु कक्षकों के बीच आबंधन अंतःक्रियाएं रचनात्मक (इन-फेज) अंतःक्रियाएं हैं।
बॉन्डिंग एमओ उन परमाणु ऑर्बिटल्स की तुलना में ऊर्जा में कम होते हैं जो उन्हें उत्पन्न करने के लिए संयोजित होते हैं।

प्रतिरक्षी आण्विक कक्षाएँ:

परमाणु ऑर्बिटल्स के बीच एंटीबॉन्डिंग इंटरैक्शन विनाशकारी (आउट-ऑफ़-फ़ेज़) इंटरैक्शन हैं, नोड (भौतिकी) के साथ जहां दो इंटरैक्टिंग परमाणुओं के बीच एंटीबॉन्डिंग ऑर्बिटल की तरंग फ़ंक्शन शून्य है
एंटीबॉन्डिंग एमओ उन परमाणु ऑर्बिटल्स की तुलना में ऊर्जा में अधिक होते हैं जो उन्हें उत्पन्न करने के लिए संयोजित होते हैं।

गैर-बंधन कक्षक:

संगत समरूपता की कमी के कारण नॉनबॉन्डिंग एमओ परमाणु ऑर्बिटल्स के बीच कोई बातचीत नहीं होने का परिणाम हैं।
नॉनबॉन्डिंग एमओ में अणु में किसी परमाणु के परमाणु ऑर्बिटल्स के समान ऊर्जा होगी।

एमओ के लिए सिग्मा और पीआई लेबल

परमाणु कक्षाओं के बीच परस्पर क्रिया के प्रकार को आणविक-कक्षीय समरूपता लेबल σ (सिग्मा), π (pi), δ (डेल्टा), φ (phi), γ (गामा) आदि द्वारा वर्गीकृत किया जा सकता है। ये संबंधित ग्रीक अक्षर हैं परमाणु कक्षाओं में क्रमशः s, p, d, f और g। संबंधित परमाणुओं के बीच आंतरिक परमाणु अक्ष वाले नोडल विमानों की संख्या σ MOs के लिए शून्य है, π के लिए एक, δ के लिए दो, φ के लिए तीन और γ के लिए चार है।

σ समरूपता

σ समरूपता वाला MO या तो दो परमाणु s-ऑर्बिटल्स या दो परमाणु p की परस्पर क्रिया से उत्पन्न होता है_z-ऑर्बिटल्स. MO में σ-समरूपता होगी यदि कक्षक दो परमाणु केंद्रों, आंतरिक परमाणु अक्ष को जोड़ने वाली धुरी के संबंध में सममित है। इसका मतलब यह है कि आंतरिक परमाणु अक्ष के बारे में एमओ के घूमने से चरण परिवर्तन नहीं होता है। σ* ऑर्बिटल, सिग्मा एंटीबॉन्डिंग ऑर्बिटल, आंतरिक परमाणु अक्ष के चारों ओर घूमने पर भी उसी चरण को बनाए रखता है। σ* ऑर्बिटल में नोडल प्लेन होता है जो नाभिक के बीच होता है और आंतरिक अक्ष के लंबवत होता है।^[14]

π समरूपता

π समरूपता वाला MO दो परमाणु p की परस्पर क्रिया से उत्पन्न होता है_x ऑर्बिटल्स या पी_y कक्षाएँ। यदि आंतरिक परमाणु अक्ष के बारे में घूर्णन के संबंध में कक्षीय असममित है तो MO में π समरूपता होगी। इसका मतलब यह है कि आंतरिक परमाणु अक्ष के बारे में एमओ के घूमने से चरण परिवर्तन होगा। यदि परमाणु कक्षक#वास्तविक कक्षकों पर विचार किया जाए तो नोडल तल है जिसमें आंतरिक अक्ष होता है।

एक π* ऑर्बिटल, पीआई एंटीबॉन्डिंग ऑर्बिटल, आंतरिक परमाणु अक्ष के बारे में घुमाए जाने पर भी चरण परिवर्तन उत्पन्न करेगा। π* कक्षक में नाभिक के बीच दूसरा नोडल तल भी होता है।^[14]^[15]^[16]^[17]

δ समरूपता

δ समरूपता वाला MO दो परमाणु d की परस्पर क्रिया से उत्पन्न होता है_xy या डी_x²-y² कक्षाएँ। क्योंकि इन आणविक कक्षाओं में कम-ऊर्जा डी परमाणु कक्षाएँ शामिल होती हैं, उन्हें संक्रमण धातु | संक्रमण-धातु परिसरों में देखा जाता है। δ आबंधन कक्षक में आंतरिक नाभिकीय अक्ष वाले दो नोडल तल होते हैं, और δ* प्रतिरक्षी कक्षक में नाभिक के बीच तीसरा नोडल तल भी होता है।

φ समरूपता

Suitably aligned f atomic orbitals overlap to form phi molecular orbital (a phi bond)

सैद्धांतिक रसायनज्ञों ने अनुमान लगाया है कि उच्च-क्रम के बंधन, जैसे कि एफ परमाणु कक्षाओं के ओवरलैप के अनुरूप फाई बांड, संभव हैं। फाई बांड युक्त अणु का कोई ज्ञात उदाहरण नहीं है।

गेरेड और अनगेरेड समरूपता

उन अणुओं के लिए जिनमें व्युत्क्रम केंद्र (सेंट्रोसममेट्री ) होता है, समरूपता के अतिरिक्त लेबल होते हैं जिन्हें आणविक कक्षाओं पर लागू किया जा सकता है। सेंट्रोसिमेट्रिक अणुओं में शामिल हैं:

गैर-सेंट्रोसिमेट्रिक अणुओं में शामिल हैं:

हेटेरोन्यूक्लियर अणु डायटोमिक्स, XY
टेट्राहेड्रल आणविक ज्यामिति, EX₄.

यदि किसी अणु में समरूपता के केंद्र के माध्यम से व्युत्क्रमण के परिणामस्वरूप आणविक कक्षीय के लिए समान चरण होते हैं, तो एमओ को जर्मन शब्द सम से गेराडे (जी) समरूपता कहा जाता है। यदि किसी अणु में समरूपता के केंद्र के माध्यम से व्युत्क्रमण के परिणामस्वरूप आणविक कक्षक के लिए चरण परिवर्तन होता है, तो एमओ को विषम के लिए जर्मन शब्द से अनगेरेड (यू) समरूपता कहा जाता है। σ-समरूपता के साथ बंधन MO के लिए, कक्षीय σ है_g (s'+ s सममित है), जबकि σ-समरूपता के साथ प्रतिरक्षी MO कक्षीय σ है_u, क्योंकि s' – s का व्युत्क्रमण प्रतिसममिति है। π-समरूपता के साथ बंधन MO के लिए कक्षीय π है_u क्योंकि समरूपता के केंद्र के माध्यम से व्युत्क्रमण संकेत परिवर्तन उत्पन्न करेगा (दो पी परमाणु कक्षाएँ दूसरे के साथ चरण में हैं लेकिन दो पालियों के विपरीत संकेत हैं), जबकि π-समरूपता के साथ प्रतिरक्षी MO π है_g क्योंकि समरूपता के केंद्र के माध्यम से व्युत्क्रमण से कोई संकेत परिवर्तन नहीं होगा (दो पी ऑर्बिटल्स चरण द्वारा एंटीसिमेट्रिक हैं)।^[14]

एमओ आरेख

एमओ विश्लेषण का गुणात्मक दृष्टिकोण अणु में बॉन्डिंग इंटरैक्शन को देखने के लिए आणविक कक्षीय आरेख का उपयोग करता है। इस प्रकार के आरेख में, आणविक कक्षाओं को क्षैतिज रेखाओं द्वारा दर्शाया जाता है; रेखा जितनी ऊँची होगी, कक्षक की ऊर्जा उतनी ही अधिक होगी, और पतित कक्षकों को उनके बीच स्थान के साथ समान स्तर पर रखा जाएगा। फिर, पॉली अपवर्जन सिद्धांत और हंड के अधिकतम बहुलता के नियम को ध्यान में रखते हुए, आणविक कक्षाओं में रखे जाने वाले इलेक्ट्रॉनों को एक-एक करके व्यवस्थित किया जाता है (केवल 2 इलेक्ट्रॉन, विपरीत स्पिन वाले, प्रति कक्षक; पर कई अयुग्मित इलेक्ट्रॉन रखें उन्हें जोड़ना शुरू करने से पहले जितना संभव हो सके ऊर्जा स्तर)। अधिक जटिल अणुओं के लिए, तरंग यांत्रिकी दृष्टिकोण संबंध की गुणात्मक समझ में उपयोगिता खो देता है (हालांकि मात्रात्मक दृष्टिकोण के लिए अभी भी आवश्यक है)। कुछ गुण:

ऑर्बिटल्स के आधार सेट में वे परमाणु ऑर्बिटल्स शामिल होते हैं जो आणविक ऑर्बिटल इंटरैक्शन के लिए उपलब्ध होते हैं, जो बॉन्डिंग या एंटीबॉन्डिंग हो सकते हैं
आणविक कक्षकों की संख्या रैखिक विस्तार या आधार सेट में शामिल परमाणु कक्षकों की संख्या के बराबर है
यदि अणु में कुछ समरूपता है, तो विकृत परमाणु कक्षाएँ (समान परमाणु ऊर्जा के साथ) रैखिक संयोजनों में समूहीकृत की जाती हैं (जिन्हें समरूपता-अनुकूलित परमाणु कक्षाएँ (SO) कहा जाता है), जो समरूपता समूह के परिमित समूहों के प्रतिनिधित्व सिद्धांत से संबंधित हैं, इसलिए समूह का वर्णन करने वाले तरंग कार्यों को समरूपता-अनुकूलित रैखिक संयोजन (एसएएलसी) के रूप में जाना जाता है।
एक समूह प्रतिनिधित्व से संबंधित आणविक कक्षाओं की संख्या इस प्रतिनिधित्व से संबंधित समरूपता-अनुकूलित परमाणु कक्षाओं की संख्या के बराबर है
परिमित समूहों के विशेष प्रतिनिधित्व सिद्धांत के भीतर, समरूपता-अनुकूलित परमाणु कक्षाएँ अधिक मिश्रित होती हैं यदि उनकी परमाणु ऊर्जा का स्तर करीब हो।

एक यथोचित सरल अणु के लिए आणविक कक्षीय आरेख के निर्माण की सामान्य प्रक्रिया को निम्नानुसार संक्षेपित किया जा सकता है:

1. अणु को बिंदु समूह निर्दिष्ट करें।

2. SALCs की आकृतियों को देखें।

3. प्रत्येक आणविक टुकड़े के SALC को ऊर्जा के क्रम में व्यवस्थित करें, पहले यह ध्यान दें कि क्या वे s, p, या d ऑर्बिटल्स से आते हैं (और उन्हें s < p < d क्रम में रखें), और फिर उनके आंतरिक नोड्स की संख्या।

4. दो टुकड़ों से समान समरूपता प्रकार के SALCs को मिलाएं, और N SALCs से N आणविक कक्षाएँ बनाएं।

5. ओवरलैप और मूल ऑर्बिटल्स की सापेक्ष ऊर्जाओं पर विचार करके आणविक ऑर्बिटल्स की सापेक्ष ऊर्जा का अनुमान लगाएं, और आणविक ऑर्बिटल्स ऊर्जा स्तर आरेख (ऑर्बिटल्स की उत्पत्ति दिखाते हुए) पर स्तर बनाएं।

6. वाणिज्यिक सॉफ़्टवेयर का उपयोग करके आणविक कक्षीय गणना करके इस गुणात्मक क्रम की पुष्टि करें, सही करें और संशोधित करें।^[18]

आणविक कक्षाओं में बंधन

कक्षीय अध:पतन

यदि आणविक कक्षाओं में समान ऊर्जा हो तो उन्हें पतित कहा जाता है। उदाहरण के लिए, पहले दस तत्वों के होमोन्यूक्लियर डायटोमिक अणुओं में, पी से प्राप्त आणविक कक्षाएँ_x और पी_y परमाणु कक्षाओं के परिणामस्वरूप दो पतित बंधन कक्षाएँ (कम ऊर्जा की) और दो पतित प्रतिरक्षी कक्षाएँ (उच्च ऊर्जा की) बनती हैं।^[13]

आयनिक बंधन

जब दो परमाणुओं के परमाणु ऑर्बिटल्स के बीच ऊर्जा का अंतर काफी बड़ा होता है, तो परमाणु के ऑर्बिटल्स लगभग पूरी तरह से बॉन्डिंग ऑर्बिटल्स में योगदान करते हैं, और दूसरे परमाणु के ऑर्बिटल्स लगभग पूरी तरह से एंटीबॉन्डिंग ऑर्बिटल्स में योगदान करते हैं। इस प्रकार, स्थिति प्रभावी रूप से यह है कि या अधिक इलेक्ट्रॉनों को परमाणु से दूसरे में स्थानांतरित कर दिया गया है। इसे (अधिकतर) आयनिक बंधन कहा जाता है।

बांड आदेश

किसी अणु का बंधन क्रम, या बंधनों की संख्या, बंधन और प्रतिरक्षी आणविक कक्षाओं में इलेक्ट्रॉनों की संख्या को मिलाकर निर्धारित की जा सकती है। बॉन्डिंग ऑर्बिटल में इलेक्ट्रॉनों की जोड़ी बंधन बनाती है, जबकि एंटीबॉडी ऑर्बिटल में इलेक्ट्रॉनों की जोड़ी बॉन्ड को नकार देती है। उदाहरण के लिए, एन₂बॉन्डिंग ऑर्बिटल्स में आठ इलेक्ट्रॉनों और एंटीबॉन्डिंग ऑर्बिटल्स में दो इलेक्ट्रॉनों के साथ, तीन का बॉन्ड ऑर्डर होता है, जो ट्रिपल बॉन्ड का गठन करता है।

बॉन्ड की ताकत बॉन्ड ऑर्डर के समानुपाती होती है - बॉन्डिंग की अधिक मात्रा अधिक स्थिर बॉन्ड बनाती है - और बॉन्ड की लंबाई इसके व्युत्क्रमानुपाती होती है - मजबूत बॉन्ड छोटा होता है।

सकारात्मक बंधन क्रम वाले अणु की आवश्यकता के दुर्लभ अपवाद हैं। यद्यपि हो₂ एमओ विश्लेषण के अनुसार 0 का बॉन्ड ऑर्डर है, अत्यधिक अस्थिर बीई का प्रयोगात्मक सबूत है₂ अणु की बंधन लंबाई 245 pm और बंधन ऊर्जा 10 kJ/mol है।^[14]^[19]

होमो और लूमो

उच्चतम व्याप्त आणविक कक्षक और सबसे कम रिक्त आणविक कक्षक को अक्सर क्रमशः HOMO और LUMO कहा जाता है। HOMO और LUMO की ऊर्जाओं के अंतर को HOMO-LUMO अंतर कहा जाता है। यह धारणा अक्सर साहित्य में भ्रम का विषय है और इस पर सावधानी से विचार किया जाना चाहिए। इसका मान आमतौर पर मूलभूत अंतर (आयनीकरण क्षमता और इलेक्ट्रॉन आत्मीयता के बीच अंतर) और ऑप्टिकल अंतर के बीच स्थित होता है। इसके अलावा, HOMO-LUMO गैप थोक सामग्री ऊर्जा अंतराल या ट्रांसपोर्ट गैप से संबंधित हो सकता है, जो आमतौर पर मौलिक गैप से बहुत छोटा होता है।

उदाहरण

होमोन्यूक्लियर डायटोमिक्स

होमोन्यूक्लियर डायटोमिक एमओ में आधार सेट में प्रत्येक परमाणु कक्षक से समान योगदान होता है। यह एच के लिए होमोन्यूक्लियर डायटोमिक एमओ आरेख में दिखाया गया है₂, वह₂, और ली₂, जिनमें से सभी में सममित कक्षाएँ हैं।^[14]

एच₂

एक अकेले हाइड्रोजन परमाणु (बाएं और दाएं) के परमाणु कक्षक और एच के संबंधित बंधन (नीचे) और प्रतिरक्षी (ऊपर) आणविक कक्षा के लिए इलेक्ट्रॉन तरंग कार्य₂ अणु. तरंगक्रिया का वास्तविक भाग नीला वक्र है, और काल्पनिक भाग लाल वक्र है। लाल बिंदु नाभिक के स्थान को चिह्नित करते हैं। इलेक्ट्रॉन तरंग फ़ंक्शन श्रोडिंगर तरंग समीकरण के अनुसार दोलन करता है, और ऑर्बिटल्स इसकी खड़ी तरंगें हैं। स्थायी तरंग आवृत्ति कक्षीय की गतिज ऊर्जा के समानुपाती होती है। (यह कथानक त्रि-आयामी प्रणाली का आयामी टुकड़ा है।)

एक सरल MO उदाहरण के रूप में, हाइड्रोजन अणु, H में इलेक्ट्रॉनों पर विचार करें₂ (MO आरेख#डायटोमिक MO आरेख देखें), दो परमाणुओं को H' और H लेबल के साथ। सबसे कम ऊर्जा वाले परमाणु कक्षक, 1s' और 1s, अणु की समरूपता के अनुसार परिवर्तित नहीं होते हैं। हालाँकि, निम्नलिखित समरूपता अनुकूलित परमाणु कक्षाएँ करती हैं:

1s' – 1s"	Antisymmetric combination: negated by reflection, unchanged by other operations
1s' + 1s"	Symmetric combination: unchanged by all symmetry operations

सममित संयोजन (जिसे बॉन्डिंग ऑर्बिटल कहा जाता है) आधार ऑर्बिटल्स की तुलना में ऊर्जा में कम है, और एंटीसिमेट्रिक संयोजन ( प्रतिरक्षी ऑर्बिटल कहा जाता है) अधिक है। क्योंकि एच₂ अणु में दो इलेक्ट्रॉन होते हैं, वे दोनों बंधन कक्ष में जा सकते हैं, जिससे प्रणाली दो मुक्त हाइड्रोजन परमाणुओं की तुलना में कम ऊर्जा (इसलिए अधिक स्थिर) हो जाती है। इसे सहसंयोजक बंधन कहा जाता है। अनुबंध आदेश, बॉन्डिंग इलेक्ट्रॉनों की संख्या घटा एंटीबॉडी इलेक्ट्रॉनों की संख्या के बराबर है, जिसे 2 से विभाजित किया गया है। इस उदाहरण में, बॉन्डिंग ऑर्बिटल में 2 इलेक्ट्रॉन हैं और एंटीबॉन्डिंग ऑर्बिटल में कोई भी नहीं है; बंधन क्रम 1 है, और दो हाइड्रोजन परमाणुओं के बीच एकल बंधन है।

वह₂

दूसरी ओर, He के काल्पनिक अणु पर विचार करें₂ He' और He लेबल वाले परमाणुओं के साथ। जैसा कि एच के साथ है₂, सबसे कम ऊर्जा वाले परमाणु ऑर्बिटल्स 1s' और 1s हैं, और अणु की समरूपता के अनुसार परिवर्तित नहीं होते हैं, जबकि समरूपता अनुकूलित परमाणु ऑर्बिटल्स करते हैं। सममित संयोजन - बॉन्डिंग ऑर्बिटल - आधार ऑर्बिटल्स की तुलना में ऊर्जा में कम है, और एंटीसिमेट्रिक संयोजन - एंटीबॉन्डिंग ऑर्बिटल - अधिक है। एच के विपरीत₂, दो वैलेंस इलेक्ट्रॉनों के साथ, वह₂ इसकी तटस्थ जमीनी अवस्था में चार हैं। दो इलेक्ट्रॉन निम्न-ऊर्जा बंधन कक्षक, σ को भरते हैं_g(1s), जबकि शेष दो उच्च-ऊर्जा प्रतिरक्षी कक्षक, σ को भरते हैं_u*(1s). इस प्रकार, अणु के चारों ओर परिणामी इलेक्ट्रॉन घनत्व दो परमाणुओं के बीच बंधन के गठन का समर्थन नहीं करता है; परमाणुओं को साथ बांधे रखने वाले स्थिर बंधन के बिना, अणु के अस्तित्व की उम्मीद नहीं की जा सकती। इसे देखने का दूसरा तरीका यह है कि दो बंधनकारी इलेक्ट्रॉन और दो प्रतिरक्षी इलेक्ट्रॉन हैं; इसलिए, बंधन क्रम 0 है और कोई बंधन मौजूद नहीं है (अणु में वान डेर वाल्स क्षमता द्वारा समर्थित बाध्य अवस्था है)।

वह₂

डिलिथियम ली₂ दो ली परमाणुओं के 1s और 2s परमाणु कक्षाओं (आधार सेट) के ओवरलैप से बनता है। प्रत्येक ली परमाणु बॉन्डिंग इंटरैक्शन के लिए तीन इलेक्ट्रॉनों का योगदान देता है, और छह इलेक्ट्रॉन सबसे कम ऊर्जा के तीन एमओ को भरते हैं, σ_g(1एस), पी_u*(1एस), और पी_g(2s). बांड क्रम के लिए समीकरण का उपयोग करते हुए, यह पाया गया है कि डाइलिथियम का बंधन क्रम एक, एकल बंधन है।^[20]

उत्कृष्ट गैसें

He के काल्पनिक अणु पर विचार करना₂, चूँकि परमाणु कक्षकों का आधार समुच्चय H के मामले जैसा ही है₂, हम पाते हैं कि बॉन्डिंग और एंटीबॉन्डिंग ऑर्बिटल्स दोनों भरे हुए हैं, इसलिए जोड़ी को कोई ऊर्जा लाभ नहीं है। HeH को थोड़ा ऊर्जा लाभ होगा, लेकिन H जितना नहीं₂ + 2 वह, इसलिए अणु बहुत अस्थिर है और हाइड्रोजन और हीलियम में विघटित होने से पहले केवल कुछ समय के लिए ही मौजूद रहता है। सामान्य तौर पर, हम पाते हैं कि हे जैसे परमाणु जिनमें पूर्ण ऊर्जा कोश होते हैं वे शायद ही कभी अन्य परमाणुओं के साथ बंधते हैं। अल्पकालिक वैन डेर वाल्स बॉन्डिंग को छोड़कर, बहुत कम उत्कृष्ट गैस यौगिक ज्ञात हैं।

हेटेरोन्यूक्लियर डायटोमिक्स

जबकि होमोन्यूक्लियर डायटोमिक अणुओं के लिए एमओ में प्रत्येक परस्पर क्रिया करने वाले परमाणु कक्षक का समान योगदान होता है, हेटेरोन्यूक्लियर डायटोमिक अणुओं के लिए एमओ में अलग-अलग परमाणु कक्षीय योगदान होता है। हेटेरोन्यूक्लियर डायटोमिक्स में बॉन्डिंग या एंटीबॉन्डिंग ऑर्बिटल्स का उत्पादन करने के लिए ऑर्बिटल इंटरैक्शन तब होता है, जब परमाणु ऑर्बिटल्स के बीच पर्याप्त ओवरलैप होता है, जैसा कि उनकी समरूपता और ऑर्बिटल ऊर्जा में समानता से निर्धारित होता है।

एचएफ

हाइड्रोजिन फ्लोराइड में एच 1 एस और एफ 2 एस ऑर्बिटल्स के बीच एचएफ ओवरलैप को समरूपता द्वारा अनुमति दी जाती है लेकिन दो परमाणु ऑर्बिटल्स के बीच ऊर्जा में अंतर उन्हें आणविक ऑर्बिटल बनाने के लिए बातचीत करने से रोकता है। H 1s और F 2p के बीच ओवरलैप_z ऑर्बिटल्स में भी समरूपता की अनुमति है, और इन दो परमाणु ऑर्बिटल्स में थोड़ी ऊर्जा पृथक्करण है। इस प्रकार, वे परस्पर क्रिया करते हैं, जिससे σ और σ* MOs और 1 के बंधन क्रम के साथ अणु का निर्माण होता है। चूंकि HF गैर-सेंट्रोसिमेट्रिक अणु है, समरूपता लेबल g और u इसके आणविक कक्षाओं पर लागू नहीं होते हैं।^[21]

मात्रात्मक दृष्टिकोण

आणविक ऊर्जा स्तरों के लिए मात्रात्मक मान प्राप्त करने के लिए, किसी को ऐसे आणविक ऑर्बिटल्स की आवश्यकता होती है जो कॉन्फ़िगरेशन इंटरैक्शन (सीआई) विस्तार पूर्ण कॉन्फ़िगरेशन इंटरैक्शन सीमा की ओर तेजी से परिवर्तित हो। ऐसे कार्यों को प्राप्त करने की सबसे आम विधि हार्ट्री-फॉक विधि है, जो आणविक कक्षाओं को फॉक ऑपरेटर के eigenfunction के रूप में व्यक्त करती है। आम तौर पर परमाणु नाभिक पर केंद्रित गाऊसी कार्यों के रैखिक संयोजन के रूप में आणविक कक्षाओं का विस्तार करके इस समस्या को हल किया जाता है (परमाणु कक्षाओं का रैखिक संयोजन आणविक कक्षीय विधि और आधार सेट (रसायन विज्ञान) देखें)। इन रैखिक संयोजनों के गुणांकों के लिए समीकरण सामान्यीकृत eigenvalue समीकरण है जिसे रूथान समीकरण के रूप में जाना जाता है, जो वास्तव में हार्ट्री-फॉक समीकरण का विशेष प्रतिनिधित्व है। ऐसे कई कार्यक्रम हैं जिनमें स्पार्टन (रसायन विज्ञान सॉफ्टवेयर) सहित एमओ की क्वांटम रासायनिक गणना की जा सकती है।

सरल खाते अक्सर सुझाव देते हैं कि प्रयोगात्मक आणविक कक्षीय ऊर्जा वैलेंस ऑर्बिटल्स के लिए पराबैंगनी फोटोइलेक्ट्रॉन स्पेक्ट्रोस्कोपी और कोर ऑर्बिटल्स के लिए एक्स - रे फ़ोटोइलैक्ट्रॉन स्पेक्ट्रोस्कोपी के तरीकों से प्राप्त की जा सकती है। हालाँकि, यह गलत है क्योंकि ये प्रयोग आयनीकरण ऊर्जा को मापते हैं, अणु और इलेक्ट्रॉन को हटाने के परिणामस्वरूप आयनों में से के बीच ऊर्जा में अंतर। कूपमैन्स प्रमेय द्वारा आयनीकरण ऊर्जाएँ लगभग कक्षीय ऊर्जाओं से जुड़ी होती हैं। जबकि कुछ अणुओं के लिए इन दोनों मूल्यों के बीच समझौता करीब हो सकता है, अन्य मामलों में यह बहुत खराब हो सकता है।

↑ Prior to Mulliken, the word "orbital" was used only as an adjective, for example "orbital velocity" or "orbital wave function."^[1] Mulliken used orbital as a noun, when he suggested the terms "atomic orbitals" and "molecular orbitals" to describe the electronic structures of polyatomic molecules.^[2]^[3]

संदर्भ

↑ orbital. Retrieved April 18, 2021. {{cite book}}: |work= ignored (help)
↑ ^2.0 ^2.1 Mulliken, Robert S. (July 1932). "बहुपरमाणुक अणुओं और संयोजकता की इलेक्ट्रॉनिक संरचनाएँ। द्वितीय. सामान्य विचार". Physical Review. 41 (1): 49–71. Bibcode:1932PhRv...41...49M. doi:10.1103/PhysRev.41.49.
↑ Brown, Theodore (2002). Chemistry : the central science. Upper Saddle River, NJ: Prentice Hall. ISBN 0-13-066997-0.
↑ Cotton, F. Albert (1990). समूह सिद्धांत के रासायनिक अनुप्रयोग (3rd ed.). New York: Wiley. pp. 102. ISBN 0471510947. OCLC 19975337.
↑ Albright, T. A.; Burdett, J. K.; Whangbo, M.-H. (2013). रसायन विज्ञान में कक्षीय अंतःक्रियाएँ. Hoboken, N.J.: Wiley. ISBN 9780471080398.
↑ Hund, F. (1926). "आणविक स्पेक्ट्रा में कुछ घटनाओं की व्याख्या पर" [On the interpretation of some phenomena in molecular spectra]. Zeitschrift für Physik (in Deutsch). Springer Science and Business Media LLC. 36 (9–10): 657–674. Bibcode:1926ZPhy...36..657H. doi:10.1007/bf01400155. ISSN 1434-6001. S2CID 123208730.
↑ F. Hund, "Zur Deutung der Molekelspektren", Zeitschrift für Physik, Part I, vol. 40, pages 742-764 (1927); Part II, vol. 42, pages 93–120 (1927); Part III, vol. 43, pages 805-826 (1927); Part IV, vol. 51, pages 759-795 (1928); Part V, vol. 63, pages 719-751 (1930).
↑ Mulliken, Robert S. (1 May 1927). "Electronic States and Band Spectrum Structure in Diatomic Molecules. IV. Hund's Theory; Second Positive Nitrogen and Swan Bands; Alternating Intensities". Physical Review. American Physical Society (APS). 29 (5): 637–649. Bibcode:1927PhRv...29..637M. doi:10.1103/physrev.29.637. ISSN 0031-899X.
↑ Mulliken, Robert S. (1928). "The assignment of quantum numbers for electrons in molecules. Extracts from Phys. Rev. 32, 186-222 (1928), plus currently written annotations". International Journal of Quantum Chemistry. Wiley. 1 (1): 103–117. doi:10.1002/qua.560010106. ISSN 0020-7608.
↑ Friedrich Hund and Chemistry, Werner Kutzelnigg, on the occasion of Hund's 100th birthday, Angewandte Chemie International Edition, 35, 573–586, (1996)
↑ Robert S. Mulliken's Nobel Lecture, Science, 157, no. 3785, 13-24. Available on-line at: Nobelprize.org
↑ Lennard-Jones, John (Sir) (1929). "कुछ द्विपरमाणुक अणुओं की इलेक्ट्रॉनिक संरचना". Transactions of the Faraday Society. 25: 668–686. Bibcode:1929FaTr...25..668L. doi:10.1039/tf9292500668.
↑ ^13.0 ^13.1 Miessler, G.L.; Tarr, Donald A. (2008). अकार्बनिक रसायन शास्त्र. Pearson Education. ISBN 978-81-317-1885-8.
↑ ^14.0 ^14.1 ^14.2 ^14.3 ^14.4 Catherine E. Housecroft, Alan G. Sharpe, Inorganic Chemistry, Pearson Prentice Hall; 2nd Edition, 2005, p. 29-33.
↑ Peter Atkins; Julio De Paula. Atkins’ Physical Chemistry. Oxford University Press, 8th ed., 2006.
↑ Yves Jean; François Volatron. An Introduction to Molecular Orbitals. Oxford University Press, 1993.
↑ Michael Munowitz, Principles of Chemistry, Norton & Company, 2000, p. 229-233.
↑ Atkins, Peter; et al. (2006). अकार्बनिक रसायन शास्त्र (4. ed.). New York: W.H. Freeman. p. 208. ISBN 978-0-7167-4878-6.
↑ Bondybey, V.E. (1984). "Electronic structure and bonding of Be2". Chemical Physics Letters. 109 (5): 436–441. Bibcode:1984CPL...109..436B. doi:10.1016/0009-2614(84)80339-5.
↑ König, Burkhard (1995-02-21). "Chemical Bonding. VonM. J. Winter. 90 S., ISBN 0-19-855694-2. – Organometallics 1. Complexes with Transition Metal-Carbon σ-Bonds. VonM. Bochmann. 91 S., ISBN 0-19-855751-5. – Organometallics 2. Complexes with Transition Metal-Carbon π-Bonds. VonM. Bochmann. 89 S., ISBN 0-19-855813-9. – Bifunctional Compounds. VonR. S. Ward. 90 S., ISBN 0-19-855808-2. – Alle aus der Reihe: Oxford Chemistry Primers, Oxford University Press, Oxford, 1994, Broschur, je 4.99 £". Angewandte Chemie (in Deutsch). 107 (4): 540–540. doi:10.1002/ange.19951070434.
↑ Catherine E. Housecroft, Alan G, Sharpe, Inorganic Chemistry, Pearson Prentice Hall; 2nd Edition, 2005, ISBN 0130-39913-2, p. 41-43.

[4] Prior to Mulliken, the word "orbital" was used only as an adjective, for example "orbital velocity" or "orbital wave function."^[1] Mulliken used orbital as a noun, when he suggested the terms "atomic orbitals" and "molecular orbitals" to describe the electronic structures of polyatomic molecules.^[2]^[3]

[1] orbital. Retrieved April 18, 2021. {{cite book}}: |work= ignored (help)

[muller1932-2] 2.0 ^2.1 Mulliken, Robert S. (July 1932). "बहुपरमाणुक अणुओं और संयोजकता की इलेक्ट्रॉनिक संरचनाएँ। द्वितीय. सामान्य विचार". Physical Review. 41 (1): 49–71. Bibcode:1932PhRv...41...49M. doi:10.1103/PhysRev.41.49.

[3] Brown, Theodore (2002). Chemistry : the central science. Upper Saddle River, NJ: Prentice Hall. ISBN 0-13-066997-0.

[5] Cotton, F. Albert (1990). समूह सिद्धांत के रासायनिक अनुप्रयोग (3rd ed.). New York: Wiley. pp. 102. ISBN 0471510947. OCLC 19975337.

[6] Albright, T. A.; Burdett, J. K.; Whangbo, M.-H. (2013). रसायन विज्ञान में कक्षीय अंतःक्रियाएँ. Hoboken, N.J.: Wiley. ISBN 9780471080398.

[Hund1926-7] Hund, F. (1926). "आणविक स्पेक्ट्रा में कुछ घटनाओं की व्याख्या पर" [On the interpretation of some phenomena in molecular spectra]. Zeitschrift für Physik (in Deutsch). Springer Science and Business Media LLC. 36 (9–10): 657–674. Bibcode:1926ZPhy...36..657H. doi:10.1007/bf01400155. ISSN 1434-6001. S2CID 123208730.

[8] F. Hund, "Zur Deutung der Molekelspektren", Zeitschrift für Physik, Part I, vol. 40, pages 742-764 (1927); Part II, vol. 42, pages 93–120 (1927); Part III, vol. 43, pages 805-826 (1927); Part IV, vol. 51, pages 759-795 (1928); Part V, vol. 63, pages 719-751 (1930).

[Mulliken1927-9] Mulliken, Robert S. (1 May 1927). "Electronic States and Band Spectrum Structure in Diatomic Molecules. IV. Hund's Theory; Second Positive Nitrogen and Swan Bands; Alternating Intensities". Physical Review. American Physical Society (APS). 29 (5): 637–649. Bibcode:1927PhRv...29..637M. doi:10.1103/physrev.29.637. ISSN 0031-899X.

[Mulliken1928-10] Mulliken, Robert S. (1928). "The assignment of quantum numbers for electrons in molecules. Extracts from Phys. Rev. 32, 186-222 (1928), plus currently written annotations". International Journal of Quantum Chemistry. Wiley. 1 (1): 103–117. doi:10.1002/qua.560010106. ISSN 0020-7608.

[11] Friedrich Hund and Chemistry, Werner Kutzelnigg, on the occasion of Hund's 100th birthday, Angewandte Chemie International Edition, 35, 573–586, (1996)

[12] Robert S. Mulliken's Nobel Lecture, Science, 157, no. 3785, 13-24. Available on-line at: Nobelprize.org

[13] Lennard-Jones, John (Sir) (1929). "कुछ द्विपरमाणुक अणुओं की इलेक्ट्रॉनिक संरचना". Transactions of the Faraday Society. 25: 668–686. Bibcode:1929FaTr...25..668L. doi:10.1039/tf9292500668.

[Gary_L._Miessler_2004-14] 13.0 ^13.1 Miessler, G.L.; Tarr, Donald A. (2008). अकार्बनिक रसायन शास्त्र. Pearson Education. ISBN 978-81-317-1885-8.

[H&C-15] 14.0 ^14.1 ^14.2 ^14.3 ^14.4 Catherine E. Housecroft, Alan G. Sharpe, Inorganic Chemistry, Pearson Prentice Hall; 2nd Edition, 2005, p. 29-33.

[16] Peter Atkins; Julio De Paula. Atkins’ Physical Chemistry. Oxford University Press, 8th ed., 2006.

[17] Yves Jean; François Volatron. An Introduction to Molecular Orbitals. Oxford University Press, 1993.

[18] Michael Munowitz, Principles of Chemistry, Norton & Company, 2000, p. 229-233.

[19] Atkins, Peter; et al. (2006). अकार्बनिक रसायन शास्त्र (4. ed.). New York: W.H. Freeman. p. 208. ISBN 978-0-7167-4878-6.

[20] Bondybey, V.E. (1984). "Electronic structure and bonding of Be2". Chemical Physics Letters. 109 (5): 436–441. Bibcode:1984CPL...109..436B. doi:10.1016/0009-2614(84)80339-5.

[21] König, Burkhard (1995-02-21). "Chemical Bonding. VonM. J. Winter. 90 S., ISBN 0-19-855694-2. – Organometallics 1. Complexes with Transition Metal-Carbon σ-Bonds. VonM. Bochmann. 91 S., ISBN 0-19-855751-5. – Organometallics 2. Complexes with Transition Metal-Carbon π-Bonds. VonM. Bochmann. 89 S., ISBN 0-19-855813-9. – Bifunctional Compounds. VonR. S. Ward. 90 S., ISBN 0-19-855808-2. – Alle aus der Reihe: Oxford Chemistry Primers, Oxford University Press, Oxford, 1994, Broschur, je 4.99 £". Angewandte Chemie (in Deutsch). 107 (4): 540–540. doi:10.1002/ange.19951070434.

[22] Catherine E. Housecroft, Alan G, Sharpe, Inorganic Chemistry, Pearson Prentice Hall; 2nd Edition, 2005, ISBN 0130-39913-2, p. 41-43.

[lower-alpha 1]

[2]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[1]

[3]

@@ Line 1: / Line 1: @@
 {{Short description|Wave-like behavior of an electron in a molecule}}
 {{See also|Molecular orbital theory|Molecular orbital diagram}}
-[[File:Orbitals acetylene.jpg|right|thumb|पूर्ण [[एसिटिलीन]] (H-C≡C-H) आणविक कक्षीय सेट। बायां स्तंभ एमओ को दर्शाता है जो जमीनी अवस्था में व्याप्त हैं, शीर्ष पर सबसे कम ऊर्जा कक्षीय है। कुछ MO में दिखाई देने वाली सफेद और भूरे रंग की रेखा नाभिक से गुजरने वाली आणविक धुरी है। कक्षीय तरंग कार्य लाल क्षेत्रों में सकारात्मक और नीले क्षेत्रों में नकारात्मक होते हैं। दायां कॉलम आभासी एमओ को दर्शाता है जो जमीनी अवस्था में खाली हैं, लेकिन उत्तेजित अवस्था में व्याप्त हो सकते हैं।]][[रसायन विज्ञान]] में, एक आणविक कक्षक ({{IPAc-en|ɒr|b|ə|d|l}}) एक [[फ़ंक्शन (गणित)]] है जो एक [[अणु]] में एक [[इलेक्ट्रॉन]] के स्थान और पदार्थ तरंग | तरंग जैसे व्यवहार का वर्णन करता है। इस फ़ंक्शन का उपयोग रासायनिक और भौतिक गुणों की गणना करने के लिए किया जा सकता है जैसे कि किसी विशिष्ट क्षेत्र में इलेक्ट्रॉन खोजने की संभावना। परमाणु कक्षक और आणविक कक्षक शब्द{{efn|Prior to Mulliken, the word "orbital" was used only as an [[adjective]], for example "orbital velocity" or "orbital wave function."<ref>{{cite book |title=orbital |publisher=[[Merriam-Webster]]  |work=Dictionary by Merriam-Webster: America's most-trusted online dictionary |url=https://www.merriam-webster.com/dictionary/orbital |accessdate=April 18, 2021}}</ref> Mulliken used orbital as a [[noun]], when he suggested the terms "atomic orbitals" and "molecular orbitals" to describe the electronic structures of polyatomic molecules.<ref name="muller1932"/><ref>{{cite book | last = Brown | first = Theodore | title = Chemistry : the central science | publisher = Prentice Hall | location = Upper Saddle River, NJ | year = 2002 | isbn = 0-13-066997-0 }}</ref>}} को 1932 में रॉबर्ट एस. मुल्लिकेन द्वारा एक-इलेक्ट्रॉन कक्षीय तरंग कार्यों के अर्थ में पेश किया गया था।<ref name="muller1932">{{cite journal| last=Mulliken | first=Robert S. | title=बहुपरमाणुक अणुओं और संयोजकता की इलेक्ट्रॉनिक संरचनाएँ। द्वितीय. सामान्य विचार|date=July 1932| journal=[[Physical Review]] | volume=41 | issue=1 | pages=49–71 | bibcode = 1932PhRv...41...49M | doi = 10.1103/PhysRev.41.49}}</ref> प्रारंभिक स्तर पर, उनका उपयोग अंतरिक्ष के उस क्षेत्र का वर्णन करने के लिए किया जाता है जिसमें किसी फ़ंक्शन का महत्वपूर्ण आयाम होता है।
+[[File:Orbitals acetylene.jpg|right|thumb|पूर्ण [[एसिटिलीन]] (H-C≡C-H) आणविक कक्षीय सेट। बायां स्तंभ एमओ को दर्शाता है जो जमीनी अवस्था में व्याप्त हैं, शीर्ष पर सबसे कम ऊर्जा कक्षीय है। कुछ MO में दिखाई देने वाली सफेद और भूरे रंग की रेखा नाभिक से गुजरने वाली आणविक धुरी है। कक्षीय तरंग कार्य लाल क्षेत्रों में सकारात्मक और नीले क्षेत्रों में नकारात्मक होते हैं। दायां कॉलम आभासी एमओ को दर्शाता है जो जमीनी अवस्था में खाली हैं, लेकिन उत्तेजित अवस्था में व्याप्त हो सकते हैं।]][[रसायन विज्ञान]] में, आणविक कक्षक ({{IPAc-en|ɒr|b|ə|d|l}}) [[फ़ंक्शन (गणित)]] है जो [[अणु]] में [[इलेक्ट्रॉन]] के स्थान और पदार्थ तरंग | तरंग जैसे व्यवहार का वर्णन करता है। इस फ़ंक्शन का उपयोग रासायनिक और भौतिक गुणों की गणना करने के लिए किया जा सकता है जैसे कि किसी विशिष्ट क्षेत्र में इलेक्ट्रॉन खोजने की संभावना। परमाणु कक्षक और आणविक कक्षक शब्द{{efn|Prior to Mulliken, the word "orbital" was used only as an [[adjective]], for example "orbital velocity" or "orbital wave function."<ref>{{cite book |title=orbital |publisher=[[Merriam-Webster]]  |work=Dictionary by Merriam-Webster: America's most-trusted online dictionary |url=https://www.merriam-webster.com/dictionary/orbital |accessdate=April 18, 2021}}</ref> Mulliken used orbital as a [[noun]], when he suggested the terms "atomic orbitals" and "molecular orbitals" to describe the electronic structures of polyatomic molecules.<ref name="muller1932"/><ref>{{cite book | last = Brown | first = Theodore | title = Chemistry : the central science | publisher = Prentice Hall | location = Upper Saddle River, NJ | year = 2002 | isbn = 0-13-066997-0 }}</ref>}} को 1932 में रॉबर्ट एस. मुल्लिकेन द्वारा एक-इलेक्ट्रॉन कक्षीय तरंग कार्यों के अर्थ में पेश किया गया था।<ref name="muller1932">{{cite journal| last=Mulliken | first=Robert S. | title=बहुपरमाणुक अणुओं और संयोजकता की इलेक्ट्रॉनिक संरचनाएँ। द्वितीय. सामान्य विचार|date=July 1932| journal=[[Physical Review]] | volume=41 | issue=1 | pages=49–71 | bibcode = 1932PhRv...41...49M | doi = 10.1103/PhysRev.41.49}}</ref> प्रारंभिक स्तर पर, उनका उपयोग अंतरिक्ष के उस क्षेत्र का वर्णन करने के लिए किया जाता है जिसमें किसी फ़ंक्शन का महत्वपूर्ण आयाम होता है।
-एक पृथक परमाणु में, कक्षीय इलेक्ट्रॉनों का स्थान [[परमाणु कक्षक]] नामक कार्यों द्वारा निर्धारित होता है। जब कई परमाणु रासायनिक रूप से एक अणु में संयोजित होते हैं, तो इलेक्ट्रॉनों का स्थान समग्र रूप से अणु द्वारा निर्धारित होता है, इसलिए परमाणु कक्षाएँ मिलकर आणविक कक्षाएँ बनाती हैं। घटक परमाणुओं से इलेक्ट्रॉन आणविक कक्षाओं पर कब्जा कर लेते हैं। गणितीय रूप से, आणविक कक्षाएँ अणु के [[परमाणु नाभिक]] के क्षेत्र में इलेक्ट्रॉनों के लिए श्रोडिंगर समीकरण का एक अनुमानित समाधान हैं। इनका निर्माण आम तौर पर अणु के प्रत्येक परमाणु से परमाणु ऑर्बिटल्स परमाणु ऑर्बिटल्स या [[ संकर कक्षीय ]]्स या परमाणुओं के समूहों से अन्य आणविक ऑर्बिटल्स के रैखिक संयोजन द्वारा किया जाता है। उन्हें हार्ट्री-फॉक विधि | हार्ट्री-फॉक या सेल्फ-कंसिस्टेंट फील्ड (एससीएफ) विधियों का उपयोग करके मात्रात्मक रूप से गणना की जा सकती है।
+एक पृथक परमाणु में, कक्षीय इलेक्ट्रॉनों का स्थान [[परमाणु कक्षक]] नामक कार्यों द्वारा निर्धारित होता है। जब कई परमाणु रासायनिक रूप से अणु में संयोजित होते हैं, तो इलेक्ट्रॉनों का स्थान समग्र रूप से अणु द्वारा निर्धारित होता है, इसलिए परमाणु कक्षाएँ मिलकर आणविक कक्षाएँ बनाती हैं। घटक परमाणुओं से इलेक्ट्रॉन आणविक कक्षाओं पर कब्जा कर लेते हैं। गणितीय रूप से, आणविक कक्षाएँ अणु के [[परमाणु नाभिक]] के क्षेत्र में इलेक्ट्रॉनों के लिए श्रोडिंगर समीकरण का अनुमानित समाधान हैं। इनका निर्माण आम तौर पर अणु के प्रत्येक परमाणु से परमाणु ऑर्बिटल्स परमाणु ऑर्बिटल्स या [[ संकर कक्षीय |संकर कक्षीय]] ्स या परमाणुओं के समूहों से अन्य आणविक ऑर्बिटल्स के रैखिक संयोजन द्वारा किया जाता है। उन्हें हार्ट्री-फॉक विधि | हार्ट्री-फॉक या सेल्फ-कंसिस्टेंट फील्ड (एससीएफ) विधियों का उपयोग करके मात्रात्मक रूप से गणना की जा सकती है।
-आणविक कक्षाएँ तीन प्रकार की होती हैं: आबंधन आणविक कक्षाएँ जिनकी ऊर्जा उन्हें बनाने वाले परमाणु कक्षाओं की ऊर्जा से कम होती है, और इस प्रकार उन रासायनिक बंधों को बढ़ावा देती है जो अणु को एक साथ रखते हैं; प्रतिरक्षी आणविक ऑर्बिटल्स जिनकी ऊर्जा उनके घटक परमाणु ऑर्बिटल्स की ऊर्जा से अधिक होती है, और इसलिए अणु के बंधन का विरोध करते हैं, और गैर-बंधन ऑर्बिटल्स जिनकी ऊर्जा उनके घटक परमाणु ऑर्बिटल्स के समान होती है और इस प्रकार बॉन्डिंग पर कोई प्रभाव नहीं पड़ता है अणु.
+आणविक कक्षाएँ तीन प्रकार की होती हैं: आबंधन आणविक कक्षाएँ जिनकी ऊर्जा उन्हें बनाने वाले परमाणु कक्षाओं की ऊर्जा से कम होती है, और इस प्रकार उन रासायनिक बंधों को बढ़ावा देती है जो अणु को साथ रखते हैं; प्रतिरक्षी आणविक ऑर्बिटल्स जिनकी ऊर्जा उनके घटक परमाणु ऑर्बिटल्स की ऊर्जा से अधिक होती है, और इसलिए अणु के बंधन का विरोध करते हैं, और गैर-बंधन ऑर्बिटल्स जिनकी ऊर्जा उनके घटक परमाणु ऑर्बिटल्स के समान होती है और इस प्रकार बॉन्डिंग पर कोई प्रभाव नहीं पड़ता है अणु.
 ==अवलोकन==
-एक आणविक कक्षक (एमओ) का उपयोग अणु में उन क्षेत्रों का प्रतिनिधित्व करने के लिए किया जा सकता है जहां उस कक्षक पर कब्जा करने वाले एक [[ऋणावेशित सूक्ष्म अणु का विन्यास]] पाए जाने की संभावना है। आणविक कक्षाएँ अणु के [[परमाणु नाभिक]] के विद्युत क्षेत्र में इलेक्ट्रॉनों के लिए श्रोडिंगर समीकरण के अनुमानित समाधान हैं। हालाँकि इस समीकरण से सीधे ऑर्बिटल्स की गणना करना बहुत ही कठिन समस्या है। इसके बजाय वे परमाणु कक्षाओं के संयोजन से प्राप्त होते हैं, जो एक परमाणु में एक इलेक्ट्रॉन के स्थान की भविष्यवाणी करते हैं। एक आणविक कक्षक एक अणु के इलेक्ट्रॉन विन्यास को निर्दिष्ट कर सकता है: एक (या एक जोड़ी) इलेक्ट्रॉन का स्थानिक वितरण और ऊर्जा। आमतौर पर एक एमओ को परमाणु कक्षाओं के रैखिक संयोजन आणविक कक्षीय विधि (एलसीएओ-एमओ विधि) के रूप में दर्शाया जाता है, विशेष रूप से गुणात्मक या बहुत अनुमानित उपयोग में। वे [[आणविक कक्षीय सिद्धांत]] के माध्यम से समझे गए अणुओं में बंधन का एक सरल मॉडल प्रदान करने में अमूल्य हैं।
+एक आणविक कक्षक (एमओ) का उपयोग अणु में उन क्षेत्रों का प्रतिनिधित्व करने के लिए किया जा सकता है जहां उस कक्षक पर कब्जा करने वाले [[ऋणावेशित सूक्ष्म अणु का विन्यास]] पाए जाने की संभावना है। आणविक कक्षाएँ अणु के [[परमाणु नाभिक]] के विद्युत क्षेत्र में इलेक्ट्रॉनों के लिए श्रोडिंगर समीकरण के अनुमानित समाधान हैं। हालाँकि इस समीकरण से सीधे ऑर्बिटल्स की गणना करना बहुत ही कठिन समस्या है। इसके बजाय वे परमाणु कक्षाओं के संयोजन से प्राप्त होते हैं, जो परमाणु में इलेक्ट्रॉन के स्थान की भविष्यवाणी करते हैं। आणविक कक्षक अणु के इलेक्ट्रॉन विन्यास को निर्दिष्ट कर सकता है: (या जोड़ी) इलेक्ट्रॉन का स्थानिक वितरण और ऊर्जा। आमतौर पर एमओ को परमाणु कक्षाओं के रैखिक संयोजन आणविक कक्षीय विधि (एलसीएओ-एमओ विधि) के रूप में दर्शाया जाता है, विशेष रूप से गुणात्मक या बहुत अनुमानित उपयोग में। वे [[आणविक कक्षीय सिद्धांत]] के माध्यम से समझे गए अणुओं में बंधन का सरल मॉडल प्रदान करने में अमूल्य हैं।
-कम्प्यूटेशनल रसायन विज्ञान में अधिकांश वर्तमान विधियां सिस्टम के एमओ की गणना से शुरू होती हैं। एक आणविक कक्षक नाभिक द्वारा उत्पन्न विद्युत क्षेत्र में एक इलेक्ट्रॉन के व्यवहार और अन्य इलेक्ट्रॉनों के कुछ औसत वितरण का वर्णन करता है। एक ही कक्षा में रहने वाले दो इलेक्ट्रॉनों के मामले में, [[पाउली सिद्धांत]] की मांग है कि उनके पास विपरीत स्पिन हो। आवश्यक रूप से यह एक अनुमान है, और आणविक इलेक्ट्रॉनिक तरंग फ़ंक्शन के अत्यधिक सटीक विवरण में ऑर्बिटल्स नहीं होते हैं ([[कॉन्फ़िगरेशन इंटरेक्शन]] देखें)।
+कम्प्यूटेशनल रसायन विज्ञान में अधिकांश वर्तमान विधियां सिस्टम के एमओ की गणना से शुरू होती हैं। आणविक कक्षक नाभिक द्वारा उत्पन्न विद्युत क्षेत्र में इलेक्ट्रॉन के व्यवहार और अन्य इलेक्ट्रॉनों के कुछ औसत वितरण का वर्णन करता है। ही कक्षा में रहने वाले दो इलेक्ट्रॉनों के मामले में, [[पाउली सिद्धांत]] की मांग है कि उनके पास विपरीत स्पिन हो। आवश्यक रूप से यह अनुमान है, और आणविक इलेक्ट्रॉनिक तरंग फ़ंक्शन के अत्यधिक सटीक विवरण में ऑर्बिटल्स नहीं होते हैं ([[कॉन्फ़िगरेशन इंटरेक्शन]] देखें)।
-सामान्य तौर पर, आणविक कक्षाएँ पूरे अणु में स्थानीयकृत होती हैं। इसके अलावा, यदि अणु में समरूपता तत्व हैं, तो इसके गैर-अपक्षयी आणविक कक्षाएँ इनमें से किसी भी समरूपता के संबंध में या तो सममित या एंटीसिमेट्रिक हैं। दूसरे शब्दों में, आणविक कक्षीय ψ में एक समरूपता ऑपरेशन एस (उदाहरण के लिए, एक प्रतिबिंब, घूर्णन, या व्युत्क्रम) के अनुप्रयोग के परिणामस्वरूप आणविक कक्षक अपरिवर्तित होता है या इसके गणितीय चिह्न को उलट देता है: Sψ = ±ψ। उदाहरण के लिए, तलीय अणुओं में, आणविक तल में परावर्तन के संबंध में आणविक कक्षाएँ या तो सममित ([[सिग्मा बांड]]) या एंटीसिमेट्रिक (पीआई बांड) होती हैं। यदि विकृत कक्षीय ऊर्जा वाले अणुओं पर भी विचार किया जाता है, तो एक अधिक सामान्य कथन यह है कि आणविक कक्षाएँ अणु के [[समरूपता समूह]] के [[अघुलनशील प्रतिनिधित्व]] के लिए आधार बनाती हैं।<ref>{{Cite book|url=https://archive.org/details/isbn_9780471510949/page/102|title=समूह सिद्धांत के रासायनिक अनुप्रयोग|last=Cotton|first=F. Albert|date=1990|publisher=Wiley|isbn=0471510947|edition=3rd|location=New York|pages=[https://archive.org/details/isbn_9780471510949/page/102 102]|oclc=19975337|url-access=registration}}</ref> आणविक ऑर्बिटल्स के समरूपता गुणों का मतलब है कि डेलोकलाइज़ेशन आणविक ऑर्बिटल सिद्धांत की एक अंतर्निहित विशेषता है और इसे मूल रूप से (और पूरक) वैलेंस बॉन्ड सिद्धांत से अलग बनाता है, जिसमें बॉन्ड को स्थानीयकृत इलेक्ट्रॉन जोड़े के रूप में देखा जाता है, [[अनुनाद (रसायन विज्ञान)]] के लिए छूट के साथ स्थानीयकरण के लिए खाता.
+सामान्य तौर पर, आणविक कक्षाएँ पूरे अणु में स्थानीयकृत होती हैं। इसके अलावा, यदि अणु में समरूपता तत्व हैं, तो इसके गैर-अपक्षयी आणविक कक्षाएँ इनमें से किसी भी समरूपता के संबंध में या तो सममित या एंटीसिमेट्रिक हैं। दूसरे शब्दों में, आणविक कक्षीय ψ में समरूपता ऑपरेशन एस (उदाहरण के लिए, प्रतिबिंब, घूर्णन, या व्युत्क्रम) के अनुप्रयोग के परिणामस्वरूप आणविक कक्षक अपरिवर्तित होता है या इसके गणितीय चिह्न को उलट देता है: Sψ = ±ψ। उदाहरण के लिए, तलीय अणुओं में, आणविक तल में परावर्तन के संबंध में आणविक कक्षाएँ या तो सममित ([[सिग्मा बांड]]) या एंटीसिमेट्रिक (पीआई बांड) होती हैं। यदि विकृत कक्षीय ऊर्जा वाले अणुओं पर भी विचार किया जाता है, तो अधिक सामान्य कथन यह है कि आणविक कक्षाएँ अणु के [[समरूपता समूह]] के [[अघुलनशील प्रतिनिधित्व]] के लिए आधार बनाती हैं।<ref>{{Cite book|url=https://archive.org/details/isbn_9780471510949/page/102|title=समूह सिद्धांत के रासायनिक अनुप्रयोग|last=Cotton|first=F. Albert|date=1990|publisher=Wiley|isbn=0471510947|edition=3rd|location=New York|pages=[https://archive.org/details/isbn_9780471510949/page/102 102]|oclc=19975337|url-access=registration}}</ref> आणविक ऑर्बिटल्स के समरूपता गुणों का मतलब है कि डेलोकलाइज़ेशन आणविक ऑर्बिटल सिद्धांत की अंतर्निहित विशेषता है और इसे मूल रूप से (और पूरक) वैलेंस बॉन्ड सिद्धांत से अलग बनाता है, जिसमें बॉन्ड को स्थानीयकृत इलेक्ट्रॉन जोड़े के रूप में देखा जाता है, [[अनुनाद (रसायन विज्ञान)]] के लिए छूट के साथ स्थानीयकरण के लिए खाता.
-इन समरूपता-अनुकूलित विहित आणविक कक्षाओं के विपरीत, विहित कक्षाओं में कुछ गणितीय परिवर्तन लागू करके [[स्थानीयकृत आणविक कक्षाएँ]] बनाई जा सकती हैं। इस दृष्टिकोण का लाभ यह है कि ऑर्बिटल्स एक अणु के बंधनों के अधिक निकट से मेल खाएंगे जैसा कि लुईस संरचना द्वारा दर्शाया गया है। एक नुकसान के रूप में, इन स्थानीयकृत कक्षाओं के ऊर्जा स्तर का अब भौतिक अर्थ नहीं रह गया है। (इस लेख के बाकी हिस्से में चर्चा कैनोनिकल आणविक ऑर्बिटल्स पर केंद्रित होगी। स्थानीयकृत आणविक ऑर्बिटल्स पर आगे की चर्चा के लिए, देखें: प्राकृतिक बॉन्ड ऑर्बिटल और सिग्मा-पीआई और समकक्ष-ऑर्बिटल मॉडल।)
+इन समरूपता-अनुकूलित विहित आणविक कक्षाओं के विपरीत, विहित कक्षाओं में कुछ गणितीय परिवर्तन लागू करके [[स्थानीयकृत आणविक कक्षाएँ]] बनाई जा सकती हैं। इस दृष्टिकोण का लाभ यह है कि ऑर्बिटल्स अणु के बंधनों के अधिक निकट से मेल खाएंगे जैसा कि लुईस संरचना द्वारा दर्शाया गया है। नुकसान के रूप में, इन स्थानीयकृत कक्षाओं के ऊर्जा स्तर का अब भौतिक अर्थ नहीं रह गया है। (इस लेख के बाकी हिस्से में चर्चा कैनोनिकल आणविक ऑर्बिटल्स पर केंद्रित होगी। स्थानीयकृत आणविक ऑर्बिटल्स पर आगे की चर्चा के लिए, देखें: प्राकृतिक बॉन्ड ऑर्बिटल और सिग्मा-पीआई और समकक्ष-ऑर्बिटल मॉडल।)
 ==आणविक कक्षकों का निर्माण==
-आणविक कक्षाएँ परमाणु कक्षाओं के बीच अनुमत अंतःक्रियाओं से उत्पन्न होती हैं, जिन्हें अनुमति दी जाती है यदि परमाणु कक्षाओं की समरूपता ([[समूह सिद्धांत]] से निर्धारित) एक दूसरे के साथ संगत हैं। परमाणु कक्षीय अंतःक्रियाओं की दक्षता दो परमाणु कक्षकों के बीच [[कक्षीय ओवरलैप]] (दो कक्षक एक दूसरे के साथ कितनी अच्छी तरह से रचनात्मक रूप से बातचीत करते हैं इसका एक माप) से निर्धारित की जाती है, जो महत्वपूर्ण है यदि परमाणु कक्षक ऊर्जा में करीब हैं। अंत में, बनने वाले आणविक कक्षकों की संख्या अणु बनाने के लिए संयोजित होने वाले परमाणुओं में परमाणु कक्षकों की संख्या के बराबर होनी चाहिए।
+आणविक कक्षाएँ परमाणु कक्षाओं के बीच अनुमत अंतःक्रियाओं से उत्पन्न होती हैं, जिन्हें अनुमति दी जाती है यदि परमाणु कक्षाओं की समरूपता ([[समूह सिद्धांत]] से निर्धारित) दूसरे के साथ संगत हैं। परमाणु कक्षीय अंतःक्रियाओं की दक्षता दो परमाणु कक्षकों के बीच [[कक्षीय ओवरलैप]] (दो कक्षक दूसरे के साथ कितनी अच्छी तरह से रचनात्मक रूप से बातचीत करते हैं इसका माप) से निर्धारित की जाती है, जो महत्वपूर्ण है यदि परमाणु कक्षक ऊर्जा में करीब हैं। अंत में, बनने वाले आणविक कक्षकों की संख्या अणु बनाने के लिए संयोजित होने वाले परमाणुओं में परमाणु कक्षकों की संख्या के बराबर होनी चाहिए।
 ==गुणात्मक चर्चा==
-आणविक संरचना की एक अस्पष्ट, लेकिन गुणात्मक रूप से उपयोगी चर्चा के लिए, आणविक कक्षकों को परमाणु कक्षकों के [[रैखिक संयोजन]] आणविक कक्षीय विधि [[ansatz]] से प्राप्त किया जा सकता है। यहां, आणविक कक्षाओं को परमाणु कक्षाओं के रैखिक संयोजन के रूप में व्यक्त किया गया है।<ref>{{Cite book|title=रसायन विज्ञान में कक्षीय अंतःक्रियाएँ|last1=Albright|first1=T. A.|last2=Burdett|first2=J. K.|last3=Whangbo|first3=M.-H.|publisher=Wiley|year=2013|isbn=9780471080398|location=Hoboken, N.J.}}</ref>
+आणविक संरचना की अस्पष्ट, लेकिन गुणात्मक रूप से उपयोगी चर्चा के लिए, आणविक कक्षकों को परमाणु कक्षकों के [[रैखिक संयोजन]] आणविक कक्षीय विधि [[ansatz]] से प्राप्त किया जा सकता है। यहां, आणविक कक्षाओं को परमाणु कक्षाओं के रैखिक संयोजन के रूप में व्यक्त किया गया है।<ref>{{Cite book|title=रसायन विज्ञान में कक्षीय अंतःक्रियाएँ|last1=Albright|first1=T. A.|last2=Burdett|first2=J. K.|last3=Whangbo|first3=M.-H.|publisher=Wiley|year=2013|isbn=9780471080398|location=Hoboken, N.J.}}</ref>
@@ Line 25: / Line 25: @@
 {{main|Linear combination of atomic orbitals}}
-आणविक कक्षाएँ पहली बार [[फ्रेडरिक कुत्ता]] द्वारा प्रस्तुत की गईं<ref name="Hund1926">{{cite journal | last=Hund | first=F. | title=आणविक स्पेक्ट्रा में कुछ घटनाओं की व्याख्या पर|trans-title=On the interpretation of some phenomena in molecular spectra | journal=Zeitschrift für Physik | publisher=Springer Science and Business Media LLC | volume=36 | issue=9–10 | year=1926 | issn=1434-6001 | doi=10.1007/bf01400155 | pages=657–674 | bibcode=1926ZPhy...36..657H | s2cid=123208730 | language=de}}</ref><ref>F. Hund, "Zur Deutung der Molekelspektren", ''Zeitschrift für Physik'', Part I, vol. 40, pages 742-764 (1927); Part II, vol. 42, pages 93–120 (1927); Part III, vol. 43, pages 805-826 (1927); Part IV, vol. 51, pages 759-795 (1928); Part V, vol. 63, pages 719-751 (1930).</ref> और रॉबर्ट एस. मुल्लिकेन<ref name="Mulliken1927">{{cite journal | last=Mulliken | first=Robert S. | title=Electronic States and Band Spectrum Structure in Diatomic Molecules. IV. Hund's Theory; Second Positive Nitrogen and Swan Bands; Alternating Intensities | journal=[[Physical Review]] | publisher=American Physical Society (APS) | volume=29 | issue=5 | date=1 May 1927 | issn=0031-899X | doi=10.1103/physrev.29.637 | pages=637–649| bibcode=1927PhRv...29..637M }}</ref><ref name="Mulliken1928">{{cite journal | last=Mulliken | first=Robert S. | title=The assignment of quantum numbers for electrons in molecules. Extracts from Phys. Rev. 32, 186-222 (1928), plus currently written annotations | journal=International Journal of Quantum Chemistry | publisher=Wiley | volume=1 | issue=1 | year=1928 | issn=0020-7608 | doi=10.1002/qua.560010106 | pages=103–117}}</ref> 1927 और 1928 में.<ref>[[Friedrich Hund]] and Chemistry, [[Werner Kutzelnigg]], on the occasion of Hund's 100th birthday, ''[[Angewandte Chemie International Edition]]'', 35, 573–586, (1996)</ref><ref>[[Robert S. Mulliken]]'s Nobel Lecture, ''[[Science (journal)|Science]]'', 157, no. 3785, 13-24. Available on-line at: [http://nobelprize.org/nobel_prizes/chemistry/laureates/1966/mulliken-lecture.pdf Nobelprize.org]</ref> परमाणु ऑर्बिटल्स का रैखिक संयोजन या आणविक ऑर्बिटल्स के लिए एलसीएओ सन्निकटन 1929 में [[जॉन लेनार्ड-जोन्स]]|सर जॉन लेनार्ड-जोन्स द्वारा पेश किया गया था।<ref>{{cite journal| url=https://www.chemteam.info/Chem-History/Lennard-Jones-1929/Lennard-Jones-1929.html |last1=Lennard-Jones |first1=John (Sir) |author1-link=John Lennard-Jones |title=कुछ द्विपरमाणुक अणुओं की इलेक्ट्रॉनिक संरचना|journal=Transactions of the Faraday Society |volume=25 |pages=668–686 |date=1929|doi=10.1039/tf9292500668 |bibcode=1929FaTr...25..668L }}</ref> उनके अभूतपूर्व पेपर में दिखाया गया कि क्वांटम सिद्धांतों से [[एक अधातु तत्त्व]] और [[ऑक्सीजन]] अणुओं की इलेक्ट्रॉनिक संरचना कैसे प्राप्त की जाए। आणविक कक्षीय सिद्धांत का यह गुणात्मक दृष्टिकोण आधुनिक क्वांटम रसायन विज्ञान की शुरुआत का हिस्सा है।
+आणविक कक्षाएँ पहली बार [[फ्रेडरिक कुत्ता]] द्वारा प्रस्तुत की गईं<ref name="Hund1926">{{cite journal | last=Hund | first=F. | title=आणविक स्पेक्ट्रा में कुछ घटनाओं की व्याख्या पर|trans-title=On the interpretation of some phenomena in molecular spectra | journal=Zeitschrift für Physik | publisher=Springer Science and Business Media LLC | volume=36 | issue=9–10 | year=1926 | issn=1434-6001 | doi=10.1007/bf01400155 | pages=657–674 | bibcode=1926ZPhy...36..657H | s2cid=123208730 | language=de}}</ref><ref>F. Hund, "Zur Deutung der Molekelspektren", ''Zeitschrift für Physik'', Part I, vol. 40, pages 742-764 (1927); Part II, vol. 42, pages 93–120 (1927); Part III, vol. 43, pages 805-826 (1927); Part IV, vol. 51, pages 759-795 (1928); Part V, vol. 63, pages 719-751 (1930).</ref> और रॉबर्ट एस. मुल्लिकेन<ref name="Mulliken1927">{{cite journal | last=Mulliken | first=Robert S. | title=Electronic States and Band Spectrum Structure in Diatomic Molecules. IV. Hund's Theory; Second Positive Nitrogen and Swan Bands; Alternating Intensities | journal=[[Physical Review]] | publisher=American Physical Society (APS) | volume=29 | issue=5 | date=1 May 1927 | issn=0031-899X | doi=10.1103/physrev.29.637 | pages=637–649| bibcode=1927PhRv...29..637M }}</ref><ref name="Mulliken1928">{{cite journal | last=Mulliken | first=Robert S. | title=The assignment of quantum numbers for electrons in molecules. Extracts from Phys. Rev. 32, 186-222 (1928), plus currently written annotations | journal=International Journal of Quantum Chemistry | publisher=Wiley | volume=1 | issue=1 | year=1928 | issn=0020-7608 | doi=10.1002/qua.560010106 | pages=103–117}}</ref> 1927 और 1928 में.<ref>[[Friedrich Hund]] and Chemistry, [[Werner Kutzelnigg]], on the occasion of Hund's 100th birthday, ''[[Angewandte Chemie International Edition]]'', 35, 573–586, (1996)</ref><ref>[[Robert S. Mulliken]]'s Nobel Lecture, ''[[Science (journal)|Science]]'', 157, no. 3785, 13-24. Available on-line at: [http://nobelprize.org/nobel_prizes/chemistry/laureates/1966/mulliken-lecture.pdf Nobelprize.org]</ref> परमाणु ऑर्बिटल्स का रैखिक संयोजन या आणविक ऑर्बिटल्स के लिए एलसीएओ सन्निकटन 1929 में [[जॉन लेनार्ड-जोन्स]]|सर जॉन लेनार्ड-जोन्स द्वारा पेश किया गया था।<ref>{{cite journal| url=https://www.chemteam.info/Chem-History/Lennard-Jones-1929/Lennard-Jones-1929.html |last1=Lennard-Jones |first1=John (Sir) |author1-link=John Lennard-Jones |title=कुछ द्विपरमाणुक अणुओं की इलेक्ट्रॉनिक संरचना|journal=Transactions of the Faraday Society |volume=25 |pages=668–686 |date=1929|doi=10.1039/tf9292500668 |bibcode=1929FaTr...25..668L }}</ref> उनके अभूतपूर्व पेपर में दिखाया गया कि क्वांटम सिद्धांतों से [[एक अधातु तत्त्व|अधातु तत्त्व]] और [[ऑक्सीजन]] अणुओं की इलेक्ट्रॉनिक संरचना कैसे प्राप्त की जाए। आणविक कक्षीय सिद्धांत का यह गुणात्मक दृष्टिकोण आधुनिक क्वांटम रसायन विज्ञान की शुरुआत का हिस्सा है।
-परमाणु ऑर्बिटल्स (एलसीएओ) के रैखिक संयोजन का उपयोग आणविक ऑर्बिटल्स का अनुमान लगाने के लिए किया जा सकता है जो अणु के घटक परमाणुओं के बीच बंधन पर बनते हैं। परमाणु कक्षक के समान, एक श्रोडिंगर समीकरण, जो एक इलेक्ट्रॉन के व्यवहार का वर्णन करता है, एक आणविक कक्षक के लिए भी बनाया जा सकता है। परमाणु कक्षाओं के रैखिक संयोजन, या परमाणु तरंग कार्यों के योग और अंतर, हार्ट्री-फॉक विधि के लिए अनुमानित समाधान प्रदान करते हैं। हार्ट्री-फॉक समीकरण जो आणविक श्रोडिंगर समीकरण के स्वतंत्र-कण सन्निकटन के अनुरूप हैं। सरल द्विपरमाणुक अणुओं के लिए, प्राप्त तरंगक्रियाओं को समीकरणों द्वारा गणितीय रूप से दर्शाया जाता है
+परमाणु ऑर्बिटल्स (एलसीएओ) के रैखिक संयोजन का उपयोग आणविक ऑर्बिटल्स का अनुमान लगाने के लिए किया जा सकता है जो अणु के घटक परमाणुओं के बीच बंधन पर बनते हैं। परमाणु कक्षक के समान, श्रोडिंगर समीकरण, जो इलेक्ट्रॉन के व्यवहार का वर्णन करता है, आणविक कक्षक के लिए भी बनाया जा सकता है। परमाणु कक्षाओं के रैखिक संयोजन, या परमाणु तरंग कार्यों के योग और अंतर, हार्ट्री-फॉक विधि के लिए अनुमानित समाधान प्रदान करते हैं। हार्ट्री-फॉक समीकरण जो आणविक श्रोडिंगर समीकरण के स्वतंत्र-कण सन्निकटन के अनुरूप हैं। सरल द्विपरमाणुक अणुओं के लिए, प्राप्त तरंगक्रियाओं को समीकरणों द्वारा गणितीय रूप से दर्शाया जाता है
 :<math>\Psi = c_a \psi_a + c_b \psi_b</math>
 :<math>\Psi^* = c_a \psi_a - c_b \psi_b</math>
-कहाँ <math>\Psi</math> और <math>\Psi^*</math> क्रमशः आबंधन और प्रतिरक्षी आण्विक कक्षकों के लिए आण्विक तरंगक्रियाएँ हैं, <math>\psi_a</math> और <math>\psi_b</math> क्रमशः परमाणु a और b से परमाणु तरंग फलन हैं, और <math>c_a</math> और <math>c_b</math> समायोज्य गुणांक हैं. ये गुणांक व्यक्तिगत परमाणु कक्षाओं की ऊर्जा और समरूपता के आधार पर सकारात्मक या नकारात्मक हो सकते हैं। जैसे-जैसे दो परमाणु एक-दूसरे के करीब आते हैं, उनके परमाणु कक्षक उच्च इलेक्ट्रॉन घनत्व के क्षेत्रों का निर्माण करने के लिए ओवरलैप होते हैं, और, परिणामस्वरूप, दोनों परमाणुओं के बीच आणविक कक्षक बनते हैं। परमाणु सकारात्मक रूप से चार्ज किए गए नाभिक और बॉन्डिंग आणविक कक्षाओं में मौजूद नकारात्मक चार्ज वाले इलेक्ट्रॉनों के बीच इलेक्ट्रोस्टैटिक आकर्षण द्वारा एक साथ बंधे रहते हैं।<ref name="Gary L. Miessler 2004">{{cite book | last1=Miessler | first1=G.L. |last2=Tarr |first2=Donald A. | title=अकार्बनिक रसायन शास्त्र| publisher=Pearson Education | year=2008 | isbn=978-81-317-1885-8 | url=https://books.google.com/books?id=rBfolO_rhf8C}}</ref>
+कहाँ <math>\Psi</math> और <math>\Psi^*</math> क्रमशः आबंधन और प्रतिरक्षी आण्विक कक्षकों के लिए आण्विक तरंगक्रियाएँ हैं, <math>\psi_a</math> और <math>\psi_b</math> क्रमशः परमाणु a और b से परमाणु तरंग फलन हैं, और <math>c_a</math> और <math>c_b</math> समायोज्य गुणांक हैं. ये गुणांक व्यक्तिगत परमाणु कक्षाओं की ऊर्जा और समरूपता के आधार पर सकारात्मक या नकारात्मक हो सकते हैं। जैसे-जैसे दो परमाणु एक-दूसरे के करीब आते हैं, उनके परमाणु कक्षक उच्च इलेक्ट्रॉन घनत्व के क्षेत्रों का निर्माण करने के लिए ओवरलैप होते हैं, और, परिणामस्वरूप, दोनों परमाणुओं के बीच आणविक कक्षक बनते हैं। परमाणु सकारात्मक रूप से चार्ज किए गए नाभिक और बॉन्डिंग आणविक कक्षाओं में मौजूद नकारात्मक चार्ज वाले इलेक्ट्रॉनों के बीच इलेक्ट्रोस्टैटिक आकर्षण द्वारा साथ बंधे रहते हैं।<ref name="Gary L. Miessler 2004">{{cite book | last1=Miessler | first1=G.L. |last2=Tarr |first2=Donald A. | title=अकार्बनिक रसायन शास्त्र| publisher=Pearson Education | year=2008 | isbn=978-81-317-1885-8 | url=https://books.google.com/books?id=rBfolO_rhf8C}}</ref>
@@ Line 40: / Line 40: @@
 * बॉन्डिंग एमओ उन परमाणु ऑर्बिटल्स की तुलना में ऊर्जा में कम होते हैं जो उन्हें उत्पन्न करने के लिए संयोजित होते हैं।
 प्रतिरक्षी आण्विक कक्षाएँ:
-* परमाणु ऑर्बिटल्स के बीच एंटीबॉन्डिंग इंटरैक्शन विनाशकारी (आउट-ऑफ़-फ़ेज़) इंटरैक्शन हैं, एक [[नोड (भौतिकी)]] के साथ जहां दो इंटरैक्टिंग परमाणुओं के बीच एंटीबॉन्डिंग ऑर्बिटल की तरंग फ़ंक्शन शून्य है
+* परमाणु ऑर्बिटल्स के बीच एंटीबॉन्डिंग इंटरैक्शन विनाशकारी (आउट-ऑफ़-फ़ेज़) इंटरैक्शन हैं, [[नोड (भौतिकी)]] के साथ जहां दो इंटरैक्टिंग परमाणुओं के बीच एंटीबॉन्डिंग ऑर्बिटल की तरंग फ़ंक्शन शून्य है
 * एंटीबॉन्डिंग एमओ उन परमाणु ऑर्बिटल्स की तुलना में ऊर्जा में अधिक होते हैं जो उन्हें उत्पन्न करने के लिए संयोजित होते हैं।
 गैर-बंधन कक्षक:
 * संगत समरूपता की कमी के कारण नॉनबॉन्डिंग एमओ परमाणु ऑर्बिटल्स के बीच कोई बातचीत नहीं होने का परिणाम हैं।
-* नॉनबॉन्डिंग एमओ में अणु में किसी एक परमाणु के परमाणु ऑर्बिटल्स के समान ऊर्जा होगी।
+* नॉनबॉन्डिंग एमओ में अणु में किसी परमाणु के परमाणु ऑर्बिटल्स के समान ऊर्जा होगी।
-===एमओ के लिए सिग्मा और पीआई लेबल===<!-- this section-title is linked from some redirect pages...do not change it here without also updating them -->
+===एमओ के लिए सिग्मा और पीआई लेबल===
 परमाणु कक्षाओं के बीच परस्पर क्रिया के प्रकार को आणविक-कक्षीय समरूपता लेबल σ (सिग्मा), π (pi), δ (डेल्टा), φ (phi), γ (गामा) आदि द्वारा वर्गीकृत किया जा सकता है। ये संबंधित ग्रीक अक्षर हैं परमाणु कक्षाओं में क्रमशः s, p, d, f और g। संबंधित परमाणुओं के बीच आंतरिक परमाणु अक्ष वाले नोडल विमानों की संख्या σ MOs के लिए शून्य है, π के लिए एक, δ के लिए दो, φ के लिए तीन और γ के लिए चार है।
 ====σ समरूपता====
 {{Further|Sigma bond}}
-σ समरूपता वाला एक MO या तो दो परमाणु s-ऑर्बिटल्स या दो परमाणु p की परस्पर क्रिया से उत्पन्न होता है<sub>z</sub>-ऑर्बिटल्स. एक MO में σ-समरूपता होगी यदि कक्षक दो परमाणु केंद्रों, आंतरिक परमाणु अक्ष को जोड़ने वाली धुरी के संबंध में सममित है। इसका मतलब यह है कि आंतरिक परमाणु अक्ष के बारे में एमओ के घूमने से चरण परिवर्तन नहीं होता है। एक σ* ऑर्बिटल, सिग्मा एंटीबॉन्डिंग ऑर्बिटल, आंतरिक परमाणु अक्ष के चारों ओर घूमने पर भी उसी चरण को बनाए रखता है। σ* ऑर्बिटल में एक नोडल प्लेन होता है जो नाभिक के बीच होता है और आंतरिक अक्ष के लंबवत होता है।<ref name = H&C>Catherine E. Housecroft, Alan G. Sharpe, ''Inorganic Chemistry'', Pearson Prentice Hall; 2nd Edition, 2005, p. 29-33.</ref>
+σ समरूपता वाला MO या तो दो परमाणु s-ऑर्बिटल्स या दो परमाणु p की परस्पर क्रिया से उत्पन्न होता है<sub>z</sub>-ऑर्बिटल्स. MO में σ-समरूपता होगी यदि कक्षक दो परमाणु केंद्रों, आंतरिक परमाणु अक्ष को जोड़ने वाली धुरी के संबंध में सममित है। इसका मतलब यह है कि आंतरिक परमाणु अक्ष के बारे में एमओ के घूमने से चरण परिवर्तन नहीं होता है। σ* ऑर्बिटल, सिग्मा एंटीबॉन्डिंग ऑर्बिटल, आंतरिक परमाणु अक्ष के चारों ओर घूमने पर भी उसी चरण को बनाए रखता है। σ* ऑर्बिटल में नोडल प्लेन होता है जो नाभिक के बीच होता है और आंतरिक अक्ष के लंबवत होता है।<ref name = H&C>Catherine E. Housecroft, Alan G. Sharpe, ''Inorganic Chemistry'', Pearson Prentice Hall; 2nd Edition, 2005, p. 29-33.</ref>
 ====π समरूपता====
 {{Further|Pi bond}}
-π समरूपता वाला एक MO दो परमाणु p की परस्पर क्रिया से उत्पन्न होता है<sub>x</sub> ऑर्बिटल्स या पी<sub>y</sub> कक्षाएँ। यदि आंतरिक परमाणु अक्ष के बारे में घूर्णन के संबंध में कक्षीय असममित है तो एक MO में π समरूपता होगी। इसका मतलब यह है कि आंतरिक परमाणु अक्ष के बारे में एमओ के घूमने से चरण परिवर्तन होगा। यदि परमाणु कक्षक#वास्तविक कक्षकों पर विचार किया जाए तो एक नोडल तल है जिसमें आंतरिक अक्ष होता है।
+π समरूपता वाला MO दो परमाणु p की परस्पर क्रिया से उत्पन्न होता है<sub>x</sub> ऑर्बिटल्स या पी<sub>y</sub> कक्षाएँ। यदि आंतरिक परमाणु अक्ष के बारे में घूर्णन के संबंध में कक्षीय असममित है तो MO में π समरूपता होगी। इसका मतलब यह है कि आंतरिक परमाणु अक्ष के बारे में एमओ के घूमने से चरण परिवर्तन होगा। यदि परमाणु कक्षक#वास्तविक कक्षकों पर विचार किया जाए तो नोडल तल है जिसमें आंतरिक अक्ष होता है।
-एक π* ऑर्बिटल, पीआई एंटीबॉन्डिंग ऑर्बिटल, आंतरिक परमाणु अक्ष के बारे में घुमाए जाने पर भी एक चरण परिवर्तन उत्पन्न करेगा। π* कक्षक में नाभिक के बीच एक दूसरा नोडल तल भी होता है।<ref name = H&C /><ref>Peter Atkins; Julio De Paula. ''Atkins’ Physical Chemistry''. Oxford University Press, 8th ed., 2006.</ref><ref>Yves Jean; François Volatron. ''An Introduction to Molecular Orbitals''. Oxford University Press, 1993.</ref><ref>Michael Munowitz, ''Principles of Chemistry'', Norton & Company, 2000, p. 229-233.</ref>
+एक π* ऑर्बिटल, पीआई एंटीबॉन्डिंग ऑर्बिटल, आंतरिक परमाणु अक्ष के बारे में घुमाए जाने पर भी चरण परिवर्तन उत्पन्न करेगा। π* कक्षक में नाभिक के बीच दूसरा नोडल तल भी होता है।<ref name = H&C /><ref>Peter Atkins; Julio De Paula. ''Atkins’ Physical Chemistry''. Oxford University Press, 8th ed., 2006.</ref><ref>Yves Jean; François Volatron. ''An Introduction to Molecular Orbitals''. Oxford University Press, 1993.</ref><ref>Michael Munowitz, ''Principles of Chemistry'', Norton & Company, 2000, p. 229-233.</ref>
 ====δ समरूपता====
 {{Further|Delta bond}}
-δ समरूपता वाला एक MO दो परमाणु d की परस्पर क्रिया से उत्पन्न होता है<sub>xy</sub> या डी<sub>x<sup>2</sup>-y<sup>2</sup></sub> कक्षाएँ। क्योंकि इन आणविक कक्षाओं में कम-ऊर्जा डी परमाणु कक्षाएँ शामिल होती हैं, उन्हें [[संक्रमण धातु]] | संक्रमण-धातु परिसरों में देखा जाता है। एक δ आबंधन कक्षक में आंतरिक नाभिकीय अक्ष वाले दो नोडल तल होते हैं, और एक δ* प्रतिरक्षी कक्षक में नाभिक के बीच एक तीसरा नोडल तल भी होता है।
+δ समरूपता वाला MO दो परमाणु d की परस्पर क्रिया से उत्पन्न होता है<sub>xy</sub> या डी<sub>x<sup>2</sup>-y<sup>2</sup></sub> कक्षाएँ। क्योंकि इन आणविक कक्षाओं में कम-ऊर्जा डी परमाणु कक्षाएँ शामिल होती हैं, उन्हें [[संक्रमण धातु]] | संक्रमण-धातु परिसरों में देखा जाता है। δ आबंधन कक्षक में आंतरिक नाभिकीय अक्ष वाले दो नोडल तल होते हैं, और δ* प्रतिरक्षी कक्षक में नाभिक के बीच तीसरा नोडल तल भी होता है।
-====φ समरूपता====<!-- this section-title is linked from some redirect pages...do not change it here without also updating them -->
+====φ समरूपता====
 {{Further|Phi bond}}
 {{multiple image
@@ Line 86: / Line 86: @@
 * [[टेट्राहेड्रल आणविक ज्यामिति]], EX<sub>4</sub>.
 यदि किसी अणु में समरूपता के केंद्र के माध्यम से व्युत्क्रमण के परिणामस्वरूप आणविक कक्षीय के लिए समान चरण होते हैं, तो एमओ को जर्मन शब्द सम से गेराडे (जी) समरूपता कहा जाता है।
-यदि किसी अणु में समरूपता के केंद्र के माध्यम से व्युत्क्रमण के परिणामस्वरूप आणविक कक्षक के लिए एक चरण परिवर्तन होता है, तो एमओ को विषम के लिए जर्मन शब्द से अनगेरेड (यू) समरूपता कहा जाता है।
+यदि किसी अणु में समरूपता के केंद्र के माध्यम से व्युत्क्रमण के परिणामस्वरूप आणविक कक्षक के लिए चरण परिवर्तन होता है, तो एमओ को विषम के लिए जर्मन शब्द से अनगेरेड (यू) समरूपता कहा जाता है।
-σ-समरूपता के साथ एक बंधन MO के लिए, कक्षीय σ है<sub>g</sub> (s'+ s<nowiki></nowiki> सममित है), जबकि σ-समरूपता के साथ एक प्रतिरक्षी MO कक्षीय σ है<sub>u</sub>, क्योंकि s' – s<nowiki></nowiki> का व्युत्क्रमण प्रतिसममिति है।
+σ-समरूपता के साथ बंधन MO के लिए, कक्षीय σ है<sub>g</sub> (s'+ s सममित है), जबकि σ-समरूपता के साथ प्रतिरक्षी MO कक्षीय σ है<sub>u</sub>, क्योंकि s' – s का व्युत्क्रमण प्रतिसममिति है।
-π-समरूपता के साथ एक बंधन MO के लिए कक्षीय π है<sub>u</sub> क्योंकि समरूपता के केंद्र के माध्यम से व्युत्क्रमण एक संकेत परिवर्तन उत्पन्न करेगा (दो पी परमाणु कक्षाएँ एक दूसरे के साथ चरण में हैं लेकिन दो पालियों के विपरीत संकेत हैं), जबकि π-समरूपता के साथ एक प्रतिरक्षी MO π है<sub>g</sub> क्योंकि समरूपता के केंद्र के माध्यम से व्युत्क्रमण से कोई संकेत परिवर्तन नहीं होगा (दो पी ऑर्बिटल्स चरण द्वारा एंटीसिमेट्रिक हैं)।<ref name = H&C />
+π-समरूपता के साथ बंधन MO के लिए कक्षीय π है<sub>u</sub> क्योंकि समरूपता के केंद्र के माध्यम से व्युत्क्रमण संकेत परिवर्तन उत्पन्न करेगा (दो पी परमाणु कक्षाएँ दूसरे के साथ चरण में हैं लेकिन दो पालियों के विपरीत संकेत हैं), जबकि π-समरूपता के साथ प्रतिरक्षी MO π है<sub>g</sub> क्योंकि समरूपता के केंद्र के माध्यम से व्युत्क्रमण से कोई संकेत परिवर्तन नहीं होगा (दो पी ऑर्बिटल्स चरण द्वारा एंटीसिमेट्रिक हैं)।<ref name = H&C />
@@ Line 94: / Line 94: @@
 {{main|Molecular orbital diagram}}
-एमओ विश्लेषण का गुणात्मक दृष्टिकोण एक अणु में बॉन्डिंग इंटरैक्शन को देखने के लिए आणविक कक्षीय आरेख का उपयोग करता है। इस प्रकार के आरेख में, आणविक कक्षाओं को क्षैतिज रेखाओं द्वारा दर्शाया जाता है; रेखा जितनी ऊँची होगी, कक्षक की ऊर्जा उतनी ही अधिक होगी, और पतित कक्षकों को उनके बीच एक स्थान के साथ समान स्तर पर रखा जाएगा। फिर, पॉली अपवर्जन सिद्धांत और हंड के अधिकतम बहुलता के नियम को ध्यान में रखते हुए, आणविक कक्षाओं में रखे जाने वाले इलेक्ट्रॉनों को एक-एक करके व्यवस्थित किया जाता है (केवल 2 इलेक्ट्रॉन, विपरीत स्पिन वाले, प्रति कक्षक; एक पर कई अयुग्मित इलेक्ट्रॉन रखें उन्हें जोड़ना शुरू करने से पहले जितना संभव हो सके [[ऊर्जा स्तर]])। अधिक जटिल अणुओं के लिए, तरंग यांत्रिकी दृष्टिकोण संबंध की गुणात्मक समझ में उपयोगिता खो देता है (हालांकि मात्रात्मक दृष्टिकोण के लिए अभी भी आवश्यक है)।
+एमओ विश्लेषण का गुणात्मक दृष्टिकोण अणु में बॉन्डिंग इंटरैक्शन को देखने के लिए आणविक कक्षीय आरेख का उपयोग करता है। इस प्रकार के आरेख में, आणविक कक्षाओं को क्षैतिज रेखाओं द्वारा दर्शाया जाता है; रेखा जितनी ऊँची होगी, कक्षक की ऊर्जा उतनी ही अधिक होगी, और पतित कक्षकों को उनके बीच स्थान के साथ समान स्तर पर रखा जाएगा। फिर, पॉली अपवर्जन सिद्धांत और हंड के अधिकतम बहुलता के नियम को ध्यान में रखते हुए, आणविक कक्षाओं में रखे जाने वाले इलेक्ट्रॉनों को एक-एक करके व्यवस्थित किया जाता है (केवल 2 इलेक्ट्रॉन, विपरीत स्पिन वाले, प्रति कक्षक; पर कई अयुग्मित इलेक्ट्रॉन रखें उन्हें जोड़ना शुरू करने से पहले जितना संभव हो सके [[ऊर्जा स्तर]])। अधिक जटिल अणुओं के लिए, तरंग यांत्रिकी दृष्टिकोण संबंध की गुणात्मक समझ में उपयोगिता खो देता है (हालांकि मात्रात्मक दृष्टिकोण के लिए अभी भी आवश्यक है)।
 कुछ गुण:
 * ऑर्बिटल्स के आधार सेट में वे परमाणु ऑर्बिटल्स शामिल होते हैं जो आणविक ऑर्बिटल इंटरैक्शन के लिए उपलब्ध होते हैं, जो बॉन्डिंग या एंटीबॉन्डिंग हो सकते हैं
@@ Line 100: / Line 100: @@
 * यदि अणु में कुछ समरूपता है, तो विकृत परमाणु कक्षाएँ (समान परमाणु ऊर्जा के साथ) रैखिक संयोजनों में समूहीकृत की जाती हैं (जिन्हें समरूपता-अनुकूलित परमाणु कक्षाएँ (SO) कहा जाता है), जो समरूपता समूह के परिमित समूहों के प्रतिनिधित्व सिद्धांत से संबंधित हैं, इसलिए समूह का वर्णन करने वाले तरंग कार्यों को समरूपता-अनुकूलित रैखिक संयोजन (एसएएलसी) के रूप में जाना जाता है।
 * एक समूह प्रतिनिधित्व से संबंधित आणविक कक्षाओं की संख्या इस प्रतिनिधित्व से संबंधित समरूपता-अनुकूलित परमाणु कक्षाओं की संख्या के बराबर है
-* परिमित समूहों के एक विशेष प्रतिनिधित्व सिद्धांत के भीतर, समरूपता-अनुकूलित परमाणु कक्षाएँ अधिक मिश्रित होती हैं यदि उनकी परमाणु ऊर्जा का स्तर करीब हो।
+* परिमित समूहों के विशेष प्रतिनिधित्व सिद्धांत के भीतर, समरूपता-अनुकूलित परमाणु कक्षाएँ अधिक मिश्रित होती हैं यदि उनकी परमाणु ऊर्जा का स्तर करीब हो।
 एक यथोचित सरल अणु के लिए आणविक कक्षीय आरेख के निर्माण की सामान्य प्रक्रिया को निम्नानुसार संक्षेपित किया जा सकता है:
-. अणु को एक बिंदु समूह निर्दिष्ट करें।
+. अणु को बिंदु समूह निर्दिष्ट करें।
 . SALCs की आकृतियों को देखें।
@@ Line 128: / Line 128: @@
 {{main|Ionic bond}}
-जब दो परमाणुओं के परमाणु ऑर्बिटल्स के बीच ऊर्जा का अंतर काफी बड़ा होता है, तो एक परमाणु के ऑर्बिटल्स लगभग पूरी तरह से बॉन्डिंग ऑर्बिटल्स में योगदान करते हैं, और दूसरे परमाणु के ऑर्बिटल्स लगभग पूरी तरह से एंटीबॉन्डिंग ऑर्बिटल्स में योगदान करते हैं। इस प्रकार, स्थिति प्रभावी रूप से यह है कि एक या अधिक इलेक्ट्रॉनों को एक परमाणु से दूसरे में स्थानांतरित कर दिया गया है। इसे (अधिकतर) आयनिक बंधन कहा जाता है।{{cn|date=June 2022}}
+जब दो परमाणुओं के परमाणु ऑर्बिटल्स के बीच ऊर्जा का अंतर काफी बड़ा होता है, तो परमाणु के ऑर्बिटल्स लगभग पूरी तरह से बॉन्डिंग ऑर्बिटल्स में योगदान करते हैं, और दूसरे परमाणु के ऑर्बिटल्स लगभग पूरी तरह से एंटीबॉन्डिंग ऑर्बिटल्स में योगदान करते हैं। इस प्रकार, स्थिति प्रभावी रूप से यह है कि या अधिक इलेक्ट्रॉनों को परमाणु से दूसरे में स्थानांतरित कर दिया गया है। इसे (अधिकतर) आयनिक बंधन कहा जाता है।
 ====बांड आदेश====
 {{main|Bond order}}
-किसी अणु का बंधन क्रम, या बंधनों की संख्या, बंधन और प्रतिरक्षी आणविक कक्षाओं में इलेक्ट्रॉनों की संख्या को मिलाकर निर्धारित की जा सकती है। बॉन्डिंग ऑर्बिटल में इलेक्ट्रॉनों की एक जोड़ी एक बंधन बनाती है, जबकि एक एंटीबॉडी ऑर्बिटल में इलेक्ट्रॉनों की एक जोड़ी एक बॉन्ड को नकार देती है। उदाहरण के लिए, एन<sub>2</sub>बॉन्डिंग ऑर्बिटल्स में आठ इलेक्ट्रॉनों और एंटीबॉन्डिंग ऑर्बिटल्स में दो इलेक्ट्रॉनों के साथ, तीन का बॉन्ड ऑर्डर होता है, जो एक ट्रिपल बॉन्ड का गठन करता है।
+किसी अणु का बंधन क्रम, या बंधनों की संख्या, बंधन और प्रतिरक्षी आणविक कक्षाओं में इलेक्ट्रॉनों की संख्या को मिलाकर निर्धारित की जा सकती है। बॉन्डिंग ऑर्बिटल में इलेक्ट्रॉनों की जोड़ी बंधन बनाती है, जबकि एंटीबॉडी ऑर्बिटल में इलेक्ट्रॉनों की जोड़ी बॉन्ड को नकार देती है। उदाहरण के लिए, एन<sub>2</sub>बॉन्डिंग ऑर्बिटल्स में आठ इलेक्ट्रॉनों और एंटीबॉन्डिंग ऑर्बिटल्स में दो इलेक्ट्रॉनों के साथ, तीन का बॉन्ड ऑर्डर होता है, जो ट्रिपल बॉन्ड का गठन करता है।
-बॉन्ड की ताकत बॉन्ड ऑर्डर के समानुपाती होती है - बॉन्डिंग की अधिक मात्रा अधिक स्थिर बॉन्ड बनाती है - और बॉन्ड की लंबाई इसके व्युत्क्रमानुपाती होती है - एक मजबूत बॉन्ड छोटा होता है।
+बॉन्ड की ताकत बॉन्ड ऑर्डर के समानुपाती होती है - बॉन्डिंग की अधिक मात्रा अधिक स्थिर बॉन्ड बनाती है - और बॉन्ड की लंबाई इसके व्युत्क्रमानुपाती होती है - मजबूत बॉन्ड छोटा होता है।
 सकारात्मक बंधन क्रम वाले अणु की आवश्यकता के दुर्लभ अपवाद हैं। यद्यपि हो<sub>2</sub> एमओ विश्लेषण के अनुसार 0 का बॉन्ड ऑर्डर है, अत्यधिक अस्थिर बीई का प्रयोगात्मक सबूत है<sub>2</sub> अणु की बंधन लंबाई 245 pm और बंधन ऊर्जा 10 kJ/mol है।<ref name = H&C /><ref>{{cite journal | last1 = Bondybey | first1 = V.E. | year = 1984 | title = Electronic structure and bonding of Be2 | journal = Chemical Physics Letters | volume = 109 | issue = 5| pages = 436–441 | doi = 10.1016/0009-2614(84)80339-5 | bibcode = 1984CPL...109..436B }}</ref>
@@ Line 141: / Line 141: @@
 ====होमो और लूमो====
 {{main|HOMO and LUMO}}
-उच्चतम व्याप्त आणविक कक्षक और सबसे कम रिक्त आणविक कक्षक को अक्सर क्रमशः HOMO और LUMO कहा जाता है। HOMO और LUMO की ऊर्जाओं के अंतर को HOMO-LUMO अंतर कहा जाता है। यह धारणा अक्सर साहित्य में भ्रम का विषय है और इस पर सावधानी से विचार किया जाना चाहिए। इसका मान आमतौर पर मूलभूत अंतर (आयनीकरण क्षमता और इलेक्ट्रॉन आत्मीयता के बीच अंतर) और ऑप्टिकल अंतर के बीच स्थित होता है। इसके अलावा, HOMO-LUMO गैप थोक सामग्री [[ऊर्जा अंतराल]] या ट्रांसपोर्ट गैप से संबंधित हो सकता है, जो आमतौर पर मौलिक गैप से बहुत छोटा होता है।{{cn|date=June 2022}}
+उच्चतम व्याप्त आणविक कक्षक और सबसे कम रिक्त आणविक कक्षक को अक्सर क्रमशः HOMO और LUMO कहा जाता है। HOMO और LUMO की ऊर्जाओं के अंतर को HOMO-LUMO अंतर कहा जाता है। यह धारणा अक्सर साहित्य में भ्रम का विषय है और इस पर सावधानी से विचार किया जाना चाहिए। इसका मान आमतौर पर मूलभूत अंतर (आयनीकरण क्षमता और इलेक्ट्रॉन आत्मीयता के बीच अंतर) और ऑप्टिकल अंतर के बीच स्थित होता है। इसके अलावा, HOMO-LUMO गैप थोक सामग्री [[ऊर्जा अंतराल]] या ट्रांसपोर्ट गैप से संबंधित हो सकता है, जो आमतौर पर मौलिक गैप से बहुत छोटा होता है।
 ==उदाहरण==
@@ Line 151: / Line 151: @@
 ====एच<sub>2</sub>====
-[[File:H2OrbitalsAnimation.gif|thumb|right|300px|एक अकेले हाइड्रोजन परमाणु (बाएं और दाएं) के परमाणु कक्षक और एच के संबंधित बंधन (नीचे) और प्रतिरक्षी (ऊपर) आणविक कक्षा के लिए इलेक्ट्रॉन तरंग कार्य<sub>2</sub> अणु. तरंगक्रिया का वास्तविक भाग नीला वक्र है, और [[काल्पनिक भाग]] लाल वक्र है। लाल बिंदु नाभिक के स्थान को चिह्नित करते हैं। इलेक्ट्रॉन तरंग फ़ंक्शन श्रोडिंगर तरंग समीकरण के अनुसार दोलन करता है, और ऑर्बिटल्स इसकी खड़ी तरंगें हैं। स्थायी तरंग आवृत्ति कक्षीय की गतिज ऊर्जा के समानुपाती होती है। (यह कथानक त्रि-आयामी प्रणाली का एक आयामी टुकड़ा है।)]]एक सरल MO उदाहरण के रूप में, [[हाइड्रोजन]] अणु, H में इलेक्ट्रॉनों पर विचार करें<sub>2</sub> (MO आरेख#डायटोमिक MO आरेख देखें), दो परमाणुओं को H' और H लेबल के साथ। सबसे कम ऊर्जा वाले परमाणु कक्षक, 1s' और 1s, अणु की समरूपता के अनुसार परिवर्तित नहीं होते हैं। हालाँकि, निम्नलिखित समरूपता अनुकूलित परमाणु कक्षाएँ करती हैं:
+[[File:H2OrbitalsAnimation.gif|thumb|right|300px|एक अकेले हाइड्रोजन परमाणु (बाएं और दाएं) के परमाणु कक्षक और एच के संबंधित बंधन (नीचे) और प्रतिरक्षी (ऊपर) आणविक कक्षा के लिए इलेक्ट्रॉन तरंग कार्य<sub>2</sub> अणु. तरंगक्रिया का वास्तविक भाग नीला वक्र है, और [[काल्पनिक भाग]] लाल वक्र है। लाल बिंदु नाभिक के स्थान को चिह्नित करते हैं। इलेक्ट्रॉन तरंग फ़ंक्शन श्रोडिंगर तरंग समीकरण के अनुसार दोलन करता है, और ऑर्बिटल्स इसकी खड़ी तरंगें हैं। स्थायी तरंग आवृत्ति कक्षीय की गतिज ऊर्जा के समानुपाती होती है। (यह कथानक त्रि-आयामी प्रणाली का आयामी टुकड़ा है।)]]एक सरल MO उदाहरण के रूप में, [[हाइड्रोजन]] अणु, H में इलेक्ट्रॉनों पर विचार करें<sub>2</sub> (MO आरेख#डायटोमिक MO आरेख देखें), दो परमाणुओं को H' और H लेबल के साथ। सबसे कम ऊर्जा वाले परमाणु कक्षक, 1s' और 1s, अणु की समरूपता के अनुसार परिवर्तित नहीं होते हैं। हालाँकि, निम्नलिखित समरूपता अनुकूलित परमाणु कक्षाएँ करती हैं:
 {| class="wikitable"
@@ Line 161: / Line 161: @@
 |Symmetric combination: unchanged by all symmetry operations
 |}
-सममित संयोजन (जिसे बॉन्डिंग ऑर्बिटल कहा जाता है) आधार ऑर्बिटल्स की तुलना में ऊर्जा में कम है, और एंटीसिमेट्रिक संयोजन ([[ प्रतिरक्षी ]] ऑर्बिटल कहा जाता है) अधिक है। क्योंकि एच<sub>2</sub> अणु में दो इलेक्ट्रॉन होते हैं, वे दोनों बंधन कक्ष में जा सकते हैं, जिससे प्रणाली दो मुक्त हाइड्रोजन परमाणुओं की तुलना में कम ऊर्जा (इसलिए अधिक स्थिर) हो जाती है। इसे [[सहसंयोजक बंधन]] कहा जाता है। [[अनुबंध आदेश]], बॉन्डिंग इलेक्ट्रॉनों की संख्या घटा एंटीबॉडी इलेक्ट्रॉनों की संख्या के बराबर है, जिसे 2 से विभाजित किया गया है। इस उदाहरण में, बॉन्डिंग ऑर्बिटल में 2 इलेक्ट्रॉन हैं और एंटीबॉन्डिंग ऑर्बिटल में कोई भी नहीं है; बंधन क्रम 1 है, और दो हाइड्रोजन परमाणुओं के बीच एक एकल बंधन है।{{cn|date=June 2022}}
+सममित संयोजन (जिसे बॉन्डिंग ऑर्बिटल कहा जाता है) आधार ऑर्बिटल्स की तुलना में ऊर्जा में कम है, और एंटीसिमेट्रिक संयोजन ([[ प्रतिरक्षी | प्रतिरक्षी]] ऑर्बिटल कहा जाता है) अधिक है। क्योंकि एच<sub>2</sub> अणु में दो इलेक्ट्रॉन होते हैं, वे दोनों बंधन कक्ष में जा सकते हैं, जिससे प्रणाली दो मुक्त हाइड्रोजन परमाणुओं की तुलना में कम ऊर्जा (इसलिए अधिक स्थिर) हो जाती है। इसे [[सहसंयोजक बंधन]] कहा जाता है। [[अनुबंध आदेश]], बॉन्डिंग इलेक्ट्रॉनों की संख्या घटा एंटीबॉडी इलेक्ट्रॉनों की संख्या के बराबर है, जिसे 2 से विभाजित किया गया है। इस उदाहरण में, बॉन्डिंग ऑर्बिटल में 2 इलेक्ट्रॉन हैं और एंटीबॉन्डिंग ऑर्बिटल में कोई भी नहीं है; बंधन क्रम 1 है, और दो हाइड्रोजन परमाणुओं के बीच एकल बंधन है।
 ====वह<sub>2</sub>====
-दूसरी ओर, He के काल्पनिक अणु पर विचार करें<sub>2</sub> He' और He लेबल वाले परमाणुओं के साथ। जैसा कि एच के साथ है<sub>2</sub>, सबसे कम ऊर्जा वाले परमाणु ऑर्बिटल्स 1s' और 1s हैं, और अणु की समरूपता के अनुसार परिवर्तित नहीं होते हैं, जबकि समरूपता अनुकूलित परमाणु ऑर्बिटल्स करते हैं। सममित संयोजन - बॉन्डिंग ऑर्बिटल - आधार ऑर्बिटल्स की तुलना में ऊर्जा में कम है, और एंटीसिमेट्रिक संयोजन - एंटीबॉन्डिंग ऑर्बिटल - अधिक है। एच के विपरीत<sub>2</sub>, दो वैलेंस इलेक्ट्रॉनों के साथ, वह<sub>2</sub> इसकी तटस्थ जमीनी अवस्था में चार हैं। दो इलेक्ट्रॉन निम्न-ऊर्जा बंधन कक्षक, σ को भरते हैं<sub>g</sub>(1s), जबकि शेष दो उच्च-ऊर्जा प्रतिरक्षी कक्षक, σ को भरते हैं<sub>u</sub>*(1s). इस प्रकार, अणु के चारों ओर परिणामी इलेक्ट्रॉन घनत्व दो परमाणुओं के बीच बंधन के गठन का समर्थन नहीं करता है; परमाणुओं को एक साथ बांधे रखने वाले स्थिर बंधन के बिना, अणु के अस्तित्व की उम्मीद नहीं की जा सकती। इसे देखने का दूसरा तरीका यह है कि दो बंधनकारी इलेक्ट्रॉन और दो प्रतिरक्षी इलेक्ट्रॉन हैं; इसलिए, बंधन क्रम 0 है और कोई बंधन मौजूद नहीं है (अणु में वान डेर वाल्स क्षमता द्वारा समर्थित एक बाध्य अवस्था है)।{{citation needed|date=January 2014}}
+दूसरी ओर, He के काल्पनिक अणु पर विचार करें<sub>2</sub> He' और He लेबल वाले परमाणुओं के साथ। जैसा कि एच के साथ है<sub>2</sub>, सबसे कम ऊर्जा वाले परमाणु ऑर्बिटल्स 1s' और 1s हैं, और अणु की समरूपता के अनुसार परिवर्तित नहीं होते हैं, जबकि समरूपता अनुकूलित परमाणु ऑर्बिटल्स करते हैं। सममित संयोजन - बॉन्डिंग ऑर्बिटल - आधार ऑर्बिटल्स की तुलना में ऊर्जा में कम है, और एंटीसिमेट्रिक संयोजन - एंटीबॉन्डिंग ऑर्बिटल - अधिक है। एच के विपरीत<sub>2</sub>, दो वैलेंस इलेक्ट्रॉनों के साथ, वह<sub>2</sub> इसकी तटस्थ जमीनी अवस्था में चार हैं। दो इलेक्ट्रॉन निम्न-ऊर्जा बंधन कक्षक, σ को भरते हैं<sub>g</sub>(1s), जबकि शेष दो उच्च-ऊर्जा प्रतिरक्षी कक्षक, σ को भरते हैं<sub>u</sub>*(1s). इस प्रकार, अणु के चारों ओर परिणामी इलेक्ट्रॉन घनत्व दो परमाणुओं के बीच बंधन के गठन का समर्थन नहीं करता है; परमाणुओं को साथ बांधे रखने वाले स्थिर बंधन के बिना, अणु के अस्तित्व की उम्मीद नहीं की जा सकती। इसे देखने का दूसरा तरीका यह है कि दो बंधनकारी इलेक्ट्रॉन और दो प्रतिरक्षी इलेक्ट्रॉन हैं; इसलिए, बंधन क्रम 0 है और कोई बंधन मौजूद नहीं है (अणु में वान डेर वाल्स क्षमता द्वारा समर्थित बाध्य अवस्था है)।
 ====वह<sub>2</sub>====
@@ Line 171: / Line 171: @@
 ====उत्कृष्ट गैसें====
-He के एक काल्पनिक अणु पर विचार करना<sub>2</sub>, चूँकि परमाणु कक्षकों का आधार समुच्चय H के मामले जैसा ही है<sub>2</sub>, हम पाते हैं कि बॉन्डिंग और एंटीबॉन्डिंग ऑर्बिटल्स दोनों भरे हुए हैं, इसलिए जोड़ी को कोई ऊर्जा लाभ नहीं है। HeH को थोड़ा ऊर्जा लाभ होगा, लेकिन H जितना नहीं<sub>2</sub> + 2 वह, इसलिए अणु बहुत अस्थिर है और हाइड्रोजन और हीलियम में विघटित होने से पहले केवल कुछ समय के लिए ही मौजूद रहता है। सामान्य तौर पर, हम पाते हैं कि हे जैसे परमाणु जिनमें पूर्ण ऊर्जा कोश होते हैं वे शायद ही कभी अन्य परमाणुओं के साथ बंधते हैं। अल्पकालिक [[वैन डेर वाल्स बॉन्डिंग]] को छोड़कर, बहुत कम [[उत्कृष्ट गैस यौगिक]] ज्ञात हैं।{{cn|date=June 2022}}
+He के काल्पनिक अणु पर विचार करना<sub>2</sub>, चूँकि परमाणु कक्षकों का आधार समुच्चय H के मामले जैसा ही है<sub>2</sub>, हम पाते हैं कि बॉन्डिंग और एंटीबॉन्डिंग ऑर्बिटल्स दोनों भरे हुए हैं, इसलिए जोड़ी को कोई ऊर्जा लाभ नहीं है। HeH को थोड़ा ऊर्जा लाभ होगा, लेकिन H जितना नहीं<sub>2</sub> + 2 वह, इसलिए अणु बहुत अस्थिर है और हाइड्रोजन और हीलियम में विघटित होने से पहले केवल कुछ समय के लिए ही मौजूद रहता है। सामान्य तौर पर, हम पाते हैं कि हे जैसे परमाणु जिनमें पूर्ण ऊर्जा कोश होते हैं वे शायद ही कभी अन्य परमाणुओं के साथ बंधते हैं। अल्पकालिक [[वैन डेर वाल्स बॉन्डिंग]] को छोड़कर, बहुत कम [[उत्कृष्ट गैस यौगिक]] ज्ञात हैं।
 ===हेटेरोन्यूक्लियर डायटोमिक्स===
-जबकि होमोन्यूक्लियर डायटोमिक अणुओं के लिए एमओ में प्रत्येक परस्पर क्रिया करने वाले परमाणु कक्षक का समान योगदान होता है, हेटेरोन्यूक्लियर डायटोमिक अणुओं के लिए एमओ में अलग-अलग परमाणु कक्षीय योगदान होता है। हेटेरोन्यूक्लियर डायटोमिक्स में बॉन्डिंग या एंटीबॉन्डिंग ऑर्बिटल्स का उत्पादन करने के लिए ऑर्बिटल इंटरैक्शन तब होता है, जब परमाणु ऑर्बिटल्स के बीच पर्याप्त ओवरलैप होता है, जैसा कि उनकी समरूपता और ऑर्बिटल ऊर्जा में समानता से निर्धारित होता है।{{cn|date=June 2022}}
+जबकि होमोन्यूक्लियर डायटोमिक अणुओं के लिए एमओ में प्रत्येक परस्पर क्रिया करने वाले परमाणु कक्षक का समान योगदान होता है, हेटेरोन्यूक्लियर डायटोमिक अणुओं के लिए एमओ में अलग-अलग परमाणु कक्षीय योगदान होता है। हेटेरोन्यूक्लियर डायटोमिक्स में बॉन्डिंग या एंटीबॉन्डिंग ऑर्बिटल्स का उत्पादन करने के लिए ऑर्बिटल इंटरैक्शन तब होता है, जब परमाणु ऑर्बिटल्स के बीच पर्याप्त ओवरलैप होता है, जैसा कि उनकी समरूपता और ऑर्बिटल ऊर्जा में समानता से निर्धारित होता है।
 ====एचएफ====
-[[ हाइड्रोजिन फ्लोराइड ]] में एच 1 एस और एफ 2 एस ऑर्बिटल्स के बीच एचएफ ओवरलैप को समरूपता द्वारा अनुमति दी जाती है लेकिन दो परमाणु ऑर्बिटल्स के बीच ऊर्जा में अंतर उन्हें आणविक ऑर्बिटल बनाने के लिए बातचीत करने से रोकता है। H 1s और F 2p के बीच ओवरलैप<sub>z</sub> ऑर्बिटल्स में भी समरूपता की अनुमति है, और इन दो परमाणु ऑर्बिटल्स में थोड़ी ऊर्जा पृथक्करण है। इस प्रकार, वे परस्पर क्रिया करते हैं, जिससे σ और σ* MOs और 1 के बंधन क्रम के साथ एक अणु का निर्माण होता है। चूंकि HF एक गैर-सेंट्रोसिमेट्रिक अणु है, समरूपता लेबल g और u इसके आणविक कक्षाओं पर लागू नहीं होते हैं।<ref>Catherine E. Housecroft, Alan G, Sharpe, Inorganic Chemistry, Pearson Prentice Hall; 2nd Edition, 2005, {{ISBN|0130-39913-2}}, p. 41-43.</ref>
+[[ हाइड्रोजिन फ्लोराइड | हाइड्रोजिन फ्लोराइड]] में एच 1 एस और एफ 2 एस ऑर्बिटल्स के बीच एचएफ ओवरलैप को समरूपता द्वारा अनुमति दी जाती है लेकिन दो परमाणु ऑर्बिटल्स के बीच ऊर्जा में अंतर उन्हें आणविक ऑर्बिटल बनाने के लिए बातचीत करने से रोकता है। H 1s और F 2p के बीच ओवरलैप<sub>z</sub> ऑर्बिटल्स में भी समरूपता की अनुमति है, और इन दो परमाणु ऑर्बिटल्स में थोड़ी ऊर्जा पृथक्करण है। इस प्रकार, वे परस्पर क्रिया करते हैं, जिससे σ और σ* MOs और 1 के बंधन क्रम के साथ अणु का निर्माण होता है। चूंकि HF गैर-सेंट्रोसिमेट्रिक अणु है, समरूपता लेबल g और u इसके आणविक कक्षाओं पर लागू नहीं होते हैं।<ref>Catherine E. Housecroft, Alan G, Sharpe, Inorganic Chemistry, Pearson Prentice Hall; 2nd Edition, 2005, {{ISBN|0130-39913-2}}, p. 41-43.</ref>
 ==मात्रात्मक दृष्टिकोण==
-आणविक ऊर्जा स्तरों के लिए मात्रात्मक मान प्राप्त करने के लिए, किसी को ऐसे आणविक ऑर्बिटल्स की आवश्यकता होती है जो कॉन्फ़िगरेशन इंटरैक्शन (सीआई) विस्तार [[पूर्ण कॉन्फ़िगरेशन इंटरैक्शन]] सीमा की ओर तेजी से परिवर्तित हो। ऐसे कार्यों को प्राप्त करने की सबसे आम विधि हार्ट्री-फॉक विधि है, जो आणविक कक्षाओं को [[फॉक ऑपरेटर]] के [[eigenfunction]] के रूप में व्यक्त करती है। आम तौर पर परमाणु नाभिक पर केंद्रित गाऊसी कार्यों के रैखिक संयोजन के रूप में आणविक कक्षाओं का विस्तार करके इस समस्या को हल किया जाता है (परमाणु कक्षाओं का रैखिक संयोजन आणविक कक्षीय विधि और [[आधार सेट (रसायन विज्ञान)]] देखें)। इन रैखिक संयोजनों के गुणांकों के लिए समीकरण एक सामान्यीकृत [[eigenvalue]] समीकरण है जिसे [[रूथान समीकरण]] के रूप में जाना जाता है, जो वास्तव में हार्ट्री-फॉक समीकरण का एक विशेष प्रतिनिधित्व है। ऐसे कई कार्यक्रम हैं जिनमें [[स्पार्टन (रसायन विज्ञान सॉफ्टवेयर)]] सहित एमओ की क्वांटम रासायनिक गणना की जा सकती है।{{cn|date=June 2022}}
+आणविक ऊर्जा स्तरों के लिए मात्रात्मक मान प्राप्त करने के लिए, किसी को ऐसे आणविक ऑर्बिटल्स की आवश्यकता होती है जो कॉन्फ़िगरेशन इंटरैक्शन (सीआई) विस्तार [[पूर्ण कॉन्फ़िगरेशन इंटरैक्शन]] सीमा की ओर तेजी से परिवर्तित हो। ऐसे कार्यों को प्राप्त करने की सबसे आम विधि हार्ट्री-फॉक विधि है, जो आणविक कक्षाओं को [[फॉक ऑपरेटर]] के [[eigenfunction]] के रूप में व्यक्त करती है। आम तौर पर परमाणु नाभिक पर केंद्रित गाऊसी कार्यों के रैखिक संयोजन के रूप में आणविक कक्षाओं का विस्तार करके इस समस्या को हल किया जाता है (परमाणु कक्षाओं का रैखिक संयोजन आणविक कक्षीय विधि और [[आधार सेट (रसायन विज्ञान)]] देखें)। इन रैखिक संयोजनों के गुणांकों के लिए समीकरण सामान्यीकृत [[eigenvalue]] समीकरण है जिसे [[रूथान समीकरण]] के रूप में जाना जाता है, जो वास्तव में हार्ट्री-फॉक समीकरण का विशेष प्रतिनिधित्व है। ऐसे कई कार्यक्रम हैं जिनमें [[स्पार्टन (रसायन विज्ञान सॉफ्टवेयर)]] सहित एमओ की क्वांटम रासायनिक गणना की जा सकती है।
-सरल खाते अक्सर सुझाव देते हैं कि प्रयोगात्मक आणविक कक्षीय ऊर्जा वैलेंस ऑर्बिटल्स के लिए [[पराबैंगनी फोटोइलेक्ट्रॉन स्पेक्ट्रोस्कोपी]] और कोर ऑर्बिटल्स के लिए [[एक्स - रे फ़ोटोइलैक्ट्रॉन स्पेक्ट्रोस्कोपी]] के तरीकों से प्राप्त की जा सकती है। हालाँकि, यह गलत है क्योंकि ये प्रयोग आयनीकरण ऊर्जा को मापते हैं, अणु और एक इलेक्ट्रॉन को हटाने के परिणामस्वरूप आयनों में से एक के बीच ऊर्जा में अंतर। कूपमैन्स प्रमेय द्वारा आयनीकरण ऊर्जाएँ लगभग कक्षीय ऊर्जाओं से जुड़ी होती हैं। जबकि कुछ अणुओं के लिए इन दोनों मूल्यों के बीच समझौता करीब हो सकता है, अन्य मामलों में यह बहुत खराब हो सकता है।{{cn|date=June 2022}}
+सरल खाते अक्सर सुझाव देते हैं कि प्रयोगात्मक आणविक कक्षीय ऊर्जा वैलेंस ऑर्बिटल्स के लिए [[पराबैंगनी फोटोइलेक्ट्रॉन स्पेक्ट्रोस्कोपी]] और कोर ऑर्बिटल्स के लिए [[एक्स - रे फ़ोटोइलैक्ट्रॉन स्पेक्ट्रोस्कोपी]] के तरीकों से प्राप्त की जा सकती है। हालाँकि, यह गलत है क्योंकि ये प्रयोग आयनीकरण ऊर्जा को मापते हैं, अणु और इलेक्ट्रॉन को हटाने के परिणामस्वरूप आयनों में से के बीच ऊर्जा में अंतर। कूपमैन्स प्रमेय द्वारा आयनीकरण ऊर्जाएँ लगभग कक्षीय ऊर्जाओं से जुड़ी होती हैं। जबकि कुछ अणुओं के लिए इन दोनों मूल्यों के बीच समझौता करीब हो सकता है, अन्य मामलों में यह बहुत खराब हो सकता है।
 ==टिप्पणियाँ==
@@ Line 193: / Line 193: @@
 {{Wikiquote}}
-{{Chemical bonding theory}}
-{{Authority control}}
 [[Category: आणविक भौतिकी]] [[Category: क्वांटम रसायन शास्त्र]] [[Category: सैद्धांतिक रसायन शास्त्र]] [[Category: कम्प्यूटेशनल रसायन शास्त्र]] [[Category: रासायनिक संबंध]]

Anonymous

Search

आणविक कक्षक: Difference between revisions

Namespaces

More

Page actions

Revision as of 09:33, 11 July 2023

Contents

अवलोकन

आणविक कक्षकों का निर्माण