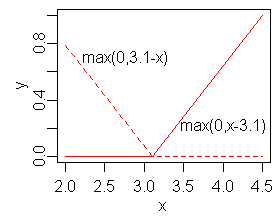बहुभिन्नरूपी अनुकूली प्रतिगमन तख़्ता: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Non-parametric regression technique}} | {{Short description|Non-parametric regression technique}} | ||
आंकड़ों में, बहुभिन्नरूपी अनुकूली प्रतिगमन स्प्लिन ( | आंकड़ों में, '''बहुभिन्नरूपी अनुकूली प्रतिगमन स्प्लिन''' (मार्स) 1991 में जेरोम एच. फ्रीडमैन द्वारा प्रस्तुत [[प्रतिगमन विश्लेषण]] का रूप है।<ref>{{Cite journal | last1 = Friedman | first1 = J. H. | doi = 10.1214/aos/1176347963 | title = बहुभिन्नरूपी अनुकूली प्रतिगमन स्प्लिंस| journal = The Annals of Statistics | volume = 19 | issue = 1 | pages = 1–67 | year = 1991 |mr=1091842 | zbl = 0765.62064 | jstor = 2241837| citeseerx = 10.1.1.382.970 }}</ref> यह [[गैर-पैरामीट्रिक प्रतिगमन|अपैरामीट्रिक प्रतिगमन]] तकनीक है और इसे [[रैखिक मॉडल]] के विस्तार के रूप में देखा जा सकता है जो स्वचालित रूप से चर के मध्य अरैखिकता और इंटरैक्शन को मॉडल करता है। | ||
मार्स सैलफोर्ड प्रणाली द्वारा ट्रेडमार्क और लाइसेंसीकृत है। ट्रेडमार्क उल्लंघनों से बचने के लिए, मार्स के कई विवृत-सोर्स कार्यान्वयनों को भूमि कहा जाता है।<ref>[https://cran.r-project.org/web/packages/earth/index.html CRAN Package earth]</ref><ref>[http://orange.biolab.si/blog/2011/12/20/earth-multivariate-adaptive-regression-splines/ Earth – Multivariate adaptive regression splines in Orange (Python machine learning library)]</ref> | |||
== | == आधार == | ||
यह खंड कुछ उदाहरणों का उपयोग करके मंगल ग्रह का परिचय देता है। हम डेटा के | यह खंड कुछ उदाहरणों का उपयोग करके मंगल ग्रह का परिचय देता है। हम डेटा के सेट से प्रारंभ करते हैं: इनपुट चर x का मैट्रिक्स, और देखी गई प्रतिक्रियाओं y का वेक्टर, x में प्रत्येक पंक्ति के लिए प्रतिक्रिया के साथ है। उदाहरण के लिए, डेटा हो सकता है: | ||
{| | {| | ||
| Line 20: | Line 20: | ||
| 20.6 || 77.0 | | 20.6 || 77.0 | ||
|} | |} | ||
यहां केवल | यहां केवल [[आश्रित और स्वतंत्र चर]] है, इसलिए x मैट्रिक्स केवल कॉलम है। इन मापों को देखते हुए, हम मॉडल बनाना चाहेंगे जो किसी दिए गए x के लिए अपेक्षित y की भविष्यवाणी करता है। | ||
[[File:Friedmans mars linear model.png|frame|right|रेखीय मॉडल]]उपरोक्त डेटा के लिए | [[File:Friedmans mars linear model.png|frame|right|रेखीय मॉडल]]उपरोक्त डेटा के लिए रैखिक मॉडल है: | ||
: <math> | : <math> | ||
\widehat{y} = -37 + 5.1 x | \widehat{y} = -37 + 5.1 x | ||
</math> | </math> | ||
हैट <math>\widehat{y}</math> दर्शाता है कि <math>\widehat{y}</math> डेटा से अनुमान लगाया गया है। दाईं ओर का चित्र इस फलन का प्लॉट दिखाता है: पूर्वानुमान बताने वाली पंक्ति <math>\widehat{y}</math> के प्रति x, y के मूल मान को लाल बिंदुओं के रूप में दिखाया गया है। | |||
x के | x के शीर्ष पर डेटा प्रदर्शित करता है कि y और x के मध्य संबंध अरैखिक हो सकता है (x के निम्न और उच्च मूल्यों पर प्रतिगमन रेखा के सापेक्ष लाल बिंदुओं को देखें)। इस प्रकार अरैखिकताओं को ध्यान में रखते हुए स्वचालित रूप से मॉडल बनाने के लिए मार्स की ओर संकेत करते हैं। मार्स सॉफ़्टवेयर दिए गए x और y से निम्नानुसार मॉडल बनाता है: | ||
: <math> | : <math> | ||
| Line 40: | Line 39: | ||
</math> | </math> | ||
[[File:Friedmans mars simple model.png|frame|right|समान डेटा का सरल | [[File:Friedmans mars simple model.png|frame|right|समान डेटा का सरल मार्स मॉडल]]दाईं ओर का चित्र इस फलन का प्लॉट दिखाता है: पूर्वानुमानित <math>\widehat{y}</math> के प्रति x, y के मूल मानों को एक बार फिर लाल बिंदुओं के रूप में दिखाया गया है। पूर्वानुमानित प्रतिक्रिया अब मूल y मानों के लिए उत्तम अनुकूल है। | ||
अरैखिकता को ध्यान में रखने के लिए मार्स ने स्वचालित रूप से अनुमानित y में घुमाव उत्पन्न किया है। किंक का निर्माण हिंज कार्यों द्वारा होता है। हिंज फलन से प्रारंभ होने वाले भाव <math>\max</math> (जहाँ <math>\max(a,b)</math> है <math>a</math> यदि <math>a > b</math>, अन्य <math>b</math>) हिंज फलन का नीचे अधिक विस्तार से वर्णन किया गया है। | |||
इस सरल उदाहरण में, हम प्लॉट से | इस सरल उदाहरण में, हम प्लॉट से सरलता से देख सकते हैं कि y का x के साथ अरैखिक संबंध है (और संभवतः अनुमान लगा सकते हैं कि y, x के वर्ग के साथ परिवर्तित होता रहता है)। चूँकि, सामान्यतः कई आश्रित और स्वतंत्र चर होंगे, y और इन चर के मध्य संबंध अस्पष्ट होगा और प्लॉटिंग द्वारा सरलता से दिखाई नहीं देगा। हम उस अरैखिक संबंध का परिक्षण करने के लिए मार्स का उपयोग कर सकते हैं। | ||
अनेक चरों के साथ | अनेक चरों के साथ मार्स अभिव्यक्ति का उदाहरण है: | ||
: <math> | : <math> | ||
| Line 57: | Line 56: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
[[File:Friedmans mars ozone model.png|frame|right| | [[File:Friedmans mars ozone model.png|frame|right|मार्स मॉडल में परिवर्तनीय अंतःक्रिया]]यह अभिव्यक्ति वायु प्रदूषण (ओजोन स्तर) को तापमान और कुछ अन्य चर के आधार पर दर्शाती है। ध्यान दें कि सूत्र में अंतिम पद (अंतिम पंक्ति पर) के मध्य परस्पर क्रिया <math>\mathrm{wind} </math> और <math>\mathrm{vis}</math> सम्मिलित है। | ||
उत्तम प्लॉट पर दिए गए आंकड़े की भविष्यवाणी की गई है <math>\mathrm{ozone}</math> जैसा <math>\mathrm{wind}</math> और <math>\mathrm{vis}</math> भिन्न-भिन्न होते हैं, अन्य चर उनके मध्य मानों पर निश्चित होते हैं। यह आंकड़ा दर्शाता है कि वायु ओजोन स्तर को तब तक प्रभावित नहीं करती जब तक दृश्यता कम न हो। हम देखते हैं कि मार्स कार्यों के संयोजन से अधिक प्रतिगमन सतहों का निर्माण कर सकता है। | |||
उपरोक्त अभिव्यक्ति प्राप्त करने के लिए, | उपरोक्त अभिव्यक्ति प्राप्त करने के लिए, मार्स मॉडल निर्माण प्रक्रिया स्वचालित रूप से चयन करती है कि कौन से चर का उपयोग करना है (कुछ चर महत्वपूर्ण हैं, अन्य नहीं), कार्यों में किंक की स्थिति, और कार्यों को कैसे संयोजित किया जाता है। | ||
== मंगल मॉडल == | == मंगल ग्रह मॉडल == | ||
मार्स फॉर्म के मॉडल बनाता है: | |||
: <math>\widehat{f}(x) = \sum_{i=1}^k c_i B_i(x). </math> | : <math>\widehat{f}(x) = \sum_{i=1}^k c_i B_i(x). </math> | ||
मॉडल आधार कार्यों का | मॉडल आधार कार्यों का भारित योग <math>B_i(x)</math> है प्रत्येक <math>c_i</math> स्थिर गुणांक है, उदाहरण के लिए, उपरोक्त ओजोन के सूत्र में प्रत्येक पंक्ति उसके गुणांक से गुणा किया गया [[आधार कार्य]] है। | ||
<math>B_i(x)</math> | |||
प्रत्येक <math>c_i</math> | |||
उदाहरण के लिए, उपरोक्त ओजोन के सूत्र में प्रत्येक पंक्ति [[आधार कार्य]] | |||
प्रत्येक आधार कार्य <math>B_i(x)</math> निम्नलिखित तीन रूपों में से | प्रत्येक आधार कार्य <math>B_i(x)</math> निम्नलिखित तीन रूपों में से प्राप्त करता है: | ||
1) | 1) अचर 1 ऐसा पद है, अंतःखंड उपरोक्त ओजोन सूत्र में, अवरोधन पद 5.2 है। | ||
उपरोक्त ओजोन सूत्र में, अवरोधन पद 5.2 है। | |||
2) | 2) कार्य फलन का ऐसा रूप होता है <math> \max(0, x - \text{constant}) </math> या <math> \max(0, \text{constant} - x) </math> मार्स हिंज फलन के लिए स्वचालित रूप से उन चरों के चर और मानों का चयन करता है। ऐसे आधार कार्यों के उदाहरण ओजोन सूत्र की मध्य तीन पंक्तियों में देखे जा सकते हैं। | ||
3) दो या दो से अधिक | 3) दो या दो से अधिक फलनो का उत्पाद ये आधार फलन दो या दो से अधिक चरों के मध्य अंतःक्रिया को मॉडल कर सकते हैं। उदाहरण ओजोन सूत्र की अंतिम पंक्ति है। | ||
ये आधार | |||
उदाहरण ओजोन सूत्र की अंतिम पंक्ति है। | |||
== | == कार्य के फलन == | ||
[[File:Friedmans mars hinge functions.png|frame|right|काज की प्रतिबिंबित जोड़ी x=3.1 पर गाँठ के साथ कार्य करती है]] | [[File:Friedmans mars hinge functions.png|frame|right|काज की प्रतिबिंबित जोड़ी x=3.1 पर गाँठ के साथ कार्य करती है]] | ||
{{further|Hinge function}} | {{further|Hinge function}} | ||
मार्स मॉडल का प्रमुख भाग रूप धारण करने वाले हिंज फलन हैं: | |||
: <math>\max(0,x-c)</math> | : <math>\max(0,x-c)</math> | ||
या | या | ||
: <math>\max(0,c-x)</math> | : <math>\max(0,c-x)</math> | ||
जहाँ <math>c</math> स्थिरांक है, जिसे कनॉट कहा जाता है। दाईं ओर का चित्र 3.1 पर गाँठ के साथ कार्य के फलन की प्रतिबिंबित जोड़ी को दर्शाता है। | |||
दाईं ओर का चित्र 3.1 पर | |||
हिंज | हिंज फलन इसकी सीमा के भाग के लिए शून्य है, इसलिए इसका उपयोग डेटा को असंयुक्त क्षेत्रों में विभाजित करने के लिए किया जा सकता है, जिनमें से प्रत्येक को स्वतंत्र रूप से व्यवहार किया जा सकता है। इस प्रकार, उदाहरण के लिए अभिव्यक्ति में कार्य की प्रतिबिंबित जोड़ी कार्य करती है: | ||
: <math> | : <math> | ||
6.1 \max(0, x - 13) | 6.1 \max(0, x - 13) | ||
- 3.1 \max(0, 13 - x) | - 3.1 \max(0, 13 - x) | ||
</math> | </math> | ||
पूर्व अनुभाग में सरल मार्स मॉडल के लिए दिखाया गया भाग रैखिक ग्राफ़ बनाता है। | |||
कोई यह मान सकता है कि हिंज | कोई यह मान सकता है कि हिंज फलन के भाग से रैखिक फलन बनाए जा सकते हैं, किंतु नॉन-लीनियर फलन बनाने के लिए हिंज फलन के साथ गुणा किया जा सकता है। | ||
हिंज | हिंज फलन को [[रैंप समारोह|रैंप फलन]], [[आइस हॉकी स्टिक]], या रेक्टिफायर (तंत्रिका नेटवर्क) फलन भी कहा जाता है। परिवर्तन में अधिकतम इस आलेख में उपयोग किए गए <math>\max</math> नोटेशन में, हिंज फलन को प्रायः <math>[\pm(x_i - c)]_+</math> से दर्शाया जाता है जहाँ <math>[\cdot]_+</math> का तात्पर्य सकारात्मक भाग है। | ||
== मॉडल निर्माण प्रक्रिया == | == मॉडल निर्माण प्रक्रिया == | ||
{{see also|Stepwise regression}} | {{see also|Stepwise regression}} | ||
मार्स दो चरणों में मॉडल बनाता है: आगे और पीछे का मार्ग। यह दो-चरणीय दृष्टिकोण वही है जो [[पुनरावर्ती विभाजन]] वृक्षों द्वारा उपयोग किया जाता है। | |||
आगे और पीछे का मार्ग। | |||
यह दो-चरणीय दृष्टिकोण | |||
[[पुनरावर्ती विभाजन]] | |||
=== फॉरवर्ड पास === | === फॉरवर्ड पास === | ||
मार्स मॉडल से प्रारंभ होता है जिसमें केवल इंटरसेप्ट टर्म होता है (जो प्रतिक्रिया मूल्यों का माध्य है)। | |||
(जो प्रतिक्रिया मूल्यों का माध्य है)। | |||
मार्स फिर मॉडल में जोड़े में आधार फलन को बार-बार जोड़ता है। प्रत्येक चरण में यह आधार फलनों की जोड़ी का शोध करता है जो वर्गों के योग में अवशिष्ट त्रुटि में अधिकतम कमी देता है (यह [[लालची एल्गोरिदम|ग्रेडी एल्गोरिदम]] है)। जोड़ी में दो आधार फलन समान हैं, अतिरिक्त इसके कि प्रत्येक फलन के लिए मिरर किए गए हिंज फलन का भिन्न पक्ष उपयोग किया जाता है। प्रत्येक नए आधार फलन में मॉडल में पूर्व से ही शब्द सम्मिलित होता है (जो संभवतः इंटरसेप्ट शब्द हो सकता है) नए हिंज फलन द्वारा गुणा किया जाता है। हिंज फलन को चर और कनॉट द्वारा परिभाषित किया जाता है, इसलिए नया आधार फलन जोड़ने के लिए, मार्स को निम्नलिखित के सभी संयोजनों का परिक्षण करना होगा: | |||
1) मौजूदा शब्द (इस संदर्भ में मूल शब्द कहे जाते हैं) | 1) मौजूदा शब्द (इस संदर्भ में मूल शब्द कहे जाते हैं) | ||
2) सभी चर (नए आधार | 2) सभी चर (नए आधार फलन के लिए का चयन करने के लिए) | ||
3) प्रत्येक चर के सभी मान (नए काज | 3) प्रत्येक चर के सभी मान (नए काज फलन की गाँठ के लिए)। | ||
प्रत्येक पद के गुणांक की गणना करने के लिए | प्रत्येक पद के गुणांक की गणना करने के लिए मार्स पदों पर रेखीय प्रतिगमन लागू करता है। | ||
शब्दों को जोड़ने की यह प्रक्रिया तब तक जारी रहती है जब तक कि शेष त्रुटि में परिवर्तन जारी रखने के लिए बहुत छोटा न हो या जब तक शब्दों की अधिकतम संख्या न हो जाए। मॉडल निर्माण | शब्दों को जोड़ने की यह प्रक्रिया तब तक जारी रहती है जब तक कि शेष त्रुटि में परिवर्तन जारी रखने के लिए बहुत छोटा न हो या जब तक शब्दों की अधिकतम संख्या न हो जाए। मॉडल निर्माण प्रारंभ होने से पहले उपयोगकर्ता द्वारा शर्तों की अधिकतम संख्या निर्दिष्ट की जाती है। | ||
प्रत्येक चरण पर | प्रत्येक चरण पर परिक्षण [[ पाशविक बल खोज | पाशविक बल परिक्षण]] |ब्रूट-फोर्स फैशन में की जाती है, किंतु मार्स का प्रमुख पहलू यह है कि हिंज कार्यों की प्रकृति के कारण तेजी से न्यूनतम-वर्ग अद्यतन तकनीक का उपयोग करके परिक्षण अपेक्षाकृत तेज़ी से की जा सकती है। दरअसल, परिक्षण बिल्कुल क्रूर बल नहीं है. परिक्षण को [[ heuristics ]] के साथ तेज किया जा सकता है जो प्रत्येक चरण पर विचार करने के लिए मूल शब्दों की संख्या को कम कर देता है (फास्ट मार्स)<ref>[[Friedman, J. H.]] (1993) ''Fast MARS'', Stanford University Department of Statistics, Technical Report 110</ref>). | ||
=== पिछड़ा पास === | === पिछड़ा पास === | ||
फॉरवर्ड पास आमतौर पर [[ ओवरफ़िट ]] मॉडल बनाता है। ( ओवरफिट मॉडल मॉडल बनाने के लिए उपयोग किए गए डेटा के लिए अच्छी तरह से फिट होता है | फॉरवर्ड पास आमतौर पर [[ ओवरफ़िट ]] मॉडल बनाता है। ( ओवरफिट मॉडल मॉडल बनाने के लिए उपयोग किए गए डेटा के लिए अच्छी तरह से फिट होता है किंतु नए डेटा के लिए अच्छी तरह से सामान्यीकृत नहीं होगा।) उत्तम सामान्यीकरण क्षमता के साथ मॉडल बनाने के लिए, बैकवर्ड पास मॉडल को काटता है। यह - करके शब्दों को हटाता है, प्रत्येक चरण में सबसे कम प्रभावी शब्द को हटाता है जब तक कि उसे सबसे अच्छा सबमॉडल नहीं मिल जाता। मॉडल उपसमुच्चय की तुलना नीचे वर्णित सामान्यीकृत क्रॉस सत्यापन (जीसीवी) मानदंड का उपयोग करके की जाती है। | ||
फॉरवर्ड पास की तुलना में बैकवर्ड पास का फायदा है: किसी भी चरण पर यह हटाने के लिए कोई भी शब्द चुन सकता है, जबकि प्रत्येक चरण पर फॉरवर्ड पास केवल शब्दों की अगली जोड़ी देख सकता है। | फॉरवर्ड पास की तुलना में बैकवर्ड पास का फायदा है: किसी भी चरण पर यह हटाने के लिए कोई भी शब्द चुन सकता है, जबकि प्रत्येक चरण पर फॉरवर्ड पास केवल शब्दों की अगली जोड़ी देख सकता है। | ||
फॉरवर्ड पास जोड़े में शब्द जोड़ता है, | फॉरवर्ड पास जोड़े में शब्द जोड़ता है, किंतु बैकवर्ड पास आम तौर पर जोड़े के तरफ को हटा देता है और इसलिए अंतिम मॉडल में शब्द प्रायः जोड़े में नहीं देखे जाते हैं। के समीकरण में युग्मित काज देखा जा सकता है <math>\widehat{y}</math> उपरोक्त पहले मंगल उदाहरण में; ओजोन उदाहरण में कोई पूर्ण युग्म नहीं रखा गया है। | ||
==== सामान्यीकृत क्रॉस सत्यापन ==== | ==== सामान्यीकृत क्रॉस सत्यापन ==== | ||
{{further|Cross-validation (statistics)|Model selection}} | {{further|Cross-validation (statistics)|Model selection}} | ||
सबसे अच्छा सबसेट चुनने के लिए मॉडल सबसेट के प्रदर्शन की तुलना करने के लिए बैकवर्ड पास सामान्यीकृत क्रॉस वैलिडेशन (जीसीवी) का उपयोग करता है: जीसीवी के निचले मान | सबसे अच्छा सबसेट चुनने के लिए मॉडल सबसेट के प्रदर्शन की तुलना करने के लिए बैकवर्ड पास सामान्यीकृत क्रॉस वैलिडेशन (जीसीवी) का उपयोग करता है: जीसीवी के निचले मान उत्तम होते हैं। जीसीवी [[नियमितीकरण (मशीन लर्निंग)]] का रूप है: यह मॉडल जटिलता के मुकाबले फिट की अच्छाई का व्यापार करता है। | ||
(हम यह अनुमान लगाना चाहते हैं कि कोई मॉडल नए डेटा पर कितना अच्छा प्रदर्शन करता है, प्रशिक्षण डेटा पर नहीं। ऐसा नया डेटा आमतौर पर मॉडल निर्माण के समय उपलब्ध नहीं होता है, इसलिए इसके बजाय हम नए डेटा पर प्रदर्शन क्या होगा इसका अनुमान लगाने के लिए जीसीवी का उपयोग करते हैं। प्रशिक्षण डेटा पर वर्गों का कच्चा अवशिष्ट योग | [[वर्गों का अवशिष्ट योग]] (RSS) मॉडल की तुलना करने के लिए अपर्याप्त है, क्योंकि | (हम यह अनुमान लगाना चाहते हैं कि कोई मॉडल नए डेटा पर कितना अच्छा प्रदर्शन करता है, प्रशिक्षण डेटा पर नहीं। ऐसा नया डेटा आमतौर पर मॉडल निर्माण के समय उपलब्ध नहीं होता है, इसलिए इसके बजाय हम नए डेटा पर प्रदर्शन क्या होगा इसका अनुमान लगाने के लिए जीसीवी का उपयोग करते हैं। प्रशिक्षण डेटा पर वर्गों का कच्चा अवशिष्ट योग | [[वर्गों का अवशिष्ट योग]] (RSS) मॉडल की तुलना करने के लिए अपर्याप्त है, क्योंकि मार्स शब्द हटा दिए जाने पर RSS हमेशा बढ़ता है। दूसरे शब्दों में, यदि RSS का उपयोग मॉडलों की तुलना करने के लिए किया जाता था, तो बैकवर्ड पास हमेशा सबसे बड़े मॉडल को चुनेगा - किंतु सबसे बड़े मॉडल में आमतौर पर सबसे अच्छा सामान्यीकरण प्रदर्शन नहीं होता है।) | ||
जीसीवी का सूत्र है | जीसीवी का सूत्र है | ||
| Line 166: | Line 153: | ||
: (मंगल पदों की संख्या − 1 ) / 2 | : (मंगल पदों की संख्या − 1 ) / 2 | ||
हिंज- | हिंज-फलन गांठों की संख्या है, इसलिए सूत्र गांठों को जोड़ने पर जुर्माना लगाता है। इस प्रकार जीसीवी फॉर्मूला मॉडल के लचीलेपन को ध्यान में रखते हुए प्रशिक्षण आरएसएस को समायोजित (यानी बढ़ाता है) करता है। हम लचीलेपन को दंडित करते हैं क्योंकि जो मॉडल बहुत लचीले हैं वे डेटा की व्यवस्थित संरचना के बजाय डेटा में शोर के विशिष्ट अहसास को मॉडल करेंगे। | ||
सामान्यीकृत क्रॉस-सत्यापन को यह नाम दिया गया है क्योंकि यह त्रुटि का अनुमान लगाने के लिए सूत्र का उपयोग करता है जिसे लीव-वन-आउट सत्यापन द्वारा निर्धारित किया जाएगा। यह सिर्फ अनुमान है | सामान्यीकृत क्रॉस-सत्यापन को यह नाम दिया गया है क्योंकि यह त्रुटि का अनुमान लगाने के लिए सूत्र का उपयोग करता है जिसे लीव-वन-आउट सत्यापन द्वारा निर्धारित किया जाएगा। यह सिर्फ अनुमान है किंतु व्यवहार में अच्छा काम करता है। जीसीवी को क्रेवेन और [[ग्रेस वाहबा]] द्वारा पेश किया गया था और फ्रीडमैन द्वारा मार्स के लिए विस्तारित किया गया था। | ||
===बाधाएँ === | ===बाधाएँ === | ||
| Line 178: | Line 165: | ||
बातचीत की अधिकतम स्वीकार्य डिग्री निर्दिष्ट करके। | बातचीत की अधिकतम स्वीकार्य डिग्री निर्दिष्ट करके। | ||
आम तौर पर केवल या दो डिग्री की बातचीत की अनुमति होती है, | आम तौर पर केवल या दो डिग्री की बातचीत की अनुमति होती है, | ||
किंतु उच्च डिग्री का उपयोग तब किया जा सकता है जब डेटा इसकी गारंटी देता है। | |||
पहले | पहले मार्स उदाहरण में अंतःक्रिया की अधिकतम डिग्री | ||
उपरोक्त है ( | उपरोक्त है (भूमिात् कोई इंटरैक्शन या कोई योगात्मक मॉडल नहीं); | ||
ओजोन उदाहरण में यह दो है। | ओजोन उदाहरण में यह दो है। | ||
| Line 192: | Line 179: | ||
कोई भी प्रतिगमन मॉडलिंग तकनीक सभी स्थितियों के लिए सर्वोत्तम नहीं है। | कोई भी प्रतिगमन मॉडलिंग तकनीक सभी स्थितियों के लिए सर्वोत्तम नहीं है। | ||
नीचे दिए गए दिशानिर्देशों का उद्देश्य मंगल ग्रह के फायदे और नुकसान का विचार देना है। | नीचे दिए गए दिशानिर्देशों का उद्देश्य मंगल ग्रह के फायदे और नुकसान का विचार देना है। | ||
किंतु दिशानिर्देशों के अपवाद होंगे। | |||
मंगल की तुलना पुनरावर्ती विभाजन से करना उपयोगी है और यह नीचे किया गया है। | मंगल की तुलना पुनरावर्ती विभाजन से करना उपयोगी है और यह नीचे किया गया है। | ||
(पुनरावर्ती विभाजन को सामान्यतः प्रतिगमन वृक्ष भी कहा जाता है, | (पुनरावर्ती विभाजन को सामान्यतः प्रतिगमन वृक्ष भी कहा जाता है, | ||
| Line 198: | Line 185: | ||
विवरण के लिए [[ निर्णय वृक्ष सीखना ]] लेख देखें)। | विवरण के लिए [[ निर्णय वृक्ष सीखना ]] लेख देखें)। | ||
* | *मार्स मॉडल रैखिक प्रतिगमन मॉडल की तुलना में अधिक लचीले होते हैं। | ||
* | *मार्स मॉडल समझने और व्याख्या करने में सरल हैं।<ref name=":0">{{Cite book|title=एप्लाइड प्रेडिक्टिव मॉडलिंग|last1=Kuhn|first1=Max|last2=Johnson|first2=Kjell|date=2013|publisher=Springer New York|isbn=9781461468486|location=New York, NY|language=en|doi=10.1007/978-1-4614-6849-3}}</ref> उपरोक्त ओजोन सांद्रता के समीकरण की तुलना, मान लीजिए, प्रशिक्षित [[कृत्रिम तंत्रिका नेटवर्क]] या यादृच्छिक जंगल के अंदरूनी हिस्सों से करें। | ||
* | *मार्स निरंतर और श्रेणीबद्ध डेटा दोनों को संभाल सकता है।<ref>{{cite book | last=Friedman | first=Jerome H. | chapter=Estimating Functions of Mixed Ordinal and Categorical Variables Using Adaptive Splines | author-link=Friedman, J. H.|year=1993|title=सांख्यिकीय डेटा विश्लेषण और मजबूती में नई दिशाएँ|editor=Stephan Morgenthaler |editor2=Elvezio Ronchetti |editor3=Werner Stahel|publisher=Birkhauser}}</ref><ref name="Friedman 1991">{{cite journal | last=Friedman | first=Jerome H. | title=अनुकूली स्प्लाइन का उपयोग करके मिश्रित क्रमसूचक और श्रेणीबद्ध चर के कार्यों का अनुमान लगाना| website=DTIC | date=1991-06-01 | url=https://apps.dtic.mil/sti/citations/ADA590939 | archive-url=https://web.archive.org/web/20220411085148/https://apps.dtic.mil/sti/citations/ADA590939 | url-status=live | archive-date=April 11, 2022 | access-date=2022-04-11}}</ref> मार्स संख्यात्मक डेटा के लिए पुनरावर्ती विभाजन से उत्तम होता है क्योंकि पुनरावर्ती विभाजन द्वारा उपयोग किए जाने वाले टुकड़े-टुकड़े निरंतर विभाजन की तुलना में संख्यात्मक चर के लिए टिका अधिक उपयुक्त होती है। | ||
* | *मार्स मॉडल के निर्माण के लिए प्रायः बहुत कम या कोई डेटा तैयारी की आवश्यकता नहीं होती है।<ref name=":0" />हिंज फलन स्वचालित रूप से इनपुट डेटा को विभाजित करता है, इसलिए आउटलेर्स का प्रभाव निहित होता है। इस संबंध में मार्स पुनरावर्ती विभाजन के समान है जो डेटा को असंयुक्त क्षेत्रों में भी विभाजित करता है, हालांकि भिन्न विधि का उपयोग करता है। (फिर भी, अधिकांश सांख्यिकीय मॉडलिंग तकनीकों की तरह, मार्स मॉडल को प्रशिक्षित करने से पहले ज्ञात आउटलेर्स को हटाने पर विचार किया जाना चाहिए।{{Citation needed|date=March 2019}}) | ||
* | *मार्स (पुनरावर्ती विभाजन की तरह) स्वचालित फ़ीचर चयन करता है (जिसका भूमि है कि यह मॉडल में महत्वपूर्ण चर सम्मिलित करता है और महत्वहीन को बाहर कर देता है)। चूँकि, चयन में कुछ मनमानी हो सकती है, खासकर जब सहसंबद्ध भविष्यवक्ता हों, और यह व्याख्या को प्रभावित कर सकता है<ref name=":0" />*मार्स मॉडल में पूर्वाग्रह-विचरण का अच्छा समझौता होता है। मॉडल अरैखिकता और परिवर्तनीय इंटरैक्शन को मॉडल करने के लिए पर्याप्त लचीले हैं (इस प्रकार मार्स मॉडल में अधिक कम पूर्वाग्रह है), फिर भी मार्स आधार कार्यों का बाधित रूप बहुत अधिक लचीलेपन को रोकता है (इस प्रकार मार्स मॉडल में अधिक कम भिन्नता होती है)। | ||
* | *मार्स अधिक बड़े डेटासेट को संभालने के लिए उपयुक्त है। 100 भविष्यवक्ताओं और 10 के साथ इनपुट मैट्रिक्स से मार्स मॉडल बनाना नियमित मामला है<sup>5</sup>अवलोकन. ऐसा मॉडल 1 गीगाहर्ट्ज मशीन पर लगभग मिनट में बनाया जा सकता है, यह मानते हुए कि मार्स शब्दों की परस्पर क्रिया की अधिकतम डिग्री तक सीमित है (यानी केवल योगात्मक शब्द)। समान 1 गीगाहर्ट्ज़ मशीन पर समान डेटा वाले डिग्री दो मॉडल को अधिक समय लगता है - लगभग 12 मिनट। ध्यान रखें कि यह समय अत्यधिक डेटा पर निर्भर है। पुनरावर्ती विभाजन मार्स की तुलना में बहुत तेज़ है।{{Citation needed|date=March 2019}} | ||
* | *मार्स मॉडल के साथ, किसी भी गैर-पैरामीट्रिक प्रतिगमन की तरह, पैरामीटर आत्मविश्वास अंतराल और मॉडल पर अन्य जांचों की गणना सीधे नहीं की जा सकती (रैखिक प्रतिगमन मॉडल के विपरीत)। क्रॉस-वैलिडेशन (सांख्यिकी)|इसके बजाय मॉडल को मान्य करने के लिए क्रॉस-वैलिडेशन और संबंधित तकनीकों का उपयोग किया जाना चाहिए। | ||
* | *मार्स मॉडल [[बूस्टिंग (मेटा-एल्गोरिदम)]] पेड़ों के समान अच्छे फिट नहीं देते हैं, किंतु इन्हें अधिक तेज़ी से बनाया जा सकता है और ये अधिक व्याख्या योग्य हैं। ( 'व्याख्यात्मक' मॉडल ऐसे रूप में है जो यह स्पष्ट करता है कि प्रत्येक भविष्यवक्ता का प्रभाव क्या है।) | ||
* <code> | * <code>भूमि</code>का>, <code>mda</code>, और <code>polspline</code> कार्यान्वयन भविष्यवक्ताओं में लापता मूल्यों की अनुमति नहीं देता है, किंतु प्रतिगमन पेड़ों (जैसे) के मुफ्त कार्यान्वयन की अनुमति देता है <code>rpart</code> और <code>party</code>) सरोगेट स्प्लिट्स नामक तकनीक का उपयोग करके लापता मानों की अनुमति दें। | ||
* | *मार्स मॉडल शीघ्रता से भविष्यवाणियां कर सकते हैं। भविष्यवाणी फलन को बस मार्स मॉडल सूत्र का मूल्यांकन करना है। इसकी तुलना [[ समर्थन वेक्टर यंत्र ]] के साथ भविष्यवाणी करने से करें, जहां प्रत्येक वेरिएबल को प्रत्येक सपोर्ट वेक्टर के संबंधित तत्व से गुणा करना होता है। यदि कई चर और कई समर्थन वैक्टर हैं तो यह धीमी प्रक्रिया हो सकती है। | ||
*परिणामस्वरूप फिट किया गया | *परिणामस्वरूप फिट किया गया फलन सुचारू नहीं है (टिका के साथ भिन्न-भिन्न नहीं)। | ||
== विस्तार और संबंधित अवधारणाएँ == | == विस्तार और संबंधित अवधारणाएँ == | ||
* [[सामान्यीकृत रैखिक मॉडल]] (जीएलएम) को | * [[सामान्यीकृत रैखिक मॉडल]] (जीएलएम) को मार्स मॉडल के निर्माण के बाद लिंक फलन लागू करके मार्स मॉडल में सम्मिलित किया जा सकता है। इस प्रकार, उदाहरण के लिए, मार्स मॉडल संभावनाओं की भविष्यवाणी करने के लिए [[ संभार तन्त्र परावर्तन ]] को सम्मिलित कर सकते हैं। | ||
* [[अरेखीय प्रतिगमन]]|नॉन-लीनियर रिग्रेशन का उपयोग तब किया जाता है जब | * [[अरेखीय प्रतिगमन]]|नॉन-लीनियर रिग्रेशन का उपयोग तब किया जाता है जब फलन का अंतर्निहित रूप ज्ञात होता है और रिग्रेशन का उपयोग केवल उस फलन के मापदंडों का अनुमान लगाने के लिए किया जाता है। दूसरी ओर, मंगल स्वयं कार्यों का अनुमान लगाता है, यद्यपि कार्यों की प्रकृति पर गंभीर बाधाएं होती हैं। (ये बाधाएँ आवश्यक हैं क्योंकि डेटा से मॉडल की परिक्षण करना विपरीत समस्या है जो मॉडल पर बाधाओं के बिना [[अच्छी तरह से प्रस्तुत समस्या]] नहीं है।) | ||
* पुनरावर्ती विभाजन (आमतौर पर कार्ट कहा जाता है)। | * पुनरावर्ती विभाजन (आमतौर पर कार्ट कहा जाता है)। मार्स को पुनरावर्ती विभाजन के सामान्यीकरण के रूप में देखा जा सकता है जो मॉडल को संख्यात्मक (यानी गैर-श्रेणीबद्ध) डेटा को उत्तम ढंग से संभालने की अनुमति देता है। | ||
* [[सामान्यीकृत योगात्मक मॉडल]]। उपयोगकर्ता के नजरिए से GAM, | * [[सामान्यीकृत योगात्मक मॉडल]]। उपयोगकर्ता के नजरिए से GAM, मार्स के समान हैं, किंतु (ए) मार्स आधार कार्यों के बजाय सुचारू [[स्थानीय प्रतिगमन]] या बहुपद स्पलाइन (गणित) में फिट होते हैं, और (बी) स्वचालित रूप से परिवर्तनीय इंटरैक्शन को मॉडल नहीं करते हैं। GAMs द्वारा आंतरिक रूप से उपयोग की जाने वाली फिटिंग विधि मार्स से बहुत भिन्न है। ऐसे मॉडलों के लिए जिन्हें परिवर्तनीय इंटरैक्शन की स्वचालित परिक्षण की आवश्यकता नहीं होती है, GAMs प्रायः मार्स के साथ अनुकूल प्रतिस्पर्धा करते हैं। | ||
* [[टीएसएमएआरएस]]। टाइम सीरीज़ मार्स वह शब्द है जिसका उपयोग तब किया जाता है जब | * [[टीएसएमएआरएस]]। टाइम सीरीज़ मार्स वह शब्द है जिसका उपयोग तब किया जाता है जब मार्स मॉडल को टाइम सीरीज़ संदर्भ में लागू किया जाता है। आमतौर पर इस सेट अप में भविष्यवक्ता विलंबित समय श्रृंखला मान होते हैं जिसके परिणामस्वरूप ऑटोरेग्रेसिव स्पलाइन मॉडल होते हैं। मूविंग एवरेज स्पलाइन मॉडल को सम्मिलित करने के लिए इन मॉडलों और ्सटेंशनों को टीएसएमएआरएस का उपयोग करके यूनीवेरिएट टाइम सीरीज़ मॉडलिंग और पूर्वानुमान में वर्णित किया गया है: टीएसएमएआरएस का उपयोग करके थ्रेशोल्ड टाइम सीरीज़ ऑटोरेग्रेसिव, मौसमी और मूविंग औसत मॉडल का अध्ययन। | ||
* [[ बायेसियन मंगल ]] (बीएमएआरएस) ही मॉडल फॉर्म का उपयोग करता है, | * [[ बायेसियन मंगल ]] (बीएमएआरएस) ही मॉडल फॉर्म का उपयोग करता है, किंतु बायेसियन दृष्टिकोण का उपयोग करके मॉडल बनाता है। यह विभिन्न इष्टतम मार्स मॉडल पर पहुंच सकता है क्योंकि मॉडल निर्माण का दृष्टिकोण भिन्न है। Bमार्स का परिणाम आम तौर पर मार्स मॉडल के पिछले नमूनों का समूह होता है, जो संभाव्य भविष्यवाणी की अनुमति देता है।<ref>{{cite journal |last1=Denison |first1=D. G. T. |last2=Mallick |first2=B. K. |last3=Smith |first3=A. F. M. |title=बायेसियन मंगल|journal=Statistics and Computing |date=1 December 1998 |volume=8 |issue=4 |pages=337–346 |doi=10.1023/A:1008824606259 |s2cid=12570055 |url=https://link.springer.com/content/pdf/10.1023/A:1008824606259.pdf |language=en |issn=1573-1375}}</ref> | ||
== यह भी देखें == | == यह भी देखें == | ||
| Line 231: | Line 218: | ||
== अग्रिम पठन == | == अग्रिम पठन == | ||
* Hastie T., Tibshirani R., and Friedman J.H. (2009) [http://www-stat.stanford.edu/~tibs/ElemStatLearn ''The Elements of Statistical Learning''], 2nd edition. Springer, {{ISBN|978-0-387-84857-0}} (has a section on | * Hastie T., Tibshirani R., and Friedman J.H. (2009) [http://www-stat.stanford.edu/~tibs/ElemStatLearn ''The Elements of Statistical Learning''], 2nd edition. Springer, {{ISBN|978-0-387-84857-0}} (has a section on मार्स) | ||
* Faraway J. (2005) [http://www.maths.bath.ac.uk/~jjf23 ''Extending the Linear Model with R''], CRC, {{ISBN|978-1-58488-424-8}} (has an example using | * Faraway J. (2005) [http://www.maths.bath.ac.uk/~jjf23 ''Extending the Linear Model with R''], CRC, {{ISBN|978-1-58488-424-8}} (has an example using मार्स with R) | ||
* Heping Zhang and Burton H. Singer (2010) [https://www.amazon.com/Recursive-Partitioning-Applications-Springer-Statistics/dp/1441968237 ''Recursive Partitioning and Applications''], 2nd edition. Springer, {{ISBN|978-1-4419-6823-4}} (has a chapter on | * Heping Zhang and Burton H. Singer (2010) [https://www.amazon.com/Recursive-Partitioning-Applications-Springer-Statistics/dp/1441968237 ''Recursive Partitioning and Applications''], 2nd edition. Springer, {{ISBN|978-1-4419-6823-4}} (has a chapter on मार्स and discusses some tweaks to the algorithm) | ||
* Denison D.G.T., Holmes C.C., Mallick B.K., and Smith A.F.M. (2004) [http://www.stat.tamu.edu/~bmallick/wileybook/book_code.html ''Bayesian Methods for Nonlinear Classification and Regression''], Wiley, {{ISBN|978-0-471-49036-4}} | * Denison D.G.T., Holmes C.C., Mallick B.K., and Smith A.F.M. (2004) [http://www.stat.tamu.edu/~bmallick/wileybook/book_code.html ''Bayesian Methods for Nonlinear Classification and Regression''], Wiley, {{ISBN|978-0-471-49036-4}} | ||
* Berk R.A. (2008) ''Statistical learning from a regression perspective'', Springer, {{ISBN|978-0-387-77500-5}} | * Berk R.A. (2008) ''Statistical learning from a regression perspective'', Springer, {{ISBN|978-0-387-77500-5}} | ||
| Line 239: | Line 226: | ||
== बाहरी संबंध == | == बाहरी संबंध == | ||
Several free and commercial software packages are available for fitting | Several free and commercial software packages are available for fitting मार्स-type models. | ||
; Free software: | ; Free software: | ||
* [[R (programming language)|R]] packages: | * [[R (programming language)|R]] packages: | ||
** <code> | ** <code>भूमि</code> function in the <code>[https://cran.r-project.org/web/packages/earth/index.html भूमि]</code> package | ||
** <code> | ** <code>मार्स</code> function in the <code>[https://cran.r-project.org/web/packages/mda/index.html mda]</code> package | ||
** <code> | ** <code>polyमार्स</code> function in the <code>[https://cran.r-project.org/web/packages/polspline/index.html polspline]</code> package. Not Friedman's मार्स. | ||
** <code>bass</code> function in the <code>[https://cran.r-project.org/web/packages/BASS/index.html BASS]</code> package for Bayesian | ** <code>bass</code> function in the <code>[https://cran.r-project.org/web/packages/BASS/index.html BASS]</code> package for Bayesian मार्स. | ||
* Matlab code: | * Matlab code: | ||
** [http://www.cs.rtu.lv/jekabsons/regression.html ARESLab: Adaptive Regression Splines toolbox for Matlab] | ** [http://www.cs.rtu.lv/jekabsons/regression.html ARESLab: Adaptive Regression Splines toolbox for Matlab] | ||
** [https://web.stat.tamu.edu/~bmallick/wileybook/book_code.html Code] from the book ''Bayesian Methods for Nonlinear Classification and Regression''<ref>{{cite book |last1=Denison |first1=D. G. T. |last2=Holmes |first2=C. C. |last3=Mallick |first3=B. K. |last4=Smith |first4=A. F. M. |title=Bayesian methods for nonlinear classification and regression |date=2002 |publisher=Wiley |location=Chichester, England |isbn=978-0-471-49036-4}}</ref> for Bayesian | ** [https://web.stat.tamu.edu/~bmallick/wileybook/book_code.html Code] from the book ''Bayesian Methods for Nonlinear Classification and Regression''<ref>{{cite book |last1=Denison |first1=D. G. T. |last2=Holmes |first2=C. C. |last3=Mallick |first3=B. K. |last4=Smith |first4=A. F. M. |title=Bayesian methods for nonlinear classification and regression |date=2002 |publisher=Wiley |location=Chichester, England |isbn=978-0-471-49036-4}}</ref> for Bayesian मार्स. | ||
* Python | * Python | ||
** [http://orange.biolab.si/blog/2011/12/20/earth-multivariate-adaptive-regression-splines/ | ** [http://orange.biolab.si/blog/2011/12/20/earth-multivariate-adaptive-regression-splines/ भूमि – Multivariate adaptive regression splines] | ||
** [https://github.com/jcrudy/py-earth/ py- | ** [https://github.com/jcrudy/py-earth/ py-भूमि] | ||
** [https://github.com/lanl/pyBASS pyBASS] for Bayesian | ** [https://github.com/lanl/pyBASS pyBASS] for Bayesian मार्स. | ||
; Commercial software: | ; Commercial software: | ||
* [http://www.salford-systems.com/mars.php | * [http://www.salford-systems.com/mars.php मार्स] from Salford Systems. Based on Friedman's implementation. | ||
* [https://web.archive.org/web/20101203023609/http://www.statsoft.com/products/data-mining-solutions/ STATISTICA Data Miner] from StatSoft | * [https://web.archive.org/web/20101203023609/http://www.statsoft.com/products/data-mining-solutions/ STATISTICA Data Miner] from StatSoft | ||
* [http://support.sas.com/documentation/cdl/en/statug/65328/HTML/default/viewer.htm#statug_adaptivereg_overview.htm ADAPTIVEREG] from SAS. | * [http://support.sas.com/documentation/cdl/en/statug/65328/HTML/default/viewer.htm#statug_adaptivereg_overview.htm ADAPTIVEREG] from SAS. | ||
Revision as of 19:37, 11 July 2023
आंकड़ों में, बहुभिन्नरूपी अनुकूली प्रतिगमन स्प्लिन (मार्स) 1991 में जेरोम एच. फ्रीडमैन द्वारा प्रस्तुत प्रतिगमन विश्लेषण का रूप है।[1] यह अपैरामीट्रिक प्रतिगमन तकनीक है और इसे रैखिक मॉडल के विस्तार के रूप में देखा जा सकता है जो स्वचालित रूप से चर के मध्य अरैखिकता और इंटरैक्शन को मॉडल करता है।
मार्स सैलफोर्ड प्रणाली द्वारा ट्रेडमार्क और लाइसेंसीकृत है। ट्रेडमार्क उल्लंघनों से बचने के लिए, मार्स के कई विवृत-सोर्स कार्यान्वयनों को भूमि कहा जाता है।[2][3]
आधार
यह खंड कुछ उदाहरणों का उपयोग करके मंगल ग्रह का परिचय देता है। हम डेटा के सेट से प्रारंभ करते हैं: इनपुट चर x का मैट्रिक्स, और देखी गई प्रतिक्रियाओं y का वेक्टर, x में प्रत्येक पंक्ति के लिए प्रतिक्रिया के साथ है। उदाहरण के लिए, डेटा हो सकता है:
| x | y |
|---|---|
| 10.5 | 16.4 |
| 10.7 | 18.8 |
| 10.8 | 19.7 |
| ... | ... |
| 20.6 | 77.0 |
यहां केवल आश्रित और स्वतंत्र चर है, इसलिए x मैट्रिक्स केवल कॉलम है। इन मापों को देखते हुए, हम मॉडल बनाना चाहेंगे जो किसी दिए गए x के लिए अपेक्षित y की भविष्यवाणी करता है।
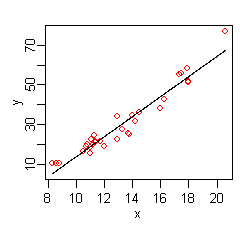
उपरोक्त डेटा के लिए रैखिक मॉडल है:
हैट दर्शाता है कि डेटा से अनुमान लगाया गया है। दाईं ओर का चित्र इस फलन का प्लॉट दिखाता है: पूर्वानुमान बताने वाली पंक्ति के प्रति x, y के मूल मान को लाल बिंदुओं के रूप में दिखाया गया है।
x के शीर्ष पर डेटा प्रदर्शित करता है कि y और x के मध्य संबंध अरैखिक हो सकता है (x के निम्न और उच्च मूल्यों पर प्रतिगमन रेखा के सापेक्ष लाल बिंदुओं को देखें)। इस प्रकार अरैखिकताओं को ध्यान में रखते हुए स्वचालित रूप से मॉडल बनाने के लिए मार्स की ओर संकेत करते हैं। मार्स सॉफ़्टवेयर दिए गए x और y से निम्नानुसार मॉडल बनाता है:
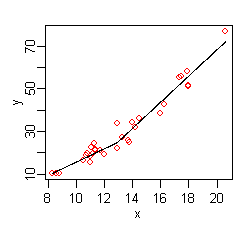
दाईं ओर का चित्र इस फलन का प्लॉट दिखाता है: पूर्वानुमानित के प्रति x, y के मूल मानों को एक बार फिर लाल बिंदुओं के रूप में दिखाया गया है। पूर्वानुमानित प्रतिक्रिया अब मूल y मानों के लिए उत्तम अनुकूल है।
अरैखिकता को ध्यान में रखने के लिए मार्स ने स्वचालित रूप से अनुमानित y में घुमाव उत्पन्न किया है। किंक का निर्माण हिंज कार्यों द्वारा होता है। हिंज फलन से प्रारंभ होने वाले भाव (जहाँ है यदि , अन्य ) हिंज फलन का नीचे अधिक विस्तार से वर्णन किया गया है।
इस सरल उदाहरण में, हम प्लॉट से सरलता से देख सकते हैं कि y का x के साथ अरैखिक संबंध है (और संभवतः अनुमान लगा सकते हैं कि y, x के वर्ग के साथ परिवर्तित होता रहता है)। चूँकि, सामान्यतः कई आश्रित और स्वतंत्र चर होंगे, y और इन चर के मध्य संबंध अस्पष्ट होगा और प्लॉटिंग द्वारा सरलता से दिखाई नहीं देगा। हम उस अरैखिक संबंध का परिक्षण करने के लिए मार्स का उपयोग कर सकते हैं।
अनेक चरों के साथ मार्स अभिव्यक्ति का उदाहरण है:
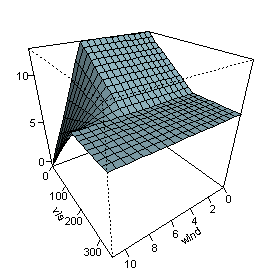
यह अभिव्यक्ति वायु प्रदूषण (ओजोन स्तर) को तापमान और कुछ अन्य चर के आधार पर दर्शाती है। ध्यान दें कि सूत्र में अंतिम पद (अंतिम पंक्ति पर) के मध्य परस्पर क्रिया और सम्मिलित है।
उत्तम प्लॉट पर दिए गए आंकड़े की भविष्यवाणी की गई है जैसा और भिन्न-भिन्न होते हैं, अन्य चर उनके मध्य मानों पर निश्चित होते हैं। यह आंकड़ा दर्शाता है कि वायु ओजोन स्तर को तब तक प्रभावित नहीं करती जब तक दृश्यता कम न हो। हम देखते हैं कि मार्स कार्यों के संयोजन से अधिक प्रतिगमन सतहों का निर्माण कर सकता है।
उपरोक्त अभिव्यक्ति प्राप्त करने के लिए, मार्स मॉडल निर्माण प्रक्रिया स्वचालित रूप से चयन करती है कि कौन से चर का उपयोग करना है (कुछ चर महत्वपूर्ण हैं, अन्य नहीं), कार्यों में किंक की स्थिति, और कार्यों को कैसे संयोजित किया जाता है।
मंगल ग्रह मॉडल
मार्स फॉर्म के मॉडल बनाता है:
मॉडल आधार कार्यों का भारित योग है प्रत्येक स्थिर गुणांक है, उदाहरण के लिए, उपरोक्त ओजोन के सूत्र में प्रत्येक पंक्ति उसके गुणांक से गुणा किया गया आधार कार्य है।
प्रत्येक आधार कार्य निम्नलिखित तीन रूपों में से प्राप्त करता है:
1) अचर 1 ऐसा पद है, अंतःखंड उपरोक्त ओजोन सूत्र में, अवरोधन पद 5.2 है।
2) कार्य फलन का ऐसा रूप होता है या मार्स हिंज फलन के लिए स्वचालित रूप से उन चरों के चर और मानों का चयन करता है। ऐसे आधार कार्यों के उदाहरण ओजोन सूत्र की मध्य तीन पंक्तियों में देखे जा सकते हैं।
3) दो या दो से अधिक फलनो का उत्पाद ये आधार फलन दो या दो से अधिक चरों के मध्य अंतःक्रिया को मॉडल कर सकते हैं। उदाहरण ओजोन सूत्र की अंतिम पंक्ति है।
कार्य के फलन
मार्स मॉडल का प्रमुख भाग रूप धारण करने वाले हिंज फलन हैं:
या
जहाँ स्थिरांक है, जिसे कनॉट कहा जाता है। दाईं ओर का चित्र 3.1 पर गाँठ के साथ कार्य के फलन की प्रतिबिंबित जोड़ी को दर्शाता है।
हिंज फलन इसकी सीमा के भाग के लिए शून्य है, इसलिए इसका उपयोग डेटा को असंयुक्त क्षेत्रों में विभाजित करने के लिए किया जा सकता है, जिनमें से प्रत्येक को स्वतंत्र रूप से व्यवहार किया जा सकता है। इस प्रकार, उदाहरण के लिए अभिव्यक्ति में कार्य की प्रतिबिंबित जोड़ी कार्य करती है:
पूर्व अनुभाग में सरल मार्स मॉडल के लिए दिखाया गया भाग रैखिक ग्राफ़ बनाता है।
कोई यह मान सकता है कि हिंज फलन के भाग से रैखिक फलन बनाए जा सकते हैं, किंतु नॉन-लीनियर फलन बनाने के लिए हिंज फलन के साथ गुणा किया जा सकता है।
हिंज फलन को रैंप फलन, आइस हॉकी स्टिक, या रेक्टिफायर (तंत्रिका नेटवर्क) फलन भी कहा जाता है। परिवर्तन में अधिकतम इस आलेख में उपयोग किए गए नोटेशन में, हिंज फलन को प्रायः से दर्शाया जाता है जहाँ का तात्पर्य सकारात्मक भाग है।
मॉडल निर्माण प्रक्रिया
मार्स दो चरणों में मॉडल बनाता है: आगे और पीछे का मार्ग। यह दो-चरणीय दृष्टिकोण वही है जो पुनरावर्ती विभाजन वृक्षों द्वारा उपयोग किया जाता है।
फॉरवर्ड पास
मार्स मॉडल से प्रारंभ होता है जिसमें केवल इंटरसेप्ट टर्म होता है (जो प्रतिक्रिया मूल्यों का माध्य है)।
मार्स फिर मॉडल में जोड़े में आधार फलन को बार-बार जोड़ता है। प्रत्येक चरण में यह आधार फलनों की जोड़ी का शोध करता है जो वर्गों के योग में अवशिष्ट त्रुटि में अधिकतम कमी देता है (यह ग्रेडी एल्गोरिदम है)। जोड़ी में दो आधार फलन समान हैं, अतिरिक्त इसके कि प्रत्येक फलन के लिए मिरर किए गए हिंज फलन का भिन्न पक्ष उपयोग किया जाता है। प्रत्येक नए आधार फलन में मॉडल में पूर्व से ही शब्द सम्मिलित होता है (जो संभवतः इंटरसेप्ट शब्द हो सकता है) नए हिंज फलन द्वारा गुणा किया जाता है। हिंज फलन को चर और कनॉट द्वारा परिभाषित किया जाता है, इसलिए नया आधार फलन जोड़ने के लिए, मार्स को निम्नलिखित के सभी संयोजनों का परिक्षण करना होगा:
1) मौजूदा शब्द (इस संदर्भ में मूल शब्द कहे जाते हैं)
2) सभी चर (नए आधार फलन के लिए का चयन करने के लिए)
3) प्रत्येक चर के सभी मान (नए काज फलन की गाँठ के लिए)।
प्रत्येक पद के गुणांक की गणना करने के लिए मार्स पदों पर रेखीय प्रतिगमन लागू करता है।
शब्दों को जोड़ने की यह प्रक्रिया तब तक जारी रहती है जब तक कि शेष त्रुटि में परिवर्तन जारी रखने के लिए बहुत छोटा न हो या जब तक शब्दों की अधिकतम संख्या न हो जाए। मॉडल निर्माण प्रारंभ होने से पहले उपयोगकर्ता द्वारा शर्तों की अधिकतम संख्या निर्दिष्ट की जाती है।
प्रत्येक चरण पर परिक्षण पाशविक बल परिक्षण |ब्रूट-फोर्स फैशन में की जाती है, किंतु मार्स का प्रमुख पहलू यह है कि हिंज कार्यों की प्रकृति के कारण तेजी से न्यूनतम-वर्ग अद्यतन तकनीक का उपयोग करके परिक्षण अपेक्षाकृत तेज़ी से की जा सकती है। दरअसल, परिक्षण बिल्कुल क्रूर बल नहीं है. परिक्षण को heuristics के साथ तेज किया जा सकता है जो प्रत्येक चरण पर विचार करने के लिए मूल शब्दों की संख्या को कम कर देता है (फास्ट मार्स)[4]).
पिछड़ा पास
फॉरवर्ड पास आमतौर पर ओवरफ़िट मॉडल बनाता है। ( ओवरफिट मॉडल मॉडल बनाने के लिए उपयोग किए गए डेटा के लिए अच्छी तरह से फिट होता है किंतु नए डेटा के लिए अच्छी तरह से सामान्यीकृत नहीं होगा।) उत्तम सामान्यीकरण क्षमता के साथ मॉडल बनाने के लिए, बैकवर्ड पास मॉडल को काटता है। यह - करके शब्दों को हटाता है, प्रत्येक चरण में सबसे कम प्रभावी शब्द को हटाता है जब तक कि उसे सबसे अच्छा सबमॉडल नहीं मिल जाता। मॉडल उपसमुच्चय की तुलना नीचे वर्णित सामान्यीकृत क्रॉस सत्यापन (जीसीवी) मानदंड का उपयोग करके की जाती है।
फॉरवर्ड पास की तुलना में बैकवर्ड पास का फायदा है: किसी भी चरण पर यह हटाने के लिए कोई भी शब्द चुन सकता है, जबकि प्रत्येक चरण पर फॉरवर्ड पास केवल शब्दों की अगली जोड़ी देख सकता है।
फॉरवर्ड पास जोड़े में शब्द जोड़ता है, किंतु बैकवर्ड पास आम तौर पर जोड़े के तरफ को हटा देता है और इसलिए अंतिम मॉडल में शब्द प्रायः जोड़े में नहीं देखे जाते हैं। के समीकरण में युग्मित काज देखा जा सकता है उपरोक्त पहले मंगल उदाहरण में; ओजोन उदाहरण में कोई पूर्ण युग्म नहीं रखा गया है।
सामान्यीकृत क्रॉस सत्यापन
सबसे अच्छा सबसेट चुनने के लिए मॉडल सबसेट के प्रदर्शन की तुलना करने के लिए बैकवर्ड पास सामान्यीकृत क्रॉस वैलिडेशन (जीसीवी) का उपयोग करता है: जीसीवी के निचले मान उत्तम होते हैं। जीसीवी नियमितीकरण (मशीन लर्निंग) का रूप है: यह मॉडल जटिलता के मुकाबले फिट की अच्छाई का व्यापार करता है।
(हम यह अनुमान लगाना चाहते हैं कि कोई मॉडल नए डेटा पर कितना अच्छा प्रदर्शन करता है, प्रशिक्षण डेटा पर नहीं। ऐसा नया डेटा आमतौर पर मॉडल निर्माण के समय उपलब्ध नहीं होता है, इसलिए इसके बजाय हम नए डेटा पर प्रदर्शन क्या होगा इसका अनुमान लगाने के लिए जीसीवी का उपयोग करते हैं। प्रशिक्षण डेटा पर वर्गों का कच्चा अवशिष्ट योग | वर्गों का अवशिष्ट योग (RSS) मॉडल की तुलना करने के लिए अपर्याप्त है, क्योंकि मार्स शब्द हटा दिए जाने पर RSS हमेशा बढ़ता है। दूसरे शब्दों में, यदि RSS का उपयोग मॉडलों की तुलना करने के लिए किया जाता था, तो बैकवर्ड पास हमेशा सबसे बड़े मॉडल को चुनेगा - किंतु सबसे बड़े मॉडल में आमतौर पर सबसे अच्छा सामान्यीकरण प्रदर्शन नहीं होता है।)
जीसीवी का सूत्र है
- जीसीवी = आरएसएस / (एन · (1 - (पैरामीटर की प्रभावी संख्या) / एन)2)
जहां RSS प्रशिक्षण डेटा पर मापा गया वर्गों का अवशिष्ट योग है और N अवलोकनों की संख्या ('x' मैट्रिक्स में पंक्तियों की संख्या) है।
EffectiveNumberOfParameters को परिभाषित किया गया है मंगल ग्रह संदर्भ के रूप में
- (मापदंडों की प्रभावी संख्या) = (मंगल के पदों की संख्या) + (दंड) · ((मंगल के पदों की संख्या) − 1 ) / 2
जहां 'जुर्माना' लगभग 2 या 3 है (एमएआरएस सॉफ्टवेयर उपयोगकर्ता को जुर्माना पूर्व निर्धारित करने की अनुमति देता है)।
ध्यान दें कि
- (मंगल पदों की संख्या − 1 ) / 2
हिंज-फलन गांठों की संख्या है, इसलिए सूत्र गांठों को जोड़ने पर जुर्माना लगाता है। इस प्रकार जीसीवी फॉर्मूला मॉडल के लचीलेपन को ध्यान में रखते हुए प्रशिक्षण आरएसएस को समायोजित (यानी बढ़ाता है) करता है। हम लचीलेपन को दंडित करते हैं क्योंकि जो मॉडल बहुत लचीले हैं वे डेटा की व्यवस्थित संरचना के बजाय डेटा में शोर के विशिष्ट अहसास को मॉडल करेंगे।
सामान्यीकृत क्रॉस-सत्यापन को यह नाम दिया गया है क्योंकि यह त्रुटि का अनुमान लगाने के लिए सूत्र का उपयोग करता है जिसे लीव-वन-आउट सत्यापन द्वारा निर्धारित किया जाएगा। यह सिर्फ अनुमान है किंतु व्यवहार में अच्छा काम करता है। जीसीवी को क्रेवेन और ग्रेस वाहबा द्वारा पेश किया गया था और फ्रीडमैन द्वारा मार्स के लिए विस्तारित किया गया था।
बाधाएँ
बाधा का पहले ही उल्लेख किया जा चुका है: उपयोगकर्ता फॉरवर्ड पास में शब्दों की अधिकतम संख्या निर्दिष्ट कर सकता है।
फॉरवर्ड पास पर और बाधा लगाई जा सकती है बातचीत की अधिकतम स्वीकार्य डिग्री निर्दिष्ट करके। आम तौर पर केवल या दो डिग्री की बातचीत की अनुमति होती है, किंतु उच्च डिग्री का उपयोग तब किया जा सकता है जब डेटा इसकी गारंटी देता है। पहले मार्स उदाहरण में अंतःक्रिया की अधिकतम डिग्री उपरोक्त है (भूमिात् कोई इंटरैक्शन या कोई योगात्मक मॉडल नहीं); ओजोन उदाहरण में यह दो है।
फॉरवर्ड पास पर अन्य बाधाएँ संभव हैं। उदाहरण के लिए, उपयोगकर्ता निर्दिष्ट कर सकता है कि इंटरैक्शन की अनुमति है केवल कुछ इनपुट वेरिएबल के लिए। ज्ञान के कारण ऐसी बाधाएँ समझ में आ सकती हैं उस प्रक्रिया का जिसने डेटा उत्पन्न किया।
पक्ष और विपक्ष
कोई भी प्रतिगमन मॉडलिंग तकनीक सभी स्थितियों के लिए सर्वोत्तम नहीं है। नीचे दिए गए दिशानिर्देशों का उद्देश्य मंगल ग्रह के फायदे और नुकसान का विचार देना है। किंतु दिशानिर्देशों के अपवाद होंगे। मंगल की तुलना पुनरावर्ती विभाजन से करना उपयोगी है और यह नीचे किया गया है। (पुनरावर्ती विभाजन को सामान्यतः प्रतिगमन वृक्ष भी कहा जाता है, निर्णय वृक्ष, या पूर्वानुमानित विश्लेषण#वर्गीकरण और प्रतिगमन वृक्ष; विवरण के लिए निर्णय वृक्ष सीखना लेख देखें)।
- मार्स मॉडल रैखिक प्रतिगमन मॉडल की तुलना में अधिक लचीले होते हैं।
- मार्स मॉडल समझने और व्याख्या करने में सरल हैं।[5] उपरोक्त ओजोन सांद्रता के समीकरण की तुलना, मान लीजिए, प्रशिक्षित कृत्रिम तंत्रिका नेटवर्क या यादृच्छिक जंगल के अंदरूनी हिस्सों से करें।
- मार्स निरंतर और श्रेणीबद्ध डेटा दोनों को संभाल सकता है।[6][7] मार्स संख्यात्मक डेटा के लिए पुनरावर्ती विभाजन से उत्तम होता है क्योंकि पुनरावर्ती विभाजन द्वारा उपयोग किए जाने वाले टुकड़े-टुकड़े निरंतर विभाजन की तुलना में संख्यात्मक चर के लिए टिका अधिक उपयुक्त होती है।
- मार्स मॉडल के निर्माण के लिए प्रायः बहुत कम या कोई डेटा तैयारी की आवश्यकता नहीं होती है।[5]हिंज फलन स्वचालित रूप से इनपुट डेटा को विभाजित करता है, इसलिए आउटलेर्स का प्रभाव निहित होता है। इस संबंध में मार्स पुनरावर्ती विभाजन के समान है जो डेटा को असंयुक्त क्षेत्रों में भी विभाजित करता है, हालांकि भिन्न विधि का उपयोग करता है। (फिर भी, अधिकांश सांख्यिकीय मॉडलिंग तकनीकों की तरह, मार्स मॉडल को प्रशिक्षित करने से पहले ज्ञात आउटलेर्स को हटाने पर विचार किया जाना चाहिए।[citation needed])
- मार्स (पुनरावर्ती विभाजन की तरह) स्वचालित फ़ीचर चयन करता है (जिसका भूमि है कि यह मॉडल में महत्वपूर्ण चर सम्मिलित करता है और महत्वहीन को बाहर कर देता है)। चूँकि, चयन में कुछ मनमानी हो सकती है, खासकर जब सहसंबद्ध भविष्यवक्ता हों, और यह व्याख्या को प्रभावित कर सकता है[5]*मार्स मॉडल में पूर्वाग्रह-विचरण का अच्छा समझौता होता है। मॉडल अरैखिकता और परिवर्तनीय इंटरैक्शन को मॉडल करने के लिए पर्याप्त लचीले हैं (इस प्रकार मार्स मॉडल में अधिक कम पूर्वाग्रह है), फिर भी मार्स आधार कार्यों का बाधित रूप बहुत अधिक लचीलेपन को रोकता है (इस प्रकार मार्स मॉडल में अधिक कम भिन्नता होती है)।
- मार्स अधिक बड़े डेटासेट को संभालने के लिए उपयुक्त है। 100 भविष्यवक्ताओं और 10 के साथ इनपुट मैट्रिक्स से मार्स मॉडल बनाना नियमित मामला है5अवलोकन. ऐसा मॉडल 1 गीगाहर्ट्ज मशीन पर लगभग मिनट में बनाया जा सकता है, यह मानते हुए कि मार्स शब्दों की परस्पर क्रिया की अधिकतम डिग्री तक सीमित है (यानी केवल योगात्मक शब्द)। समान 1 गीगाहर्ट्ज़ मशीन पर समान डेटा वाले डिग्री दो मॉडल को अधिक समय लगता है - लगभग 12 मिनट। ध्यान रखें कि यह समय अत्यधिक डेटा पर निर्भर है। पुनरावर्ती विभाजन मार्स की तुलना में बहुत तेज़ है।[citation needed]
- मार्स मॉडल के साथ, किसी भी गैर-पैरामीट्रिक प्रतिगमन की तरह, पैरामीटर आत्मविश्वास अंतराल और मॉडल पर अन्य जांचों की गणना सीधे नहीं की जा सकती (रैखिक प्रतिगमन मॉडल के विपरीत)। क्रॉस-वैलिडेशन (सांख्यिकी)|इसके बजाय मॉडल को मान्य करने के लिए क्रॉस-वैलिडेशन और संबंधित तकनीकों का उपयोग किया जाना चाहिए।
- मार्स मॉडल बूस्टिंग (मेटा-एल्गोरिदम) पेड़ों के समान अच्छे फिट नहीं देते हैं, किंतु इन्हें अधिक तेज़ी से बनाया जा सकता है और ये अधिक व्याख्या योग्य हैं। ( 'व्याख्यात्मक' मॉडल ऐसे रूप में है जो यह स्पष्ट करता है कि प्रत्येक भविष्यवक्ता का प्रभाव क्या है।)
भूमिका>,mda, औरpolsplineकार्यान्वयन भविष्यवक्ताओं में लापता मूल्यों की अनुमति नहीं देता है, किंतु प्रतिगमन पेड़ों (जैसे) के मुफ्त कार्यान्वयन की अनुमति देता हैrpartऔरparty) सरोगेट स्प्लिट्स नामक तकनीक का उपयोग करके लापता मानों की अनुमति दें।- मार्स मॉडल शीघ्रता से भविष्यवाणियां कर सकते हैं। भविष्यवाणी फलन को बस मार्स मॉडल सूत्र का मूल्यांकन करना है। इसकी तुलना समर्थन वेक्टर यंत्र के साथ भविष्यवाणी करने से करें, जहां प्रत्येक वेरिएबल को प्रत्येक सपोर्ट वेक्टर के संबंधित तत्व से गुणा करना होता है। यदि कई चर और कई समर्थन वैक्टर हैं तो यह धीमी प्रक्रिया हो सकती है।
- परिणामस्वरूप फिट किया गया फलन सुचारू नहीं है (टिका के साथ भिन्न-भिन्न नहीं)।
विस्तार और संबंधित अवधारणाएँ
- सामान्यीकृत रैखिक मॉडल (जीएलएम) को मार्स मॉडल के निर्माण के बाद लिंक फलन लागू करके मार्स मॉडल में सम्मिलित किया जा सकता है। इस प्रकार, उदाहरण के लिए, मार्स मॉडल संभावनाओं की भविष्यवाणी करने के लिए संभार तन्त्र परावर्तन को सम्मिलित कर सकते हैं।
- अरेखीय प्रतिगमन|नॉन-लीनियर रिग्रेशन का उपयोग तब किया जाता है जब फलन का अंतर्निहित रूप ज्ञात होता है और रिग्रेशन का उपयोग केवल उस फलन के मापदंडों का अनुमान लगाने के लिए किया जाता है। दूसरी ओर, मंगल स्वयं कार्यों का अनुमान लगाता है, यद्यपि कार्यों की प्रकृति पर गंभीर बाधाएं होती हैं। (ये बाधाएँ आवश्यक हैं क्योंकि डेटा से मॉडल की परिक्षण करना विपरीत समस्या है जो मॉडल पर बाधाओं के बिना अच्छी तरह से प्रस्तुत समस्या नहीं है।)
- पुनरावर्ती विभाजन (आमतौर पर कार्ट कहा जाता है)। मार्स को पुनरावर्ती विभाजन के सामान्यीकरण के रूप में देखा जा सकता है जो मॉडल को संख्यात्मक (यानी गैर-श्रेणीबद्ध) डेटा को उत्तम ढंग से संभालने की अनुमति देता है।
- सामान्यीकृत योगात्मक मॉडल। उपयोगकर्ता के नजरिए से GAM, मार्स के समान हैं, किंतु (ए) मार्स आधार कार्यों के बजाय सुचारू स्थानीय प्रतिगमन या बहुपद स्पलाइन (गणित) में फिट होते हैं, और (बी) स्वचालित रूप से परिवर्तनीय इंटरैक्शन को मॉडल नहीं करते हैं। GAMs द्वारा आंतरिक रूप से उपयोग की जाने वाली फिटिंग विधि मार्स से बहुत भिन्न है। ऐसे मॉडलों के लिए जिन्हें परिवर्तनीय इंटरैक्शन की स्वचालित परिक्षण की आवश्यकता नहीं होती है, GAMs प्रायः मार्स के साथ अनुकूल प्रतिस्पर्धा करते हैं।
- टीएसएमएआरएस। टाइम सीरीज़ मार्स वह शब्द है जिसका उपयोग तब किया जाता है जब मार्स मॉडल को टाइम सीरीज़ संदर्भ में लागू किया जाता है। आमतौर पर इस सेट अप में भविष्यवक्ता विलंबित समय श्रृंखला मान होते हैं जिसके परिणामस्वरूप ऑटोरेग्रेसिव स्पलाइन मॉडल होते हैं। मूविंग एवरेज स्पलाइन मॉडल को सम्मिलित करने के लिए इन मॉडलों और ्सटेंशनों को टीएसएमएआरएस का उपयोग करके यूनीवेरिएट टाइम सीरीज़ मॉडलिंग और पूर्वानुमान में वर्णित किया गया है: टीएसएमएआरएस का उपयोग करके थ्रेशोल्ड टाइम सीरीज़ ऑटोरेग्रेसिव, मौसमी और मूविंग औसत मॉडल का अध्ययन।
- बायेसियन मंगल (बीएमएआरएस) ही मॉडल फॉर्म का उपयोग करता है, किंतु बायेसियन दृष्टिकोण का उपयोग करके मॉडल बनाता है। यह विभिन्न इष्टतम मार्स मॉडल पर पहुंच सकता है क्योंकि मॉडल निर्माण का दृष्टिकोण भिन्न है। Bमार्स का परिणाम आम तौर पर मार्स मॉडल के पिछले नमूनों का समूह होता है, जो संभाव्य भविष्यवाणी की अनुमति देता है।[8]
यह भी देखें
- रेखीय प्रतिगमन
- स्थानीय प्रतिगमन
- तर्कसंगत कार्य मॉडलिंग
- खंडित प्रतिगमन
- तख़्ता प्रक्षेप
- तख़्ता प्रतिगमन
संदर्भ
- ↑ Friedman, J. H. (1991). "बहुभिन्नरूपी अनुकूली प्रतिगमन स्प्लिंस". The Annals of Statistics. 19 (1): 1–67. CiteSeerX 10.1.1.382.970. doi:10.1214/aos/1176347963. JSTOR 2241837. MR 1091842. Zbl 0765.62064.
- ↑ CRAN Package earth
- ↑ Earth – Multivariate adaptive regression splines in Orange (Python machine learning library)
- ↑ Friedman, J. H. (1993) Fast MARS, Stanford University Department of Statistics, Technical Report 110
- ↑ 5.0 5.1 5.2 Kuhn, Max; Johnson, Kjell (2013). एप्लाइड प्रेडिक्टिव मॉडलिंग (in English). New York, NY: Springer New York. doi:10.1007/978-1-4614-6849-3. ISBN 9781461468486.
- ↑ Friedman, Jerome H. (1993). "Estimating Functions of Mixed Ordinal and Categorical Variables Using Adaptive Splines". In Stephan Morgenthaler; Elvezio Ronchetti; Werner Stahel (eds.). सांख्यिकीय डेटा विश्लेषण और मजबूती में नई दिशाएँ. Birkhauser.
- ↑ Friedman, Jerome H. (1991-06-01). "अनुकूली स्प्लाइन का उपयोग करके मिश्रित क्रमसूचक और श्रेणीबद्ध चर के कार्यों का अनुमान लगाना". DTIC. Archived from the original on April 11, 2022. Retrieved 2022-04-11.
- ↑ Denison, D. G. T.; Mallick, B. K.; Smith, A. F. M. (1 December 1998). "बायेसियन मंगल" (PDF). Statistics and Computing (in English). 8 (4): 337–346. doi:10.1023/A:1008824606259. ISSN 1573-1375. S2CID 12570055.
अग्रिम पठन
- Hastie T., Tibshirani R., and Friedman J.H. (2009) The Elements of Statistical Learning, 2nd edition. Springer, ISBN 978-0-387-84857-0 (has a section on मार्स)
- Faraway J. (2005) Extending the Linear Model with R, CRC, ISBN 978-1-58488-424-8 (has an example using मार्स with R)
- Heping Zhang and Burton H. Singer (2010) Recursive Partitioning and Applications, 2nd edition. Springer, ISBN 978-1-4419-6823-4 (has a chapter on मार्स and discusses some tweaks to the algorithm)
- Denison D.G.T., Holmes C.C., Mallick B.K., and Smith A.F.M. (2004) Bayesian Methods for Nonlinear Classification and Regression, Wiley, ISBN 978-0-471-49036-4
- Berk R.A. (2008) Statistical learning from a regression perspective, Springer, ISBN 978-0-387-77500-5
बाहरी संबंध
Several free and commercial software packages are available for fitting मार्स-type models.
- Free software
- R packages:
- Matlab code:
- ARESLab: Adaptive Regression Splines toolbox for Matlab
- Code from the book Bayesian Methods for Nonlinear Classification and Regression[1] for Bayesian मार्स.
- Python
- भूमि – Multivariate adaptive regression splines
- py-भूमि
- pyBASS for Bayesian मार्स.
- Commercial software
- मार्स from Salford Systems. Based on Friedman's implementation.
- STATISTICA Data Miner from StatSoft
- ADAPTIVEREG from SAS.
- ↑ Denison, D. G. T.; Holmes, C. C.; Mallick, B. K.; Smith, A. F. M. (2002). Bayesian methods for nonlinear classification and regression. Chichester, England: Wiley. ISBN 978-0-471-49036-4.