क्विकसेलेक्ट: Difference between revisions
No edit summary |
No edit summary |
||
| Line 19: | Line 19: | ||
==एल्गोरिदम== | ==एल्गोरिदम== | ||
क्विकसॉर्ट में, एक उपप्रक्रिया होती है जिसे कहा जाता है <code>partition</code> जो, रैखिक समय में, एक सूची को समूहित कर सकता है (सूचकांकों से लेकर)। <code>left</code> को <code>right</code>) दो भागों में: वे जो एक निश्चित तत्व से छोटे हैं, और वे जो तत्व से बड़े या उसके | क्विकसॉर्ट में, एक उपप्रक्रिया होती है जिसे कहा जाता है <code>partition</code> जो, रैखिक समय में, एक सूची को समूहित कर सकता है (सूचकांकों से लेकर)। <code>left</code> को <code>right</code>) दो भागों में: वे जो एक निश्चित तत्व से छोटे हैं, और वे जो तत्व से बड़े या उसके सामान्तर हैं। यहां स्यूडोकोड है जो तत्व के बारे में एक विभाजन करता है <code>list[pivotIndex]</code>: | ||
फलन विभाजन (सूची, बाएँ, दाएँ, पिवोटइंडेक्स) है | |||
पिवोटवैल्यू�:= सूची[पिवोटइंडेक्स] | |||
स्वैप सूची[पिवोटइंडेक्स] और सूची[दाएं] ''//पिवोट को अंत तक ले जाएं'' | स्वैप सूची[पिवोटइंडेक्स] और सूची[दाएं] ''//पिवोट को अंत तक ले जाएं'' | ||
स्टोरइंडेक्स�:= बाएँ | |||
i के लिए बाएँ से दाएँ - 1 करो | i के लिए बाएँ से दाएँ - 1 करो | ||
यदि सूची[i] <pivotValue | यदि सूची[i] <pivotValue तब | ||
स्वैप सूची[स्टोरइंडेक्स] और सूची[i] | स्वैप सूची[स्टोरइंडेक्स] और सूची[i] | ||
वेतन वृद्धि स्टोर इंडेक्स | वेतन वृद्धि स्टोर इंडेक्स | ||
| Line 34: | Line 34: | ||
इसे क्विकॉर्ट#लोमुटो विभाजन योजना के रूप में जाना जाता है, जो क्विकॉर्ट#होरे विभाजन योजना|होरे की मूल विभाजन योजना की तुलना में सरल किन्तु कम कुशल है। | इसे क्विकॉर्ट#लोमुटो विभाजन योजना के रूप में जाना जाता है, जो क्विकॉर्ट#होरे विभाजन योजना|होरे की मूल विभाजन योजना की तुलना में सरल किन्तु कम कुशल है। | ||
क्विकसॉर्ट में, हम दोनों शाखाओं को पुनरावर्ती रूप से क्रमबद्ध करते हैं, जिससे सर्वोत्तम स्थिति बनती है <math>O(n\log n)</math> समय। चूँकि, चयन करते समय, हम पहले से ही जानते हैं कि हमारा वांछित तत्व किस विभाजन में है, क्योंकि धुरी अपनी अंतिम क्रमबद्ध स्थिति में है, इसके पहले वाले सभी तत्व अवर्गीकृत क्रम में हैं और इसके | क्विकसॉर्ट में, हम दोनों शाखाओं को पुनरावर्ती रूप से क्रमबद्ध करते हैं, जिससे सर्वोत्तम स्थिति बनती है <math>O(n\log n)</math> समय। चूँकि, चयन करते समय, हम पहले से ही जानते हैं कि हमारा वांछित तत्व किस विभाजन में है, क्योंकि धुरी अपनी अंतिम क्रमबद्ध स्थिति में है, इसके पहले वाले सभी तत्व अवर्गीकृत क्रम में हैं और इसके पश्चात् वाले सभी तत्व अवर्गीकृत क्रम में हैं। इसलिए, एक एकल पुनरावर्ती कॉल सही विभाजन में वांछित तत्व का पता लगाती है, और हम त्वरित चयन के लिए इस पर काम करते हैं: | ||
// बाएँ..दाएँ सहित सूची का k-वाँ सबसे छोटा तत्व लौटाता है | // बाएँ..दाएँ सहित सूची का k-वाँ सबसे छोटा तत्व लौटाता है | ||
// (अर्थात् बाएँ <= k <= दाएँ)। | // (अर्थात् बाएँ <= k <= दाएँ)। | ||
' | 'फलन' चुनें (सूची, बाएँ, दाएँ, k) 'है' | ||
'यदि' बाएँ = दाएँ 'तब' // यदि सूची में केवल एक तत्व है, | 'यदि' बाएँ = दाएँ 'तब' // यदि सूची में केवल एक तत्व है, | ||
'वापसी' सूची[बाएं] // उस तत्व को लौटाएं | 'वापसी' सूची[बाएं] // उस तत्व को लौटाएं | ||
pivotIndexI:= ... // बाएँ और दाएँ के मध्य एक pivotIndex चुनें, | |||
// उदाहरण के लिए, बाएं + फर्श (रैंड() % (दाएं - बाएं + 1)) | // उदाहरण के लिए, बाएं + फर्श (रैंड()�% (दाएं - बाएं + 1)) | ||
पिवोटइंडेक्स�:= विभाजन (सूची, बाएँ, दाएँ, पिवोटइंडेक्स) | |||
// धुरी अपनी अंतिम क्रमबद्ध स्थिति में है | // धुरी अपनी अंतिम क्रमबद्ध स्थिति में है | ||
'यदि' k = pivotIndex 'तब' | 'यदि' k = pivotIndex 'तब' | ||
| Line 54: | Line 54: | ||
---- क्विकॉर्ट से समानता पर ध्यान दें: जिस तरह न्यूनतम-आधारित चयन एल्गोरिथ्म एक आंशिक चयन सॉर्ट है, यह एक आंशिक क्विकॉर्ट है, जो केवल उत्पन्न और विभाजन करता है <math>O(\log n)</math> उसके जैसा <math>O(n)</math> विभाजन. इस सरल प्रक्रिया में रैखिक प्रदर्शन की उम्मीद है, और, क्विकसॉर्ट की तरह, व्यवहार में इसका प्रदर्शन अधिक अच्छा है। यह एक इन-प्लेस एल्गोरिदम भी है, यदि [[ पूंछ कॉल ]] ऑप्टिमाइज़ेशन उपलब्ध है, या लूप के साथ [[ पूँछ प्रत्यावर्तन ]] को खत्म करने पर केवल निरंतर मेमोरी ओवरहेड की आवश्यकता होती है: | ---- क्विकॉर्ट से समानता पर ध्यान दें: जिस तरह न्यूनतम-आधारित चयन एल्गोरिथ्म एक आंशिक चयन सॉर्ट है, यह एक आंशिक क्विकॉर्ट है, जो केवल उत्पन्न और विभाजन करता है <math>O(\log n)</math> उसके जैसा <math>O(n)</math> विभाजन. इस सरल प्रक्रिया में रैखिक प्रदर्शन की उम्मीद है, और, क्विकसॉर्ट की तरह, व्यवहार में इसका प्रदर्शन अधिक अच्छा है। यह एक इन-प्लेस एल्गोरिदम भी है, यदि [[ पूंछ कॉल ]] ऑप्टिमाइज़ेशन उपलब्ध है, या लूप के साथ [[ पूँछ प्रत्यावर्तन ]] को खत्म करने पर केवल निरंतर मेमोरी ओवरहेड की आवश्यकता होती है: | ||
फलन चयन(सूची, बाएँ, दाएँ, k) है | |||
कुंडली | कुंडली | ||
यदि बाएँ = दाएँ | यदि बाएँ = दाएँ तब | ||
वापसी सूची[बाएं] | वापसी सूची[बाएं] | ||
पिवोटइंडेक्स�:= ... ''// बाएँ और दाएँ के मध्य पिवोटइंडेक्स चुनें'' | |||
पिवोटइंडेक्स�:= विभाजन (सूची, बाएँ, दाएँ, पिवोटइंडेक्स) | |||
यदि k = pivotIndex | यदि k = pivotIndex तब | ||
वापसी सूची[के] | वापसी सूची[के] | ||
अन्यथा यदि k < pivotIndex तब | अन्यथा यदि k < pivotIndex तब | ||
दाएँ�:= पिवोटइंडेक्स − 1 | |||
अन्य | अन्य | ||
बाएँ�:= पिवोटइंडेक्स + 1 | |||
==समय जटिलता== | ==समय जटिलता== | ||
क्विकसॉर्ट की तरह, क्विकसेलेक्ट का औसत प्रदर्शन अच्छा है, किन्तु चुनी गई धुरी के प्रति संवेदनशील है। यदि अच्छे पिवोट्स चुने जाते हैं, अर्थात वे जो किसी दिए गए अंश द्वारा खोज | क्विकसॉर्ट की तरह, क्विकसेलेक्ट का औसत प्रदर्शन अच्छा है, किन्तु चुनी गई धुरी के प्रति संवेदनशील है। यदि अच्छे पिवोट्स चुने जाते हैं, अर्थात वे जो किसी दिए गए अंश द्वारा खोज समूह को लगातार कम करते हैं, तब खोज समूह आकार में तेजी से घटता है और प्रेरण (या ज्यामितीय श्रृंखला को संक्षेप में) से कोई देखता है कि प्रदर्शन रैखिक है, क्योंकि प्रत्येक चरण रैखिक है और कुल समय इसका एक स्थिर समय है (यह इस पर निर्भर करता है कि खोज समूह कितनी तेजी से कम होता है)। चूँकि, यदि खराब पिवोट्स को लगातार चुना जाता है, जैसे कि हर बार केवल एक ही तत्व कम होना, तब सबसे खराब स्थिति का प्रदर्शन द्विघात होता है: <math>O(n^2).</math> उदाहरण के लिए, किसी समूह के अधिकतम तत्व की खोज करने, पहले तत्व को धुरी के रूप में उपयोग करने और डेटा को क्रमबद्ध करने में ऐसा होता है। चूँकि, बेतरतीब ढंग से चुने गए पिवोट्स के लिए, यह सबसे खराब स्थिति बहुत ही असंभावित है: से अधिक का उपयोग करने की संभावना <math>Cn</math> किसी भी पर्याप्त बड़े स्थिरांक के लिए तुलना <math>C</math>, एक फलन के रूप में अतिघातीय रूप से छोटा है <math>C</math>.<ref>{{cite journal | ||
| last = Devroye | first = Luc | | last = Devroye | first = Luc | ||
| doi = 10.1016/0022-0000(84)90009-6 | | doi = 10.1016/0022-0000(84)90009-6 | ||
Revision as of 20:55, 14 July 2023
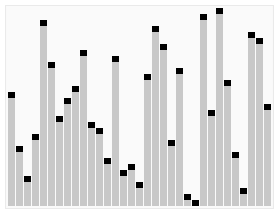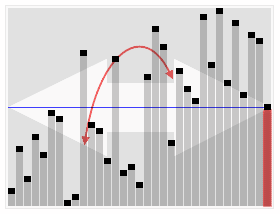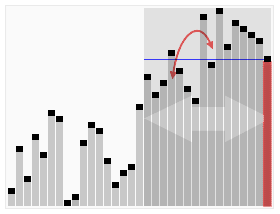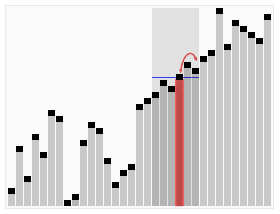 Animated visualization of the quickselect algorithm. Selecting the 22nd smallest value. | |
| Class | Selection algorithm |
|---|---|
| Data structure | Array |
| Worst-case performance | (n2) |
| Best-case performance | (n) |
| Average performance | (n) |
कंप्यूटर विज्ञान में, क्विकसेलेक्ट एक अव्यवस्थित सूची में kवें सबसे छोटे तत्व को खोजने के लिए एक चयन एल्गोरिदम है, जिसे kवें क्रम के आंकड़ों के रूप में भी जाना जाता है। संबंधित जल्दी से सुलझाएं सॉर्टिंग एल्गोरिदम की तरह, इसे टोनी होरे द्वारा विकसित किया गया था, और इस प्रकार इसे होरे के चयन एल्गोरिदम के रूप में भी जाना जाता है।[1] क्विकसॉर्ट की तरह, यह अभ्यास में कुशल है और इसका औसत-मामला प्रदर्शन अच्छा है, किन्तु सबसे खराब स्थिति में इसका प्रदर्शन खराब है। क्विकसेलेक्ट और इसके वेरिएंट चयन एल्गोरिदम हैं जिनका उपयोग अधिकांशतः कुशल वास्तविक विश्व के कार्यान्वयन में किया जाता है।
क्विकसेलेक्ट क्विकॉर्ट के समान समग्र दृष्टिकोण का उपयोग करता है, एक तत्व को धुरी के रूप में चुनता है और धुरी के आधार पर डेटा को दो भागों में विभाजित करता है, तदनुसार धुरी से कम या अधिक। चूँकि, क्विकसॉर्ट की तरह, दोनों तरफ पुनरावृत्ति करने के अतिरिक्त, क्विकसेलेक्ट केवल एक तरफ पुनरावृत्ति करता है - वह तत्व वाला पक्ष जिसे वह खोज रहा है। इससे औसत जटिलता कम हो जाती है को , की सबसे खराब स्थिति के साथ .
क्विकॉर्ट की तरह, क्विकसेलेक्ट को सामान्यतः इन-प्लेस एल्गोरिदम के रूप में और चयन से परे प्रयुक्त किया जाता है kवां तत्व, यह डेटा को आंशिक रूप से सॉर्ट भी करता है। सॉर्टिंग के साथ कनेक्शन की आगे की चर्चा के लिए चयन एल्गोरिदम देखें।
एल्गोरिदम
क्विकसॉर्ट में, एक उपप्रक्रिया होती है जिसे कहा जाता है partition जो, रैखिक समय में, एक सूची को समूहित कर सकता है (सूचकांकों से लेकर)। left को right) दो भागों में: वे जो एक निश्चित तत्व से छोटे हैं, और वे जो तत्व से बड़े या उसके सामान्तर हैं। यहां स्यूडोकोड है जो तत्व के बारे में एक विभाजन करता है list[pivotIndex]:
फलन विभाजन (सूची, बाएँ, दाएँ, पिवोटइंडेक्स) है
पिवोटवैल्यू�:= सूची[पिवोटइंडेक्स]
स्वैप सूची[पिवोटइंडेक्स] और सूची[दाएं] //पिवोट को अंत तक ले जाएं
स्टोरइंडेक्स�:= बाएँ
i के लिए बाएँ से दाएँ - 1 करो
यदि सूची[i] <pivotValue तब
स्वैप सूची[स्टोरइंडेक्स] और सूची[i]
वेतन वृद्धि स्टोर इंडेक्स
स्वैप सूची [दाएं] और सूची [स्टोर इंडेक्स] // धुरी को उसके अंतिम स्थान पर ले जाएं
रिटर्न स्टोर इंडेक्स
इसे क्विकॉर्ट#लोमुटो विभाजन योजना के रूप में जाना जाता है, जो क्विकॉर्ट#होरे विभाजन योजना|होरे की मूल विभाजन योजना की तुलना में सरल किन्तु कम कुशल है।
क्विकसॉर्ट में, हम दोनों शाखाओं को पुनरावर्ती रूप से क्रमबद्ध करते हैं, जिससे सर्वोत्तम स्थिति बनती है समय। चूँकि, चयन करते समय, हम पहले से ही जानते हैं कि हमारा वांछित तत्व किस विभाजन में है, क्योंकि धुरी अपनी अंतिम क्रमबद्ध स्थिति में है, इसके पहले वाले सभी तत्व अवर्गीकृत क्रम में हैं और इसके पश्चात् वाले सभी तत्व अवर्गीकृत क्रम में हैं। इसलिए, एक एकल पुनरावर्ती कॉल सही विभाजन में वांछित तत्व का पता लगाती है, और हम त्वरित चयन के लिए इस पर काम करते हैं:
// बाएँ..दाएँ सहित सूची का k-वाँ सबसे छोटा तत्व लौटाता है
// (अर्थात् बाएँ <= k <= दाएँ)।
'फलन' चुनें (सूची, बाएँ, दाएँ, k) 'है'
'यदि' बाएँ = दाएँ 'तब' // यदि सूची में केवल एक तत्व है,
'वापसी' सूची[बाएं] // उस तत्व को लौटाएं
pivotIndexI:= ... // बाएँ और दाएँ के मध्य एक pivotIndex चुनें,
// उदाहरण के लिए, बाएं + फर्श (रैंड()�% (दाएं - बाएं + 1))
पिवोटइंडेक्स�:= विभाजन (सूची, बाएँ, दाएँ, पिवोटइंडेक्स)
// धुरी अपनी अंतिम क्रमबद्ध स्थिति में है
'यदि' k = pivotIndex 'तब'
'वापसी' सूची[के]
'अन्यथा यदि' k < पिवोटइंडेक्स 'तब'
'वापसी' चुनें (सूची, बाएँ, पिवोटइंडेक्स - 1, के)
'अन्य'
'वापसी' चयन करें (सूची, पिवोटइंडेक्स + 1, दाएँ, के)
क्विकॉर्ट से समानता पर ध्यान दें: जिस तरह न्यूनतम-आधारित चयन एल्गोरिथ्म एक आंशिक चयन सॉर्ट है, यह एक आंशिक क्विकॉर्ट है, जो केवल उत्पन्न और विभाजन करता है उसके जैसा विभाजन. इस सरल प्रक्रिया में रैखिक प्रदर्शन की उम्मीद है, और, क्विकसॉर्ट की तरह, व्यवहार में इसका प्रदर्शन अधिक अच्छा है। यह एक इन-प्लेस एल्गोरिदम भी है, यदि पूंछ कॉल ऑप्टिमाइज़ेशन उपलब्ध है, या लूप के साथ पूँछ प्रत्यावर्तन को खत्म करने पर केवल निरंतर मेमोरी ओवरहेड की आवश्यकता होती है:
फलन चयन(सूची, बाएँ, दाएँ, k) है
कुंडली
यदि बाएँ = दाएँ तब
वापसी सूची[बाएं]
पिवोटइंडेक्स�:= ... // बाएँ और दाएँ के मध्य पिवोटइंडेक्स चुनें
पिवोटइंडेक्स�:= विभाजन (सूची, बाएँ, दाएँ, पिवोटइंडेक्स)
यदि k = pivotIndex तब
वापसी सूची[के]
अन्यथा यदि k < pivotIndex तब
दाएँ�:= पिवोटइंडेक्स − 1
अन्य
बाएँ�:= पिवोटइंडेक्स + 1
समय जटिलता
क्विकसॉर्ट की तरह, क्विकसेलेक्ट का औसत प्रदर्शन अच्छा है, किन्तु चुनी गई धुरी के प्रति संवेदनशील है। यदि अच्छे पिवोट्स चुने जाते हैं, अर्थात वे जो किसी दिए गए अंश द्वारा खोज समूह को लगातार कम करते हैं, तब खोज समूह आकार में तेजी से घटता है और प्रेरण (या ज्यामितीय श्रृंखला को संक्षेप में) से कोई देखता है कि प्रदर्शन रैखिक है, क्योंकि प्रत्येक चरण रैखिक है और कुल समय इसका एक स्थिर समय है (यह इस पर निर्भर करता है कि खोज समूह कितनी तेजी से कम होता है)। चूँकि, यदि खराब पिवोट्स को लगातार चुना जाता है, जैसे कि हर बार केवल एक ही तत्व कम होना, तब सबसे खराब स्थिति का प्रदर्शन द्विघात होता है: उदाहरण के लिए, किसी समूह के अधिकतम तत्व की खोज करने, पहले तत्व को धुरी के रूप में उपयोग करने और डेटा को क्रमबद्ध करने में ऐसा होता है। चूँकि, बेतरतीब ढंग से चुने गए पिवोट्स के लिए, यह सबसे खराब स्थिति बहुत ही असंभावित है: से अधिक का उपयोग करने की संभावना किसी भी पर्याप्त बड़े स्थिरांक के लिए तुलना , एक फलन के रूप में अतिघातीय रूप से छोटा है .[2]
वेरिएंट
सबसे आसान समाधान एक यादृच्छिक धुरी चुनना है, जो लगभग निश्चित रैखिक समय उत्पन्न करता है। निश्चित रूप से, कोई मीडियन-ऑफ़-3 पिवट रणनीति (जैसे कि क्विकसॉर्ट में) का उपयोग कर सकता है, जो आंशिक रूप से सॉर्ट किए गए डेटा पर रैखिक प्रदर्शन देता है, जैसा कि वास्तविक विश्व में आम है। चूँकि, काल्पनिक अनुक्रम अभी भी सबसे खराब स्थिति का कारण बन सकते हैं; डेविड मूसर ने 3 के मध्यस्थ हत्यारा अनुक्रम का वर्णन किया है जो उस रणनीति के विरुद्ध हमले की अनुमति देता है, जो उनके आत्मचयन एल्गोरिदम के लिए एक प्रेरणा थी।
अधिक परिष्कृत धुरी रणनीति का उपयोग करके सबसे खराब स्थिति में भी रैखिक प्रदर्शन सुनिश्चित किया जा सकता है; यह माध्यिका एल्गोरिदम के माध्यिका में किया जाता है। चूँकि, धुरी की गणना का ओवरहेड अधिक है, और इस प्रकार इसका उपयोग सामान्यतः व्यवहार में नहीं किया जाता है। तेज औसत स्थितियोंके प्रदर्शन और रैखिक सबसे खराब प्रदर्शन दोनों को प्राप्त करने के लिए फ़ॉलबैक के रूप में मध्यस्थों के माध्यिका के साथ मूलभूतत्वरित चयन को जोड़ा जा सकता है; यह इंट्रोसेलेक्ट में किया जाता है।
औसत समय जटिलता की उत्तम गणना से सबसे खराब स्थिति उत्पन्न होती है यादृच्छिक पिवोट्स के लिए (माध्यिका के स्थितियोंमें; अन्य k तेज़ हैं)।[3] अधिक जटिल धुरी रणनीति द्वारा स्थिरांक को 3/2 तक सुधारा जा सकता है, जिससे फ्लॉयड-रिवेस्ट एल्गोरिथ्म प्राप्त होता है, जिसकी औसत जटिलता है माध्यिका के लिए, अन्य k तेज़ होने के साथ।
यह भी देखें
- फ्लोयड-रिवेस्ट एल्गोरिदम
- अंतःचयन करें
- माध्यिकाओं का माध्यिका
संदर्भ
- ↑ Hoare, C. A. R. (1961). "Algorithm 65: Find". Comm. ACM. 4 (7): 321–322. doi:10.1145/366622.366647.
- ↑ Devroye, Luc (1984). "Exponential bounds for the running time of a selection algorithm" (PDF). Journal of Computer and System Sciences. 29 (1): 1–7. doi:10.1016/0022-0000(84)90009-6. MR 0761047. Devroye, Luc (2001). "On the probabilistic worst-case time of 'find'" (PDF). Algorithmica. 31 (3): 291–303. doi:10.1007/s00453-001-0046-2. MR 1855252.
- ↑ Blum-style analysis of Quickselect, David Eppstein, October 9, 2007.
बाहरी संबंध
- "qselect", Quickselect algorithm in Matlab, Manolis Lourakis