कॉम्ब सॉर्ट: Difference between revisions
m (Abhishek moved page कंघी सॉर्ट करें to कॉम्ब सॉर्ट without leaving a redirect) |
No edit summary |
||
| Line 18: | Line 18: | ||
|optimal= | |optimal= | ||
}} | }} | ||
'''कॉम्ब सॉर्ट''' एक अपेक्षाकृत सरल [[छँटाई | '''कॉम्ब सॉर्ट''' एक अपेक्षाकृत सरल [[छँटाई एल्गोरिथ्म]] है जिसे मूल रूप से 1980 में व्लोड्ज़िमिएर्ज़ डोबोसिविज़ और आर्टूर बोरोवी द्वारा डिज़ाइन किया गया था।<ref name=BB/><ref>{{Cite journal | ||
|title=An efficient variation of bubble sort | |title=An efficient variation of bubble sort | ||
|first=Wlodzimierz |last=Dobosiewicz | |first=Wlodzimierz |last=Dobosiewicz | ||
| Line 24: | Line 24: | ||
|volume=11 |issue=1 |date=29 August 1980 |pages=5–6 | |volume=11 |issue=1 |date=29 August 1980 |pages=5–6 | ||
|doi=10.1016/0020-0190(80)90022-8 | |doi=10.1016/0020-0190(80)90022-8 | ||
}}</ref> बाद में 1991 में स्टीफन लेसी और रिचर्ड बॉक्स | }}</ref> बाद में 1991 में स्टीफन लेसी और रिचर्ड बॉक्स (और इसे कॉम्बसॉर्ट नाम दिया गया) द्वारा इसे फिर से खोजा गया है।<ref>{{cite news | ||
|url=http://cs.clackamas.cc.or.us/molatore/cs260Spr03/combsort.htm | |url=http://cs.clackamas.cc.or.us/molatore/cs260Spr03/combsort.htm | ||
|title=A Fast, Easy Sort: A novel enhancement makes a bubble sort into one of the fastest sorting routines | |title=A Fast, Easy Sort: A novel enhancement makes a bubble sort into one of the fastest sorting routines | ||
| Line 30: | Line 30: | ||
|department=Hands On |date=April 1991 | |department=Hands On |date=April 1991 | ||
|volume=16 |issue=4 |pages=315–318, 320 | |volume=16 |issue=4 |pages=315–318, 320 | ||
}} [https://archive.org/details/eu_BYTE-1991-04_OCR Entire magazine] available at archive.org.</ref> कॉम्ब सॉर्ट [[ बुलबुले की तरह |बबल सॉर्ट]] में उसी | }} [https://archive.org/details/eu_BYTE-1991-04_OCR Entire magazine] available at archive.org.</ref> कॉम्ब सॉर्ट [[ बुलबुले की तरह |बबल सॉर्ट]] में उसी प्रकार सुधार करता है जैसे [[शैलसॉर्ट]] [[ सम्मिलन सॉर्ट |इंसर्शन सॉर्ट]] में सुधार करता है। | ||
nist.gov की "डिमिनिशिंग इंक्रीमेंट सॉर्ट" परिभाषा में 'कॉम्ब सॉर्ट' शब्द का उल्लेख डेटा के पुनरावृत्त पास को देखने के रूप में किया गया है, जहां कॉम्ब के दांत स्पर्श करते हैं; पहला शब्द [[डोनाल्ड नुथ]] से जुड़ा है।<ref>{{cite web | nist.gov की "डिमिनिशिंग इंक्रीमेंट सॉर्ट" परिभाषा में 'कॉम्ब सॉर्ट' शब्द का उल्लेख डेटा के पुनरावृत्त पास को देखने के रूप में किया गया है, जहां कॉम्ब के दांत स्पर्श करते हैं; पहला शब्द [[डोनाल्ड नुथ]] से जुड़ा है।<ref>{{cite web | ||
| Line 39: | Line 39: | ||
==एल्गोरिदम== | ==एल्गोरिदम== | ||
मूल विचार | मूल विचार टर्टल, या सूची के अंत के पास छोटे मानों को खत्म करना है, क्योंकि बबल सॉर्ट में ये सॉर्टिंग को काफी धीमा कर देते हैं। सूची के प्रारंभ में रैबिट के बड़े मान बबल सॉर्ट में कोई समस्या उत्पन्न नहीं करते हैं। | ||
बबल सॉर्ट में, जब किन्हीं दो तत्वों की तुलना की जाती है, तो उनमें सदैव 1 का अंतर (दूसरे से दूरी) होता है।<ref>{{cite web | बबल सॉर्ट में, जब किन्हीं दो तत्वों की तुलना की जाती है, तो उनमें सदैव 1 का अंतर (दूसरे से दूरी) होता है।<ref>{{cite web | ||
| Line 47: | Line 47: | ||
|accessdate=March 9, 2021}}</ref> कॉम्ब सॉर्ट का मूल विचार यह है कि अंतर 1 से अधिक हो सकता है। बबल सॉर्ट का आंतरिक लूप, जो वास्तविक स्वैप करता है, जिसको इस प्रकार संशोधित किया जाता है कि स्वैप किए गए तत्वों के बीच अंतर "सिकुड़ कारक" k के चरणों में कम (बाहरी लूप के प्रत्येक पुनरावृत्ति के लिए) हो जाता है: {{math|[{{sfrac|''n''|''k''}}, {{sfrac|''n''|''k''<sup>2</sup>}}, {{sfrac|''n''|''k''<sup>3</sup>}}, ..., 1]}} | |accessdate=March 9, 2021}}</ref> कॉम्ब सॉर्ट का मूल विचार यह है कि अंतर 1 से अधिक हो सकता है। बबल सॉर्ट का आंतरिक लूप, जो वास्तविक स्वैप करता है, जिसको इस प्रकार संशोधित किया जाता है कि स्वैप किए गए तत्वों के बीच अंतर "सिकुड़ कारक" k के चरणों में कम (बाहरी लूप के प्रत्येक पुनरावृत्ति के लिए) हो जाता है: {{math|[{{sfrac|''n''|''k''}}, {{sfrac|''n''|''k''<sup>2</sup>}}, {{sfrac|''n''|''k''<sup>3</sup>}}, ..., 1]}} | ||
अंतर तब | अंतर तब प्रारंभ होता है जब सूची n की लंबाई को सिकुड़न कारक k द्वारा विभाजित करके क्रमबद्ध किया जाता है (सामान्यतः 1.3; नीचे देखें) और उपरोक्त संशोधित बबल सॉर्ट का एक पास उस अंतर के साथ लागू किया जाता है। फिर अंतर को सिकुड़न कारक द्वारा विभाजित किया जाता है, फिर से सूची को इस नए अंतर के साथ क्रमबद्ध किया जाता है और प्रक्रिया तब तक दोहराई जाती है जब तक कि अंतर 1 न हो जाए। इस बिंदु पर, कंघी क्रमबद्धता 1 के अंतर का उपयोग करके जारी रहती है जब तक कि सूची पूरी तरह से क्रमबद्ध न हो जाए। प्रकार का अंतिम चरण इस प्रकार बबल प्रकार के बराबर होता है किन्तु इस समय तक अधिकांश टर्टल का समाधान हो चुका होता है इसलिए बबल प्रकार प्रभावी होगा। | ||
सिकुड़न कारक का कॉम्ब छंटाई की दक्षता पर बहुत प्रभाव पड़ता है। 200,000 से अधिक यादृच्छिक सूचियों पर प्रयोगसिद्ध परीक्षण के बाद मूल लेख के लेखकों द्वारा k = 1.3 को आदर्श सिकुड़न कारक के रूप में सुझाया गया है। बहुत छोटा मान अनावश्यक रूप से कई तुलनाएँ करके एल्गोरिदम को धीमा कर देता है, जबकि बहुत बड़ा मान | सिकुड़न कारक का कॉम्ब छंटाई की दक्षता पर बहुत प्रभाव पड़ता है। 200,000 से अधिक यादृच्छिक सूचियों पर प्रयोगसिद्ध परीक्षण के बाद मूल लेख के लेखकों द्वारा k = 1.3 को आदर्श सिकुड़न कारक के रूप में सुझाया गया है। बहुत छोटा मान अनावश्यक रूप से कई तुलनाएँ करके एल्गोरिदम को धीमा कर देता है, जबकि बहुत बड़ा मान टर्टल से प्रभावी रूप से निपटने में विफल रहता है, जिससे उसे 1 गैप आकार के साथ कई पास की आवश्यकता होती है। | ||
घटते अंतराल के साथ बार-बार सॉर्टिंग पास का पैटर्न शेलसॉर्ट के समान है, किन्तु शेलसॉर्ट में सरणी को अगले सबसे छोटे अंतराल पर जाने से पहले प्रत्येक पास को पूरी तरह से सॉर्ट किया जाता है। कॉम्ब सॉर्ट के पास तत्वों को पूरी तरह से सॉर्ट नहीं करते हैं। यही कारण है कि शेलसॉर्ट गैप अनुक्रमों में लगभग 2.2 का बड़ा इष्टतम सिकुड़न कारक होता है। | घटते अंतराल के साथ बार-बार सॉर्टिंग पास का पैटर्न शेलसॉर्ट के समान है, किन्तु शेलसॉर्ट में सरणी को अगले सबसे छोटे अंतराल पर जाने से पहले प्रत्येक पास को पूरी तरह से सॉर्ट किया जाता है। कॉम्ब सॉर्ट के पास तत्वों को पूरी तरह से सॉर्ट नहीं करते हैं। यही कारण है कि शेलसॉर्ट गैप अनुक्रमों में लगभग 2.2 का बड़ा इष्टतम सिकुड़न कारक होता है। | ||
| Line 132: | Line 132: | ||
{{Wikibooks|Algorithm Implementation|Sorting/Comb sort|Comb sort}} | {{Wikibooks|Algorithm Implementation|Sorting/Comb sort|Comb sort}} | ||
* बबल सॉर्ट, सामान्यतः धीमी एल्गोरिथ्म, कॉम्ब सॉर्ट का आधार है। | * बबल सॉर्ट, सामान्यतः धीमी एल्गोरिथ्म, कॉम्ब सॉर्ट का आधार है। | ||
* [[ कॉकटेल प्रकार ]], या द्विदिशात्मक बबल सॉर्ट, बबल सॉर्ट का रूप है जो | * [[ कॉकटेल प्रकार ]], या द्विदिशात्मक बबल सॉर्ट, बबल सॉर्ट का रूप है जो टर्टल की समस्या का भी समाधान करता है, यद्यपि कम प्रभावी ढंग से। | ||
== संदर्भ == | == संदर्भ == | ||
Revision as of 10:07, 19 July 2023
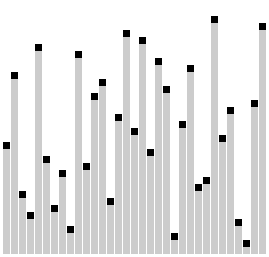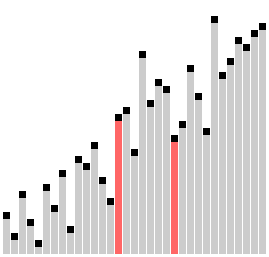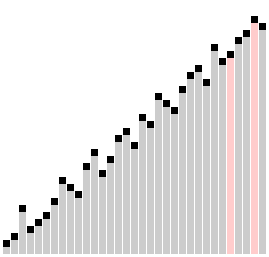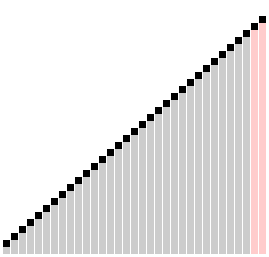 Comb sort with shrink factor k=1.24733 | |
| Class | Sorting algorithm |
|---|---|
| Data structure | Array |
| Worst-case performance | [1] |
| Best-case performance | |
| Average performance | , where p is the number of increments[1] |
| Worst-case space complexity | |
कॉम्ब सॉर्ट एक अपेक्षाकृत सरल छँटाई एल्गोरिथ्म है जिसे मूल रूप से 1980 में व्लोड्ज़िमिएर्ज़ डोबोसिविज़ और आर्टूर बोरोवी द्वारा डिज़ाइन किया गया था।[1][2] बाद में 1991 में स्टीफन लेसी और रिचर्ड बॉक्स (और इसे कॉम्बसॉर्ट नाम दिया गया) द्वारा इसे फिर से खोजा गया है।[3] कॉम्ब सॉर्ट बबल सॉर्ट में उसी प्रकार सुधार करता है जैसे शैलसॉर्ट इंसर्शन सॉर्ट में सुधार करता है।
nist.gov की "डिमिनिशिंग इंक्रीमेंट सॉर्ट" परिभाषा में 'कॉम्ब सॉर्ट' शब्द का उल्लेख डेटा के पुनरावृत्त पास को देखने के रूप में किया गया है, जहां कॉम्ब के दांत स्पर्श करते हैं; पहला शब्द डोनाल्ड नुथ से जुड़ा है।[4]
एल्गोरिदम
मूल विचार टर्टल, या सूची के अंत के पास छोटे मानों को खत्म करना है, क्योंकि बबल सॉर्ट में ये सॉर्टिंग को काफी धीमा कर देते हैं। सूची के प्रारंभ में रैबिट के बड़े मान बबल सॉर्ट में कोई समस्या उत्पन्न नहीं करते हैं।
बबल सॉर्ट में, जब किन्हीं दो तत्वों की तुलना की जाती है, तो उनमें सदैव 1 का अंतर (दूसरे से दूरी) होता है।[5] कॉम्ब सॉर्ट का मूल विचार यह है कि अंतर 1 से अधिक हो सकता है। बबल सॉर्ट का आंतरिक लूप, जो वास्तविक स्वैप करता है, जिसको इस प्रकार संशोधित किया जाता है कि स्वैप किए गए तत्वों के बीच अंतर "सिकुड़ कारक" k के चरणों में कम (बाहरी लूप के प्रत्येक पुनरावृत्ति के लिए) हो जाता है: [n/k, n/k2, n/k3, ..., 1]
अंतर तब प्रारंभ होता है जब सूची n की लंबाई को सिकुड़न कारक k द्वारा विभाजित करके क्रमबद्ध किया जाता है (सामान्यतः 1.3; नीचे देखें) और उपरोक्त संशोधित बबल सॉर्ट का एक पास उस अंतर के साथ लागू किया जाता है। फिर अंतर को सिकुड़न कारक द्वारा विभाजित किया जाता है, फिर से सूची को इस नए अंतर के साथ क्रमबद्ध किया जाता है और प्रक्रिया तब तक दोहराई जाती है जब तक कि अंतर 1 न हो जाए। इस बिंदु पर, कंघी क्रमबद्धता 1 के अंतर का उपयोग करके जारी रहती है जब तक कि सूची पूरी तरह से क्रमबद्ध न हो जाए। प्रकार का अंतिम चरण इस प्रकार बबल प्रकार के बराबर होता है किन्तु इस समय तक अधिकांश टर्टल का समाधान हो चुका होता है इसलिए बबल प्रकार प्रभावी होगा।
सिकुड़न कारक का कॉम्ब छंटाई की दक्षता पर बहुत प्रभाव पड़ता है। 200,000 से अधिक यादृच्छिक सूचियों पर प्रयोगसिद्ध परीक्षण के बाद मूल लेख के लेखकों द्वारा k = 1.3 को आदर्श सिकुड़न कारक के रूप में सुझाया गया है। बहुत छोटा मान अनावश्यक रूप से कई तुलनाएँ करके एल्गोरिदम को धीमा कर देता है, जबकि बहुत बड़ा मान टर्टल से प्रभावी रूप से निपटने में विफल रहता है, जिससे उसे 1 गैप आकार के साथ कई पास की आवश्यकता होती है।
घटते अंतराल के साथ बार-बार सॉर्टिंग पास का पैटर्न शेलसॉर्ट के समान है, किन्तु शेलसॉर्ट में सरणी को अगले सबसे छोटे अंतराल पर जाने से पहले प्रत्येक पास को पूरी तरह से सॉर्ट किया जाता है। कॉम्ब सॉर्ट के पास तत्वों को पूरी तरह से सॉर्ट नहीं करते हैं। यही कारण है कि शेलसॉर्ट गैप अनुक्रमों में लगभग 2.2 का बड़ा इष्टतम सिकुड़न कारक होता है।
स्यूडोकोड
function combsort(array input) is
gap := input.size // Initialize gap size
shrink := 1.3 // Set the gap shrink factor
sorted := false
loop while sorted = false
// Update the gap value for a next comb
gap := floor(gap / shrink)
if gap ≤ 1 then
gap := 1
sorted := true // If there are no swaps this pass, we are done
end if
// A single "comb" over the input list
i := 0
loop while i + gap < input.size // See Shell sort for a similar idea
if input[i] > input[i+gap] then
swap(input[i], input[i+gap])
sorted := false
// If this assignment never happens within the loop,
// then there have been no swaps and the list is sorted.
end if
i := i + 1
end loop
end loop
end function
पायथन कोड
साथ ही, दो त्वरित पायथन (प्रोग्रामिंग भाषा) कार्यान्वयन: सूची (या सरणी, या अन्य परिवर्तनीय प्रकार जहां उस पर उपयोग किए गए संचालन भाषा को समझ में आता है) में स्थान पर काम करता है, दूसरा दिए गए डेटा के समान मूल्यों के साथ एक सूची बनाता है और इसे (अंतर्निहित sorted किए गए फ़ंक्शन के समान) सॉर्ट करने के बाद वापस कर देता है।
from math import floor
def combsort_inplace(data):
length = len(data)
shrink = 1.3
gap = length
sorted = False
while not sorted:
gap = floor(gap / shrink)
if gap <= 1:
sorted = True
gap = 1
# equivalent to `i = 0; while (i + gap) < length: ...{loop body}... i += 1`
for i in range(length - gap):
sm = gap + i
if data[i] > data[sm]:
# because Python is very nice, this accomplishes the swap
data[i], data[sm] = data[sm], data[i]
sorted = False
def combsort(data):
length = len(data)
shrink = 1.3
gap = length
out = list(data)
is_sorted = False
while not is_sorted:
gap = floor(gap / shrink)
if gap <= 1:
is_sorted = True
gap = 1
for i in range(length - gap):
sm = gap + i
if out[i] > out[sm]:
out[i], out[sm] = out[sm], out[i]
is_sorted = False
return out
यह भी देखें
- बबल सॉर्ट, सामान्यतः धीमी एल्गोरिथ्म, कॉम्ब सॉर्ट का आधार है।
- कॉकटेल प्रकार , या द्विदिशात्मक बबल सॉर्ट, बबल सॉर्ट का रूप है जो टर्टल की समस्या का भी समाधान करता है, यद्यपि कम प्रभावी ढंग से।
संदर्भ
- ↑ 1.0 1.1 1.2 Brejová, Bronislava (15 September 2001). "Analyzing variants of Shellsort". Information Processing Letters. 79 (5): 223–227. doi:10.1016/S0020-0190(00)00223-4.
- ↑ Dobosiewicz, Wlodzimierz (29 August 1980). "An efficient variation of bubble sort". Information Processing Letters. 11 (1): 5–6. doi:10.1016/0020-0190(80)90022-8.
- ↑ Lacey, Stephen; Box, Richard (April 1991). "A Fast, Easy Sort: A novel enhancement makes a bubble sort into one of the fastest sorting routines". Hands On. Byte Magazine. Vol. 16, no. 4. pp. 315–318, 320. Entire magazine available at archive.org.
- ↑ "diminishing increment sort". Retrieved March 9, 2021.
- ↑ "comb sort". National Institute of Standards and Technology (nist.gov). Retrieved March 9, 2021.