बेलनाकार और गोलाकार निर्देशांक में सदिश फ़ील्ड
|
|
| Line 1: |
Line 1: |
| {{Use American English|date = March 2019}}
| | |
| {{Short description|Vector field representation in 3D curvilinear coordinate systems}} | | {{Short description|Vector field representation in 3D curvilinear coordinate systems}} |
| [[File:3D Spherical.svg|thumb|240px|right|गोलाकार निर्देशांक (r, θ, φ) जैसा कि आमतौर पर भौतिकी में उपयोग किया जाता है: रेडियल दूरी r, ध्रुवीय कोण θ ([[थीटा]]), और अज़ीमुथल कोण φ ([[phi]])। प्रतीक ρ ([[rho]]) का प्रयोग अक्सर r के स्थान पर किया जाता है।]]नोट: यह पृष्ठ गोलाकार निर्देशांक के लिए सामान्य भौतिकी संकेतन का उपयोग करता है, जिसमें <math>\theta</math> z अक्ष और मूल बिंदु को विचाराधीन बिंदु से जोड़ने वाले त्रिज्या वेक्टर के बीच का कोण है, जबकि <math>\phi</math> x-y तल और x अक्ष पर त्रिज्या वेक्टर के प्रक्षेपण के बीच का कोण है। कई अन्य परिभाषाएँ उपयोग में हैं, और इसलिए विभिन्न स्रोतों की तुलना करते समय सावधानी बरतनी चाहिए।<ref name="wolfram">[http://mathworld.wolfram.com/CylindricalCoordinates.html Wolfram Mathworld, spherical coordinates]</ref> | | [[File:3D Spherical.svg|thumb|240px|right|गोलाकार निर्देशांक (r, θ, φ) जैसा कि आमतौर पर भौतिकी में उपयोग किया जाता है: रेडियल दूरी r, ध्रुवीय कोण θ ([[थीटा]]), और अज़ीमुथल कोण φ ([[phi]])। प्रतीक ρ ([[rho]]) का प्रयोग अक्सर r के स्थान पर किया जाता है।]]नोट: यह पृष्ठ गोलाकार निर्देशांक के लिए सामान्य भौतिकी संकेतन का उपयोग करता है, जिसमें <math>\theta</math> z अक्ष और मूल बिंदु को विचाराधीन बिंदु से जोड़ने वाले त्रिज्या वेक्टर के बीच का कोण है, जबकि <math>\phi</math> x-y तल और x अक्ष पर त्रिज्या वेक्टर के प्रक्षेपण के बीच का कोण है। कई अन्य परिभाषाएँ उपयोग में हैं, और इसलिए विभिन्न स्रोतों की तुलना करते समय सावधानी बरतनी चाहिए।<ref name="wolfram">[http://mathworld.wolfram.com/CylindricalCoordinates.html Wolfram Mathworld, spherical coordinates]</ref> |
| Line 34: |
Line 34: |
| \end{bmatrix} | | \end{bmatrix} |
| \begin{bmatrix} \mathbf{\hat x} \\ \mathbf{\hat y} \\ \mathbf{\hat z} \end{bmatrix}</math> | | \begin{bmatrix} \mathbf{\hat x} \\ \mathbf{\hat y} \\ \mathbf{\hat z} \end{bmatrix}</math> |
| ध्यान दें: मैट्रिक्स एक [[ऑर्थोगोनल मैट्रिक्स]] है, यानी इसका व्युत्क्रमणीय मैट्रिक्स बस इसका स्थानान्तरण है। | | ध्यान दें: मैट्रिक्स [[ऑर्थोगोनल मैट्रिक्स]] है, यानी इसका व्युत्क्रमणीय मैट्रिक्स बस इसका स्थानान्तरण है। |
|
| |
|
| === एक सदिश क्षेत्र का समय व्युत्पन्न === | | === एक सदिश क्षेत्र का समय व्युत्पन्न === |
| Line 63: |
Line 63: |
|
| |
|
| दूसरी बार व्युत्पन्न भौतिकी में रुचि का है, क्योंकि यह [[शास्त्रीय यांत्रिकी]] प्रणालियों के लिए [[गति के समीकरण]]ों में पाया जाता है। | | दूसरी बार व्युत्पन्न भौतिकी में रुचि का है, क्योंकि यह [[शास्त्रीय यांत्रिकी]] प्रणालियों के लिए [[गति के समीकरण]]ों में पाया जाता है। |
| बेलनाकार निर्देशांक में एक वेक्टर क्षेत्र का दूसरी बार व्युत्पन्न निम्न द्वारा दिया गया है: | | बेलनाकार निर्देशांक में वेक्टर क्षेत्र का दूसरी बार व्युत्पन्न निम्न द्वारा दिया गया है: |
| <math display="block">\mathbf{\ddot A} | | <math display="block">\mathbf{\ddot A} |
| = \mathbf{\hat \rho} \left(\ddot A_\rho - A_\phi \ddot\phi - 2 \dot A_\phi \dot\phi - A_\rho \dot\phi^2\right) | | = \mathbf{\hat \rho} \left(\ddot A_\rho - A_\phi \ddot\phi - 2 \dot A_\phi \dot\phi - A_\rho \dot\phi^2\right) |
| Line 116: |
Line 116: |
| -\sin\phi & \cos\phi & 0 \end{bmatrix} | | -\sin\phi & \cos\phi & 0 \end{bmatrix} |
| \begin{bmatrix} \mathbf{\hat x} \\ \mathbf{\hat y} \\ \mathbf{\hat z} \end{bmatrix}</math> | | \begin{bmatrix} \mathbf{\hat x} \\ \mathbf{\hat y} \\ \mathbf{\hat z} \end{bmatrix}</math> |
| ध्यान दें: मैट्रिक्स एक ऑर्थोगोनल मैट्रिक्स है, यानी इसका व्युत्क्रम बस इसका स्थानान्तरण है। | | ध्यान दें: मैट्रिक्स ऑर्थोगोनल मैट्रिक्स है, यानी इसका व्युत्क्रम बस इसका स्थानान्तरण है। |
|
| |
|
| कार्तीय इकाई सदिश इस प्रकार गोलाकार इकाई सदिशों से संबंधित हैं: | | कार्तीय इकाई सदिश इस प्रकार गोलाकार इकाई सदिशों से संबंधित हैं: |
Revision as of 23:32, 13 July 2023

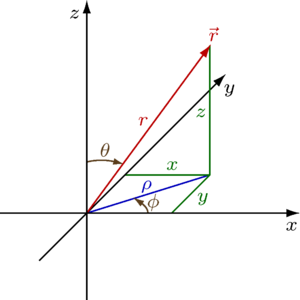
गोलाकार निर्देशांक (r, θ, φ) जैसा कि आमतौर पर भौतिकी में उपयोग किया जाता है: रेडियल दूरी r, ध्रुवीय कोण θ (
थीटा), और अज़ीमुथल कोण φ (
phi)। प्रतीक ρ (
rho) का प्रयोग अक्सर r के स्थान पर किया जाता है।
नोट: यह पृष्ठ गोलाकार निर्देशांक के लिए सामान्य भौतिकी संकेतन का उपयोग करता है, जिसमें  z अक्ष और मूल बिंदु को विचाराधीन बिंदु से जोड़ने वाले त्रिज्या वेक्टर के बीच का कोण है, जबकि
z अक्ष और मूल बिंदु को विचाराधीन बिंदु से जोड़ने वाले त्रिज्या वेक्टर के बीच का कोण है, जबकि  x-y तल और x अक्ष पर त्रिज्या वेक्टर के प्रक्षेपण के बीच का कोण है। कई अन्य परिभाषाएँ उपयोग में हैं, और इसलिए विभिन्न स्रोतों की तुलना करते समय सावधानी बरतनी चाहिए।[1]
x-y तल और x अक्ष पर त्रिज्या वेक्टर के प्रक्षेपण के बीच का कोण है। कई अन्य परिभाषाएँ उपयोग में हैं, और इसलिए विभिन्न स्रोतों की तुलना करते समय सावधानी बरतनी चाहिए।[1]
बेलनाकार समन्वय प्रणाली
वेक्टर फ़ील्ड
सदिशों को बेलनाकार निर्देशांकों में (ρ, φ, z) द्वारा परिभाषित किया जाता है, जहाँ
- ρ xy-तल पर प्रक्षेपित वेक्टर की लंबाई है,
- φ, xy-तल (यानी ρ) और सकारात्मक x-अक्ष (0 ≤ φ < 2π) पर वेक्टर के प्रक्षेपण के बीच का कोण है।
- z नियमित z-निर्देशांक है।
(ρ, φ, z) कार्तीय निर्देशांक में दिया गया है:

या इसके विपरीत:

किसी भी सदिश क्षेत्र को इकाई सदिशों के संदर्भ में इस प्रकार लिखा जा सकता है:

बेलनाकार इकाई वैक्टर कार्टेशियन इकाई वैक्टर से संबंधित हैं:

ध्यान दें: मैट्रिक्स
ऑर्थोगोनल मैट्रिक्स है, यानी इसका व्युत्क्रमणीय मैट्रिक्स बस इसका स्थानान्तरण है।
एक सदिश क्षेत्र का समय व्युत्पन्न
यह पता लगाने के लिए कि सदिश क्षेत्र A समय में कैसे बदलता है, समय व्युत्पन्न की गणना की जानी चाहिए।
इस प्रयोजन के लिए समय व्युत्पन्न के लिए न्यूटन के अंकन का उपयोग किया जाएगा ( ).
कार्टेशियन निर्देशांक में यह बस है:
).
कार्टेशियन निर्देशांक में यह बस है:

हालाँकि, बेलनाकार निर्देशांक में यह बन जाता है:

यूनिट वैक्टर के समय व्युत्पन्न की आवश्यकता है।
वे इसके द्वारा दिए गए हैं:

तो समय व्युत्पन्न सरल हो जाता है:

सदिश क्षेत्र का दूसरी बार व्युत्पन्न
दूसरी बार व्युत्पन्न भौतिकी में रुचि का है, क्योंकि यह शास्त्रीय यांत्रिकी प्रणालियों के लिए गति के समीकरणों में पाया जाता है।
बेलनाकार निर्देशांक में वेक्टर क्षेत्र का दूसरी बार व्युत्पन्न निम्न द्वारा दिया गया है:

इस अभिव्यक्ति को समझने के लिए, P के स्थान पर A प्रतिस्थापित किया जाता है, जहाँ P सदिश (
ρ,
φ,
z) है।
इस का मतलब है कि  .
.
प्रतिस्थापित करने के बाद, परिणाम दिया गया है:

यांत्रिकी में, इस अभिव्यक्ति के पदों को कहा जाता है:

गोलाकार समन्वय प्रणाली
वेक्टर फ़ील्ड
वेक्टर को गोलाकार निर्देशांक में (r, θ, φ) द्वारा परिभाषित किया जाता है, जहां
- r वेक्टर की लंबाई है,
- θ सकारात्मक Z-अक्ष और प्रश्न में वेक्टर के बीच का कोण है (0 ≤ θ ≤ π), और
- φ xy-तल पर वेक्टर के प्रक्षेपण और सकारात्मक X-अक्ष (0 ≤ φ < 2π) के बीच का कोण है।
(r, θ, φ) कार्तीय निर्देशांक में दिया गया है:

या इसके विपरीत:

किसी भी सदिश क्षेत्र को इकाई सदिशों के संदर्भ में इस प्रकार लिखा जा सकता है:

गोलाकार इकाई सदिश कार्तीय इकाई सदिशों से इस प्रकार संबंधित हैं:

ध्यान दें: मैट्रिक्स ऑर्थोगोनल मैट्रिक्स है, यानी इसका व्युत्क्रम बस इसका स्थानान्तरण है।
कार्तीय इकाई सदिश इस प्रकार गोलाकार इकाई सदिशों से संबंधित हैं:

एक सदिश क्षेत्र का समय व्युत्पन्न
यह पता लगाने के लिए कि सदिश क्षेत्र A समय में कैसे बदलता है, समय व्युत्पन्न की गणना की जानी चाहिए।
कार्टेशियन निर्देशांक में यह बस है:

हालाँकि, गोलाकार निर्देशांक में यह बन जाता है:

यूनिट वैक्टर के समय व्युत्पन्न की आवश्यकता है। वे इसके द्वारा दिए गए हैं:

इस प्रकार समय व्युत्पन्न बन जाता है:

यह भी देखें
संदर्भ