|
|
| Line 1: |
Line 1: |
|
| |
|
| {{Short description|Vector field representation in 3D curvilinear coordinate systems}} | | {{Short description|Vector field representation in 3D curvilinear coordinate systems}} |
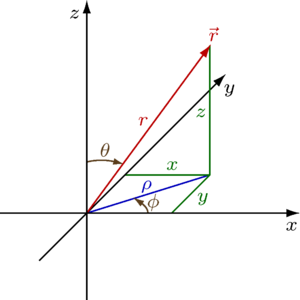
| [[File:3D Spherical.svg|thumb|240px|right|गोलाकार निर्देशांक (r, θ, φ) जैसा कि सामान्यतः भौतिकी में उपयोग किया जाता है: रेडियल दूरी r, ध्रुवीय कोण θ ([[थीटा]]), और अज़ीमुथल कोण φ ([[phi]])। प्रतीक ρ ([[rho]]) का प्रयोग अक्सर r के स्थान पर किया जाता है।]]नोट: यह पृष्ठ गोलाकार निर्देशांक के लिए सामान्य भौतिकी संकेतन का उपयोग करता है, इस प्रकार जिसमें <math>\theta</math> z अक्ष और मूल बिंदु को विचाराधीन बिंदु से जोड़ने वाले त्रिज्या सदिश के बीच का कोण है, जबकि <math>\phi</math> x-y तल और x अक्ष पर त्रिज्या सदिश के प्रक्षेपण के बीच का कोण है। इस प्रकार कई अन्य परिभाषाएँ उपयोग में हैं, और इसलिए विभिन्न स्रोतों की तुलना करते समय सावधानी रखनी चाहिए।<ref name="wolfram">[http://mathworld.wolfram.com/CylindricalCoordinates.html Wolfram Mathworld, spherical coordinates]</ref> | | [[File:3D Spherical.svg|thumb|240px|right|गोलाकार निर्देशांक (r, θ, φ) जैसा कि सामान्यतः भौतिकी में उपयोग किया जाता है: रेडियल दूरी r, ध्रुवीय कोण θ ([[थीटा]]), और अज़ीमुथल कोण φ ([[phi]])। प्रतीक ρ ([[rho]]) का प्रयोग अक्सर r के स्थान पर किया जाता है।]]नोट: यह पृष्ठ गोलाकार निर्देशांक के लिए सामान्य भौतिकी संकेतन का उपयोग करता है, इस प्रकार जिसमें <math>\theta</math> z अक्ष और मूल बिंदु को विचाराधीन बिंदु से जोड़ने वाले त्रिज्या सदिश के मध्य का कोण है, जबकि <math>\phi</math> x-y तल और x अक्ष पर त्रिज्या सदिश के प्रक्षेपण के मध्य का कोण है। इस प्रकार कई अन्य परिभाषाएँ उपयोग में हैं, और इसलिए विभिन्न स्रोतों की तुलना करते समय सावधानी रखनी चाहिए।<ref name="wolfram">[http://mathworld.wolfram.com/CylindricalCoordinates.html Wolfram Mathworld, spherical coordinates]</ref> |
| == बेलनाकार निर्देशांक प्रणाली == | | == बेलनाकार निर्देशांक प्रणाली == |
|
| |
|
| Line 8: |
Line 8: |
| सदिशों को [[बेलनाकार निर्देशांक]] में (ρ, φ, z) द्वारा परिभाषित किया जाता है, जहाँ | | सदिशों को [[बेलनाकार निर्देशांक]] में (ρ, φ, z) द्वारा परिभाषित किया जाता है, जहाँ |
| * ρ xy-तल पर प्रक्षेपित सदिश की लंबाई है, | | * ρ xy-तल पर प्रक्षेपित सदिश की लंबाई है, |
| * φ, xy-तल (अर्थात ρ) और सकारात्मक x-अक्ष (0 ≤ φ < 2π) पर सदिश के प्रक्षेपण के बीच का कोण है। | | * φ, xy-तल (अर्थात ρ) और सकारात्मक x-अक्ष (0 ≤ φ < 2π) पर सदिश के प्रक्षेपण के मध्य का कोण है। |
| * z नियमित z-निर्देशांक है। | | * z नियमित z-निर्देशांक है। |
|
| |
|
| Line 36: |
Line 36: |
| === एक सदिश क्षेत्र का समय व्युत्पन्न === | | === एक सदिश क्षेत्र का समय व्युत्पन्न === |
|
| |
|
| यह पता लगाने के लिए कि सदिश क्षेत्र A समय में कैसे बदलता है, इस प्रकार समय व्युत्पन्न की गणना की जानी चाहिए। इस प्रयोजन के लिए समय व्युत्पन्न के लिए न्यूटन के अंकन (<math>\dot{\mathbf{A}}</math>) का उपयोग किया जाता है कार्तीय निर्देशांक में यह केवल है: | | यह पता लगाने के लिए कि सदिश क्षेत्र A समय में कैसे परिवर्तित होते है, इस प्रकार समय व्युत्पन्न की गणना की जानी चाहिए। इस प्रयोजन के लिए समय व्युत्पन्न के लिए न्यूटन के अंकन (<math>\dot{\mathbf{A}}</math>) का उपयोग किया जाता है कार्तीय निर्देशांक में यह केवल है: |
| <math display="block">\dot{\mathbf{A}} = \dot{A}_x \hat{\mathbf{x}} + \dot{A}_y \hat{\mathbf{y}} + \dot{A}_z \hat{\mathbf{z}}</math> | | <math display="block">\dot{\mathbf{A}} = \dot{A}_x \hat{\mathbf{x}} + \dot{A}_y \hat{\mathbf{y}} + \dot{A}_z \hat{\mathbf{z}}</math> |
| चूँकि, बेलनाकार निर्देशांक में यह बन जाता है: | | चूँकि, बेलनाकार निर्देशांक में यह बन जाता है: |
| Line 64: |
Line 64: |
| इस का कारण है कि <math>\mathbf{A} = \mathbf{P} = \rho \mathbf{\hat \rho} + z \mathbf{\hat z}</math>. | | इस का कारण है कि <math>\mathbf{A} = \mathbf{P} = \rho \mathbf{\hat \rho} + z \mathbf{\hat z}</math>. |
|
| |
|
| प्रतिस्थापित करने के बाद, परिणाम दिया गया है: | | प्रतिस्थापित करने के पश्चात , परिणाम दिया गया है: |
| <math display="block">\ddot\mathbf{P} | | <math display="block">\ddot\mathbf{P} |
| = \mathbf{\hat \rho} \left(\ddot \rho - \rho \dot\phi^2\right) | | = \mathbf{\hat \rho} \left(\ddot \rho - \rho \dot\phi^2\right) |
| Line 86: |
Line 86: |
| सदिश को [[गोलाकार निर्देशांक]] में (r, θ, φ) द्वारा परिभाषित किया जाता है, जहां | | सदिश को [[गोलाकार निर्देशांक]] में (r, θ, φ) द्वारा परिभाषित किया जाता है, जहां |
| *r सदिश की लंबाई है, | | *r सदिश की लंबाई है, |
| * θ सकारात्मक Z-अक्ष और प्रश्न में सदिश (0 ≤ θ ≤ π), के बीच का कोण है और | | * θ सकारात्मक Z-अक्ष और प्रश्न में सदिश (0 ≤ θ ≤ π), के मध्य का कोण है और |
| * φ xy-तल पर सदिश के प्रक्षेपण और सकारात्मक X-अक्ष (0 ≤ φ < 2π) के बीच का कोण है। | | * φ xy-तल पर सदिश के प्रक्षेपण और सकारात्मक X-अक्ष (0 ≤ φ < 2π) के मध्य का कोण है। |
|
| |
|
| (r, θ, φ) कार्तीय निर्देशांक में दिया गया है: | | (r, θ, φ) कार्तीय निर्देशांक में दिया गया है: |
| Line 118: |
Line 118: |
| === एक सदिश क्षेत्र का समय व्युत्पन्न === | | === एक सदिश क्षेत्र का समय व्युत्पन्न === |
|
| |
|
| यह पता लगाने के लिए कि सदिश क्षेत्र A समय में कैसे बदलता है, इस प्रकार समय व्युत्पन्न की गणना की जानी चाहिए। कार्तीय निर्देशांक में यह पर्याप्त है: | | यह पता लगाने के लिए कि सदिश क्षेत्र A समय में कैसे परिवर्तित है, इस प्रकार समय व्युत्पन्न की गणना की जानी चाहिए। कार्तीय निर्देशांक में यह पर्याप्त है: |
| <math display="block">\mathbf{\dot A} = \dot A_x \mathbf{\hat x} + \dot A_y \mathbf{\hat y} + \dot A_z \mathbf{\hat z}</math> | | <math display="block">\mathbf{\dot A} = \dot A_x \mathbf{\hat x} + \dot A_y \mathbf{\hat y} + \dot A_z \mathbf{\hat z}</math> |
| चूँकि, गोलाकार निर्देशांक में यह बन जाता है: | | चूँकि, गोलाकार निर्देशांक में यह बन जाता है: |

गोलाकार निर्देशांक (r, θ, φ) जैसा कि सामान्यतः भौतिकी में उपयोग किया जाता है: रेडियल दूरी r, ध्रुवीय कोण θ (
थीटा), और अज़ीमुथल कोण φ (
phi)। प्रतीक ρ (
rho) का प्रयोग अक्सर r के स्थान पर किया जाता है।
नोट: यह पृष्ठ गोलाकार निर्देशांक के लिए सामान्य भौतिकी संकेतन का उपयोग करता है, इस प्रकार जिसमें  z अक्ष और मूल बिंदु को विचाराधीन बिंदु से जोड़ने वाले त्रिज्या सदिश के मध्य का कोण है, जबकि
z अक्ष और मूल बिंदु को विचाराधीन बिंदु से जोड़ने वाले त्रिज्या सदिश के मध्य का कोण है, जबकि  x-y तल और x अक्ष पर त्रिज्या सदिश के प्रक्षेपण के मध्य का कोण है। इस प्रकार कई अन्य परिभाषाएँ उपयोग में हैं, और इसलिए विभिन्न स्रोतों की तुलना करते समय सावधानी रखनी चाहिए।[1]
x-y तल और x अक्ष पर त्रिज्या सदिश के प्रक्षेपण के मध्य का कोण है। इस प्रकार कई अन्य परिभाषाएँ उपयोग में हैं, और इसलिए विभिन्न स्रोतों की तुलना करते समय सावधानी रखनी चाहिए।[1]
बेलनाकार निर्देशांक प्रणाली
सदिश क्षेत्र
सदिशों को बेलनाकार निर्देशांक में (ρ, φ, z) द्वारा परिभाषित किया जाता है, जहाँ
- ρ xy-तल पर प्रक्षेपित सदिश की लंबाई है,
- φ, xy-तल (अर्थात ρ) और सकारात्मक x-अक्ष (0 ≤ φ < 2π) पर सदिश के प्रक्षेपण के मध्य का कोण है।
- z नियमित z-निर्देशांक है।
(ρ, φ, z) कार्तीय निर्देशांक में दिया गया है:

या इसके विपरीत:

किसी भी सदिश क्षेत्र को इकाई सदिशों के संदर्भ में इस प्रकार लिखा जा सकता है:

बेलनाकार इकाई सदिश कार्तीय इकाई सदिश से संबंधित हैं:

ध्यान दें: आव्यूह
ऑर्थोगोनल आव्यूह है, अर्थात इसका व्युत्क्रमणीय आव्यूह इसका स्थानान्तरण है।
एक सदिश क्षेत्र का समय व्युत्पन्न
यह पता लगाने के लिए कि सदिश क्षेत्र A समय में कैसे परिवर्तित होते है, इस प्रकार समय व्युत्पन्न की गणना की जानी चाहिए। इस प्रयोजन के लिए समय व्युत्पन्न के लिए न्यूटन के अंकन ( ) का उपयोग किया जाता है कार्तीय निर्देशांक में यह केवल है:
) का उपयोग किया जाता है कार्तीय निर्देशांक में यह केवल है:

चूँकि, बेलनाकार निर्देशांक में यह बन जाता है:

यूनिट सदिश के समय व्युत्पन्न की आवश्यकता है। वे इसके द्वारा दिए गए हैं:

तो समय व्युत्पन्न सरल हो जाता है:

सदिश क्षेत्र का दूसरी बार व्युत्पन्न
दूसरी बार व्युत्पन्न भौतिकी में रुचि का है, क्योंकि यह मौलिक यांत्रिकी प्रणालियों के लिए गति के समीकरण में पाया जाता है। इस प्रकार बेलनाकार निर्देशांक में सदिश क्षेत्र का दूसरी बार व्युत्पन्न निम्न द्वारा दिया गया है:

इस एक्सप्रेशन को समझने के लिए, P के स्थान पर A प्रतिस्थापित किया जाता है, जहाँ P सदिश (
ρ,
φ,
z) है।
इस का कारण है कि  .
.
प्रतिस्थापित करने के पश्चात , परिणाम दिया गया है:

यांत्रिकी में, इस एक्सप्रेशन के पदों को कहा जाता है:

गोलाकार निर्देशांक प्रणाली
सदिश क्षेत्र
सदिश को गोलाकार निर्देशांक में (r, θ, φ) द्वारा परिभाषित किया जाता है, जहां
- r सदिश की लंबाई है,
- θ सकारात्मक Z-अक्ष और प्रश्न में सदिश (0 ≤ θ ≤ π), के मध्य का कोण है और
- φ xy-तल पर सदिश के प्रक्षेपण और सकारात्मक X-अक्ष (0 ≤ φ < 2π) के मध्य का कोण है।
(r, θ, φ) कार्तीय निर्देशांक में दिया गया है:

या इसके विपरीत:

किसी भी सदिश क्षेत्र को इकाई सदिशों के संदर्भ में इस प्रकार लिखा जा सकता है:

गोलाकार इकाई सदिश कार्तीय इकाई सदिशों से इस प्रकार संबंधित हैं:

ध्यान दें: आव्यूह ऑर्थोगोनल आव्यूह है, अर्थात इसका व्युत्क्रम केवल इसका स्थानान्तरण है।
कार्तीय इकाई सदिश इस प्रकार गोलाकार इकाई सदिशों से संबंधित हैं:

एक सदिश क्षेत्र का समय व्युत्पन्न
यह पता लगाने के लिए कि सदिश क्षेत्र A समय में कैसे परिवर्तित है, इस प्रकार समय व्युत्पन्न की गणना की जानी चाहिए। कार्तीय निर्देशांक में यह पर्याप्त है:

चूँकि, गोलाकार निर्देशांक में यह बन जाता है:

यूनिट सदिश के समय व्युत्पन्न की आवश्यकता है। वे इसके द्वारा दिए गए हैं:

इस प्रकार समय व्युत्पन्न बन जाता है:

यह भी देखें
संदर्भ