प्रक्रिया क्षमता सूचकांक

प्रक्रिया क्षमता सूचकांक, या प्रक्रिया क्षमता अनुपात, प्रक्रिया क्षमता का एक सांख्यिकीय माप है: विशिष्टता (तकनीकी मानक) सीमा के भीतर उत्पादन उत्पन्न करने के लिए एक इंजीनियरिंग प्रक्रिया की क्षमता। प्रक्रिया क्षमता की अवधारणा केवल उन प्रक्रियाओं के लिए अर्थ रखती है जो सांख्यिकीय नियंत्रण की स्थिति में हैं। इसका मतलब यह है कि यह उन विचलनों का विवरण नहीं दे सकता है जिनकी अपेक्षा नहीं की जाती है, जैसे कि गलत तरीके से संरेखित, क्षतिग्रस्त, या घिसे हुए उपकरण। प्रक्रिया क्षमता सूचकांक मापते हैं कि एक प्रक्रिया अपनी विशिष्टता सीमाओं के सापेक्ष कितनी "प्राकृतिक भिन्नता" का अनुभव करती है, और विभिन्न प्रक्रियाओं की तुलना इस बात से करने की अनुमति देती है कि कोई संगठन उन्हें कितनी अच्छी तरह नियंत्रित करता है। कुछ हद तक विपरीत रूप से, उच्च सूचकांक मान बेहतर प्रदर्शन का संकेत देते हैं, जबकि शून्य उच्च विचलन का संकेत देता है।

गैर-विशेषज्ञों के लिए उदाहरण

एक कंपनी एक खराद पर नाममात्र व्यास 20 मिमी के साथ धुरी का उत्पादन करती है। चूँकि कोई भी धुरी बिल्कुल 20 मिमी तक नहीं बनाई जा सकती है, डिज़ाइनर अधिकतम स्वीकार्य विचलन (जिन्हें सहनशीलता या विनिर्देश सीमा कहा जाता है) निर्दिष्ट करता है। उदाहरण के लिए, आवश्यकता यह हो सकती है कि धुरी 19.9 और 20.2 मिमी के बीच होनी चाहिए। प्रक्रिया क्षमता सूचकांक एक माप है कि यह कितनी संभावना है कि एक उत्पादित धुरी इस आवश्यकता को पूरा करती है। सूचकांक केवल सांख्यिकीय (प्राकृतिक) विविधताओं से संबंधित है। ये ऐसी विविधताएँ हैं जो बिना किसी विशेष कारण के स्वाभाविक रूप से घटित होती हैं। जिन त्रुटियों पर ध्यान नहीं दिया गया उनमें ऑपरेटर त्रुटियां, या लेथ तंत्र में गड़बड़ी शामिल है जिसके परिणामस्वरूप उपकरण की गलत या अप्रत्याशित स्थिति उत्पन्न हो जाती है। यदि बाद वाले प्रकार की त्रुटियां होती हैं, तो प्रक्रिया सांख्यिकीय नियंत्रण की स्थिति में नहीं है। जब यह मामला है, तो प्रक्रिया क्षमता सूचकांक अर्थहीन है।

परिचय

यदि प्रक्रिया की ऊपरी और निचली विनिर्देश (तकनीकी मानक) सीमाएं यूएसएल और एलएसएल हैं, तो लक्ष्य प्रक्रिया माध्य T है, प्रक्रिया का अनुमानित माध्य ${\hat {\mu }}$ है और प्रक्रिया की अनुमानित परिवर्तनशीलता (मानक विचलन के रूप में व्यक्त) ${\hat {\sigma }}$ है, तो आम तौर पर स्वीकृत प्रक्रिया क्षमता सूचकांकों में सम्मिलित हैं:

Index	Description
${\hat {C}}_{p}={\frac {\text{USL - LSL}}{6{\hat {\sigma }}}}$	यह अनुमान लगाता है कि यदि प्रक्रिया माध्य को विनिर्देश सीमाओं के बीच केंद्रित किया जाए तो प्रक्रिया क्या उत्पादन करने में सक्षम है। मानता है कि प्रक्रिया का उत्पादन लगभग सामान्य रूप से वितरित है।
${\hat {C}}_{p,{\text{lower}}}={{\hat {\mu }}-{\text{LSL}} \over 3{\hat {\sigma }}}$	उन विशिष्टताओं के लिए प्रक्रिया क्षमता का अनुमान लगाता है जिनमें केवल निचली सीमा निहित होती है (उदाहरण के लिए, ताकत)। मानता है कि प्रक्रिया का उत्पादन लगभग सामान्य रूप से वितरित है।
${\hat {C}}_{p,{\text{upper}}}={{\text{USL}}-{\hat {\mu }} \over 3{\hat {\sigma }}}$	उन विशिष्टताओं के लिए प्रक्रिया क्षमता का अनुमान लगाता है जिनमें केवल ऊपरी सीमा होती है (उदाहरण के लिए, एकाग्रता)। मानता है कि प्रक्रिया का उत्पादन लगभग सामान्य रूप से वितरित है।
${\hat {C}}_{pk}=\min {\Bigg [}{{\text{USL}}-{\hat {\mu }} \over 3{\hat {\sigma }}},{{\hat {\mu }}-{\text{LSL}} \over 3{\hat {\sigma }}}{\Bigg ]}$	अनुमान लगाता है कि प्रक्रिया क्या उत्पादन करने में सक्षम है, यह ध्यान में रखते हुए कि प्रक्रिया माध्य विनिर्देश सीमाओं के बीच केंद्रित नहीं हो सकता है। (यदि प्रक्रिया माध्य केन्द्रित नहीं है, तो ${\hat {C}}_{p}$ प्रक्रिया क्षमता को अधिक महत्व देता है।) ${\hat {C}}_{pk}<0$ यदि प्रक्रिया माध्य विनिर्देश सीमा से बाहर आता है। मानता है कि प्रक्रिया का उत्पादन लगभग सामान्य रूप से वितरित है।
${\hat {C}}_{pm}={\frac {{\hat {C}}_{p}}{\sqrt {1+\left({\frac {{\hat {\mu }}-T}{\hat {\sigma }}}\right)^{2}}}}$	लक्ष्य T के आसपास प्रक्रिया क्षमता का अनुमान लगाता है। ${\hat {C}}_{pm}$ हमेशा शून्य से बड़ा होता है। यह मानता है कि प्रक्रिया का उत्पादन लगभग सामान्य रूप से वितरित होता है। ${\hat {C}}_{pm}$ को तागुची क्षमता सूचकांक के रूप में भी जाना जाता है।
${\hat {C}}_{pkm}={\frac {{\hat {C}}_{pk}}{\sqrt {1+\left({\frac {{\hat {\mu }}-T}{\hat {\sigma }}}\right)^{2}}}}$	किसी लक्ष्य, T के आसपास प्रक्रिया क्षमता का अनुमान लगाता है, और केन्द्र के बाहर प्रक्रिया माध्य का हिसाब रखता है। मानता है कि प्रक्रिया का उत्पादन लगभग सामान्य रूप से वितरित है।

${\hat {\sigma }}$ का अनुमान मानक विचलन के निष्पक्ष अनुमान का उपयोग करके लगाया जाता है।

अनुशंसित मान

प्रक्रिया क्षमता सूचकांकों का निर्माण तेजी से उच्च मूल्यों के साथ अधिक वांछनीय क्षमता को व्यक्त करने के लिए किया जाता है। शून्य के करीब या नीचे के मान लक्ष्य से बाहर चल रही प्रक्रियाओं को दर्शाते हैं (${\hat {\mu }}$ T से दूर) या उच्च भिन्नता के साथ।

न्यूनतम स्वीकार्य प्रक्रिया क्षमता लक्ष्यों के लिए मूल्य तय करना व्यक्तिगत राय का मामला है, और जो सर्वसम्मति मौजूद है वह उद्योग, सुविधा और विचाराधीन प्रक्रिया के अनुसार भिन्न होती है। उदाहरण के लिए, ऑटोमोटिव उद्योग में, ऑटोमोटिव इंडस्ट्री एक्शन ग्रुप अनुशंसित सी के लिए उत्पादन भाग अनुमोदन प्रक्रिया, चौथे संस्करण में दिशानिर्देश निर्धारित करता है।_pk महत्वपूर्ण-से-गुणवत्ता प्रक्रिया विशेषताओं के लिए न्यूनतम मान। हालाँकि, ये मानदंड बहस योग्य हैं और कई प्रक्रियाओं का मूल्यांकन क्षमता के लिए नहीं किया जा सकता है क्योंकि उनका उचित मूल्यांकन नहीं किया गया है।

चूँकि प्रक्रिया क्षमता विनिर्देश का एक कार्य है, प्रक्रिया क्षमता सूचकांक केवल विनिर्देश जितना ही अच्छा है। उदाहरण के लिए, यदि विनिर्देश भाग के कार्य और आलोचनात्मकता पर विचार किए बिना एक इंजीनियरिंग दिशानिर्देश से आया है, तो प्रक्रिया क्षमता के बारे में चर्चा बेकार है, और यदि इस पर ध्यान केंद्रित किया जाए कि विनिर्देश के बाहर एक भाग की सीमा रेखा होने के वास्तविक जोखिम क्या हैं, तो अधिक लाभ होंगे। . तागुची विधियों का हानि कार्य इस अवधारणा को बेहतर ढंग से दर्शाता है।

कम से कम एक अकादमिक विशेषज्ञ अनुशंसा करता है निम्नलिखित:

Situation	Recommended minimum process capability for two-sided specifications	Recommended minimum process capability for one-sided specification
Existing process	1.33	1.25
New process	1.50	1.45
Safety or critical parameter for existing process	1.50	1.45
Safety or critical parameter for new process	1.67	1.60
Six Sigma quality process	2.00	2.00

हालाँकि, जहां एक प्रक्रिया 2.5 से अधिक क्षमता सूचकांक के साथ एक विशेषता उत्पन्न करती है, अनावश्यक परिशुद्धता महंगी हो सकती है।

प्रक्रिया के नतीजों के उपायों से संबंध

प्रक्रिया क्षमता सूचकांकों से मैपिंग, जैसे सी_pk, प्रक्रिया के नतीजों के उपाय सीधे हैं। प्रोसेस फॉलआउट यह निर्धारित करता है कि एक प्रक्रिया कितने दोष पैदा करती है और इसे प्रति मिलियन अवसरों में दोष या प्रति मिलियन पार्ट्स में मापा जाता है। प्रक्रिया उपज प्रक्रिया परिणाम का पूरक है और संभाव्यता घनत्व फ़ंक्शन के तहत क्षेत्र के लगभग बराबर है Failed to parse (Conversion error. Server ("cli") reported: "SyntaxError: Expected "-", "[", "\\", "\\begin", "\\begin{", "]", "^", "_", "{", "}", [ \t\n\r], [%$], [().], [,:;?!'], [/|], [0-9], [><~], [\-+*=], or [a-zA-Z] but "प" found.in 1:53"): {\displaystyle \Phi(\sigma) = \frac{1}{\sqrt{2\pi>< प्रक्रिया आउटपुट लगभग [[सामान्य रूप से वितरित]] होता है। अल्पावधि (शॉर्ट सिग्मा) में, रिश्ते हैं: {| class="wikitable" |- ! C_p ! Sigma level (σ) ! Area under the [[probability density function]] <math>\Phi(\sigma)} ! Process yield ! Process fallout (in terms of DPMO/PPM) |- | 0.33 || 1 ||0.6826894921||68.27%||317311 |- | 0.67 || 2 ||0.9544997361||95.45%||45500 |- | 1.00 || 3 ||0.9973002039||99.73%||2700 |- | 1.33 || 4 ||0.9999366575||99.99%||63 |- | 1.67 || 5 ||0.9999994267||99.9999%||1 |- | 2.00 || 6 ||0.9999999980||99.9999998%||0.002 |} लंबी अवधि में, प्रक्रियाएं महत्वपूर्ण रूप से स्थानांतरित या बहाव कर सकती हैं (अधिकांश नियंत्रण चार्ट केवल प्रक्रिया उत्पादन में 1.5σ या उससे अधिक के परिवर्तनों के प्रति संवेदनशील होते हैं)। यदि प्रक्रियाओं में लक्ष्य से 1.5 सिग्मा शिफ्ट 1.5σ दूर था (सिक्स सिग्मा#सिग्मा स्तर देखें), तो यह इन रिश्तों का उत्पादन करेगा:

Cp	Adjusted Sigma level (σ)	Area under the probability density function $\Phi (\sigma )$	Process yield	Process fallout (in terms of DPMO/PPM)
0.33	1	0.3085375387	30.85%	691462
0.67	2	0.6914624613	69.15%	308538
1.00	3	0.9331927987	93.32%	66807
1.33	4	0.9937903347	99.38%	6209
1.67	5	0.9997673709	99.9767%	232.6
2.00	6	0.9999966023	99.99966%	3.40

चूँकि प्रक्रियाएँ लंबे समय तक महत्वपूर्ण रूप से स्थानांतरित या बहाव कर सकती हैं, प्रत्येक प्रक्रिया में एक अद्वितीय सिग्मा शिफ्ट मान होगा, इस प्रकार प्रक्रिया क्षमता सूचकांक कम लागू होते हैं क्योंकि उन्हें सांख्यिकीय नियंत्रण की आवश्यकता होती है।

उदाहरण

100.00 माइक्रोमीटर|μm के लक्ष्य और क्रमशः 106.00 μm और 94.00 μm की ऊपरी और निचली विनिर्देश सीमा के साथ एक गुणवत्ता विशेषता पर विचार करें। यदि, कुछ समय तक प्रक्रिया की सावधानीपूर्वक निगरानी करने के बाद, यह प्रतीत होता है कि प्रक्रिया नियंत्रण में है और अनुमानित रूप से उत्पादन दे रही है (जैसा कि नीचे रन चार्ट में दर्शाया गया है), तो हम इसके माध्य और मानक विचलन का सार्थक अनुमान लगा सकते हैं।

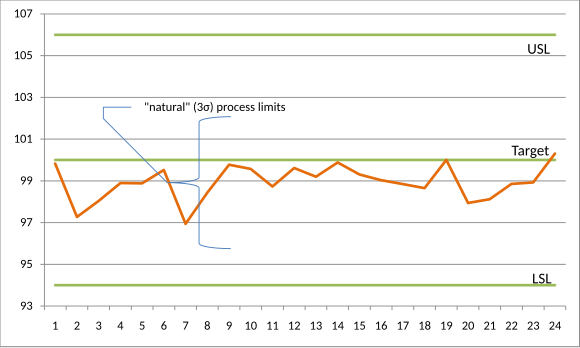अगर ${\hat {\mu }}$ और ${\hat {\sigma }}$ का अनुमान क्रमशः 98.94 μm और 1.03 μm है, तो

Index
${\hat {C}}_{p}={\frac {\text{USL - LSL}}{6{\hat {\sigma }}}}={\frac {106.00-94.00}{6\times 1.03}}=1.94$
${\hat {C}}_{pk}=\min {\Bigg [}{{\text{USL}}-{\hat {\mu }} \over 3{\hat {\sigma }}},{{\hat {\mu }}-{\text{LSL}} \over 3{\hat {\sigma }}}{\Bigg ]}=\min {\Bigg [}{106.00-98.94 \over 3\times 1.03},{98.94-94 \over 3\times 1.03}{\Bigg ]}=1.60$
${\hat {C}}_{pm}={\frac {{\hat {C}}_{p}}{\sqrt {1+\left({\frac {{\hat {\mu }}-T}{\hat {\sigma }}}\right)^{2}}}}={\frac {1.94}{\sqrt {1+\left({\frac {98.94-100.00}{1.03}}\right)^{2}}}}=1.35$
${\hat {C}}_{pkm}={\frac {{\hat {C}}_{pk}}{\sqrt {1+\left({\frac {{\hat {\mu }}-T}{\hat {\sigma }}}\right)^{2}}}}={\frac {1.60}{\sqrt {1+\left({\frac {98.94-100.00}{1.03}}\right)^{2}}}}=1.11$

तथ्य यह है कि प्रक्रिया ऑफ-सेंटर (अपने लक्ष्य से लगभग 1σ नीचे) चल रही है, सी के लिए स्पष्ट रूप से भिन्न मूल्यों में परिलक्षित होता है_{पी</उप>, सीपीके</उप>, सीpm, और सीपीकेएम</उप>.}

यह भी देखें

• प्रक्रिया अभियंता)
• प्रक्रिया क्षमता
• प्रक्रिया प्रदर्शन सूचकांक