जैककार्ड सूचकांक: Difference between revisions
No edit summary |
No edit summary |
||
| Line 5: | Line 5: | ||
| image1 = Intersection of sets A and B.svg | | image1 = Intersection of sets A and B.svg | ||
| image2 = Union of sets A and B.svg | | image2 = Union of sets A and B.svg | ||
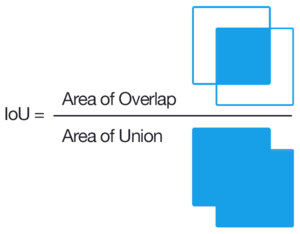
| footer = | | footer = दो समुच्चयों A और B का प्रतिच्छेदन और मिलन | ||
}} | }} | ||
| Line 16: | Line 16: | ||
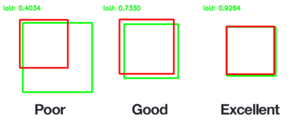
| footer = Intersection over Union as a similarity measure for [[object detection]] on images - an important task in [[computer vision]]. | | footer = Intersection over Union as a similarity measure for [[object detection]] on images - an important task in [[computer vision]]. | ||
}} | }} | ||
'''जैककार्ड सूचकांक''', जिसे '''जैकार्ड समानता गुणांक''' के रूप में भी जाना जाता है, एक आँकड़ा है जिसका उपयोग [[नमूना (सांख्यिकी)]] समुच्चय की [[समानता माप]] और [[विविधता सूचकांक]] को मापने के लिए किया जाता है। इसे 1884 में [[ग्रोव कार्ल गिल्बर्ट]] द्वारा उनके ''' | '''जैककार्ड इंडेक्स (सूचकांक'''), जिसे '''जैकार्ड समानता गुणांक''' के रूप में भी जाना जाता है, एक आँकड़ा है जिसका उपयोग [[नमूना (सांख्यिकी)]] समुच्चय की [[समानता माप]] और [[विविधता सूचकांक|विविधता इंडेक्स]] को मापने के लिए किया जाता है। इसे 1884 में [[ग्रोव कार्ल गिल्बर्ट]] द्वारा उनके वेरिफिकेशन '''(प्रमाणन) के अनुपात''' के रूप में विकसित किया गया था (v)<ref>{{Cite journal | url=https://doi.org/10.1175/1520-0434(1996)011%3C0003:TFAASE%3E2.0.CO;2 | doi=10.1175/1520-0434(1996)011<0003:TFAASE>2.0.CO;2 | issn=1520-0434 | year=1996 | volume=11 | page=3 | title=The Finley Affair: A Signal Event in the History of Forecast Verification | last1=Murphy | first1=Allan H. | journal=Weather and Forecasting | issue=1 | bibcode=1996WtFor..11....3M | s2cid=54532560 }}</ref> और अब इसे प्रायः मौसम विज्ञान में '''क्रिटिकल सक्सेस इंडेक्स''' के रूप में जाना जाता है।<ref>{{cite web|url=https://www.swpc.noaa.gov/sites/default/files/images/u30/Forecast%20Verification%20Glossary.pdf|title=पूर्वानुमान सत्यापन शब्दावली|website=noaa.gov|access-date=21 May 2023}}</ref> इसे बाद में [[पॉल जैकार्ड]] द्वारा स्वतंत्र रूप से विकसित किया गया था, जिसे मूल रूप से फ्रांसीसी नाम गुणांक डी कम्युनॉटे दिया गया था,<ref>{{Cite journal|last=Jaccard|first=Paul| title=अल्पाइन क्षेत्र में वनस्पतियों का वितरण.1|date=February 1912|journal=New Phytologist|volume=11|issue=2|pages=37–50|doi=10.1111/j.1469-8137.1912.tb05611.x|issn=0028-646X}}</ref> और टी. टैनिमोटो द्वारा फिर से स्वतंत्र रूप से तैयार किया गया।<ref name=":1" />इस प्रकार, कुछ क्षेत्रों में '''टैनिमोटो इंडेक्स''' या '''टैनिमोटो गुणांक''' का भी उपयोग किया जाता है। हालाँकि, सामान्यतः '''यूनियन ओवर इंटरसेक्शन''' का अनुपात लेने में वे समान हैं। जैकार्ड गुणांक परिमित नमूना समुच्चय के बीच समानता को मापता है, और इसे नमूना समुच्चय के [[संघ (सेट सिद्धांत)|संघ (समुच्चय सिद्धांत)]] के आकार से विभाजित प्रतिच्छेदन (इंटरसेक्शन) के आकार (समुच्चय सिद्धांत) के रूप में परिभाषित किया जाता है: | ||
:<math> J(A,B) = {{|A \cap B|}\over{|A \cup B|}} = {{|A \cap B|}\over{|A| + |B| - |A \cap B|}}.</math> | :<math> J(A,B) = {{|A \cap B|}\over{|A \cup B|}} = {{|A \cap B|}\over{|A| + |B| - |A \cap B|}}.</math> | ||
ध्यान दें कि डिज़ाइन के अनुसार, <math> 0\le J(A,B)\le 1.</math> यदि A प्रतिच्छेदन B रिक्त है, तो J(A,B) = 0. जैककार्ड गुणांक का व्यापक रूप से कंप्यूटर विज्ञान, पारिस्थितिकी, जीनोमिक्स और अन्य विज्ञानों में उपयोग किया जाता है, जहां [[बाइनरी डेटा]] का उपयोग किया जाता है। जैकार्ड गुणांक के साथ परिकल्पना परीक्षण के लिए सटीक समाधान और सन्निकटन दोनों विधियाँ उपलब्ध हैं।<ref name=":0">{{cite journal | vauthors = Chung NC, Miasojedow B, Startek M, Gambin A | title = Jaccard/Tanimoto similarity test and estimation methods for biological presence-absence data | journal = BMC Bioinformatics | volume = 20 | issue = Suppl 15 | pages = 644 | date = December 2019 | pmid = 31874610 | pmc = 6929325 | doi = 10.1186/s12859-019-3118-5 | arxiv=1903.11372 | url = }}</ref> | ध्यान दें कि डिज़ाइन के अनुसार, <math> 0\le J(A,B)\le 1.</math> यदि A प्रतिच्छेदन B रिक्त है, तो J(A,B) = 0. जैककार्ड गुणांक का व्यापक रूप से कंप्यूटर विज्ञान, पारिस्थितिकी, जीनोमिक्स और अन्य विज्ञानों में उपयोग किया जाता है, जहां [[बाइनरी डेटा]] का उपयोग किया जाता है। जैकार्ड गुणांक के साथ परिकल्पना परीक्षण के लिए सटीक समाधान और सन्निकटन दोनों विधियाँ उपलब्ध हैं।<ref name=":0">{{cite journal | vauthors = Chung NC, Miasojedow B, Startek M, Gambin A | title = Jaccard/Tanimoto similarity test and estimation methods for biological presence-absence data | journal = BMC Bioinformatics | volume = 20 | issue = Suppl 15 | pages = 644 | date = December 2019 | pmid = 31874610 | pmc = 6929325 | doi = 10.1186/s12859-019-3118-5 | arxiv=1903.11372 | url = }}</ref> | ||
जैककार्ड समानता बैग यानी [[मल्टीसेट|मल्टीसमुच्चय]] | |||
बैग | जैककार्ड समानता बैग यानी [[मल्टीसेट|मल्टीसमुच्चय]] पर भी लागू होती है। इसका एक समान सूत्र है,<ref>{{cite book | vauthors = Leskovec J, Rajaraman A, Ullman J |title=बड़े पैमाने पर डेटासेट का खनन|publisher=Cambridge |year=2020 |isbn=9781108476348 }} and p. 76-77 in an earlier version http://infolab.stanford.edu/~ullman/mmds/ch3.pdf</ref> लेकिन प्रतीकों का मतलब है बैग प्रतिच्छेदन और बैग योग (संघ नहीं)। अधिकतम मान 1/2 है. | ||
:<math> J(A,B) = {{|A \cap B|}\over{|A \uplus B|}} = {{|A \cap B|}\over{|A| + |B|}}.</math> | :<math> J(A,B) = {{|A \cap B|}\over{|A \uplus B|}} = {{|A \cap B|}\over{|A| + |B|}}.</math> | ||
जैकार्ड दूरी, जो नमूना समुच्चय के बीच ''असमानता'' को मापती है, जैकार्ड गुणांक का पूरक है और इसे जैकर्ड गुणांक को 1 से घटाकर, या समकक्ष रूप से, संघ और प्रतिच्छेदन के आकार के अंतर को विभाजित करके प्राप्त किया जाता है। संघ के आकार के अनुसार दो समुच्चय में से: | '''जैकार्ड दूरी''', जो नमूना समुच्चय के बीच ''असमानता'' को मापती है, जैकार्ड गुणांक का पूरक है और इसे जैकर्ड गुणांक को 1 से घटाकर, या समकक्ष रूप से, संघ और प्रतिच्छेदन के आकार के अंतर को विभाजित करके प्राप्त किया जाता है। संघ के आकार के अनुसार दो समुच्चय में से: | ||
:<math> d_J(A,B) = 1 - J(A,B) = { { |A \cup B| - |A \cap B| } \over |A \cup B| }.</math> | :<math> d_J(A,B) = 1 - J(A,B) = { { |A \cup B| - |A \cap B| } \over |A \cup B| }.</math> | ||
जैकार्ड दूरी की एक वैकल्पिक व्याख्या [[सममित अंतर]] के आकार के अनुपात के रूप में है <math>A \triangle B = (A \cup B) - (A \cap B)</math> संघ को जैककार्ड दूरी का उपयोग सामान्यतः [[क्लस्टर विश्लेषण]] और ''n'' नमूना समुच्चय के [[बहुआयामी स्केलिंग]] के लिए n × n आव्यूह की गणना करने के लिए किया जाता है। | |||
यह दूरी सभी परिमित समुच्चय के संग्रह पर एक दूरी फलन है।<ref>{{cite journal | vauthors = Kosub S | title = जैकार्ड दूरी के लिए त्रिभुज असमानता पर एक नोट।| journal = Pattern Recognition Letters | date = April 2019 | volume = 120 | pages = 36–8 | doi = 10.1016/j.patrec.2018.12.007 | arxiv = 1612.02696 | bibcode = 2019PaReL.120...36K | s2cid = 564831 }}</ref><ref name="lipkus">{{cite journal | vauthors = Lipkus AH | title=तनिमोटो दूरी के लिए त्रिभुज असमानता का प्रमाण|journal=Journal of Mathematical Chemistry |volume=26 |number=1–3 |year=1999 |pages=263–265 |doi=10.1023/A:1019154432472| s2cid=118263043 }}</ref><ref>{{cite journal | vauthors = Levandowsky M, Winter D |title=सेट के बीच की दूरी|journal=Nature |volume=234 |number=5 |year=1971 |pages=34–35 |doi=10.1038/234034a0|bibcode=1971Natur.234...34L |s2cid=4283015 }}</ref> | यह दूरी सभी परिमित समुच्चय के संग्रह पर एक दूरी फलन है।<ref>{{cite journal | vauthors = Kosub S | title = जैकार्ड दूरी के लिए त्रिभुज असमानता पर एक नोट।| journal = Pattern Recognition Letters | date = April 2019 | volume = 120 | pages = 36–8 | doi = 10.1016/j.patrec.2018.12.007 | arxiv = 1612.02696 | bibcode = 2019PaReL.120...36K | s2cid = 564831 }}</ref><ref name="lipkus">{{cite journal | vauthors = Lipkus AH | title=तनिमोटो दूरी के लिए त्रिभुज असमानता का प्रमाण|journal=Journal of Mathematical Chemistry |volume=26 |number=1–3 |year=1999 |pages=263–265 |doi=10.1023/A:1019154432472| s2cid=118263043 }}</ref><ref>{{cite journal | vauthors = Levandowsky M, Winter D |title=सेट के बीच की दूरी|journal=Nature |volume=234 |number=5 |year=1971 |pages=34–35 |doi=10.1038/234034a0|bibcode=1971Natur.234...34L |s2cid=4283015 }}</ref> | ||
[[माप (गणित)]] के लिए जैककार्ड दूरी का संस्करण भी है, जिसमें [[संभाव्यता माप]] भी सम्मिलित है। अगर <math>\mu</math> [[मापने योग्य स्थान]] पर एक माप है <math>X</math>, फिर हम जैकार्ड गुणांक को परिभाषित करते हैं | [[माप (गणित)]] के लिए जैककार्ड दूरी का संस्करण भी है, जिसमें [[संभाव्यता माप]] भी सम्मिलित है। अगर <math>\mu</math> [[मापने योग्य स्थान]] पर एक माप है <math>X</math>, फिर हम जैकार्ड गुणांक को परिभाषित करते हैं | ||
| Line 67: | Line 68: | ||
जैककार्ड समानता गुणांक और परिणामस्वरूप संबंधित आव्यूह के आधार पर सांख्यिकीय अनुमान लगाया जा सकता है।<ref name=":0" />एन विशेषताओं के साथ दो नमूना समुच्चय ''A'' और ''B'' दिए जाने पर, यह देखने के लिए एक सांख्यिकीय परीक्षण आयोजित किया जा सकता है कि क्या ओवरलैप सांख्यिकीय महत्व है। सटीक समाधान उपलब्ध है, हालाँकि n बढ़ने पर गणना महंगी हो सकती है।<ref name=":0" />अनुमान विधियाँ या तो [[बहुपद वितरण]] का अनुमान लगाकर या बूटस्ट्रैपिंग द्वारा उपलब्ध हैं।<ref name=":0" /> | जैककार्ड समानता गुणांक और परिणामस्वरूप संबंधित आव्यूह के आधार पर सांख्यिकीय अनुमान लगाया जा सकता है।<ref name=":0" />एन विशेषताओं के साथ दो नमूना समुच्चय ''A'' और ''B'' दिए जाने पर, यह देखने के लिए एक सांख्यिकीय परीक्षण आयोजित किया जा सकता है कि क्या ओवरलैप सांख्यिकीय महत्व है। सटीक समाधान उपलब्ध है, हालाँकि n बढ़ने पर गणना महंगी हो सकती है।<ref name=":0" />अनुमान विधियाँ या तो [[बहुपद वितरण]] का अनुमान लगाकर या बूटस्ट्रैपिंग द्वारा उपलब्ध हैं।<ref name=":0" /> | ||
=== [[सरल मिलान गुणांक]] (एसएमसी) के साथ अंतर === | === [[सरल मिलान गुणांक]] (एसएमसी) के साथ अंतर === | ||
जब बाइनरी विशेषताओं के लिए उपयोग किया जाता है, तो जैककार्ड इंडेक्स सरल मिलान गुणांक के समान होता है। मुख्य अंतर यह है कि एसएमसी के पास शब्द है <math>M_{00}</math> इसके अंश और हर में, जबकि जैककार्ड | जब बाइनरी विशेषताओं के लिए उपयोग किया जाता है, तो जैककार्ड इंडेक्स सरल मिलान गुणांक के समान होता है। मुख्य अंतर यह है कि एसएमसी के पास शब्द है <math>M_{00}</math> इसके अंश और हर में, जबकि जैककार्ड इंडेक्स में ऐसा नहीं है। इस प्रकार, एसएमसी दोनों पारस्परिक उपस्थिति (जब एक विशेषता दोनों समुच्चय में उपस्थित है) और पारस्परिक अनुपस्थिति (जब एक विशेषता दोनों समुच्चय में अनुपस्थित है) को मिलान के रूप में गिनती है और इसकी तुलना ब्रह्मांड में विशेषताओं की कुल संख्या से करती है, जबकि जैककार्ड इंडेक्स केवल पारस्परिक उपस्थिति को मिलान के रूप में गिनता है और इसकी तुलना उन विशेषताओं की संख्या से करता है जिन्हें दो समुच्चय में से कम से कम एक द्वारा चुना गया है। | ||
एफ़िनिटी विश्लेषण में, उदाहरण के लिए, दो उपभोक्ताओं की बास्केट जिनकी हम तुलना करना चाहते हैं, उनमें स्टोर में सभी उपलब्ध उत्पादों का केवल एक छोटा सा अंश हो सकता है, इसलिए एसएमसी सामान्यतः समानता के बहुत उच्च मूल्य लौटाएगा, भले ही टोकरियाँ बहुत कम हों समानता, इस प्रकार जैकार्ड | एफ़िनिटी विश्लेषण में, उदाहरण के लिए, दो उपभोक्ताओं की बास्केट जिनकी हम तुलना करना चाहते हैं, उनमें स्टोर में सभी उपलब्ध उत्पादों का केवल एक छोटा सा अंश हो सकता है, इसलिए एसएमसी सामान्यतः समानता के बहुत उच्च मूल्य लौटाएगा, भले ही टोकरियाँ बहुत कम हों समानता, इस प्रकार जैकार्ड इंडेक्स उस संदर्भ में समानता का अधिक उपयुक्त माप बन जाता है। उदाहरण के लिए, 1000 उत्पादों और दो ग्राहकों वाले एक सुपरमार्केट पर विचार करें। पहले ग्राहक की बास्केट में नमक और काली मिर्च है और दूसरे की बास्केट में नमक और चीनी है। इस परिदृश्य में, जैककार्ड इंडेक्स द्वारा मापी गई दो बास्केट के बीच समानता 1/3 होगी, लेकिन एसएमसी का उपयोग करके समानता 0.998 हो जाती है। | ||
अन्य संदर्भों में, जहां 0 और 1 समतुल्य जानकारी (समरूपता) रखते हैं, एसएमसी समानता का एक बेहतर उपाय है। उदाहरण के लिए, [[डमी वैरिएबल (सांख्यिकी)]] में संग्रहीत जनसांख्यिकीय चर के सदिश, जैसे कि लिंग, एसएमसी के साथ जैककार्ड इंडेक्स की तुलना में बेहतर होंगे क्योंकि समानता पर लिंग का प्रभाव बराबर होना चाहिए, चाहे पुरुष को 0 के रूप में परिभाषित किया गया हो और महिला 1 या दूसरे तरीके से या नहीं। हालाँकि, जब हमारे पास सममित डमी चर होते हैं, तो कोई डमी को दो बाइनरी विशेषताओं (इस मामले में, पुरुष और महिला) में विभाजित करके एसएमसी के व्यवहार को दोहरा सकता है, इस प्रकार उन्हें असममित विशेषताओं में बदल सकता है, जिससे बिना जैककार्ड इंडेक्स के उपयोग की अनुमति मिलती है। किसी भी पूर्वाग्रह का परिचय देना। हालाँकि, सममित डमी चर के मामले में एसएमसी अधिक कम्प्यूटेशनल रूप से कुशल बनी हुई है क्योंकि इसमें अतिरिक्त आयाम जोड़ने की आवश्यकता नहीं है। | अन्य संदर्भों में, जहां 0 और 1 समतुल्य जानकारी (समरूपता) रखते हैं, एसएमसी समानता का एक बेहतर उपाय है। उदाहरण के लिए, [[डमी वैरिएबल (सांख्यिकी)]] में संग्रहीत जनसांख्यिकीय चर के सदिश, जैसे कि लिंग, एसएमसी के साथ जैककार्ड इंडेक्स की तुलना में बेहतर होंगे क्योंकि समानता पर लिंग का प्रभाव बराबर होना चाहिए, चाहे पुरुष को 0 के रूप में परिभाषित किया गया हो और महिला 1 या दूसरे तरीके से या नहीं। हालाँकि, जब हमारे पास सममित डमी चर होते हैं, तो कोई डमी को दो बाइनरी विशेषताओं (इस मामले में, पुरुष और महिला) में विभाजित करके एसएमसी के व्यवहार को दोहरा सकता है, इस प्रकार उन्हें असममित विशेषताओं में बदल सकता है, जिससे बिना जैककार्ड इंडेक्स के उपयोग की अनुमति मिलती है। किसी भी पूर्वाग्रह का परिचय देना। हालाँकि, सममित डमी चर के मामले में एसएमसी अधिक कम्प्यूटेशनल रूप से कुशल बनी हुई है क्योंकि इसमें अतिरिक्त आयाम जोड़ने की आवश्यकता नहीं है। | ||
| Line 98: | Line 99: | ||
:<math>J_\mathcal{W}(x,y) = \frac{|X\cap Y|}{|X\setminus Y| + |X|} < J(X,Y).</math> | :<math>J_\mathcal{W}(x,y) = \frac{|X\cap Y|}{|X\setminus Y| + |X|} < J(X,Y).</math> | ||
[[File:Geometric interpretation of the Probability Jaccard Index as Simplices.png|thumb|upright=1.75|संभाव्यता जैककार्ड | [[File:Geometric interpretation of the Probability Jaccard Index as Simplices.png|thumb|upright=1.75|संभाव्यता जैककार्ड इंडेक्स की व्याख्या सरलताओं के प्रतिच्छेदन के रूप में की जा सकती है।]]इसके अतिरिक्त, एक सामान्यीकरण जो संभाव्यता वितरण और उनके संबंधित समर्थन समुच्चय के बीच निरंतर है | ||
:<math>J_\mathcal{P}(x,y) = \sum_{x_i\neq 0, y_i \neq 0} \frac{1}{\sum_{j} \max\left(\frac{x_j}{x_i}, \frac{y_j}{y_i}\right)}</math> | :<math>J_\mathcal{P}(x,y) = \sum_{x_i\neq 0, y_i \neq 0} \frac{1}{\sum_{j} \max\left(\frac{x_j}{x_i}, \frac{y_j}{y_i}\right)}</math> | ||
| Line 107: | Line 108: | ||
संगत दूरी, <math>1 - J_\mathcal{P}(x,y)</math>, संभाव्यता वितरण पर एक मीट्रिक है, और गैर-ऋणात्मक सदिश पर एक छद्ममिति स्थान|छद्म-मीट्रिक है। | संगत दूरी, <math>1 - J_\mathcal{P}(x,y)</math>, संभाव्यता वितरण पर एक मीट्रिक है, और गैर-ऋणात्मक सदिश पर एक छद्ममिति स्थान|छद्म-मीट्रिक है। | ||
संभाव्यता जैकार्ड इंडेक्स की [[सिंप्लेक्स]] के एक प्रतिच्छेदन के क्षेत्र के रूप में एक ज्यामितीय व्याख्या है। एक इकाई पर प्रत्येक बिंदु <math>k</math>-सिम्पलेक्स एक संभाव्यता वितरण से मेल खाता है <math>k+1</math> तत्व, क्योंकि इकाई <math>k</math>-सिम्प्लेक्स बिंदुओं का समूह है <math>k+1</math> ऐसे आयाम जिनका योग 1 है। संभाव्यता जैककार्ड | संभाव्यता जैकार्ड इंडेक्स की [[सिंप्लेक्स]] के एक प्रतिच्छेदन के क्षेत्र के रूप में एक ज्यामितीय व्याख्या है। एक इकाई पर प्रत्येक बिंदु <math>k</math>-सिम्पलेक्स एक संभाव्यता वितरण से मेल खाता है <math>k+1</math> तत्व, क्योंकि इकाई <math>k</math>-सिम्प्लेक्स बिंदुओं का समूह है <math>k+1</math> ऐसे आयाम जिनका योग 1 है। संभाव्यता जैककार्ड इंडेक्स को ज्यामितीय रूप से प्राप्त करने के लिए, प्रत्येक आइटम के द्रव्यमान के अनुसार इकाई सिंप्लेक्स को उप-सरलताओं में विभाजित करके एक संभाव्यता वितरण का प्रतिनिधित्व करें। यदि आप इस तरह दर्शाए गए दो वितरणों को एक-दूसरे के ऊपर रखते हैं, और प्रत्येक आइटम के अनुरूप सरलताओं को काटते हैं, तो जो क्षेत्र बचता है वह वितरण के संभाव्यता जैककार्ड इंडेक्स के बराबर होता है। | ||
=== संभाव्यता जैककार्ड | === संभाव्यता जैककार्ड इंडेक्स की इष्टतमता === | ||
[[File:Visual proof of the optimality of the Probability Jaccard Index on Three element distributions.png|thumb|upright=1.75|तीन तत्व वितरणों पर संभाव्यता जैककार्ड | [[File:Visual proof of the optimality of the Probability Jaccard Index on Three element distributions.png|thumb|upright=1.75|तीन तत्व वितरणों पर संभाव्यता जैककार्ड इंडेक्स की इष्टतमता का एक दृश्य प्रमाण।]]यादृच्छिक चर बनाने की समस्या पर विचार करें ताकि वे यथासंभव एक-दूसरे से टकराएं। अर्थात यदि <math>X\sim x</math> और <math>Y\sim y</math>, हम निर्माण करना चाहेंगे <math>X</math> और <math>Y</math> बढ़ाने के लिए <math>\Pr[X=Y]</math>. यदि हम केवल दो वितरणों को देखें <math>x,y</math> अलगाव में, उच्चतम <math>\Pr[X=Y]</math> हम प्राप्त कर सकते हैं द्वारा दिया गया है <math>1 - \text{TV}(x,y)</math>जहाँ <math>\text{TV}</math> [[संभाव्यता माप की कुल भिन्नता दूरी]] है। हालाँकि, मान लीजिए कि हम केवल उस विशेष जोड़ी को अधिकतम करने के बारे में चिंतित नहीं थे, मान लीजिए कि हम किसी भी मनमानी जोड़ी की टकराव की संभावना को अधिकतम करना चाहते हैं। प्रत्येक वितरण के लिए एक अनंत संख्या में यादृच्छिक चर का निर्माण किया जा सकता है <math>x</math>, और अधिकतम करने का प्रयास करें <math>\Pr[X=Y]</math> सभी जोड़ियों के लिए <math>x,y</math>. नीचे वर्णित काफी मजबूत अर्थ में, संभाव्यता जैककार्ड इंडेक्स इन यादृच्छिक चर को संरेखित करने का एक इष्टतम तरीका है। | ||
किसी भी नमूनाकरण विधि के लिए <math>G</math> और असतत वितरण <math>x,y</math>, अगर <math>\Pr[G(x) = G(y)] > J_\mathcal{P}(x,y)</math> फिर कुछ के लिए <math>z</math>जहाँ <math>J_\mathcal{P}(x,z)>J_\mathcal{P}(x,y)</math> और <math>J_\mathcal{P}(y,z)>J_\mathcal{P}(x,y)</math>, दोनों में से एक <math>\Pr[G(x) = G(z)] < J_\mathcal{P}(x,z)</math> या <math>\Pr[G(y) = G(z)] < J_\mathcal{P}(y,z)</math>.<ref name="pminhash" /> | किसी भी नमूनाकरण विधि के लिए <math>G</math> और असतत वितरण <math>x,y</math>, अगर <math>\Pr[G(x) = G(y)] > J_\mathcal{P}(x,y)</math> फिर कुछ के लिए <math>z</math>जहाँ <math>J_\mathcal{P}(x,z)>J_\mathcal{P}(x,y)</math> और <math>J_\mathcal{P}(y,z)>J_\mathcal{P}(x,y)</math>, दोनों में से एक <math>\Pr[G(x) = G(z)] < J_\mathcal{P}(x,z)</math> या <math>\Pr[G(y) = G(z)] < J_\mathcal{P}(y,z)</math>.<ref name="pminhash" /> | ||
अर्थात्, कोई भी नमूनाकरण विधि इससे अधिक टकराव प्राप्त नहीं कर सकती है <math>J_\mathcal{P}</math> की तुलना में कम टकराव प्राप्त किए बिना एक जोड़ी पर <math>J_\mathcal{P}</math> दूसरे युग्म पर, जहाँ घटा हुआ युग्म नीचे अधिक समान है <math>J_\mathcal{P}</math> बढ़ी हुई जोड़ी की तुलना में. यह प्रमेय समुच्चय के जैकार्ड | अर्थात्, कोई भी नमूनाकरण विधि इससे अधिक टकराव प्राप्त नहीं कर सकती है <math>J_\mathcal{P}</math> की तुलना में कम टकराव प्राप्त किए बिना एक जोड़ी पर <math>J_\mathcal{P}</math> दूसरे युग्म पर, जहाँ घटा हुआ युग्म नीचे अधिक समान है <math>J_\mathcal{P}</math> बढ़ी हुई जोड़ी की तुलना में. यह प्रमेय समुच्चय के जैकार्ड इंडेक्स (यदि समान वितरण के रूप में व्याख्या की जाए) और संभाव्यता जैकार्ड के लिए सत्य है, लेकिन भारित जैकार्ड के लिए नहीं। (प्रमेय किसी स्थान पर सभी वितरणों पर संयुक्त वितरण का वर्णन करने के लिए नमूनाकरण विधि शब्द का उपयोग करता है, क्योंकि यह मिनहैश # इनकॉर्पोरेटिंग वेट के उपयोग से प्राप्त होता है जो इसे उनकी टकराव की संभावना के रूप में प्राप्त करता है।) | ||
इस प्रमेय में सिंप्लेक्स प्रतिनिधित्व का उपयोग करके तीन तत्व वितरण पर एक दृश्य प्रमाण है। | इस प्रमेय में सिंप्लेक्स प्रतिनिधित्व का उपयोग करके तीन तत्व वितरण पर एक दृश्य प्रमाण है। | ||
== | == टैनिमोटो समानता और दूरी == | ||
टैनिमोटो समानता और टैनिमोटो दूरी के रूप में वर्णित कार्यों के विभिन्न रूप साहित्य और इंटरनेट पर पाए जाते हैं। इनमें से अधिकांश जैककार्ड समानता और जैककार्ड दूरी के पर्यायवाची हैं, लेकिन कुछ गणितीय रूप से भिन्न हैं। कई स्रोत<ref>For example {{cite book | vauthors = Huihuan Q, Xinyu W, Yangsheng X |title=Intelligent Surveillance Systems |publisher=Springer |year=2011 |page=161 |isbn=978-94-007-1137-2 }}</ref> आईबीएम तकनीकी रिपोर्ट का हवाला दें<ref name=":1">{{cite journal | vauthors = Tanimoto TT |title=वर्गीकरण और भविष्यवाणी का एक प्राथमिक गणितीय सिद्धांत|journal=Internal IBM Technical Report |date=17 Nov 1958 |issue=8? |volume=1957 }}</ref> मौलिक संदर्भ के रूप में. रिपोर्ट [https://www.worldcat.org/oclc/10917698 कई पुस्तकालयों] से उपलब्ध है। | टैनिमोटो समानता और टैनिमोटो दूरी के रूप में वर्णित कार्यों के विभिन्न रूप साहित्य और इंटरनेट पर पाए जाते हैं। इनमें से अधिकांश जैककार्ड समानता और जैककार्ड दूरी के पर्यायवाची हैं, लेकिन कुछ गणितीय रूप से भिन्न हैं। कई स्रोत<ref>For example {{cite book | vauthors = Huihuan Q, Xinyu W, Yangsheng X |title=Intelligent Surveillance Systems |publisher=Springer |year=2011 |page=161 |isbn=978-94-007-1137-2 }}</ref> आईबीएम तकनीकी रिपोर्ट का हवाला दें<ref name=":1">{{cite journal | vauthors = Tanimoto TT |title=वर्गीकरण और भविष्यवाणी का एक प्राथमिक गणितीय सिद्धांत|journal=Internal IBM Technical Report |date=17 Nov 1958 |issue=8? |volume=1957 }}</ref> मौलिक संदर्भ के रूप में. रिपोर्ट [https://www.worldcat.org/oclc/10917698 कई पुस्तकालयों] से उपलब्ध है। | ||
अक्टूबर 1960 में प्रकाशित पौधों को वर्गीकृत करने के लिए | अक्टूबर 1960 में प्रकाशित पौधों को वर्गीकृत करने के लिए "कंप्यूटर प्रोग्राम में,<ref>{{cite journal | vauthors = Rogers DJ, Tanimoto TT | title = पौधों को वर्गीकृत करने के लिए एक कंप्यूटर प्रोग्राम| journal = Science | volume = 132 | issue = 3434 | pages = 1115–8 | date = October 1960 | pmid = 17790723 | doi = 10.1126/science.132.3434.1115 | bibcode = 1960Sci...132.1115R }}</ref> समानता अनुपात" और व्युत्पन्न दूरी फलन के आधार पर वर्गीकरण की एक विधि दी गई है। ऐसा लगता है कि यह "टैनिमोटो समानता" और "टैनिमोटो दूरी" शब्दों के अर्थ के लिए सबसे आधिकारिक स्रोत है। समानता अनुपात जैकार्ड समानता के बराबर है, लेकिन दूरी फलन जैकार्ड दूरी के समान नहीं है। | ||
=== | === टैनिमोटो की समानता और दूरी की परिभाषाएँ === | ||
उस पेपर में, [[बिट सरणी]] पर एक समानता अनुपात दिया गया है, जहां एक निश्चित आकार की सरणी का प्रत्येक बिट मॉडल किए जा रहे पौधे में एक विशेषता की उपस्थिति या अनुपस्थिति का प्रतिनिधित्व करता है। अनुपात की परिभाषा सामान्य बिट्स की संख्या है, जो किसी भी नमूने में समुच्चय बिट्स (यानी गैर-शून्य) की संख्या से विभाजित होती है। | उस पेपर में, [[बिट सरणी]] पर एक समानता अनुपात दिया गया है, जहां एक निश्चित आकार की सरणी का प्रत्येक बिट मॉडल किए जा रहे पौधे में एक विशेषता की उपस्थिति या अनुपस्थिति का प्रतिनिधित्व करता है। अनुपात की परिभाषा सामान्य बिट्स की संख्या है, जो किसी भी नमूने में समुच्चय बिट्स (यानी गैर-शून्य) की संख्या से विभाजित होती है। | ||
| Line 132: | Line 133: | ||
: <math> T_s(X,Y) = \frac{\sum_i ( X_i \land Y_i)}{\sum_i ( X_i \lor Y_i)}</math> | : <math> T_s(X,Y) = \frac{\sum_i ( X_i \land Y_i)}{\sum_i ( X_i \lor Y_i)}</math> | ||
यदि प्रत्येक नमूने को विशेषताओं के एक समुच्चय के रूप में तैयार किया जाता है, तो यह मान दो समुच्चय के जैकार्ड गुणांक के बराबर है। पेपर में जैकार्ड का उल्लेख नहीं किया गया है, और ऐसा लगता है कि लेखकों को इसकी जानकारी नहीं थी। | यदि प्रत्येक नमूने को विशेषताओं के एक समुच्चय के रूप में तैयार किया जाता है, तो यह मान दो समुच्चय के जैकार्ड गुणांक के बराबर है। पेपर में जैकार्ड का उल्लेख नहीं किया गया है, और ऐसा लगता है कि लेखकों को इसकी जानकारी नहीं थी। | ||
टैनिमोटो इस अनुपात के आधार पर दूरी गुणांक को परिभाषित करता है, जो गैर-शून्य समानता वाले बिटमैप्स के लिए परिभाषित है: | टैनिमोटो इस अनुपात के आधार पर <nowiki>''</nowiki>दूरी गुणांक<nowiki>''</nowiki> को परिभाषित करता है, जो गैर-शून्य समानता वाले बिटमैप्स के लिए परिभाषित है: | ||
: <math>T_d(X,Y) = -\log_2 ( T_s(X,Y) ) </math> | : <math>T_d(X,Y) = -\log_2 ( T_s(X,Y) ) </math> | ||
यह गुणांक, जानबूझकर, दूरी मीट्रिक नहीं है। इसे दो नमूनों की संभावना को अनुमति देने के लिए चुना गया है, जो एक दूसरे से काफी भिन्न हैं, दोनों एक तिहाई के समान हैं। ऐसा उदाहरण बनाना आसान है जो त्रिभुज असमानता | यह गुणांक, जानबूझकर, दूरी मीट्रिक (मापीय) नहीं है। इसे दो नमूनों की संभावना को अनुमति देने के लिए चुना गया है, जो एक दूसरे से काफी भिन्न हैं, दोनों एक तिहाई के समान हैं। ऐसा उदाहरण बनाना आसान है जो त्रिभुज असमानता मीट्रिक स्पेस की संपत्ति को अस्वीकार करता है। | ||
=== | === टैनिमोटो दूरी की अन्य परिभाषाएँ === | ||
टैनिमोटो दूरी को प्रायः ग़लती से जैककार्ड दूरी के पर्याय के रूप में संदर्भित किया जाता है <math>1-T_s</math>. यह फलन एक उचित दूरी मीट्रिक है. टैनिमोटो दूरी को प्रायः एक उचित दूरी मीट्रिक के रूप में कहा जाता है, शायद जैककार्ड दूरी के साथ इसके भ्रम के कारण। | टैनिमोटो दूरी को प्रायः ग़लती से जैककार्ड दूरी के पर्याय के रूप में संदर्भित किया जाता है <math>1-T_s</math>. यह फलन एक उचित दूरी मीट्रिक है. टैनिमोटो दूरी को प्रायः एक उचित दूरी मीट्रिक के रूप में कहा जाता है, शायद जैककार्ड दूरी के साथ इसके भ्रम के कारण। | ||
| Line 152: | Line 153: | ||
:<math>\|A\|^2 = \sum_i A_i^2 = \sum_i A_i.</math> | :<math>\|A\|^2 = \sum_i A_i^2 = \sum_i A_i.</math> | ||
यह संभावित रूप से भ्रमित करने वाला प्रतिनिधित्व है, क्योंकि सदिश पर व्यक्त किया गया फलन अधिक सामान्य है, जब तक कि इसका डोमेन स्पष्ट रूप से प्रतिबंधित न हो। के गुण <math> T_s </math> जरूरी नहीं कि इसका विस्तार हो <math>f</math>. विशेष रूप से, अंतर | यह संभावित रूप से भ्रमित करने वाला प्रतिनिधित्व है, क्योंकि सदिश पर व्यक्त किया गया फलन अधिक सामान्य है, जब तक कि इसका डोमेन स्पष्ट रूप से प्रतिबंधित न हो। के गुण <math> T_s </math> जरूरी नहीं कि इसका विस्तार हो <math>f</math>. विशेष रूप से, अंतर फलन <math>1-f</math> जबकि, त्रिभुज असमानता को संरक्षित नहीं करता है, और इसलिए यह एक उचित दूरी मीट्रिक नहीं है <math>1 - T_s </math> है। | ||
एक वास्तविक ख़तरा है कि इस सूत्र का उपयोग करके टैनिमोटो दूरी के संयोजन को परिभाषित किया जा रहा है, साथ ही यह कथन कि टैनिमोटो दूरी एक उचित दूरी मीट्रिक है, गलत निष्कर्ष पर ले जाएगा कि फलन <math>1-f</math> वास्तव में सामान्य तौर पर सदिश या मल्टीसमुच्चय पर एक दूरी मीट्रिक है, जबकि समानता खोज या क्लस्टरिंग एल्गोरिदम में इसका उपयोग सही परिणाम देने में विफल हो सकता है। | एक वास्तविक ख़तरा है कि इस सूत्र का उपयोग करके टैनिमोटो दूरी के संयोजन को परिभाषित किया जा रहा है, साथ ही यह कथन कि टैनिमोटो दूरी एक उचित दूरी मीट्रिक है, गलत निष्कर्ष पर ले जाएगा कि फलन <math>1-f</math> वास्तव में सामान्य तौर पर सदिश या मल्टीसमुच्चय पर एक दूरी मीट्रिक है, जबकि समानता खोज या क्लस्टरिंग एल्गोरिदम में इसका उपयोग सही परिणाम देने में विफल हो सकता है। | ||
| Line 180: | Line 181: | ||
* [[हैमिंग दूरी]] | * [[हैमिंग दूरी]] | ||
* सोरेनसेन-डाइस गुणांक, जो समतुल्य है: <math>J=S/(2-S)</math> और <math>S=2J/(1+J)</math> (<math>J</math>: जैकार्ड इंडेक्स, <math>S</math>: सोरेनसेन-डाइस गुणांक) | * सोरेनसेन-डाइस गुणांक, जो समतुल्य है: <math>J=S/(2-S)</math> और <math>S=2J/(1+J)</math> (<math>J</math>: जैकार्ड इंडेक्स, <math>S</math>: सोरेनसेन-डाइस गुणांक) | ||
* [[टावर्सकी सूचकांक]] | * [[टावर्सकी सूचकांक|टावर्सकी इंडेक्स]] | ||
* [[सह - संबंध]] | * [[सह - संबंध]] | ||
*पारस्परिक जानकारी, एक सामान्यीकृत पारस्परिक जानकारी#मीट्रिक संस्करण, जो एक एंट्रोपिक जैककार्ड दूरी है। | *पारस्परिक जानकारी, एक सामान्यीकृत पारस्परिक जानकारी#मीट्रिक संस्करण, जो एक एंट्रोपिक जैककार्ड दूरी है। | ||
Revision as of 22:17, 18 July 2023
जैककार्ड इंडेक्स (सूचकांक), जिसे जैकार्ड समानता गुणांक के रूप में भी जाना जाता है, एक आँकड़ा है जिसका उपयोग नमूना (सांख्यिकी) समुच्चय की समानता माप और विविधता इंडेक्स को मापने के लिए किया जाता है। इसे 1884 में ग्रोव कार्ल गिल्बर्ट द्वारा उनके वेरिफिकेशन (प्रमाणन) के अनुपात के रूप में विकसित किया गया था (v)[1] और अब इसे प्रायः मौसम विज्ञान में क्रिटिकल सक्सेस इंडेक्स के रूप में जाना जाता है।[2] इसे बाद में पॉल जैकार्ड द्वारा स्वतंत्र रूप से विकसित किया गया था, जिसे मूल रूप से फ्रांसीसी नाम गुणांक डी कम्युनॉटे दिया गया था,[3] और टी. टैनिमोटो द्वारा फिर से स्वतंत्र रूप से तैयार किया गया।[4]इस प्रकार, कुछ क्षेत्रों में टैनिमोटो इंडेक्स या टैनिमोटो गुणांक का भी उपयोग किया जाता है। हालाँकि, सामान्यतः यूनियन ओवर इंटरसेक्शन का अनुपात लेने में वे समान हैं। जैकार्ड गुणांक परिमित नमूना समुच्चय के बीच समानता को मापता है, और इसे नमूना समुच्चय के संघ (समुच्चय सिद्धांत) के आकार से विभाजित प्रतिच्छेदन (इंटरसेक्शन) के आकार (समुच्चय सिद्धांत) के रूप में परिभाषित किया जाता है:
ध्यान दें कि डिज़ाइन के अनुसार, यदि A प्रतिच्छेदन B रिक्त है, तो J(A,B) = 0. जैककार्ड गुणांक का व्यापक रूप से कंप्यूटर विज्ञान, पारिस्थितिकी, जीनोमिक्स और अन्य विज्ञानों में उपयोग किया जाता है, जहां बाइनरी डेटा का उपयोग किया जाता है। जैकार्ड गुणांक के साथ परिकल्पना परीक्षण के लिए सटीक समाधान और सन्निकटन दोनों विधियाँ उपलब्ध हैं।[5]
जैककार्ड समानता बैग यानी मल्टीसमुच्चय पर भी लागू होती है। इसका एक समान सूत्र है,[6] लेकिन प्रतीकों का मतलब है बैग प्रतिच्छेदन और बैग योग (संघ नहीं)। अधिकतम मान 1/2 है.
जैकार्ड दूरी, जो नमूना समुच्चय के बीच असमानता को मापती है, जैकार्ड गुणांक का पूरक है और इसे जैकर्ड गुणांक को 1 से घटाकर, या समकक्ष रूप से, संघ और प्रतिच्छेदन के आकार के अंतर को विभाजित करके प्राप्त किया जाता है। संघ के आकार के अनुसार दो समुच्चय में से:
जैकार्ड दूरी की एक वैकल्पिक व्याख्या सममित अंतर के आकार के अनुपात के रूप में है संघ को जैककार्ड दूरी का उपयोग सामान्यतः क्लस्टर विश्लेषण और n नमूना समुच्चय के बहुआयामी स्केलिंग के लिए n × n आव्यूह की गणना करने के लिए किया जाता है।
यह दूरी सभी परिमित समुच्चय के संग्रह पर एक दूरी फलन है।[7][8][9]
माप (गणित) के लिए जैककार्ड दूरी का संस्करण भी है, जिसमें संभाव्यता माप भी सम्मिलित है। अगर मापने योग्य स्थान पर एक माप है , फिर हम जैकार्ड गुणांक को परिभाषित करते हैं
और जैकार्ड दूरी द्वारा
अगर सावधानी बरतनी होगी या , क्योंकि इन स्थितियोमें ये सूत्र अच्छी तरह से परिभाषित नहीं हैं।
मिनहैश न्यूनतम-वार स्वतंत्र क्रमपरिवर्तन स्थानीयता संवेदनशील हैशिंग योजना का उपयोग समुच्चय के जोड़े के जैकार्ड समानता गुणांक के सटीक अनुमान की कुशलता से गणना करने के लिए किया जा सकता है, जहां प्रत्येक समुच्चय को हैश फलन के न्यूनतम मूल्यों से प्राप्त स्थिर आकार के हस्ताक्षर द्वारा दर्शाया जाता है। .
असममित द्विआधारी विशेषताओं की समानता
दो वस्तुओं, A और B, प्रत्येक को n बाइनरी अंक प्रणाली विशेषताओं के साथ देखते हुए, जैककार्ड गुणांक ओवरलैप का एक उपयोगी माप है जिसे A और B अपनी विशेषताओं के साथ साझा करते हैं। A और B की प्रत्येक विशेषता या तो 0 या 1 हो सकती है। A और B दोनों के लिए विशेषताओं के प्रत्येक संयोजन की कुल संख्या निम्नानुसार निर्दिष्ट है:
- विशेषताओं की कुल संख्या को दर्शाता है जहाँ A और B दोनों का मान 1 है।
- विशेषताओं की कुल संख्या का प्रतिनिधित्व करता है जहां A की विशेषता 0 है और B की विशेषता 1 है।
- विशेषताओं की कुल संख्या का प्रतिनिधित्व करता है जहां A की विशेषता 1 है और B की विशेषता 0 है।
- विशेषताओं की कुल संख्या को दर्शाता है जहाँ A और B दोनों का मान 0 है।
A B |
0 | 1 |
|---|---|---|
| 0 | ||
| 1 |
प्रत्येक विशेषता को इन चार श्रेणियों में से एक में आना चाहिए, जिसका अर्थ है
जैककार्ड समानता गुणांक, J, इस प्रकार दिया गया है
जैकार्ड दूरी, dJ, के रूप में दिया गया है
जैककार्ड समानता गुणांक और परिणामस्वरूप संबंधित आव्यूह के आधार पर सांख्यिकीय अनुमान लगाया जा सकता है।[5]एन विशेषताओं के साथ दो नमूना समुच्चय A और B दिए जाने पर, यह देखने के लिए एक सांख्यिकीय परीक्षण आयोजित किया जा सकता है कि क्या ओवरलैप सांख्यिकीय महत्व है। सटीक समाधान उपलब्ध है, हालाँकि n बढ़ने पर गणना महंगी हो सकती है।[5]अनुमान विधियाँ या तो बहुपद वितरण का अनुमान लगाकर या बूटस्ट्रैपिंग द्वारा उपलब्ध हैं।[5]
सरल मिलान गुणांक (एसएमसी) के साथ अंतर
जब बाइनरी विशेषताओं के लिए उपयोग किया जाता है, तो जैककार्ड इंडेक्स सरल मिलान गुणांक के समान होता है। मुख्य अंतर यह है कि एसएमसी के पास शब्द है इसके अंश और हर में, जबकि जैककार्ड इंडेक्स में ऐसा नहीं है। इस प्रकार, एसएमसी दोनों पारस्परिक उपस्थिति (जब एक विशेषता दोनों समुच्चय में उपस्थित है) और पारस्परिक अनुपस्थिति (जब एक विशेषता दोनों समुच्चय में अनुपस्थित है) को मिलान के रूप में गिनती है और इसकी तुलना ब्रह्मांड में विशेषताओं की कुल संख्या से करती है, जबकि जैककार्ड इंडेक्स केवल पारस्परिक उपस्थिति को मिलान के रूप में गिनता है और इसकी तुलना उन विशेषताओं की संख्या से करता है जिन्हें दो समुच्चय में से कम से कम एक द्वारा चुना गया है।
एफ़िनिटी विश्लेषण में, उदाहरण के लिए, दो उपभोक्ताओं की बास्केट जिनकी हम तुलना करना चाहते हैं, उनमें स्टोर में सभी उपलब्ध उत्पादों का केवल एक छोटा सा अंश हो सकता है, इसलिए एसएमसी सामान्यतः समानता के बहुत उच्च मूल्य लौटाएगा, भले ही टोकरियाँ बहुत कम हों समानता, इस प्रकार जैकार्ड इंडेक्स उस संदर्भ में समानता का अधिक उपयुक्त माप बन जाता है। उदाहरण के लिए, 1000 उत्पादों और दो ग्राहकों वाले एक सुपरमार्केट पर विचार करें। पहले ग्राहक की बास्केट में नमक और काली मिर्च है और दूसरे की बास्केट में नमक और चीनी है। इस परिदृश्य में, जैककार्ड इंडेक्स द्वारा मापी गई दो बास्केट के बीच समानता 1/3 होगी, लेकिन एसएमसी का उपयोग करके समानता 0.998 हो जाती है।
अन्य संदर्भों में, जहां 0 और 1 समतुल्य जानकारी (समरूपता) रखते हैं, एसएमसी समानता का एक बेहतर उपाय है। उदाहरण के लिए, डमी वैरिएबल (सांख्यिकी) में संग्रहीत जनसांख्यिकीय चर के सदिश, जैसे कि लिंग, एसएमसी के साथ जैककार्ड इंडेक्स की तुलना में बेहतर होंगे क्योंकि समानता पर लिंग का प्रभाव बराबर होना चाहिए, चाहे पुरुष को 0 के रूप में परिभाषित किया गया हो और महिला 1 या दूसरे तरीके से या नहीं। हालाँकि, जब हमारे पास सममित डमी चर होते हैं, तो कोई डमी को दो बाइनरी विशेषताओं (इस मामले में, पुरुष और महिला) में विभाजित करके एसएमसी के व्यवहार को दोहरा सकता है, इस प्रकार उन्हें असममित विशेषताओं में बदल सकता है, जिससे बिना जैककार्ड इंडेक्स के उपयोग की अनुमति मिलती है। किसी भी पूर्वाग्रह का परिचय देना। हालाँकि, सममित डमी चर के मामले में एसएमसी अधिक कम्प्यूटेशनल रूप से कुशल बनी हुई है क्योंकि इसमें अतिरिक्त आयाम जोड़ने की आवश्यकता नहीं है।
भारित जैककार्ड समानता और दूरी
अगर और सभी वास्तविक के साथ दो सदिश हैं , तो उनके जैककार्ड समानता गुणांक (जिसे रुज़िका समानता के रूप में भी जाना जाता है) को इस प्रकार परिभाषित किया गया है
और जैकार्ड दूरी (उस समय इसे सोर्जेल दूरी के नाम से भी जाना जाता था)
और भी अधिक व्यापकता के साथ, यदि और मापने योग्य स्थान पर दो गैर-ऋणात्मक मापने योग्य कार्य हैं माप के साथ , तो हम परिभाषित कर सकते हैं
जहाँ और बिंदुवार ऑपरेटर हैं. फिर जैकार्ड दूरी है
फिर, उदाहरण के लिए, दो मापने योग्य समुच्चय के लिए , अपने पास जहाँ और संबंधित समुच्चय के विशिष्ट कार्य हैं।
संभाव्यता जैककार्ड समानता और दूरी
ऊपर वर्णित भारित जैककार्ड समानता, जैकार्ड इंडेक्स को घनात्मक सदिश में सामान्यीकृत करती है, जहां एक समुच्चय संकेतक फलन द्वारा दिए गए बाइनरी सदिश से मेल खाता है, यानी। . हालाँकि, यह जैकार्ड इंडेक्स को संभाव्यता वितरण के लिए सामान्यीकृत नहीं करता है, जहां एक समुच्चय एक समान संभाव्यता वितरण से मेल खाता है, अर्थात।
यदि समुच्चय आकार में भिन्न हो तो यह हमेशा कम होता है। अगर , और तब
इसके अतिरिक्त, एक सामान्यीकरण जो संभाव्यता वितरण और उनके संबंधित समर्थन समुच्चय के बीच निरंतर है
जिसे प्रोबेबिलिटी जैकार्ड कहा जाता है।[10] संभाव्यता सदिश पर भारित जैकार्ड के विरुद्ध इसकी निम्नलिखित सीमाएँ हैं।
यहां ऊपरी सीमा (भारित) सोरेंसन-डाइस गुणांक जैकार्ड|सोरेनसेन-डाइस गुणांक से अंतर है। संगत दूरी, , संभाव्यता वितरण पर एक मीट्रिक है, और गैर-ऋणात्मक सदिश पर एक छद्ममिति स्थान|छद्म-मीट्रिक है।
संभाव्यता जैकार्ड इंडेक्स की सिंप्लेक्स के एक प्रतिच्छेदन के क्षेत्र के रूप में एक ज्यामितीय व्याख्या है। एक इकाई पर प्रत्येक बिंदु -सिम्पलेक्स एक संभाव्यता वितरण से मेल खाता है तत्व, क्योंकि इकाई -सिम्प्लेक्स बिंदुओं का समूह है ऐसे आयाम जिनका योग 1 है। संभाव्यता जैककार्ड इंडेक्स को ज्यामितीय रूप से प्राप्त करने के लिए, प्रत्येक आइटम के द्रव्यमान के अनुसार इकाई सिंप्लेक्स को उप-सरलताओं में विभाजित करके एक संभाव्यता वितरण का प्रतिनिधित्व करें। यदि आप इस तरह दर्शाए गए दो वितरणों को एक-दूसरे के ऊपर रखते हैं, और प्रत्येक आइटम के अनुरूप सरलताओं को काटते हैं, तो जो क्षेत्र बचता है वह वितरण के संभाव्यता जैककार्ड इंडेक्स के बराबर होता है।
संभाव्यता जैककार्ड इंडेक्स की इष्टतमता
यादृच्छिक चर बनाने की समस्या पर विचार करें ताकि वे यथासंभव एक-दूसरे से टकराएं। अर्थात यदि और , हम निर्माण करना चाहेंगे और बढ़ाने के लिए . यदि हम केवल दो वितरणों को देखें अलगाव में, उच्चतम हम प्राप्त कर सकते हैं द्वारा दिया गया है जहाँ संभाव्यता माप की कुल भिन्नता दूरी है। हालाँकि, मान लीजिए कि हम केवल उस विशेष जोड़ी को अधिकतम करने के बारे में चिंतित नहीं थे, मान लीजिए कि हम किसी भी मनमानी जोड़ी की टकराव की संभावना को अधिकतम करना चाहते हैं। प्रत्येक वितरण के लिए एक अनंत संख्या में यादृच्छिक चर का निर्माण किया जा सकता है , और अधिकतम करने का प्रयास करें सभी जोड़ियों के लिए . नीचे वर्णित काफी मजबूत अर्थ में, संभाव्यता जैककार्ड इंडेक्स इन यादृच्छिक चर को संरेखित करने का एक इष्टतम तरीका है।
किसी भी नमूनाकरण विधि के लिए और असतत वितरण , अगर फिर कुछ के लिए जहाँ और , दोनों में से एक या .[10]
अर्थात्, कोई भी नमूनाकरण विधि इससे अधिक टकराव प्राप्त नहीं कर सकती है की तुलना में कम टकराव प्राप्त किए बिना एक जोड़ी पर दूसरे युग्म पर, जहाँ घटा हुआ युग्म नीचे अधिक समान है बढ़ी हुई जोड़ी की तुलना में. यह प्रमेय समुच्चय के जैकार्ड इंडेक्स (यदि समान वितरण के रूप में व्याख्या की जाए) और संभाव्यता जैकार्ड के लिए सत्य है, लेकिन भारित जैकार्ड के लिए नहीं। (प्रमेय किसी स्थान पर सभी वितरणों पर संयुक्त वितरण का वर्णन करने के लिए नमूनाकरण विधि शब्द का उपयोग करता है, क्योंकि यह मिनहैश # इनकॉर्पोरेटिंग वेट के उपयोग से प्राप्त होता है जो इसे उनकी टकराव की संभावना के रूप में प्राप्त करता है।)
इस प्रमेय में सिंप्लेक्स प्रतिनिधित्व का उपयोग करके तीन तत्व वितरण पर एक दृश्य प्रमाण है।
टैनिमोटो समानता और दूरी
टैनिमोटो समानता और टैनिमोटो दूरी के रूप में वर्णित कार्यों के विभिन्न रूप साहित्य और इंटरनेट पर पाए जाते हैं। इनमें से अधिकांश जैककार्ड समानता और जैककार्ड दूरी के पर्यायवाची हैं, लेकिन कुछ गणितीय रूप से भिन्न हैं। कई स्रोत[11] आईबीएम तकनीकी रिपोर्ट का हवाला दें[4] मौलिक संदर्भ के रूप में. रिपोर्ट कई पुस्तकालयों से उपलब्ध है।
अक्टूबर 1960 में प्रकाशित पौधों को वर्गीकृत करने के लिए "कंप्यूटर प्रोग्राम में,[12] समानता अनुपात" और व्युत्पन्न दूरी फलन के आधार पर वर्गीकरण की एक विधि दी गई है। ऐसा लगता है कि यह "टैनिमोटो समानता" और "टैनिमोटो दूरी" शब्दों के अर्थ के लिए सबसे आधिकारिक स्रोत है। समानता अनुपात जैकार्ड समानता के बराबर है, लेकिन दूरी फलन जैकार्ड दूरी के समान नहीं है।
टैनिमोटो की समानता और दूरी की परिभाषाएँ
उस पेपर में, बिट सरणी पर एक समानता अनुपात दिया गया है, जहां एक निश्चित आकार की सरणी का प्रत्येक बिट मॉडल किए जा रहे पौधे में एक विशेषता की उपस्थिति या अनुपस्थिति का प्रतिनिधित्व करता है। अनुपात की परिभाषा सामान्य बिट्स की संख्या है, जो किसी भी नमूने में समुच्चय बिट्स (यानी गैर-शून्य) की संख्या से विभाजित होती है।
गणितीय शब्दों में प्रस्तुत किया गया है, यदि नमूने X और Y बिटमैप हैं, X का iवां बिट है, और क्रमशः बिटवाइज़ ऑपरेशन तार्किक संयोजन , तार्किक विच्छेदन ऑपरेटर हैं, फिर समानता अनुपात है
यदि प्रत्येक नमूने को विशेषताओं के एक समुच्चय के रूप में तैयार किया जाता है, तो यह मान दो समुच्चय के जैकार्ड गुणांक के बराबर है। पेपर में जैकार्ड का उल्लेख नहीं किया गया है, और ऐसा लगता है कि लेखकों को इसकी जानकारी नहीं थी।
टैनिमोटो इस अनुपात के आधार पर ''दूरी गुणांक'' को परिभाषित करता है, जो गैर-शून्य समानता वाले बिटमैप्स के लिए परिभाषित है:
यह गुणांक, जानबूझकर, दूरी मीट्रिक (मापीय) नहीं है। इसे दो नमूनों की संभावना को अनुमति देने के लिए चुना गया है, जो एक दूसरे से काफी भिन्न हैं, दोनों एक तिहाई के समान हैं। ऐसा उदाहरण बनाना आसान है जो त्रिभुज असमानता मीट्रिक स्पेस की संपत्ति को अस्वीकार करता है।
टैनिमोटो दूरी की अन्य परिभाषाएँ
टैनिमोटो दूरी को प्रायः ग़लती से जैककार्ड दूरी के पर्याय के रूप में संदर्भित किया जाता है . यह फलन एक उचित दूरी मीट्रिक है. टैनिमोटो दूरी को प्रायः एक उचित दूरी मीट्रिक के रूप में कहा जाता है, शायद जैककार्ड दूरी के साथ इसके भ्रम के कारण।
यदि जैकार्ड या टैनिमोटो समानता को बिट सदिश पर व्यक्त किया जाता है, तो इसे इस प्रकार लिखा जा सकता है
जहां समान गणना सदिश अदिश उत्पाद और परिमाण के संदर्भ में व्यक्त की जाती है। यह प्रतिनिधित्व इस तथ्य पर निर्भर करता है कि, एक बिट सदिश के लिए (जहां प्रत्येक आयाम का मान या तो 0 या 1 है)
और
यह संभावित रूप से भ्रमित करने वाला प्रतिनिधित्व है, क्योंकि सदिश पर व्यक्त किया गया फलन अधिक सामान्य है, जब तक कि इसका डोमेन स्पष्ट रूप से प्रतिबंधित न हो। के गुण जरूरी नहीं कि इसका विस्तार हो . विशेष रूप से, अंतर फलन जबकि, त्रिभुज असमानता को संरक्षित नहीं करता है, और इसलिए यह एक उचित दूरी मीट्रिक नहीं है है।
एक वास्तविक ख़तरा है कि इस सूत्र का उपयोग करके टैनिमोटो दूरी के संयोजन को परिभाषित किया जा रहा है, साथ ही यह कथन कि टैनिमोटो दूरी एक उचित दूरी मीट्रिक है, गलत निष्कर्ष पर ले जाएगा कि फलन वास्तव में सामान्य तौर पर सदिश या मल्टीसमुच्चय पर एक दूरी मीट्रिक है, जबकि समानता खोज या क्लस्टरिंग एल्गोरिदम में इसका उपयोग सही परिणाम देने में विफल हो सकता है।
लिपकस[8]टैनिमोटो समानता की एक परिभाषा का उपयोग करता है जो इसके बराबर है , और फलन के रूप में टैनिमोटो दूरी को संदर्भित करता है . हालाँकि, पेपर में यह स्पष्ट कर दिया गया है कि संदर्भ (घनात्मक) वेटिंग सदिश के उपयोग से प्रतिबंधित है ऐसा कि, किसी भी सदिश ए के लिए विचार किया जा रहा है, इन परिस्थितियों में, फलन एक उचित दूरी मीट्रिक है, और इसलिए ऐसे वेटिंग सदिश द्वारा शासित सदिश का एक समुच्चय इस फलन के तहत एक मीट्रिक स्थान बनाता है।
बाइनरी वर्गीकरण भ्रम आव्यूह में जैकार्ड इंडेक्स
बाइनरी वर्गीकरण के लिए नियोजित भ्रम आव्यूह में, जैककार्ड इंडेक्स को निम्नलिखित सूत्र में तैयार किया जा सकता है:
जहां TP सच्चे घनात्मक हैं, एफपी गलत घनात्मक हैं और FN गलत ऋणात्मक हैं।[13]
यह भी देखें
- ओवरलैप गुणांक
- सरल मिलान गुणांक
- हैमिंग दूरी
- सोरेनसेन-डाइस गुणांक, जो समतुल्य है: और (: जैकार्ड इंडेक्स, : सोरेनसेन-डाइस गुणांक)
- टावर्सकी इंडेक्स
- सह - संबंध
- पारस्परिक जानकारी, एक सामान्यीकृत पारस्परिक जानकारी#मीट्रिक संस्करण, जो एक एंट्रोपिक जैककार्ड दूरी है।
संदर्भ
- ↑ Murphy, Allan H. (1996). "The Finley Affair: A Signal Event in the History of Forecast Verification". Weather and Forecasting. 11 (1): 3. Bibcode:1996WtFor..11....3M. doi:10.1175/1520-0434(1996)011<0003:TFAASE>2.0.CO;2. ISSN 1520-0434. S2CID 54532560.
- ↑ "पूर्वानुमान सत्यापन शब्दावली" (PDF). noaa.gov. Retrieved 21 May 2023.
- ↑ Jaccard, Paul (February 1912). "अल्पाइन क्षेत्र में वनस्पतियों का वितरण.1". New Phytologist. 11 (2): 37–50. doi:10.1111/j.1469-8137.1912.tb05611.x. ISSN 0028-646X.
- ↑ 4.0 4.1 Tanimoto TT (17 Nov 1958). "वर्गीकरण और भविष्यवाणी का एक प्राथमिक गणितीय सिद्धांत". Internal IBM Technical Report. 1957 (8?).
- ↑ 5.0 5.1 5.2 5.3 Chung NC, Miasojedow B, Startek M, Gambin A (December 2019). "Jaccard/Tanimoto similarity test and estimation methods for biological presence-absence data". BMC Bioinformatics. 20 (Suppl 15): 644. arXiv:1903.11372. doi:10.1186/s12859-019-3118-5. PMC 6929325. PMID 31874610.
- ↑ Leskovec J, Rajaraman A, Ullman J (2020). बड़े पैमाने पर डेटासेट का खनन. Cambridge. ISBN 9781108476348. and p. 76-77 in an earlier version http://infolab.stanford.edu/~ullman/mmds/ch3.pdf
- ↑ Kosub S (April 2019). "जैकार्ड दूरी के लिए त्रिभुज असमानता पर एक नोट।". Pattern Recognition Letters. 120: 36–8. arXiv:1612.02696. Bibcode:2019PaReL.120...36K. doi:10.1016/j.patrec.2018.12.007. S2CID 564831.
- ↑ 8.0 8.1 Lipkus AH (1999). "तनिमोटो दूरी के लिए त्रिभुज असमानता का प्रमाण". Journal of Mathematical Chemistry. 26 (1–3): 263–265. doi:10.1023/A:1019154432472. S2CID 118263043.
- ↑ Levandowsky M, Winter D (1971). "सेट के बीच की दूरी". Nature. 234 (5): 34–35. Bibcode:1971Natur.234...34L. doi:10.1038/234034a0. S2CID 4283015.
- ↑ 10.0 10.1 Moulton R, Jiang Y (2018). "अधिकतम सुसंगत नमूनाकरण और संभाव्यता वितरण का जैकार्ड सूचकांक". International Conference on Data Mining, Workshop on High Dimensional Data Mining: 347–356. arXiv:1809.04052. doi:10.1109/ICDM.2018.00050. ISBN 978-1-5386-9159-5. S2CID 49746072.
- ↑ For example Huihuan Q, Xinyu W, Yangsheng X (2011). Intelligent Surveillance Systems. Springer. p. 161. ISBN 978-94-007-1137-2.
- ↑ Rogers DJ, Tanimoto TT (October 1960). "पौधों को वर्गीकृत करने के लिए एक कंप्यूटर प्रोग्राम". Science. 132 (3434): 1115–8. Bibcode:1960Sci...132.1115R. doi:10.1126/science.132.3434.1115. PMID 17790723.
- ↑ Aziz Taha, Abdel (2015). "Metrics for evaluating 3D medical image segmentation: analysis, selection, and tool". BMC Medical Imaging. 15 (29): 1–28. doi:10.1186/s12880-015-0068-x. PMC 4533825. PMID 26263899.
अग्रिम पठन
- Tan PN, Steinbach M, Kumar V (2005). Introduction to Data Mining. ISBN 0-321-32136-7.
- Jaccard P (1901). "Étude comparative de la distribution florale dans une portion des Alpes et des Jura". Bulletin de la Société vaudoise des sciences naturelles. 37: 547–579.
- Jaccard P (1912). "The Distribution of the flora in the alpine zone". New Phytologist. 11 (2): 37–50. doi:10.1111/j.1469-8137.1912.tb05611.x.
बाहरी संबंध
- Introduction to Data Mining lecture notes from Tan, Steinbach, Kumar
- SimMetrics a sourceforge implementation of Jaccard index and many other similarity metrics
- A web-based calculator for finding the Jaccard Coefficient
- Tutorial on how to calculate different similarities
- Intersection over Union (IoU) for object detection
- Kaggle Dstl Satellite Imagery Feature Detection - Evaluation
- Similarity and dissimilarity measures used in data science