चतुर्भुज आयाम मॉड्यूलेशन: Difference between revisions

Revision as of 19:50, 27 July 2023

चतुर्भुज आयाम मॉड्यूलेशन (क्यूएएम) डिजिटल मॉड्यूलेशन विधियों के सदस्य और सूचना प्रसारित करने के लिए आधुनिक दूरसंचार में व्यापक रूप से उपयोग किए जाने वाले एनालॉग मॉड्यूलेशन विधियों के संबंधित सदस्य का नाम है। यह आयाम-शिफ्ट कुंजीयन (एएसके) डिजिटल मॉड्यूलेशन योजना अथवा आयाम मॉड्यूलेशन (एएम) एनालॉग मॉड्यूलेशन योजना का उपयोग करके, दो वाहक तरंगों के आयामों को परिवर्तित (मॉड्यूलेटेड) करके दो एनालॉग संदेश सिग्नल, अथवा दो डिजिटल बिट स्ट्रीम संप्रेषित करता है। दो वाहक तरंगें समान आवृत्ति की हैं और एक-दूसरे के साथ 90° तक चरण से बाहर हैं, इस स्थिति को ओर्थोगोनालिटी अथवा चतुर्भुज चरण के रूप में भी जाना जाता है। इस प्रकार प्रेषित सिग्नल दो वाहक तरंगों को साथ जोड़कर बनाया जाता है। रिसीवर पर, दो तरंगों को उनके ऑर्थोगोनैलिटी गुण के कारण सुसंगत रूप से पृथक (डिमॉड्यूलेटेड) किया जा सकता है। अन्य प्रमुख गुण यह भी है कि मॉड्यूलेशन वाहक आवृत्ति की तुलना में कम-आवृत्ति/कम-बैंडविड्थ तरंग रूप हैं, जिसे इन-फेज और क्वाडरेचर घटकों अथवा नैरोबैंड धारणा के रूप में जाना जाता है।

चरण मॉड्यूलेशन (एनालॉग पीएम) और चरण-शिफ्ट कुंजीयन (डिजिटल पीएसके) को क्यूएएम की विशेष स्थिति माना जा सकता है, जहां प्रेषित सिग्नल का आयाम स्थिर होता है, किन्तु इसका चरण भिन्न होता है। इसे आवृति मॉड्यूलेशन (एफएम) और आवृत्ति शिफ्ट कुंजीयन (एफएसके) तक भी विस्तारित किया जा सकता है, क्योंकि इन्हें चरण मॉड्यूलेशन की विशेष स्थिति माना जा सकता है।

क्यूएएम का उपयोग बड़े स्तर पर डिजिटल दूरसंचार प्रणालियों के लिए मॉड्यूलेशन योजना के रूप में किया जाता है, जिस प्रकार 802.11 वाई-फाई मानकों में होता है। क्यूएएम के साथ आरबिटरेरी रूप से उच्च वर्णक्रमीय दक्षता उपयुक्त तारामंडल आरेख आकार निर्धारित करके प्राप्त की जा सकती है, जो केवल संचार चैनल के ध्वनि स्तर और रैखिकता द्वारा सीमित है।^[1] क्यूएएम का उपयोग ऑप्टिकल फाइबर प्रणाली में बिट रेट वृद्धि के रूप में किया जा रहा है; क्यूएएम 16 और क्यूएएम 64 का 3-पथ इंटरफेरोमीटर के साथ वैकल्पिक रूप से अनुकरण किया जा सकता है।^[2]^[3]

क्यूएएम का डिमॉड्यूलेशन

एनालॉग क्यूएएम: वेक्टर विश्लेषक स्क्रीन पर मापा गया PAL रंग बार सिग्नल।

क्यूएएम सिग्नल में, वाहक अन्य वाहक से 90° पीछे रहता है, और इसके आयाम मॉड्यूलेशन को प्रथागत रूप से इन-फेज घटक के रूप में संदर्भित किया जाता है, जिसे $I (t).$ द्वारा दर्शाया जाता है। अन्य मॉड्यूलेटिंग फलन इन-फ़ेज़ और चतुर्भुज घटक $Q (t).$ हैं। तब समग्र तरंग को गणितीय रूप से इस प्रकार प्रस्तुत किया जा सकता है:

s_{s}(t)\triangleq \sin(2\pi f_{c}t)I(t)\ +\ \underbrace {\sin \left(2\pi f_{c}t+{\tfrac {\pi }{2}}\right)} _{\cos \left(2\pi f_{c}t\right)}\;Q(t),

अथवा:

s_{c}(t)\triangleq \cos(2\pi f_{c}t)I(t)\ +\ \underbrace {\cos \left(2\pi f_{c}t+{\tfrac {\pi }{2}}\right)} _{-\sin \left(2\pi f_{c}t\right)}\;Q(t),

(Eq.1)

जहाँ $f c$ वाहक आवृत्ति है। रिसीवर पर, सुसंगत डेमोडुलेटर $I (t)$ और $Q (t)$ के प्राप्त अनुमानों को उत्पन्न करने के लिए प्राप्त सिग्नल को कोसाइन और साइन दोनों के साथ भिन्न-भिन्न रूप से गुणा करता है। उदाहरण के लिए:

r(t)\triangleq s_{c}(t)\cos(2\pi f_{c}t)=I(t)\cos(2\pi f_{c}t)\cos(2\pi f_{c}t)-Q(t)\sin(2\pi f_{c}t)\cos(2\pi f_{c}t).

मानक त्रिकोणमितीय सर्वसमिकाओं का उपयोग करके, हम इसे इस प्रकार अंकित कर सकते हैं:

{\begin{aligned}r(t)&={\tfrac {1}{2}}I(t)\left[1+\cos(4\pi f_{c}t)\right]-{\tfrac {1}{2}}Q(t)\sin(4\pi f_{c}t)\\&={\tfrac {1}{2}}I(t)+{\tfrac {1}{2}}\left[I(t)\cos(4\pi f_{c}t)-Q(t)\sin(4\pi f_{c}t)\right].\end{aligned}}

लो-पास फ़िल्टरिंग $r (t)$ उच्च आवृत्ति वाले शब्दों ( $4π f c t$ युक्त) को विस्थापित कर देता है, केवल $I (t)$ शब्द को त्याग देता है। यह फ़िल्टर किया गया सिग्नल $Q (t)$ से अप्रभावित रहता है, यह दर्शाता है कि इन-फेज घटक को चतुर्भुज घटक से स्वतंत्र रूप से प्राप्त किया जा सकता है। इसी प्रकार, हम $s c (t)$ का गुणा साइन तरंग से कर सकते हैं और तत्पश्चात $Q (t)$ प्राप्त करने के लिए लो-पास फ़िल्टर का उपयोग कर सकते हैं।

साइन (ठोस लाल) और कोसाइन (बिंदीदार नीला) फ़ंक्शन के ग्राफ़ विभिन्न चरणों के साइनसॉइड हैं।

दो साइनसोइड्स का जोड़ रैखिक ऑपरेशन है जो कोई नया आवृत्ति घटक नहीं बनाता है। इसलिए मिश्रित सिग्नल की बैंडविड्थ डीएसबी (डबल-साइडबैंड) घटकों की बैंडविड्थ के बराबर है। प्रभावी रूप से, डीएसबी की वर्णक्रमीय अतिरेक इस तकनीक का उपयोग करके सूचना क्षमता को दोगुना करने में सक्षम बनाती है। यह डिमोड्यूलेशन जटिलता की कीमत पर आता है। विशेष रूप से, डीएसबी सिग्नल में नियमित आवृत्ति पर शून्य-क्रॉसिंग होती है, जिससे वाहक साइनसॉइड के चरण को पुनर्प्राप्त करना आसान हो जाता है। इसे स्व-घड़ी संकेत|सेल्फ-क्लॉकिंग कहा जाता है। किन्तु क्वाडरेचर-मॉड्यूलेटेड सिग्नल के प्रेषक और रिसीवर को घड़ी साझा करनी होगी या अन्यथा घड़ी सिग्नल भेजना होगा। यदि घड़ी के चरण अलग-अलग हो जाते हैं, तो डिमोड्युलेटेड I और Q सिग्नल -दूसरे में प्रवाहित हो जाते हैं, जिससे क्रॉसस्टॉक उत्पन्न होता है। इस संदर्भ में, घड़ी संकेत को चरण संदर्भ कहा जाता है। क्लॉक सिंक्रोनाइज़ेशन आम तौर पर बर्स्ट सबकैरियर या दोस्त सिग्नल को संचारित करके प्राप्त किया जाता है। उदाहरण के लिए, एनटीएससी के लिए चरण संदर्भ, इसके रंग-विस्फोट सिग्नल में शामिल है।

एनालॉग क्यूएएम का उपयोग इसमें किया जाता है:

एनटीएससी और पीएएल एनालॉग रंगीन टेलीविजन सिस्टम, जहां आई- और क्यू-सिग्नल क्रोमा (रंग) जानकारी के घटकों को ले जाते हैं। क्यूएएम वाहक चरण को प्रत्येक स्कैन लाइन की शुरुआत में प्रसारित विशेष कलरबर्स्ट से पुनर्प्राप्त किया जाता है।
C-QUAM (संगत क्यूएएम) का उपयोग AM स्टीरियो रेडियो एएम स्टीरियो अंतर जानकारी ले जाने के लिए किया जाता है।

क्यूएएम का फूरियर विश्लेषण

आवृत्ति डोमेन में, क्यूएएम का वर्णक्रमीय पैटर्न DSB-SC मॉड्यूलेशन के समान है। यूलर के फार्मूले को साइनसोइड्स पर लागू करना Eq.1, का सकारात्मक-आवृत्ति भाग $s c$ (या विश्लेषणात्मक प्रतिनिधित्व) है:

s_{c}(t)_{+}={\tfrac {1}{2}}e^{i2\pi f_{c}t}[I(t)+iQ(t)]\quad {\stackrel {\mathcal {F}}{\Longrightarrow }}\quad {\tfrac {1}{2}}\left[{\widehat {I\ }}(f-f_{c})+e^{i\pi /2}{\widehat {Q}}(f-f_{c})\right],

जहाँ ${\mathcal {F}}$ फूरियर रूपांतरण को दर्शाता है, और $︿ I$ और $︿ Q$ के रूपांतर हैं $I (t)$ और $Q (t).$ यह परिणाम समान केंद्र आवृत्ति वाले दो डीएसबी-एससी संकेतों के योग का प्रतिनिधित्व करता है। का कारक $i (= e iπ /2)$ 90° चरण बदलाव का प्रतिनिधित्व करता है जो उनके व्यक्तिगत डिमोड्यूलेशन को सक्षम बनाता है।

डिजिटल क्यूएएम

उदाहरण नक्षत्र बिंदुओं के साथ डिजिटल 16-क्यूएएम

4-क्यूएएम, 16-क्यूएएम, 32-क्यूएएम और 64-क्यूएएम के लिए तारामंडल बिंदु ओवरलैप किए गए

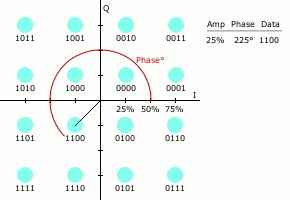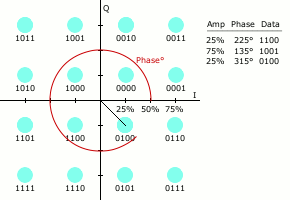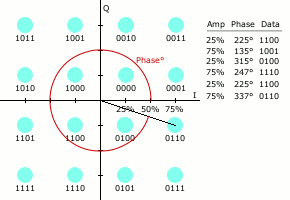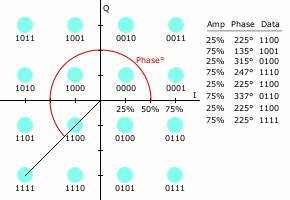
कई डिजिटल मॉड्यूलेशन योजनाओं की तरह, तारामंडल आरेख क्यूएएम के लिए उपयोगी है। क्यूएएम में, तारामंडल बिंदु आमतौर पर समान ऊर्ध्वाधर और क्षैतिज रिक्ति के साथ वर्ग ग्रिड में व्यवस्थित होते हैं, हालांकि अन्य कॉन्फ़िगरेशन संभव हैं (उदाहरण के लिए हेक्सागोनल या त्रिकोणीय ग्रिड)। डिजिटल दूरसंचार में डेटा आमतौर पर बाइनरी अंक प्रणाली है, इसलिए ग्रिड में बिंदुओं की संख्या आम तौर पर प्रति प्रतीक अंश ्स की संख्या के अनुरूप 2 (2, 4, 8, ...) की शक्ति होती है। सबसे सरल और सबसे अधिक इस्तेमाल किए जाने वाले क्यूएएम तारामंडल में वर्ग में व्यवस्थित बिंदु शामिल होते हैं, यानी 16-क्यूएएम, 64-क्यूएएम और 256-क्यूएएम (दो की घात भी)। क्रॉस-क्यूएएम जैसे गैर-वर्ग तारामंडल, अधिक दक्षता प्रदान कर सकते हैं किन्तु बढ़ी हुई मॉडेम जटिलता की लागत के कारण शायद ही कभी इसका उपयोग किया जाता है।

उच्च-क्रम तारामंडल में जाने से, प्रति प्रतीक (डेटा) अधिक बिट्स संचारित करना संभव है। हालाँकि, यदि तारामंडल की औसत ऊर्जा को समान रहना है (निष्पक्ष तुलना के माध्यम से), तो बिंदुओं को साथ करीब होना चाहिए और इस प्रकार शोर और अन्य भ्रष्टाचार के प्रति अधिक संवेदनशील होते हैं; इसके परिणामस्वरूप उच्च बिट त्रुटि दर होती है और इसलिए उच्च-क्रम क्यूएएम निरंतर औसत तारामंडल ऊर्जा के लिए निचले-क्रम क्यूएएम की तुलना में कम विश्वसनीय रूप से अधिक डेटा प्रदान कर सकता है। बिट त्रुटि दर को बढ़ाए बिना उच्च-क्रम क्यूएएम का उपयोग करने के लिए सिग्नल ऊर्जा को बढ़ाकर, शोर को कम करके, या दोनों द्वारा उच्च सिग्नल-टू-शोर अनुपात (एसएनआर) की आवश्यकता होती है।

यदि 8-चरण-शिफ्ट कुंजीयन द्वारा प्रस्तावित डेटा-दरों से अधिक की आवश्यकता होती है, तो क्यूएएम पर जाना अधिक सामान्य है क्योंकि यह बिंदुओं को अधिक समान रूप से वितरित करके I-Q विमान में आसन्न बिंदुओं के बीच अधिक दूरी प्राप्त करता है। जटिल कारक यह है कि बिंदु अब सभी समान आयाम नहीं हैं और इसलिए डिमॉड्युलेटर को अब केवल चरण के बजाय चरण (तरंगों) और आयाम दोनों का सही ढंग से पता लगाना होगा।

64-क्यूएएम और 256-क्यूएएम का उपयोग अक्सर डिजिटल केबल टेलीविजन और केबल मॉडेम अनुप्रयोगों में किया जाता है। संयुक्त राज्य अमेरिका में, 64-क्यूएएम और 256-क्यूएएम डिजिटल केबल के लिए अनिवार्य मॉड्यूलेशन योजनाएं हैं (क्यूएएम ट्यूनर देखें) जैसा कि केबल दूरसंचार इंजीनियरों की सोसायटी द्वारा मानक ANSI/SCTE 07 2013 में मानकीकृत किया गया है। . ध्यान दें कि कई मार्केटिंग लोग इन्हें क्यूएएम-64 और क्यूएएम-256 के रूप में संदर्भित करेंगे।^{[citation needed]} यूके में, 64-क्यूएएम का उपयोग डिजिटल टेरेस्ट्रियल टेलीविजन (फ्रीव्यू (यूके)) के लिए किया जाता है जबकि 256-क्यूएएम का उपयोग फ्रीव्यू-एचडी के लिए किया जाता है।

ADSL लाइन पर बिट-लोडिंग (बिट्स प्रति क्यूएएम तारामंडल)।

वर्णक्रमीय दक्षता के बहुत उच्च स्तर को प्राप्त करने के लिए डिज़ाइन की गई संचार प्रणालियाँ आमतौर पर बहुत घने क्यूएएम तारामंडल का उपयोग करती हैं। उदाहरण के लिए, वर्तमान होमप्लग AV2 500-Mbit/s पावर लाइन संचार#होम नेटवर्किंग (LAN) डिवाइस 1024-क्यूएएम और 4096-क्यूएएम का उपयोग करते हैं,^[4] साथ ही मौजूदा होम वायरिंग (को्स, फोन लाइनों और पावर लाइन संचार पर ईथरनेट) पर नेटवर्किंग के लिए आईटीयू-टी जी.एचएन मानक का उपयोग करने वाले भविष्य के उपकरण; 4096-क्यूएएम 12 बिट/प्रतीक प्रदान करता है। अन्य उदाहरण कॉपर ट्विस्टेड जोड़े के लिए एडीएसएल तकनीक है, जिसका तारामंडल आकार 32768-क्यूएएम तक जाता है (एडीएसएल शब्दावली में इसे बिट-लोडिंग या बिट प्रति टोन कहा जाता है, 32768-क्यूएएम 15 बिट प्रति टोन के बराबर है)।^[5]

अल्ट्रा-उच्च क्षमता वाले माइक्रोवेव बैकहॉल सिस्टम भी 1024-क्यूएएम का उपयोग करते हैं।^[6] 1024-क्यूएएम, अनुकूली कोडिंग और मॉड्यूलेशन (ACM) और XPIC के साथ, विक्रेता ल 56 मेगाहर्ट्ज चैनल में गीगाबिट क्षमता प्राप्त कर सकते हैं।^[6]

हस्तक्षेप और शोर

प्रसारण या दूरसंचार जैसे प्रतिकूल आकाशवाणी आवृति /माइक्रोवेव क्यूएएम अनुप्रयोग वातावरण में उच्च क्रम क्यूएएम तारामंडल (उच्च डेटा दर और मोड) में जाने पर, मल्टीपाथ हस्तक्षेप आम तौर पर बढ़ जाता है। तारामंडल में धब्बों का प्रसार हो रहा है, जिससे आसन्न राज्यों के बीच अलगाव कम हो गया है, जिससे रिसीवर के लिए सिग्नल को उचित रूप से डिकोड करना मुश्किल हो गया है। दूसरे शब्दों में, शोर#इलेक्ट्रॉनिक शोर प्रतिरोधक क्षमता कम हो गई है। ऐसे कई परीक्षण पैरामीटर माप हैं जो विशिष्ट ऑपरेटिंग वातावरण के लिए इष्टतम क्यूएएम मोड निर्धारित करने में मदद करते हैं। निम्नलिखित तीन सबसे महत्वपूर्ण हैं:^[7]

वाहक संकेत/हस्तक्षेप अनुपात
वाहक-से-शोर अनुपात
सीमा-से-शोर अनुपात

यह भी देखें

आयाम और चरण-शिफ्ट कुंजीयन या असममित चरण-शिफ्ट कुंजीयन (एपीएसके)
वाहक रहित आयाम चरण मॉड्यूलेशन (सीएपी)
Circle packing § Applications
इन-फेज और चतुर्भुज घटक
मॉडुलन तकनीकों के अन्य उदाहरणों के लिए मॉड्यूलेशन
चरण-शिफ्ट कुंजीयन
एचडीटीवी के लिए क्यूएएम ट्यूनर
यादृच्छिक मॉड्यूलेशन

संदर्भ

↑ "डिजिटल मॉड्यूलेशन दक्षताएँ". Barnard Microsystems. Archived from the original on 2011-04-30.
↑ "Ciena tests 200G via 16-QAM with Japan-U.S. Cable Network". lightwave. April 17, 2014. Retrieved 7 November 2016.
↑ Kylia products Archived July 13, 2011, at the Wayback Machine, dwdm mux demux, 90 degree optical hybrid, d(q) psk demodulatorssingle polarization
↑ http://www.homeplug.org/media/filer_public/a1/46/a1464318-f5df-46c5-89dc-7243d8ccfcee/homeplug_av2_whitepaper_150907.pdf Homeplug_AV2 whitepaper
↑ http://www.itu.int/rec/T-REC-G.992.3-200904-I section 8.6.3 Constellation mapper - maximum number of bits per constellation BIMAX ≤ 15
↑ ^6.0 ^6.1 http://www.trangosys.com/products/point-to-point-wireless-backhaul/licensed-wireless/trangolink-apex-orion.shtml A Apex Orion
↑ Howard Friedenberg and Sunil Naik. "हिटलेस स्पेस डायवर्सिटी एसटीएल संकीर्ण एसटीएल बैंड में आईपी+ऑडियो सक्षम करता है" (PDF). 2005 National Association of Broadcasters Annual Convention. Archived from the original (PDF) on March 23, 2006. Retrieved April 17, 2005.

अग्रिम पठन

Jonqyin (Russell) Sun "Linear diversity analysis for QAM in Rician fading channels", IEEE WOCC 2014
John G. Proakis, "Digital Communications, 3rd Edition"

बाहरी संबंध

QAM Demodulation
Interactive webdemo of QAM constellation with additive noise Institute of Telecommunicatons, University of Stuttgart
QAM bit error rate for AWGN channel – online experiment
How imperfections affect QAM constellation
Microwave Phase Shifters Overview by Herley General Microwave
Simulation of dual-polarization QPSK (DP-QPSK) for 100G optical transmission

[1] "डिजिटल मॉड्यूलेशन दक्षताएँ". Barnard Microsystems. Archived from the original on 2011-04-30.

[2] "Ciena tests 200G via 16-QAM with Japan-U.S. Cable Network". lightwave. April 17, 2014. Retrieved 7 November 2016.

[3] Kylia products Archived July 13, 2011, at the Wayback Machine, dwdm mux demux, 90 degree optical hybrid, d(q) psk demodulatorssingle polarization

[4] ttp://www.homeplug.org/media/filer_public/a1/46/a1464318-f5df-46c5-89dc-7243d8ccfcee/homeplug_av2_whitepaper_150907.pdf Homeplug_AV2 whitepaper

[5] ttp://www.itu.int/rec/T-REC-G.992.3-200904-I section 8.6.3 Constellation mapper - maximum number of bits per constellation BIMAX ≤ 15

[auto-6] 6.0 ^6.1 http://www.trangosys.com/products/point-to-point-wireless-backhaul/licensed-wireless/trangolink-apex-orion.shtml A Apex Orion

[7] Howard Friedenberg and Sunil Naik. "हिटलेस स्पेस डायवर्सिटी एसटीएल संकीर्ण एसटीएल बैंड में आईपी+ऑडियो सक्षम करता है" (PDF). 2005 National Association of Broadcasters Annual Convention. Archived from the original (PDF) on March 23, 2006. Retrieved April 17, 2005.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

@@ Line 16: / Line 16: @@
 == क्यूएएम का डिमॉड्यूलेशन ==
-[[File:PAL colour bar signal measured vector edit.svg|200px|right|thumb|एनालॉग क्यूएएम: वेक्टर विश्लेषक स्क्रीन पर मापा गया PAL रंग बार सिग्नल।]]क्यूएएम सिग्नल में, वाहक दूसरे से 90° पीछे रहता है, और इसके आयाम मॉड्यूलेशन को पारंपरिक रूप से In-phase_and_quadrature_components|in-phase घटक के रूप में संदर्भित किया जाता है, जिसे इसके द्वारा दर्शाया जाता है। {{math|''I''(''t'').}} अन्य मॉड्यूलेटिंग फ़ंक्शन इन-फ़ेज़ और क्वाडरेचर घटक हैं, {{math|''Q''(''t'').}} तो समग्र तरंग को गणितीय रूप से इस प्रकार तैयार किया गया है:
+[[File:PAL colour bar signal measured vector edit.svg|200px|right|thumb|एनालॉग क्यूएएम: वेक्टर विश्लेषक स्क्रीन पर मापा गया PAL रंग बार सिग्नल।]]क्यूएएम सिग्नल में, वाहक अन्य वाहक से 90° पीछे रहता है, और इसके आयाम मॉड्यूलेशन को प्रथागत रूप से इन-फेज घटक के रूप में संदर्भित किया जाता है, जिसे {{math|''I''(''t'').}} द्वारा दर्शाया जाता है। अन्य मॉड्यूलेटिंग फलन इन-फ़ेज़ और चतुर्भुज घटक {{math|''Q''(''t'').}} हैं। तब समग्र तरंग को गणितीय रूप से इस प्रकार प्रस्तुत किया जा सकता है:
-:<math>s_s(t) \triangleq \sin(2\pi f_c t) I(t)\ +\ \underbrace{\sin\left(2\pi f_c t + \tfrac{\pi}{2} \right)}_{\cos\left(2\pi f_c t\right)}\; Q(t),</math> या:
+:<math>s_s(t) \triangleq \sin(2\pi f_c t) I(t)\ +\ \underbrace{\sin\left(2\pi f_c t + \tfrac{\pi}{2} \right)}_{\cos\left(2\pi f_c t\right)}\; Q(t),</math> अथवा:
 {{NumBlk|:|<math>s_c(t) \triangleq \cos(2\pi f_c t) I(t)\ +\ \underbrace{\cos\left(2\pi f_c t + \tfrac{\pi}{2} \right)}_{-\sin\left(2\pi f_c t\right)}\; Q(t),</math>|{{EquationRef|Eq.1}}}}
-कहाँ {{math|''f''{{sub|c}}}} वाहक आवृत्ति है. रिसीवर पर, [[उत्पाद डिटेक्टर]] प्राप्त अनुमानों को उत्पन्न करने के लिए [[ कोज्या |कोज्या]] और [[ उन लोगों के |उन लोगों के]] सिग्नल दोनों के साथ प्राप्त सिग्नल को अलग-अलग गुणा करता है। {{math|''I''(''t'')}} और {{math|''Q''(''t'')}}. उदाहरण के लिए:
+जहाँ {{math|''f''{{sub|c}}}} वाहक आवृत्ति है। रिसीवर पर, [[उत्पाद डिटेक्टर|सुसंगत डेमोडुलेटर]] {{math|''I''(''t'')}} और {{math|''Q''(''t'')}} के प्राप्त अनुमानों को उत्पन्न करने के लिए प्राप्त सिग्नल को [[ कोज्या |कोसाइन]] और [[ उन लोगों के |साइन]] दोनों के साथ भिन्न-भिन्न रूप से गुणा करता है। उदाहरण के लिए:
 :<math>r(t) \triangleq s_c(t) \cos (2 \pi f_c t) = I(t) \cos (2 \pi f_c t) \cos (2 \pi f_c t) - Q(t) \sin (2 \pi f_c t) \cos (2 \pi f_c t).</math>
-त्रिकोणमितीय सर्वसमिकाओं#उत्पाद-से-योग और योग-से-उत्पाद सर्वसमिकाओं की मानक सूची का उपयोग करके, हम इसे इस प्रकार लिख सकते हैं:
+मानक त्रिकोणमितीय सर्वसमिकाओं का उपयोग करके, हम इसे इस प्रकार अंकित कर सकते हैं:
 :<math>\begin{align}
@@ Line 30: / Line 30: @@
         &= \tfrac{1}{2} I(t) + \tfrac{1}{2} \left[I(t) \cos (4 \pi f_c t) - Q(t) \sin (4 \pi f_c t)\right].
 \end{align}</math>
-कम-पास फ़िल्टरिंग {{math|''r''(''t'')}} उच्च आवृत्ति वाले शब्दों (युक्त) को हटा देता है {{math|4π''f''{{sub|c}}''t''}}), केवल छोड़कर {{math|''I''(''t'')}} अवधि। यह फ़िल्टर किया गया सिग्नल इससे अप्रभावित रहता है {{math|''Q''(''t''),}} यह दर्शाता है कि इन-फेज घटक को चतुर्भुज घटक से स्वतंत्र रूप से प्राप्त किया जा सकता है। इसी प्रकार, हम गुणा कर सकते हैं {{math|''s''{{sub|c}}(''t'')}} साइन वेव द्वारा और फिर निकालने के लिए लो-पास फ़िल्टर द्वारा {{math|''Q''(''t'').}}
+लो-पास फ़िल्टरिंग {{math|''r''(''t'')}} उच्च आवृत्ति वाले शब्दों ({{math|4π''f''{{sub|c}}''t''}} युक्त) को विस्थापित कर देता है, केवल {{math|''I''(''t'')}} शब्द को त्याग देता है। यह फ़िल्टर किया गया सिग्नल {{math|''Q''(''t'')}} से अप्रभावित रहता है, यह दर्शाता है कि इन-फेज घटक को चतुर्भुज घटक से स्वतंत्र रूप से प्राप्त किया जा सकता है। इसी प्रकार, हम {{math|''s''{{sub|c}}(''t'')}} का गुणा साइन तरंग से कर सकते हैं और तत्पश्चात {{math|''Q''(''t'')}} प्राप्त करने के लिए लो-पास फ़िल्टर का उपयोग कर सकते हैं।
 [[File:Sine and Cosine.svg|thumb|180px|right|साइन (ठोस लाल) और कोसाइन (बिंदीदार नीला) फ़ंक्शन के ग्राफ़ विभिन्न चरणों के साइनसॉइड हैं।]]दो साइनसोइड्स का जोड़ रैखिक ऑपरेशन है जो कोई नया आवृत्ति घटक नहीं बनाता है। इसलिए मिश्रित सिग्नल की बैंडविड्थ डीएसबी (डबल-साइडबैंड) घटकों की बैंडविड्थ के बराबर है। प्रभावी रूप से, डीएसबी की वर्णक्रमीय अतिरेक इस तकनीक का उपयोग करके सूचना क्षमता को दोगुना करने में सक्षम बनाती है। यह डिमोड्यूलेशन जटिलता की कीमत पर आता है। विशेष रूप से, डीएसबी सिग्नल में नियमित आवृत्ति पर शून्य-क्रॉसिंग होती है, जिससे वाहक साइनसॉइड के चरण को पुनर्प्राप्त करना आसान हो जाता है। इसे [[स्व-घड़ी संकेत]]|सेल्फ-क्लॉकिंग कहा जाता है। किन्तु क्वाडरेचर-मॉड्यूलेटेड सिग्नल के प्रेषक और रिसीवर को घड़ी साझा करनी होगी या अन्यथा घड़ी सिग्नल भेजना होगा। यदि घड़ी के चरण अलग-अलग हो जाते हैं, तो डिमोड्युलेटेड I और Q सिग्नल -दूसरे में प्रवाहित हो जाते हैं, जिससे [[क्रॉसस्टॉक]] उत्पन्न होता है। इस संदर्भ में, घड़ी संकेत को चरण संदर्भ कहा जाता है। क्लॉक सिंक्रोनाइज़ेशन आम तौर पर बर्स्ट [[सबकैरियर]] या [[दोस्त]] सिग्नल को संचारित करके प्राप्त किया जाता है। उदाहरण के लिए, [[एनटीएससी]] के लिए चरण संदर्भ, इसके [[ रंग-विस्फोट |रंग-विस्फोट]] सिग्नल में शामिल है।
@@ Line 47: / Line 47: @@
    \tfrac{1}{2}\left[\widehat{I\ }(f - f_c) + e^{i\pi/2} \widehat Q(f - f_c)\right],
 </math>
-कहाँ <math>\mathcal{F}</math> फूरियर रूपांतरण को दर्शाता है, और {{math|{{overset|︿|I}}}} और {{math|{{overset|︿|Q}}}} के रूपांतर हैं {{math|''I''(''t'')}} और {{math|''Q''(''t'').}} यह परिणाम समान केंद्र आवृत्ति वाले दो डीएसबी-एससी संकेतों के योग का प्रतिनिधित्व करता है। का कारक {{math|1='''i''' (= ''e''{{sup|''iπ''/2}})}} 90° चरण बदलाव का प्रतिनिधित्व करता है जो उनके व्यक्तिगत डिमोड्यूलेशन को सक्षम बनाता है।
+जहाँ <math>\mathcal{F}</math> फूरियर रूपांतरण को दर्शाता है, और {{math|{{overset|︿|I}}}} और {{math|{{overset|︿|Q}}}} के रूपांतर हैं {{math|''I''(''t'')}} और {{math|''Q''(''t'').}} यह परिणाम समान केंद्र आवृत्ति वाले दो डीएसबी-एससी संकेतों के योग का प्रतिनिधित्व करता है। का कारक {{math|1='''i''' (= ''e''{{sup|''iπ''/2}})}} 90° चरण बदलाव का प्रतिनिधित्व करता है जो उनके व्यक्तिगत डिमोड्यूलेशन को सक्षम बनाता है।
 == डिजिटल क्यूएएम ==

v t e Analog television broadcasting topics
Systems	180-line 343-line 375-line 405-line (System A) 441-line 525-line (System M) 625-line (System B, System C, System D, System G, System H, System I, System K, System L, System N) 819-line ( System E , System F )
Color systems	NTSC NTSC-J Clear-Vision PAL PAL-M PAL-S PALplus SECAM
Video	Back porch and front porch Black level Blanking level Chrominance Chrominance subcarrier Colorburst Color killer Color TV Composite video Frame (video) Horizontal scan rate Horizontal blanking interval Luma Nominal analogue blanking Overscan Raster scan Safe area Television lines Vertical blanking interval White clipper
Sound	Multichannel television sound NICAM Sound-in-Syncs Zweikanalton
Modulation	Frequency modulation Quadrature amplitude modulation Vestigial sideband modulation (VSB)
Transmission	Amplifiers Antenna (radio) Broadcast transmitter/Transmitter station Cavity amplifier Differential gain Differential phase Diplexer Dipole antenna Dummy load Frequency mixer Intercarrier method Intermediate frequency Output power of an analog TV transmitter Pre-emphasis Residual carrier Split sound system Superheterodyne transmitter Television receive-only Direct-broadcast satellite television Television transmitter Terrestrial television Transposer Digital television transition
Frequencies & Bands	Frequency offset Microwave transmission Television channel frequencies UHF VHF
Propagation	Beam tilt Distortion Earth bulge Field strength in free space Noise (electronics) Null fill Path loss Radiation pattern Skew Television interference
Testing	Distortionmeter Field strength meter Vectorscope VIT signals Zero reference pulse
Artifacts	Dot crawl Ghosting Hanover bars Sparklies

v t e Telecommunications
History	Beacon Broadcasting Cable protection system Cable TV Communications satellite Computer network Data compression audio DCT image video Digital media Internet video online video platform social media streaming Drums Edholm's law Electrical telegraph Fax Heliographs Hydraulic telegraph Information Age Information revolution Internet Mass media Mobile phone Smartphone Optical telecommunication Optical telegraphy Pager Photophone Prepaid mobile phone Radio Radiotelephone Satellite communications Semaphore Semiconductor device MOSFET transistor Smoke signals Telecommunications history Telautograph Telegraphy Teleprinter (teletype) Telephone The Telephone Cases Television digital streaming Undersea telegraph line Videotelephony Whistled language Wireless revolution
Pioneers	Nasir Ahmed Edwin Howard Armstrong Mohamed M. Atalla John Logie Baird Paul Baran John Bardeen Alexander Graham Bell Emile Berliner Tim Berners-Lee Francis Blake (telephone) Jagadish Chandra Bose Charles Bourseul Walter Houser Brattain Vint Cerf Claude Chappe Yogen Dalal Daniel Davis Jr. Donald Davies Amos Dolbear Thomas Edison Lee de Forest Philo Farnsworth Reginald Fessenden Elisha Gray Oliver Heaviside Robert Hooke Erna Schneider Hoover Harold Hopkins Gardiner Greene Hubbard Internet pioneers Bob Kahn Dawon Kahng Charles K. Kao Narinder Singh Kapany Hedy Lamarr Innocenzo Manzetti Guglielmo Marconi Robert Metcalfe Antonio Meucci Samuel Morse Jun-ichi Nishizawa Charles Grafton Page Radia Perlman Alexander Stepanovich Popov Tivadar Puskás Johann Philipp Reis Claude Shannon Almon Brown Strowger Henry Sutton Charles Sumner Tainter Nikola Tesla Camille Tissot Alfred Vail Thomas A. Watson Charles Wheatstone Vladimir K. Zworykin
Transmission media	Coaxial cable Fiber-optic communication optical fiber Free-space optical communication Molecular communication Radio waves wireless Transmission line data transmission circuit telecommunication circuit
Network topology and switching	Bandwidth Links Nodes terminal Network switching circuit packet Telephone exchange
Multiplexing	Space-division Frequency-division Time-division Polarization-division Orbital angular-momentum Code-division
Concepts	Communication protocol Computer network Data transmission Store and forward Telecommunications equipment
Types of network	Cellular network Ethernet ISDN LAN Mobile NGN Public Switched Telephone Radio Television Telex UUCP WAN Wireless network
Notable networks	ARPANET BITNET CYCLADES FidoNet Internet Internet2 JANET NPL network Toasternet Usenet
Locations	Africa Americas North South Antarctica Asia Europe Oceania (Global telecommunications regulation bodies)
Category Outline Commons

Anonymous

Search

चतुर्भुज आयाम मॉड्यूलेशन: Difference between revisions

Namespaces

More

Page actions

Revision as of 19:50, 27 July 2023

Contents

क्यूएएम का डिमॉड्यूलेशन

क्यूएएम का फूरियर विश्लेषण

डिजिटल क्यूएएम

हस्तक्षेप और शोर

यह भी देखें

संदर्भ

अग्रिम पठन

बाहरी संबंध

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

चतुर्भुज आयाम मॉड्यूलेशन: Difference between revisions

Revision as of 19:50, 27 July 2023

क्यूएएम का डिमॉड्यूलेशन

क्यूएएम का फूरियर विश्लेषण

डिजिटल क्यूएएम

हस्तक्षेप और शोर

यह भी देखें

संदर्भ

अग्रिम पठन

बाहरी संबंध

Navigation

Wiki tools

Page tools

Other projects

Categories