मिट्टाग-लेफ़लर फ़ंक्शन: Difference between revisions
(Created page with "{{Short description|Mathematical function}} {{distinguish|Mittag-Leffler polynomials}} File:MittagLeffler GaussToLorentz.gif|thumb|right|300px|मिट्टाग-ले...") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Mathematical function}} | {{Short description|Mathematical function}} | ||
{{distinguish|Mittag-Leffler polynomials}} | {{distinguish|Mittag-Leffler polynomials}} | ||
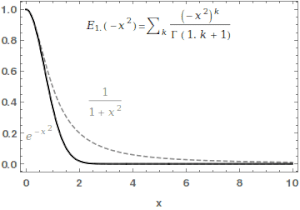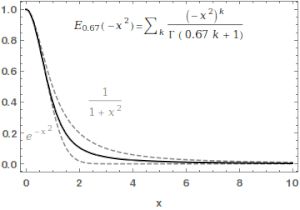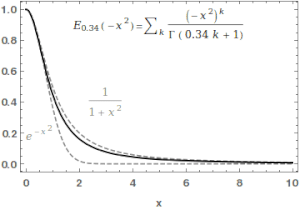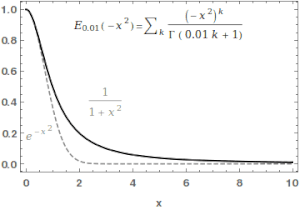
[[File:MittagLeffler GaussToLorentz.gif|thumb|right|300px|मिट्टाग-लेफ़लर फ़ंक्शन का उपयोग गाऊसी और लोरेंत्ज़ियन फ़ंक्शन के बीच लगातार अंतरण करने के लिए किया जा सकता है।]]गणित में, मिट्टाग-लेफ़लर फ़ंक्शन <math>E_{\alpha,\beta}</math> | [[File:MittagLeffler GaussToLorentz.gif|thumb|right|300px|मिट्टाग-लेफ़लर फ़ंक्शन का उपयोग गाऊसी और लोरेंत्ज़ियन फ़ंक्शन के बीच लगातार अंतरण करने के लिए किया जा सकता है।]]गणित में, मिट्टाग-लेफ़लर फ़ंक्शन <math>E_{\alpha,\beta}</math> विशेष फ़ंक्शन है, [[जटिल संख्या]] [[फ़ंक्शन (गणित)]] जो दो जटिल मापदंडों पर निर्भर करता है <math>\alpha</math> और <math>\beta</math>. इसका वास्तविक भाग होने पर इसे निम्नलिखित [[श्रृंखला (गणित)]] द्वारा परिभाषित किया जा सकता है <math>\alpha</math> पूर्णतः सकारात्मक है:<ref name=":0">{{cite arXiv|last1=Saxena|first1=R. K.|last2=Mathai|first2=A. M.|last3=Haubold|first3=H. J.|date=2009-09-01|title=मिट्टाग-लेफ़लर फ़ंक्शंस और उनके अनुप्रयोग|class=math.CA |eprint=0909.0230|language=en}}</ref><ref>{{Cite web|url=http://mathworld.wolfram.com/Mittag-LefflerFunction.html|title=मिट्टाग-लेफ़लर फ़ंक्शन|last=Weisstein|first=Eric W.|website=mathworld.wolfram.com|language=en|access-date=2019-09-11}}</ref> | ||
:<math>E_{\alpha, \beta} (z) = \sum_{k=0}^\infty \frac{z^k}{\Gamma(\alpha k + \beta)},</math> | :<math>E_{\alpha, \beta} (z) = \sum_{k=0}^\infty \frac{z^k}{\Gamma(\alpha k + \beta)},</math> | ||
कहाँ <math>\Gamma(x) </math> [[गामा फ़ंक्शन]] है. कब <math>\beta=1</math>, इसका संक्षिप्त रूप इस प्रकार है <math>E_\alpha(z) = E_{\alpha,1}(z)</math>. | कहाँ <math>\Gamma(x) </math> [[गामा फ़ंक्शन]] है. कब <math>\beta=1</math>, इसका संक्षिप्त रूप इस प्रकार है <math>E_\alpha(z) = E_{\alpha,1}(z)</math>. | ||
के लिए <math>\alpha=0</math>, उपरोक्त श्रृंखला ज्यामितीय श्रृंखला के टेलर विस्तार के बराबर है और परिणामस्वरूप <math>E_{0,\beta}(z)=\frac{1}{\Gamma(\beta)}\frac{1}{1-z}</math>. | के लिए <math>\alpha=0</math>, उपरोक्त श्रृंखला ज्यामितीय श्रृंखला के टेलर विस्तार के बराबर है और परिणामस्वरूप <math>E_{0,\beta}(z)=\frac{1}{\Gamma(\beta)}\frac{1}{1-z}</math>. | ||
यदि <math>\alpha</math> और <math>\beta</math> वास्तविक और सकारात्मक हैं, श्रृंखला तर्क के सभी मूल्यों के लिए अभिसरण करती है <math>z</math>, इसलिए मिट्टाग-लेफ़लर फ़ंक्शन | यदि <math>\alpha</math> और <math>\beta</math> वास्तविक और सकारात्मक हैं, श्रृंखला तर्क के सभी मूल्यों के लिए अभिसरण करती है <math>z</math>, इसलिए मिट्टाग-लेफ़लर फ़ंक्शन संपूर्ण फ़ंक्शन है। इस फ़ंक्शन का नाम गोस्टा मिट्टाग-लेफ़लर के नाम पर रखा गया है। [[भिन्नात्मक कलन]] के सिद्धांत में कार्यों का यह वर्ग महत्वपूर्ण है। | ||
के लिए <math>\alpha >0 </math>, मिट्टाग-लेफ़लर फ़ंक्शन <math>E_{\alpha,1}(z)</math> व्यवस्था का | के लिए <math>\alpha >0 </math>, मिट्टाग-लेफ़लर फ़ंक्शन <math>E_{\alpha,1}(z)</math> व्यवस्था का संपूर्ण कार्य है <math>1/\alpha</math>, और कुछ अर्थों में इसके क्रम का सबसे सरल संपूर्ण कार्य है। | ||
मिट्टाग-लेफ़लर फ़ंक्शन पुनरावृत्ति गुण को संतुष्ट करता है (प्रमेय 5.1)। <ref name=":0" /> | मिट्टाग-लेफ़लर फ़ंक्शन पुनरावृत्ति गुण को संतुष्ट करता है (प्रमेय 5.1)। <ref name=":0" /> | ||
| Line 50: | Line 50: | ||
==मिटाग-लेफ़लर फ़ंक्शन के अनुप्रयोग== | ==मिटाग-लेफ़लर फ़ंक्शन के अनुप्रयोग== | ||
मिट्टाग-लेफ़लर फ़ंक्शन के अनुप्रयोगों में से | मिट्टाग-लेफ़लर फ़ंक्शन के अनुप्रयोगों में से भिन्नात्मक क्रम विस्कोलेस्टिक सामग्रियों के मॉडलिंग में है। विस्कोइलास्टिक सामग्रियों के समय-निर्भर विश्राम व्यवहार की प्रायोगिक जांच में विश्राम प्रक्रिया की शुरुआत में तनाव में बहुत तेजी से कमी और बड़े समय के लिए बेहद धीमी गति से गिरावट की विशेषता है। स्थिर स्पर्शोन्मुख मूल्य तक पहुंचने में काफी समय भी लग सकता है। इसलिए, पर्याप्त सटीकता के साथ विश्राम व्यवहार का वर्णन करने के लिए बहुत सारे मैक्सवेल तत्वों की आवश्यकता होती है। यह बड़ी संख्या में सामग्री मापदंडों की पहचान करने के लिए कठिन अनुकूलन समस्या में समाप्त होता है। दूसरी ओर, पिछले कुछ वर्षों में, भिन्नात्मक व्युत्पन्न की अवधारणा को [[viscoelasticity]] के सिद्धांत से परिचित कराया गया है। इन मॉडलों में, स्टैंडर्ड_लीनियर_सॉलिड_मॉडल मॉडल केवल कुछ ही सामग्री मापदंडों के साथ रबर जैसी सामग्रियों की गतिशील प्रकृति की भविष्यवाणी करने के लिए बहुत प्रभावी पाया गया। संबंधित संवैधानिक समीकरण का समाधान मिट्टाग-लेफ़लर प्रकार के विश्राम फ़ंक्शन की ओर ले जाता है। इसे नकारात्मक तर्कों के साथ शक्ति श्रृंखला द्वारा परिभाषित किया गया है। यह फ़ंक्शन मूल पर छलांग के साथ मनमाना और निरंतर संकेत के प्रभाव में विश्राम प्रक्रिया के सभी आवश्यक गुणों का प्रतिनिधित्व करता है।<ref>Pritz, T. (2003). Five-parameter fractional derivative model for polymeric damping materials. Journal of Sound and Vibration, 265(5), 935-952.</ref><ref>Nonnenmacher, T. F., & Glöckle, W. G. (1991). A fractional model for mechanical stress relaxation. Philosophical magazine letters, 64(2), 89-93.</ref> | ||
| Line 64: | Line 64: | ||
==संदर्भ== | ==संदर्भ== | ||
{{reflist}} | {{reflist}} | ||
* Mittag-Leffler, M.G.: Sur la nouvelle fonction E(x). C. R. Acad. Sci. Paris 137, 554–558 (1903) | * Mittag-Leffler, M.G.: Sur la nouvelle fonction E(x). C. R. Acad. Sci. Paris 137, 554–558 (1903) | ||
* Mittag-Leffler, M.G.: Sopra la funzione E˛.x/. Rend. R. Acc. Lincei, (Ser. 5) 13, 3–5 (1904) | * Mittag-Leffler, M.G.: Sopra la funzione E˛.x/. Rend. R. Acc. Lincei, (Ser. 5) 13, 3–5 (1904) | ||
Revision as of 21:23, 7 July 2023
गणित में, मिट्टाग-लेफ़लर फ़ंक्शन विशेष फ़ंक्शन है, जटिल संख्या फ़ंक्शन (गणित) जो दो जटिल मापदंडों पर निर्भर करता है और . इसका वास्तविक भाग होने पर इसे निम्नलिखित श्रृंखला (गणित) द्वारा परिभाषित किया जा सकता है पूर्णतः सकारात्मक है:[1][2]
कहाँ गामा फ़ंक्शन है. कब , इसका संक्षिप्त रूप इस प्रकार है . के लिए , उपरोक्त श्रृंखला ज्यामितीय श्रृंखला के टेलर विस्तार के बराबर है और परिणामस्वरूप .
यदि और वास्तविक और सकारात्मक हैं, श्रृंखला तर्क के सभी मूल्यों के लिए अभिसरण करती है , इसलिए मिट्टाग-लेफ़लर फ़ंक्शन संपूर्ण फ़ंक्शन है। इस फ़ंक्शन का नाम गोस्टा मिट्टाग-लेफ़लर के नाम पर रखा गया है। भिन्नात्मक कलन के सिद्धांत में कार्यों का यह वर्ग महत्वपूर्ण है।
के लिए , मिट्टाग-लेफ़लर फ़ंक्शन व्यवस्था का संपूर्ण कार्य है , और कुछ अर्थों में इसके क्रम का सबसे सरल संपूर्ण कार्य है।
मिट्टाग-लेफ़लर फ़ंक्शन पुनरावृत्ति गुण को संतुष्ट करता है (प्रमेय 5.1)। [1]
जिससे एसिम्प्टोटिक विस्तार|पोंकारे एसिम्प्टोटिक विस्तार
अनुसरण करता है, जो सत्य है .
विशेष मामले
के लिए हम पाते हैं: (धारा 2 [1] त्रुटि फ़ंक्शन:
ज्यामितीय प्रगति का योग:
के लिए , अपने पास
के लिए , अभिन्न
क्रमशः देता है: , , .
मिट्टाग-लेफ़लर का अभिन्न प्रतिनिधित्व
मिट्टाग-लेफ़लर फ़ंक्शन का अभिन्न प्रतिनिधित्व (धारा 6) है [1]
जहां रूपरेखा प्रारंभ और समाप्त होता है और इंटीग्रैंड की विलक्षणताओं और शाखा बिंदुओं के चारों ओर वृत्त।
लाप्लास परिवर्तन और मिट्टाग-लेफ़लर योग से संबंधित अभिव्यक्ति (Eq (7.5)) है [1]साथ )
मिटाग-लेफ़लर फ़ंक्शन के अनुप्रयोग
मिट्टाग-लेफ़लर फ़ंक्शन के अनुप्रयोगों में से भिन्नात्मक क्रम विस्कोलेस्टिक सामग्रियों के मॉडलिंग में है। विस्कोइलास्टिक सामग्रियों के समय-निर्भर विश्राम व्यवहार की प्रायोगिक जांच में विश्राम प्रक्रिया की शुरुआत में तनाव में बहुत तेजी से कमी और बड़े समय के लिए बेहद धीमी गति से गिरावट की विशेषता है। स्थिर स्पर्शोन्मुख मूल्य तक पहुंचने में काफी समय भी लग सकता है। इसलिए, पर्याप्त सटीकता के साथ विश्राम व्यवहार का वर्णन करने के लिए बहुत सारे मैक्सवेल तत्वों की आवश्यकता होती है। यह बड़ी संख्या में सामग्री मापदंडों की पहचान करने के लिए कठिन अनुकूलन समस्या में समाप्त होता है। दूसरी ओर, पिछले कुछ वर्षों में, भिन्नात्मक व्युत्पन्न की अवधारणा को viscoelasticity के सिद्धांत से परिचित कराया गया है। इन मॉडलों में, स्टैंडर्ड_लीनियर_सॉलिड_मॉडल मॉडल केवल कुछ ही सामग्री मापदंडों के साथ रबर जैसी सामग्रियों की गतिशील प्रकृति की भविष्यवाणी करने के लिए बहुत प्रभावी पाया गया। संबंधित संवैधानिक समीकरण का समाधान मिट्टाग-लेफ़लर प्रकार के विश्राम फ़ंक्शन की ओर ले जाता है। इसे नकारात्मक तर्कों के साथ शक्ति श्रृंखला द्वारा परिभाषित किया गया है। यह फ़ंक्शन मूल पर छलांग के साथ मनमाना और निरंतर संकेत के प्रभाव में विश्राम प्रक्रिया के सभी आवश्यक गुणों का प्रतिनिधित्व करता है।[3][4]
यह भी देखें
- मित्तग-लेफ़लर सारांश
- मिट्टाग-लेफ़लर वितरण
- फॉक्स-राइट फ़ंक्शन
टिप्पणियाँ
- R Package 'MittagLeffleR' by Gurtek Gill, Peter Straka. Implements the Mittag-Leffler function, distribution, random variate generation, and estimation.
संदर्भ
- ↑ 1.0 1.1 1.2 1.3 1.4 Saxena, R. K.; Mathai, A. M.; Haubold, H. J. (2009-09-01). "मिट्टाग-लेफ़लर फ़ंक्शंस और उनके अनुप्रयोग" (in English). arXiv:0909.0230 [math.CA].
- ↑ Weisstein, Eric W. "मिट्टाग-लेफ़लर फ़ंक्शन". mathworld.wolfram.com (in English). Retrieved 2019-09-11.
- ↑ Pritz, T. (2003). Five-parameter fractional derivative model for polymeric damping materials. Journal of Sound and Vibration, 265(5), 935-952.
- ↑ Nonnenmacher, T. F., & Glöckle, W. G. (1991). A fractional model for mechanical stress relaxation. Philosophical magazine letters, 64(2), 89-93.
- Mittag-Leffler, M.G.: Sur la nouvelle fonction E(x). C. R. Acad. Sci. Paris 137, 554–558 (1903)
- Mittag-Leffler, M.G.: Sopra la funzione E˛.x/. Rend. R. Acc. Lincei, (Ser. 5) 13, 3–5 (1904)
- Gorenflo R., Kilbas A.A., Mainardi F., Rogosin S.V., Mittag-Leffler Functions, Related Topics and Applications (Springer, New York, 2014) 443 pages ISBN 978-3-662-43929-6
- Igor Podlubny (1998). "chapter 1". Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, Some Methods of Their Solution and Some of Their Applications. Mathematics in Science and Engineering. Academic Press. ISBN 0-12-558840-2.
- Kai Diethelm (2010). "chapter 4". The analysis of fractional differential equations: an application-oriented exposition using differential operators of Caputo type. Lecture Notes in Mathematics. Heidelberg and New York: Springer-Verlag. ISBN 978-3-642-14573-5.
बाहरी संबंध
- Mittag-Leffler function: MATLAB code
- Mittag-Leffler and stable random numbers: Continuous-time random walks and stochastic solution of space-time fractional diffusion equations
This article incorporates material from Mittag-Leffler function on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.