केन्द्रीयता: Difference between revisions
m (29 revisions imported from alpha:केन्द्रीयता) |
No edit summary |
||
| Line 219: | Line 219: | ||
==अग्रिम पठन== | ==अग्रिम पठन== | ||
* Koschützki, D.; Lehmann, K. A.; Peeters, L.; Richter, S.; Tenfelde-Podehl, D. and Zlotowski, O. (2005) Centrality Indices. In Brandes, U. and Erlebach, T. (Eds.) ''Network Analysis: Methodological Foundations'', pp. 16–61, LNCS 3418, Springer-Verlag. | * Koschützki, D.; Lehmann, K. A.; Peeters, L.; Richter, S.; Tenfelde-Podehl, D. and Zlotowski, O. (2005) Centrality Indices. In Brandes, U. and Erlebach, T. (Eds.) ''Network Analysis: Methodological Foundations'', pp. 16–61, LNCS 3418, Springer-Verlag. | ||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category:CS1 English-language sources (en)]] | |||
[[Category: | [[Category:CS1 errors]] | ||
[[Category:CS1 maint]] | |||
[[Category:Created On 09/07/2023]] | [[Category:Created On 09/07/2023]] | ||
[[Category:Vigyan Ready]] | [[Category:Lua-based templates]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Webarchive template wayback links]] | |||
[[Category:ग्राफ दूरी]] | |||
[[Category:ग्राफ सिद्धांत]] | |||
[[Category:ग्राफ़ एल्गोरिदम]] | |||
[[Category:नेटवर्क]] | |||
[[Category:नेटवर्क विश्लेषण]] | |||
[[Category:नेटवर्क सिद्धांत]] | |||
[[Category:बीजगणितीय ग्राफ सिद्धांत]] | |||
Latest revision as of 15:00, 2 August 2023
| a series का हिस्सा चालू | ||||
| नेटवर्क विज्ञान | ||||
|---|---|---|---|---|
| नेटवर्क प्रकार | ||||
| ग्राफ | ||||
|
||||
| मॉडल | ||||
|
||||
| ||||
ग्राफ सिद्धांत और केंद्रीयता के नेटवर्क विश्लेषण सूचक ग्राफ के भीतर अपनी नेटवर्क स्थिति के अनुरूप नोड्स को संख्या या रैंकिंग के रूप में निर्दिष्ट करते हैं। जबकि अनुप्रयोगों में सोशल नेटवर्क में सबसे प्रभावशाली व्यक्तियों की पहचान करते है और इस प्रकार इंटरनेट या अर्बन नेटवर्क में प्रमुख मौलिक ढांचे के नोड्स, डिजीज के सुपर-स्प्रेडर्स और ब्रेन नेटवर्क के रूप में सम्मलित होते है।[1][2] केंद्रीयता अवधारणाओं को सबसे पहले सोशल नेटवर्क विश्लेषण में विकसित किया गया था और केंद्रीयता को मापने के लिए उपयोग किए जाने वाले कई शब्द उनके समाजशास्त्र मूल को दर्शाते हैं।
केंद्रीयता सूचकांकों की परिभाषा और कैरिक्टरिज़ेशन
केंद्रीयता घातांक इस प्रश्न का उत्तर हैं कि एक महत्वपूर्ण शीर्ष की फीचर क्या है? इसका उत्तर ग्राफ़ के शीर्षों पर एक वास्तविक-मूल्यवान फलन के संदर्भ में दिया जाता है, जहां उत्पादन मान एक रैंकिंग प्रदान करने की उम्मीद कर रहे हैं, जो सबसे महत्वपूर्ण नोड्स की पहचान करती है।[3][4][5]
वाइड शब्द के व्यापक अर्थ हैं, इसके परिणामस्वरूप केंद्रीयता की कई भिन्न -भिन्न परिभाषाएँ होती हैं। दो वर्गीकरण योजनाएं प्रस्तावित की गई हैं और इस प्रकार पूरे नेटवर्क में एक प्रकार के प्रवाह या स्थानांतरण के संबंध में महत्व की कल्पना की जा सकती है। इससे केंद्रीयताओं को प्रवाह के आधार पर वर्गीकृत किया जा सकता है जिसे वे महत्वपूर्ण मानते हैं।[4] जबकि महत्व को वैकल्पिक रूप से नेटवर्क की एकीकरण में भागीदारी के रूप में माना जाता है। यह केंद्रीयताओं को इस आधार पर वर्गीकृत करने की अनुमति देता है कि वे एकीकरण को कैसे मापते हैं।[6] इन दोनों दृष्टिकोंण के माध्यम से भिन्न -भिन्न श्रेणी के संकेतकों को विभाजित किया जाता है। एक अन्य निष्कर्ष यह है कि एक केंद्रीयता जो एक श्रेणी के लिए उपयुक्त है, वह किसी अन्य श्रेणी पर प्रयुक्त होने पर अधिकांशतः गलत मान लिया जाता है।[4]
केंद्रीयता के उपाय यद्यपि सभी नहीं होते हैं पर केंद्रीयता के मापन में किसी दिये गये शीर्ष से गुजरने वाले किसी प्रकार के पथ (ग्राफ सिद्धांत) की संख्या को भी सम्मलित किया जा सकता है। जिसे वॉक भी कहा जाता है प्रासंगिक वॉक को कैसे परिभाषित और प्रभावी ढंग से गिना जाता है, इसके उपाय भिन्न -भिन्न हैं। इस समूह पर विचार को सीमित करने से टैक्सोनॉमी की अनुमति मिलती है जो एक स्पेक्ट्रम पर कई केंद्रीयताओं को रखती है, जो कि एक डिग्री की केंद्रीयता की लंबाई से लेकर अनंत वॉक की अभिलक्षणिक मान केंद्रीयता तक होता है। [3][7] अन्य केंद्रीयता उपाय, जैसे मध्यनेस की केंद्रीयता न केवल समग्र कनेक्टिविटी पर ध्यान केंद्रित करती है, बल्कि उन स्थितियों पर ध्यान केंद्रित करती है, जो नेटवर्क की कनेक्टिविटी के लिए महत्वपूर्ण होते हैं।
नेटवर्क प्रवाह द्वारा कैरिक्टरिज़ेशन
नेटवर्क को पथ का विवरण माना जा सकता है जिनके साथ कुछ प्रवाह होता है। यह प्रवाह के प्रकार और केंद्रीयता द्वारा एन्कोड किए गए पथ प्रकार के आधार पर लक्षण वर्णन की अनुमति देता है और इस प्रकार प्रवाह स्थानांतरण पर आधारित हो सकता है, जहां प्रत्येक अविभाज्य वस्तु एक नोड से दूसरे नोड में जाती है, जैसे पैकेज डिलीवरी साइट से ग्राहक के घर तक जाती है। दूसरी स्थिति क्रमिक दोहराव के रूप में होती है, जिसमें एक आइटम को दोहराया जाता है जिससे कि स्रोत और लक्ष्य दोनों के पास वह हो सकती है। इसका एक उदाहरण गॉसिप के माध्यम से सूचना का प्रसार किया जाता है, जिसमें सूचना को निजी तरीके से प्रचारित किया जाता है और प्रक्रिया के अंत में स्रोत और लक्ष्य नोड्स दोनों को सूचित किया जाता है। अंतिम विषय समानांतर दोहराव के रूप में होता है, जिसमें आइटम को एक ही समय में कई लिंक पर डुप्लिकेट किया जाता है, जैसे एक रेडियो प्रसारण जो एक ही समय में कई श्रोताओं को एक ही जानकारी प्रदान करता है।[4]
इसी तरह, पथ के प्रकार को दूरी (ग्राफ़ सिद्धांत) के सबसे छोटे पथ पर बाध्य किया जा सकता है इससे अधिक बार किसी भी शीर्ष पर एक से अधिक बार निरीक्षण नहीं किया जा सकता है और इस प्रकार ग्राफ़ सिद्धांत के शब्दों की शब्दावली शीर्षों पर कई बार जाया जा सकता है, किसी भी किनारे को एक से अधिक बार पार नहीं किया जाता है या ग्राफ़ सिद्धांत शब्दों की शब्दावली वॉक शीर्षों और किनारों पर अनेक बार देखा और पार किया जा सकता है।[4]
वॉक संरचना द्वारा कैरिक्टरिज़ेशन
वैकल्पिक वर्गीकरण इस बात से प्राप्त किया जा सकता है कि केंद्रीयता का निर्माण कैसे किया जाता है। यह पुनः दो वर्गों में विभाजित हो जाता है। केन्द्रीयताएँ या तो रेडियल या औसत दर्जे की होती हैं। रेडियल केन्द्रीयताएँ उन वॉक की गिनती करती हैं जो दिए गए शीर्ष से प्रारंभ या समाप्ति होती हैं। डिग्री केंद्रीयता और अभिलक्षणिक मान केंद्रीयताएं रेडियल केंद्रीयता के उदाहरण हैं और इस प्रकार रेडियल केंद्रीयताएं लंबाई अनन्तता क्षेत्र की संख्या की गणना मध्यवर्ती केंद्रता में दूरी की गणना होती है। जो दिए गए शीर्ष से होकर गुजरती हैं। इसका कैनोनिकल उदाहरण है और इस प्रकार फ्रीमैन की मध्यवर्ती केंद्रीयता है और दिए गए शीर्ष से गुजरने वाले सबसे छोटे रास्तों की संख्या के रूप में होता है।[6]
इसी तरह, गिनती या तो वॉक की मात्रा या लंबाई को कैप्चर कर सकती है। वॉल्यूम दिए गए प्रकार के वॉक की कुल संख्या होती है। पिछले पैराग्राफ के तीन उदाहरण इस श्रेणी में आते हैं। इस प्रकार लंबाई ग्राफ़ में दिए गए शीर्ष से शेष शीर्ष तक की दूरी को दर्शाती है। जिससे निकटता केंद्रीयता किसी दिए गए शीर्ष से अन्य सभी शीर्षों तक की कुल भूभौतिकी दूरी का सबसे अच्छा ज्ञात उदाहरण है।[6] ध्यान दें कि यह वर्गीकरण गिने जाने वाले वॉक के प्रकार से स्वतंत्र है अर्थात वॉक, ट्रेल, पगडंडी, पथ, जियोडेसिक के रूप में होते है।
बोर्गट्टी और एवरेट का प्रस्ताव है कि यह टाइपोलॉजी केंद्रीयता मापन की तुलना करने के सर्वोत्तम तरीके के बारे में अंतर्दृष्टि प्रदान करती है। इस 2×2 वर्गीकरण में एक ही बॉक्स में रखी गई केन्द्रीयताएँ प्रशंसनीय विकल्प बनाने के लिए पर्याप्त समान हैं और इस प्रकार कोई भी उचित रूप से तुलना कर सकता है कि किसी दिए गए एप्लिकेशन के लिए कौन सा अच्छा है। चूंकि, विभिन्न बक्सों के माप स्पष्ट रूप से भिन्न होते हैं। जबकि सापेक्ष फिटनेस का कोई भी मूल्यांकन केवल पूर्व निर्धारित करने के संदर्भ में हो सकता है कि कौन सी श्रेणी अधिक प्रयुक्त है, जिससे तुलना विवादास्पद रूप में हो सकती है।[6]
रेडियल-वॉल्यूम केंद्रीयताएं स्पेक्ट्रम पर उपस्थित होती हैं
वॉक संरचना द्वारा कैरिक्टरिज़ेशन से पता चलता है कि व्यापक उपयोग में लगभग सभी केंद्रीयताएं रेडियल-वॉल्यूम माप के रूप में होती है। ये इस बिलीफ को कूटबद्ध करते हैं कि एक शीर्ष की केंद्रीयता उन शीर्षों की केंद्रीयता का एक कार्य है जिनके साथ यह जुड़ा हुआ होता है। केंद्रीयताएं खुद को भिन्न करती हैं कि एसोसिएशन कैसे परिभाषित किया जाता है।
बोनाकिच ने दिखाया कि यदि एसोसिएशन को ग्राफ सिद्धांत की शब्दावली वॉक के संदर्भ में परिभाषित किया जाता है, तो वॉक की लंबाई के आधार पर केंद्रीयताओं के एक फॅमिली को परिभाषित किया जा सकता है।[3] डिग्री केंद्रीयता लंबाई वॉक को गिनती है, जबकि अभिलक्षणिक मान केंद्रीयता लंबाई अनंत के वॉक को गिनती है और इस प्रकार संघ की वैकल्पिक परिभाषाएँ भी उचित हैं। अल्फ़ा केंद्रीयता शीर्षों को प्रभाव का बाहरी स्रोत रखने की अनुमति देती है। एस्ट्राडा की सबग्राफ केंद्रीयता केवल बंद रास्तों त्रिकोण वर्ग आदि की गिनती का प्रस्ताव करती है।
ऐसे मापन का मूल अवलोकन यह है कि ग्राफ़ के आसन्न आव्यूह की घात उस घात द्वारा दी गई लंबाई के वॉक की संख्या देती हैं। इसी प्रकार आव्यूह घातांक भी किसी दी गई लंबाई के वॉक की संख्या से निकटता से संबंधित होते है और इस प्रकार आसन्न आव्यूह का प्रारंभिक परिवर्तन गणना किए गए वॉक के प्रकार की एक भिन्न परिभाषा की अनुमति देता है। किसी भी दृष्टिकोण के अनुसार किसी शीर्ष की केंद्रीयता को अनंत योग के रूप में व्यक्त किया जाता है
आव्यूह घात या
आव्यूह घातांक, जहां
- वॉक की लंबाई है,
- परिवर्तित आसन्नता आव्यूह है और
- डिस्कॉउंट पैरामीटर है, जो योग का अभिसरण सुनिश्चित करता है।
- डी एक डिस्काउंट पैरामीटर है जो योग के अभिसरण सुनिश्चित करता है।
बोनासिच के मापन का फॅमिली आसन्नता आव्यूह को परिवर्तित नहीं करता है। अल्फ़ा केंद्रीयता आसन्नता आव्यूह को उसके संकल्पात्मक औपचारिकता के साथ प्रतिस्थापित करती है। सबग्राफ केंद्रीयता आसन्न आव्यूह को उसके ट्रेस से बदल देती है। एक चौंकाने वाला निष्कर्ष यह है कि आसन्न आव्यूह के प्रारंभिक परिवर्तन की परवाह किए बिना, ऐसे सभी दृष्टिकोणों में सामान्य सीमित व्यवहार होता है। जैसा शून्य के करीब, घातांक #डिग्री केंद्रीयता में परिवर्तित हो जाते हैं। जैसा अपने अधिकतम मूल्य के निकटतम पहुंचने पर, घातांक #अभिलक्षणिक सदिश केंद्रीयता में परिवर्तित हो जाते हैं।[7]
खेल-सैद्धांतिक केंद्रीयता
उपर्युक्त मानक मापन में अधिकांश का सामान्य फीचर यह है कि वे नोड की उस भूमिका पर ही ध्यान केंद्रित करके उसके महत्व का मूल्यांकन करते हैं, जो एक नोड स्वयं निभाता है। चूंकि, कई अनुप्रयोगों में तालमेल के कारण ऐसा दृष्टिकोण अपर्याप्त है क्योंकि समूहों में नोड्स की कार्यविधि को ध्यान में रखा जाता है।
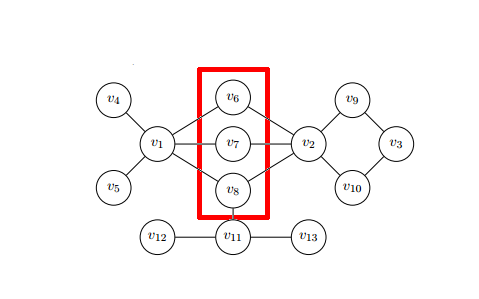
उदाहरण के लिए, किसी महामारी को रोकने की समस्या पर विचार करते है और इस प्रकार नेटवर्क की उपरोक्त छवि को देखते हुए हमें इन नोड्स का टीकाकरण करना होता है और जबकि पहले वर्णित मापन के आधार पर हम उन नोड्स की पहचान करते हैं। जो डिजीज फैलाने में सबसे महत्वपूर्ण होते है। केवल केंद्रीयताओं पर आधारित दृष्टिकोण जो नोड्स की व्यक्तिगत फीचर पर ध्यान केंद्रित करता है, यह एक अच्छा विचार नहीं हो सकता है। लाल वर्ग में नोड्स, व्यक्तिगत रूप से डिजीज को फैलने से नहीं रोक सकते हैं, लेकिन उन्हें एक समूह के रूप में विचार करने पर हम स्पष्ट रूप से देखते हैं कि यदि नोड्स में डिजीज प्रारंभ हो गई है तो वे डिजीज को रोक सकते हैं। इस प्रकार , , और . गेम-सैद्धांतिक केंद्रीयताएं गेम-थ्योरी के टूल का उपयोग करके वर्णित समस्याओं और अपॉर्चुनिटी से परामर्श करने का प्रयास करती हैं और इस प्रकार प्रस्तावित दृष्टिकोण [8] शैप्ले मान का उपयोग करता है। शेपली मूल्य गणना की समय सम्मिश्र कठोरता के कारण होता है, इस डोमेन में अधिकांश प्रयास नवीन कलनविधि और विधियो को प्रयुक्त करने में प्रेरित होते हैं, जो नेटवर्क की एक विशिष्ट टोपोलॉजी या समस्या के एक विशेष करैक्टर पर निर्भर करते हैं। इस तरह के दृष्टिकोण से समय सम्मिश्र को घातांक से बहुपद तक कम करने में मदद मिलती है।
इसी प्रकार, समाधान अवधारणा प्राधिकरण वितरण ([9]) खिलाड़ियों के बीच द्विपक्षीय प्रत्यक्ष प्रभाव को मापने के लिए शेपली मूल्य के अतिरिक्त शेपली-शुबिक पावर इंडेक्स प्रयुक्त करता है। वितरण वास्तव में एक प्रकार की अभिलक्षणिक मान केंद्रीयता के रूप में है। इसका उपयोग (2020) में बड़े डेटा ऑब्जेक्ट को सॉर्ट करने के लिए किया जाता है।[10] जैसे कि अमेरिकी कॉलेजों की रैंकिंग इत्यादि में होता है ।
महत्वपूर्ण लिमिटेशन
केंद्रीयता सूचकांकों की दो महत्वपूर्ण लिमिटेशन होती है, एक स्पष्ट और दूसरी सूक्ष्म रूप में होती है और इस प्रकार स्पष्ट सीमा यह है कि एक केंद्रीयता जो एक अनुप्रयोग के लिए इष्टतम रूप में होती है, इस प्रकार अधिकांशतः भिन्न अनुप्रयोग के लिए उप-इष्टतम होती है और यदि ऐसा नहीं होता है तो हमें इतनी सारी भिन्न -भिन्न केंद्रीयताओं की आवश्यकता नहीं होती हैं। इस घटना का एक उदाहरण क्रैकहार्ट काईट ग्राफ द्वारा प्रदान किया जाता है, जिसके लिए केंद्रीयता की तीन भिन्न -भिन्न धारणाएं सबसे केंद्रीय शीर्ष के तीन भिन्न -भिन्न विकल्प देती हैं।[11]
अतिसूक्ष्म सीमा सामान्यतः मानी जाने वाली भ्रांति के रूप में होती है और शीर्ष केंद्रीयता के सापेक्ष महत्व को इंगित करती है। केंद्रीयता घातांक विशेष रूप से एक रैंकिंग उत्पन्न करने के लिए डिज़ाइन किए गए हैं जो सबसे महत्वपूर्ण शीर्षों के संकेत की अनुमति देता है।[3][4] यह इस प्रकार बताई गई सीमा के अनुसार अच्छा करते हैं। वे सामान्य रूप से नोड्स के प्रभाव को मापने के लिए डिज़ाइन नहीं किए गए हैं। वर्तमान में, नेटवर्क भौतिकविदों ने इस समस्या के समाधान के लिए नोड प्रभाव आव्यूह विकसित करना प्रारंभ कर देते है।
एरर दो तरफा है और सबसे पहले रैंकिंग केवल महत्व के आधार पर शीर्षों को क्रमित करती है, यह रैंकिंग के विभिन्न स्तरों के बीच महत्व के अंतर को निर्धारित नहीं करती है। प्रश्न में केंद्रीयता माप के लिए फ्रीमैन केंद्रीकरण को प्रयुक्त करके इसे कम किया जा सकता है, जो उनके केंद्रीकरण स्कोर के अंतर के आधार पर नोड्स के महत्व के बारे में कुछ जानकारी प्रदान करता है। इसके अतिरिक्त फ्रीमैन केंद्रीकरण किसी को उनके उच्चतम केंद्रीकरण स्कोर की तुलना करके कई नेटवर्क की तुलना करने में सक्षम बनाता है।[12]चूंकि, यह दृष्टिकोण व्यवहार में शायद कम ही देखा जाता है।
दूसरे, जो फीचर सही ढंग से किसी दिए गए नेटवर्क एप्लिकेशन में सबसे महत्वपूर्ण शीर्षों की पहचान करती हैं और इस प्रकार वे आवश्यक रूप से शेष शीर्षों के लिए सामान्यीकृत नहीं होती हैं। अधिकांश अन्य नेटवर्क नोड्स के लिए रैंकिंग अर्थहीन रूप में होती है।[13][14][15][16] यह बताता है कि उदाहरण के लिए गूगल छवि खोज के केवल पहले कुछ परिणाम ही उचित क्रम में दिखाई देते हैं। पेजरैंक एक अत्यधिक अस्थिर माप है, जो जंप पैरामीटर के छोटे समायोजन के बाद लगातार रैंक उलटफेर दिखाता है।[17]
चूंकि, शेष नेटवर्क के लिए केंद्रीयता सूचकांकों को सामान्यीकृत करने में विफलता पहली बार में प्रति-सहज ज्ञान युक्त लगती है, यह उपरोक्त परिभाषाओं के रूप में सीधे अनुसरण करती है। सम्मिश्र नेटवर्क में विषम टोपोलॉजी होती है। इस सीमा तक कि इष्टतम माप सबसे महत्वपूर्ण शीर्षों की नेटवर्क संरचना पर निर्भर करता है, जबकि माप जो ऐसे शीर्षों के लिए इष्टतम नेटवर्क के शेष भाग के लिए उप-इष्टतम होता है।[13]
डिग्री केंद्रीयता

ऐतिहासिक रूप से पहला और संकल्पनात्मक रूप से सबसे सरल डिग्री केंद्रीयता होती है, जिसे एक नोड पर घटने वाले लिंक की संख्या अर्थात एक नोड में उपस्थित संबंधों की संख्या के रूप में परिभाषित किया जाता है। नेटवर्क के माध्यम से जो कुछ भी प्रवाहित होता है, जैसे वायरस या कुछ जानकारी को पकड़ने के लिए नोड के तत्काल रिस्क के संदर्भ में डिग्री की व्याख्या की जाती है। डायरेक्टेड नेटवर्क की स्थितियों में जहां संबंधों की दिशा होती है और इस प्रकार डिग्री केंद्रीयता के दो भिन्न -भिन्न मापन को परिभाषित करते हैं, अर्थात् इंडिग्री और आउटडिग्री तदनुसार इंडिग्री नोड को निर्देशित संबंधों की संख्या की गिनती है और आउटडिग्री उन संबंधों की संख्या है जो नोड दूसरों को निर्देशित करता है। जब संबंध मित्रता या सहयोग जैसे कुछ धनात्मक पहलुओं से जुड़े होते हैं, तो इंडिग्री को अधिकांशतः लोकप्रियता के रूप में और आउटडिग्री को मिलनसारिता के रूप में व्याख्यायित किया जाता है।
एक शीर्ष की डिग्री केंद्रीयता , किसी दिए गए ग्राफ़ के लिए साथ शिखर और किनारों को इस प्रकार परिभाषित किया जाता है,
ग्राफ़ में सभी नोड्स के लिए डिग्री केंद्रीयता की गणना करने के लिए बड़ी थीटा की आवश्यकता होती है| सघन आव्यूह में ग्राफ़ का आसन्न आव्यूह प्रतिनिधित्व और किनारों के लिए लेता है विरल आव्यूह प्रतिनिधित्व के रूप में होते है।
नोड स्तर पर केंद्रीयता की परिभाषा को पूरे ग्राफ़ तक बढ़ाया जा सकता है, इस स्थिति में हम ग्राफ़ केंद्रीकरण की बात करते है।[18] और इस प्रकार उच्चतम डिग्री केंद्रीयता वाला नोड . के रूप में बनें होते है और इस प्रकार माना , नोड से जुड़ा ग्राफ़ जो निम्नलिखित मात्रा को अधिकतम करता है, जिसमें में उच्चतम डिग्री केंद्रीयता वाला नोड है,
इस प्रकार ग्राफ की डिग्री केंद्रीकरण इस प्रकार है
ग्राफ़ को अधिकतम किया जाता है इसमें एक केंद्रीय नोड के रूप में होता है, जिससे अन्य सभी नोड जुड़े होते हैं ( स्टार ग्राफ) और इस स्थिति में
- के रूप में होते है,
तो, किसी भी ग्राफ़ के लिए
- के रूप में होते है,
इसके अतिरिक्त डिग्री केंद्रीयता के लिए टेंडेंसी टू मेक हब (टीएमएच) नाम का एक नया व्यापक वैश्विक उपाय इस प्रकार परिभाषित होता है[2]
जहां नेटवर्क में डिग्री केंद्रीयता की उपस्थिति से टीएमएच बढ़ता है।
निकटता केंद्रीयता
एक कनेक्टेड घटक (ग्राफ़ सिद्धांत) ग्राफ़ असतत गणित में, एक नोड का सामान्यीकरण सांख्यिकी निकटता केंद्रीयता या निकटता नोड और ग्राफ़ में अन्य सभी नोड्स के बीच सबसे छोटी पथ समस्या की औसत लंबाई होती है। इस प्रकार एक नोड जितना अधिक केंद्रीय होता है, वह अन्य सभी नोड्स के उतना ही निकटतम होता है।
निकटता को एलेक्स बेवेलस (1950) ने दूरता के गुणक व्युत्क्रम के रूप में परिभाषित किया है,[19][20] इस प्रकार जहाँ शीर्ष u और v के बीच की दूरी ग्राफ सिद्धांत को दर्शाती है। चूंकि, जब निकटता केंद्रीयता की बात की जाती है, तो सामान्यतः लोग इसके सामान्यीकृत रूप का उल्लेख करते हैं, जो पिछले सूत्र द्वारा गुणा किया गया है , जहाँ ग्राफ़ में नोड्स की संख्या के रूप में होती है,
यह सामान्यीकरण विभिन्न आकारों के ग्राफ़ के नोड्स के बीच तुलना की अनुमति देता है। कई ग्राफ़ के लिए निकटता के व्युत्क्रम और डिग्री के लघुगणक के बीच एक मजबूत संबंध है,[21] जहाँ शीर्ष v की डिग्री है जबकि α और β प्रत्येक नेटवर्क के लिए स्थिरांक हैं।
अन्य सभी नोड्स से दूरी लेना अप्रत्यक्ष ग्राफ़ में अप्रासंगिक है, जबकि यह निर्देशित ग्राफ में पूरी तरह से भिन्न परिणाम उत्पन्न कर सकता है, उदाहरण के लिए एक वेबसाइट में आउटगोइंग लिंक से उच्च निकटता केंद्रीयता हो सकती है, लेकिन आने वाले लिंक से कम निकटता केंद्रीयता हो सकती है।
हार्मोनिक केंद्रीयता
आवश्यक रूप से जुड़े हुए ग्राफ़ में, हार्मोनिक केंद्रीयता निकटता केंद्रीयता की परिभाषा में योग और पारस्परिक संचालन को उलट देती है:
जहाँ यदि u से v तक कोई पाथ नहीं है और इस प्रकार हार्मोनिक केंद्रीयता को विभाजित करके सामान्यीकृत किया जा सकता है , जहाँ ग्राफ़ में नोड्स की संख्या है.
हार्मोनिक केंद्रीयता को मास्सिमो मार्चियोरी और विटो लटोरा (2000) द्वारा प्रस्तावित किया गया था और फिर स्वतंत्र रूप से डेकर (2005) द्वारा मूल्यांकित केंद्रीयता नाम का उपयोग करके और रोचैट (2009) द्वारा प्रस्तावित किया गया था।[22]
बिटवीननेस की केंद्रीयता
बिटवीननेस एक ग्राफ़ (असतत गणित) के भीतर एक शीर्ष ग्राफ़ सिद्धांत की एक केंद्रीयता माप है और बीच में किनारे (ग्राफ़ सिद्धांत) के रूप में होते है, जिस पर यहां चर्चा नहीं की गई है और बीच की केंद्रीयता यह निर्धारित करती है कि एक नोड दो अन्य नोड्स के बीच सबसे छोटे पथ पर एक पुल के रूप में कितनी बार कार्य करता है। इसे लिंटन फ्रीमैन द्वारा एक सोशल नेटवर्क में अन्य मनुष्यों के बीच संचार पर एक मानव के नियंत्रण को मापने के लिए एक उपाय के रूप में प्रयुक्त किया जाता है।[23] और इस प्रकार उनकी अवधारणा में दो अनियमित ढंग से चुने गए शीर्षों के बीच यादृच्छिक रूप से चुने गए सबसे छोटे पथ समस्या पर जिन शीर्षों के घटित होने की उच्च संभावना होती है उनमें बीच की स्थिति अधिक होती है।
एक शीर्ष की मध्यता एक ग्राफ में साथ शीर्षों की गणना इस प्रकार की जाती है।
- शीर्षों (s,t) के प्रत्येक जोड़े के लिए, उनके बीच सबसे छोटी पथ समस्या की गणना करते है।
- शीर्षों (s,t) के प्रत्येक जोड़े के लिए, सबसे छोटे पथों का अंश निर्धारित करते है, जो प्रश्न में शीर्ष से होकर गुजरते हैं यहां, शीर्ष v के रूप में दर्शाते है।
- शीर्षों (s,t) के सभी युग्मों पर इस भिन्न का योग करते है।
अधिक सघनता से बीच की स्थिति को इस प्रकार दर्शाया जा सकता है[24]
जहाँ नोड से सबसे छोटे पथों की कुल संख्या है नोड करने के लिए और उन पथों की संख्या है, जो .से गुजरते हैं और इस प्रकार v बीच की स्थिति को शीर्षों के जोड़े की संख्या से विभाजित करके सामान्यीकृत किया जा सकता है, जो डिग्राफ (गणित) के लिए के रूप में होता है और अप्रत्यक्ष ग्राफ़ के लिए .के रूप में होता है, उदाहरण के लिए, एक अप्रत्यक्ष स्टार ग्राफ सिद्धांत में, केंद्र शीर्ष के बीच की दूरी के रूप में होती है, जो प्रत्येक संभव सबसे छोटे पथ में समाहित होता है और 1, यदि सामान्यीकृत किया जाता है) जबकि लीवस जो किसी भी सबसे छोटे पथ में सम्मलित नहीं हैं और उनके बीच 0 का अंतर होता है।
गणना के पहलू से, एक ग्राफ़ में सभी शीर्षों की बीच और निकटता दोनों केंद्रीयताओं में एक ग्राफ़ पर सभी शीर्षों के जोड़े के बीच सबसे छोटे पथ की गणना के रूप में सम्मलित होती है, जिसके लिए फ्लोयड वारशाल कलनविधि के साथ समय की आवश्यकता होती है। चूंकि, विरल ग्राफ़ पर, जॉनसन का कलन विधि समय नोटेशन लेते हुए अधिक कुशल रूप में हो सकता है, इस प्रकार बिना भारित ग्राफ़ की स्थिति में गणना ब्रैंड्स कलनविधि के साथ की जाती है[24] जिसमें समय लगता है। सामान्यतः इसे कलन विधि के रूप में जानते हैं और ग्राफ़ का अप्रत्यक्ष रूप हैं लूप और एकाधिक किनारों के भत्ते से जुड़े हुए हैं। विशेष रूप से नेटवर्क ग्राफ़ के साथ काम करते समय सरल संबंध बनाए रखने के लिए अधिकांशतः ग्राफ़ लूप या एकाधिक किनारों के बिना होते हैं, जहां किनारे दो लोगों या शीर्षों के बीच कनेक्शन का प्रतिनिधित्व करते हैं। इस स्थिति में, ब्रैंड्स के कलन विधि का उपयोग करके प्रत्येक सबसे छोटे पथ को दो बार गिना जाने के लिए अंतिम केंद्रीयता स्कोर को 2 से विभाजित किया जाता है।[24]
अभिलक्षणिक सदिश केंद्रीयता
अभिलक्षणिक सदिश केंद्रीयता जिसे आइजेनसेंट्रैलिटी भी कहा जाता है और इस प्रकार एक नेटवर्क (गणित) में एक नोड (नेटवर्किंग) के प्रभाव का एक माप होता है। यह इस अवधारणा के आधार पर नेटवर्क में सभी नोड्स को सापेक्ष स्कोर प्रदान करता है कि उच्च स्कोरिंग नोड्स के कनेक्शन कम स्कोरिंग नोड्स के बराबर कनेक्शन की तुलना में नोड के स्कोर में अधिक योगदान देते हैं।[25][5] गूगल की पृष्ठ रैंक और काट्ज़ केंद्रीयता अभिलक्षणिक सदिश केंद्रीयता के भिन्न रूप हैं।[26]
अभिलक्षणिक सदिश केंद्रीयता खोजने के लिए आसन्न आव्यूह का उपयोग करना
किसी दिए गए ग्राफ़ के लिए साथ शीर्षों की संख्या दें आसन्न आव्यूह के रूप में होते है, अर्थात यदि शीर्ष शीर्ष से जुड़ा हुआ है , और अन्यथा शीर्ष का सापेक्ष केंद्रीयता स्कोर इस प्रकार परिभाषित किया जा सकता है,
जहाँ के निकटतम का एक समूह है और एक स्थिरांक है और इस प्रकार एक छोटी सी पुनर्व्यवस्था के साथ इसे सदिश नोटेशन में अभिलक्षणिक सदिश समीकरण के रूप में फिर से लिखा जा सकता है
सामान्य रुप से, कई भिन्न -भिन्न अभिलक्षणिक मान के रूप में होते है, जिसके लिए एक गैर-शून्य अभिलक्षणिक मान समाधान के रूप में उपस्थित है। चूँकि आसन्न आव्यूह में प्रविष्टियाँ गैर-ऋणात्मक होती हैं, जो पेरोन-फ्रोबेनियस प्रमेय द्वारा एक अद्वितीय सबसे बड़ा अभिलक्षणिक मान है, जो वास्तविक और धनात्मक होता है। इस सबसे बड़े अभिलक्षणिक मान के परिणामस्वरूप वांछित केंद्रीयता माप प्राप्त होता है।[27] इस प्रकार h> संबंधित अभिलक्षणिक सदिश का घटक फिर शीर्ष का सापेक्ष केंद्रीयता स्कोर देता है और नेटवर्क में. अभिलक्षणिक सदिश को केवल एक सामान्य कारक तक परिभाषित किया जाता है, इसलिए केवल शीर्षों की केंद्रीयताओं के अनुपात को अच्छी तरह से परिभाषित किया जाता है। निरपेक्ष स्कोर को परिभाषित करने के लिए किसी को अभिलक्षणिक सदिश को सामान्य रूप में करना होता है उदाहरण के लिए, जैसे कि सभी शीर्षों का योग 1 या शीर्षों की कुल संख्या n है। पावर पुनरावृत्ति कई अभिलक्षणिक मान कलनविधि में से एक है जिसका उपयोग इस प्रमुख अभिलक्षणिक सदिश को फाइंड करने के लिए किया जाता है।[26] इसके अतिरिक्त इसे सामान्यीकृत किया जा सकता है जिससे कि A में प्रविष्टियां कनेक्शन के गुण का प्रतिनिधित्व करने वाली वास्तविक संख्याएं के रूप में हो सकती है, जैसा कि स्टोकेस्टिक आव्यूह में होता है।
काट्ज़ केंद्रीयता
काट्ज़ केंद्रीयता डिग्री केंद्रीयता का एक सामान्यीकरण है।[28] डिग्री केंद्रीयता प्रत्यक्ष निकटतम की संख्या को मापती है और काट्ज़ केंद्रीयता उन सभी नोड्स की संख्या को मापती है जिन्हें एक पथ के माध्यम से जोड़ा जा सकता है, जबकि दूर के नोड्स के योगदान को दंडित किया जाता है और गणितीय रूप से इसे इस प्रकार परिभाषित किया जाता है।
जहाँ में एटीन्यूएशन कारक है .
काट्ज़ केंद्रीयता को अभिलक्षणिक सदिश केंद्रीयता के एक प्रकार के रूप में देखा जा सकता है और इस प्रकार काट्ज़ केंद्रीयता का दूसरा रूप है।
अभिलक्षणिक सदिश केंद्रीयता की अभिव्यक्ति की तुलना में, को द्वारा प्रतिस्थापित किया जाता है।
ऐसा दिखाया गया है[29] कि प्रमुख अभिलक्षणिक सदिश काट्ज़ केंद्रीयता की सीमा है क्योंकि यह नीचे से की ओर बढ़ता है और इस प्रकार सबसे बड़े अभिलक्षणिक मान आसन्न आव्यूह से जुड़ा हुआ होता है।
पेजरैंक केंद्रीयता
पेजरैंक निम्नलिखित समीकरण को संतुष्ट करता है,
जहाँ
नोड के निकटतम की संख्या या निर्देशित ग्राफ़ में आउटबाउंड लिंक की संख्या है। अभिलक्षणिक मान केंद्रीयता और काट्ज़ केंद्रीयता की तुलना में एक बड़ा अंतर स्केलिंग कारक है।. पेजरैंक और अभिलक्षणिक मान केंद्रीयता के बीच एक और अंतर यह है कि पेजरैंक सदिश बाएं हाथ का अभिलक्षणिक मान है और ध्यान दें कि कारक घातांक के विपरीत रूप में होते है।[30]
परकोलेशन केंद्रीयता
एक सम्मिश्र नेटवर्क में एकल नोड के 'महत्व' को निर्धारित करने के लिए कई केंद्रीयता उपाय उपस्थित होते है। चूंकि, ये उपाय विशुद्ध रूप से टोपोलॉजिकल शब्दों में एक नोड के महत्व को मापते हैं और नोड का मूल्य किसी भी तरह से नोड की 'स्थिति' पर निर्भर नहीं करता है। यह नेटवर्क गतिशीलता की परवाह किए बिना स्थिर रहता है। यह भारित मध्यवर्ती मापों के लिए भी सत्य है। चूंकि, एक नोड बहुत अच्छी तरह से बीच की केंद्रीयता या किसी अन्य केंद्रीयता माप के संदर्भ में केंद्रीय रूप से स्थित हो सकता है, लेकिन उस नेटवर्क के संदर्भ में 'केंद्रीय रूप से' स्थित नहीं हो सकता है जिसमें रिसाव होता है। कई परिदृश्यों में सम्मिश्र नेटवर्क में 'संक्रमण' का प्रसार होता है। उदाहरण के लिए वायरल या बैक्टीरियल संक्रमण लोगों के सोशल नेटवर्क पर फैल सकता है, जिसे संपर्क नेटवर्क के रूप में जाना जाता है और इस प्रकार सड़क रेल या हवाई संपर्क से जुड़े कस्बों या जनसंख्या केंद्रों के नेटवर्क पर विचार करके डिजीज के प्रसार को उच्च स्तर पर भी माना जा सकता है। कंप्यूटर वायरस कंप्यूटर नेटवर्क पर फैल सकते हैं। इस प्रकार व्यावसायिक प्रस्तावों और सौदों के बारे में अफवाहें या खबरें लोगों के सोशल नेटवर्क के माध्यम से भी फैल सकती हैं। इन सभी परिदृश्यों में, 'संक्रमण' एक सम्मिश्र नेटवर्क के लिंक पर फैलता है जैसे-जैसे यह फैलता है नोड्स की 'स्थितियों' को बदलता है या तो पुनर्प्राप्ति पूर्वक होता है। उदाहरण के लिए महामारी विज्ञान के परिदृश्य में संक्रमण फैलते ही व्यक्ति 'अतिसंवेदनशील' से 'संक्रमित' अवस्था में चले जाते हैं। इस प्रकार उपरोक्त उदाहरणों में भिन्न -भिन्न नोड्स जिन राज्यों को ले सकते हैं वे द्विआधारी रूप में हो सकते हैं, जैसे कि समाचार का एक टुकड़ा प्राप्त नहीं होता है और इस प्रकार अतिसंवेदनशील/संक्रमित/पुनर्प्राप्त के रूप में होते है, जैसे कि किसी कस्बे में संक्रमित लोगों का अनुपात जैसे-जैसे संक्रमण फैलता है। इन सभी परिदृश्यों में सामान्य फीचर यह है कि संक्रमण फैलने के परिणामस्वरूप नेटवर्क में नोड स्थिति में परिवर्तन होता है। इसे ध्यान में रखते हुए परकोलेशन सेंट्रलिटी (पीसी) का प्रस्ताव किया गया था, जो विशेष रूप से नेटवर्क के माध्यम से परकोलेशन में सहायता के संदर्भ में नोड्स के महत्व को मापता है। यह उपाय पिरवीनन एट अल द्वारा प्रस्तावित किया गया था।[31]
किसी निश्चित समय पर, किसी दिए गए नोड के लिए पर्कोलेशन केंद्रीयता को उस नोड से गुजरने वाले 'पेरकोलेटेड पथों' के अनुपात के रूप में परिभाषित किया जाता है। 'पेरकोलेटेड पाथ' नोड्स की एक जोड़ी के बीच का सबसे छोटा रास्ता है, जहां स्रोत नोड को रिसोर्ट किया जाता है, उदाहरण के लिए, संक्रमित लक्ष्य नोड को परकोलेशन या गैर-अंतरित या आंशिक रूप से परकोलेशन अवस्था में किया जा सकता है।
जहाँ नोड से सबसे छोटे पथों की कुल संख्या है नोड करने के लिए और उन पथों की संख्या है जो . गुजरते हैं और समय पर नोड की परकोलेशन स्थिति को द्वारा निरूपित किया जाता है, और दो विशेष स्थिति हैं जब जो समय पर गैर-छिद्रित स्थिति को इंगित करता है। जबकि जब जो समय .पर पूरी तरह से व्याप्त स्थिति को इंगित करता है और इस प्रकार बीच के मान आंशिक रूप से प्रभावित राज्यों को दर्शाते हैं, उदाहरण के लिए, टाउनशिप के नेटवर्क में यह उस शहर में संक्रमित लोगों का प्रतिशत होता है।
परकोलेशन पथों से जुड़ा भार स्रोत नोड्स को निर्दिष्ट परकोलेशन स्तरों पर निर्भर करते हैं, इस आधार पर कि स्रोत नोड का परकोलेशन स्तर जितना अधिक होता है उस नोड से निकलने वाले पथ उतने ही महत्वपूर्ण रूप में होते है। वे नोड्स जो अत्यधिक परकोलेशन नोड्स से उत्पन्न होने वाले सबसे छोटे पथ पर स्थित होते है, इसलिए संभावित रूप से परकोलेशन के लिए अधिक महत्वपूर्ण हैं। पीसी की परिभाषा को लक्ष्य नोड भार के रूप में सम्मलित करने के लिए बढ़ाया जाता है। जबकि ब्रैंड्स के तेज़ कलन विधि से अपनाए गए कुशल कार्यान्वयन के साथ परकोलेशन केंद्रीयता गणनाओ समय में चलती है और यदि गणना के लिए लक्ष्य नोड्स के वेट पर विचार करने की आवश्यकता होती है, तो सबसे खराब स्थिति का समय .के रूप में है।
क्रॉस-क्लिक केंद्रीयता
एक सम्मिश्र ग्राफ़ में एकल नोड की क्रॉस-क्लिक केंद्रीयता नोड की विभिन्न क्लिक ग्राफ़ सिद्धांत से कनेक्टिविटी निर्धारित करती है। उच्च क्रॉस-क्लिक कनेक्टिविटी वाला नोड ग्राफ़ में सूचना या डिजीज के प्रसार की सुविधा प्रदान करता है। क्लिक्स सबग्राफ होते हैं जिनमें प्रत्येक नोड क्लिक में हर दूसरे नोड से जुड़ा होता है। एक नोड की क्रॉस-क्लिक कनेक्टिविटी किसी दिए गए ग्राफ़ के लिए के साथ शीर्ष और किनारों को इस प्रकार परिभाषित किया गया है, जहाँ उन क्लिकों की संख्या है जिनसे शीर्ष संबंधित है. इस उपाय का उपयोग 2013 में फघानी द्वारा किया गया था [32] लेकिन पहली बार 1998 में एवरेट और बोर्गट्टी द्वारा प्रस्तावित किया गया था, जहां उन्होंने इसे क्लिक ओवरलैप केंद्रीयता कहा था।
फ्रीमैन केंद्रीकरण
किसी भी नेटवर्क का केंद्रीकरण इस बात का माप है कि अन्य सभी नोड्स कितने केंद्रीय हैं और इसकी तुलना में उसका सबसे केंद्रीय नोड कितना केंद्रीय है।[12] केंद्रीकरण के उपाय तब (a) नेटवर्क में सबसे केंद्रीय नोड और अन्य सभी नोड्स के बीच केंद्रीयता में अंतर के योग की गणना करते हैं और (b) इस मात्रा को समान आकार के किसी भी नेटवर्क में सैद्धांतिक रूप से सबसे बड़े अंतर के योग से विभाजित करते हैं।[12] इस प्रकार, प्रत्येक केंद्रीयता माप का अपना केंद्रीकरण माप औपचारिक रूप से परिभाषित होता है। यदि बिंदु की कोई केंद्रीयता माप है , यदि नेटवर्क में इस तरह का सबसे बड़ा माप है और यदि,
- को इस प्रकार दर्शाते है,
बिंदु केंद्रीयता में अंतर का सबसे बड़ा योग है समान संख्या में नोड्स वाले किसी भी ग्राफ़ के लिए, नेटवर्क का केंद्रीकरण है:[12]
समान संख्या में नोड्स वाले किसी भी ग्राफ़ के लिए बिंदु केंद्रीयता C_{x} में अंतर का सबसे बड़ा योग है, तो नेटवर्क का केंद्रीकरण है:
यह अवधारणा लिंटन फ्रीमैन की देन है।
असमानता-आधारित केंद्रीयता माप

किसी दिए गए नेटवर्क के नोड्स की रैंकिंग में अच्छे परिणाम प्राप्त करने के लिए,[33] सम्मिश्र नेटवर्क में केंद्रीयता मापन को समृद्ध करने के लिए वर्गीकरण और डेटा माइनिंग के सिद्धांत के लिए विशिष्ट असमानता मापन का उपयोग किया जाता है। इसे अभिलक्षणिक सदिश केंद्रीयता के साथ चित्रित किया गया है और इस प्रकार अभिलक्षणिक मान समस्या के समाधान के माध्यम से प्रत्येक नोड की केंद्रीयता की गणना करता है।
जहाँ निर्देशांक के गुणन और एक यादृच्छिक आव्यूह समानता के रूप में होते है, जिसे एक असमानता माप के माध्यम से परिभाषित किया जाता है, उदाहरण के लिए जैककार्ड घातांक असमानता को इस प्रकार दर्शाया गया है,
जहां यह माप हमें किसी दिए गए नोड की केंद्रीयता के लिए प्रत्येक नोड के टोपोलॉजिकल योगदान को मापने की अनुमति देता है, जिसे योगदान केंद्रीयता कहा जाता है, उन नोड्स को अधिक असमानता के साथ अधिक वेट/प्रासंगिकता के रूप में होता है, क्योंकि ये दिए गए नोड तक पहुंच की अनुमति देते हैं और इस प्रकार नोड्स जो स्वयं सीधे नहीं पहुंच सकते हैं।
उल्लेखनीय है कि गैर-ऋणात्मक है क्योंकि और गैर-ऋणात्मक आव्यूह के रूप में है, इसलिए हम यह सुनिश्चित करने के लिए पेरोन-फ्रोबेनियस प्रमेय का उपयोग करते हैं कि उपरोक्त समस्या का λ = λmax एक अद्वितीय समाधान है और इस प्रकार c' गैर-ऋणात्मक के साथ हमें नेटवर्क में प्रत्येक नोड की केंद्रीयता का अनुमान लगाने की अनुमति देता है। इसलिए, i-th नोड की केंद्रीयता है और इसे इस प्रकार दर्शाया गया है
जहाँ नेटवर्क में नोड्स की संख्या है, कई असमानता मापन और नेटवर्क का परीक्षण किया गया है [34] अध्ययन किए गए स्थितियों में अच्छे परिणाम प्राप्त करना है।
यह भी देखें
- अल्फ़ा केंद्रीयता
- कोर-परिधि संरचना
- दूरी (ग्राफ़ सिद्धांत)
नोट्स और संदर्भ
- ↑ van den Heuvel MP, Sporns O (December 2013). "मानव मस्तिष्क में नेटवर्क हब". Trends in Cognitive Sciences. 17 (12): 683–96. doi:10.1016/j.tics.2013.09.012. PMID 24231140. S2CID 18644584.
- ↑ 2.0 2.1 Saberi M, Khosrowabadi R, Khatibi A, Misic B, Jafari G (January 2021). "आराम-अवस्था मस्तिष्क नेटवर्क की स्थिरता पर नकारात्मक लिंक का टोपोलॉजिकल प्रभाव". Scientific Reports. 11 (1): 2176. doi:10.1038/s41598-021-81767-7. PMC 7838299. PMID 33500525.
- ↑ 3.0 3.1 3.2 3.3 Bonacich, Phillip (1987). "Power and Centrality: A Family of Measures". American Journal of Sociology. 92 (5): 1170–1182. doi:10.1086/228631. S2CID 145392072.
- ↑ 4.0 4.1 4.2 4.3 4.4 4.5 Borgatti, Stephen P. (2005). "केंद्रीयता और नेटवर्क प्रवाह". Social Networks. 27: 55–71. CiteSeerX 10.1.1.387.419. doi:10.1016/j.socnet.2004.11.008.
- ↑ 5.0 5.1 Christian F. A. Negre, Uriel N. Morzan, Heidi P. Hendrickson, Rhitankar Pal, George P. Lisi, J. Patrick Loria, Ivan Rivalta, Junming Ho, Victor S. Batista. (2018). "Eigenvector centrality for characterization of protein allosteric pathways". Proceedings of the National Academy of Sciences. 115 (52): E12201–E12208. doi:10.1073/pnas.1810452115. PMC 6310864. PMID 30530700.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ 6.0 6.1 6.2 6.3 Borgatti, Stephen P.; Everett, Martin G. (2006). "केंद्रीयता पर एक ग्राफ़-सैद्धांतिक परिप्रेक्ष्य". Social Networks. 28 (4): 466–484. doi:10.1016/j.socnet.2005.11.005.
- ↑ 7.0 7.1 Benzi, Michele; Klymko, Christine (2013). "विभिन्न केंद्रीयता उपायों का एक मैट्रिक्स विश्लेषण". SIAM Journal on Matrix Analysis and Applications. 36 (2): 686–706. arXiv:1312.6722. doi:10.1137/130950550. S2CID 7088515.
- ↑ Michalak, Aadithya, Szczepański, Ravindran, & Jennings arXiv:1402.0567
- ↑ Hu, Xingwei; Shapley, Lloyd (2003). "संगठनों में प्राधिकरण वितरण पर". Games and Economic Behavior. 45: 132–170. doi:10.1016/s0899-8256(03)00130-1.
- ↑ Hu, Xingwei (2020). "कॉलेज रैंकिंग के अनुप्रयोग के साथ प्रकट प्राथमिकता के आधार पर बड़े डेटा को क्रमबद्ध करना". Journal of Big Data. 7. arXiv:2003.12198. doi:10.1186/s40537-020-00300-1.
- ↑ Krackhardt, David (June 1990). "Assessing the Political Landscape: Structure, Cognition, and Power in Organizations". Administrative Science Quarterly. 35 (2): 342–369. doi:10.2307/2393394. JSTOR 2393394.
- ↑ 12.0 12.1 12.2 12.3 Freeman, Linton C. (1979), "centrality in social networks: Conceptual clarification" (PDF), Social Networks, 1 (3): 215–239, CiteSeerX 10.1.1.227.9549, doi:10.1016/0378-8733(78)90021-7, archived from the original (PDF) on 2016-02-22, retrieved 2014-07-31
- ↑ 13.0 13.1 Lawyer, Glenn (2015). "Understanding the spreading power of all nodes in a network: a continuous-time perspective". Sci Rep. 5: 8665. arXiv:1405.6707. Bibcode:2015NatSR...5E8665L. doi:10.1038/srep08665. PMC 4345333. PMID 25727453.
- ↑ da Silva, Renato; Viana, Matheus; da F. Costa, Luciano (2012). "प्रसारकों की व्यक्तिगत विशेषताओं से महामारी फैलने की भविष्यवाणी करना". J. Stat. Mech.: Theory Exp. 2012 (7): P07005. arXiv:1202.0024. Bibcode:2012JSMTE..07..005A. doi:10.1088/1742-5468/2012/07/p07005. S2CID 2530998.
- ↑ Bauer, Frank; Lizier, Joseph (2012). "Identifying influential spreaders and efficiently estimating infection numbers in epidemic models: A walk counting approach". Europhys Lett. 99 (6): 68007. arXiv:1203.0502. Bibcode:2012EL.....9968007B. doi:10.1209/0295-5075/99/68007. S2CID 9728486.
- ↑ Sikic, Mile; Lancic, Alen; Antulov-Fantulin, Nino; Stefanic, Hrvoje (2013). "Epidemic centrality -- is there an underestimated epidemic impact of network peripheral nodes?". The European Physical Journal B. 86 (10): 1–13. arXiv:1110.2558. Bibcode:2013EPJB...86..440S. doi:10.1140/epjb/e2013-31025-5. S2CID 12052238.
- ↑ Ghoshal, G.; Barabsi, A L (2011). "जटिल नेटवर्क में रैंकिंग स्थिरता और सुपर-स्थिर नोड्स।". Nat Commun. 2: 394. Bibcode:2011NatCo...2..394G. doi:10.1038/ncomms1396. PMID 21772265.
- ↑ Freeman, Linton C. "Centrality in social networks conceptual clarification." Social networks 1.3 (1979): 215–239.
- ↑ Alex Bavelas. Communication patterns in task-oriented groups. J. Acoust. Soc. Am, 22(6):725–730, 1950.
- ↑ Sabidussi, G (1966). "किसी ग्राफ़ का केंद्रीयता सूचकांक". Psychometrika. 31 (4): 581–603. doi:10.1007/bf02289527. hdl:10338.dmlcz/101401. PMID 5232444. S2CID 119981743.
- ↑ Evans, Tim S.; Chen, Bingsheng (2022). "नेटवर्क केंद्रीयता को जोड़ने से निकटता और डिग्री मापी जाती है". Communications Physics (in English). 5 (1): 172. doi:10.1038/s42005-022-00949-5. ISSN 2399-3650. S2CID 236881169.
- ↑ Yannick Rochat. Closeness centrality extended to unconnected graphs: The harmonic centrality index (PDF). Applications of Social Network Analysis, ASNA 2009. Archived (PDF) from the original on 2017-08-16. Retrieved 2017-02-19.
- ↑ Freeman, Linton (1977). "बीच के आधार पर केंद्रीयता के उपायों का एक सेट". Sociometry. 40 (1): 35–41. doi:10.2307/3033543. JSTOR 3033543.
- ↑ 24.0 24.1 24.2 Brandes, Ulrik (2001). "बीच की केंद्रीयता के लिए एक तेज़ एल्गोरिदम" (PDF). Journal of Mathematical Sociology. 25 (2): 163–177. CiteSeerX 10.1.1.11.2024. doi:10.1080/0022250x.2001.9990249. hdl:10983/23603. S2CID 13971996. Archived from the original on March 4, 2016. Retrieved October 11, 2011.
- ↑ M. E. J. Newman. "नेटवर्क का गणित" (PDF). Archived (PDF) from the original on 2021-01-22. Retrieved 2006-11-09.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ 26.0 26.1 "अमेरिकन गणितीय सोसायटी". Archived from the original on 2018-01-11. Retrieved 2011-08-24.
- ↑ M. E. J. Newman. "नेटवर्क का गणित" (PDF). Archived (PDF) from the original on 2021-01-22. Retrieved 2006-11-09.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Katz, L. 1953. A New Status Index Derived from Sociometric Index. Psychometrika, 39–43.
- ↑ Bonacich, P (1991). "एक साथ समूह और व्यक्तिगत केंद्रीयताएँ". Social Networks. 13 (2): 155–168. doi:10.1016/0378-8733(91)90018-o.
- ↑ How does Google rank webpages? Archived January 31, 2012, at the Wayback Machine 20Q: About Networked Life
- ↑ Piraveenan, M.; Prokopenko, M.; Hossain, L. (2013). "Percolation Centrality: Quantifying Graph-Theoretic Impact of Nodes during Percolation in Networks". PLOS ONE. 8 (1): e53095. Bibcode:2013PLoSO...853095P. doi:10.1371/journal.pone.0053095. PMC 3551907. PMID 23349699.
- ↑ Faghani, Mohamamd Reza (2013). "ऑनलाइन सोशल नेटवर्क में एक्सएसएस वर्म प्रसार और जांच तंत्र का एक अध्ययन". IEEE Transactions on Information Forensics and Security. 8 (11): 1815–1826. doi:10.1109/TIFS.2013.2280884. S2CID 13587900.
- ↑ Alvarez-Socorro, A. J.; Herrera-Almarza, G. C.; González-Díaz, L. A. (2015-11-25). "असमानता के उपायों पर आधारित आइजेनसेंट्रैलिटी जटिल नेटवर्क में केंद्रीय नोड्स को प्रकट करती है". Scientific Reports. 5: 17095. Bibcode:2015NatSR...517095A. doi:10.1038/srep17095. PMC 4658528. PMID 26603652.
- ↑ Alvarez-Socorro, A.J.; Herrera-Almarza; González-Díaz, L. A. "असमानता के उपायों के आधार पर ईजेनसेंट्रैलिटी के लिए अनुपूरक जानकारी जटिल नेटवर्क में केंद्रीय नोड्स का खुलासा करती है" (PDF). Nature Publishing Group. Archived (PDF) from the original on 2016-03-07. Retrieved 2015-12-29.
अग्रिम पठन
- Koschützki, D.; Lehmann, K. A.; Peeters, L.; Richter, S.; Tenfelde-Podehl, D. and Zlotowski, O. (2005) Centrality Indices. In Brandes, U. and Erlebach, T. (Eds.) Network Analysis: Methodological Foundations, pp. 16–61, LNCS 3418, Springer-Verlag.