पुनरावर्ती बायेसियन अनुमान: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{About| | {{About|बेयस फ़िल्टर, एक सामान्य संभाव्य दृष्टिकोण|समान नाम वाला स्पैम फ़िल्टर|नाइव बेयस स्पैम फ़िल्टरिंग}} | ||
संभाव्यता सिद्धांत, सांख्यिकी और [[ यंत्र अधिगम | | संभाव्यता सिद्धांत, सांख्यिकी और [[ यंत्र अधिगम |मशीन लर्निंग]] में, '''पुनरावर्ती बायेसियन अनुमान''', जिसे बेयस फ़िल्टर के रूप में भी जाना जाता है, आने वाले माप और गणितीय प्रक्रिया मॉडल का उपयोग करके समय के साथ अज्ञात संभाव्यता [[घनत्व अनुमान|घनत्व]] फ़ंक्शन (पीडीएफ) का [[घनत्व अनुमान|अनुमान]] लगाने के लिए एक सामान्य संभाव्य दृष्टिकोण है। इस प्रकार से प्रक्रिया गणितीय अवधारणाओं और मॉडलों पर अधिक निर्भर करता है जिन्हें बायेसियन सांख्यिकी के रूप में ज्ञात पूर्व और पश्च संभावनाओं के अध्ययन के अन्दर सिद्धांतित किया जाता है। | ||
== | ==रोबोटिक्स में== | ||
बेयस फ़िल्टर एल्गोरिदम है जिसका उपयोग [[कंप्यूटर विज्ञान]] में रोबोट को उसकी स्थिति और अभिविन्यास का अनुमान लगाने की अनुमति देने के लिए कई मान्यताओं की संभावनाओं की गणना करने के लिए किया जाता है। अनिवार्य रूप से, बेयस फ़िल्टर रोबोटों को | इस प्रकार से बेयस फ़िल्टर एल्गोरिदम है जिसका उपयोग [[कंप्यूटर विज्ञान]] में रोबोट को उसकी स्थिति और अभिविन्यास का अनुमान लगाने की अनुमति देने के लिए कई मान्यताओं की संभावनाओं की गणना करने के लिए किया जाता है। और अनिवार्य रूप से, बेयस फ़िल्टर रोबोटों को वर्तमान समय में प्राप्त सेंसर डेटा के आधार पर, समन्वय प्रणाली के अन्दर अपनी अधिक संभावित स्थिति को निरंतर अपडेट करने की अनुमति देते हैं। किन्तु यह पुनरावर्ती एल्गोरिदम है. इसमें दो भाग सम्मिलित किये गए हैं: पूर्वानुमान और नवाचार सम्मिलित है । यदि वरिएबल [[सामान्य वितरण]] होते हैं और संक्रमण रैखिक होते हैं, तो बेयस फ़िल्टर [[कलमन फ़िल्टर]] के समान हो जाता है। | ||
किन्तु साधारण उदाहरण में ग्रिड में घूमने वाले एक रोबोट में कई अलग-अलग सेंसर हो सकते हैं जो की उसे अपने परिवेश के अतिरिक्त में सूचना प्रदान करते हैं। और रोबोट निश्चितता के साथ प्रारंभ हो सकता है कि वह स्थिति (0,0) पर है। चूंकि जैसे-जैसे यह अपनी मूल स्थिति से दूर और दूर जाता है, बेयस फ़िल्टर का उपयोग करके रोबोट को अपनी स्थिति के अतिरिक्त में निरंतर कम निश्चितता मिलती है, अर्थात संभावना को उसकी वर्तमान स्थिति के अतिरिक्त में रोबोट के विश्वास को सौंपा जा सकता है और उस संभावना को अतिरिक्त सेंसर सूचना से निरंतर अपडेट किया जा सकता है। | |||
== मॉडल == | == मॉडल == | ||
माप <math>z</math> | इस प्रकार से माप <math>z</math> [[छिपा हुआ मार्कोव मॉडल|गुप्त मार्कोव मॉडल]] (एचएमएम) के [[प्रकट चर|प्रकट वरिएबल]] हैं, जिसका अर्थ है वास्तविक स्थिति <math>x</math> इसे न देखी गई [[मार्कोव प्रक्रिया]] माना जाता है। निम्नलिखित चित्र एचएमएम का [[बायेसियन नेटवर्क]] प्रस्तुत करता है। | ||
[[Image:HMM Kalman Filter Derivation.svg|हिडन मार्कोव मॉडल|केंद्र]]मार्कोव धारणा के कारण, तत्काल | [[Image:HMM Kalman Filter Derivation.svg|हिडन मार्कोव मॉडल|केंद्र]]मार्कोव धारणा के कारण, तत्काल अंतिम स्थिति को देखते हुए वर्तमान वास्तविक स्थिति की संभावना अन्य अंतिम स्थितियों से सशर्त रूप से स्वतंत्र है। | ||
:<math>p(\textbf{x}_k|\textbf{x}_{k-1},\textbf{x}_{k-2},\dots,\textbf{x}_0) = p(\textbf{x}_k|\textbf{x}_{k-1} )</math> | :<math>p(\textbf{x}_k|\textbf{x}_{k-1},\textbf{x}_{k-2},\dots,\textbf{x}_0) = p(\textbf{x}_k|\textbf{x}_{k-1} )</math> | ||
इसी प्रकार, k- | इसी प्रकार, ''k''-th टाइमस्टेप पर माप केवल वर्तमान स्थिति पर निर्भर होते है, इसलिए वर्तमान स्थिति को देखते हुए यह सशर्त रूप से अन्य सभी स्तिथियों से स्वतंत्र है। | ||
:<math>p(\textbf{z}_k|\textbf{x}_k,\textbf{x}_{k-1},\dots,\textbf{x}_{0}) = p(\textbf{z}_k|\textbf{x}_{k} )</math> | :<math>p(\textbf{z}_k|\textbf{x}_k,\textbf{x}_{k-1},\dots,\textbf{x}_{0}) = p(\textbf{z}_k|\textbf{x}_{k} )</math> | ||
इन मान्यताओं का उपयोग करके एचएमएम के सभी | इन मान्यताओं का उपयोग करके एचएमएम के सभी स्तिथियों पर संभाव्यता वितरण को सरलता से लिखा जा सकता है: | ||
:<math>p(\textbf{x}_0,\dots,\textbf{x}_k,\textbf{z}_1,\dots,\textbf{z}_k) = p(\textbf{x}_0)\prod_{i=1}^k p(\textbf{z}_i|\textbf{x}_i)p(\textbf{x}_i|\textbf{x}_{i-1}).</math> | :<math>p(\textbf{x}_0,\dots,\textbf{x}_k,\textbf{z}_1,\dots,\textbf{z}_k) = p(\textbf{x}_0)\prod_{i=1}^k p(\textbf{z}_i|\textbf{x}_i)p(\textbf{x}_i|\textbf{x}_{i-1}).</math> | ||
चूंकि , जब स्थिति x का अनुमान लगाने के लिए कलमन फ़िल्टर का उपयोग किया जाता है, तो ब्याज की संभाव्यता वितरण वर्तमान टाइमस्टेप तक माप पर वातानुकूलित वर्तमान स्थितियों से जुड़ी होती है। (यह अंतिम स्तिथियों को मार्जिनलाईजिंग पर रखकर और माप सेट की संभावना से विभाजित करके प्राप्त किया जाता है।) | |||
इससे कलमन फ़िल्टर के | इससे कलमन फ़िल्टर के पूर्वानुमान और ''अद्यतन'' चरण संभाव्य रूप से लिखे जाते हैं। इस प्रकार से अनुमानित स्थिति से जुड़ा संभाव्यता वितरण (''k'' - 1)-th टाइमस्टेप से ''k''-th और अंतिम स्थिति से जुड़े संभाव्यता वितरण के उत्पादों का योग (अभिन्न) है। अंतिम स्थिति से संबद्ध संभाव्यता वितरण, सभी संभावित <math>x_{k-1}</math> से अधिक है . | ||
:<math> p(\textbf{x}_k|\textbf{z}_{1:k-1}) = \int p(\textbf{x}_k | \textbf{x}_{k-1}) p(\textbf{x}_{k-1} | \textbf{z}_{1:k-1} ) \, d\textbf{x}_{k-1} </math> | :<math> p(\textbf{x}_k|\textbf{z}_{1:k-1}) = \int p(\textbf{x}_k | \textbf{x}_{k-1}) p(\textbf{x}_{k-1} | \textbf{z}_{1:k-1} ) \, d\textbf{x}_{k-1} </math> | ||
| Line 30: | Line 30: | ||
भाजक | भाजक | ||
:<math>p(\textbf{z}_k|\textbf{z}_{1:k-1}) = \int p(\textbf{z}_k|\textbf{x}_k) p(\textbf{x}_k|\textbf{z}_{1:k-1}) d\textbf{x}_{k}</math> | :<math>p(\textbf{z}_k|\textbf{z}_{1:k-1}) = \int p(\textbf{z}_k|\textbf{x}_k) p(\textbf{x}_k|\textbf{z}_{1:k-1}) d\textbf{x}_{k}</math> | ||
<math>x</math> के सापेक्ष स्थिर है , इसलिए हम इसे सदैव गुणांक <math>\alpha</math> के स्थान पर प्रतिस्थापित कर सकते हैं , जिसे समान्यतः व्यवहार में अनदेखा किया जा सकता है।इस प्रकार से अंश की गणना की जा सकती है और फिर इसे सामान्यीकृत किया जा सकता है, क्योंकि इसका अभिन्न अंग एकता होना चाहिए। | |||
== अनुप्रयोग == | == अनुप्रयोग == | ||
| Line 38: | Line 38: | ||
==अनुक्रमिक बायेसियन फ़िल्टरिंग== | ==अनुक्रमिक बायेसियन फ़िल्टरिंग== | ||
अनुक्रमिक बायेसियन फ़िल्टरिंग | इस प्रकार से अनुक्रमिक बायेसियन फ़िल्टरिंग यह स्तिथियों के लिए बायेसियन अनुमान का विस्तार है यह दर्शाया गया की मूल्य समय में परिवर्तित किया जाता है। यह समय के साथ विकसित होने वाले प्रेक्षित वरिएबल के वास्तविक मूल्य का अनुमान लगाने की विधि कहलाती है। | ||
विधि का नाम है: | इस प्रकार विधि का नाम है: | ||
;फ़िल्टरिंग: अतीत और वर्तमान अवलोकनों को | ;फ़िल्टरिंग: अतीत और वर्तमान अवलोकनों को दर्शाते हुए वर्तमान मूल्य का अनुमान लगाते समय उपयोग किया जाता है। | ||
; | ;स्मूथिंग : अतीत और वर्तमान टिप्पणियों को दर्शाते हुए अंतिम और मूल्यों का अनुमान लगाते समय उपयोग किया जाता है। | ||
; | ;पूर्वानुमान : अतः अतीत और वर्तमान टिप्पणियों को दर्शाते हुए संभावित भविष्य के मूल्य का अनुमान लगाते समय उपयोग किया जाता है।। | ||
अनुक्रमिक बायेसियन फ़िल्टरिंग की धारणा का [[नियंत्रण सिद्धांत]] और [[रोबोटिक]] | अनुक्रमिक बायेसियन फ़िल्टरिंग की धारणा का [[नियंत्रण सिद्धांत]] और [[रोबोटिक]] में उच्च माप पर उपयोग किया जाता है। | ||
== अग्रिम पठन == | == अग्रिम पठन == | ||
Revision as of 14:58, 13 July 2023
संभाव्यता सिद्धांत, सांख्यिकी और मशीन लर्निंग में, पुनरावर्ती बायेसियन अनुमान, जिसे बेयस फ़िल्टर के रूप में भी जाना जाता है, आने वाले माप और गणितीय प्रक्रिया मॉडल का उपयोग करके समय के साथ अज्ञात संभाव्यता घनत्व फ़ंक्शन (पीडीएफ) का अनुमान लगाने के लिए एक सामान्य संभाव्य दृष्टिकोण है। इस प्रकार से प्रक्रिया गणितीय अवधारणाओं और मॉडलों पर अधिक निर्भर करता है जिन्हें बायेसियन सांख्यिकी के रूप में ज्ञात पूर्व और पश्च संभावनाओं के अध्ययन के अन्दर सिद्धांतित किया जाता है।
रोबोटिक्स में
इस प्रकार से बेयस फ़िल्टर एल्गोरिदम है जिसका उपयोग कंप्यूटर विज्ञान में रोबोट को उसकी स्थिति और अभिविन्यास का अनुमान लगाने की अनुमति देने के लिए कई मान्यताओं की संभावनाओं की गणना करने के लिए किया जाता है। और अनिवार्य रूप से, बेयस फ़िल्टर रोबोटों को वर्तमान समय में प्राप्त सेंसर डेटा के आधार पर, समन्वय प्रणाली के अन्दर अपनी अधिक संभावित स्थिति को निरंतर अपडेट करने की अनुमति देते हैं। किन्तु यह पुनरावर्ती एल्गोरिदम है. इसमें दो भाग सम्मिलित किये गए हैं: पूर्वानुमान और नवाचार सम्मिलित है । यदि वरिएबल सामान्य वितरण होते हैं और संक्रमण रैखिक होते हैं, तो बेयस फ़िल्टर कलमन फ़िल्टर के समान हो जाता है।
किन्तु साधारण उदाहरण में ग्रिड में घूमने वाले एक रोबोट में कई अलग-अलग सेंसर हो सकते हैं जो की उसे अपने परिवेश के अतिरिक्त में सूचना प्रदान करते हैं। और रोबोट निश्चितता के साथ प्रारंभ हो सकता है कि वह स्थिति (0,0) पर है। चूंकि जैसे-जैसे यह अपनी मूल स्थिति से दूर और दूर जाता है, बेयस फ़िल्टर का उपयोग करके रोबोट को अपनी स्थिति के अतिरिक्त में निरंतर कम निश्चितता मिलती है, अर्थात संभावना को उसकी वर्तमान स्थिति के अतिरिक्त में रोबोट के विश्वास को सौंपा जा सकता है और उस संभावना को अतिरिक्त सेंसर सूचना से निरंतर अपडेट किया जा सकता है।
मॉडल
इस प्रकार से माप गुप्त मार्कोव मॉडल (एचएमएम) के प्रकट वरिएबल हैं, जिसका अर्थ है वास्तविक स्थिति इसे न देखी गई मार्कोव प्रक्रिया माना जाता है। निम्नलिखित चित्र एचएमएम का बायेसियन नेटवर्क प्रस्तुत करता है।
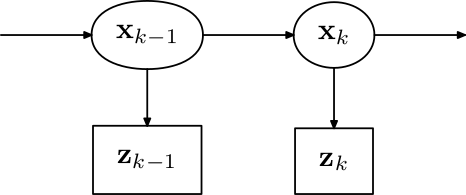 मार्कोव धारणा के कारण, तत्काल अंतिम स्थिति को देखते हुए वर्तमान वास्तविक स्थिति की संभावना अन्य अंतिम स्थितियों से सशर्त रूप से स्वतंत्र है।
मार्कोव धारणा के कारण, तत्काल अंतिम स्थिति को देखते हुए वर्तमान वास्तविक स्थिति की संभावना अन्य अंतिम स्थितियों से सशर्त रूप से स्वतंत्र है।
इसी प्रकार, k-th टाइमस्टेप पर माप केवल वर्तमान स्थिति पर निर्भर होते है, इसलिए वर्तमान स्थिति को देखते हुए यह सशर्त रूप से अन्य सभी स्तिथियों से स्वतंत्र है।
इन मान्यताओं का उपयोग करके एचएमएम के सभी स्तिथियों पर संभाव्यता वितरण को सरलता से लिखा जा सकता है:
चूंकि , जब स्थिति x का अनुमान लगाने के लिए कलमन फ़िल्टर का उपयोग किया जाता है, तो ब्याज की संभाव्यता वितरण वर्तमान टाइमस्टेप तक माप पर वातानुकूलित वर्तमान स्थितियों से जुड़ी होती है। (यह अंतिम स्तिथियों को मार्जिनलाईजिंग पर रखकर और माप सेट की संभावना से विभाजित करके प्राप्त किया जाता है।)
इससे कलमन फ़िल्टर के पूर्वानुमान और अद्यतन चरण संभाव्य रूप से लिखे जाते हैं। इस प्रकार से अनुमानित स्थिति से जुड़ा संभाव्यता वितरण (k - 1)-th टाइमस्टेप से k-th और अंतिम स्थिति से जुड़े संभाव्यता वितरण के उत्पादों का योग (अभिन्न) है। अंतिम स्थिति से संबद्ध संभाव्यता वितरण, सभी संभावित से अधिक है .
अद्यतन की संभाव्यता वितरण माप संभावना और अनुमानित स्थिति के उत्पाद के समानुपाती होती है।
भाजक
के सापेक्ष स्थिर है , इसलिए हम इसे सदैव गुणांक के स्थान पर प्रतिस्थापित कर सकते हैं , जिसे समान्यतः व्यवहार में अनदेखा किया जा सकता है।इस प्रकार से अंश की गणना की जा सकती है और फिर इसे सामान्यीकृत किया जा सकता है, क्योंकि इसका अभिन्न अंग एकता होना चाहिए।
अनुप्रयोग
- कलमन फ़िल्टर, बहुभिन्नरूपी सामान्य वितरण के लिए पुनरावर्ती बायेसियन फ़िल्टर
- कण फ़िल्टर, अनुक्रमिक मोंटे कार्लो (एसएमसी) आधारित तकनीक, जो असतत बिंदुओं के सेट का उपयोग करके संभाव्यता घनत्व फ़ंक्शन को मॉडल करती है
- ग्रिड-आधारित अनुमानक, जो पीडीएफ को नियतात्मक असतत ग्रिड में उप-विभाजित करते हैं
अनुक्रमिक बायेसियन फ़िल्टरिंग
इस प्रकार से अनुक्रमिक बायेसियन फ़िल्टरिंग यह स्तिथियों के लिए बायेसियन अनुमान का विस्तार है यह दर्शाया गया की मूल्य समय में परिवर्तित किया जाता है। यह समय के साथ विकसित होने वाले प्रेक्षित वरिएबल के वास्तविक मूल्य का अनुमान लगाने की विधि कहलाती है।
इस प्रकार विधि का नाम है:
- फ़िल्टरिंग
- अतीत और वर्तमान अवलोकनों को दर्शाते हुए वर्तमान मूल्य का अनुमान लगाते समय उपयोग किया जाता है।
- स्मूथिंग
- अतीत और वर्तमान टिप्पणियों को दर्शाते हुए अंतिम और मूल्यों का अनुमान लगाते समय उपयोग किया जाता है।
- पूर्वानुमान
- अतः अतीत और वर्तमान टिप्पणियों को दर्शाते हुए संभावित भविष्य के मूल्य का अनुमान लगाते समय उपयोग किया जाता है।।
अनुक्रमिक बायेसियन फ़िल्टरिंग की धारणा का नियंत्रण सिद्धांत और रोबोटिक में उच्च माप पर उपयोग किया जाता है।
अग्रिम पठन
- Arulampalam, M. Sanjeev; Maskell, Simon; Gordon, Neil (2002). "A Tutorial on Particle Filters for On-line Non-linear/Non-Gaussian Bayesian Tracking". IEEE Transactions on Signal Processing. 50 (2): 174–188. CiteSeerX 10.1.1.117.1144. doi:10.1109/78.978374.
- Burkhart, Michael C. (2019). "Chapter 1. An Overview of Bayesian Filtering". A Discriminative Approach to Bayesian Filtering with Applications to Human Neural Decoding. Providence, RI, USA: Brown University. doi:10.26300/nhfp-xv22.
- Chen, Zhe Sage (2003). "Bayesian Filtering: From Kalman Filters to Particle Filters, and Beyond". Statistics: A Journal of Theoretical and Applied Statistics. 182 (1): 1–69.
- Diard, Julien; Bessière, Pierre; Mazer, Emmanuel (2003). "A survey of probabilistic models, using the Bayesian Programming methodology as a unifying framework" (PDF). cogprints.org.
- Särkkä, Simo (2013). Bayesian Filtering and Smoothing (PDF). Cambridge University Press.
- Volkov, Alexander (2015). "Accuracy bounds of non-Gaussian Bayesian tracking in a NLOS environment". Signal Processing. 108: 498–508. doi:10.1016/j.sigpro.2014.10.025.