आर्किमिडीज़ संपत्ति: Difference between revisions

Revision as of 12:37, 23 July 2023

आर्किमिडीज़ गुण का चित्रण।

अमूर्त बीजगणित और गणितीय विश्लेषण में आर्किमिडीज गुण का नाम सिरैक्यूज़ के प्राचीन यूनानी गणितज्ञ आर्किमिडीज़ के नाम पर रखा गया है, जो कुछ बीजगणितीय संरचनाओं जैसे कि आदेशित या मानक समूह (बीजगणित) और क्षेत्रों के माध्यम से धारित गुण है। गुण, सामान्यतः समझा जाता है, और यह बताता है कि दो सकारात्मक संख्याएं $x$ और $y$ दिए जाने पर एक पूर्णांक $n$ होता है जैसे कि कि $nx>y$ है। इसका अर्थ यह भी है कि प्राकृतिक संख्याओं का समूह उपरोक्त परिबद्ध नहीं है।^[1] साधारणतया कहा जाये तो यह कोई उन्‍नत रूप से बड़े या उन्‍नत रूप से छोटे घटक न होने का गुण है। यह ओटो स्टोल्ज़ ही थे जिन्होंने आर्किमिडीज़ के सूत्रीकरण को इसका नाम दिया चूँकि यह आर्किमिडीज़ के 'ऑन द स्फीयर एंड सिलेंडर' के सूत्रीकरण V के रूप में प्रकट होता है।^[2]

यह धारणा प्राचीन ग्रीस के परिमाण (गणित) के सिद्धांत से उत्पन्न हुई; यह अभी भी आधुनिक गणित में एक महत्वपूर्ण भूमिका निभाता है जैसे कि ज्यामिति के लिए डेविड हिल्बर्ट के सिद्धांत, रैखिक रूप से आदेशित समूह के सिद्धांत, आदेशित क्षेत्र और स्थानीय क्षेत्र के सिद्धांत है।

एक बीजगणितीय संरचना जिसमें कोई भी दो शून्यतर घटक तुलनीय हैं, इस अर्थ में कि उनमें से कोई भी दूसरे के संबंध में अपरिमेय नहीं है, उसे 'आर्किमिडीयन' कहा जाता है। एक संरचना जिसमें शून्यतर घटक ों की एक युग्म होता है, जिनमें से एक दूसरे के संबंध में अतिसूक्ष्म है, उसे 'अ-आर्किमिडीज' कहा जाता है।उदाहरण के रूप मे एक रैखिक रूप से आदेशित समूह जो कि आर्किमिडीज़ है, एक आर्किमिडीज़ समूह है।

इसे भिन्न-भिन्न संदर्भों में थोड़ा भिन्न सूत्रीकरण के साथ स्पष्ट करा जा सकता है। उदाहरण के रूप मे क्रमित क्षेत्रों के संदर्भ में, एक के पास आर्किमिडीज़ का सूत्रीकरण है जो इस गुण को सज्जित करता है, जिस स्थान पर वास्तविक संख्याओं का क्षेत्र आर्किमिडीज़ है, किन्तु वास्तविक गुणांक में तर्कसंगत कार्यो का क्षेत्र आर्किमिडीज़ नहीं है।

आर्किमिडीज़ गुण के नाम का इतिहास और उत्पत्ति

इस अवधारणा का नाम ओटो स्टोल्ज़ के माध्यम से (1880 के दशक में) प्राचीन ग्रीक के ज्यामिति और सिरैक्यूज़ के भौतिक विज्ञानी आर्किमिडीज़ के नाम पर रखा गया था।

आर्किमिडीज़ गुण यूक्लिड के घटक ों की पुस्तक V में परिभाषा 4 के रूप में प्रदर्शित करी गई है:

कहा जाता है कि परिमाण का एक दूसरे से अनुपात होता है जिसे गुणा करने पर एक दूसरे से अधिक हो सकता है।

चूँकि आर्किमिडीज़ ने इसका श्रेय कनिडस के यूडोक्सस को दिया है, इसलिए इसे "यूडोक्सस का प्रमेय" या यूडोक्सस सूत्रीकरण के रूप में भी जाना जाता है।^[3]

आर्किमिडीज़ ने अनुमानी तर्कों में अत्यंत सूक्ष्म का उपयोग किया है, चूंकि उन्होंने अस्वीकार किया कि वह पूर्ण गणितीय प्रमाण थे।

रैखिक रूप से आदेशित समूहों के लिए परिभाषा

मान लीजिए कि x और y एक रैखिक क्रम वाले समूह G के सकारात्मक घटक हैं। तत्पश्चात $y$ के संबंध में $x$ अतिसूक्ष्म है (या समकक्ष $y$ , $x$ के संबंध में अनंत है) यदि किसी प्राकृतिक संख्या $n$ के लिए $nx$ का गुणज $y$ से कम है, तो निम्नलिखित असमानता है:

\underbrace {x+\cdots +x} _{n{\text{ terms}}}<y.\,

निरपेक्ष मान लेकर इस परिभाषा को समस्त समूह तक प्रेषित करा जा सकता है।

समूह $G$ आर्किमिडीज़ है यदि कोई जोड़ी नहीं है $(x,y)$ ऐसा है कि $x$ एवं $y$ के संबंध में अपरिमेय है।

इसके अतिरिक्त, यदि $K$ इकाई (1) के साथ एक बीजगणितीय संरचना है - उदाहरण के रूप मे, एक चक्र (गणित) - तो एक समान परिभाषा $K$ पर प्रयुक्त होती है। यदि $1$ के संबंध में $x$ अतिसूक्ष्म है तो $x$ एक अतिसूक्ष्म घटक है। इसी प्रकार, यदि $1$ के संबंध में $y$ अनंत है, तो $y$ एक अनंत घटक है। बीजगणितीय संरचना $K$ आर्किमिडीयन है यदि इसमें कोई अनंत घटक और कोई अतिसूक्ष्म घटक नहीं है।

आदेशित किए गए क्षेत्र

आदेशित क्षेत्र में कुछ अतिरिक्त गुण होते हैं:

परिमेय संख्याएँ किसी भी क्रमित क्षेत्र में एम्बेडिंग हो रही हैं। अर्थात्, किसी भी क्रमित क्षेत्र में अभिलक्षणिक (बीजगणित) शून्य होता है।
यदि $x$ अनंत है, तब $1/x$ अनंत है, और इसके विपरीत। इसलिए, यह सत्यापित करने के लिए कि एक क्षेत्र आर्किमिडीयन है, यह केवल यह जाँचने के लिए पर्याप्त है कि कोई अतिसूक्ष्म घटक नहीं हैं, या यह जाँचने के लिए कि कोई अनंत घटक नहीं हैं।
यदि $x$ अतिसूक्ष्म है और $r$ तब एक परिमेय संख्या है $rx$ अतिसूक्ष्म भी है। परिणाम स्वरुप , एक सामान्य घटक दिया $c$ , तीन नंबर $c/2$ , $c$ , और $2c$ या तब सभी अपरिमित हैं या सभी अपरिमित हैं।

इस समुच्चयिंग में, एक आदेशित क्षेत्र $K$ आर्किमिडीज़ ठीक है जब निम्न कथन, जिसे आर्किमिडीज़ का अभिगृहीत कहा जाता है, धारण करता है:

होने देना

x

का कोई भी घटक हो

K

. फिर एक प्राकृतिक संख्या उपस्थित है

n

ऐसा है कि

n>x

.

वैकल्पिक रूप से कोई निम्नलिखित लक्षण वर्णन का उपयोग कर सकता है:

\forall \,\varepsilon \in K{\big (}\varepsilon >0\implies \exists \ n\in N:1/n<\varepsilon {\big )}.

आदर्श क्षेत्रों के लिए परिभाषा

क्वालिफायर आर्किमिडीज़ को वैल्यूएशन रिंग के सिद्धांत में भी तैयार किया गया है और रैंक वन वैल्यू वाले क्षेत्र ्स पर नॉर्म्ड स्पेस निम्नानुसार है। होने देना $K$ एक ऐसा क्षेत्र हो जो एक निरपेक्ष मान फलन से संपन्न हो, अर्थात एक ऐसा फलन जो वास्तविक संख्या को जोड़ता हो $0$ क्षेत्र घटक 0 के साथ और एक धनात्मक वास्तविक संख्या को संबद्ध करता है $|x|$ प्रत्येक शून्य के साथ $x\in K$ और संतुष्ट करता है $|xy|=|x||y|$ और $|x+y|\leq |x|+|y|$ . फिर, $K$ यदि किसी अशून्य के लिए आर्किमिडीयन कहा जाता है $x\in K$ एक प्राकृतिक संख्या उपस्थित है $n$ ऐसा है कि

|\underbrace {x+\cdots +x} _{n{\text{ terms}}}|>1.

इसी तरह, एक आदर्श स्थान आर्किमिडीयन है यदि का योग

n

शर्तें, प्रत्येक एक गैर-शून्य सदिश के सामान्तर है

x

, पर्याप्त रूप से बड़े के लिए एक से अधिक का मानदंड है

n

. एक निरपेक्ष मान या एक आदर्श स्थान वाला क्षेत्र या तब आर्किमिडीयन है या शक्तिशाली स्थिति को संतुष्ट करता है, जिसे अल्ट्रामेट्रिक त्रिकोण असमानता कहा जाता है,

|x+y|\leq \max(|x|,|y|),

क्रमश। अल्ट्रामैट्रिक त्रिकोण असमानता को संतुष्ट करने वाले क्षेत्र या आदर्श स्थान को गैर-आर्किमिडीयन कहा जाता है।

एक गैर-आर्किमिडीयन मानक रैखिक स्थान की अवधारणा ए.एफ. मोन्ना के माध्यम से प्रस्तुत की गई थी।^[4]

उदाहरण और गैर उदाहरण

वास्तविक संख्या का आर्किमिडीयन गुण

परिमेय संख्याओं के क्षेत्र को तुच्छ कार्य सहित अनेक निरपेक्ष मान कार्यों में से एक सौंपा जा सकता है $|x|=1$ , जब $x\neq 0$ , अधिक सामान्य ${\textstyle |x|={\sqrt {x^{2}}}}$ , और यह $p$ -adic निरपेक्ष मूल्य कार्य करता है। ओस्ट्रोव्स्की के प्रमेय के अनुसार, परिमेय संख्याओं पर प्रत्येक गैर-तुच्छ निरपेक्ष मान या तब सामान्य निरपेक्ष मान या कुछ के सामान्तर होता है $p$ -एडिक निरपेक्ष मूल्य। गैर-तुच्छ निरपेक्ष मूल्यों के संबंध में तर्कसंगत क्षेत्र पूर्ण नहीं है; तुच्छ निरपेक्ष मूल्य के संबंध में, तर्कसंगत क्षेत्र एक असतत स्थलीय स्थान है, इसलिए पूर्ण है। सामान्य निरपेक्ष मान (आदेश से) के संबंध में पूर्णता वास्तविक संख्याओं का क्षेत्र है। इस निर्माण के के माध्यम से वास्तविक संख्या का क्षेत्र एक आदेशित क्षेत्र और एक मानक क्षेत्र के रूप में आर्किमिडीयन है।^[5] दूसरी ओर, अन्य गैर-तुच्छ निरपेक्ष मूल्यों के संबंध में पूर्णता मेरा कारणसंख्या हैों के क्षेत्र देती है। पी-एडिक नंबर, जिस स्थान पर $p$ एक अभाज्य पूर्णांक संख्या है (नीचे देखें); के पश्चात् से $p$ -adic निरपेक्ष मान अल्ट्रामेट्रिक गुण को संतुष्ट करते हैं, फिर $p$ -ऐडिक संख्या क्षेत्र गैर-आर्किमिडीयन हैं जो मानक क्षेत्र के रूप में हैं (उन्हें आदेशित क्षेत्र में नहीं बनाया जा सकता है)।

वास्तविक संख्याओं के सूत्रीकरण सिद्धांत में, शून्येतर अतिसूक्ष्म वास्तविक संख्याओं की गैर-उपस्थितगी निम्नतम ऊपरी बाध्य गुण के माध्यम से निहित है। के माध्यम से निरूपित करें $Z$ वह समुच्चय जिसमें सभी धनात्मक अपरिमित गुण होते हैं। यह समुच्चय ऊपर से घिरा है $1$ . वर्तमान विरोधाभास से प्रमाण है कि $Z$ खाली नहीं है। फिर इसकी कम से कम ऊपरी सीमा होती है $c$ , जो धनात्मक भी है, इसलिए $c/2<c<2c$ . तब से $c$ की ऊपरी सीमा है $Z$ और $2c$ से सख्ती से बड़ा है $c$ , $2c$ एक धनात्मक अपरिमेय नहीं है। अर्थात कुछ प्राकृतिक संख्या है $n$ जिसके लिए $1/n<2c$ . दूसरी ओर, $c/2$ एक धनात्मक अतिसूक्ष्म है, चूँकि कम से कम ऊपरी सीमा की परिभाषा के अनुसार एक अतिसूक्ष्म होना चाहिए $x$ के मध्य $c/2$ और $c$ , और यदि $1/k<c/2\leq x$ तब $x$ अतिसूक्ष्म नहीं है। परंतु $1/(4n)<c/2$ , इसलिए $c/2$ अतिसूक्ष्म नहीं है, और यह एक विरोधाभास है। इस का कारणहै कि $Z$ आखिर खाली है: कोई धनात्मक, अतिसूक्ष्म वास्तविक संख्याएँ नहीं हैं।

वास्तविक संख्याओं की आर्किमिडीयन गुण भी रचनात्मक विश्लेषण में रखती है, तथापि उस संदर्भ में कम से कम ऊपरी बाध्य गुण विफल हो सकती है।

गैर-आर्किमिडीयन आदेशित क्षेत्र

एक आदेशित क्षेत्र के उदाहरण के रूप मे जो आर्किमिडीयन नहीं है, वास्तविक गुणांक वाले तर्कसंगत कार्यों के क्षेत्र को लें। (एक परिमेय फलन कोई भी ऐसा फलन है जिसे एक बहुपद के माध्यम से दूसरे बहुपद से विभाजित करके व्यक्त किया जा सकता है; हम मानेंगे कि यह इस तरह से किया गया है कि हर का प्रमुख गुणांक धनात्मक है।) इसे एक आदेशित क्षेत्र बनाने के लिए, किसी को जोड़ और गुणा संचालन के साथ संगत आदेश देना होगा। अभी $f>g$ यदि और केवल यदि $f-g>0$ , इसलिए हमें केवल यह कहना है कि कौन से तर्कसंगत कार्यों को धनात्मक माना जाता है। यदि अंश का प्रमुख गुणांक धनात्मक है, तब फलन को धनात्मक कहें। (किसी को यह जांचना चाहिए कि यह क्रम अच्छी तरह से परिभाषित है और जोड़ और गुणा के साथ संगत है।) इस परिभाषा के अनुसार, तर्कसंगत कार्य $1/x$ धनात्मक है किन्तु तर्कसंगत कार्य से कम है $1$ . वास्तव में, यदि $n$ कोई प्राकृतिक संख्या है, तब $n(1/x)=n/x$ धनात्मक है किन्तु अभी भी कम है $1$ , चाहे कितना भी बड़ा क्यों न हो $n$ है। इसलिए, $1/x$ इस क्षेत्र में एक अपरिमेय है।

यह उदाहरण अन्य गुणांकों का सामान्यीकरण करता है। वास्तविक गुणांकों के अतिरिक्त तर्कसंगत कार्यों को तर्कसंगत के साथ लेने से एक गणनीय गैर-आर्किमिडीयन आदेशित क्षेत्र उत्पन्न होता है। गुणांकों को एक भिन्न चर में तर्कसंगत कार्यों के रूप में लेते हुए, कहते हैं $y$ , भिन्न आदेशित प्रकार के साथ एक उदाहरण बनाता है।

गैर-आर्किमिडीयन मूल्यवान क्षेत्र

p-adic मेट्रिक और p-adic नंबर क्षेत्र से संपन्न परिमेय संख्याओं का क्षेत्र जो पूर्णताएँ हैं, उनके पास निरपेक्ष मान वाले क्षेत्र के रूप में आर्किमिडीज़ गुण नहीं है। सभी आर्किमिडीयन मूल्यवान क्षेत्र सामान्य निरपेक्ष मान की शक्ति के साथ जटिल संख्याओं के एक उपक्षेत्र के लिए आइसोमेट्रिक रूप से आइसोमोर्फिक हैं।^[6]

=== आर्किमिडीयन आदेशित क्षेत्र === की समतुल्य परिभाषाएँ

प्रत्येक रैखिक रूप से आदेशित क्षेत्र $K$ एक आदेशित सब क्षेत्र के रूप में परिमेय (एक आइसोमोर्फिक कॉपी) सम्मिलित हैं, अर्थात् गुणक इकाई के माध्यम से उत्पन्न सब क्षेत्र $1$ का $K$ , जिसमें क्रमित उपसमूह के रूप में पूर्णांक होते हैं, जिसमें क्रमित मोनोइड के रूप में प्राकृतिक संख्याएँ होती हैं. परिमेय का एम्बेडिंग तब परिमेय, पूर्णांक और प्राकृतिक संख्याओं के बारे में बोलने का एक विधि देता है $K$ . इन अवसंरचनाओं के संदर्भ में आर्किमिडीयन क्षेत्रों के समतुल्य लक्षण निम्नलिखित हैं।^[7]

प्राकृतिक संख्याएं कोफिनल (गणित) में होती हैं $K$ . अर्थात हर घटक $K$ किसी प्राकृतिक संख्या से कम है। (यह स्थितिा नहीं है जब अनंत घटक उपस्थित हों।) इस प्रकार एक आर्किमिडीयन क्षेत्र वह है जिसकी प्राकृतिक संख्या बिना किसी सीमा के बढ़ती है।
शून्य सबसे कम है $K$ समुच्चय का $\{1/2,1/3,1/4,\dots \}$ . (यदि $K$ एक धनात्मक अपरिमेय समाहित करता है, यह समुच्चय के लिए एक निचली सीमा होगी जहाँ से शून्य सबसे बड़ी निचली सीमा नहीं होगी।)
के घटक ों का समुच्चय $K$ धनात्मक और ऋणात्मक परिमेय के मध्य खुला नहीं है। ऐसा इसलिए है चूँकि समुच्चय में सभी अपरिमेय होते हैं, जो कि केवल समुच्चय है $\{0\}$ जब कोई शून्येतर अतिसूक्ष्म नहीं होता है, और अन्यथा खुला होता है, तब न तब कोई न्यूनतम और न ही सबसे बड़ा अशून्य अतिसूक्ष्म होता है। ध्यान दें कि दोनों स्थितियोंमें, अत्यंत सूक्ष्म का समुच्चय बंद है। पश्चात् वाले स्थितिे में, (i) प्रत्येक अतिसूक्ष्म प्रत्येक धनात्मक परिमेय से कम है, (ii) न तब सबसे बड़ा अत्यल्प है और न ही सबसे कम धनात्मक परिमेय है, और (iii) मध्य में और कुछ नहीं है। परिणाम स्वरुप , कोई भी गैर-आर्किमिडीयन आदेशित क्षेत्र अधूरा और डिस्कनेक्ट दोनों है।
किसी के लिए $x$ में $K$ से अधिक पूर्णांकों का समूह $x$ सबसे कम घटक होता है। (यदि $x$ एक ऋणात्मक अनंत मात्रा थी तब प्रत्येक पूर्णांक इससे बड़ा होगा।)
हर गैर-खाली खुला अंतराल $K$ एक तर्कसंगत सम्मिलित है। (यदि $x$ एक धनात्मक अतिसूक्ष्म, खुला अंतराल है $(x,2x)$ अपरिमित रूप से अनेक अपरिमित हैं किन्तु एक भी परिमेय नहीं है।)
परिमेय घने समुच्चय हैं $K$ sup और inf दोनों के संबंध में। (अर्थात, का हर घटक $K$ परिमेय के कुछ समुच्चय का समर्थन है, और परिमेय के कुछ अन्य समुच्चय का inf है।) इस प्रकार एक आर्किमिडीयन क्षेत्र किसी भी क्रमित क्षेत्र के अर्थ में परिमेय का कोई सघन क्रमित विस्तार है, जो अपने परिमेय घटक ों को घनीभूत रूप से एम्बेड करता है।

यह भी देखें

0.999...
आर्किमिडीज़ ने वेक्टर स्पेस का आदेश दिया
वास्तविक संख्याओं का निर्माण – Axiomatic definitions of the real numbers

↑ https://www.math.cuhk.edu.hk/course_builder/2021/math2050c/MATH%202050C%20Lecture%204%20(Jan%2021).pdf^{[bare URL PDF]}
↑ G. Fisher (1994) in P. Ehrlich(ed.), Real Numbers, Generalizations of the Reals, and Theories of continua, 107-145, Kluwer Academic
↑ Knopp, Konrad (1951). Theory and Application of Infinite Series (English 2nd ed.). London and Glasgow: Blackie & Son, Ltd. p. 7. ISBN 0-486-66165-2.
↑ Monna, A. F. (1943). "Over een lineaire P-adische ruimte". Nederl. Akad. Wetensch. Verslag Afd. Natuurk. (52): 74–84. MR 0015678.
↑ Neal Koblitz, "p-adic Numbers, p-adic Analysis, and Zeta-Functions", Springer-Verlag,1977.
↑ Shell, Niel, Topological Fields and Near Valuations, Dekker, New York, 1990. ISBN 0-8247-8412-X
↑ Schechter 1997, §10.3

संदर्भ

Schechter, Eric (1997). Handbook of Analysis and its Foundations. Academic Press. ISBN 0-12-622760-8. Archived from the original on 2015-03-07. Retrieved 2009-01-30.

[1] ttps://www.math.cuhk.edu.hk/course_builder/2021/math2050c/MATH%202050C%20Lecture%204%20(Jan%2021).pdf^{[bare URL PDF]}

[2] G. Fisher (1994) in P. Ehrlich(ed.), Real Numbers, Generalizations of the Reals, and Theories of continua, 107-145, Kluwer Academic

[Knopp1951-3] Knopp, Konrad (1951). Theory and Application of Infinite Series (English 2nd ed.). London and Glasgow: Blackie & Son, Ltd. p. 7. ISBN 0-486-66165-2.

[monna1943-4] Monna, A. F. (1943). "Over een lineaire P-adische ruimte". Nederl. Akad. Wetensch. Verslag Afd. Natuurk. (52): 74–84. MR 0015678.

[5] Neal Koblitz, "p-adic Numbers, p-adic Analysis, and Zeta-Functions", Springer-Verlag,1977.

[shell1-6] Shell, Niel, Topological Fields and Near Valuations, Dekker, New York, 1990. ISBN 0-8247-8412-X

[Schechter-7] Schechter 1997, §10.3

[1]

[2]

[3]

[4]

[5]

[6]

[7]

@@ Line 1: / Line 1: @@
 {{Short description|Mathematical property of algebraic structures}}
 {{about|अमूर्त बीजगणित|भौतिक नियम|आर्किमिडीज़ का सिद्धांत}}
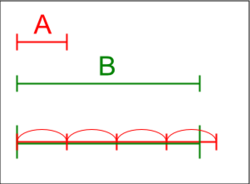
-[[File:Archimedean property.png|thumb|250px|आर्किमिडीज़ गुण का चित्रण।]]अमूर्त बीजगणित और [[गणितीय विश्लेषण]] में, प्राचीन यूनानी गणितज्ञ [[आर्किमिडीज]]़ ऑफ सिरैक्यूज़, इटली के नाम पर रखा गया आर्किमिडीयन गुण, कुछ [[बीजगणितीय संरचना]]ओं, जैसे आदेशित या आदर्श [[समूह (बीजगणित)]], और फ़ील्ड (गणित) द्वारा धारित गुण है।
+[[File:Archimedean property.png|thumb|250px|आर्किमिडीज़ गुण का चित्रण।]]अमूर्त बीजगणित और [[गणितीय विश्लेषण]] में [[आर्किमिडीज]] गुण का नाम सिरैक्यूज़ के प्राचीन यूनानी गणितज्ञ आर्किमिडीज़ के नाम पर रखा गया है, जो कुछ [[बीजगणितीय संरचना]]ओं जैसे कि आदेशित या मानक [[समूह (बीजगणित)]] और क्षेत्रों के माध्यम से  धारित गुण है। गुण, सामान्यतः समझा जाता है, और यह बताता है कि दो सकारात्मक संख्याएं  <math>x</math> और <math>y</math>  दिए जाने पर एक पूर्णांक  <math>n</math> होता है जैसे कि कि <math>nx > y</math> है। इसका अर्थ यह भी है कि [[प्राकृतिक संख्या]]ओं का समूह  उपरोक्त परिबद्ध नहीं है।<ref>https://www.math.cuhk.edu.hk/course_builder/2021/math2050c/MATH%202050C%20Lecture%204%20(Jan%2021).pdf {{Bare URL PDF|date=March 2022}}</ref> साधारणतया   कहा जाये तो यह कोई उन्‍नत रूप से बड़े या उन्‍नत रूप से छोटे घटक  न होने का गुण है। यह [[ओटो स्टोल्ज़]] ही थे जिन्होंने आर्किमिडीज़ के सूत्रीकरण को इसका नाम दिया चूँकि यह आर्किमिडीज़ के 'ऑन द स्फीयर एंड सिलेंडर' के सूत्रीकरण V के रूप में प्रकट होता है।<ref>G. Fisher (1994) in P. Ehrlich(ed.), Real Numbers, Generalizations of the Reals, and Theories of continua, 107-145, Kluwer Academic</ref>
-गुण, सामान्यतः समझा जाता है, बताता है कि दो धनात्मक संख्याएं दी गई हैं <math>x</math> और <math>y</math>, एक पूर्णांक है <math>n</math> ऐसा है कि <math>nx > y</math>. इसका अर्थ यह भी है कि [[प्राकृतिक संख्या]]ओं का समुच्चय ऊपर परिबद्ध नहीं है।<ref>https://www.math.cuhk.edu.hk/course_builder/2021/math2050c/MATH%202050C%20Lecture%204%20(Jan%2021).pdf {{Bare URL PDF|date=March 2022}}</ref> मोटे तौर पर बोलना, यह असीम रूप से बड़े या असीम रूप से छोटे तत्वों के न होने का गुण है।
+यह धारणा प्राचीन ग्रीस के [[परिमाण (गणित)]] के सिद्धांत से उत्पन्न हुई; यह अभी भी आधुनिक गणित में एक महत्वपूर्ण भूमिका निभाता है जैसे कि ज्यामिति के लिए [[डेविड हिल्बर्ट]] के सिद्धांत,  [[रैखिक रूप से आदेशित समूह]] के सिद्धांत, [[आदेशित क्षेत्र]] और  [[स्थानीय क्षेत्र]] के सिद्धांत है।
-यह [[ओटो स्टोल्ज़]] था जिसने आर्किमिडीज़ के स्वयंसिद्ध को अपना नाम दिया क्योंकि यह आर्किमिडीज़ के स्वयंसिद्ध V के रूप में स्फीयर और सिलेंडर पर प्रकट होता है।<ref>G. Fisher (1994) in P. Ehrlich(ed.), Real Numbers, Generalizations of the Reals, and Theories of continua, 107-145, Kluwer Academic</ref>
-यह धारणा प्राचीन ग्रीस के [[परिमाण (गणित)]] के सिद्धांत से उत्पन्न हुई; यह अभी भी आधुनिक गणित में एक महत्वपूर्ण भूमिका निभाता है जैसे कि [[डेविड हिल्बर्ट]] के हिल्बर्ट के स्वयंसिद्ध, और [[रैखिक रूप से आदेशित समूह]] के सिद्धांत, [[आदेशित क्षेत्र]] और [[स्थानीय क्षेत्र]]।
-एक बीजगणितीय संरचना जिसमें कोई भी दो गैर-शून्य तत्व तुलनीय हैं, इस अर्थ में कि उनमें से कोई भी दूसरे के संबंध में अपरिमेय नहीं है, उसे 'आर्किमिडीयन' कहा जाता है।
+एक बीजगणितीय संरचना जिसमें कोई भी दो शून्यतर घटक  तुलनीय हैं, इस अर्थ में कि उनमें से कोई भी दूसरे के संबंध में अपरिमेय नहीं है, उसे 'आर्किमिडीयन' कहा जाता है। एक संरचना जिसमें शून्यतर घटक ों की एक युग्म  होता है, जिनमें से एक दूसरे के संबंध में अतिसूक्ष्म है, उसे 'अ-आर्किमिडीज' कहा जाता है।उदाहरण के रूप मे  एक रैखिक रूप से आदेशित समूह जो कि आर्किमिडीज़ है, एक [[आर्किमिडीज़ समूह]] है।
-एक संरचना जिसमें गैर-शून्य तत्वों की एक जोड़ी होती है, जिनमें से एक दूसरे के संबंध में अतिसूक्ष्म है, 'गैर-आर्किमिडीज' कहा जाता है।
-उदाहरण के लिए, एक रैखिक रूप से आदेशित समूह जो कि आर्किमिडीज़ है, एक [[आर्किमिडीज़ समूह]] है।
-इसे भिन्न-भिन्न संदर्भों में थोड़ा भिन्न फॉर्मूलेशन के साथ स्पष्ट    बनाया जा सकता है।
+इसे भिन्न-भिन्न संदर्भों में थोड़ा भिन्न सूत्रीकरण के साथ स्पष्ट    करा  जा सकता है। उदाहरण के रूप मे क्रमित क्षेत्रों के संदर्भ में, एक  के पास आर्किमिडीज़ का सूत्रीकरण है जो इस गुण  को  सज्जित करता है, जिस स्थान पर  वास्तविक संख्याओं का क्षेत्र आर्किमिडीज़ है, किन्तु [[वास्तविक संख्या|वास्तविक गुणांक]]    में [[तर्कसंगत कार्य|तर्कसंगत कार्यो]] का क्षेत्र आर्किमिडीज़ नहीं है।
-उदाहरण के लिए, आदेशित क्षेत्रों के संदर्भ में, किसी के पास 'आर्किमिडीज़ का स्वयंसिद्ध' है जो इस गुण को तैयार करता है, जहाँ [[वास्तविक संख्या]]ओं का क्षेत्र आर्किमिडीज़ है, किन्तु वास्तविक गुणांकों में [[तर्कसंगत कार्य]]ों का नहीं है।
 == आर्किमिडीज़ गुण के नाम का इतिहास और उत्पत्ति ==
-इस अवधारणा का नाम ओटो स्टोल्ज़ (1880 के दशक में) ने [[प्राचीन ग्रीस]] के जियोमीटर और सिरैक्यूज़, इटली के भौतिक विज्ञानी आर्किमिडीज़ के नाम पर रखा था।
+इस अवधारणा का नाम ओटो स्टोल्ज़ के माध्यम से  (1880 के दशक में) [[प्राचीन ग्रीस|प्राचीन ग्रीक]]  के  ज्यामिति और सिरैक्यूज़ के भौतिक विज्ञानी आर्किमिडीज़ के नाम पर रखा गया था।
-आर्किमिडीयन गुण यूक्लिड के तत्वों की पुस्तक V में प्रकट होता है | परिभाषा 4 के रूप में यूक्लिड के तत्व:
+आर्किमिडीज़ गुण यूक्लिड के घटक ों की पुस्तक V में परिभाषा 4 के रूप में प्रदर्शित करी  गई है:
-{{Blockquote|Magnitudes are said to have a ratio to one another which can, when multiplied, exceed one another.}}
+{{Blockquote|कहा जाता है कि परिमाण का एक दूसरे से अनुपात होता है जिसे गुणा करने पर एक दूसरे से अधिक हो सकता है।}}
-क्योंकि आर्किमिडीज़ ने इसका श्रेय कनिडस के यूडोक्सस को दिया, इसे यूडोक्सस के प्रमेय या यूडोक्सस स्वयंसिद्ध के रूप में भी जाना जाता है।<ref name="Knopp1951">{{cite book|last=Knopp|first=Konrad|author-link=Konrad Knopp|title=Theory and Application of Infinite Series|url=https://archive.org/details/theoryapplicatio00knop|url-access=registration|edition=English 2nd|page=[https://archive.org/details/theoryapplicatio00knop/page/7 7]|year=1951|publisher=Blackie & Son, Ltd.|location=London and Glasgow|isbn=0-486-66165-2}}</ref>
-आर्किमिडीज़ ने [[अनुमानी]] तर्कों में इनफिनिटिमल्स का उपयोग किया, चूंकि उन्होंने अस्वीकार किया कि वह पूर्ण [[गणितीय प्रमाण]] थे।
+चूँकि आर्किमिडीज़ ने इसका श्रेय कनिडस के यूडोक्सस को दिया है, इसलिए इसे "यूडोक्सस का प्रमेय" या यूडोक्सस सूत्रीकरण के रूप में भी जाना जाता है।<ref name="Knopp1951">{{cite book|last=Knopp|first=Konrad|author-link=Konrad Knopp|title=Theory and Application of Infinite Series|url=https://archive.org/details/theoryapplicatio00knop|url-access=registration|edition=English 2nd|page=[https://archive.org/details/theoryapplicatio00knop/page/7 7]|year=1951|publisher=Blackie & Son, Ltd.|location=London and Glasgow|isbn=0-486-66165-2}}</ref>
+आर्किमिडीज़ ने [[अनुमानी]] तर्कों में अत्यंत सूक्ष्म का उपयोग किया है, चूंकि उन्होंने अस्वीकार किया कि वह पूर्ण [[गणितीय प्रमाण]] थे।
 == रैखिक रूप से आदेशित समूहों के लिए परिभाषा ==
 {{Main|आर्किमिडीज़ समूह}}
-होने देना {{mvar|x}} और {{mvar|y}} रैखिक रूप से आदेशित समूह # रैखिक रूप से आदेशित समूह G की परिभाषाएँ।
+मान लीजिए कि x और y एक रैखिक क्रम वाले समूह G के सकारात्मक घटक  हैं। तत्पश्चात  <math>y</math> के संबंध में  <math>x</math> अतिसूक्ष्म है (या समकक्ष  <math>y</math>,  <math>x</math> के संबंध में अनंत है) यदि किसी  [[प्राकृतिक संख्या]]  <math>n</math> के लिए  <math>nx</math> का गुणज  <math>y</math> से कम है, तो निम्नलिखित असमानता  है:
-फिर <math>x</math> के संबंध में अपरिमेय है <math>y</math> (या समकक्ष, <math>y</math> के संबंध में अनंत है <math>x</math>) यदि, किसी [[प्राकृतिक संख्या]] के लिए <math>n</math>, बहु <math>nx</math> मै रुक जाना <math>y</math>, अर्थात्, निम्नलिखित असमानता रखती है:
 <math display="block"> \underbrace{x+\cdots+x}_{n\text{ terms}} < y. \, </math>
-निरपेक्ष मान लेकर इस परिभाषा को पूरे समूह तक बढ़ाया जा सकता है।
+निरपेक्ष मान लेकर इस परिभाषा को समस्त समूह तक प्रेषित करा जा सकता है।
-समूह <math>G</math> आर्किमिडीज़ है यदि कोई जोड़ी नहीं है <math>(x,y)</math> ऐसा है कि <math>x</math> के संबंध में अपरिमेय है <math>y</math>.
+समूह <math>G</math> आर्किमिडीज़ है यदि कोई जोड़ी नहीं है <math>(x,y)</math> ऐसा है कि <math>x</math> एवं  <math>y</math>  के संबंध में अपरिमेय है।
-इसके अतिरिक्त, यदि <math>K</math> एक इकाई (1) के साथ एक बीजगणितीय संरचना है - उदाहरण के लिए, एक [[अंगूठी (गणित)]] - एक समान परिभाषा प्रयुक्त  होती है <math>K</math>.
+इसके अतिरिक्त, यदि  <math>K</math> इकाई (1) के साथ एक बीजगणितीय संरचना है - उदाहरण के रूप मे, एक [[अंगूठी (गणित)|चक्र (गणित)]] - तो एक समान परिभाषा  <math>K</math> पर प्रयुक्त होती है। यदि  <math>1</math> के संबंध में  {{mvar|x}} अतिसूक्ष्म है तो  {{mvar|x}} एक अतिसूक्ष्म घटक  है। इसी प्रकार, यदि  <math>1</math> के संबंध में  <math>y</math> अनंत है, तो  <math>y</math> एक अनंत घटक  है। बीजगणितीय संरचना  <math>K</math> आर्किमिडीयन है यदि इसमें कोई अनंत घटक  और कोई अतिसूक्ष्म घटक  नहीं है।
-यदि {{mvar|x}} के संबंध में अपरिमेय है <math>1</math>, तब <math>1</math> अतिसूक्ष्म तत्व है।
-इसी तरह यदि <math>y</math> के संबंध में अनंत है <math>1</math>, तब <math>y</math> अनंत तत्व है।
-बीजगणितीय संरचना <math>K</math> आर्किमिडीज़ है यदि इसमें कोई अनंत तत्व नहीं है और कोई अतिसूक्ष्म तत्व नहीं है।
-=== ऑर्डर किए गए फ़ील्ड ===
+=== आदेशित  किए गए  क्षेत्र ===
-आदेशित फ़ील्ड में कुछ अतिरिक्त गुण होते हैं:
+आदेशित  क्षेत्र  में कुछ अतिरिक्त गुण होते हैं:
-* परिमेय संख्याएँ किसी भी क्रमित फ़ील्ड में [[एम्बेडिंग]] हो रही हैं। अर्थात्, किसी भी क्रमित क्षेत्र में अभिलक्षणिक (बीजगणित) शून्य होता है।
+* परिमेय संख्याएँ किसी भी क्रमित  क्षेत्र  में [[एम्बेडिंग]] हो रही हैं। अर्थात्, किसी भी क्रमित क्षेत्र में अभिलक्षणिक (बीजगणित) शून्य होता है।
-* यदि <math>x</math> अनंत है, तब  <math>1/x</math> अनंत है, और इसके विपरीत। इसलिए, यह सत्यापित करने के लिए कि एक क्षेत्र आर्किमिडीयन है, यह केवल यह जाँचने के लिए पर्याप्त है कि कोई अतिसूक्ष्म तत्व नहीं हैं, या यह जाँचने के लिए कि कोई अनंत तत्व नहीं हैं।
+* यदि <math>x</math> अनंत है, तब  <math>1/x</math> अनंत है, और इसके विपरीत। इसलिए, यह सत्यापित करने के लिए कि एक क्षेत्र आर्किमिडीयन है, यह केवल यह जाँचने के लिए पर्याप्त है कि कोई अतिसूक्ष्म घटक  नहीं हैं, या यह जाँचने के लिए कि कोई अनंत घटक  नहीं हैं।
-* यदि <math>x</math> अतिसूक्ष्म है और <math>r</math> तब एक परिमेय संख्या है <math>rx</math> अतिसूक्ष्म भी है। परिणाम स्वरुप , एक सामान्य तत्व दिया <math>c</math>, तीन नंबर <math>c/2</math>, <math>c</math>, और <math>2c</math> या तब  सभी अपरिमित हैं या सभी अपरिमित हैं।
+* यदि <math>x</math> अतिसूक्ष्म है और <math>r</math> तब एक परिमेय संख्या है <math>rx</math> अतिसूक्ष्म भी है। परिणाम स्वरुप , एक सामान्य घटक  दिया <math>c</math>, तीन नंबर <math>c/2</math>, <math>c</math>, और <math>2c</math> या तब  सभी अपरिमित हैं या सभी अपरिमित हैं।
-इस समुच्चयिंग में, एक आदेशित फ़ील्ड {{mvar|K}} आर्किमिडीज़ ठीक है जब निम्न कथन, जिसे आर्किमिडीज़ का अभिगृहीत कहा जाता है, धारण करता है:
+इस समुच्चयिंग में, एक आदेशित  क्षेत्र  {{mvar|K}} आर्किमिडीज़ ठीक है जब निम्न कथन, जिसे आर्किमिडीज़ का अभिगृहीत कहा जाता है, धारण करता है:
-:  होने देना <math>x</math> का कोई भी तत्व हो <math>K</math>. फिर एक प्राकृतिक संख्या उपस्थित है <math>n</math> ऐसा है कि <math>n > x</math>.
+:  होने देना <math>x</math> का कोई भी घटक  हो <math>K</math>. फिर एक प्राकृतिक संख्या उपस्थित है <math>n</math> ऐसा है कि <math>n > x</math>.
 वैकल्पिक रूप से कोई निम्नलिखित लक्षण वर्णन का उपयोग कर सकता है:
 <math display="block">\forall\, \varepsilon \in K\big(\varepsilon > 0 \implies \exists\ n \in N : 1/n < \varepsilon\big).</math>
@@ Line 51: / Line 44: @@
 == आदर्श क्षेत्रों के लिए परिभाषा ==
-क्वालिफायर आर्किमिडीज़ को [[वैल्यूएशन रिंग]] के सिद्धांत में भी तैयार किया गया है और रैंक वन वैल्यू वाले फ़ील्ड्स पर नॉर्म्ड स्पेस निम्नानुसार है।
+क्वालिफायर आर्किमिडीज़ को [[वैल्यूएशन रिंग]] के सिद्धांत में भी तैयार किया गया है और रैंक वन वैल्यू वाले  क्षेत्र ्स पर नॉर्म्ड स्पेस निम्नानुसार है।
-होने देना <math>K</math> एक ऐसा क्षेत्र हो जो एक निरपेक्ष मान फलन  से संपन्न हो, अर्थात एक ऐसा फलन  जो वास्तविक संख्या को जोड़ता हो <math>0</math> क्षेत्र तत्व 0 के साथ और एक धनात्मक वास्तविक संख्या को संबद्ध करता है <math>|x|</math> प्रत्येक शून्य के साथ <math>x \in K</math> और संतुष्ट करता है
+होने देना <math>K</math> एक ऐसा क्षेत्र हो जो एक निरपेक्ष मान फलन  से संपन्न हो, अर्थात एक ऐसा फलन  जो वास्तविक संख्या को जोड़ता हो <math>0</math> क्षेत्र घटक  0 के साथ और एक धनात्मक वास्तविक संख्या को संबद्ध करता है <math>|x|</math> प्रत्येक शून्य के साथ <math>x \in K</math> और संतुष्ट करता है
 <math>|xy|=|x| |y|</math> और <math>|x+y| \le |x|+|y|</math>.
 फिर, <math>K</math> यदि किसी अशून्य के लिए आर्किमिडीयन कहा जाता है <math>x \in K</math> एक प्राकृतिक संख्या उपस्थित है <math>n</math> ऐसा है कि
@@ Line 62: / Line 55: @@
 अल्ट्रामैट्रिक त्रिकोण असमानता को संतुष्ट करने वाले क्षेत्र या आदर्श स्थान को गैर-आर्किमिडीयन कहा जाता है।
-एक गैर-आर्किमिडीयन मानक रैखिक स्थान की अवधारणा ए.एफ. मोन्ना द्वारा प्रस्तुत   की गई थी।<ref name=monna1943>{{cite journal |last1=Monna |first1=A. F. |title=Over een lineaire ''P''-adische ruimte |journal=Nederl. Akad. Wetensch. Verslag Afd. Natuurk. |issue=52 |date=1943 |pages=74–84 |mr=15678 }}</ref>
+एक गैर-आर्किमिडीयन मानक रैखिक स्थान की अवधारणा ए.एफ. मोन्ना के माध्यम से  प्रस्तुत   की गई थी।<ref name=monna1943>{{cite journal |last1=Monna |first1=A. F. |title=Over een lineaire ''P''-adische ruimte |journal=Nederl. Akad. Wetensch. Verslag Afd. Natuurk. |issue=52 |date=1943 |pages=74–84 |mr=15678 }}</ref>
@@ Line 73: / Line 66: @@
 गैर-तुच्छ निरपेक्ष मूल्यों के संबंध में तर्कसंगत क्षेत्र पूर्ण नहीं है; तुच्छ निरपेक्ष मूल्य के संबंध में, तर्कसंगत क्षेत्र एक असतत स्थलीय स्थान है, इसलिए पूर्ण है।
 सामान्य निरपेक्ष मान (आदेश से) के संबंध में पूर्णता वास्तविक संख्याओं का क्षेत्र है।
-इस निर्माण के द्वारा वास्तविक संख्या का क्षेत्र एक आदेशित क्षेत्र और एक मानक क्षेत्र के रूप में आर्किमिडीयन है।<ref>[[Neal Koblitz]], "p-adic Numbers, p-adic Analysis, and Zeta-Functions",  Springer-Verlag,1977.</ref> दूसरी ओर, अन्य गैर-तुच्छ निरपेक्ष मूल्यों के संबंध में पूर्णता [[मेरा मतलब संख्या है|मेरा कारणसंख्या है]]ों के क्षेत्र देती है। पी-एडिक नंबर, जहां <math>p</math> एक अभाज्य पूर्णांक संख्या है (नीचे देखें); के पश्चात् से <math>p</math>-adic निरपेक्ष मान अल्ट्रामेट्रिक गुण को संतुष्ट करते हैं, फिर <math>p</math>-ऐडिक संख्या फ़ील्ड गैर-आर्किमिडीयन हैं जो मानक फ़ील्ड के रूप में हैं (उन्हें आदेशित फ़ील्ड में नहीं बनाया जा सकता है)।
+इस निर्माण के के माध्यम से  वास्तविक संख्या का क्षेत्र एक आदेशित क्षेत्र और एक मानक क्षेत्र के रूप में आर्किमिडीयन है।<ref>[[Neal Koblitz]], "p-adic Numbers, p-adic Analysis, and Zeta-Functions",  Springer-Verlag,1977.</ref> दूसरी ओर, अन्य गैर-तुच्छ निरपेक्ष मूल्यों के संबंध में पूर्णता [[मेरा मतलब संख्या है|मेरा कारणसंख्या है]]ों के क्षेत्र देती है। पी-एडिक नंबर, जिस स्थान पर  <math>p</math> एक अभाज्य पूर्णांक संख्या है (नीचे देखें); के पश्चात् से <math>p</math>-adic निरपेक्ष मान अल्ट्रामेट्रिक गुण को संतुष्ट करते हैं, फिर <math>p</math>-ऐडिक संख्या  क्षेत्र  गैर-आर्किमिडीयन हैं जो मानक  क्षेत्र  के रूप में हैं (उन्हें आदेशित  क्षेत्र  में नहीं बनाया जा सकता है)।
-वास्तविक संख्याओं के स्वयंसिद्ध सिद्धांत में, शून्येतर अतिसूक्ष्म वास्तविक संख्याओं की गैर-उपस्थितगी निम्नतम ऊपरी बाध्य गुण द्वारा निहित है।
+वास्तविक संख्याओं के सूत्रीकरण सिद्धांत में, शून्येतर अतिसूक्ष्म वास्तविक संख्याओं की गैर-उपस्थितगी निम्नतम ऊपरी बाध्य गुण के माध्यम से  निहित है।
-द्वारा निरूपित करें <math>Z</math> वह समुच्चय जिसमें सभी धनात्मक अपरिमित गुण होते हैं।
+के माध्यम से  निरूपित करें <math>Z</math> वह समुच्चय जिसमें सभी धनात्मक अपरिमित गुण होते हैं।
 यह समुच्चय ऊपर से घिरा है <math>1</math>.
 वर्तमान विरोधाभास से प्रमाण है कि <math>Z</math> खाली नहीं है।
@@ Line 82: / Line 75: @@
 तब से {{mvar|c}} की [[ऊपरी सीमा]] है <math>Z</math> और <math>2c</math> से सख्ती से बड़ा है <math>c</math>, <math>2c</math> एक धनात्मक अपरिमेय नहीं है।
 अर्थात कुछ प्राकृतिक संख्या है <math>n</math> जिसके लिए <math>1/n < 2c</math>.
-दूसरी ओर, <math>c/2</math> एक धनात्मक अतिसूक्ष्म है, क्योंकि कम से कम ऊपरी सीमा की परिभाषा के अनुसार एक अतिसूक्ष्म होना चाहिए <math>x</math> के मध्य  <math>c/2</math> और <math>c</math>, और यदि <math>1/k < c/2 \leq x</math> तब <math>x</math> अतिसूक्ष्म नहीं है।
+दूसरी ओर, <math>c/2</math> एक धनात्मक अतिसूक्ष्म है, चूँकि कम से कम ऊपरी सीमा की परिभाषा के अनुसार एक अतिसूक्ष्म होना चाहिए <math>x</math> के मध्य  <math>c/2</math> और <math>c</math>, और यदि <math>1/k < c/2 \leq x</math> तब <math>x</math> अतिसूक्ष्म नहीं है।
 परंतु <math>1/(4n) < c/2</math>, इसलिए <math>c/2</math> अतिसूक्ष्म नहीं है, और यह एक विरोधाभास है।
 इस का कारणहै कि <math>Z</math> आखिर खाली है: कोई धनात्मक, अतिसूक्ष्म वास्तविक संख्याएँ नहीं हैं।
@@ Line 90: / Line 83: @@
 === गैर-आर्किमिडीयन आदेशित क्षेत्र ===
 {{main article|गैर-आर्किमिडीयन आदेशित क्षेत्र}}
-एक आदेशित क्षेत्र के उदाहरण के लिए जो आर्किमिडीयन नहीं है, वास्तविक गुणांक वाले [[तर्कसंगत कार्य]]ों के क्षेत्र को लें।
+एक आदेशित क्षेत्र के उदाहरण के रूप मे  जो आर्किमिडीयन नहीं है, वास्तविक गुणांक वाले [[तर्कसंगत कार्य]]ों के क्षेत्र को लें।
-(एक परिमेय फलन कोई भी ऐसा फलन है जिसे एक [[बहुपद]] द्वारा दूसरे बहुपद से विभाजित करके व्यक्त किया जा सकता है; हम मानेंगे कि यह इस तरह से किया गया है कि हर का प्रमुख गुणांक धनात्मक है।)
+(एक परिमेय फलन कोई भी ऐसा फलन है जिसे एक [[बहुपद]] के माध्यम से  दूसरे बहुपद से विभाजित करके व्यक्त किया जा सकता है; हम मानेंगे कि यह इस तरह से किया गया है कि हर का प्रमुख गुणांक धनात्मक है।)
 इसे एक आदेशित क्षेत्र बनाने के लिए, किसी को जोड़ और गुणा संचालन के साथ संगत आदेश देना होगा।
 अभी <math>f > g</math> यदि और केवल यदि <math>f - g > 0</math>, इसलिए हमें केवल यह कहना है कि कौन से तर्कसंगत कार्यों को धनात्मक माना जाता है।
@@ Line 101: / Line 94: @@
 यह उदाहरण अन्य गुणांकों का सामान्यीकरण करता है।
 वास्तविक गुणांकों के अतिरिक्त तर्कसंगत कार्यों को तर्कसंगत के साथ लेने से एक गणनीय गैर-आर्किमिडीयन आदेशित क्षेत्र उत्पन्न होता है।
-गुणांकों को एक भिन्न चर में तर्कसंगत कार्यों के रूप में लेते हुए, कहते हैं <math>y</math>, भिन्न ऑर्डर प्रकार के साथ एक उदाहरण बनाता है।
+गुणांकों को एक भिन्न चर में तर्कसंगत कार्यों के रूप में लेते हुए, कहते हैं <math>y</math>, भिन्न आदेशित  प्रकार के साथ एक उदाहरण बनाता है।
 === गैर-आर्किमिडीयन मूल्यवान क्षेत्र ===
-p-adic मेट्रिक और p-adic नंबर फ़ील्ड से संपन्न परिमेय संख्याओं का क्षेत्र जो पूर्णताएँ हैं, उनके पास निरपेक्ष मान वाले फ़ील्ड के रूप में आर्किमिडीज़ गुण नहीं है।  सभी आर्किमिडीयन मूल्यवान फ़ील्ड सामान्य निरपेक्ष मान की शक्ति के साथ जटिल संख्याओं के एक उपक्षेत्र के लिए आइसोमेट्रिक रूप से आइसोमोर्फिक हैं।<ref name=shell1>Shell, Niel, Topological Fields and Near Valuations, Dekker, New York, 1990. {{ISBN|0-8247-8412-X}}</ref>
+p-adic मेट्रिक और p-adic नंबर  क्षेत्र  से संपन्न परिमेय संख्याओं का क्षेत्र जो पूर्णताएँ हैं, उनके पास निरपेक्ष मान वाले  क्षेत्र  के रूप में आर्किमिडीज़ गुण नहीं है।  सभी आर्किमिडीयन मूल्यवान  क्षेत्र  सामान्य निरपेक्ष मान की शक्ति के साथ जटिल संख्याओं के एक उपक्षेत्र के लिए आइसोमेट्रिक रूप से आइसोमोर्फिक हैं।<ref name=shell1>Shell, Niel, Topological Fields and Near Valuations, Dekker, New York, 1990. {{ISBN|0-8247-8412-X}}</ref>
-=== आर्किमिडीयन आदेशित फ़ील्ड === की समतुल्य परिभाषाएँ
+=== आर्किमिडीयन आदेशित  क्षेत्र  === की समतुल्य परिभाषाएँ
-प्रत्येक रैखिक रूप से आदेशित क्षेत्र <math>K</math> एक आदेशित सबफ़ील्ड के रूप में परिमेय (एक आइसोमोर्फिक कॉपी) सम्मिलित  हैं, अर्थात् गुणक इकाई द्वारा उत्पन्न सबफ़ील्ड <math>1</math> का <math>K</math>, जिसमें क्रमित उपसमूह के रूप में पूर्णांक होते हैं, जिसमें क्रमित [[मोनोइड]] के रूप में प्राकृतिक संख्याएँ होती हैं.
+प्रत्येक रैखिक रूप से आदेशित क्षेत्र <math>K</math> एक आदेशित सब क्षेत्र  के रूप में परिमेय (एक आइसोमोर्फिक कॉपी) सम्मिलित  हैं, अर्थात् गुणक इकाई के माध्यम से  उत्पन्न सब क्षेत्र  <math>1</math> का <math>K</math>, जिसमें क्रमित उपसमूह के रूप में पूर्णांक होते हैं, जिसमें क्रमित [[मोनोइड]] के रूप में प्राकृतिक संख्याएँ होती हैं.
 परिमेय का एम्बेडिंग तब परिमेय, पूर्णांक और प्राकृतिक संख्याओं के बारे में बोलने का एक विधि देता है <math>K</math>.
 इन अवसंरचनाओं के संदर्भ में आर्किमिडीयन क्षेत्रों के समतुल्य लक्षण निम्नलिखित हैं।<ref name="Schechter">{{harvnb|Schechter|1997|loc=§10.3}}</ref>
-# प्राकृतिक संख्याएं [[कोफिनल (गणित)]] में होती हैं <math>K</math>. अर्थात हर तत्व <math>K</math> किसी प्राकृतिक संख्या से कम है। (यह स्थितिा नहीं है जब अनंत तत्व उपस्थित हों।) इस प्रकार एक आर्किमिडीयन क्षेत्र वह है जिसकी प्राकृतिक संख्या बिना किसी सीमा के बढ़ती है।
+# प्राकृतिक संख्याएं [[कोफिनल (गणित)]] में होती हैं <math>K</math>. अर्थात हर घटक  <math>K</math> किसी प्राकृतिक संख्या से कम है। (यह स्थितिा नहीं है जब अनंत घटक  उपस्थित हों।) इस प्रकार एक आर्किमिडीयन क्षेत्र वह है जिसकी प्राकृतिक संख्या बिना किसी सीमा के बढ़ती है।
 # शून्य [[सबसे कम]] है <math>K</math> समुच्चय का <math>\{1/2, 1/3, 1/4, \dots\}</math>. (यदि <math>K</math> एक धनात्मक अपरिमेय समाहित करता है, यह समुच्चय के लिए एक निचली सीमा होगी जहाँ से शून्य सबसे बड़ी निचली सीमा नहीं होगी।)
-# के तत्वों का समुच्चय <math>K</math> धनात्मक और ऋणात्मक परिमेय के मध्य  खुला नहीं है। ऐसा इसलिए है क्योंकि समुच्चय में सभी अपरिमेय होते हैं, जो कि केवल समुच्चय है <math>\{0\}</math> जब कोई शून्येतर अतिसूक्ष्म नहीं होता है, और अन्यथा खुला होता है, तब  न तब  कोई न्यूनतम और न ही सबसे बड़ा अशून्य अतिसूक्ष्म होता है। ध्यान दें कि दोनों स्थितियोंमें, इनफिनिटिमल्स का समुच्चय बंद है। पश्चात् वाले स्थितिे में, (i) प्रत्येक अतिसूक्ष्म प्रत्येक धनात्मक परिमेय से कम है, (ii) न तब  सबसे बड़ा अत्यल्प है और न ही सबसे कम धनात्मक परिमेय है, और (iii) मध्य  में और कुछ नहीं है। परिणाम स्वरुप , कोई भी गैर-आर्किमिडीयन आदेशित क्षेत्र अधूरा और डिस्कनेक्ट दोनों है।
+# के घटक ों का समुच्चय <math>K</math> धनात्मक और ऋणात्मक परिमेय के मध्य  खुला नहीं है। ऐसा इसलिए है चूँकि समुच्चय में सभी अपरिमेय होते हैं, जो कि केवल समुच्चय है <math>\{0\}</math> जब कोई शून्येतर अतिसूक्ष्म नहीं होता है, और अन्यथा खुला होता है, तब  न तब  कोई न्यूनतम और न ही सबसे बड़ा अशून्य अतिसूक्ष्म होता है। ध्यान दें कि दोनों स्थितियोंमें, अत्यंत सूक्ष्म का समुच्चय बंद है। पश्चात् वाले स्थितिे में, (i) प्रत्येक अतिसूक्ष्म प्रत्येक धनात्मक परिमेय से कम है, (ii) न तब  सबसे बड़ा अत्यल्प है और न ही सबसे कम धनात्मक परिमेय है, और (iii) मध्य  में और कुछ नहीं है। परिणाम स्वरुप , कोई भी गैर-आर्किमिडीयन आदेशित क्षेत्र अधूरा और डिस्कनेक्ट दोनों है।
-# किसी के लिए <math>x</math> में <math>K</math> से अधिक पूर्णांकों का समूह <math>x</math> सबसे कम तत्व होता है। (यदि <math>x</math> एक ऋणात्मक अनंत मात्रा थी तब  प्रत्येक पूर्णांक इससे बड़ा होगा।)
+# किसी के लिए <math>x</math> में <math>K</math> से अधिक पूर्णांकों का समूह <math>x</math> सबसे कम घटक  होता है। (यदि <math>x</math> एक ऋणात्मक अनंत मात्रा थी तब  प्रत्येक पूर्णांक इससे बड़ा होगा।)
 # हर गैर-खाली खुला अंतराल <math>K</math> एक तर्कसंगत सम्मिलित  है। (यदि <math>x</math> एक धनात्मक अतिसूक्ष्म, खुला अंतराल है <math>(x,2x)</math> अपरिमित रूप से अनेक अपरिमित हैं किन्तु एक भी परिमेय नहीं है।)
-# परिमेय घने समुच्चय हैं <math>K</math> sup और inf दोनों के संबंध में। (अर्थात, का हर तत्व <math>K</math> परिमेय के कुछ समुच्चय का समर्थन है, और परिमेय के कुछ अन्य समुच्चय का inf है।) इस प्रकार एक आर्किमिडीयन क्षेत्र किसी भी क्रमित क्षेत्र के अर्थ में परिमेय का कोई सघन क्रमित विस्तार है, जो अपने परिमेय तत्वों को घनीभूत रूप से एम्बेड करता है।
+# परिमेय घने समुच्चय हैं <math>K</math> sup और inf दोनों के संबंध में। (अर्थात, का हर घटक  <math>K</math> परिमेय के कुछ समुच्चय का समर्थन है, और परिमेय के कुछ अन्य समुच्चय का inf है।) इस प्रकार एक आर्किमिडीयन क्षेत्र किसी भी क्रमित क्षेत्र के अर्थ में परिमेय का कोई सघन क्रमित विस्तार है, जो अपने परिमेय घटक ों को घनीभूत रूप से एम्बेड करता है।
 == यह भी देखें ==

Anonymous

Search

आर्किमिडीज़ संपत्ति: Difference between revisions

Namespaces

More

Page actions

Revision as of 12:37, 23 July 2023

Contents

आर्किमिडीज़ गुण के नाम का इतिहास और उत्पत्ति