रेडिएटर संख्या: Difference between revisions
No edit summary |
No edit summary |
||
| Line 15: | Line 15: | ||
समान संख्याएँ कृंतन प्रक्रिया के माध्यम से भी उत्पन्न की जा सकती हैं जिसमें ट्री को चरणों के अनुक्रम में सरल बनाया जाता है, जहाँ प्रत्येक चरण में सभी पत्ती के नोड्स और पत्तियों तक जाने वाले डिग्री-एक नोड्स के सभी रास्तों को हटा दिया जाता है: एक नोड का स्ट्राहलर नंबर वह चरण है जिस पर इसे इस प्रक्रिया द्वारा हटा दिया जाएगा, और एक ट्री का स्ट्राहलर नंबर उसके सभी नोड्स को हटाने के लिए आवश्यक चरणों की संख्या है। एक ट्री की स्ट्राहलर संख्या की एक और समकक्ष परिभाषा यह है कि यह सबसे बड़े पूर्ण द्विआधारी ट्री की ऊंचाई है जो दिए गए ट्री में होमोमोर्फिज्म का ग्राफ़ हो सकता है; एक ट्री में एक नोड की स्ट्राहलर संख्या इसी तरह सबसे बड़े पूर्ण द्विआधारी ट्री की ऊंचाई है जिसे उस नोड के नीचे अंत:स्थापित किया जा सकता है। | समान संख्याएँ कृंतन प्रक्रिया के माध्यम से भी उत्पन्न की जा सकती हैं जिसमें ट्री को चरणों के अनुक्रम में सरल बनाया जाता है, जहाँ प्रत्येक चरण में सभी पत्ती के नोड्स और पत्तियों तक जाने वाले डिग्री-एक नोड्स के सभी रास्तों को हटा दिया जाता है: एक नोड का स्ट्राहलर नंबर वह चरण है जिस पर इसे इस प्रक्रिया द्वारा हटा दिया जाएगा, और एक ट्री का स्ट्राहलर नंबर उसके सभी नोड्स को हटाने के लिए आवश्यक चरणों की संख्या है। एक ट्री की स्ट्राहलर संख्या की एक और समकक्ष परिभाषा यह है कि यह सबसे बड़े पूर्ण द्विआधारी ट्री की ऊंचाई है जो दिए गए ट्री में होमोमोर्फिज्म का ग्राफ़ हो सकता है; एक ट्री में एक नोड की स्ट्राहलर संख्या इसी तरह सबसे बड़े पूर्ण द्विआधारी ट्री की ऊंचाई है जिसे उस नोड के नीचे अंत:स्थापित किया जा सकता है। | ||
स्ट्राहलर नंबर i वाले किसी भी नोड में स्ट्राहलर नंबर i - 1 के साथ कम से कम दो वंशज होने चाहिए, स्ट्राहलर नंबर i - 2, आदि के साथ कम से कम चार वंशज होने चाहिए, और कम से कम 2<sup>i − 1</sup>पत्ती वंशज, इसलिए, n नोड्स वाले ट्री में, सबसे बड़ी संभव स्ट्राहलर संख्या लॉग <sub>2</sub>n+1है। {{sfnp|Devroye|Kruszewski|1996}} | स्ट्राहलर नंबर i वाले किसी भी नोड में स्ट्राहलर नंबर i - 1 के साथ कम से कम दो वंशज होने चाहिए, स्ट्राहलर नंबर i - 2, आदि के साथ कम से कम चार वंशज होने चाहिए, और कम से कम 2<sup>i − 1</sup>पत्ती वंशज, इसलिए, n नोड्स वाले ट्री में, सबसे बड़ी संभव स्ट्राहलर संख्या लॉग <sub>2</sub>n+1है। {{sfnp|Devroye|Kruszewski|1996}} चूंकि, जब तक ट्री एक पूर्ण [[ द्विआधारी वृक्ष | द्विआधारी ट्री]] नहीं बनाता, तब तक इसकी स्ट्राहलर संख्या इस सीमा से कम होगी। n-नोड द्विआधारी ट्री में[[यादृच्छिक बाइनरी पेड़|यादृच्छिक द्विआधारी ट्री]] चुना जाता है, रूट का अपेक्षित सूचकांक उच्च संभावना के साथ लॉग<sub>4</sub>n के बहुत करीब होता है।<ref>{{harvs|last1=Devroye|last2=Kruszewski|year=1995|year2=1996|txt}}.</ref> | ||
| Line 21: | Line 21: | ||
===नदी नेटवर्क=== | ===नदी नेटवर्क=== | ||
जल विज्ञान के लिए स्ट्राहलर [[धारा क्रम]] के अनुप्रयोग में, नदी नेटवर्क के भीतर एक धारा या नदी के प्रत्येक खंड को एक ट्री में एक नोड के रूप में माना जाता है, और अगले खंड को उसके मूल के रूप में नीचे की ओर माना जाता है। जब दो प्रथम क्रम की धाराएँ एक साथ आती हैं, तो वे दूसरे क्रम की धारा बनाती हैं। जब दो दूसरे क्रम की धाराएँ एक साथ आती हैं, तो वे तीसरे क्रम की धारा बनाती हैं। निचले क्रम की धाराएँ उच्च क्रम की धारा में | जल विज्ञान के लिए स्ट्राहलर [[धारा क्रम]] के अनुप्रयोग में, नदी नेटवर्क के भीतर एक धारा या नदी के प्रत्येक खंड को एक ट्री में एक नोड के रूप में माना जाता है, और अगले खंड को उसके मूल के रूप में नीचे की ओर माना जाता है। जब दो प्रथम क्रम की धाराएँ एक साथ आती हैं, तो वे दूसरे क्रम की धारा बनाती हैं। जब दो दूसरे क्रम की धाराएँ एक साथ आती हैं, तो वे तीसरे क्रम की धारा बनाती हैं। निचले क्रम की धाराएँ उच्च क्रम की धारा में सम्मलित होने से उच्च धारा का क्रम नहीं बदलती हैं। इस प्रकार, यदि प्रथम-क्रम की धारा दूसरे-क्रम की धारा से जुड़ती है, तो यह दूसरे-क्रम की धारा बनी रहती है। ऐसा तब तक नहीं है जब तक कि एक दूसरे क्रम की धारा दूसरे दूसरे क्रम की धारा के साथ संयोजित न हो जाए कि वह तीसरे क्रम की धारा बन जाए। गणितीय ट्री की तरह, सूचकांक ''i'' वाले एक खंड को कम से कम 2<sup>i − 1</sup> द्वारा खिलाया जाना चाहिए सूचकांक 1 की विभिन्न सहायक नदियाँ। श्रेव ने नोट किया कि हॉर्टन और स्ट्राहलर के नियमों की किसी भी टोपोलॉजिकली यादृच्छिक वितरण से अपेक्षा की जानी चाहिए। संबंध की एक बाद की समीक्षा ने इस तर्क की पुष्टि की, यह स्थापित करते हुए कि, नियमों द्वारा वर्णित गुणों से, स्ट्रीम नेटवर्क की संरचना या उत्पत्ति की व्याख्या करने के लिए कोई निष्कर्ष नहीं निकाला जा सकता है।<ref name="Hodgkinson, J.H. 2006"/><ref>Kirchner, J.W., 1993. Statistical inevitability of Horton Laws and the apparent randomness of stream channel networks. Geology 21, 591–594.</ref> | ||
एक जलधारा के रूप में अर्हता प्राप्त करने के लिए जलवैज्ञानिक विशेषता या तो आवर्ती या [[बारहमासी धारा]] होनी चाहिए। आवर्ती (या रुक-रुक कर) धाराओं में वर्ष के कम से कम भाग के लिए चैनल में पानी रहता है। किसी धारा या नदी का सूचकांक 1 (बिना सहायक नदी वाली धारा) से 12 (विश्व स्तर पर सबसे शक्तिशाली नदी, अमेज़ॅन नदी, इसके मुहाने पर) तक हो सकता है। [[ओहियो नदी]] क्रम आठ की है और [[मिसिसिपी नदी]] क्रम 10 की है। अनुमान है कि ग्रह पर 80% धाराएँ पहले से तीसरे क्रम की हेडवाटर धाराएँ हैं।<ref name="urlStreamOrder-about.com">{{cite web | एक जलधारा के रूप में अर्हता प्राप्त करने के लिए जलवैज्ञानिक विशेषता या तो आवर्ती या [[बारहमासी धारा]] होनी चाहिए। आवर्ती (या रुक-रुक कर) धाराओं में वर्ष के कम से कम भाग के लिए चैनल में पानी रहता है। किसी धारा या नदी का सूचकांक 1 (बिना सहायक नदी वाली धारा) से 12 (विश्व स्तर पर सबसे शक्तिशाली नदी, अमेज़ॅन नदी, इसके मुहाने पर) तक हो सकता है। [[ओहियो नदी]] क्रम आठ की है और [[मिसिसिपी नदी]] क्रम 10 की है। अनुमान है कि ग्रह पर 80% धाराएँ पहले से तीसरे क्रम की हेडवाटर धाराएँ हैं।<ref name="urlStreamOrder-about.com">{{cite web | ||
|url=http://geography.about.com/od/physicalgeography/a/streamorder.htm | |url=http://geography.about.com/od/physicalgeography/a/streamorder.htm | ||
| Line 30: | Line 30: | ||
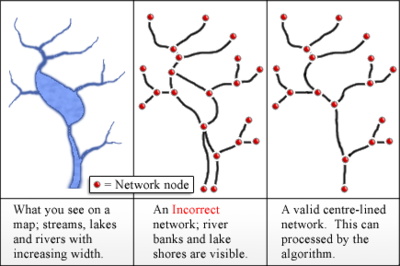
[[Image:NetworkType.png|thumb|400px|जल निकायों के ट्री नेटवर्क में गलत और सही रूपांतरण की तुलना]] | [[Image:NetworkType.png|thumb|400px|जल निकायों के ट्री नेटवर्क में गलत और सही रूपांतरण की तुलना]] | ||
{{harvtxt|ग्लीज़ेर|डेनिस्युक|रिमर|सालिंगार|2004}} वर्णन करें कि [[भौगोलिक सूचना प्रणाली]] अनुप्रयोग में स्ट्राहलर स्ट्रीम ऑर्डर मानों की गणना कैसे करें, यह कलन विधि [http://www.rivex.co.uk RivEX], एक ईएसआरआई [[Arcgis]] 10.7 टूल द्वारा कार्यान्वित किया गया है। उनके कलन विधि का इनपुट पानी के पिंडों की केंद्र रेखाओं का एक नेटवर्क है, जिसे नोड्स पर जुड़े आर्क (या किनारों) के रूप में दर्शाया जाता है। झील की सीमाओं और नदी के किनारों को चाप के रूप में उपयोग नहीं किया जाना चाहिए, क्योंकि ये | {{harvtxt|ग्लीज़ेर|डेनिस्युक|रिमर|सालिंगार|2004}} वर्णन करें कि [[भौगोलिक सूचना प्रणाली]] अनुप्रयोग में स्ट्राहलर स्ट्रीम ऑर्डर मानों की गणना कैसे करें, यह कलन विधि [http://www.rivex.co.uk RivEX], एक ईएसआरआई [[Arcgis]] 10.7 टूल द्वारा कार्यान्वित किया गया है। उनके कलन विधि का इनपुट पानी के पिंडों की केंद्र रेखाओं का एक नेटवर्क है, जिसे नोड्स पर जुड़े आर्क (या किनारों) के रूप में दर्शाया जाता है। झील की सीमाओं और नदी के किनारों को चाप के रूप में उपयोग नहीं किया जाना चाहिए, क्योंकि ये सामान्यत: गलत टोपोलॉजी के साथ एक गैर-ट्री नेटवर्क बनाएंगे। | ||
वैकल्पिक धारा क्रम श्रेव द्वारा विकसित किया गया है<ref>Shreve, R.L., 1966. Statistical law of stream numbers. Journal of Geology 74, 17–37.</ref><ref>Shreve, R.L., 1967. Infinite topologically random channel networks. Journal of Geology 75, 178–186.</ref> और हॉजकिंसन एट अल।<ref name="Hodgkinson, J.H. 2006">Hodgkinson, J.H., McLoughlin, S. & Cox, M.E. 2006. The influence of structural grain on drainage in a metamorphic sub-catchment: Laceys Creek, southeast Queensland, Australia. Geomorphology, 81: 394–407.</ref> स्ट्रीम/लिंक लंबाई के विश्लेषण के साथ स्ट्राहलर और श्रेवे सिस्टम की एक सांख्यिकीय तुलना, स्मार्ट द्वारा दी गई है।<ref>Smart, J.S. 1968, Statistical properties of stream lengths, Water Resources Research, 4, No 5. 1001–1014 </ref> | वैकल्पिक धारा क्रम श्रेव द्वारा विकसित किया गया है<ref>Shreve, R.L., 1966. Statistical law of stream numbers. Journal of Geology 74, 17–37.</ref><ref>Shreve, R.L., 1967. Infinite topologically random channel networks. Journal of Geology 75, 178–186.</ref> और हॉजकिंसन एट अल।<ref name="Hodgkinson, J.H. 2006">Hodgkinson, J.H., McLoughlin, S. & Cox, M.E. 2006. The influence of structural grain on drainage in a metamorphic sub-catchment: Laceys Creek, southeast Queensland, Australia. Geomorphology, 81: 394–407.</ref> स्ट्रीम/लिंक लंबाई के विश्लेषण के साथ स्ट्राहलर और श्रेवे सिस्टम की एक सांख्यिकीय तुलना, स्मार्ट द्वारा दी गई है।<ref>Smart, J.S. 1968, Statistical properties of stream lengths, Water Resources Research, 4, No 5. 1001–1014 </ref> | ||
| Line 38: | Line 38: | ||
स्ट्राहलर नंबरिंग को केवल नदियों के लिए ही नहीं, बल्कि किसी भी पदानुक्रमित प्रणाली के सांख्यिकीय विश्लेषण में लागू किया जा सकता है। | स्ट्राहलर नंबरिंग को केवल नदियों के लिए ही नहीं, बल्कि किसी भी पदानुक्रमित प्रणाली के सांख्यिकीय विश्लेषण में लागू किया जा सकता है। | ||
* {{harvtxt|एरेनास|दानोन|डियाज़-गुइलेरा|ग्लीसेर|2004}} सामाजिक नेटवर्क के विश्लेषण में हॉर्टन-स्ट्राहलर सूचकांक के अनुप्रयोग का वर्णन करता है। | * {{harvtxt|एरेनास|दानोन|डियाज़-गुइलेरा|ग्लीसेर|2004}} सामाजिक नेटवर्क के विश्लेषण में हॉर्टन-स्ट्राहलर सूचकांक के अनुप्रयोग का वर्णन करता है। | ||
*{{harvtxt|एहरनफ्यूच्ट|रोज़ेनबर्ग|वर्मीर|1981}} ने L-सिस्टम के विश्लेषण के लिए स्ट्राहलर नंबरिंग का एक प्रकार लागू किया (पत्तियों पर एक के | *{{harvtxt|एहरनफ्यूच्ट|रोज़ेनबर्ग|वर्मीर|1981}} ने L-सिस्टम के विश्लेषण के लिए स्ट्राहलर नंबरिंग का एक प्रकार लागू किया (पत्तियों पर एक के अतिरिक्त शून्य से प्रारंभ), जिसे उन्होंने ट्री-रैंक कहा है। | ||
*स्ट्रैलर नंबरिंग को ट्री की शाखा संरचनाओं जैसे जैविक पदानुक्रमों पर भी लागू किया गया है<ref>{{harvtxt|Borchert|Slade|1981}}</ref> और जानवरों की श्वसन और संचार प्रणाली है।<ref>{{harvtxt|Horsfield|1976}}.</ref> | *स्ट्रैलर नंबरिंग को ट्री की शाखा संरचनाओं जैसे जैविक पदानुक्रमों पर भी लागू किया गया है<ref>{{harvtxt|Borchert|Slade|1981}}</ref> और जानवरों की श्वसन और संचार प्रणाली है।<ref>{{harvtxt|Horsfield|1976}}.</ref> | ||
| Line 56: | Line 56: | ||
===पथ-चौड़ाई=== | ===पथ-चौड़ाई=== | ||
एक यादृच्छिक [[अप्रत्यक्ष ग्राफ]] G की पथ चौड़ाई को सबसे छोटी संख्या w के रूप में परिभाषित किया जा सकता है, जैसे कि एक [[अंतराल ग्राफ]] H | एक यादृच्छिक [[अप्रत्यक्ष ग्राफ]] G की पथ चौड़ाई को सबसे छोटी संख्या w के रूप में परिभाषित किया जा सकता है, जैसे कि एक [[अंतराल ग्राफ]] H सम्मलित है जिसमें G को एक उपग्राफ के रूप में सम्मलित किया गया है, H में सबसे बड़े क्लिक (ग्राफ सिद्धांत) में w + 1 कोने हैं। ट्री के लिए (उनके अभिविन्यास और जड़ को भूलकर अप्रत्यक्ष ग्राफ़ के रूप में देखा जाता है) पथ चौड़ाई स्ट्राहलर संख्या से भिन्न होती है, लेकिन इसके साथ निकटता से संबंधित होती है: पथ चौड़ाई w और स्ट्राहलर संख्या s वाले ट्री में, ये दो संख्याएं असमानताओं से संबंधित होती हैं<ref>{{harvtxt|Luttenberger|Schlund|2011}}, using a definition of the "dimension" of a tree that is one less than the Strahler number.</ref> | ||
:w ≤ s ≤ 2w + 2. | :w ≤ s ≤ 2w + 2. | ||
चक्रों के साथ ग्राफ़ को संभालने की क्षमता, न कि केवल ट्री के साथ, स्ट्राहलर संख्या की तुलना में पथ-चौड़ाई को अतिरिक्त बहुमुखी प्रतिभा प्रदान करती है। | चक्रों के साथ ग्राफ़ को संभालने की क्षमता, न कि केवल ट्री के साथ, स्ट्राहलर संख्या की तुलना में पथ-चौड़ाई को अतिरिक्त बहुमुखी प्रतिभा प्रदान करती है। | ||
चूंकि, स्ट्राहलर संख्या के विपरीत, पथ चौड़ाई केवल पूरे ग्राफ़ के लिए परिभाषित किया गया है, और ग्राफ़ में प्रत्येक नोड के लिए अलग से नहीं है। | |||
==यह भी देखें== | ==यह भी देखें== | ||
*नदी का मुख्य तना, | *नदी का मुख्य तना, सामान्यत: उच्चतम स्ट्राहलर संख्या वाली शाखा का अनुसरण करके पाया जाता है | ||
*[[Index.php?title=पीएफएफ्स्टेटर कोडिंग प्रणाली|पीएफएफ्स्टेटर कोडिंग प्रणाली]] | *[[Index.php?title=पीएफएफ्स्टेटर कोडिंग प्रणाली|पीएफएफ्स्टेटर कोडिंग प्रणाली]] | ||
Revision as of 14:28, 30 July 2023
गणित में, गणितीय ट्री (ग्राफ सिद्धांत) की स्ट्राहलर संख्या या हॉर्टन-स्ट्राहलर संख्या इसकी शाखा जटिलता का एक संख्यात्मक माप है।
इन नंबरों को सबसे पहले जल विज्ञान में नदियों और झरनों की जटिलता को मापने के एक तरीके के रूप में विकसित किया गया था रॉबर्ट ई हॉर्टन (1945) और आर्थर न्यूवेल स्ट्राहलर (1952, 1957). इस एप्लिकेशन में, उन्हें स्ट्राहलर स्ट्रीम ऑर्डर के रूप में संदर्भित किया जाता है और सहायक नदी के पदानुक्रम के आधार पर स्ट्रीम आकार को परिभाषित करने के लिए उपयोग किया जाता है। उच्च-स्तरीय प्रोग्रामिंग भाषाओं के संकलक के लिए रजिस्टर आवंटन और सामाजिक नेटवर्क के विश्लेषण में L प्रणाली और पदानुक्रमित जैविक संरचनाओं जैसे (जैविक) ट्रीों और पशु श्वसन और परिसंचरण प्रणालियों के विश्लेषण में भी वही संख्याएं उत्पन्न होती हैं।
परिभाषा
इस संदर्भ में सभी ट्री निर्देशित ग्राफ हैं, जो जड़ से पत्तियों की ओर उन्मुख हैं; दूसरे शब्दों में, वे आर्बोरेसेंस (ग्राफ सिद्धांत) हैं। एक ट्री में एक नोड की डिग्री (ग्राफ़ सिद्धांत) केवल उसके बच्चों की संख्या है। कोई किसी ट्री के सभी नोड्स को नीचे से ऊपर के क्रम में एक स्ट्राहलर नंबर इस प्रकार निर्दिष्ट कर सकता है:
- यदि नोड एक पत्ता है (इसकी कोई संतान नहीं है), तो इसका स्ट्राहलर नंबर एक है।
- यदि नोड में स्ट्राहलर संख्या i वाला एक बच्चा है, और अन्य सभी बच्चों की स्ट्राहलर संख्या i से कम है, तो नोड का स्ट्राहलर संख्या फिर से i है।
- यदि नोड में स्ट्राहलर संख्या i वाले दो या दो से अधिक बच्चे हैं, और अधिक संख्या वाले कोई संतान नहीं है, तो नोड की स्ट्राहलर संख्या i + 1 है।
किसी ट्री की स्ट्राहलर संख्या उसके मूल नोड की संख्या होती है।
कलन विधि रूप से, इन नंबरों को गहराई से पहली खोज करके और मेल आदेश में प्रत्येक नोड की संख्या निर्दिष्ट करके निर्दिष्ट किया जा सकता है। समान संख्याएँ कृंतन प्रक्रिया के माध्यम से भी उत्पन्न की जा सकती हैं जिसमें ट्री को चरणों के अनुक्रम में सरल बनाया जाता है, जहाँ प्रत्येक चरण में सभी पत्ती के नोड्स और पत्तियों तक जाने वाले डिग्री-एक नोड्स के सभी रास्तों को हटा दिया जाता है: एक नोड का स्ट्राहलर नंबर वह चरण है जिस पर इसे इस प्रक्रिया द्वारा हटा दिया जाएगा, और एक ट्री का स्ट्राहलर नंबर उसके सभी नोड्स को हटाने के लिए आवश्यक चरणों की संख्या है। एक ट्री की स्ट्राहलर संख्या की एक और समकक्ष परिभाषा यह है कि यह सबसे बड़े पूर्ण द्विआधारी ट्री की ऊंचाई है जो दिए गए ट्री में होमोमोर्फिज्म का ग्राफ़ हो सकता है; एक ट्री में एक नोड की स्ट्राहलर संख्या इसी तरह सबसे बड़े पूर्ण द्विआधारी ट्री की ऊंचाई है जिसे उस नोड के नीचे अंत:स्थापित किया जा सकता है।
स्ट्राहलर नंबर i वाले किसी भी नोड में स्ट्राहलर नंबर i - 1 के साथ कम से कम दो वंशज होने चाहिए, स्ट्राहलर नंबर i - 2, आदि के साथ कम से कम चार वंशज होने चाहिए, और कम से कम 2i − 1पत्ती वंशज, इसलिए, n नोड्स वाले ट्री में, सबसे बड़ी संभव स्ट्राहलर संख्या लॉग 2n+1है। [1] चूंकि, जब तक ट्री एक पूर्ण द्विआधारी ट्री नहीं बनाता, तब तक इसकी स्ट्राहलर संख्या इस सीमा से कम होगी। n-नोड द्विआधारी ट्री मेंयादृच्छिक द्विआधारी ट्री चुना जाता है, रूट का अपेक्षित सूचकांक उच्च संभावना के साथ लॉग4n के बहुत करीब होता है।[2]
अनुप्रयोग
नदी नेटवर्क
जल विज्ञान के लिए स्ट्राहलर धारा क्रम के अनुप्रयोग में, नदी नेटवर्क के भीतर एक धारा या नदी के प्रत्येक खंड को एक ट्री में एक नोड के रूप में माना जाता है, और अगले खंड को उसके मूल के रूप में नीचे की ओर माना जाता है। जब दो प्रथम क्रम की धाराएँ एक साथ आती हैं, तो वे दूसरे क्रम की धारा बनाती हैं। जब दो दूसरे क्रम की धाराएँ एक साथ आती हैं, तो वे तीसरे क्रम की धारा बनाती हैं। निचले क्रम की धाराएँ उच्च क्रम की धारा में सम्मलित होने से उच्च धारा का क्रम नहीं बदलती हैं। इस प्रकार, यदि प्रथम-क्रम की धारा दूसरे-क्रम की धारा से जुड़ती है, तो यह दूसरे-क्रम की धारा बनी रहती है। ऐसा तब तक नहीं है जब तक कि एक दूसरे क्रम की धारा दूसरे दूसरे क्रम की धारा के साथ संयोजित न हो जाए कि वह तीसरे क्रम की धारा बन जाए। गणितीय ट्री की तरह, सूचकांक i वाले एक खंड को कम से कम 2i − 1 द्वारा खिलाया जाना चाहिए सूचकांक 1 की विभिन्न सहायक नदियाँ। श्रेव ने नोट किया कि हॉर्टन और स्ट्राहलर के नियमों की किसी भी टोपोलॉजिकली यादृच्छिक वितरण से अपेक्षा की जानी चाहिए। संबंध की एक बाद की समीक्षा ने इस तर्क की पुष्टि की, यह स्थापित करते हुए कि, नियमों द्वारा वर्णित गुणों से, स्ट्रीम नेटवर्क की संरचना या उत्पत्ति की व्याख्या करने के लिए कोई निष्कर्ष नहीं निकाला जा सकता है।[3][4] एक जलधारा के रूप में अर्हता प्राप्त करने के लिए जलवैज्ञानिक विशेषता या तो आवर्ती या बारहमासी धारा होनी चाहिए। आवर्ती (या रुक-रुक कर) धाराओं में वर्ष के कम से कम भाग के लिए चैनल में पानी रहता है। किसी धारा या नदी का सूचकांक 1 (बिना सहायक नदी वाली धारा) से 12 (विश्व स्तर पर सबसे शक्तिशाली नदी, अमेज़ॅन नदी, इसके मुहाने पर) तक हो सकता है। ओहियो नदी क्रम आठ की है और मिसिसिपी नदी क्रम 10 की है। अनुमान है कि ग्रह पर 80% धाराएँ पहले से तीसरे क्रम की हेडवाटर धाराएँ हैं।[5] यदि नदी नेटवर्क का द्विभाजन अनुपात अधिक है, तो बाढ़ की संभावना अधिक है। एकाग्रता का समय भी कम होगा।[6] अलग-अलग अनुपातों को देखकर, द्विभाजन अनुपात यह भी दिखा सकता है कि जल निकासी बेसिन के किन हिस्सों में बाढ़ आने की संभावना अधिक है। अधिकांश ब्रिटिश नदियों का द्विभाजन अनुपात 3 और 5 के बीच है।[7]
ग्लीज़ेर et al. (2004) वर्णन करें कि भौगोलिक सूचना प्रणाली अनुप्रयोग में स्ट्राहलर स्ट्रीम ऑर्डर मानों की गणना कैसे करें, यह कलन विधि RivEX, एक ईएसआरआई Arcgis 10.7 टूल द्वारा कार्यान्वित किया गया है। उनके कलन विधि का इनपुट पानी के पिंडों की केंद्र रेखाओं का एक नेटवर्क है, जिसे नोड्स पर जुड़े आर्क (या किनारों) के रूप में दर्शाया जाता है। झील की सीमाओं और नदी के किनारों को चाप के रूप में उपयोग नहीं किया जाना चाहिए, क्योंकि ये सामान्यत: गलत टोपोलॉजी के साथ एक गैर-ट्री नेटवर्क बनाएंगे।
वैकल्पिक धारा क्रम श्रेव द्वारा विकसित किया गया है[8][9] और हॉजकिंसन एट अल।[3] स्ट्रीम/लिंक लंबाई के विश्लेषण के साथ स्ट्राहलर और श्रेवे सिस्टम की एक सांख्यिकीय तुलना, स्मार्ट द्वारा दी गई है।[10]
अन्य पदानुक्रमित प्रणालियाँ
स्ट्राहलर नंबरिंग को केवल नदियों के लिए ही नहीं, बल्कि किसी भी पदानुक्रमित प्रणाली के सांख्यिकीय विश्लेषण में लागू किया जा सकता है।
- एरेनास et al. (2004) सामाजिक नेटवर्क के विश्लेषण में हॉर्टन-स्ट्राहलर सूचकांक के अनुप्रयोग का वर्णन करता है।
- एहरनफ्यूच्ट, रोज़ेनबर्ग & वर्मीर (1981) ने L-सिस्टम के विश्लेषण के लिए स्ट्राहलर नंबरिंग का एक प्रकार लागू किया (पत्तियों पर एक के अतिरिक्त शून्य से प्रारंभ), जिसे उन्होंने ट्री-रैंक कहा है।
- स्ट्रैलर नंबरिंग को ट्री की शाखा संरचनाओं जैसे जैविक पदानुक्रमों पर भी लागू किया गया है[11] और जानवरों की श्वसन और संचार प्रणाली है।[12]
आवंटन पंजीकृत करें
उच्च-स्तरीय प्रोग्रामिंग भाषा को असेंबली भाषा में अनुवाद करते समय एक अभिव्यक्ति ट्री का मूल्यांकन करने के लिए आवश्यक रजिस्टर आवंटन की न्यूनतम संख्या वास्तव में इसकी स्ट्राहलर संख्या होती है। इस संदर्भ में, स्ट्राहलर संख्या को रजिस्टर संख्या भी कहा जा सकता है।[13] उन अभिव्यक्ति ट्री के लिए जिन्हें उपलब्ध से अधिक रजिस्टरों की आवश्यकता होती है, सेठी-उल्मन कलन विधि का उपयोग एक अभिव्यक्ति ट्री को मशीन निर्देशों के अनुक्रम में अनुवाद करने के लिए किया जा सकता है जो रजिस्टरों का यथासंभव कुशलता से उपयोग करता है, रजिस्टरों से मुख्य मेमोरी में मध्यवर्ती मूल्यों को फैलाने की संख्या को कम करता है और परिणामी संकलित कोड में निर्देशों की कुल संख्या को कम करता है।
संबंधित मापदंड
द्विभाजन अनुपात
किसी ट्री की स्ट्राहलर संख्याओं के साथ द्विभाजन अनुपात जुड़े होते हैं, संख्याएँ बताती हैं कि एक ट्री संतुलित होने के कितने करीब है। पदानुक्रम में प्रत्येक क्रम के लिए, ith द्विभाजन अनुपात है
जहां niक्रम i के साथ नोड्स की संख्या को दर्शाता है।
समग्र पदानुक्रम का द्विभाजन अनुपात विभिन्न क्रमों पर द्विभाजन अनुपातों के औसत से लिया जा सकता है। एक पूर्ण द्विआधारी ट्री में, द्विभाजन अनुपात 2 होगा, जबकि अन्य ट्री में बड़ा द्विभाजन अनुपात होगा। यह एक आयामहीन संख्या है।
पथ-चौड़ाई
एक यादृच्छिक अप्रत्यक्ष ग्राफ G की पथ चौड़ाई को सबसे छोटी संख्या w के रूप में परिभाषित किया जा सकता है, जैसे कि एक अंतराल ग्राफ H सम्मलित है जिसमें G को एक उपग्राफ के रूप में सम्मलित किया गया है, H में सबसे बड़े क्लिक (ग्राफ सिद्धांत) में w + 1 कोने हैं। ट्री के लिए (उनके अभिविन्यास और जड़ को भूलकर अप्रत्यक्ष ग्राफ़ के रूप में देखा जाता है) पथ चौड़ाई स्ट्राहलर संख्या से भिन्न होती है, लेकिन इसके साथ निकटता से संबंधित होती है: पथ चौड़ाई w और स्ट्राहलर संख्या s वाले ट्री में, ये दो संख्याएं असमानताओं से संबंधित होती हैं[14]
- w ≤ s ≤ 2w + 2.
चक्रों के साथ ग्राफ़ को संभालने की क्षमता, न कि केवल ट्री के साथ, स्ट्राहलर संख्या की तुलना में पथ-चौड़ाई को अतिरिक्त बहुमुखी प्रतिभा प्रदान करती है। चूंकि, स्ट्राहलर संख्या के विपरीत, पथ चौड़ाई केवल पूरे ग्राफ़ के लिए परिभाषित किया गया है, और ग्राफ़ में प्रत्येक नोड के लिए अलग से नहीं है।
यह भी देखें
- नदी का मुख्य तना, सामान्यत: उच्चतम स्ट्राहलर संख्या वाली शाखा का अनुसरण करके पाया जाता है
- पीएफएफ्स्टेटर कोडिंग प्रणाली
टिप्पणियाँ
- ↑ Devroye & Kruszewski (1996).
- ↑ Devroye and Kruszewski (1995, 1996).
- ↑ 3.0 3.1 Hodgkinson, J.H., McLoughlin, S. & Cox, M.E. 2006. The influence of structural grain on drainage in a metamorphic sub-catchment: Laceys Creek, southeast Queensland, Australia. Geomorphology, 81: 394–407.
- ↑ Kirchner, J.W., 1993. Statistical inevitability of Horton Laws and the apparent randomness of stream channel networks. Geology 21, 591–594.
- ↑ "Stream Order – The Classification of Streams and Rivers". Retrieved 2011-12-11.
- ↑ Bogale, Alemsha (2021). "गिलगेल अबे वाटरशेड, लेक टाना बेसिन, ऊपरी ब्लू नील बेसिन, इथियोपिया में भौगोलिक सूचना प्रणाली का उपयोग करके जल निकासी बेसिन का मॉर्फोमेट्रिक विश्लेषण". Applied Water Science. 11 (7): 122. Bibcode:2021ApWS...11..122B. doi:10.1007/s13201-021-01447-9. S2CID 235630850.
- ↑ Waugh (2002).
- ↑ Shreve, R.L., 1966. Statistical law of stream numbers. Journal of Geology 74, 17–37.
- ↑ Shreve, R.L., 1967. Infinite topologically random channel networks. Journal of Geology 75, 178–186.
- ↑ Smart, J.S. 1968, Statistical properties of stream lengths, Water Resources Research, 4, No 5. 1001–1014
- ↑ Borchert & Slade (1981)
- ↑ Horsfield (1976).
- ↑ Ershov (1958); Flajolet, Raoult & Vuillemin (1979).
- ↑ Luttenberger & Schlund (2011), using a definition of the "dimension" of a tree that is one less than the Strahler number.
संदर्भ
- Arenas, A.; Danon, L.; Díaz-Guilera, A.; Gleiser, P. M.; Guimerá, R. (2004), "Community analysis in social networks", European Physical Journal B, 38 (2): 373–380, arXiv:cond-mat/0312040, Bibcode:2004EPJB...38..373A, doi:10.1140/epjb/e2004-00130-1, S2CID 9764926.
- Borchert, Rolf; Slade, Norman A. (1981), "Bifurcation ratios and the adaptive geometry of trees", Botanical Gazette, 142 (3): 394–401, doi:10.1086/337238, hdl:1808/9253, JSTOR 2474363, S2CID 84145477.
- Devroye, Luc; Kruszewski, Paul (1995), "A note on the Horton–Strahler number for random trees", Information Processing Letters, 56 (2): 95–99, doi:10.1016/0020-0190(95)00114-R.
- Devroye, L.; Kruszewski, P. (1996), "On the Horton–Strahler number for random tries", RAIRO Informatique Théorique et Applications, 30 (5): 443–456, doi:10.1051/ita/1996300504431, MR 1435732
- Ehrenfeucht, A.; Rozenberg, G.; Vermeir, D. (1981), "On ETOL systems with finite tree-rank", SIAM Journal on Computing, 10 (1): 40–58, doi:10.1137/0210004, MR 0605602.
- Ershov, A. P. (1958), "On programming of arithmetic operations", Communications of the ACM, 1 (8): 3–6, doi:10.1145/368892.368907, S2CID 15986378.
- Flajolet, P.; Raoult, J. C.; Vuillemin, J. (1979), "The number of registers required for evaluating arithmetic expressions", Theoretical Computer Science, 9 (1): 99–125, doi:10.1016/0304-3975(79)90009-4.
- Gleyzer, A.; Denisyuk, M.; Rimmer, A.; Salingar, Y. (2004), "A fast recursive GIS algorithm for computing Strahler stream order in braided and nonbraided networks", Journal of the American Water Resources Association, 40 (4): 937–946, Bibcode:2004JAWRA..40..937G, doi:10.1111/j.1752-1688.2004.tb01057.x, S2CID 128399321.
- Horsfield, Keith (1976), "Some mathematical properties of branching trees with application to the respiratory system", Bulletin of Mathematical Biology, 38 (3): 305–315, doi:10.1007/BF02459562, PMID 1268383, S2CID 189888885.
- Horton, R. E. (1945), "Erosional development of streams and their drainage basins: hydro-physical approach to quantitative morphology", Geological Society of America Bulletin, 56 (3): 275–370, doi:10.1130/0016-7606(1945)56[275:EDOSAT]2.0.CO;2, S2CID 129509551.
- Lanfear, K. J. (1990), "A fast algorithm for automatically computing Strahler stream order", Journal of the American Water Resources Association, 26 (6): 977–981, Bibcode:1990JAWRA..26..977L, doi:10.1111/j.1752-1688.1990.tb01432.x.
- Luttenberger, Michael; Schlund, Maxmilian (2011), An extension of Parikh's theorem beyond idempotence, arXiv:1112.2864, Bibcode:2011arXiv1112.2864L
- Strahler, A. N. (1952), "Hypsometric (area-altitude) analysis of erosional topology", Geological Society of America Bulletin, 63 (11): 1117–1142, doi:10.1130/0016-7606(1952)63[1117:HAAOET]2.0.CO;2.
- Strahler, A. N. (1957), "Quantitative analysis of watershed geomorphology", Transactions of the American Geophysical Union, 38 (6): 913–920, Bibcode:1957TrAGU..38..913S, doi:10.1029/tr038i006p00913.
- Waugh, David (2002), Geography, An Integrated Approach (3rd ed.), Nelson Thornes.