डिवाइड-और-कॉन्कर आइजेनवैल्यू एल्गोरिदम: Difference between revisions
No edit summary |
|||
| Line 4: | Line 4: | ||
==पृष्ठभूमि== | ==पृष्ठभूमि== | ||
हर्मिटियन मैट्रिक्स के लिए अधिकांश | हर्मिटियन मैट्रिक्स के लिए अधिकांश अभिलक्षणिक मान एल्गोरिदम की तरह, डिवाइड-और-कॉन्कर [[त्रिविकर्णीय मैट्रिक्स|त्रिविकर्णी]] रूप में कमी के साथ प्रारम्भ होते है। <math>m \times m</math> मैट्रिक्स के लिए, इसके लिए मानक विधि, [[ गृहस्थ प्रतिबिंब |हाउसहोल्डर परावर्तन]] के माध्यम से, <math>\frac{4}{3}m^{3}</math> प्लवी बिंदु संचालन लेती है, या <math>\frac{8}{3}m^{3}</math> यदि [[eigenvector|अभिलक्षणिक सदिशों]] की भी आवश्यकता होती है। अन्य एल्गोरिदम हैं, जैसे कि अर्नोल्डी पुनरावृत्ति, जो मैट्रिक्स के कुछ वर्गों के लिए बेहतर प्रदर्शन कर सकते हैं हम यहां इस पर आगे विचार नहीं करेंगे। कुछ स्थितियों में, अभिलक्षणिक मान प्रश्न को छोटे प्रश्नों में विभाजित करना संभव है। ब्लॉक विकर्ण मैट्रिक्स पर विचार करें | ||
कुछ | |||
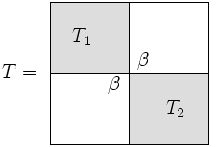
:<math>T = \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix}.</math> | :<math>T = \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix}.</math> | ||
<math>T</math> के अभिलक्षणिक मानों और अभिलक्षणिक सदिशों केवल <math>T_{1}</math> और <math>T_{2}</math> के समान हैं, और इन दो छोटे प्रश्नों को हल करना मूल प्रश्न को एक साथ हल करने की तुलना में लगभग सदैव तीव्र होगा। इस तकनीक का उपयोग कई अभिलक्षणिक मान एल्गोरिदम की दक्षता में सुधार करने के लिए किया जा सकता है, लेकिन इसके डिवाइड-और-कॉन्कर के लिए विशेष महत्व है। | |||
इस | इस लेख के शेष भाग के लिए, हम मान लेंगे कि डिवाइड-और-कॉन्कर एल्गोरिथ्म का इनपुट <math>m \times m</math> वास्तविक सममित त्रिविकर्णी मैट्रिक्स <math>T</math> है। हालाँकि हर्मिटियन मैट्रिक्स के लिए एल्गोरिदम को संशोधित किया जा सकता है, हम यहां विवरण नहीं देते हैं। | ||
== | ==डिवाइड== | ||
डिवाइड-और-कॉन्कर एल्गोरिथ्म का ''डिवाइड'' भाग इस प्रतिफलन से आता है कि त्रिविकर्णी मैट्रिक्स "लगभग" ब्लॉक विकर्ण है। | |||
:[[Image:Almost block diagonal.png]]सबमैट्रिक्स | :[[Image:Almost block diagonal.png]] | ||
:सबमैट्रिक्स <math>T_{1}</math> का आकार हम <math>n \times n</math> कहेंगे, और फिर <math>T_{2}</math> <math>(m - n) \times (m - n)</math> है। ध्यान दें कि <math>T</math> के लगभग ब्लॉक विकर्ण होने की टिप्पणी सत्य है, चाहे <math>n</math> को कैसे भी चुना जाए (अर्थात, मैट्रिक्स को विघटित करने के कई तरीके हैं)। हालाँकि, दक्षता के दृष्टिकोण से, <math>n \approx m/2</math> चुनना उचित है। | |||
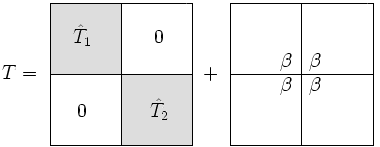
:हम <math>T</math> को एक ब्लॉक विकर्ण मैट्रिक्स के साथ-साथ [[रैंक (रैखिक बीजगणित)|रैंक]]-1 सुधार के रूप में लिखते हैं- | |||
:[[Image:Block diagonal plus correction.png]] | |||
:[[Image:Block diagonal plus correction.png]] | :<math>T_{1}</math> और <math>\hat{T}_{1}</math> के बीच एकमात्र अंतर यह है कि <math>\hat{T}_{1}</math> में निचली दाईं ओर की प्रविष्टि <math>t_{nn}</math> को <math>t_{nn} - \beta</math> से बदल दिया गया है और इसी तरह, <math>\hat{T}_{2}</math> में ऊपरी बाईं ओर की प्रविष्टि <math>t_{n+1,n+1}</math> को <math>t_{n+1,n+1} - \beta</math> से बदल दिया गया है। | ||
:विभाजन चरण का शेष भाग <math>\hat{T}_{1}</math>और <math>\hat{T}_{2}</math> के अभिलक्षणिक मानों (और यदि वांछित हो तो अभिलक्षणिक सदिशों) को हल करना है, अर्थात [[विकर्णीय मैट्रिक्स|विकर्णन]] <math>\hat{T}_{1} = Q_{1} D_{1} Q_{1}^{T}</math> और <math>\hat{T}_{2} = Q_{2} D_{2} Q_{2}^{T}</math> खोजना है। इसे डिवाइड-और-कॉन्कर एल्गोरिदम में पुनरावर्ती कॉल के साथ पूरा किया जा सकता है, हालांकि व्यावहारिक कार्यान्वयन प्रायः छोटे पर्याप्त सबमैट्रिसेस के लिए क्यूआर एल्गोरिदम पर स्विच करते हैं। | |||
==कॉन्कर== | |||
एल्गोरिथम का कॉन्कर भाग अबोधगम्य भाग है। ऊपर परिकलित उपमैट्रिक्स के विकर्णीकरण को देखते हुए, हम मूल मैट्रिक्स का विकर्णीकरण कैसे ज्ञात कर सकते हैं? | |||
सबसे पहले, <math>z^{T} = (q_{1}^{T},q_{2}^{T})</math> को परिभाषित करें, जहां <math>q_{1}^{T}</math> <math>Q_{1}</math> की अंतिम पंक्ति है और <math>q_{2}^{T}</math> <math>Q_{2}</math> की पहली पंक्ति है। यह दर्शाना अब प्राथमिक है | |||
:<math>T = \begin{bmatrix} Q_{1} & \\ & Q_{2} \end{bmatrix} \left( \begin{bmatrix} D_{1} & \\ & D_{2} \end{bmatrix} + \beta z z^{T} \right) \begin{bmatrix} Q_{1}^{T} & \\ & Q_{2}^{T} \end{bmatrix}</math> | |||
शेष कार्य को विकर्ण मैट्रिक्स के अभिलक्षणिक मानों के साथ-साथ रैंक-एक सुधार को खोजने के लिए कम कर दिया गया है। यह कैसे करना है यह दिखाने से पहले, आइए अंकन को सरल बनाएं। हम मैट्रिक्स <math>D + w w^{T}</math> के अभिलक्षणिक मानों की खोज कर रहे हैं, जहां <math>D</math> अलग-अलग प्रविष्टियों के साथ विकर्ण है और <math>w</math> गैर-शून्य प्रविष्टियों वाला कोई वेक्टर है। | |||
शून्य प्रविष्टि की स्थिति सरल है, क्योंकि यदि w<sub>i</sub> शून्य है, (<math>e_i</math>,d<sub>i</sub>) <math>D + w w^{T}</math> का अभिलक्षणिक युग्म (<math>e_i</math> मानक आधार पर है) है क्योंकि | |||
<math>(D + w w^{T})e_i = De_i = d_i e_i</math>। | |||
<math>(D + w w^{T})e_i = De_i = d_i e_i</math> | |||
यदि <math>\lambda</math> एक अभिलक्षणिक मान है, तो हमारे पास है- | |||
:<math>(D + w w^{T})q = \lambda q</math> | :<math>(D + w w^{T})q = \lambda q</math> | ||
जहां <math>q</math> संगत अभिलक्षणिक सदिश है। अब | |||
:<math>(D - \lambda I)q + w(w^{T}q) = 0</math> | :<math>(D - \lambda I)q + w(w^{T}q) = 0</math> | ||
:<math>q + (D - \lambda I)^{-1} w(w^{T}q) = 0</math> | :<math>q + (D - \lambda I)^{-1} w(w^{T}q) = 0</math> | ||
:<math>w^{T}q + w^{T}(D - \lambda I)^{-1} w(w^{T}q) = 0</math> | :<math>w^{T}q + w^{T}(D - \lambda I)^{-1} w(w^{T}q) = 0</math> | ||
ध्यान रखें कि <math>w^{T}q</math> एक शून्येतर अदिश राशि | ध्यान रखें कि <math>w^{T}q</math> एक शून्येतर अदिश राशि है। न तो <math>w</math> और न ही <math>q</math> शून्य हैं। यदि <math>w^{T}q</math> शून्य होता, तो <math>q</math> <math>(D + w w^{T})q = \lambda q</math> द्वारा <math>D</math> का अभिलक्षणिक सदिश होता है। यदि ऐसा होता, तो <math>q</math> में केवल एक गैर-शून्य स्थिति होती क्योंकि <math>D</math> अलग विकर्ण है और इस प्रकार आंतरिक उत्पाद <math>w^{T}q</math> अंततः शून्य नहीं हो सकता। इसलिए, हमारे पास है- | ||
:<math>1 + w^{T}(D - \lambda I)^{-1} w = 0</math> | :<math>1 + w^{T}(D - \lambda I)^{-1} w = 0</math> | ||
या अदिश समीकरण के रूप में लिखा गया है, | या अदिश समीकरण के रूप में लिखा गया है, | ||
:<math>1 + \sum_{j=1}^{m} \frac{w_{j}^{2}}{d_{j} - \lambda} = 0.</math> | :<math>1 + \sum_{j=1}^{m} \frac{w_{j}^{2}}{d_{j} - \lambda} = 0.</math> | ||
इस समीकरण को | इस समीकरण को ''दीर्घकालिक समीकरण'' के नाम से जाना जाता है। इसलिए प्रश्न को इस समीकरण के बाईं ओर द्वारा परिभाषित तर्कसंगत फलन के रूट्स को खोजने तक सीमित कर दिया गया है। | ||
सभी सामान्य | सभी सामान्य अभिलक्षणिक मान एल्गोरिदम पुनरावृत्त होने चाहिए, और डिवाइड-और-कॉन्कर एल्गोरिदम अलग नहीं है। [[अरेखीय]] दीर्घकालिक समीकरण को हल करने के लिए पुनरावृत्तीय तकनीक की आवश्यकता होती है, जैसे न्यूटन-रेफसन विधि। हालाँकि, प्रत्येक रूट को [[ बिग ओ अंकन |O]](1) पुनरावृत्तियों में पाया जा सकता है, जिनमें से प्रत्येक को <math>\Theta(m)</math> फ़्लॉप्स (<math>m</math>-डिग्री तर्कसंगत फलन के लिए) की आवश्यकता होती है, जिससे इस एल्गोरिदम के पुनरावृत्त भाग की लागत <math>\Theta(m^{2})</math> हो जाती है। | ||
==विश्लेषण== | ==विश्लेषण== | ||
Revision as of 22:19, 8 August 2023
डिवाइड-और-कॉन्कर अभिलक्षणिक मान एल्गोरिदम हर्मिटियन या वास्तविक सममित मैट्रिक्स के लिए अभिलक्षणिक मान एल्गोरिदम का एक वर्ग है जो हाल ही में (लगभग 1990 के दशक में) क्यूआर (QR) एल्गोरिदम जैसे अधिक पारंपरिक एल्गोरिदम के साथ स्थिरता और दक्षता की स्थिति में प्रतिस्पर्धी बन गया है। इन एल्गोरिदम के पीछे मूल अवधारणा कंप्यूटर विज्ञान से डिवाइड और कॉन्कर दृष्टिकोण है। अभिलक्षणिक मान प्रश्न को लगभग आधे आकार के दो प्रश्नों में विभाजित किया जाता है, इनमें से प्रत्येक को पुनरावर्ती रूप से हल किया जाता है, और मूल प्रश्न के अभिलक्षणिक मानों की गणना इन छोटे प्रश्नों के परिणामों से की जाती है।
यहां हम डिवाइड और कॉन्कर एल्गोरिदम का सबसे सरल संस्करण प्रस्तुत करते हैं, जो मूल रूप से 1981 में क्यूपेन द्वारा प्रस्तावित एल्गोरिदम के समान है। इस लेख के क्षेत्र से बाहर उपस्थित कई विवरण छोड़ दिए जाएंगे हालाँकि, इन विवरणों पर विचार किए बिना, एल्गोरिथ्म पूरी तरह से स्थिर नहीं है।
पृष्ठभूमि
हर्मिटियन मैट्रिक्स के लिए अधिकांश अभिलक्षणिक मान एल्गोरिदम की तरह, डिवाइड-और-कॉन्कर त्रिविकर्णी रूप में कमी के साथ प्रारम्भ होते है। मैट्रिक्स के लिए, इसके लिए मानक विधि, हाउसहोल्डर परावर्तन के माध्यम से, प्लवी बिंदु संचालन लेती है, या यदि अभिलक्षणिक सदिशों की भी आवश्यकता होती है। अन्य एल्गोरिदम हैं, जैसे कि अर्नोल्डी पुनरावृत्ति, जो मैट्रिक्स के कुछ वर्गों के लिए बेहतर प्रदर्शन कर सकते हैं हम यहां इस पर आगे विचार नहीं करेंगे। कुछ स्थितियों में, अभिलक्षणिक मान प्रश्न को छोटे प्रश्नों में विभाजित करना संभव है। ब्लॉक विकर्ण मैट्रिक्स पर विचार करें
के अभिलक्षणिक मानों और अभिलक्षणिक सदिशों केवल और के समान हैं, और इन दो छोटे प्रश्नों को हल करना मूल प्रश्न को एक साथ हल करने की तुलना में लगभग सदैव तीव्र होगा। इस तकनीक का उपयोग कई अभिलक्षणिक मान एल्गोरिदम की दक्षता में सुधार करने के लिए किया जा सकता है, लेकिन इसके डिवाइड-और-कॉन्कर के लिए विशेष महत्व है।
इस लेख के शेष भाग के लिए, हम मान लेंगे कि डिवाइड-और-कॉन्कर एल्गोरिथ्म का इनपुट वास्तविक सममित त्रिविकर्णी मैट्रिक्स है। हालाँकि हर्मिटियन मैट्रिक्स के लिए एल्गोरिदम को संशोधित किया जा सकता है, हम यहां विवरण नहीं देते हैं।
डिवाइड
डिवाइड-और-कॉन्कर एल्गोरिथ्म का डिवाइड भाग इस प्रतिफलन से आता है कि त्रिविकर्णी मैट्रिक्स "लगभग" ब्लॉक विकर्ण है।
- सबमैट्रिक्स का आकार हम कहेंगे, और फिर है। ध्यान दें कि के लगभग ब्लॉक विकर्ण होने की टिप्पणी सत्य है, चाहे को कैसे भी चुना जाए (अर्थात, मैट्रिक्स को विघटित करने के कई तरीके हैं)। हालाँकि, दक्षता के दृष्टिकोण से, चुनना उचित है।
- हम को एक ब्लॉक विकर्ण मैट्रिक्स के साथ-साथ रैंक-1 सुधार के रूप में लिखते हैं-
- और के बीच एकमात्र अंतर यह है कि में निचली दाईं ओर की प्रविष्टि को से बदल दिया गया है और इसी तरह, में ऊपरी बाईं ओर की प्रविष्टि को से बदल दिया गया है।
- विभाजन चरण का शेष भाग और के अभिलक्षणिक मानों (और यदि वांछित हो तो अभिलक्षणिक सदिशों) को हल करना है, अर्थात विकर्णन और खोजना है। इसे डिवाइड-और-कॉन्कर एल्गोरिदम में पुनरावर्ती कॉल के साथ पूरा किया जा सकता है, हालांकि व्यावहारिक कार्यान्वयन प्रायः छोटे पर्याप्त सबमैट्रिसेस के लिए क्यूआर एल्गोरिदम पर स्विच करते हैं।
कॉन्कर
एल्गोरिथम का कॉन्कर भाग अबोधगम्य भाग है। ऊपर परिकलित उपमैट्रिक्स के विकर्णीकरण को देखते हुए, हम मूल मैट्रिक्स का विकर्णीकरण कैसे ज्ञात कर सकते हैं?
सबसे पहले, को परिभाषित करें, जहां की अंतिम पंक्ति है और की पहली पंक्ति है। यह दर्शाना अब प्राथमिक है
शेष कार्य को विकर्ण मैट्रिक्स के अभिलक्षणिक मानों के साथ-साथ रैंक-एक सुधार को खोजने के लिए कम कर दिया गया है। यह कैसे करना है यह दिखाने से पहले, आइए अंकन को सरल बनाएं। हम मैट्रिक्स के अभिलक्षणिक मानों की खोज कर रहे हैं, जहां अलग-अलग प्रविष्टियों के साथ विकर्ण है और गैर-शून्य प्रविष्टियों वाला कोई वेक्टर है।
शून्य प्रविष्टि की स्थिति सरल है, क्योंकि यदि wi शून्य है, (,di) का अभिलक्षणिक युग्म ( मानक आधार पर है) है क्योंकि
।
यदि एक अभिलक्षणिक मान है, तो हमारे पास है-
जहां संगत अभिलक्षणिक सदिश है। अब
ध्यान रखें कि एक शून्येतर अदिश राशि है। न तो और न ही शून्य हैं। यदि शून्य होता, तो द्वारा का अभिलक्षणिक सदिश होता है। यदि ऐसा होता, तो में केवल एक गैर-शून्य स्थिति होती क्योंकि अलग विकर्ण है और इस प्रकार आंतरिक उत्पाद अंततः शून्य नहीं हो सकता। इसलिए, हमारे पास है-
या अदिश समीकरण के रूप में लिखा गया है,
इस समीकरण को दीर्घकालिक समीकरण के नाम से जाना जाता है। इसलिए प्रश्न को इस समीकरण के बाईं ओर द्वारा परिभाषित तर्कसंगत फलन के रूट्स को खोजने तक सीमित कर दिया गया है।
सभी सामान्य अभिलक्षणिक मान एल्गोरिदम पुनरावृत्त होने चाहिए, और डिवाइड-और-कॉन्कर एल्गोरिदम अलग नहीं है। अरेखीय दीर्घकालिक समीकरण को हल करने के लिए पुनरावृत्तीय तकनीक की आवश्यकता होती है, जैसे न्यूटन-रेफसन विधि। हालाँकि, प्रत्येक रूट को O(1) पुनरावृत्तियों में पाया जा सकता है, जिनमें से प्रत्येक को फ़्लॉप्स (-डिग्री तर्कसंगत फलन के लिए) की आवश्यकता होती है, जिससे इस एल्गोरिदम के पुनरावृत्त भाग की लागत हो जाती है।
विश्लेषण
जैसा कि फूट डालो और जीतो एल्गोरिदम के लिए आम है, हम चल रहे समय का विश्लेषण करने के लिए मास्टर प्रमेय (एल्गोरिदम का विश्लेषण) | फूट डालो और जीतो पुनरावृत्ति के लिए मास्टर प्रमेय का उपयोग करेंगे। याद रखें कि ऊपर हमने कहा था कि हम चुनते हैं . हम पुनरावृत्ति संबंध लिख सकते हैं:
मास्टर प्रमेय के अंकन में, और इस तरह . स्पष्ट रूप से, , तो हमारे पास
याद रखें कि ऊपर हमने बताया था कि हर्मिटियन मैट्रिक्स को त्रिविकर्ण रूप में कम करना होता है फ्लॉप. यह फूट डालो और जीतो भाग के चलने के समय को कम कर देता है, और इस बिंदु पर यह स्पष्ट नहीं है कि फूट डालो और जीतो एल्गोरिथ्म QR एल्गोरिथ्म पर क्या लाभ प्रदान करता है (जो कि लेता भी है) त्रिविकर्ण आव्यूहों के लिए फ़्लॉप)।
फूट डालो और राज करो का लाभ तब मिलता है जब आइजनवेक्टर की भी आवश्यकता होती है। यदि यह मामला है, तो त्रिविकर्ण रूप में कमी आती है , लेकिन एल्गोरिथ्म का दूसरा भाग लेता है भी। उचित लक्ष्य परिशुद्धता वाले क्यूआर एल्गोरिदम के लिए, यह है , जबकि फूट डालो और राज करो के लिए यह है . इस सुधार का कारण यह है कि फूट डालो और राज करो में एल्गोरिथम का भाग (गुणा करना)। मैट्रिक्स) पुनरावृत्ति से अलग है, जबकि क्यूआर में, यह प्रत्येक पुनरावृत्ति चरण में होना चाहिए। जोड़ रहा हूँ कमी के लिए फ्लॉप, कुल सुधार से है को फ्लॉप.
फूट डालो और जीतो एल्गोरिदम के व्यावहारिक उपयोग से पता चला है कि अधिकांश यथार्थवादी आइगेनवैल्यू समस्याओं में, एल्गोरिदम वास्तव में इससे बेहतर काम करता है। इसका कारण यह है कि बहुत बार मैट्रिक्स और वेक्टर संख्यात्मक रूप से विरल होते हैं, जिसका अर्थ है कि उनके पास तैरनेवाला स्थल परिशुद्धता से छोटे मानों वाली कई प्रविष्टियाँ हैं, जो संख्यात्मक अपस्फीति की अनुमति देती हैं, यानी समस्या को अयुग्मित उप-समस्याओं में तोड़ देती हैं।
विकल्प और कार्यान्वयन
यहां प्रस्तुत एल्गोरिदम सबसे सरल संस्करण है। कई व्यावहारिक कार्यान्वयन में, स्थिरता की गारंटी के लिए अधिक जटिल रैंक-1 सुधारों का उपयोग किया जाता है; कुछ वैरिएंट रैंक-2 सुधारों का भी उपयोग करते हैं।[citation needed]
तर्कसंगत कार्यों के लिए विशेष रूट-खोज तकनीकें मौजूद हैं जो प्रदर्शन और स्थिरता दोनों के मामले में न्यूटन-रैपसन पद्धति से बेहतर कर सकती हैं। इनका उपयोग फूट डालो और जीतो एल्गोरिथ्म के पुनरावृत्त भाग को बेहतर बनाने के लिए किया जा सकता है।
फूट डालो और जीतो एल्गोरिथ्म आसानी से समानांतर एल्गोरिदम है, और LAPACK जैसे रैखिक बीजगणित कंप्यूटिंग पैकेज में उच्च गुणवत्ता वाले समानांतर कार्यान्वयन होते हैं।
संदर्भ
- Demmel, James W. (1997), Applied Numerical Linear Algebra, Philadelphia, PA: Society for Industrial and Applied Mathematics, ISBN 0-89871-389-7, MR 1463942.
- Cuppen, J.J.M. (1981). "A Divide and Conquer Method for the Symmetric Tridiagonal Eigenproblem". Numerische Mathematik. 36 (2): 177–195. doi:10.1007/BF01396757. S2CID 120504744.