एटवुड मशीन: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{short description|Classroom demonstration used to illustrate principles of classical mechanics}} | {{short description|Classroom demonstration used to illustrate principles of classical mechanics}} | ||
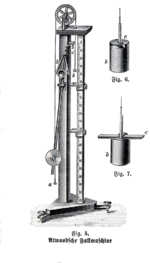
[[Image:Atwoods machine.png|thumb|150px|right|एटवुड मशीन का चित्रण, 1905।]]एटवुड मशीन (या एटवुड की मशीन) का आविष्कार 1784 में अंग्रेजी [[गणितज्ञ]] [[जॉर्ज एटवुड]] द्वारा एकसमान [[त्वरण]] के साथ गति के यांत्रिक नियमों को सत्यापित करने के लिए प्रयोगशाला प्रयोग के रूप में किया गया था। एटवुड की मशीन [[शास्त्रीय यांत्रिकी|चिरसम्मत यांत्रिकी]] के सिद्धांतों को स्पष्ट करने के लिए उपयोग की जाने वाली एक सामान्य कक्षा प्रदर्शन है। | [[Image:Atwoods machine.png|thumb|150px|right|एटवुड मशीन का चित्रण, 1905।]]'''एटवुड मशीन''' (या एटवुड की मशीन) का आविष्कार 1784 में अंग्रेजी [[गणितज्ञ]] [[जॉर्ज एटवुड]] द्वारा एकसमान [[त्वरण]] के साथ गति के यांत्रिक नियमों को सत्यापित करने के लिए प्रयोगशाला प्रयोग के रूप में किया गया था। एटवुड की मशीन [[शास्त्रीय यांत्रिकी|चिरसम्मत यांत्रिकी]] के सिद्धांतों को स्पष्ट करने के लिए उपयोग की जाने वाली एक सामान्य कक्षा प्रदर्शन है। | ||
आदर्श एटवुड मशीन में द्रव्यमान {{math|''m''<sub>1</sub>}} और {{math|''m''<sub>2</sub>}} की दो वस्तुएं होती हैं, जो एक आदर्श द्रव्यमान रहित [[ घिरनी |घिरनी]] के ऊपर अविस्तारित द्रव्यमान रहित स्ट्रिंग से जुड़ी होती हैं।<ref><!-- This is a fairly old edition, but it is the one I have. A cite to a newer edition would be better-->{{cite book |last=Tipler |first=Paul A. |year=1991 |title=Physics For Scientists and Engineers |url=https://archive.org/details/physicsforscient00tipl |url-access=registration |edition=3rd, extended |publisher=Worth Publishers |location=New York |isbn=0-87901-432-6 |page=[https://archive.org/details/physicsforscient00tipl/page/160 160]}} Chapter 6, example 6-13</ref> | आदर्श एटवुड मशीन में द्रव्यमान {{math|''m''<sub>1</sub>}} और {{math|''m''<sub>2</sub>}} की दो वस्तुएं होती हैं, जो एक आदर्श द्रव्यमान रहित [[ घिरनी |घिरनी]] के ऊपर अविस्तारित द्रव्यमान रहित स्ट्रिंग से जुड़ी होती हैं।<ref><!-- This is a fairly old edition, but it is the one I have. A cite to a newer edition would be better-->{{cite book |last=Tipler |first=Paul A. |year=1991 |title=Physics For Scientists and Engineers |url=https://archive.org/details/physicsforscient00tipl |url-access=registration |edition=3rd, extended |publisher=Worth Publishers |location=New York |isbn=0-87901-432-6 |page=[https://archive.org/details/physicsforscient00tipl/page/160 160]}} Chapter 6, example 6-13</ref> | ||
| Line 46: | Line 46: | ||
[[Category:Machine Translated Page]] | [[Category:Machine Translated Page]] | ||
[[Category:Pages with script errors]] | [[Category:Pages with script errors]] | ||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Vigyan Ready]] | [[Category:Templates Vigyan Ready]] | ||
[[Category:Templates that add a tracking category]] | [[Category:Templates that add a tracking category]] | ||
Latest revision as of 10:03, 29 August 2023
एटवुड मशीन (या एटवुड की मशीन) का आविष्कार 1784 में अंग्रेजी गणितज्ञ जॉर्ज एटवुड द्वारा एकसमान त्वरण के साथ गति के यांत्रिक नियमों को सत्यापित करने के लिए प्रयोगशाला प्रयोग के रूप में किया गया था। एटवुड की मशीन चिरसम्मत यांत्रिकी के सिद्धांतों को स्पष्ट करने के लिए उपयोग की जाने वाली एक सामान्य कक्षा प्रदर्शन है।
आदर्श एटवुड मशीन में द्रव्यमान m1 और m2 की दो वस्तुएं होती हैं, जो एक आदर्श द्रव्यमान रहित घिरनी के ऊपर अविस्तारित द्रव्यमान रहित स्ट्रिंग से जुड़ी होती हैं।[1]
दोनों द्रव्यमान समान त्वरण का अनुभव करते हैं। जब m1 = m2, भार की स्थिति की परवाह किए बिना मशीन उदासीन साम्यावस्था में होती है।
स्थिर त्वरण के लिए समीकरण

बलों का विश्लेषण करके त्वरण के लिए एक समीकरण प्राप्त किया जा सकता है। द्रव्यमान रहित, अविस्तार्य स्ट्रिंग और आदर्श द्रव्यमान रहित घिरनी को मानते हुए, विचार करने योग्य एकमात्र बल हैं- तनाव बल (T), और दो द्रव्यमानों का भार (W1 और W2)। त्वरण ज्ञात करने के लिए, प्रत्येक द्रव्यमान को प्रभावित करने वाले बलोंं पर विचार करें। न्यूटन के द्वितीय नियम () की चिह्न परिपाटी के साथ) का उपयोग करते हुए त्वरण (a) के लिए समीकरणों की एक प्रणाली प्राप्त करें।
चिह्न परिपाटी के रूप में, मान लें कि जब के लिए नीचे की ओर और के लिए ऊपर की ओर होता है तो a धनात्मक होता है। और का वजन क्रमशः और है।
m1 को प्रभावित करने वाले बल-
तनाव के लिए समीकरण
डोरी में तनाव के लिए समीकरण को जानना उपयोगी हो सकता है। तनाव का मूल्यांकन करने के लिए, दो बल समीकरणों में से किसी एक में त्वरण के लिए समीकरण को प्रतिस्थापित करें।
जड़त्व और घर्षण के साथ घिरनी के लिए समीकरण
m1 और m2 के बीच बहुत कम द्रव्यमान अंतर के लिए, त्रिज्या r की घिरनी के घूर्णी जड़त्व I की उपेक्षा नहीं की जा सकती है। घिरनी का कोणीय त्वरण असर्पण स्थिति द्वारा दिया जाता है-
त्वरण-
त्वरण-
व्यावहारिक कार्यान्वयन
बीयरिंगों से घर्षण बलों को कम करने के लिए, एटवुड के मूल स्पष्टीकरण अन्य चार पहियों की परिधि पर आराम करने वाली मुख्य घिरनी धुरी को दिखाते हैं। मशीन के कई ऐतिहासिक कार्यान्वयन इस डिजाइन का अनुसरण करते हैं।
प्रतिसंतुलन वाला एलेवेटर आदर्श एटवुड मशीन का अनुमान लगाता है और इस तरह ड्राइविंग मोटर को एलेवेटर कैब को पकड़ने के भार से राहत देता है - इसे केवल वजन के अंतर और दो द्रव्यमानों के जड़त्व को दूर करना होता है। समान सिद्धांत का उपयोग फ़्यूनिक्यूलर रेलवे के लिए किया जाता है, जिसमें झुकी हुई पटरियों पर दो जुड़ी हुई रेलवे कारें होती हैं, और एफिल टॉवर पर लिफ्ट के लिए जो एक दूसरे को प्रतिसंतुलित करती हैं। स्की लिफ्ट एक और उदाहरण है, जहां केबल कार की सीट पहाड़ के ऊपर और नीचे एक बंद (स्थिर) घिरनी प्रणाली पर चलते हैं। स्की लिफ्ट प्रति-भारित एलेवेटर के समान है, लेकिन ऊर्ध्वाधर आयाम में केबल द्वारा प्रदान की जाने वाली विवश बल के साथ क्षैतिज और ऊर्ध्वाधर दोनों आयामों में काम प्राप्त होता है। नाव लिफ्ट एक अन्य प्रकार की प्रति-भारित एलेवेटर प्रणाली है जो एटवुड मशीन का अनुमान लगाती है।
यह भी देखें
- घर्षण रहित समतल
- कैटर का लोलक
- स्फेरिकल काऊ
- स्विंगिंग एटवुड की मशीन
टिप्पणियाँ
- ↑ Tipler, Paul A. (1991). Physics For Scientists and Engineers (3rd, extended ed.). New York: Worth Publishers. p. 160. ISBN 0-87901-432-6. Chapter 6, example 6-13
- ↑ Goldstein, Herbert (1980). Classical Mechanics (2nd ed.). New Delhi: Addison-Wesley/Narosa Indian Student Edition. pp. 26–27. ISBN 81-85015-53-8. Section 1-6, example 2
बाहरी संबंध
- A treatise on the rectilinear motion and rotation of bodies; with a description of original experiments relative to the subject by George Atwood, 1764. Drawings appear on page 450.
- Professor Greenslade's account on the Atwood Machine
- Atwood's Machine by Enrique Zeleny, The Wolfram Demonstrations Project