तरंगिका पैकेट अपघटन: Difference between revisions
No edit summary |
(→परिचय) |
||
| Line 5: | Line 5: | ||
डीडब्ल्यूटी में, प्रत्येक स्तर की गणना असतत-समय निम्न- और उच्च-अस्थायी [[चतुर्भुज दर्पण फिल्टर|चतुर्भुज दर्पण निस्यंदक]] के माध्यम से केवल पिछले तरंगिका सन्निकटन गुणांक (cAj) को पारित करके की जाती है।।<ref name=coifman1992/><ref name=akansu1991/>हालाँकि, डब्ल्यूपीडी में, दोनों विवरण (cD<sub>j</sub>(1-डी स्थिति में), cHj, cVj, cDj(2-डी स्थिति में)) और सन्निकटन गुणांक पूर्ण बाइनरी ट्री बनाने के लिए वियोजित होते हैं।<ref name=Daub>Daubechies, I. (1992), Ten lectures on wavelets, SIAM.</ref><ref name=akansu1991/><ref name=caglar1991/><ref name=akansu1992/><ref name=benyassine1995/><ref name=akansu1995/> | डीडब्ल्यूटी में, प्रत्येक स्तर की गणना असतत-समय निम्न- और उच्च-अस्थायी [[चतुर्भुज दर्पण फिल्टर|चतुर्भुज दर्पण निस्यंदक]] के माध्यम से केवल पिछले तरंगिका सन्निकटन गुणांक (cAj) को पारित करके की जाती है।।<ref name=coifman1992/><ref name=akansu1991/>हालाँकि, डब्ल्यूपीडी में, दोनों विवरण (cD<sub>j</sub>(1-डी स्थिति में), cHj, cVj, cDj(2-डी स्थिति में)) और सन्निकटन गुणांक पूर्ण बाइनरी ट्री बनाने के लिए वियोजित होते हैं।<ref name=Daub>Daubechies, I. (1992), Ten lectures on wavelets, SIAM.</ref><ref name=akansu1991/><ref name=caglar1991/><ref name=akansu1992/><ref name=benyassine1995/><ref name=akansu1995/> | ||
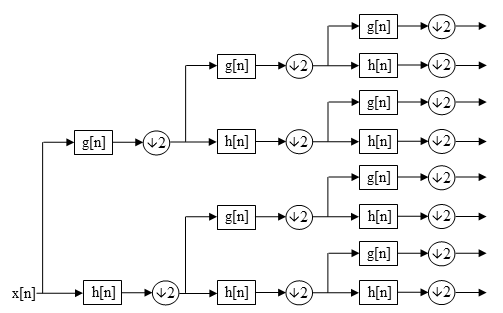
[[Image:Wavelets - WPD.png|frame|none|3 स्तरों पर तरंगिका पैकेट अपघटन। जी [एन] निम्न-पास सन्निकटन गुणांक हैं, एच [एन] उच्च-पास विस्तार गुणांक हैं।]]वियोजन के एन स्तरों के लिए डब्ल्यूपीडी डीडब्ल्यूटी के लिए{{nobr|(''एन'' + 1)}} समुच्चय के विपरीत गुणांक (या नोड्स) के 2 एन विभिन्न समुच्चय उत्पन्न करता है। हालाँकि, [[downsampling]] प्रक्रिया के कारण गुणांकों की समग्र संख्या अभी भी समान है और कोई | [[Image:Wavelets - WPD.png|frame|none|3 स्तरों पर तरंगिका पैकेट अपघटन। जी [एन] निम्न-पास सन्निकटन गुणांक हैं, एच [एन] उच्च-पास विस्तार गुणांक हैं।]]वियोजन के एन स्तरों के लिए डब्ल्यूपीडी डीडब्ल्यूटी के लिए{{nobr|(''एन'' + 1)}} समुच्चय के विपरीत गुणांक (या नोड्स) के 2 एन विभिन्न समुच्चय उत्पन्न करता है। हालाँकि, [[downsampling|उतार-चढ़ाव]] प्रक्रिया के कारण गुणांकों की समग्र संख्या अभी भी समान है और कोई अतिरेकता नहीं है। | ||
संपीड़न के दृष्टिकोण से, मानक तरंगिका रूपांतरण सर्वोत्तम परिणाम नहीं दे सकता है, क्योंकि यह तरंगिका आधारों तक सीमित है जो कम आवृत्तियों की ओर दो की शक्ति से बढ़ता है। यह हो सकता है कि आधारों का एक और संयोजन किसी विशेष सिग्नल के लिए अधिक वांछनीय प्रतिनिधित्व उत्पन्न करता है।<ref name=akansu1992>A. N. Akansu and R. A. Haddad, [https://www.amazon.com/Multiresolution-Signal-Decomposition-Second-Transforms/dp/0120471418/ref=sr_1_1?ie=UTF8&qid=1325021689&sr=8-1 Multiresolution Signal Decomposition: Transforms, Subbands, and Wavelets]. Boston, MA: Academic Press, {{ISBN|978-0-12-047141-6}}, 1992.</ref> सबबैंड ट्री संरचना के लिए कई एल्गोरिदम हैं जो इष्टतम आधारों का एक सेट ढूंढते हैं जो किसी विशेष लागत फ़ंक्शन ([[एन्ट्रापी]], ऊर्जा संघनन, आदि) के सापेक्ष डेटा का सबसे वांछनीय प्रतिनिधित्व प्रदान करते हैं।<ref name=coifman1992>Coifman R. R. & Wickerhauser M. V., 1992. [http://www.csee.wvu.edu/~xinl/library/papers/infor/coifman1992.pdf Entropy-Based Algorithms for Best Basis Selection], IEEE Transactions on Information Theory, 38(2).</ref> | संपीड़न के दृष्टिकोण से, मानक तरंगिका रूपांतरण सर्वोत्तम परिणाम नहीं दे सकता है, क्योंकि यह तरंगिका आधारों तक सीमित है जो कम आवृत्तियों की ओर दो की शक्ति से बढ़ता है। यह हो सकता है कि आधारों का एक और संयोजन किसी विशेष सिग्नल के लिए अधिक वांछनीय प्रतिनिधित्व उत्पन्न करता है।<ref name=akansu1992>A. N. Akansu and R. A. Haddad, [https://www.amazon.com/Multiresolution-Signal-Decomposition-Second-Transforms/dp/0120471418/ref=sr_1_1?ie=UTF8&qid=1325021689&sr=8-1 Multiresolution Signal Decomposition: Transforms, Subbands, and Wavelets]. Boston, MA: Academic Press, {{ISBN|978-0-12-047141-6}}, 1992.</ref> सबबैंड ट्री संरचना के लिए कई एल्गोरिदम हैं जो इष्टतम आधारों का एक सेट ढूंढते हैं जो किसी विशेष लागत फ़ंक्शन ([[एन्ट्रापी]], ऊर्जा संघनन, आदि) के सापेक्ष डेटा का सबसे वांछनीय प्रतिनिधित्व प्रदान करते हैं।<ref name=coifman1992>Coifman R. R. & Wickerhauser M. V., 1992. [http://www.csee.wvu.edu/~xinl/library/papers/infor/coifman1992.pdf Entropy-Based Algorithms for Best Basis Selection], IEEE Transactions on Information Theory, 38(2).</ref> | ||
Revision as of 22:31, 14 March 2023
मूल रूप से इष्टतम उपबैंड ट्री संरचना (एसबी-टीएस) के रूप में जाना जाता है, जिसे तरंगिका पैकेट वियोजन (डब्ल्यूपीडी) भी कहा जाता है।(कभी-कभी केवल तरंगिका पैकेट या उपबैंड ट्री के रूप में जाना जाता है), एक तरंगिका रूपांतरण है जहां असतत-समय (नमूना) संकेत असतत तरंगिका रूपांतरण (डीडब्ल्यूटी) की तुलना में अधिक निस्यंदक के माध्यम से पारित किया जाता है।
परिचय
डीडब्ल्यूटी में, प्रत्येक स्तर की गणना असतत-समय निम्न- और उच्च-अस्थायी चतुर्भुज दर्पण निस्यंदक के माध्यम से केवल पिछले तरंगिका सन्निकटन गुणांक (cAj) को पारित करके की जाती है।।[1][2]हालाँकि, डब्ल्यूपीडी में, दोनों विवरण (cDj(1-डी स्थिति में), cHj, cVj, cDj(2-डी स्थिति में)) और सन्निकटन गुणांक पूर्ण बाइनरी ट्री बनाने के लिए वियोजित होते हैं।[3][2][4][5][6][7]
वियोजन के एन स्तरों के लिए डब्ल्यूपीडी डीडब्ल्यूटी के लिए(एन + 1) समुच्चय के विपरीत गुणांक (या नोड्स) के 2 एन विभिन्न समुच्चय उत्पन्न करता है। हालाँकि, उतार-चढ़ाव प्रक्रिया के कारण गुणांकों की समग्र संख्या अभी भी समान है और कोई अतिरेकता नहीं है।
संपीड़न के दृष्टिकोण से, मानक तरंगिका रूपांतरण सर्वोत्तम परिणाम नहीं दे सकता है, क्योंकि यह तरंगिका आधारों तक सीमित है जो कम आवृत्तियों की ओर दो की शक्ति से बढ़ता है। यह हो सकता है कि आधारों का एक और संयोजन किसी विशेष सिग्नल के लिए अधिक वांछनीय प्रतिनिधित्व उत्पन्न करता है।[5] सबबैंड ट्री संरचना के लिए कई एल्गोरिदम हैं जो इष्टतम आधारों का एक सेट ढूंढते हैं जो किसी विशेष लागत फ़ंक्शन (एन्ट्रापी, ऊर्जा संघनन, आदि) के सापेक्ष डेटा का सबसे वांछनीय प्रतिनिधित्व प्रदान करते हैं।[1] [2] विभिन्न प्रकार के सबबैंड ट्री (ऑर्थोगोनल आधार) के चयन को संबोधित करने के लिए सिग्नल प्रोसेसिंग और संचार क्षेत्रों में प्रासंगिक अध्ययन किए गए थे, उदा। ऊर्जा संघनन (एन्ट्रॉपी), सबबैंड सहसंबंधों और अन्य सहित रुचि के प्रदर्शन मेट्रिक्स के संबंध में नियमित, डाइडिक, अनियमित। [4] [6] [7] असतत तरंगिका रूपांतरण सिद्धांत (समय चर में निरंतर) असतत (नमूना) संकेतों को बदलने के लिए एक सन्निकटन प्रदान करता है। इसके विपरीत, डिस्क्रीट-टाइम सबबैंड ट्रांसफॉर्म थ्योरी पहले से ही सैंपल किए गए संकेतों का सही प्रतिनिधित्व करने में सक्षम बनाती है।[5][8]
गैलरी
अनुप्रयोग
प्रीक्लिनिकल डायग्नोसिस में वेवलेट पैकेट सफलतापूर्वक लागू किए गए थे।[9]
संदर्भ
- ↑ 1.0 1.1 Coifman R. R. & Wickerhauser M. V., 1992. Entropy-Based Algorithms for Best Basis Selection, IEEE Transactions on Information Theory, 38(2).
- ↑ 2.0 2.1 2.2 A. N. Akansu and Y. Liu, On Signal Decomposition Techniques, (Invited Paper), Optical Engineering Journal, special issue Visual Communications and Image Processing, vol. 30, pp. 912–920, July 1991.
- ↑ Daubechies, I. (1992), Ten lectures on wavelets, SIAM.
- ↑ 4.0 4.1 H. Caglar, Y. Liu and A. N. Akansu, Statistically Optimized PR-QMF Design, Proc. SPIE Visual Communications and Image Processing, vol. 1605, pp. 86–94, 1991.
- ↑ 5.0 5.1 5.2 A. N. Akansu and R. A. Haddad, Multiresolution Signal Decomposition: Transforms, Subbands, and Wavelets. Boston, MA: Academic Press, ISBN 978-0-12-047141-6, 1992.
- ↑ 6.0 6.1 A. Benyassine and A. N. Akansu, Performance Analysis and Optimal Structuring of Subchannels for Discrete Multitone Transceivers , Proc. IEEE International Symposium on Circuits and Systems (ISCAS), pp. 1456–1459, April 1995.
- ↑ 7.0 7.1 M. V. Tazebay and A. N. Akansu, Adaptive Subband Transforms in Time-frequency Excisers for DSSS Communications Systems, IEEE Trans. Signal Process., vol. 43, pp. 2776–2782, Nov. 1995.
- ↑ A. N. Akansu, W. A. Serdijn, and I. W. Selesnick, Wavelet Transforms in Signal Processing: A Review of Emerging Applications, Physical Communication, Elsevier, vol. 3, issue 1, pp. 1–18, March 2010.
- ↑ Zhang, Y.; Dong, Z. (2015). "असतत वेवलेट पैकेट के माध्यम से चुंबकीय अनुनाद (एमआर) मस्तिष्क छवियों का प्रीक्लिनिकल डायग्नोसिस, सैलिस एंट्रॉपी और सामान्यीकृत ईजेनवैल्यू प्रॉक्सिमल सपोर्ट वेक्टर मशीन (जीईपीएसवीएम) के साथ बदलता है।". Entropy. 17 (4): 1795–1813. Bibcode:2015Entrp..17.1795Z. doi:10.3390/e17041795.
बाहरी संबंध
- An implementation of wavelet packet decomposition can be found in MATLAB wavelet toolbox.
- An implementation for R can be found in the wavethresh package.
- An illustration and implementation of wavelet packets along with its code in C++ can be found at: Ian Kaplan (March 2002). "The Wavelet Packet Transform". Bearcave.
- JWave: An implementation in Java for 1-D and 2-D wavelet packets using Haar, Daubechies, Coiflet, and Legendre wavelets.