स्टोक्स की समस्या: Difference between revisions
No edit summary |
|||
| Line 35: | Line 35: | ||
प्लेट के दोलन और निर्मित बल के बीच चरण बदलाव होता है। | प्लेट के दोलन और निर्मित बल के बीच चरण बदलाव होता है। | ||
=== सीमा के पास [[vorticity]] दोलन === | === सीमा के पास [[vorticity|आवर्त]] दोलन === | ||
दोलनशील स्टोक्स प्रवाह के लिए स्टोक्स के समाधान से महत्वपूर्ण अवलोकन यह है कि दीवार से दूर जाने पर | दोलनशील स्टोक्स प्रवाह के लिए स्टोक्स के समाधान से महत्वपूर्ण अवलोकन यह है कि दीवार से दूर जाने पर आवर्त दोलन पतली सीमा परत और नम [[घातीय क्षय]] तक सीमित होते हैं।<ref name=Phil46>Phillips (1977), p. 46.</ref> यह अवलोकन अशांत सीमा परत के कथन में भी मान्य है। स्टोक्स सीमा परत के बाहर - जो अधिकांशतः तरल पदार्थ की मात्रा का बड़ा भाग होता है - आवर्त दोलनों की उपेक्षा की जा सकती है। लगभग अच्छे के लिए, प्रवाह वेग दोलन सीमा परत के बाहर अघूर्णनशील होते हैं, और [[संभावित प्रवाह]] सिद्धांत को गति के दोलनशील भाग पर क्रियान्वित किया जा सकता है। यह इन प्रवाह समस्याओं के समाधान को बहुत सरल करता है, और इसे अधिकांशतः ध्वनि तरंगों और जल तरंगों के अघूर्णी प्रवाह क्षेत्रों में क्रियान्वित किया जाता है। | ||
=== | === ऊपरी दीवार से घिरा द्रव === | ||
यदि द्रव डोमेन ऊंचाई पर स्थित ऊपरी, | यदि द्रव डोमेन ऊंचाई पर स्थित ऊपरी, <math>y=h</math> स्थिर दीवार से घिरा है, प्रवाह वेग द्वारा दिया जाता है | ||
:<math>u(y,t) = \frac{U}{2(\cosh 2\lambda h -\cos 2\lambda h)}[e^{-\lambda(y-2h)}\cos(\omega t-\lambda y) + e^{\lambda(y-2h)}\cos(\omega t+\lambda y) - e^{-\lambda y} \cos(\omega t-\lambda y+2\lambda h) - e^{\lambda y}\cos(\omega t+\lambda y-2\lambda h)]</math> | :<math>u(y,t) = \frac{U}{2(\cosh 2\lambda h -\cos 2\lambda h)}[e^{-\lambda(y-2h)}\cos(\omega t-\lambda y) + e^{\lambda(y-2h)}\cos(\omega t+\lambda y) - e^{-\lambda y} \cos(\omega t-\lambda y+2\lambda h) - e^{\lambda y}\cos(\omega t+\lambda y-2\lambda h)]</math> | ||
जहाँ <math>\lambda=\sqrt{\omega/(2\nu)}</math>. | |||
=== | === स्वतंत्र सतह से घिरा द्रव === | ||
मान लीजिए द्रव डोमेन की सीमा | मान लीजिए द्रव डोमेन की सीमा <math>0<y<h</math> हो साथ <math>y=h</math> एक स्वतंत्र सतह का प्रतिनिधित्व करता हो। फिर 1968 में [[ हैं-क्या येह | चिआ-शुं यीह]] द्वारा दिखाया गया समाधान<ref>Yih, C. S. (1968). Instability of unsteady flows or configurations Part 1. Instability of a horizontal liquid layer on an oscillating plane. Journal of Fluid Mechanics, 31(4), 737-751.</ref> द्वारा दिया गया है | ||
:<math>u(y,t) = \frac{U \cos h/\delta\, \mathrm{cosh}\, h/\delta}{2(\cos^2h/\delta + \mathrm{sinh}^2h/\delta)} \Re\left\{W + W^* - i \mathrm{tanh}\, h/\delta\, \tan h/\delta \,(W-W^*)\right\},\qquad W = \mathrm{cosh}[(1+i)(h-y)/\delta] e^{i\omega t}</math> | :<math>u(y,t) = \frac{U \cos h/\delta\, \mathrm{cosh}\, h/\delta}{2(\cos^2h/\delta + \mathrm{sinh}^2h/\delta)} \Re\left\{W + W^* - i \mathrm{tanh}\, h/\delta\, \tan h/\delta \,(W-W^*)\right\},\qquad W = \mathrm{cosh}[(1+i)(h-y)/\delta] e^{i\omega t}</math> | ||
:जहाँ <math>\delta = \sqrt{2\nu/\omega}.</math> | |||
=== समतल कठोर | === समतल कठोर के पास दोलन दाब प्रवणता के कारण प्रवाह === | ||
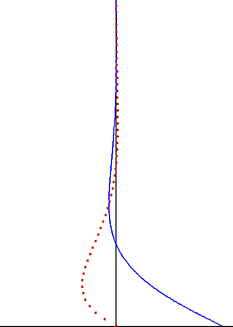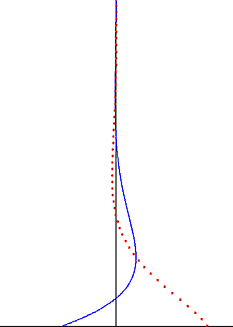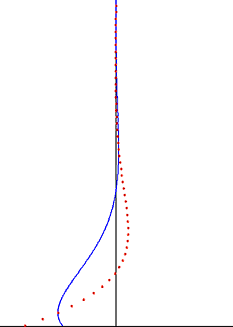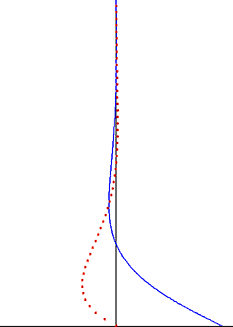
[[File:Stokes boundary layer oscillating flow.gif|frame|right|दूर-क्षेत्र प्रवाह वेग के [[sinusoidal]] दोलन के कारण स्टोक्स सीमा परत। क्षैतिज वेग नीली रेखा है, और संबंधित क्षैतिज कण भ्रमण लाल बिंदु हैं।]]एक दोलनशील दूर-क्षेत्र प्रवाह के मामले में, प्लेट को आराम से रखने के साथ, समाधान के रैखिक सुपरपोज़िशन का उपयोग करके एक ऑसिलेटिंग प्लेट के लिए पिछले समाधान से आसानी से बनाया जा सकता है। एक समान वेग दोलन पर विचार करें <math>u(\infty,t)=U_\infty \cos \omega t</math> प्लेट से दूर और प्लेट पर लुप्त वेग <math>u(0,t)=0</math>. मूल समस्या में स्थिर द्रव के विपरीत, यहाँ अनंत पर दबाव ढाल समय का एक हार्मोनिक कार्य होना चाहिए। समाधान तब द्वारा दिया जाता है | [[File:Stokes boundary layer oscillating flow.gif|frame|right|दूर-क्षेत्र प्रवाह वेग के [[sinusoidal]] दोलन के कारण स्टोक्स सीमा परत। क्षैतिज वेग नीली रेखा है, और संबंधित क्षैतिज कण भ्रमण लाल बिंदु हैं।]]एक दोलनशील दूर-क्षेत्र प्रवाह के मामले में, प्लेट को आराम से रखने के साथ, समाधान के रैखिक सुपरपोज़िशन का उपयोग करके एक ऑसिलेटिंग प्लेट के लिए पिछले समाधान से आसानी से बनाया जा सकता है। एक समान वेग दोलन पर विचार करें <math>u(\infty,t)=U_\infty \cos \omega t</math> प्लेट से दूर और प्लेट पर लुप्त वेग <math>u(0,t)=0</math>. मूल समस्या में स्थिर द्रव के विपरीत, यहाँ अनंत पर दबाव ढाल समय का एक हार्मोनिक कार्य होना चाहिए। समाधान तब द्वारा दिया जाता है | ||
Revision as of 15:35, 22 May 2023
द्रव गतिशीलता में, स्टोक्स समस्या को स्टोक्स की दूसरी समस्या के रूप में भी जाना जाता है या कभी-कभी स्टोक्स सीमा परत या दोलन सीमा परत के रूप में जाना जाता है, सर जॉर्ज स्टोक्स, प्रथम बैरोनेट के नाम पर दोलनशील ठोस सतह द्वारा बनाए गए प्रवाह को निर्धारित करने की समस्या है। इसे सबसे सरल अस्थिर समस्याओं में से एक माना जाता है जिसका नेवियर-स्टोक्स समीकरणों के लिए सटीक समाधान है।[1][2] अशांत प्रवाह में, इसे अभी भी स्टोक्स सीमा परत का नाम दिया गया है, परन्तु अब प्रवाह पर उपयोगी जानकारी प्राप्त करने के लिए प्रवाह माप, कम्प्यूटेशनल द्रव गतिकी या निकटतम पर निर्भर रहना पड़ता है।
प्रवाह विवरण[3][4]
असीम रूप से लंबी परत पर विचार करें में दिशा जो वेग से दोलन कर रही है, जो पर स्थित है | द्रव के अनंत डोमेन में, जहाँ दोलनों की आवृत्ति है। असंपीड्य नेवियर-स्टोक्स समीकरण कम हो जाते हैं
जहाँ गतिज श्यानता है। दाब प्रवणता समस्या में प्रवेश नहीं करती है। दीवार पर प्रारंभिक, नो-स्लिप स्थिति है
और दूसरी सीमा की स्थिति इस तथ्य के कारण है कि गति पर अनंत पर उत्तेजना नहीं किया जाता है। प्रवाह केवल सतह की गति के कारण होता है, कोई दाब प्रवणता नहीं होती है।
समाधान[5][6]
आवधिकता के कारण प्रारंभिक स्थिति की आवश्यकता नहीं है। चूंकि दोनों समीकरण और सीमा की स्थिति रैखिक हैं, वेग को कुछ जटिल कार्यों के वास्तविक भाग के रूप में लिखा जा सकता है
क्योंकि .
इसे आंशिक अवकल समीकरण में प्रतिस्थापित करने पर यह साधारण अवकल समीकरण में बदल जाता है
सीमा प्रतिबन्ध के साथ
उपरोक्त समस्या का समाधान है
दोलायमान सतह द्वारा बनाई गई अशांत द्रव के माध्यम से अनुप्रस्थ तरंग के रूप में जाती है, परन्तु यह घातीय कारक द्वारा अत्यधिक अवमंदित होती है। प्रवेश की गहराई इस तरंग की गति दोलन की आवृत्ति के साथ कम हो जाती है, परन्तु द्रव की गतिज श्यानता के साथ बढ़ जाती है।
द्रव द्वारा सतह पर लगाया गया बल प्रति इकाई क्षेत्र है
प्लेट के दोलन और निर्मित बल के बीच चरण बदलाव होता है।
सीमा के पास आवर्त दोलन
दोलनशील स्टोक्स प्रवाह के लिए स्टोक्स के समाधान से महत्वपूर्ण अवलोकन यह है कि दीवार से दूर जाने पर आवर्त दोलन पतली सीमा परत और नम घातीय क्षय तक सीमित होते हैं।[7] यह अवलोकन अशांत सीमा परत के कथन में भी मान्य है। स्टोक्स सीमा परत के बाहर - जो अधिकांशतः तरल पदार्थ की मात्रा का बड़ा भाग होता है - आवर्त दोलनों की उपेक्षा की जा सकती है। लगभग अच्छे के लिए, प्रवाह वेग दोलन सीमा परत के बाहर अघूर्णनशील होते हैं, और संभावित प्रवाह सिद्धांत को गति के दोलनशील भाग पर क्रियान्वित किया जा सकता है। यह इन प्रवाह समस्याओं के समाधान को बहुत सरल करता है, और इसे अधिकांशतः ध्वनि तरंगों और जल तरंगों के अघूर्णी प्रवाह क्षेत्रों में क्रियान्वित किया जाता है।
ऊपरी दीवार से घिरा द्रव
यदि द्रव डोमेन ऊंचाई पर स्थित ऊपरी, स्थिर दीवार से घिरा है, प्रवाह वेग द्वारा दिया जाता है
जहाँ .
स्वतंत्र सतह से घिरा द्रव
मान लीजिए द्रव डोमेन की सीमा हो साथ एक स्वतंत्र सतह का प्रतिनिधित्व करता हो। फिर 1968 में चिआ-शुं यीह द्वारा दिखाया गया समाधान[8] द्वारा दिया गया है
- जहाँ
समतल कठोर के पास दोलन दाब प्रवणता के कारण प्रवाह

एक दोलनशील दूर-क्षेत्र प्रवाह के मामले में, प्लेट को आराम से रखने के साथ, समाधान के रैखिक सुपरपोज़िशन का उपयोग करके एक ऑसिलेटिंग प्लेट के लिए पिछले समाधान से आसानी से बनाया जा सकता है। एक समान वेग दोलन पर विचार करें प्लेट से दूर और प्लेट पर लुप्त वेग . मूल समस्या में स्थिर द्रव के विपरीत, यहाँ अनंत पर दबाव ढाल समय का एक हार्मोनिक कार्य होना चाहिए। समाधान तब द्वारा दिया जाता है
जो दीवार z = 0 पर शून्य है, जो आराम से दीवार के लिए नो-स्लिप स्थिति के अनुरूप है। यह स्थिति अक्सर ध्वनि तरंगों में एक ठोस दीवार के पास, या पानी की लहरों में समुद्र तल के पास द्रव गति के लिए होती है। आराम की दीवार के पास दोलन प्रवाह के लिए वर्टिसिटी, ऑसिलेटिंग प्लेट के मामले में वर्टिसिटी के बराबर है, लेकिन विपरीत चिन्ह का है।
बेलनाकार ज्यामिति में स्टोक्स की समस्या
मरोड़ दोलन
त्रिज्या के एक असीम रूप से लंबे बेलन पर विचार करें कोणीय वेग के साथ मरोड़ दोलन प्रदर्शित करना कहाँ आवृत्ति है। तब वेग प्रारंभिक क्षणिक चरण के बाद पहुंचता है[9]
कहाँ दूसरी तरह का संशोधित बेसेल कार्य है। यह समाधान वास्तविक तर्क के साथ व्यक्त किया जा सकता है[10] जैसा:
कहाँ
और केल्विन कार्य हैं और आयाम रहित ऑसिलेटरी रेनॉल्ड्स संख्या के रूप में परिभाषित किया गया है , प्राणी कीनेमेटिक चिपचिपाहट।
अक्षीय दोलन
यदि बेलन अक्षीय दिशा में वेग से दोलन करता है , तो वेग क्षेत्र है
कहाँ दूसरी तरह का संशोधित बेसेल कार्य है।
स्टोक्स-कूएट प्रवाह[11]
Couette प्रवाह में, प्लेट में से किसी एक के स्थानान्तरण गति के बजाय, एक तल का दोलन किया जाएगा। अगर हमारे पास नीचे की दीवार आराम पर है और ऊपरी दीवार पर वेग से दोलन गति कर रहा है , तब वेग क्षेत्र द्वारा दिया जाता है
गतिमान तल पर प्रति एकांक क्षेत्रफल पर घर्षण बल है और नियत तल पर है .
यह भी देखें
- रेले की समस्या
संदर्भ
- ↑ Wang, C. Y. (1991). "स्थिर-अवस्था नेवियर-स्टोक्स समीकरणों का सटीक समाधान". Annual Review of Fluid Mechanics. 23: 159–177. Bibcode:1991AnRFM..23..159W. doi:10.1146/annurev.fl.23.010191.001111.
- ↑ Landau & Lifshitz (1987), pp. 83–85.
- ↑ Batchelor, George Keith. An introduction to fluid dynamics. Cambridge university press, 2000.
- ↑ Lagerstrom, Paco Axel. Laminar flow theory. Princeton University Press, 1996.
- ↑ Acheson, David J. Elementary fluid dynamics. Oxford University Press, 1990.
- ↑ Landau, Lev Davidovich, and Evgenii Mikhailovich Lifshitz. "Fluid mechanics." (1987).
- ↑ Phillips (1977), p. 46.
- ↑ Yih, C. S. (1968). Instability of unsteady flows or configurations Part 1. Instability of a horizontal liquid layer on an oscillating plane. Journal of Fluid Mechanics, 31(4), 737-751.
- ↑ Drazin, Philip G., and Norman Riley. The Navier–Stokes equations: a classification of flows and exact solutions. No. 334. Cambridge University Press, 2006.
- ↑ Rivero, M.; Garzón, F.; Núñez, J.; Figueroa, A. (2019). "मरोड़ वाले दोलन करने वाले वृत्ताकार बेलन द्वारा प्रेरित प्रवाह का अध्ययन". European Journal of Mechanics - B/Fluids (in English). 78: 245–251. doi:10.1016/j.euromechflu.2019.08.002. S2CID 201253195.
- ↑ Landau, L. D., & Sykes, J. B. (1987). Fluid Mechanics: Vol 6. pp. 88