क्यू (एब्स्ट्रैक्ट डेटा प्रकार): Difference between revisions
m (Sugatha moved page कतार (सार डेटा प्रकार) to क्यू (एब्स्ट्रैक्ट डेटा प्रकार)) |
No edit summary |
||
| Line 12: | Line 12: | ||
|delete_worst={{math|O(1)}} | |delete_worst={{math|O(1)}} | ||
}} | }} | ||
[[Index.php?title=अभिकलन विज्ञान|अभिकलन विज्ञान]] में | [[Index.php?title=अभिकलन विज्ञान|अभिकलन विज्ञान]] में क्यू संस्थाओं का संग्रह (अमूर्त तथ्य प्रकार) है जो क्रम में बनाए रखा जाता है एवं अनुक्रम के छोर पर संस्थाओं को जोड़कर एवं दूसरे छोर से संस्थाओं को हटाकर संशोधित करता है। सम्मेलन के अनुसार, जिस क्रम में तत्वों की तुलना करी जाती है उसके अंत को क्यू का पिछला भाग कहा जाता है एवं जिस अंत में तत्वों को हटा दिया जाता है उसे क्यू का अगला भाग कहा जाता है जो कि उपयोग किए गए शब्दों के अनुरूप होता है जिसके लिए लोग सामान या सेवाओं की प्रतीक्षा करने के लिए क्रम में स्थित होते हैं। | ||
क्यू के पिछले भाग में तत्व जोड़ने की क्रिया को 'एनक्यू' के रूप में जाना जाता है एवं किसी तत्व को सामने से हटाने की क्रिया को 'डीक्यू' के रूप में जाना जाता है। अन्य कार्यों की भी अनुमति दी जाती है, जिसमें अधिकांशतः ''पीक (तथ्य प्रकार संचालन)'' या ''मुख्य'' संचालन सम्मलित होता है, जो अगले तत्व के मूल्य को बिना डीक्यू किए वापस करता है। | |||
फीफो तथ्य संरचना में | फीफो तथ्य संरचना में क्यू की तुलना करा गया पहला तत्व हटा दिया जाता है। यह आवश्यक है कि एक बार नवीन तत्व की तुलना करी जाए जोकि नए तत्व को हटाए जाने से पहले सभी पहले तत्व को हटा दिया जाए। क्यू रेखीय तथ्य संरचना का उदाहरण है, या अधिक संक्षेप में यह अनुक्रमिक संग्रह है। अभिकलन योजना में क्यूें सामान्य हैं, जहां उन्हें अक्ष नित्य के साथ [[सार डेटा संरचना|सार (एब्स्ट्रैक्ट) तथ्य संरचना]] के रूप में या लक्ष्योन्मुखी भाषाओं में तथ्य संरचनाओं के रूप में कार्यान्वित किया जाता है। सामान्यतः कार्यान्वयन [[Index.php?title=Index.php?title=वृत्त बफर|वृत्त बफर]] एवं श्रृंखलित सूचियाँ हैं। | ||
अभिकलन विज्ञान, [[परिवहन]] एवं संचालन अनुसंधान में | अभिकलन विज्ञान, [[परिवहन]] एवं संचालन अनुसंधान में क्यूें सेवाएं प्रदान करती हैं जहां तथ्य बफर, व्यक्तियों या घटनाओं जैसी विभिन्न संस्थाओं को संग्रहीत एवं पश्चात संसाधित करने के लिए आयोजित किया जाता है। इन संदर्भों में, क्यू एक बफर (अभिकलन विज्ञान) का कार्य करता है। क्यू का अन्य उपयोग चौड़ाई-प्रथम खोज के कार्यान्वयन में है। | ||
== | ==क्यू कार्यान्वयन == | ||
सैद्धांतिक रूप से, | सैद्धांतिक रूप से, क्यू की विशेषता यह है कि इसकी कोई विशिष्ट क्षमता नहीं होती है। यदि कितने ही तत्व पहले से सम्मलित हों, नवीन तत्व की निरंतर तुलना करी जा सकती है। [[सरणी]] को संवृत क्षेत्र में बदलने एवं उस क्षेत्र में चित एवं पट को अंतहीन रूप से घूमने देने की सरल चाल सरणी में संग्रहीत वस्तुओं को कभी भी स्थानांतरित करने के लिए अनावश्यक बनाती है। यदि एन सरणी की बनावट है, तो अभिकलन सूची सापेक्ष एन सरणी को वृत्त में बदल देता है। यह अभी भी उच्च-स्तरीय भाषा में क्यू बनाने का वैचारिक रूप से सबसे सरल विधि है, लेकिन यह निश्चित रूप से चीजों को थोड़ा धीमा करता है, क्योंकि सरणी सूची की तुलना शून्य एवं सरणी बनावट से की जाती है, जोकि इसमें लगने वाले समय के समान है। बफर या सूचक (अभिकलन योजनािंग) के साथ अधिकांश आधुनिक भाषाएं गतिशील सूचियों के लिए पुस्तकालयों को लागू कर सकती हैं या उनके साथ आ सकती हैं। क्यू अतिप्रवाह परिणाम पूर्ण क्यू में तत्व जोड़ने की प्रयास करने से होता है एवं रिक्त क्यू से तत्व को निकालने का प्रयास करते समय क्यू अधःप्रवाह हो जाती है। | ||
बंधी हुई | बंधी हुई क्यू निश्चित संख्या में वस्तुओं तक सीमित क्यू है।<ref>{{cite web|url=http://docs.oracle.com/javase/7/docs/api/java/util/Queue.html |title=Queue (Java Platform SE 7) |publisher=Docs.oracle.com |date=2014-03-26 |access-date=2014-05-22}}</ref> फीफो क्यूों के कई कुशल कार्यान्वयन हैं जिसमे से कुशल कार्यान्वयन वह है जो [[बिग ओ नोटेशन]] समय में संचालन-एन-पंक्ति एवं डी-पंक्ति- कर सकते है। | ||
*श्रृंखलित सूची | *श्रृंखलित सूची | ||
** दोगुनी श्रंखला की गई सूची में दोनों चितों पर ओ(1) सम्मिलन एवं विलोपन होता है, इसलिए यह | ** दोगुनी श्रंखला की गई सूची में दोनों चितों पर ओ(1) सम्मिलन एवं विलोपन होता है, इसलिए यह क्यूों के लिए स्वाभाविक विकल्प है। | ||
** नियमित रूप से एकल रूप से जुड़ी सूची में चित्फ एक छोर पर प्रभावी प्रविष्टि एवं विलोपन होता है। चूंकि छोटा संशोधन पहले के अतिरिक्त अंतिम आसंधि के लिए सूचक रखना कुशल | ** नियमित रूप से एकल रूप से जुड़ी सूची में चित्फ एक छोर पर प्रभावी प्रविष्टि एवं विलोपन होता है। चूंकि छोटा संशोधन पहले के अतिरिक्त अंतिम आसंधि के लिए सूचक रखना कुशल क्यू को लागू करने में सक्षम रहेगा। | ||
* संशोधित गतिशील सरणी का उपयोग करके कार्यान्वित [[Index.php?title=दोनों ओर से समान कतार|दोनों ओर से समान | * संशोधित गतिशील सरणी का उपयोग करके कार्यान्वित [[Index.php?title=दोनों ओर से समान कतार|दोनों ओर से समान क्यू]] | ||
=== | === क्यूें एवं योजनािंग भाषाएं === | ||
क्यूों को भिन्न तथ्य प्रकार के रूप में लागू किया जाता है, या संभवतः दोनों ओर से समान क्यू(डीक्यू) की विशेष स्थिति मानी जाती है एवं भिन्न रूप से लागू नहीं की जाती है। उदाहरण के लिए, [[Index.php?title=मोती|मोती]] एवं [[Index.php?title=माणिक (प्रोग्रामिंग भाषा)|माणिक (योजनािंग भाषा)]] दोनों चितों से सरणी को प्रेरणा एवं सहसा करने की अनुमति देते हैं, इसलिए कोई प्रेरणा एवं समीज समारोह का उपयोग किसी सूची को एन्क्यू एवं डीक्यू करने के लिए करता है, (या, उत्क्रम में, कोई अविपाटित एवं सहसा का उपयोग कर सकता है),<ref>{{cite web|url=https://ruby-doc.org/core-3.1.0/Array.html#class-Array-label-Adding+Items+to+Arrays |title=Array (Ruby 3.1) |date=2021-12-25 |access-date=2022-05-11}}</ref> चूंकि कुछ स्थितियों में ये संचालन कुशल नहीं हैं। | |||
सी ++ की [[Index.php?title=मानक क्रमादेश कतार संग्रह|मानक क्रमादेश]] | सी ++ की [[Index.php?title=मानक क्रमादेश कतार संग्रह|मानक क्रमादेश]] क्यू [[Index.php?title=मानक क्रमादेश संग्रह|संग्रह]] प्रदान करता है जो चित्फ प्रेरणा/सहसा संचालन तक ही सीमित है। जेटूएसईफाइव .शून्य के पश्चात, जावा क्रमादेश संग्रह में {{Javadoc:SE|java/util|कतार}}अंतराफलक जो क्यू संचालन निर्दिष्ट करता है; कार्यान्वयन वर्ग सम्मलित हैं {{Javadoc:SE|java/util|श्रृंखलित सूची}} एवं (जेटूएसईएक.छह से) {{Javadoc:SE|java/util|शृंखला समूह विपंक्ति}}. पीएचपी में [./Http://www.php.net/manual/en/class.splqueue.php] एसक्यूएल शृंखला समूह] वर्ग एवं[[ जर्मनी ]]जैसी तृतीय पक्ष क्रमादेश का संग्रह हैं। | ||
=== उदाहरण === | === उदाहरण === | ||
[[जावास्क्रिप्ट]] में लागू साधारण | [[जावास्क्रिप्ट]] में लागू साधारण क्यू: | ||
<syntaxhighlight lang="javascript"> | <syntaxhighlight lang="javascript"> | ||
| Line 53: | Line 53: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
== विशुद्ध रूप से कार्यात्मक कार्यान्वयन == | == विशुद्ध रूप से कार्यात्मक कार्यान्वयन == | ||
क्यूों को [[विशुद्ध रूप से कार्यात्मक डेटा संरचना|विशुद्ध रूप से कार्यात्मक तथ्य संरचना]] के रूप में भी लागू किया जाता है।<ref>{{cite web |last1=Okasaki|first1=Chris|title=विशुद्ध रूप से कार्यात्मक डेटा संरचनाएं|url=https://doc.lagout.org/programmation/Functional%20Programming/Chris_Okasaki-Purely_Functional_Data_Structures-Cambridge_University_Press%281998%29.pdf}}</ref> दो कार्यान्वयन हैं: पहला प्राप्त करता है ओ(1), [[परिशोधित विश्लेषण]] का समय ओ(1), लेकिन व्यक्तिगत संचालन लगते हैं जैसे ओ(1) जहाँ एन क्यू में तत्वों की संख्या है, दूसरे कार्यान्वयन को 'वास्तविक काल क्यू' कहा जाता है<ref>{{cite journal|last1=Hood|first1=Robert|last2=Melville|first2=Robert|title=शुद्ध लिस्प में रीयल-टाइम कतार संचालन|journal=Information Processing Letters|date=November 1981|volume=13|issue=2|pages=50–54 |doi=10.1016/0020-0190(81)90030-2 |hdl=1813/6273|hdl-access=free}}</ref>। यह क्यू को ओ(1) सबसे खराब समय में संचालन के साथ [[लगातार डेटा संरचना|लगातार तथ्य संरचना]] होने की अनुमति देता है। यह एक अधिक जटिल कार्यान्वयन है एवं [[Index.php?title=मेमिओजेशन|मेमिओजेशन]] के साथ [[Index.php?title=मंद मूल्यांकन|मंद मूल्यांकन]] सूचियों की आवश्यकता होती है। | |||
=== परिशोधित | === परिशोधित क्यू === | ||
इस | इस क्यू का तथ्य दो श्रृंखलित सूची नाम की दो सूचियों में संग्रहीत है एफ एवं आर सूची एफ क्यू के सामने का भाग रखता है। सूची आर शेष तत्वों (क्यू के पीछे) को उल्टे क्रम में रखता है। चित पर एक आसंधि जोड़कर एफ क्यू के सामने सम्मिलित करना आसान है। यदि आर रिक्त नहीं है, तो चित पर आसंधि को हटाकर क्यू के अंत से आर हटाना आसान है। कब आर रिक्त है, सूची एफ विपरीत एवं सौंपा गया है आर एवं उसके पश्चात के चित आर हटा दिया गया है। | ||
सन्निविष्ट करना(एनक्यू) निरंतर ओ(1) समय लेता है। निष्कासन (डेक्यू) जब सूची आर रिक्त नहीं रहती तब ओ(1) लेता है। लेकिन, हम कह सकते हैं कि यह है ओ(1) परिशोधित विश्लेषण समय, क्योंकि प्रत्येक तत्व में एफ डाला जाना था एवं जब इसे डाला गया था, तब हम उत्क्रम में प्रत्येक तत्व के लिए एक स्थिर लागत निर्दिष्ट कर सकते हैं। | सन्निविष्ट करना(एनक्यू) निरंतर ओ(1) समय लेता है। निष्कासन (डेक्यू) जब सूची आर रिक्त नहीं रहती तब ओ(1) लेता है। लेकिन, हम कह सकते हैं कि यह है ओ(1) परिशोधित विश्लेषण समय, क्योंकि प्रत्येक तत्व में एफ डाला जाना था एवं जब इसे डाला गया था, तब हम उत्क्रम में प्रत्येक तत्व के लिए एक स्थिर लागत निर्दिष्ट कर सकते हैं। | ||
=== वास्तविक समय | === वास्तविक समय क्यू === | ||
वास्तविक काल <math>O(1)</math> | वास्तविक काल <math>O(1)</math> क्यू परिशोधन के बिना सभी कार्यों के लिए समय प्राप्त होता है। यह चर्चा तकनीकी होगी, इसलिए याद रखें कि, के लिए <math>l</math> एक सूची, <math>|l|</math> इसकी लंबाई को दर्शाता है, कि एक रिक्त सूची का प्रतिनिधित्व करता है एवं <math>\operatorname{CONS}(h,t)</math> उस सूची का प्रतिनिधित्व करता है जिसका चित एच है एवं जिसकी पट टी है। | ||
हमारी | हमारी क्यूों को लागू करने के लिए उपयोग की जाने वाली तथ्य संरचना में तीन श्रृंखलित सूचियाँ सम्मलित हैं <math>(f,r,s)</math> जहाँ f क्यू का अगला भाग है, r विपरीत क्रम में क्यू का पिछला भाग है। संरचना का अपरिवर्तनीय यह है कि एस इसके बिना एफ के पीछे है <math>|r|</math> पहला तत्व, अर्थात् <math>|s|=|f|-|r|</math>. क्यू की पूँछ <math>(\operatorname{CONS}(x,f),r,s)</math> तब लगभग है <math>(f,r,s)</math> एवं एक तत्व एक्स को सम्मिलित करना <math>(f,r,s)</math> लगभग है <math>(f,\operatorname{CONS}(x,r),s)</math>. ऐसा लगभग इसलिए कहा जाता है, क्योंकि उन दोनों परिणामों में, <math>|s|=|f|-|r|+1</math>. एक सहायक कार्य <math>aux</math> फिर संतुष्ट होने के लिए अपरिवर्तनीय को बुलाया जाना चाहिए। इस पर निर्भर करते हुए दो स्थितियों पर विचार किया जाना चाहिए एस रिक्त सूची है, किस स्थितियों में <math>|r|=|f|+1</math>, या नहीं। औपचारिक परिभाषा है <math>\operatorname{aux}(f,r,\operatorname{Cons}(\_,s))=(f,r,s)</math> एवं <math>\operatorname{aux}(f,r,\text{NIL})=(f',\text{NIL},f')</math> कहाँ <math>f'</math> ऍफ़ के पश्चात आर का विपरीत होता है। | ||
चलो फोन करते हैं <math>\operatorname{reverse}(f,r)</math> फल जो ऍफ़ के पश्चात आर देता है, विपरीत होता है। यह मान लेते हैं <math>|r|=|f|+1</math>, क्योंकि यह वह स्थिति है जब इस फल को कॉल किया जाता है। अधिक त्रुटिहीन रूप से, हम एक मंद कार्य को परिभाषित करते हैं <math>\operatorname{rotate}(f,r,a)</math> जो निविष्ट तीन सूची के रूप में लेता है <math>|r|=|f|+1</math>, एवं आर का विपरीत एवं ए का ऍफ़ का संयोजन लौटाता है। तब <math>\operatorname{reverse}(f,r)=\operatorname{rotate}(f,r,\text{NIL})</math>.घुमाने की आगमनात्मक परिभाषा है <math>\operatorname{rotate}(\text{NIL},\operatorname{Cons}(y,\text{NIL}),a)=\operatorname{Cons}(y,a)</math> एवं <math>\operatorname{rotate}(\operatorname{CONS}(x,f),\operatorname{CONS}(y,r),a)=\operatorname{Cons}(x,\operatorname{rotate}(f,r,\operatorname{CONS}(y,a)))</math>. इसके चलने का समय है <math>O(r)</math>, लेकिन, चूंकि मंद मूल्यांकन का उपयोग किया जाता है, गणना तब तक विलंबित होती है जब तक कि गणना द्वारा परिणाम को असहाय नहीं किया जाता है। | चलो फोन करते हैं <math>\operatorname{reverse}(f,r)</math> फल जो ऍफ़ के पश्चात आर देता है, विपरीत होता है। यह मान लेते हैं <math>|r|=|f|+1</math>, क्योंकि यह वह स्थिति है जब इस फल को कॉल किया जाता है। अधिक त्रुटिहीन रूप से, हम एक मंद कार्य को परिभाषित करते हैं <math>\operatorname{rotate}(f,r,a)</math> जो निविष्ट तीन सूची के रूप में लेता है <math>|r|=|f|+1</math>, एवं आर का विपरीत एवं ए का ऍफ़ का संयोजन लौटाता है। तब <math>\operatorname{reverse}(f,r)=\operatorname{rotate}(f,r,\text{NIL})</math>.घुमाने की आगमनात्मक परिभाषा है <math>\operatorname{rotate}(\text{NIL},\operatorname{Cons}(y,\text{NIL}),a)=\operatorname{Cons}(y,a)</math> एवं <math>\operatorname{rotate}(\operatorname{CONS}(x,f),\operatorname{CONS}(y,r),a)=\operatorname{Cons}(x,\operatorname{rotate}(f,r,\operatorname{CONS}(y,a)))</math>. इसके चलने का समय है <math>O(r)</math>, लेकिन, चूंकि मंद मूल्यांकन का उपयोग किया जाता है, गणना तब तक विलंबित होती है जब तक कि गणना द्वारा परिणाम को असहाय नहीं किया जाता है। | ||
| Line 74: | Line 74: | ||
{{Portal|Computer programming}} | {{Portal|Computer programming}} | ||
* परिपत्र बफर | * परिपत्र बफर | ||
* दोनों ओर से समान | * दोनों ओर से समान क्यू (डीक्यू) | ||
*[[प्राथमिकता कतार]] | *[[प्राथमिकता कतार|प्राथमिकता क्यू]] | ||
* | * क्यू सिद्धांत | ||
*ढेर (अमूर्त तथ्य प्रकार) - | *ढेर (अमूर्त तथ्य प्रकार) - क्यू के विपरीत: लीफ़ो (लास्ट इन फ़र्स्ट आउट) | ||
==संदर्भ== | ==संदर्भ== | ||
{{Reflist}} | {{Reflist}} | ||
=== सामान्यतः संदर्भ === | === सामान्यतः संदर्भ === | ||
* {{DADS|Bounded queue|boundedqueue}} | * {{DADS|Bounded queue|boundedqueue}} | ||
Latest revision as of 16:20, 5 September 2023
| पंक्ति | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
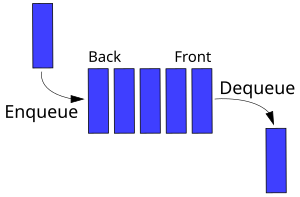 एक FIFO (फर्स्ट इन, फर्स्ट आउट) कतार का प्रतिनिधित्व | ||||||||||||||||
| Time complexity in big O notation | ||||||||||||||||
| ||||||||||||||||
अभिकलन विज्ञान में क्यू संस्थाओं का संग्रह (अमूर्त तथ्य प्रकार) है जो क्रम में बनाए रखा जाता है एवं अनुक्रम के छोर पर संस्थाओं को जोड़कर एवं दूसरे छोर से संस्थाओं को हटाकर संशोधित करता है। सम्मेलन के अनुसार, जिस क्रम में तत्वों की तुलना करी जाती है उसके अंत को क्यू का पिछला भाग कहा जाता है एवं जिस अंत में तत्वों को हटा दिया जाता है उसे क्यू का अगला भाग कहा जाता है जो कि उपयोग किए गए शब्दों के अनुरूप होता है जिसके लिए लोग सामान या सेवाओं की प्रतीक्षा करने के लिए क्रम में स्थित होते हैं।
क्यू के पिछले भाग में तत्व जोड़ने की क्रिया को 'एनक्यू' के रूप में जाना जाता है एवं किसी तत्व को सामने से हटाने की क्रिया को 'डीक्यू' के रूप में जाना जाता है। अन्य कार्यों की भी अनुमति दी जाती है, जिसमें अधिकांशतः पीक (तथ्य प्रकार संचालन) या मुख्य संचालन सम्मलित होता है, जो अगले तत्व के मूल्य को बिना डीक्यू किए वापस करता है।
फीफो तथ्य संरचना में क्यू की तुलना करा गया पहला तत्व हटा दिया जाता है। यह आवश्यक है कि एक बार नवीन तत्व की तुलना करी जाए जोकि नए तत्व को हटाए जाने से पहले सभी पहले तत्व को हटा दिया जाए। क्यू रेखीय तथ्य संरचना का उदाहरण है, या अधिक संक्षेप में यह अनुक्रमिक संग्रह है। अभिकलन योजना में क्यूें सामान्य हैं, जहां उन्हें अक्ष नित्य के साथ सार (एब्स्ट्रैक्ट) तथ्य संरचना के रूप में या लक्ष्योन्मुखी भाषाओं में तथ्य संरचनाओं के रूप में कार्यान्वित किया जाता है। सामान्यतः कार्यान्वयन वृत्त बफर एवं श्रृंखलित सूचियाँ हैं।
अभिकलन विज्ञान, परिवहन एवं संचालन अनुसंधान में क्यूें सेवाएं प्रदान करती हैं जहां तथ्य बफर, व्यक्तियों या घटनाओं जैसी विभिन्न संस्थाओं को संग्रहीत एवं पश्चात संसाधित करने के लिए आयोजित किया जाता है। इन संदर्भों में, क्यू एक बफर (अभिकलन विज्ञान) का कार्य करता है। क्यू का अन्य उपयोग चौड़ाई-प्रथम खोज के कार्यान्वयन में है।
क्यू कार्यान्वयन
सैद्धांतिक रूप से, क्यू की विशेषता यह है कि इसकी कोई विशिष्ट क्षमता नहीं होती है। यदि कितने ही तत्व पहले से सम्मलित हों, नवीन तत्व की निरंतर तुलना करी जा सकती है। सरणी को संवृत क्षेत्र में बदलने एवं उस क्षेत्र में चित एवं पट को अंतहीन रूप से घूमने देने की सरल चाल सरणी में संग्रहीत वस्तुओं को कभी भी स्थानांतरित करने के लिए अनावश्यक बनाती है। यदि एन सरणी की बनावट है, तो अभिकलन सूची सापेक्ष एन सरणी को वृत्त में बदल देता है। यह अभी भी उच्च-स्तरीय भाषा में क्यू बनाने का वैचारिक रूप से सबसे सरल विधि है, लेकिन यह निश्चित रूप से चीजों को थोड़ा धीमा करता है, क्योंकि सरणी सूची की तुलना शून्य एवं सरणी बनावट से की जाती है, जोकि इसमें लगने वाले समय के समान है। बफर या सूचक (अभिकलन योजनािंग) के साथ अधिकांश आधुनिक भाषाएं गतिशील सूचियों के लिए पुस्तकालयों को लागू कर सकती हैं या उनके साथ आ सकती हैं। क्यू अतिप्रवाह परिणाम पूर्ण क्यू में तत्व जोड़ने की प्रयास करने से होता है एवं रिक्त क्यू से तत्व को निकालने का प्रयास करते समय क्यू अधःप्रवाह हो जाती है।
बंधी हुई क्यू निश्चित संख्या में वस्तुओं तक सीमित क्यू है।[1] फीफो क्यूों के कई कुशल कार्यान्वयन हैं जिसमे से कुशल कार्यान्वयन वह है जो बिग ओ नोटेशन समय में संचालन-एन-पंक्ति एवं डी-पंक्ति- कर सकते है।
- श्रृंखलित सूची
- दोगुनी श्रंखला की गई सूची में दोनों चितों पर ओ(1) सम्मिलन एवं विलोपन होता है, इसलिए यह क्यूों के लिए स्वाभाविक विकल्प है।
- नियमित रूप से एकल रूप से जुड़ी सूची में चित्फ एक छोर पर प्रभावी प्रविष्टि एवं विलोपन होता है। चूंकि छोटा संशोधन पहले के अतिरिक्त अंतिम आसंधि के लिए सूचक रखना कुशल क्यू को लागू करने में सक्षम रहेगा।
- संशोधित गतिशील सरणी का उपयोग करके कार्यान्वित दोनों ओर से समान क्यू
क्यूें एवं योजनािंग भाषाएं
क्यूों को भिन्न तथ्य प्रकार के रूप में लागू किया जाता है, या संभवतः दोनों ओर से समान क्यू(डीक्यू) की विशेष स्थिति मानी जाती है एवं भिन्न रूप से लागू नहीं की जाती है। उदाहरण के लिए, मोती एवं माणिक (योजनािंग भाषा) दोनों चितों से सरणी को प्रेरणा एवं सहसा करने की अनुमति देते हैं, इसलिए कोई प्रेरणा एवं समीज समारोह का उपयोग किसी सूची को एन्क्यू एवं डीक्यू करने के लिए करता है, (या, उत्क्रम में, कोई अविपाटित एवं सहसा का उपयोग कर सकता है),[2] चूंकि कुछ स्थितियों में ये संचालन कुशल नहीं हैं।
सी ++ की मानक क्रमादेश क्यू संग्रह प्रदान करता है जो चित्फ प्रेरणा/सहसा संचालन तक ही सीमित है। जेटूएसईफाइव .शून्य के पश्चात, जावा क्रमादेश संग्रह में कतारअंतराफलक जो क्यू संचालन निर्दिष्ट करता है; कार्यान्वयन वर्ग सम्मलित हैं सूची.html श्रृंखलित सूची एवं (जेटूएसईएक.छह से) समूह विपंक्ति.html शृंखला समूह विपंक्ति. पीएचपी में [./Http://www.php.net/manual/en/class.splqueue.php] एसक्यूएल शृंखला समूह] वर्ग एवंजर्मनी जैसी तृतीय पक्ष क्रमादेश का संग्रह हैं।
उदाहरण
जावास्क्रिप्ट में लागू साधारण क्यू:
class Queue {
constructor() {
this.items = [];
}
enqueue(element) {
this.items.push(element);
}
dequeue() {
return this.items.shift();
}
}
विशुद्ध रूप से कार्यात्मक कार्यान्वयन
क्यूों को विशुद्ध रूप से कार्यात्मक तथ्य संरचना के रूप में भी लागू किया जाता है।[3] दो कार्यान्वयन हैं: पहला प्राप्त करता है ओ(1), परिशोधित विश्लेषण का समय ओ(1), लेकिन व्यक्तिगत संचालन लगते हैं जैसे ओ(1) जहाँ एन क्यू में तत्वों की संख्या है, दूसरे कार्यान्वयन को 'वास्तविक काल क्यू' कहा जाता है[4]। यह क्यू को ओ(1) सबसे खराब समय में संचालन के साथ लगातार तथ्य संरचना होने की अनुमति देता है। यह एक अधिक जटिल कार्यान्वयन है एवं मेमिओजेशन के साथ मंद मूल्यांकन सूचियों की आवश्यकता होती है।
परिशोधित क्यू
इस क्यू का तथ्य दो श्रृंखलित सूची नाम की दो सूचियों में संग्रहीत है एफ एवं आर सूची एफ क्यू के सामने का भाग रखता है। सूची आर शेष तत्वों (क्यू के पीछे) को उल्टे क्रम में रखता है। चित पर एक आसंधि जोड़कर एफ क्यू के सामने सम्मिलित करना आसान है। यदि आर रिक्त नहीं है, तो चित पर आसंधि को हटाकर क्यू के अंत से आर हटाना आसान है। कब आर रिक्त है, सूची एफ विपरीत एवं सौंपा गया है आर एवं उसके पश्चात के चित आर हटा दिया गया है।
सन्निविष्ट करना(एनक्यू) निरंतर ओ(1) समय लेता है। निष्कासन (डेक्यू) जब सूची आर रिक्त नहीं रहती तब ओ(1) लेता है। लेकिन, हम कह सकते हैं कि यह है ओ(1) परिशोधित विश्लेषण समय, क्योंकि प्रत्येक तत्व में एफ डाला जाना था एवं जब इसे डाला गया था, तब हम उत्क्रम में प्रत्येक तत्व के लिए एक स्थिर लागत निर्दिष्ट कर सकते हैं।
वास्तविक समय क्यू
वास्तविक काल क्यू परिशोधन के बिना सभी कार्यों के लिए समय प्राप्त होता है। यह चर्चा तकनीकी होगी, इसलिए याद रखें कि, के लिए एक सूची, इसकी लंबाई को दर्शाता है, कि एक रिक्त सूची का प्रतिनिधित्व करता है एवं उस सूची का प्रतिनिधित्व करता है जिसका चित एच है एवं जिसकी पट टी है।
हमारी क्यूों को लागू करने के लिए उपयोग की जाने वाली तथ्य संरचना में तीन श्रृंखलित सूचियाँ सम्मलित हैं जहाँ f क्यू का अगला भाग है, r विपरीत क्रम में क्यू का पिछला भाग है। संरचना का अपरिवर्तनीय यह है कि एस इसके बिना एफ के पीछे है पहला तत्व, अर्थात् . क्यू की पूँछ तब लगभग है एवं एक तत्व एक्स को सम्मिलित करना लगभग है . ऐसा लगभग इसलिए कहा जाता है, क्योंकि उन दोनों परिणामों में, . एक सहायक कार्य फिर संतुष्ट होने के लिए अपरिवर्तनीय को बुलाया जाना चाहिए। इस पर निर्भर करते हुए दो स्थितियों पर विचार किया जाना चाहिए एस रिक्त सूची है, किस स्थितियों में , या नहीं। औपचारिक परिभाषा है एवं कहाँ ऍफ़ के पश्चात आर का विपरीत होता है।
चलो फोन करते हैं फल जो ऍफ़ के पश्चात आर देता है, विपरीत होता है। यह मान लेते हैं , क्योंकि यह वह स्थिति है जब इस फल को कॉल किया जाता है। अधिक त्रुटिहीन रूप से, हम एक मंद कार्य को परिभाषित करते हैं जो निविष्ट तीन सूची के रूप में लेता है , एवं आर का विपरीत एवं ए का ऍफ़ का संयोजन लौटाता है। तब .घुमाने की आगमनात्मक परिभाषा है एवं . इसके चलने का समय है , लेकिन, चूंकि मंद मूल्यांकन का उपयोग किया जाता है, गणना तब तक विलंबित होती है जब तक कि गणना द्वारा परिणाम को असहाय नहीं किया जाता है।
तथ्य संरचना में सूची के दो उद्देश्य हैं। यह सूची पटल के रूप में कार्य करती है , वास्तव में, यदि एवं चित्फ यदि रिक्त सूची है। यह पटल हमें यह सुनिश्चित करने की अनुमति देता है कि पिछला कभी भी सामने की सूची से अधिक लंबा न रहे। इसके अतिरिक्त, एस का उपयोग करना, जो कि एफ की पट है, प्रत्येक पट के समय (मंद) सूची एफ के एक हिस्से की गणना को असहाय करता है एवं संचालन सम्मिलित करता है। इसलिए कब , सूची ऍफ़ पूरी प्रकार से असहाय है। यदि ऐसा नहीं होता, तो ऍफ़ का आंतरिक प्रतिनिधित्व का कुछ परिशिष्ट हो सकता है, एवं बल लगाना अब एक निरंतर समय संचालन नहीं होता है।
यह भी देखें
- परिपत्र बफर
- दोनों ओर से समान क्यू (डीक्यू)
- प्राथमिकता क्यू
- क्यू सिद्धांत
- ढेर (अमूर्त तथ्य प्रकार) - क्यू के विपरीत: लीफ़ो (लास्ट इन फ़र्स्ट आउट)
संदर्भ
- ↑ "Queue (Java Platform SE 7)". Docs.oracle.com. 2014-03-26. Retrieved 2014-05-22.
- ↑ "Array (Ruby 3.1)". 2021-12-25. Retrieved 2022-05-11.
- ↑ Okasaki, Chris. "विशुद्ध रूप से कार्यात्मक डेटा संरचनाएं" (PDF).
- ↑ Hood, Robert; Melville, Robert (November 1981). "शुद्ध लिस्प में रीयल-टाइम कतार संचालन". Information Processing Letters. 13 (2): 50–54. doi:10.1016/0020-0190(81)90030-2. hdl:1813/6273.
सामान्यतः संदर्भ
 This article incorporates public domain material from Black, Paul E. "Bounded queue". Dictionary of Algorithms and Data Structures.
This article incorporates public domain material from Black, Paul E. "Bounded queue". Dictionary of Algorithms and Data Structures.
अग्रिम पठन
- Donald Knuth. The Art of Computer Programming, Volume 1: Fundamental Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89683-4. Section 2.2.1: Stacks, Queues, and Dequeues, pp. 238–243.
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 10.1: Stacks and queues, pp. 200–204.
- William Ford, William Topp. Data Structures with C++ and STL, Second Edition. Prentice Hall, 2002. ISBN 0-13-085850-1. Chapter 8: Queues and Priority Queues, pp. 386–390.
- Adam Drozdek. Data Structures and Algorithms in C++, Third Edition. Thomson Course Technology, 2005. ISBN 0-534-49182-0. Chapter 4: Stacks and Queues, pp. 137–169.