ट्रैक्ट्रिक्स: Difference between revisions
No edit summary |
No edit summary |
||
| Line 4: | Line 4: | ||
'''[[आइजैक न्यूटन|न्यूटन]] (1676) और [[क्रिस्टियान ह्यूजेन्स]] (1693) द्वारा इसका अध्ययन किया गया था।<ref name=":0" />''' | '''[[आइजैक न्यूटन|न्यूटन]] (1676) और [[क्रिस्टियान ह्यूजेन्स]] (1693) द्वारा इसका अध्ययन किया गया था।<ref name=":0" />''' | ||
==गणितीय व्युत्पत्ति== | ==गणितीय व्युत्पत्ति== | ||
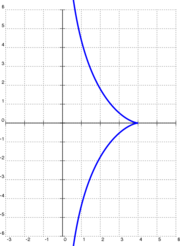
[[Image:Tractrix.png|thumb|180px|शुरुआत में ऑब्जेक्ट के साथ ट्रैक्ट्रिक्स {{math|(4, 0)}}]]मान लीजिए कि वस्तु को रखा गया है {{math|(''a'', 0)}} (या {{math|(4, 0)}} दाईं ओर दिखाए गए उदाहरण में), और मूल पर खींचने वाला (गणित), इसलिए {{mvar|a}} खींचने वाले धागे की लंबाई है (दाईं ओर उदाहरण में 4)। फिर खींचने वाला साथ चलना शुरू कर देता है {{mvar|y}} अक्ष सकारात्मक दिशा में. प्रत्येक क्षण, धागा वक्र पर [[स्पर्शरेखा]] होगा {{math|1=''y'' = ''y''(''x'')}} वस्तु द्वारा वर्णित है, ताकि यह खींचने वाले की गति से पूरी तरह से निर्धारित हो जाए। गणितीय रूप से, यदि वस्तु के निर्देशांक हैं {{math|(''x'', ''y'')}}, द {{nowrap|{{mvar|y}}-coordinate}}खींचने वाले का है <math>y + \operatorname{sign}(y)\sqrt{a^2 - x^2},</math> [[पाइथागोरस प्रमेय]] द्वारा. यह लिखने पर कि धागे की ढलान वक्र की स्पर्शरेखा के बराबर होती है, [[अंतर समीकरण]] की ओर ले जाती है | [[Image:Tractrix.png|thumb|180px|शुरुआत में ऑब्जेक्ट के साथ ट्रैक्ट्रिक्स {{math|(4, 0)}}]]मान लीजिए कि वस्तु को दाईं ओर दिखाए गए उदाहरण में {{math|(''a'', 0)}} (या {{math|(4, 0)}}) रखा गया है {{math|(''a'', 0)}} (या {{math|(4, 0)}} दाईं ओर दिखाए गए उदाहरण में), और मूल पर खींचने वाला (गणित), इसलिए {{mvar|a}} खींचने वाले धागे की लंबाई है (दाईं ओर उदाहरण में 4)। फिर खींचने वाला साथ चलना शुरू कर देता है {{mvar|y}} अक्ष सकारात्मक दिशा में. प्रत्येक क्षण, धागा वक्र पर [[स्पर्शरेखा]] होगा {{math|1=''y'' = ''y''(''x'')}} वस्तु द्वारा वर्णित है, ताकि यह खींचने वाले की गति से पूरी तरह से निर्धारित हो जाए। गणितीय रूप से, यदि वस्तु के निर्देशांक हैं {{math|(''x'', ''y'')}}, द {{nowrap|{{mvar|y}}-coordinate}}खींचने वाले का है <math>y + \operatorname{sign}(y)\sqrt{a^2 - x^2},</math> [[पाइथागोरस प्रमेय]] द्वारा. यह लिखने पर कि धागे की ढलान वक्र की स्पर्शरेखा के बराबर होती है, [[अंतर समीकरण]] की ओर ले जाती है | ||
:<math>\frac{dy}{dx} = \pm\frac{\sqrt{a^2-x^2}}{x}</math> | :<math>\frac{dy}{dx} = \pm\frac{\sqrt{a^2-x^2}}{x}</math> | ||
प्रारंभिक शर्त के साथ {{math|1=''y''(''a'') = 0}}. इसका समाधान है | प्रारंभिक शर्त के साथ {{math|1=''y''(''a'') = 0}}. इसका समाधान है | ||
Revision as of 17:23, 24 September 2023
ज्यामिति में, ट्रैक्ट्रिक्स (from Latin trahere 'to pull, drag'; बहुवचन: ट्रैक्ट्रिसेस) वह वक्र है जिसके अनुदिश कोई वस्तु घर्षण के प्रभाव में चलती है, जब खींचने वाले बिंदु (ट्रैक्टर) से जुड़े रेखा खंड द्वारा क्षैतिज विमान पर खींचा जाता है जो समकोण पर चलता है वस्तु और खींचने वाले के बीच अनंत गति से प्रारंभिक रेखा है। इसलिए यह अनुसरण का वक्र है। इसे पहली बार 1670 में क्लाउड पेरौल्ट द्वारा प्रस्तुत किया गया था, और बाद में आइजैक न्यूटन (1676) और क्रिस्टियान ह्यूजेन्स (1693) द्वारा इसका अध्ययन किया गया था।[1]
न्यूटन (1676) और क्रिस्टियान ह्यूजेन्स (1693) द्वारा इसका अध्ययन किया गया था।[1]
गणितीय व्युत्पत्ति
मान लीजिए कि वस्तु को दाईं ओर दिखाए गए उदाहरण में (a, 0) (या (4, 0)) रखा गया है (a, 0) (या (4, 0) दाईं ओर दिखाए गए उदाहरण में), और मूल पर खींचने वाला (गणित), इसलिए a खींचने वाले धागे की लंबाई है (दाईं ओर उदाहरण में 4)। फिर खींचने वाला साथ चलना शुरू कर देता है y अक्ष सकारात्मक दिशा में. प्रत्येक क्षण, धागा वक्र पर स्पर्शरेखा होगा y = y(x) वस्तु द्वारा वर्णित है, ताकि यह खींचने वाले की गति से पूरी तरह से निर्धारित हो जाए। गणितीय रूप से, यदि वस्तु के निर्देशांक हैं (x, y), द y-coordinateखींचने वाले का है पाइथागोरस प्रमेय द्वारा. यह लिखने पर कि धागे की ढलान वक्र की स्पर्शरेखा के बराबर होती है, अंतर समीकरण की ओर ले जाती है
प्रारंभिक शर्त के साथ y(a) = 0. इसका समाधान है
जहां संकेत ± खींचने वाले की गति की दिशा (सकारात्मक या नकारात्मक) पर निर्भर करता है।
इस समाधान का पहला पद भी लिखा जा सकता है
- कहाँ arsech व्युत्क्रम अतिपरवलयिक छेदक फलन है।
समाधान से पहले का संकेत इस बात पर निर्भर करता है कि खींचने वाला ऊपर की ओर जाता है या नीचे की ओर। दोनों शाखाएँ ट्रैक्ट्रिक्स से संबंधित हैं, जो शिखर (विलक्षणता) बिंदु पर मिलती हैं (a, 0).
ट्रैक्ट्रिक्स का आधार
ट्रैक्ट्रिक्स का आवश्यक गुण बिंदु के बीच की दूरी की स्थिरता है P वक्र पर और स्पर्शरेखा रेखा के प्रतिच्छेदन पर Pवक्र के अनंतस्पर्शी के साथ।
ट्रैक्ट्रिक्स को कई तरीकों से माना जा सकता है:
- यह सीधी रेखा पर (बिना फिसले) घूम रहे अतिशयोक्तिपूर्ण सर्पिल के केंद्र का लोकस (गणित) है।
- यह ज़ंजीर का फ़ंक्शन का इनवॉल्व है, जो दो बिंदुओं से जुड़ी पूरी तरह से लचीली, elastomer, सजातीय स्ट्रिंग का वर्णन करता है जो गुरुत्वाकर्षण क्षेत्र के अधीन है। कैटेनरी का समीकरण है y(x) = a cosh x/a.
- प्रक्षेपवक्र कार के पिछले धुरी के मध्य द्वारा स्थिर गति और स्थिर दिशा (प्रारंभ में वाहन के लंबवत) पर रस्सी द्वारा खींचे जाने से निर्धारित होता है।
- यह (अरैखिक) वक्र है जो त्रिज्या का वृत्त है a सीधी रेखा पर घूम रहा है, जिसका केंद्र पर है x अक्ष, हर समय लंबवत रूप से प्रतिच्छेद करता है।
फ़ंक्शन क्षैतिज अनंतस्पर्शी को स्वीकार करता है। के संबंध में वक्र सममित है y-एक्सिस। वक्रता त्रिज्या है r = a cot x/y.
ट्रैक्ट्रिक्स का बड़ा निहितार्थ इसके अनंतस्पर्शी: छद्ममंडल के बारे में इसकी क्रांति की सतह का अध्ययन था। 1868 में यूजेनियो बेल्ट्रामी द्वारा अध्ययन किया गया,[citation needed]निरंतर नकारात्मक गाऊसी वक्रता की सतह के रूप में, छद्ममंडल अतिशयोक्तिपूर्ण ज्यामिति का स्थानीय मॉडल है। इस विचार को कास्नर और न्यूमैन ने अपनी पुस्तक गणित और कल्पना में आगे बढ़ाया, जहां उन्होंने टॉय ट्रेन को ट्रैक्ट्रिक्स उत्पन्न करने के लिए पॉकेट घड़ी को खींचते हुए दिखाया।[2]
गुण
- वक्र को समीकरण द्वारा पैरामीटराइज़ किया जा सकता है .[3]
- जिस ज्यामितीय तरीके से इसे परिभाषित किया गया था, उसके कारण ट्रैक्ट्रिक्स में यह गुण है कि अनंतस्पर्शी और स्पर्शरेखा के बिंदु के बीच, इसके स्पर्शरेखा के खंड की लंबाई स्थिर होती है a.
- बीच में शाखा की चाप की लंबाई x = x1 और x = x2 है a ln x1/x2.
- ट्रैक्ट्रिक्स और उसके अनंतस्पर्शी के बीच का क्षेत्र है π a2/2, जिसे अभिन्न या मैमिकॉन प्रमेय का उपयोग करके पाया जा सकता है।
- ट्रैक्ट्रिक्स की सतह के सामान्यों का आवरण (गणित) (अर्थात्, ट्रैक्ट्रिक्स का उत्क्रांति) द्वारा दिया गया कैटेनरी (या श्रृंखला वक्र) है y = a cosh x/a.
- ट्रैक्ट्रिक्स को उसके अनंतस्पर्शी बिंदु के चारों ओर घुमाने से बनी क्रांति की सतह छद्मगोला है।
व्यावहारिक अनुप्रयोग
1927 में, पी.जी.ए.एच. वोइगट ने इस धारणा के आधार पर हॉर्न लाउडस्पीकर डिज़ाइन का पेटेंट कराया कि हॉर्न के माध्यम से यात्रा करने वाली तरंग का अग्र भाग स्थिर त्रिज्या का गोलाकार होता है। विचार यह है कि हॉर्न के भीतर ध्वनि के आंतरिक परावर्तन के कारण होने वाली विकृति को कम किया जाए। परिणामी आकृति ट्रैक्ट्रिक्स की क्रांति की सतह है।[4]
शीट मेटल के निर्माण की तकनीक में महत्वपूर्ण अनुप्रयोग है। विशेष रूप से ट्रैक्ट्रिक्स प्रोफ़ाइल का उपयोग डाई के कोने के लिए किया जाता है जिस पर गहरी ड्राइंग के दौरान शीट धातु को मोड़ा जाता है।[5]
एक दांतेदार बेल्ट-पुली डिज़ाइन अपने दांतों के लिए ट्रैक्ट्रिक्स कैटेनरी आकार का उपयोग करके यांत्रिक विद्युत संचरण के लिए बेहतर दक्षता प्रदान करता है।[6] यह आकार चरखी से जुड़े बेल्ट के दांतों के घर्षण को कम करता है, क्योंकि हिलने वाले दांत न्यूनतम स्लाइडिंग संपर्क के साथ जुड़ते और अलग होते हैं। मूल टाइमिंग बेल्ट डिज़ाइन में सरल ट्रैपेज़ॉइडल या गोलाकार दांत आकार का उपयोग किया जाता है, जो महत्वपूर्ण फिसलन और घर्षण का कारण बनता है।
ड्राइंग मशीनें
- अक्टूबर-नवंबर 1692 में, क्रिस्टियान ह्यूजेंस ने तीन ट्रैक्ट्रिक्स-ड्राइंग मशीनों का वर्णन किया।[citation needed]
- 1693 में गॉटफ्राइड विल्हेम लीबनिज़ ने सार्वभौमिक ट्रैक्शनल मशीन तैयार की, जो सिद्धांत रूप में, किसी भी साधारण अंतर समीकरण#परिभाषाओं को एकीकृत कर सकती थी।[7] यह अवधारणा ट्रैक्शनल सिद्धांत को लागू करने वाला एनालॉग कंप्यूटिंग तंत्र था। लीबनिज़ के समय की तकनीक के साथ इस उपकरण का निर्माण करना अव्यावहारिक था, और इसे कभी साकार नहीं किया गया।
- 1706 में जॉन पर्क्स ने अतिशयोक्तिपूर्ण कार्य क्वाडरेचर को साकार करने के लिए ट्रैक्शनल मशीन का निर्माण किया।[8]
- 1729 में जॉन पोलेनी ने ट्रैक्शनल उपकरण बनाया जो लॉगरिदमिक कार्यों को खींचने में सक्षम बनाता था।[9]
इन सभी मशीनों का इतिहास एच. जे. एम. बोस के लेख में देखा जा सकता है।[10]
यह भी देखें
- दीनी की सतह
- के लिए अतिशयोक्तिपूर्ण कार्य tanh, sech, csch, arcosh
- के लिए प्राकृतिक लघुगणक ln
- के लिए साइन फ़ंक्शन sgn
- त्रिकोणमितीय कार्यों के लिए sin, cos, tan, arccot, csc
टिप्पणियाँ
- ↑ 1.0 1.1 Stillwell, John (2010). गणित और उसका इतिहास (revised, 3rd ed.). Springer Science & Business Media. p. 345. ISBN 978-1-4419-6052-8., extract of page 345
- ↑ Kasner, Edward; Newman, James (2013). "Figure 45(a)". गणित और कल्पना. Dover Books on Mathematics. Courier Corporation. p. 141. ISBN 9780486320274.
- ↑ O'Connor, John J.; Robertson, Edmund F., "Tractrix", MacTutor History of Mathematics archive, University of St Andrews
- ↑ Horn loudspeaker design pp. 4–5. (Reprinted from Wireless World, March 1974)
- ↑ Lange, Kurt (1985). धातु निर्माण की पुस्तिका. McGraw Hill Book Company. p. 20.43.
- ↑ "Gates Powergrip GT3 Drive Design Manual" (PDF). Gates Corporation. 2014. p. 177. Retrieved 17 November 2017.
The GT tooth profile is based on the tractix mathematical function. Engineering handbooks describe this function as a "frictionless" system. This early development by Schiele is described as an involute form of a catenary.
- ↑ Milici, Pietro (2014). Lolli, Gabriele (ed.). From Logic to Practice: Italian Studies in the Philosophy of Mathematics. Springer.
... विशेष अंतर समीकरणों को हल करने के लिए ... यांत्रिक उपकरणों का अध्ययन किया गया ... हमें लीबनिज़ की 'यूनिवर्सल ट्रैक्शनल मशीन' को याद करना चाहिए
- ↑ Perks, John (1706). "हाइपरबोला के लिए एक नए चतुर्भुज का निर्माण और गुण". Philosophical Transactions. 25: 2253–2262. doi:10.1098/rstl.1706.0017. JSTOR 102681. S2CID 186211499.
- ↑ Poleni, John (1729). गणितीय अक्षरों का संग्रह. p. letter no. 7.
- ↑ Bos, H. J. M. (1989). "Recognition and Wonder – Huygens, Tractional Motion and Some Thoughts on the History of Mathematics" (PDF). Euclides. 63: 65–76.
संदर्भ
- Kasner, Edward; Newman, James (1940). Mathematics and the Imagination. Simon & Schuster. p. 141–143.
- Lawrence, J. Dennis (1972). A Catalog of Special Plane Curves. Dover Publications. pp. 5, 199. ISBN 0-486-60288-5.