असतत हार्टले परिवर्तन: Difference between revisions
(Created page with "{{Short description|Fourier-related mathematical transform}} असतत हार्टले परिवर्तन (DHT) सिग्नल प्रोसेस...") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Fourier-related mathematical transform}} | {{Short description|Fourier-related mathematical transform}} | ||
असतत [[ हार्टले परिवर्तन ]] ( | '''असतत[[ हार्टले परिवर्तन | हार्टले परिवर्तन]](डीएचटी)''' सिग्नल प्रोसेसिंग और संबंधित क्षेत्रों में समान अनुप्रयोगों के साथ, असतत [[फूरियर रूपांतरण]] (डीएफटी) के समान असतत, आवधिक डेटा का एक [[फूरियर-संबंधित परिवर्तन]] है। डीएफटी से इसका मुख्य अंतर यह है कि यह वास्तविक इनपुट को वास्तविक आउटपुट में बदल देता है, जिसमें सम्मिश्र संख्याओं की कोई आंतरिक भागीदारी नहीं होती है। जिस तरह डीएफटी [[असतत फूरियर रूपांतरण]] (एफटी) का असतत एनालॉग है, उसी तरह डीएचटी 1942 में राल्फ वी. एल. हार्टले द्वारा प्रस्तुत किए गए निरंतर हार्टले ट्रांसफॉर्म (एचटी) का असतत एनालॉग है।<ref name="Hartley_1942"/> | ||
क्योंकि डीएचटी के लिए [[फास्ट फूरियर ट्रांसफॉर्म]] (एफएफटी) के अनुरूप तेज़ एल्गोरिदम हैं, डीएचटी को मूल रूप से 1983 में रोनाल्ड एन. ब्रेसवेल द्वारा प्रस्तावित किया गया था।<ref name="Bracewell_1983"/>सामान्य स्थिति में एक अधिक कुशल कम्प्यूटेशनल उपकरण के रूप में जहां डेटा पूरी तरह से वास्तविक है। हालाँकि, बाद में यह तर्क दिया गया कि वास्तविक इनपुट या आउटपुट के लिए विशेष एफएफटी एल्गोरिदम | क्योंकि डीएचटी के लिए [[फास्ट फूरियर ट्रांसफॉर्म]] (एफएफटी) के अनुरूप तेज़ एल्गोरिदम हैं, डीएचटी को मूल रूप से 1983 में रोनाल्ड एन. ब्रेसवेल द्वारा प्रस्तावित किया गया था।<ref name="Bracewell_1983"/>सामान्य स्थिति में एक अधिक कुशल कम्प्यूटेशनल उपकरण के रूप में जहां डेटा पूरी तरह से वास्तविक है। हालाँकि, बाद में यह तर्क दिया गया कि वास्तविक इनपुट या आउटपुट के लिए विशेष एफएफटी एल्गोरिदम सामान्यतः डीएचटी के लिए किसी भी संबंधित एल्गोरिदम की तुलना में थोड़े कम संचालन के साथ पाए जा सकते हैं। | ||
== परिभाषा == | == परिभाषा == | ||
औपचारिक रूप से, असतत हार्टले परिवर्तन एक रैखिक, | औपचारिक रूप से, असतत हार्टले परिवर्तन एक रैखिक, इनवेर्टीबल [[फ़ंक्शन (गणित)]] ''H'':'''R'''<sup>''n''</sup> → '''R'''<sup>''n''</sup> है (जहाँ ''''R'''<nowiki/>' [[वास्तविक संख्या]]ओं के समुच्चय को दर्शाता है)। सूत्र के अनुसार N वास्तविक संख्याएँ ''x''<sub>0</sub>, ..., ''x<sub>N</sub>''<sub>−1</sub> को N वास्तविक संख्याएँ ''H''<sub>0</sub>, ..., ''H<sub>N</sub>''<sub>−1</sub> में बदल दिया जाता है | ||
:<math>H_k = \sum_{n=0}^{N-1} x_n \operatorname{cas} \left( \frac{2 \pi}{N} n k \right) = \sum_{n=0}^{N-1} x_n \left[ \cos \left( \frac{2 \pi}{N} n k \right) + \sin \left( \frac{2 \pi}{N} n k \right) \right] \quad \quad k = 0, \dots, N-1 .</math> | :<math>H_k = \sum_{n=0}^{N-1} x_n \operatorname{cas} \left( \frac{2 \pi}{N} n k \right) = \sum_{n=0}^{N-1} x_n \left[ \cos \left( \frac{2 \pi}{N} n k \right) + \sin \left( \frac{2 \pi}{N} n k \right) \right] \quad \quad k = 0, \dots, N-1 .</math> | ||
संमिश्रण <math>\cos(z) + \sin(z)</math> <math>= \sqrt{2} \cos\left(z-\frac\pi 4\right)</math> कभी-कभी निरूपित किया जाता है {{math|cas(''z'')}}, और इससे भ्रमित नहीं होना चाहिए {{math|1=[[cis (mathematics)|cis(''z'')]] = ''e<sup>iz</sup>'' = cos(''z'') + ''i'' sin(''z'')}}, या {{math|1=''e''<sup>−''iz''</sup> = cis(−''z'')}} जो डीएफटी परिभाषा में दिखाई देता है (जहां ''i'' एक [[काल्पनिक इकाई]] के रूप में है)। | |||
डीएफटी की तरह, परिवर्तन के सामने समग्र पैमाने का कारक और साइन टर्म का संकेत परंपरा का विषय है। हालाँकि ये परंपराएँ कभी-कभी लेखकों के बीच भिन्न होती हैं, लेकिन वे परिवर्तन के आवश्यक गुणों को प्रभावित नहीं करती हैं। | डीएफटी की तरह, परिवर्तन के सामने समग्र पैमाने का कारक और साइन टर्म का संकेत परंपरा का विषय है। हालाँकि ये परंपराएँ कभी-कभी लेखकों के बीच भिन्न होती हैं, लेकिन वे परिवर्तन के आवश्यक गुणों को प्रभावित नहीं करती हैं। | ||
== गुण == | == गुण == | ||
परिवर्तन की व्याख्या | परिवर्तन की व्याख्या सदिश (''x''<sub>0</sub>, ...., ''x<sub>N</sub>''<sub>−1</sub>) के गुणन के रूप में की जा सकती है, ''N''-बाय-''N'' [[मैट्रिक्स (गणित)|आव्यूह (गणित)]] द्वारा; इसलिए, असतत हार्टले रूपांतरण एक [[रैखिक ऑपरेटर]] है। आव्यूह इनवेर्टीबल है; व्युत्क्रम परिवर्तन, जो किसी को ''x<sub>n</sub>'' पुनर्प्राप्त करने की अनुमति देता है ''H<sub>k</sub>'', से बस H<sub>k</sub> का डीएचटी है 1/''N'' से गुणा किया गया है। अर्थात्, डीएचटी एक समग्र पैमाने के कारक तक अपना स्वयं का व्युत्क्रम (इनवोल्यूशन (गणित) है। | ||
डीएचटी का उपयोग डीएफटी की गणना करने के लिए किया जा सकता है, और इसके | डीएचटी का उपयोग डीएफटी की गणना करने के लिए किया जा सकता है, और इसके विपरीत किया जा सकता है। वास्तविक इनपुट के लिए x<sub>n</sub>, डीएफटी आउटपुट ''X<sub>k</sub>'' एक वास्तविक हिस्सा है (''H<sub>k</sub>'' + ''H<sub>N−k</sub>'')/2 और एक काल्पनिक भाग (''H<sub>N−k</sub>'' − ''H<sub>k</sub>'')/2. इसके विपरीत, डीएचटी ''x<sub>n</sub>'' के डीएफटी की गणना के बराबर है1 + i से गुणा किया जाता है, फिर परिणाम का वास्तविक भाग लिया जाता है। | ||
डीएफटी की तरह, दो | डीएफटी की तरह, दो सदिश x = (x<sub>n</sub>) का एक चक्रीय [[कनवल्शन]] z = x∗y) और y = (y<sub>n</sub>) एक सदिश z = (z<sub>n</sub>) उत्पन्न करने के लिए), पूरी लंबाई ''N'', डीएचटी के बाद एक सरल ऑपरेशन बन जाता है। विशेष रूप से, मान लीजिए कि सदिश '''X, Y''' और '''Z''' क्रमशः '''x, y''' और '''z''' के डीएचटी को दर्शाते हैं। फिर '''Z''' के तत्व इस प्रकार दिए गए हैं: | ||
:<math> \begin{matrix} | :<math> \begin{matrix} | ||
| Line 28: | Line 28: | ||
\end{matrix} | \end{matrix} | ||
</math> | </math> | ||
जहाँ हम सभी सदिशों को N (X) में आवर्त मानते हैं<sub>N</sub>= एक्स<sub>0</sub>, वगैरह)। इस प्रकार, जैसे डीएफटी एक कनवल्शन को | जहाँ हम सभी सदिशों को N (X) में आवर्त मानते हैं<sub>N</sub>= एक्स<sub>0</sub>, वगैरह)। इस प्रकार, जैसे डीएफटी एक कनवल्शन को सम्मिश्र संख्याओं (वास्तविक और काल्पनिक भागों के जोड़े) के बिंदुवार गुणन में बदल देता है, डीएचटी एक कनवल्शन को वास्तविक आवृत्ति घटकों के जोड़े के एक सरल संयोजन में बदल देता है। व्युत्क्रम DHT तब वांछित सदिश 'z' उत्पन्न करता है। इस तरह, डीएचटी के लिए एक तेज़ एल्गोरिदम (नीचे देखें) कनवल्शन के लिए एक तेज़ एल्गोरिदम उत्पन्न करता है। (यह डीएफटी के लिए संबंधित प्रक्रिया से थोड़ा अधिक महंगा है, इसमें नीचे दिए गए परिवर्तनों की लागत शामिल नहीं है, क्योंकि उपरोक्त जोड़ीदार ऑपरेशन के लिए जटिल गुणन के 6 की तुलना में 8 वास्तविक-अंकगणितीय संचालन की आवश्यकता होती है। इस गणना में शामिल नहीं है 2 से विभाजन, जिसे अवशोषित किया जा सकता है उदाहरण के लिए उलटा डीएचटी के 1/एन सामान्यीकरण में।) | ||
== तेज़ एल्गोरिदम == | == तेज़ एल्गोरिदम == | ||
डीएफटी की तरह, सीधे डीएचटी परिभाषा का मूल्यांकन करने के लिए ओ(एन) की आवश्यकता होगी<sup>2</sup>) अंकगणितीय परिचालन ([[ बिग ओ अंकन ]] देखें)। हालाँकि, FFT के समान तेज़ एल्गोरिदम हैं, जो केवल O(N लॉग N) संचालन में समान परिणाम की गणना करते हैं। लगभग हर एफएफटी एल्गोरिदम, कूली-टुकी एफएफटी एल्गोरिदम|कूली-ट्यूकी से [[प्राइम-फैक्टर एफएफटी एल्गोरिदम]]|प्राइम-फैक्टर से विनोग्राड (1985) तक<ref name="Sorensen_1985"/>ब्रून के FFT एल्गोरिथम के लिए|ब्रून का (1993),<ref name="Bini-Bozzo_1993"/>असतत हार्टले परिवर्तन के लिए एक सीधा एनालॉग है। (हालांकि, कुछ अधिक विदेशी एफएफटी एल्गोरिदम, जैसे कि क्यूएफटी, की अभी तक डीएचटी के संदर्भ में जांच नहीं की गई है।) | डीएफटी की तरह, सीधे डीएचटी परिभाषा का मूल्यांकन करने के लिए ओ(एन) की आवश्यकता होगी<sup>2</sup>) अंकगणितीय परिचालन ([[ बिग ओ अंकन ]] देखें)। हालाँकि, FFT के समान तेज़ एल्गोरिदम हैं, जो केवल O(N लॉग N) संचालन में समान परिणाम की गणना करते हैं। लगभग हर एफएफटी एल्गोरिदम, कूली-टुकी एफएफटी एल्गोरिदम|कूली-ट्यूकी से [[प्राइम-फैक्टर एफएफटी एल्गोरिदम]]|प्राइम-फैक्टर से विनोग्राड (1985) तक<ref name="Sorensen_1985"/>ब्रून के FFT एल्गोरिथम के लिए|ब्रून का (1993),<ref name="Bini-Bozzo_1993"/>असतत हार्टले परिवर्तन के लिए एक सीधा एनालॉग है। (हालांकि, कुछ अधिक विदेशी एफएफटी एल्गोरिदम, जैसे कि क्यूएफटी, की अभी तक डीएचटी के संदर्भ में जांच नहीं की गई है।) | ||
विशेष रूप से, Cooley-Tukey एल्गोरिदम के DHT एनालॉग को | विशेष रूप से, Cooley-Tukey एल्गोरिदम के DHT एनालॉग को सामान्यतः फास्ट हार्टले ट्रांसफॉर्म (FHT) एल्गोरिदम के रूप में जाना जाता है, और इसे पहली बार 1984 में ब्रेसवेल द्वारा वर्णित किया गया था।<ref name="Bracewell_1984"/>यह एफएचटी एल्गोरिथ्म, कम से कम जब दो|पावर-ऑफ-दो आकार एन की शक्ति पर लागू किया जाता है, तो 1987 में [[स्टैनफोर्ड विश्वविद्यालय]] को जारी संयुक्त राज्य [[सॉफ्टवेयर पेटेंट]] संख्या 4,646,256 का विषय है। स्टैनफोर्ड ने इस पेटेंट को 1994 में सार्वजनिक डोमेन में रखा (ब्रेसवेल, 1995)।<ref name="Bracewell_1995"/> | ||
जैसा कि ऊपर उल्लेख किया गया है, डीएचटी एल्गोरिदम | जैसा कि ऊपर उल्लेख किया गया है, डीएचटी एल्गोरिदम सामान्यतः वास्तविक इनपुट (या आउटपुट) के लिए विशिष्ट संबंधित डीएफटी एल्गोरिदम (एफएफटी) की तुलना में थोड़ा कम कुशल ([[ तैरनेवाला स्थल ]] ऑपरेशन की संख्या के संदर्भ में) होते हैं। यह पहली बार सोरेनसेन एट अल द्वारा तर्क दिया गया था। (1987)<ref name="Sorensen_1987"/>और डुहामेल और [[मार्टिन वेटरली]] (1987)।<ref name="Duhamel-Vetterli_1987"/>बाद के लेखकों ने एक स्प्लिट-रेडिक्स एल्गोरिदम ([[स्प्लिट-रेडिक्स एफएफटी एल्गोरिदम]] | स्प्लिट-रेडिक्स एफएफटी के समान) का उपयोग करके दो आकारों की शक्ति के डीएचटी के लिए सबसे कम प्रकाशित ऑपरेशन गणना प्राप्त की, जो डीएचटी को तोड़ता है। लंबाई N को लंबाई N/2 के DHT में और लंबाई N/4 के दो वास्तविक-इनपुट DFT (DHT नहीं) में। इस तरह, उन्होंने तर्क दिया कि पावर-टू-लंबाई के डीएचटी की गणना, वास्तविक-इनपुट डीएफटी के लिए अंकगणितीय संचालन की संबंधित संख्या की तुलना में, अधिकतम 2 अतिरिक्त के साथ की जा सकती है। | ||
वर्तमान समय के कंप्यूटरों पर, प्रदर्शन सख्त ऑपरेशन गणनाओं की तुलना में [[सीपीयू कैश]] और [[सीपीयू पाइपलाइन]] विचारों द्वारा अधिक निर्धारित होता है, और अंकगणितीय लागत में मामूली अंतर महत्वपूर्ण होने की संभावना नहीं है। चूंकि एफएचटी और वास्तविक-इनपुट एफएफटी एल्गोरिदम में समान कम्प्यूटेशनल संरचनाएं होती हैं, इसलिए ऐसा प्रतीत होता है कि इनमें से किसी को भी पर्याप्त प्राथमिक गति लाभ नहीं है ({{ill|Miodrag Popović (engineer){{!}}Popović|sr|Миодраг Поповић (електротехничар)}} और सेविक, 1994)।<ref name="Popović-Šević_1994"/>एक व्यावहारिक मामले के रूप में, अत्यधिक अनुकूलित वास्तविक-इनपुट एफएफटी लाइब्रेरी कई स्रोतों से उपलब्ध हैं (उदाहरण के लिए [[इंटेल]] जैसे सीपीयू विक्रेताओं से), जबकि अत्यधिक अनुकूलित डीएचटी लाइब्रेरी कम आम हैं। | वर्तमान समय के कंप्यूटरों पर, प्रदर्शन सख्त ऑपरेशन गणनाओं की तुलना में [[सीपीयू कैश]] और [[सीपीयू पाइपलाइन]] विचारों द्वारा अधिक निर्धारित होता है, और अंकगणितीय लागत में मामूली अंतर महत्वपूर्ण होने की संभावना नहीं है। चूंकि एफएचटी और वास्तविक-इनपुट एफएफटी एल्गोरिदम में समान कम्प्यूटेशनल संरचनाएं होती हैं, इसलिए ऐसा प्रतीत होता है कि इनमें से किसी को भी पर्याप्त प्राथमिक गति लाभ नहीं है ({{ill|Miodrag Popović (engineer){{!}}Popović|sr|Миодраг Поповић (електротехничар)}} और सेविक, 1994)।<ref name="Popović-Šević_1994"/>एक व्यावहारिक मामले के रूप में, अत्यधिक अनुकूलित वास्तविक-इनपुट एफएफटी लाइब्रेरी कई स्रोतों से उपलब्ध हैं (उदाहरण के लिए [[इंटेल]] जैसे सीपीयू विक्रेताओं से), जबकि अत्यधिक अनुकूलित डीएचटी लाइब्रेरी कम आम हैं। | ||
| Line 48: | Line 48: | ||
साथ <math>k_i = 0,1,\ldots, N_i-1</math> और कहाँ <math>{\rm cas}(x)=\cos(x)+\sin(x).</math> | साथ <math>k_i = 0,1,\ldots, N_i-1</math> और कहाँ <math>{\rm cas}(x)=\cos(x)+\sin(x).</math> | ||
1-डी मामले के समान, वास्तविक और सममित परिवर्तन के रूप में, एमडी-डीएचटी एमडी-डीएफटी की तुलना में सरल है। एक के लिए, व्युत्क्रम DHT एक स्केलिंग कारक के अतिरिक्त, आगे के परिवर्तन के समान है; | 1-डी मामले के समान, वास्तविक और सममित परिवर्तन के रूप में, एमडी-डीएचटी एमडी-डीएफटी की तुलना में सरल है। एक के लिए, व्युत्क्रम DHT एक स्केलिंग कारक के अतिरिक्त, आगे के परिवर्तन के समान है; | ||
[[File:Img DHT prop2.png|केंद्र|फ़्रेमलेस|400x400px]]और दूसरा, चूंकि कर्नेल वास्तविक है, यह | [[File:Img DHT prop2.png|केंद्र|फ़्रेमलेस|400x400px]]और दूसरा, चूंकि कर्नेल वास्तविक है, यह सम्मिश्र संख्याओं की कम्प्यूटेशनल जटिलता से बचता है। इसके अतिरिक्त, डीएफटी एक सरल एडिटिव ऑपरेशन (ब्रेसवेल, 1983) द्वारा सीधे डीएचटी से प्राप्त किया जा सकता है।<ref name="Bracewell_1983"/> | ||
एमडी-डीएचटी का व्यापक रूप से छवि और ऑप्टिकल सिग्नल प्रोसेसिंग जैसे क्षेत्रों में उपयोग किया जाता है। विशिष्ट अनुप्रयोगों में कंप्यूटर विज़न, हाई-डेफिनिशन टेलीविज़न और टेलीकांफ्रेंसिंग शामिल हैं, ऐसे क्षेत्र जो गति छवियों को संसाधित या विश्लेषण करते हैं (ज़ेंग, 2000)।<ref name="Zeng-Bi-Leyman_2000"/> | एमडी-डीएचटी का व्यापक रूप से छवि और ऑप्टिकल सिग्नल प्रोसेसिंग जैसे क्षेत्रों में उपयोग किया जाता है। विशिष्ट अनुप्रयोगों में कंप्यूटर विज़न, हाई-डेफिनिशन टेलीविज़न और टेलीकांफ्रेंसिंग शामिल हैं, ऐसे क्षेत्र जो गति छवियों को संसाधित या विश्लेषण करते हैं (ज़ेंग, 2000)।<ref name="Zeng-Bi-Leyman_2000"/> | ||
| Line 63: | Line 63: | ||
<math>X(k_1,k_2,k_3) = \frac{1}{2} [\hat{X}(k_1,k_2,-k_3)+\hat{X}(k_1,-k_2,k_3)+\hat{X}(-k_1,k_2,k_3)-\hat{X}(-k_1,-k_2,-k_3)].</math> | <math>X(k_1,k_2,k_3) = \frac{1}{2} [\hat{X}(k_1,k_2,-k_3)+\hat{X}(k_1,-k_2,k_3)+\hat{X}(-k_1,k_2,k_3)-\hat{X}(-k_1,-k_2,-k_3)].</math> | ||
के लिए <math>\hat{X}</math>, पंक्ति-स्तंभ एल्गोरिदम को तब लागू किया जा सकता है। इस तकनीक का उपयोग | के लिए <math>\hat{X}</math>, पंक्ति-स्तंभ एल्गोरिदम को तब लागू किया जा सकता है। इस तकनीक का उपयोग सामान्यतः ऐसे आर-सी एल्गोरिदम की सादगी के कारण किया जाता है, लेकिन वे सामान्य एम-डी स्थानों के लिए अनुकूलित नहीं हैं। | ||
अन्य तेज़ एल्गोरिदम विकसित किए गए हैं, जैसे मूलांक-2, मूलांक-4, और विभाजित मूलांक। उदाहरण के लिए, बौसाक्टा (2000)<ref name="Boussakta_2000"/>3-डी | अन्य तेज़ एल्गोरिदम विकसित किए गए हैं, जैसे मूलांक-2, मूलांक-4, और विभाजित मूलांक। उदाहरण के लिए, बौसाक्टा (2000)<ref name="Boussakta_2000"/>3-डी सदिश रेडिक्स विकसित किया, | ||
<math>X(k_1,k_2,...,k_r)=\sum_{n_1=0}^{N-1} \sum_{n_2=0}^{N-1}\sum_{n_r=0}^{N-1} x(n_1,n_2,n_3){\rm cas}(\frac{2\pi}{N}(n_1 k_1+n_2 k_2 +n_3 k_3))</math> | <math>X(k_1,k_2,...,k_r)=\sum_{n_1=0}^{N-1} \sum_{n_2=0}^{N-1}\sum_{n_r=0}^{N-1} x(n_1,n_2,n_3){\rm cas}(\frac{2\pi}{N}(n_1 k_1+n_2 k_2 +n_3 k_3))</math> | ||
| Line 74: | Line 74: | ||
<math>+\sum_{n_1:odd}\sum_{n_2:odd}\sum_{n_3:even}+\sum_{n_1:odd}\sum_{n_2:odd}\sum_{n_3:odd}.</math> | <math>+\sum_{n_1:odd}\sum_{n_2:odd}\sum_{n_3:even}+\sum_{n_1:odd}\sum_{n_2:odd}\sum_{n_3:odd}.</math> | ||
इसे बौसाक्टा (2000) में भी प्रस्तुत किया गया था<ref name="Boussakta_2000"/>यह 3डी- | इसे बौसाक्टा (2000) में भी प्रस्तुत किया गया था<ref name="Boussakta_2000"/>यह 3डी-सदिश रेडिक्स एल्गोरिदम लेता है <math>(\frac{7}{4})N^3 \log_2 N</math> गुणा और <math>(\frac{31}{8})N^3 \log_2 N</math> की तुलना में अतिरिक्त <math>3N^3 \log_2 N</math> गुणा और <math>(\frac{9}{2})N^3 \log_2 N+3N^2</math> पंक्ति-स्तंभ दृष्टिकोण से परिवर्धन। दोष यह है कि इन रेडिक्स-प्रकार के एल्गोरिदम के कार्यान्वयन को मनमाने आयामों के संकेतों के लिए सामान्यीकृत करना कठिन है। | ||
एमडी-डीएचटी को हल करने के लिए संख्या सैद्धांतिक परिवर्तनों का भी उपयोग किया गया है, क्योंकि वे बेहद तेज़ कनवल्शन करते हैं। बौसाक्टा (1988) में,<ref name="Boussakta_1988"/>यह दिखाया गया कि एमडी-डीएचटी रूपांतरण को कनवल्शन से युक्त एक रूप में कैसे विघटित किया जाए: | एमडी-डीएचटी को हल करने के लिए संख्या सैद्धांतिक परिवर्तनों का भी उपयोग किया गया है, क्योंकि वे बेहद तेज़ कनवल्शन करते हैं। बौसाक्टा (1988) में,<ref name="Boussakta_1988"/>यह दिखाया गया कि एमडी-डीएचटी रूपांतरण को कनवल्शन से युक्त एक रूप में कैसे विघटित किया जाए: | ||
Revision as of 22:48, 7 October 2023
असतत हार्टले परिवर्तन(डीएचटी) सिग्नल प्रोसेसिंग और संबंधित क्षेत्रों में समान अनुप्रयोगों के साथ, असतत फूरियर रूपांतरण (डीएफटी) के समान असतत, आवधिक डेटा का एक फूरियर-संबंधित परिवर्तन है। डीएफटी से इसका मुख्य अंतर यह है कि यह वास्तविक इनपुट को वास्तविक आउटपुट में बदल देता है, जिसमें सम्मिश्र संख्याओं की कोई आंतरिक भागीदारी नहीं होती है। जिस तरह डीएफटी असतत फूरियर रूपांतरण (एफटी) का असतत एनालॉग है, उसी तरह डीएचटी 1942 में राल्फ वी. एल. हार्टले द्वारा प्रस्तुत किए गए निरंतर हार्टले ट्रांसफॉर्म (एचटी) का असतत एनालॉग है।[1]
क्योंकि डीएचटी के लिए फास्ट फूरियर ट्रांसफॉर्म (एफएफटी) के अनुरूप तेज़ एल्गोरिदम हैं, डीएचटी को मूल रूप से 1983 में रोनाल्ड एन. ब्रेसवेल द्वारा प्रस्तावित किया गया था।[2]सामान्य स्थिति में एक अधिक कुशल कम्प्यूटेशनल उपकरण के रूप में जहां डेटा पूरी तरह से वास्तविक है। हालाँकि, बाद में यह तर्क दिया गया कि वास्तविक इनपुट या आउटपुट के लिए विशेष एफएफटी एल्गोरिदम सामान्यतः डीएचटी के लिए किसी भी संबंधित एल्गोरिदम की तुलना में थोड़े कम संचालन के साथ पाए जा सकते हैं।
परिभाषा
औपचारिक रूप से, असतत हार्टले परिवर्तन एक रैखिक, इनवेर्टीबल फ़ंक्शन (गणित) H:Rn → Rn है (जहाँ 'R' वास्तविक संख्याओं के समुच्चय को दर्शाता है)। सूत्र के अनुसार N वास्तविक संख्याएँ x0, ..., xN−1 को N वास्तविक संख्याएँ H0, ..., HN−1 में बदल दिया जाता है
संमिश्रण कभी-कभी निरूपित किया जाता है cas(z), और इससे भ्रमित नहीं होना चाहिए cis(z) = eiz = cos(z) + i sin(z), या e−iz = cis(−z) जो डीएफटी परिभाषा में दिखाई देता है (जहां i एक काल्पनिक इकाई के रूप में है)।
डीएफटी की तरह, परिवर्तन के सामने समग्र पैमाने का कारक और साइन टर्म का संकेत परंपरा का विषय है। हालाँकि ये परंपराएँ कभी-कभी लेखकों के बीच भिन्न होती हैं, लेकिन वे परिवर्तन के आवश्यक गुणों को प्रभावित नहीं करती हैं।
गुण
परिवर्तन की व्याख्या सदिश (x0, ...., xN−1) के गुणन के रूप में की जा सकती है, N-बाय-N आव्यूह (गणित) द्वारा; इसलिए, असतत हार्टले रूपांतरण एक रैखिक ऑपरेटर है। आव्यूह इनवेर्टीबल है; व्युत्क्रम परिवर्तन, जो किसी को xn पुनर्प्राप्त करने की अनुमति देता है Hk, से बस Hk का डीएचटी है 1/N से गुणा किया गया है। अर्थात्, डीएचटी एक समग्र पैमाने के कारक तक अपना स्वयं का व्युत्क्रम (इनवोल्यूशन (गणित) है।
डीएचटी का उपयोग डीएफटी की गणना करने के लिए किया जा सकता है, और इसके विपरीत किया जा सकता है। वास्तविक इनपुट के लिए xn, डीएफटी आउटपुट Xk एक वास्तविक हिस्सा है (Hk + HN−k)/2 और एक काल्पनिक भाग (HN−k − Hk)/2. इसके विपरीत, डीएचटी xn के डीएफटी की गणना के बराबर है1 + i से गुणा किया जाता है, फिर परिणाम का वास्तविक भाग लिया जाता है।
डीएफटी की तरह, दो सदिश x = (xn) का एक चक्रीय कनवल्शन z = x∗y) और y = (yn) एक सदिश z = (zn) उत्पन्न करने के लिए), पूरी लंबाई N, डीएचटी के बाद एक सरल ऑपरेशन बन जाता है। विशेष रूप से, मान लीजिए कि सदिश X, Y और Z क्रमशः x, y और z के डीएचटी को दर्शाते हैं। फिर Z के तत्व इस प्रकार दिए गए हैं:
जहाँ हम सभी सदिशों को N (X) में आवर्त मानते हैंN= एक्स0, वगैरह)। इस प्रकार, जैसे डीएफटी एक कनवल्शन को सम्मिश्र संख्याओं (वास्तविक और काल्पनिक भागों के जोड़े) के बिंदुवार गुणन में बदल देता है, डीएचटी एक कनवल्शन को वास्तविक आवृत्ति घटकों के जोड़े के एक सरल संयोजन में बदल देता है। व्युत्क्रम DHT तब वांछित सदिश 'z' उत्पन्न करता है। इस तरह, डीएचटी के लिए एक तेज़ एल्गोरिदम (नीचे देखें) कनवल्शन के लिए एक तेज़ एल्गोरिदम उत्पन्न करता है। (यह डीएफटी के लिए संबंधित प्रक्रिया से थोड़ा अधिक महंगा है, इसमें नीचे दिए गए परिवर्तनों की लागत शामिल नहीं है, क्योंकि उपरोक्त जोड़ीदार ऑपरेशन के लिए जटिल गुणन के 6 की तुलना में 8 वास्तविक-अंकगणितीय संचालन की आवश्यकता होती है। इस गणना में शामिल नहीं है 2 से विभाजन, जिसे अवशोषित किया जा सकता है उदाहरण के लिए उलटा डीएचटी के 1/एन सामान्यीकरण में।)
तेज़ एल्गोरिदम
डीएफटी की तरह, सीधे डीएचटी परिभाषा का मूल्यांकन करने के लिए ओ(एन) की आवश्यकता होगी2) अंकगणितीय परिचालन (बिग ओ अंकन देखें)। हालाँकि, FFT के समान तेज़ एल्गोरिदम हैं, जो केवल O(N लॉग N) संचालन में समान परिणाम की गणना करते हैं। लगभग हर एफएफटी एल्गोरिदम, कूली-टुकी एफएफटी एल्गोरिदम|कूली-ट्यूकी से प्राइम-फैक्टर एफएफटी एल्गोरिदम|प्राइम-फैक्टर से विनोग्राड (1985) तक[3]ब्रून के FFT एल्गोरिथम के लिए|ब्रून का (1993),[4]असतत हार्टले परिवर्तन के लिए एक सीधा एनालॉग है। (हालांकि, कुछ अधिक विदेशी एफएफटी एल्गोरिदम, जैसे कि क्यूएफटी, की अभी तक डीएचटी के संदर्भ में जांच नहीं की गई है।)
विशेष रूप से, Cooley-Tukey एल्गोरिदम के DHT एनालॉग को सामान्यतः फास्ट हार्टले ट्रांसफॉर्म (FHT) एल्गोरिदम के रूप में जाना जाता है, और इसे पहली बार 1984 में ब्रेसवेल द्वारा वर्णित किया गया था।[5]यह एफएचटी एल्गोरिथ्म, कम से कम जब दो|पावर-ऑफ-दो आकार एन की शक्ति पर लागू किया जाता है, तो 1987 में स्टैनफोर्ड विश्वविद्यालय को जारी संयुक्त राज्य सॉफ्टवेयर पेटेंट संख्या 4,646,256 का विषय है। स्टैनफोर्ड ने इस पेटेंट को 1994 में सार्वजनिक डोमेन में रखा (ब्रेसवेल, 1995)।[6]
जैसा कि ऊपर उल्लेख किया गया है, डीएचटी एल्गोरिदम सामान्यतः वास्तविक इनपुट (या आउटपुट) के लिए विशिष्ट संबंधित डीएफटी एल्गोरिदम (एफएफटी) की तुलना में थोड़ा कम कुशल (तैरनेवाला स्थल ऑपरेशन की संख्या के संदर्भ में) होते हैं। यह पहली बार सोरेनसेन एट अल द्वारा तर्क दिया गया था। (1987)[7]और डुहामेल और मार्टिन वेटरली (1987)।[8]बाद के लेखकों ने एक स्प्लिट-रेडिक्स एल्गोरिदम (स्प्लिट-रेडिक्स एफएफटी एल्गोरिदम | स्प्लिट-रेडिक्स एफएफटी के समान) का उपयोग करके दो आकारों की शक्ति के डीएचटी के लिए सबसे कम प्रकाशित ऑपरेशन गणना प्राप्त की, जो डीएचटी को तोड़ता है। लंबाई N को लंबाई N/2 के DHT में और लंबाई N/4 के दो वास्तविक-इनपुट DFT (DHT नहीं) में। इस तरह, उन्होंने तर्क दिया कि पावर-टू-लंबाई के डीएचटी की गणना, वास्तविक-इनपुट डीएफटी के लिए अंकगणितीय संचालन की संबंधित संख्या की तुलना में, अधिकतम 2 अतिरिक्त के साथ की जा सकती है।
वर्तमान समय के कंप्यूटरों पर, प्रदर्शन सख्त ऑपरेशन गणनाओं की तुलना में सीपीयू कैश और सीपीयू पाइपलाइन विचारों द्वारा अधिक निर्धारित होता है, और अंकगणितीय लागत में मामूली अंतर महत्वपूर्ण होने की संभावना नहीं है। चूंकि एफएचटी और वास्तविक-इनपुट एफएफटी एल्गोरिदम में समान कम्प्यूटेशनल संरचनाएं होती हैं, इसलिए ऐसा प्रतीत होता है कि इनमें से किसी को भी पर्याप्त प्राथमिक गति लाभ नहीं है (Popović और सेविक, 1994)।[9]एक व्यावहारिक मामले के रूप में, अत्यधिक अनुकूलित वास्तविक-इनपुट एफएफटी लाइब्रेरी कई स्रोतों से उपलब्ध हैं (उदाहरण के लिए इंटेल जैसे सीपीयू विक्रेताओं से), जबकि अत्यधिक अनुकूलित डीएचटी लाइब्रेरी कम आम हैं।
दूसरी ओर, ऐसे मामलों के लिए ओ (एन लॉग एन) जटिल-डेटा एल्गोरिदम के अस्तित्व के बावजूद, वास्तविक इनपुट के कारण एफएफटी में अनावश्यक गणनाओं को बड़ी अभाज्य संख्या एन के लिए खत्म करना अधिक कठिन है, क्योंकि अतिरेक जटिल के पीछे छिपे हुए हैं उन एल्गोरिदम में क्रमपरिवर्तन और/या चरण घूर्णन। इसके विपरीत, एक मानक प्राइम-आकार एफएफटी एल्गोरिदम, रेडर का एफएफटी एल्गोरिदम | रेडर का एल्गोरिदम, समकक्ष जटिल एफएफटी (फ्रिगो और जॉनसन, 2005) की तुलना में लगभग दो कम गणना के कारक के लिए वास्तविक डेटा के डीएचटी पर सीधे लागू किया जा सकता है। .[10]दूसरी ओर, वास्तविक-इनपुट डीएफटी के लिए राडार के एल्गोरिदम का एक गैर-डीएचटी-आधारित अनुकूलन भी संभव है (चू और चार्ल्स सिडनी बुरस, 1982)।[11]
बहु-आयामी असतत हार्टले ट्रांसफॉर्म (एमडी-डीएचटी)
आरडी-डीएचटी (आर आयामों के साथ एमडी-डीएचटी) द्वारा दिया गया है
साथ और कहाँ
1-डी मामले के समान, वास्तविक और सममित परिवर्तन के रूप में, एमडी-डीएचटी एमडी-डीएफटी की तुलना में सरल है। एक के लिए, व्युत्क्रम DHT एक स्केलिंग कारक के अतिरिक्त, आगे के परिवर्तन के समान है;
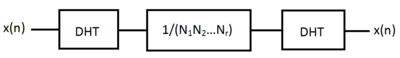 और दूसरा, चूंकि कर्नेल वास्तविक है, यह सम्मिश्र संख्याओं की कम्प्यूटेशनल जटिलता से बचता है। इसके अतिरिक्त, डीएफटी एक सरल एडिटिव ऑपरेशन (ब्रेसवेल, 1983) द्वारा सीधे डीएचटी से प्राप्त किया जा सकता है।[2]
और दूसरा, चूंकि कर्नेल वास्तविक है, यह सम्मिश्र संख्याओं की कम्प्यूटेशनल जटिलता से बचता है। इसके अतिरिक्त, डीएफटी एक सरल एडिटिव ऑपरेशन (ब्रेसवेल, 1983) द्वारा सीधे डीएचटी से प्राप्त किया जा सकता है।[2]
एमडी-डीएचटी का व्यापक रूप से छवि और ऑप्टिकल सिग्नल प्रोसेसिंग जैसे क्षेत्रों में उपयोग किया जाता है। विशिष्ट अनुप्रयोगों में कंप्यूटर विज़न, हाई-डेफिनिशन टेलीविज़न और टेलीकांफ्रेंसिंग शामिल हैं, ऐसे क्षेत्र जो गति छवियों को संसाधित या विश्लेषण करते हैं (ज़ेंग, 2000)।[12]
एमडी-डीएचटी के लिए तेज़ एल्गोरिदम
जैसे-जैसे कंप्यूटिंग गति बढ़ती जा रही है, बड़ी बहुआयामी समस्याएं कम्प्यूटेशनल रूप से व्यवहार्य हो जाती हैं, जिसके लिए तेज़ बहुआयामी एल्गोरिदम की आवश्यकता होती है। ऐसे तीन एल्गोरिदम अनुसरण करते हैं।
दक्षता के लिए पृथक्करण की खोज में, हम निम्नलिखित परिवर्तन पर विचार करते हैं (ब्रेसवेल, 1983),[2]
इसे बोर्टफेल्ड (1995) में दिखाया गया था,[13]कि दोनों को कुछ अतिरिक्त द्वारा संबंधित किया जा सकता है। उदाहरण के लिए, 3-डी में,
के लिए , पंक्ति-स्तंभ एल्गोरिदम को तब लागू किया जा सकता है। इस तकनीक का उपयोग सामान्यतः ऐसे आर-सी एल्गोरिदम की सादगी के कारण किया जाता है, लेकिन वे सामान्य एम-डी स्थानों के लिए अनुकूलित नहीं हैं।
अन्य तेज़ एल्गोरिदम विकसित किए गए हैं, जैसे मूलांक-2, मूलांक-4, और विभाजित मूलांक। उदाहरण के लिए, बौसाक्टा (2000)[14]3-डी सदिश रेडिक्स विकसित किया,
इसे बौसाक्टा (2000) में भी प्रस्तुत किया गया था[14]यह 3डी-सदिश रेडिक्स एल्गोरिदम लेता है गुणा और की तुलना में अतिरिक्त गुणा और पंक्ति-स्तंभ दृष्टिकोण से परिवर्धन। दोष यह है कि इन रेडिक्स-प्रकार के एल्गोरिदम के कार्यान्वयन को मनमाने आयामों के संकेतों के लिए सामान्यीकृत करना कठिन है।
एमडी-डीएचटी को हल करने के लिए संख्या सैद्धांतिक परिवर्तनों का भी उपयोग किया गया है, क्योंकि वे बेहद तेज़ कनवल्शन करते हैं। बौसाक्टा (1988) में,[15]यह दिखाया गया कि एमडी-डीएचटी रूपांतरण को कनवल्शन से युक्त एक रूप में कैसे विघटित किया जाए:
2-डी मामले के लिए (3-डी मामला भी बताए गए संदर्भ में शामिल है),
, निम्नानुसार 1-डी और 2-डी गोलाकार कनवल्शन में विघटित किया जा सकता है,
कहाँ
विकसित होना आगे,
इस बिंदु पर हम फ़र्मेट संख्या परिवर्तन (FNT) प्रस्तुत करते हैं। टीवेंफ़र्मेट संख्या द्वारा दिया जाता है , साथ . सुप्रसिद्ध फ़र्मेट संख्याएँ किसके लिए हैं? ( के लिए प्रमुख है ), (बास्केट, 1988)।[15]फ़र्मेट संख्या परिवर्तन द्वारा दिया गया है
साथ . और व्यवस्था की एकता की जड़ें हैं और क्रमश: .
अपघटन पर वापस जा रहे हैं, अंतिम पद के लिए के रूप में दर्शाया जाएगा , तब
अगर और के आदिम मूल मॉड्यूलो एन हैं और (यदि अस्तित्व में होने की गारंटी है और तो अभाज्य संख्या हैं) और नक्शा को तो, मैपिंग और को और , किसी को निम्नलिखित मिलता है,
.
जो अब एक वृत्ताकार कनवल्शन है। साथ , , और , किसी के पास
कहाँ पद गुणन द्वारा पद को दर्शाता है। यह भी कहा गया था (बूसाक्टा, 1988)[15]कि यह एल्गोरिदम शिफ्ट और ऐड ऑपरेशंस की संख्या में मामूली वृद्धि की कीमत पर अन्य डीएचटी एल्गोरिदम की तुलना में गुणाओं की संख्या को 8-20 के कारक से कम कर देता है, जिन्हें गुणा की तुलना में सरल माना जाता है। इस एल्गोरिथ्म का दोष यह है कि परिवर्तन के प्रत्येक आयाम में एक आदिम रूट मॉड्यूलो n होता है।
संदर्भ
- ↑ Hartley, Ralph V. L. (March 1942). "A More Symmetrical Fourier Analysis Applied to Transmission Problems". Proceedings of the IRE. 30 (3): 144–150. doi:10.1109/JRPROC.1942.234333. S2CID 51644127.
- ↑ 2.0 2.1 2.2 Bracewell, Ronald N. (1983). "Discrete Hartley Transform". Journal of the Optical Society of America. 73 (12): 1832–1835. doi:10.1364/josa.73.001832. S2CID 120611904.
- ↑ Sorensen, Henrik V.; Jones, Douglas L.; Burrus, Charles Sidney; Heideman, Michael T. (1985). "On computing the discrete Hartley transform". IEEE Transactions on Acoustics, Speech, and Signal Processing. ASSP-33 (4): 1231–1238.
- ↑ Bini, Dario Andrea; Bozzo, Enrico (1993). "Fast discrete transform by means of eigenpolynomials". Computers & Mathematics with Applications. 26 (9): 35–52. doi:10.1016/0898-1221(93)90004-f.
- ↑ Bracewell, Ronald N. (1984). "The Fast Hartley Transform". Proceedings of the IEEE. 72 (8): 1010–1018. doi:10.1109/proc.1984.12968. S2CID 21988816.
- ↑ Bracewell, Ronald N. (1995). "Computing with the Hartley Transform". Computers in Physics. 9 (4): 373–379. Bibcode:1995ComPh...9..373B. doi:10.1063/1.168534.
- ↑ Sorensen, Henrik V.; Jones, Douglas L.; Heideman, Michael T.; Burrus, Charles Sidney (1987). "Real-valued fast Fourier transform algorithms". IEEE Transactions on Acoustics, Speech, and Signal Processing. ASSP-35 (6): 849–863.
- ↑ Duhamel, Pierre; Vetterli, Martin (1987). "Improved Fourier and Hartley transform algorithms: application to cyclic convolution of real data". IEEE Transactions on Acoustics, Speech, and Signal Processing. ASSP-35: 818–824.
- ↑ Поповић [Popović], Миодраг [Miodrag] [in српски / srpski]; Šević, Dragutin (1994). "A new look at the comparison of the fast Hartley and Fourier transforms". IEEE Transactions on Signal Processing. 42 (8): 2178–2182. Bibcode:1994ITSP...42.2178P. doi:10.1109/78.301854.
- ↑ Frigo, Matteo; Johnson, Steven G. (2005). "The Design and Implementation of FFTW3" (PDF). Proceedings of the IEEE. 93 (2): 216–231. CiteSeerX 10.1.1.66.3097. doi:10.1109/jproc.2004.840301. S2CID 6644892.}
- ↑ Chu, Shuni; Burrus, Charles Sidney (1982). "A prime factor FTT [sic] algorithm using distributed arithmetic". IEEE Transactions on Acoustics, Speech, and Signal Processing. 30 (2): 217–227. doi:10.1109/tassp.1982.1163875.
- ↑ Zeng, Yonghang; Bi, Guoan; Leyman, Abdul Rahim (2000). "Polynomial Transform Algorithms for Multidimensional Discrete Hartley Transform". IEEE International Symposium on Circuits and Systems (V): 517–520.
- ↑ Bortfeld, Thomas; Dinter, Wolfgang (1995). "Calculation of Multidimensional Hartley Transforms Using One-Dimensional Fourier Transforms". IEEE Transactions on Signal Processing. 43 (5): 1306–1310. Bibcode:1995ITSP...43.1306B. doi:10.1109/78.382424.
- ↑ 14.0 14.1 Boussakta, Said; Alshibami, Osama (2000). "Fast Algorithm for the 3-D Discrete Hartley Transform". International Conference on Acoustics, Speech, and Signal Processing '00 (4): 2302–2305.
- ↑ 15.0 15.1 15.2 Boussakta, Said; Holt, Alan G. J. (1988). "Fast Multidimensional Discrete Hartley Transform using Fermat Number Transform". IEE Proceedings G - Electronic Circuits and Systems. 135 (6): 235–237. doi:10.1049/ip-g-1.1988.0036.
अग्रिम पठन
- Bracewell, Ronald N. (1986). The Hartley Transform (1 ed.). Oxford University Press. ISBN 978-0-19503969-6.
- Boussakta, Said; Holt, Alan G. J. (1988). "Fast Multidimensional Discrete Hartley Transform using Fermat Number Transform". IEE Proceedings G - Electronic Circuits and Systems. 135 (6): 235–237. doi:10.1049/ip-g-1.1988.0036.
- Hong, Jonathan; Vetterli, Martin; Duhamel, Pierre (1994). "Basefield transforms with the convolution property" (PDF). Proceedings of the IEEE. 82 (3): 400–412. doi:10.1109/5.272145.
- O'Neill, Mark A. (1988). "Faster than Fast Fourier". BYTE. 13 (4): 293–300.
- Olnejniczak, Kraig J.; Heydt, Gerald T. (March 1994). "Scanning the Special Section on the Hartley transform". Proceedings of the IEEE. 82: 372–380. (NB. Contains extensive bibliography.)