प्रकाशिकी अंतरण प्रकार्य: Difference between revisions

Revision as of 12:25, 29 September 2023

प्रकाशिकी स्थानांतरण प्रकार्य (ओटीएफ) एक प्रकाशिकी प्रणाली जैसे कि कैमरा, माइक्रोस्कोप, मानव नेत्र, या प्रोजेक्टर को, यह निर्धारित करता है कि विभिन्न स्थानिक आवृत्ति कैसे कैप्चर किए जाते हैं या प्रेषित किए जाते हैं। यह प्रकाशिकी अभियंताओ द्वारा प्रयोग किया जाता है जिससे प्रकाशिकी किसी वस्तु या दृश्य से प्रकाश को फोटोग्राफिक फिल्म, प्रतिबिंबसेंसर, रेटिना, स्क्रीन, या प्रकाशिकी ट्रांसमिशन चेन के अगले विषय पर प्रोजेक्ट कैसे करते हैं। एक रूपांतर, प्रतिरुपण स्थानतारण प्रकार्य (एमटीएफ), फेज प्रभावों की उपेक्षा करता है, परंतु बहुत सी स्थितियों में ओटीएफ के समान होता है।

किसी भी स्थानतारण प्रकार्य, लेंस प्रणाली के माध्यम से गुजरने वाले एक आवृत्ति वाले साइन-वेव पैटर्न के प्रति उसकी स्थानिक प्रकाशिकी या अवधि और उसके दिशा के आधार पर प्रतिक्रिया को निर्दिष्ट करता है। औपचारिक रूप से, ओटीएफ को बिंदु प्रसार प्रकार्य (पीएसएफ), अर्थात प्रकाशिकी की आवेग प्रतिक्रिया, एक बिंदु स्रोत की प्रतिबिंबके फूरियर रूपांतरण के रूप में परिभाषित किया गया है। फूरियर रूपांतरण के रूप में, ओटीएफ जटिल-मूल्यवान है; परंतु पीएसएफ के सामान्य विषय में इसका वास्तविक मूल्य होगा जो इसके केंद्र के बारे में सममित है। एमटीएफ को औपचारिक रूप से जटिल ओटीएफ के परिमाण (पूर्ण मूल्य) के रूप में परिभाषित किया गया है।

दाएं ओर की प्रतिबिंबमें पैनल (ए) और (डी) में दो विभिन्न प्रकाशिकी प्रणाली के लिए प्रकाशिकी अंतरण प्रकार्य दिखाए गए हैं। पहला आदर्श, विवर्तन-सीमित प्रणाली,प्रतिबिंब प्रणाली का है जिसमें एक गोल पुतली होता है। इसका स्थानांतरण कार्य स्थानिक आवृत्ति के साथ लगभग धीरे-धीरे कम हो जाता है जब तक कि यह विवर्तन-सीमा तक नहीं पहुंच जाता, इस स्थिति में 500 चक्र प्रति मिलीमीटर या 2 माइक्रोन की अवधि पर होता है, चूंकि इस अवधि जितनी छोटी आवधिक विशेषताएं इसप्रतिबिंब प्रणाली द्वारा कैप्चर की जाती हैं, इसलिए यह कहा जा सकता है कि इसका प्रस्ताव 2 माइक्रोन है।^[1] पैनल (डी) एक प्रकाशिकी प्रणाली दिखाता है जो फोकस से बाहर है। इससे विवर्तन-सीमित प्रतिबिंबप्रणाली के सापेक्ष व्यतिरेक में तेज कमी आती है। यह देखा जा सकता है कि व्यतिरेक 250 चक्र/मिमी, या 4 माइक्रोन की अवधि के आसपास शून्य है। यह बताता है कि आउट-ऑफ-फोकस प्रणाली (ई, एफ) की छवियां विवर्तन-सीमित प्रणाली (बी, सी) के सापेक्ष अधिक धुंधली क्यों हैं। ध्यान दें कि यद्यपि आउट-ऑफ-फोकस प्रणाली में 250 चक्र/मिमी के आसपास स्थानिक आवृत्तियों पर बहुत कम व्यतिरेक है, 500 चक्र/मिमी की विवर्तन सीमा के पास स्थानिक आवृत्तियों पर व्यतिरेक विवर्तन-सीमित है। पैनल (एफ) में प्रतिबिंबका बारीकी से अवलोकन करने से पता चलता है कि स्पोक लक्ष्य के केंद्र के पास बड़े स्पोक घनत्व की प्रतिबिंबअपेक्षाकृत तेज है।

परिभाषा और संबंधित अवधारणाएँ

प्रकाशिकी स्थानतारण प्रकार्य के बाद से^[2] (ओटीएफ) को बिंदु-प्रसार प्रकार्य (पीएसएफ) के फूरियर रूपांतरण के रूप में परिभाषित किया गया है, यह सामान्यतः स्थानिक आवृत्ति का एक जटिल मूल्य वाला प्रकार्य होता है। एक विशिष्ट आवधिक पैटर्न का प्रक्षेपण क्रमशः अनुमानित प्रक्षेपण के सापेक्ष विपरीत और अनुवाद के आनुपातिक पूर्ण मूल्य और जटिल तर्क के साथ एक जटिल संख्या द्वारा दर्शाया जाता है।

एक प्रकाशिकी प्रणाली की विभिन्न बारीकी से संबंधित विशेषताएँ कोमा को प्रदर्शित करती हैं, एक विशिष्ट विपथन जो अक्ष से बाहर होता है। (ए) प्वाइंट-स्प्रेड प्रकार्य (पीएसएफ) एक बिंदु स्रोत की प्रतिबिंबहै। (बी) एक रेखा की प्रतिबिंबको लाइन-स्प्रेड प्रकार्य के रूप में संदर्भित किया जाता है, इस स्थिति में एक लंबवत रेखा लाइन-स्प्रेड प्रकार्य बिंदु-स्प्रेड प्रतिबिंबके ऊर्ध्वाधर एकीकरण के सीधे आनुपातिक है। प्रकाशिकी-स्थानतारण प्रकार्य (ओटीएफ) को बिंदु-प्रसार प्रकार्य के फूरियर रूपांतरण के रूप में परिभाषित किया गया है और इस प्रकार यह सामान्यतः एक दो-आयामी जटिल प्रकार्य है। सामान्यतः केवल एक-आयामी स्लाइस दिखाया जाता है (सी), लाइन-स्प्रेड प्रकार्य के फूरियर ट्रांसफॉर्म के अनुरूप। मोटी हरी रेखा प्रकार्य के वास्तविक भाग को संकेत करती है, और पतली लाल रेखा काल्पनिक भाग को संकेत करती है। प्रायः केवल जटिल प्रकार्य का पूर्ण मान दिखाया जाता है, इससे द्वि-आयामी प्रकार्य (डी) के दृश्य की अनुमति मिलती है; यद्यपि , सामान्यतः केवल एक-आयामी प्रकार्य दिखाया जाता है। उत्तरार्द्ध को सामान्यतः स्थानिक आवृत्ति शून्य पर सामान्यीकृत किया जाता है और इसे प्रतिरुपण स्थानतारण प्रकार्य (एमटीएफ) के रूप में जाना जाता है। पूर्णता के लिए, जटिल तर्क को कभी-कभी चरण स्थानांतरण प्रकार्य (पीएचटीएफ) के रूप में प्रदान किया जाता है, जिसे पैनल (एफ) में दिखाया गया है।

विस्तार	स्थानिक कार्य	फूरियर रूपांतरण
1D	लाइन-स्प्रेड प्रकार्य (एज-स्प्रेड प्रकार्य का व्युत्पन्न)	2डी प्रकाशिकी -स्थानतारण प्रकार्य का 1डी अनुभाग
2D	बिंदु-प्रसार प्रकार्य	(2डी) प्रकाशिकी स्थानतारण प्रकार्य
3D	3डी बिंदु-प्रसार प्रकार्य	3डी प्रकाशिकी -स्थानतारण प्रकार्य

प्रायः व्यतिरेक में कमी सबसे अधिक रुचिकर होती है और पैटर्न के अनुवाद को नजरअंदाज किया जा सकता है। सापेक्ष व्यतिरेक प्रकाशिकी स्थानतारण प्रकार्य के पूर्ण मूल्य द्वारा दिया जाता है, एक प्रकार्य जिसे सामान्यतः प्रतिरुपण स्थानतारण प्रकार्य (एमटीएफ) के रूप में जाना जाता है। इसके मान दर्शाते हैं कि स्थानिक आवृत्ति के कार्य के रूप में वस्तु का कितना व्यतिरेक प्रतिबिंबमें कैप्चर किया गया है। स्थानिक आवृत्ति 1 से 0 बढ़ने के साथ एमटीएफ घटने लगता है; यद्यपि, प्रकार्य प्रायः एक जैसा नहीं होता है। दूसरी ओर, जब पैटर्न अनुवाद भी महत्वपूर्ण होता है, तो प्रकाशिकी स्थानतारण प्रकार्य के जटिल तर्क को दूसरे वास्तविक-मूल्य वाले प्रकार्य के रूप में दर्शाया जा सकता है, जिसे सामान्यतः चरण स्थानतारण प्रकार्य (पीएचटीएफ) के रूप में जाना जाता है। जटिल-मूल्यवान प्रकाशिकी स्थानतारण प्रकार्य को इन दो वास्तविक-मूल्यवान कार्यों के संयोजन के रूप में देखा जा सकता है:

\mathrm {OTF} (\nu )=\mathrm {MTF} (\nu )e^{i\,\mathrm {PhTF} (\nu )}

यहाँ

\mathrm {MTF} (\nu )=\left\vert \mathrm {OTF} (\nu )\right\vert ,

\mathrm {PhTF} (\nu )=\mathrm {arg} (\mathrm {OTF} (\nu )),

और $\mathrm {arg} (\cdot )$ जबकि, जटिल तर्क प्रकार्य का प्रतिनिधित्व करता है जबकि न्यू $\nu$ आवधिक पैटर्न की स्थानिक आवृत्ति है। सामान्य रूप में $\nu$ प्रत्येक आयाम के लिए एक स्थानिक आवृत्ति वाला एक सदिश है, अर्थात यह आवधिक पैटर्न की दिशा को भी संकेत करता है।

एक अच्छी तरह से केंद्रित प्रकाशिकी प्रणाली की आवेग प्रतिक्रिया फोकल विमान पर अधिकतम के साथ एक त्रि-आयामी तीव्रता वितरण है, और इस प्रकार डिटेक्टर को अक्षीय रूप से विस्थापित करते हुए छवियों के ढेर को रिकॉर्ड करके मापा जा सकता है। परिणामस्वरूप, त्रि-आयामी प्रकाशिकी स्थानतारण प्रकार्य को आवेग प्रतिक्रिया के त्रि-आयामी फूरियर रूपांतरण के रूप में परिभाषित किया जा सकता है। यद्यपि सामान्यतः केवल एक-आयामी, या कभी-कभी दो-आयामी अनुभाग का उपयोग किया जाता है, त्रि-आयामी प्रकाशिकी स्थानतारण प्रकार्य संरचित रोशनी माइक्रोस्कोप जैसे सूक्ष्मदर्शी की समझ में सुधार कर सकता है।

स्थानांतरण फलन की परिभाषा के अनुरूप, $\mathrm {OTF} (0)=\mathrm {MTF} (0)$ प्रकाश के उस अंश को इंगित करना चाहिए जो बिंदु स्रोत वस्तु से पता लगाया गया था। यद्यपि, सामान्यतः पता लगाए गए प्रकाश की कुल मात्रा के सापेक्ष व्यतिरेक सबसे महत्वपूर्ण है। इस प्रकार, प्रकाशिकी स्थानतारण प्रकार्य को ज्ञात तीव्रता तक सामान्य करना साधारण बात है, इसलिए $\mathrm {MTF} (0)\equiv 1$ सामान्यतः अपनाया जाता है।

प्रकाशिकी स्थानतारण प्रकार्य उत्सर्जित प्रकाश के वर्णक्रम और ध्रुवीकरण और बिंदु स्रोत की स्थिति जैसे कारकों पर निर्भर करता है। जैसे प्रतिबिंबव्यतिरेक और विश्लेषण सामान्यतः प्रतिबिंबके केंद्र में इष्टतम होते हैं, और दृश्य क्षेत्र के किनारों की ओर बिगड़ते हैं। जब महत्वपूर्ण भिन्नता होती है, तो प्रकाशिकी स्थानतारण प्रकार्य की गणना प्रतिनिधि स्थितियों या रंगों के एक समुच्चय के लिए की जा सकती है।

कभी-कभी बाइनरी ब्लैक-व्हाइट स्ट्राइप पैटर्न के आधार पर स्थानांतरण कार्यों को परिभाषित करना अधिक व्यावहारिक होता है। समान-चौड़ाई वाले काले-सफ़ेद आवधिक पैटर्न के लिए स्थानांतरण प्रकार्य को व्यतिरेक स्थानतारण प्रकार्य (सी.टी.एफ) कहा जाता है।^[3]

उदाहरण

एक आदर्श लेंस प्रणाली का ओटीएफ

एक आदर्श लेंस प्रणाली आवधिक पैटर्न को बदले बिना एक उच्च व्यतिरेक प्रक्षेपण प्रदान करेगी, इसलिए प्रकाशिकी स्थानतारण प्रकार्य प्रतिरुपण स्थानतारण प्रकार्य के समान है। सामान्यतः प्रकाशिकी के विश्लेषण द्वारा परिभाषित बिंदु पर व्यतिरेक धीरे-धीरे शून्य की ओर कम हो जाएगा। उदाहरण के लिए, 500 एनएम की दृश्यमान तरंग दैर्ध्य पर उपयोग किए जाने वाले एक आदर्श, प्रकाशिकी विपथन गैर-विपथन, एफ-नंबर एफ/4 प्रकाशिकी प्रतिबिंब प्रणाली में दाहिने हाथ की आकृति में दर्शाया गया प्रकाशिकी स्थानतारण प्रकार्य होगा।

$One-dimensional optical transfer function of a diffraction limited imaging system is identical to its modulation transfer function.$

The one-dimensional optical transfer function of a diffraction limited imaging system is identical to its modulation transfer function.

$Spoke target imaged by a diffraction limited imaging system.$

Spoke target imaged by a diffraction limited imaging system.

Transfer function and example image of an ideal, optical-aberration-free (diffraction-limited) imaging system.

कथानक से यह पढ़ा जा सकता है कि व्यतिरेक धीरे-धीरे कम हो जाता है और 500 चक्र प्रति मिलीमीटर की स्थानिक आवृत्ति पर शून्य तक पहुंच जाता है, दूसरे शब्दों में प्रतिबिंबप्रक्षेपण का प्रकाशिकी विश्लेषण 1/500 है एक मिलीमीटर, या 2 माइक्रोमीटर का होता है। तदनुसार, इस विशेषप्रतिबिंब डिवाइस के लिए, स्पोक केंद्र की ओर अधिक से अधिक धुंधले हो जाते हैं जब तक कि वे एक ग्रे, अनसुलझे, डिस्क में विलीन नहीं हो जाते। ध्यान दें कि कभी-कभी प्रकाशिकी स्थानतारण प्रकार्य ऑब्जेक्ट या नमूना स्थान की इकाइयों, अवलोकन कोण, आवरण की चौड़ाई, या सैद्धांतिक अधिकतम तक सामान्यीकृत किया जाता है। दोनों के बीच रूपांतरण सामान्यतः गुणा या भाग की स्थिति है। जैसे एक माइक्रोस्कोप सामान्यतः हर वस्तु को 10 से 100 गुना तक बढ़ा देता है, और एक रिफ्लेक्स कैमरा सामान्यतः 5 मीटर की दूरी पर वस्तुओं को 100 से 200 गुना तक बढ़ा देता है।

एक डिजिटल प्रतिबिंब डिवाइस का विश्लेषण न केवल प्रकाशिकी द्वारा सीमित होता है, बल्कि पिक्सेल की संख्या, विशेष रूप से उनकी पृथक्करण दूरी द्वारा भी सीमित होता है। जैसा कि नाइक्विस्ट-शैनन सैंपलिंग प्रमेय द्वारा समझाया गया है, दिए गए उदाहरण के प्रकाशिकी विश्लेषण से मेल खाने के लिए, प्रत्येक रंग चैनल के पिक्सल को 1 माइक्रोमीटर, प्रति मिलीमीटर 500 चक्र की आधी अवधि से अलग किया जाना चाहिए। समान सेंसर आकार पर पिक्सेल की अधिक संख्या बेहतर विवरण के विश्लेषण की अनुमति नहीं देगी। दूसरी ओर, जब पिक्सेल रिक्ति 1 माइक्रोमीटर से बड़ी होती है, तो विश्लेषण पिक्सेल के बीच पृथक्करण द्वारा सीमित होगा; इसके अतिरिक्त,एलियासिंग से प्रतिबिंबनिष्ठा में और कमी आ सकती है।

अपूर्ण लेंस प्रणाली का ओटीएफ

एक अपूर्ण, प्रकाशिकी विपथन प्रतिबिंब प्रणाली में निम्नलिखित चित्र में दर्शाए गए प्रकाशिकी स्थानतारण प्रकार्य हो सकते हैं।

The real part of the optical transfer function of an aberrated, imperfect imaging system.

The modulation transfer function of an aberrated, imperfect, imaging system.

The image of a spoke target as imaged by an aberrated optical system.

0.25 के मानक ज़र्निक गुणांक के साथ गोलाकार विपथन के साथ 500 एनएम पर एफ/4 ऑप्टिकल इमेजिंग सिस्टम का स्थानांतरण फ़ंक्शन और उदाहरण छवि।

आदर्श लेंस प्रणाली के रूप में, 500 चक्र प्रति मिलीमीटर की स्थानिक आवृत्ति पर व्यतिरेक शून्य तक पहुंच जाता है। यद्यपि, कम स्थानिक आवृत्तियों पर व्यतिरेक पिछले उदाहरण में सही प्रणाली के सापेक्ष अत्यधिक कम है। वास्तव में, 500 चक्र प्रति मिलीमीटर से कम स्थानिक आवृत्तियों के लिए भी कई अवसरों पर व्यतिरेक शून्य हो जाता है। यह उपरोक्त चित्र में दिखाई गई स्पोक प्रतिबिंब में ग्रे गोलाकार बैंड की व्याख्या करता है। ग्रे बैंड के बीच में, तीलियाँ काले से सफेद और इसके विपरीत उलटी होती दिखाई देती हैं, इसे व्यतिरेक व्युत्क्रमण के रूप में जाना जाता है, जो सीधे प्रकाशिकी स्थानतारण प्रकार्य के वास्तविक भाग में साइन रिवर्सल से संबंधित है, और कुछ सामान्य आकृतियों के लिए यह आधे एक अवधि के साथ एक स्थानांतरण के रूप में प्रस्तुत होता है।

यद्यपि यह तर्क दिया जा सकता है कि आदर्श और अपूर्ण दोनों प्रणालियों का विश्लेषण 2 माइक्रोमीटर या 500 एलपी/मिमी है, यह स्पष्ट है कि बाद वाले उदाहरण की छवियां कम तेज हैं। विश्लेषण की एक परिभाषा जो कथित गुणवत्ता के अनुरूप है, इसके अतिरिक्त स्थानिक आवृत्ति का उपयोग करेगी जिस पर पहला शून्य होता है, 10 माइक्रोमीटर, या 100 एलपी/मिमी। संपूर्णप्रतिबिंब प्रणाली के लिए भी विश्लेषण की परिभाषाएँ व्यापक रूप से भिन्न होती हैं। प्रकाशिकी स्थानतारण प्रकार्य द्वारा एक अधिक संपूर्ण, स्पष्ट चित्र प्रदान किया जाता है।

गैर-घूर्णी सममित विपथन वाले प्रकाशिकी प्रणाली का ओटीएफ

जब ट्रेफ़ोइल विपथन के साथ एक प्रकाशिकी प्रणाली के माध्यम से देखा जाता है, तो एक बिंदु वस्तु की प्रतिबिंबतीन-बिंदु वाले तारे (ए) के रूप में दिखाई देगी। चूँकि बिंदु-प्रसार प्रकार्य घूर्णी सममित नहीं है, केवल एक द्वि-आयामी प्रकाशिकी स्थानतारण प्रकार्य ही इसका अच्छी तरह से वर्णन कर सकता है (बी)। सतह प्लॉट की ऊंचाई निरपेक्ष मान को इंगित करती है और रंग प्रकार्य के जटिल तर्क को इंगित करता है। ऐसेप्रतिबिंब उपकरण द्वारा चित्रित एक स्पोक लक्ष्य (सी) में सिमुलेशन द्वारा दिखाया गया है।

प्रकाशिकी प्रणाली, और विशेष रूप से प्रकाशिकी विपथन सदैव पुनर्निर्देशनीय नहीं होते हैं। इसलिए, विभिन्न दिशा वाली आवृत्ति वाले आवर्तक पैटर्न्स को यदि उनकी आवृत्ति समान होती है, तो उनके विभिन्न बिना आवृत्ति चेतना के चित्रित किया जा सकता है। प्रकाशिकी स्थानतारण प्रकार्य या प्रतिरुपण स्थानतारण प्रकार्य सामान्यतः द्वि-आयामी प्रकार्य होते हैं। निम्नलिखित चित्र में पहले चर्चित आदर्श और अपूर्ण प्रणाली के द्वि-आयामी रूप के प्रकाशिकी प्रणाली के लिए इन दो-आयामी प्रकार्य का तुलनात्मक संकेत दिखाते हैं, जिसमें ट्रीफोइल, एक गैर-पुनर्निर्देशनीय विपथन, होता है।

प्रकाशिकी स्थानतारण प्रकार्य सदैव वास्तविक-मूल्यवान नहीं होते हैं। प्रणाली में विपथन के आधार पर, अवधि पैटर्न को किसी भी मात्रा में स्थानांतरित किया जा सकता है। यह सामान्यतः गैर-घूर्णी-सममित विपथन के स्थिति में होता है। उपरोक्त आकृति में सतह भूखंडों के रंगों का रंग चरण को दर्शाता है। यह देखा जा सकता है कि, जबकि घूर्णी सममित विपथन के लिए चरण या तो 0 या π है और इस प्रकार स्थानांतरण प्रकार्य वास्तविक मूल्य है, गैर-घूर्णी सममित विपथन के लिए स्थानांतरण प्रकार्य में एक काल्पनिक घटक होता है और चरण लगातार बदलता रहता है।

व्यावहारिक उदाहरण - उच्च परिभाषा वीडियो प्रणाली

जबकि प्रकाशिकी विश्लेषण, जैसा कि सामान्यतः कैमरा प्रणाली के संदर्भ में उपयोग किया जाता है, एक प्रतिबिंबमें केवल पिक्सेल की संख्या का वर्णन करता है, और इसलिए बारीक विवरण दिखाने की क्षमता, स्थानांतरण प्रकार्य प्रतिक्रिया में आसन्न पिक्सेल की काले से सफेद में बदलने की क्षमता का वर्णन करता है अलग-अलग स्थानिक आवृत्ति के पैटर्न, और इसलिए पूर्ण या कम व्यतिरेक के साथ, बारीक विवरण दिखाने की वास्तविक क्षमता। प्रकाशिकी स्थानतारण प्रकार्य के साथ पुनरुत्पादित एक प्रतिबिंब जो उच्च स्थानिक आवृत्तियों पर होता है, वो साधारण भाषा में 'ब्लर' या 'धुंधला' दिखाई देगी।

वर्तमान- उच्च परिभाषा (एचडी) वीडियो प्रणाली का उदाहरण लेते हुए, 1920 गुणा 1080 पिक्सल के साथ, नाइक्विस्ट-शैनन सैंपलिंग प्रमेय में कहा गया है कि एक आदर्श प्रणाली में, पूरी तरह से हल करना संभव होना चाहिए। कुल मिलाकर 1920 काली और सफेद वैकल्पिक रेखाएं, अन्यथा प्रति चित्र चौड़ाई 1920/2=960 रेखा जोड़े, या प्रति चित्र चौड़ाई 960 चक्र की स्थानिक आवृत्ति के रूप में संदर्भित की जाती हैं, संभव है परंतु कैमरे के साथ व्यवहार करते समय सामान्यतः कम स्पष्ट होता है और दूरबीन आदि के लिए अधिक उपयुक्त होता है।

व्यवहारिक दृष्टिकोण से यह बिल्कुल नहीं होता है, और स्थानिक आवृत्तियाँ जो निक्विस्ट दर की ओर आती हैं, सामान्यतः घटते हुए गुणक से पुनर्प्रक्षेपित होंगी, इसलिए मामूली विवरण की चौड़ाई में कमी होती है, हालांकि यह देखा जा सकता है कि उसे दर्शाने की क्षमता है। इससे यह दिलचस्प दृष्टिकोण उत्पन्न होता है कि, उदाहरण के लिए, एक फ़िल्म स्कैनर का उपयोग करके प्राप्त किया गया एक मानक परिभाषा टेलीविजन चित्र एक ऐसे कैमरे से जो किसी खराब प्रतिरुपण र स्थानातरण प्रकार्य वाला होता है, शार्प दिख सकता है। इन दो चित्रों में एक दिलचस्प अंतर होता है, जो अक्सर छूट जाता है, पहले में एक निश्चित सीमा तक विवरण पर पूरा दर दिखाता है, फिर असल में कोई वाकई त्वचा विवरण नहीं होता है, जबकि दूसरे में दरार विवरण तो होता है, लेकिन इसमें दर को कम किया जाता है, जिससे कुल में अधीन होने के रूप में दिखाई देता है।

त्रि-आयामी प्रकाशिकी स्थानांतरण प्रकार्य

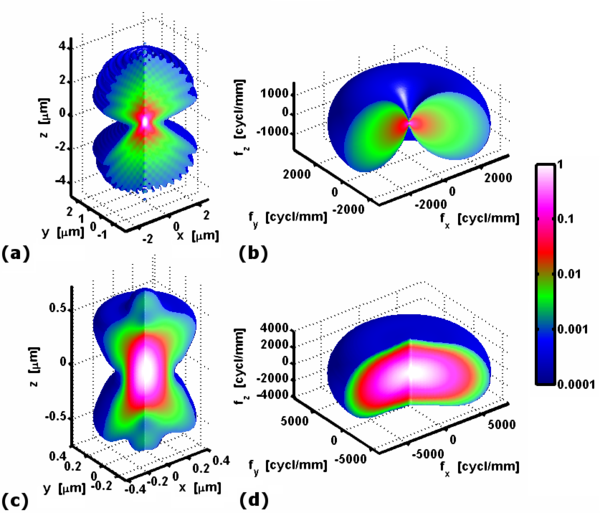
वाइड-फील्ड माइक्रोस्कोप (ए, बी) और कन्फोकल माइक्रोस्कोप (सी, डी) के त्रि-आयामी बिंदु प्रसार प्रकार्य (ए, सी) और संबंधित प्रतिरुपण स्थानतारण प्रकार्य (बी, डी)। दोनों ही स्थिति में अभिदृश्यक का संख्यात्मक छिद्र 1.49 है और माध्यम का अपवर्तनांक 1.52 है। उत्सर्जित प्रकाश की तरंग दैर्ध्य 600 एनएम मानी जाती है और, कन्फोकल माइक्रोस्कोप के स्थिति में, गोलाकार ध्रुवीकरण के साथ उत्तेजना प्रकाश की तरंग दैर्ध्य 500 एनएम होती है। आंतरिक तीव्रता वितरण को देखने के लिए एक अनुभाग काटा जाता है। लघुगणकीय रंग पैमाने पर दिखाए गए रंग अधिकतम मान के लिए सामान्यीकृत विकिरण (ए,सी) और वर्णक्रमीय घनत्व (बी,डी) को दर्शाते हैं।

यद्यपि कोई सामान्यतः किसी प्रतिबिंब को समतल या द्वि-आयामी मानता है,प्रतिबिंब प्रणाली प्रतिबिंब स्थान में त्रि-आयामी तीव्रता वितरण उत्पन्न करेगी जिसे सिद्धांत रूप से मापा जा सकता है। जैसे त्रि-आयामी तीव्रता वितरण को पकड़ने के लिए एक द्वि-आयामी सेंसर का अनुवाद किया जा सकता है। एक बिंदु स्रोत की प्रतिबिंब भी एक त्रि-आयामी (3डी) तीव्रता वितरण है जिसे 3डी बिंदु-प्रसार प्रकार्य द्वारा दर्शाया जा सकता है। उदाहरण के तौर पर, दाईं ओर का चित्र एक वाइड-फील्ड माइक्रोस्कोप (ए) के ऑब्जेक्ट स्पेस में कन्फोकल माइक्रोस्कोप (सी) के साथ 3 डी पॉइंट-स्प्रेड प्रकार्य दिखाता है। यद्यपि 1.49 के संख्यात्मक छिद्र् के साथ एक ही माइक्रोस्कोप उद्देश्य का उपयोग किया जाता है, यह स्पष्ट है कि कन्फोकल पॉइंट स्प्रेड प्रकार्य पार्श्व आयाम (एक्स, वाई) और अक्षीय आयाम (जेड) दोनों में अधिक कॉम्पैक्ट है। कोई सही निष्कर्ष निकाल सकता है कि कन्फोकल माइक्रोस्कोप का विश्लेषण तीनों आयामों में वाइड-फील्ड माइक्रोस्कोप से बेहतर है।

त्रि-आयामी प्रकाशिकी स्थानतारण प्रकार्य की गणना 3डी पॉइंट-स्प्रेड प्रकार्य के त्रि-आयामी फूरियर रूपांतरण के रूप में की जा सकती है। इसका रंग-कोडित परिमाण क्रमशः पैनल (ए) और (सी) में दिखाए गए बिंदु-प्रसार कार्यों के अनुरूप पैनल (बी) और (डी) में प्लॉट किया गया है। वाइड-फील्ड माइक्रोस्कोप के स्थानतारण प्रकार्य में एक समर्थन (गणित) होता है जो सभी तीन-आयामों में कन्फोकल माइक्रोस्कोप का आधा होता है, जो वाइड-फील्ड माइक्रोस्कोप के पहले नोट किए गए निचले विश्लेषण की पुष्टि करता है। ध्यान दें कि z-अक्ष के साथ, x = y = 0 के लिए, स्थानांतरण प्रकार्य मूल को छोड़कर हर जगह शून्य है। यह गायब शंकु एक प्रसिद्ध समस्या है जो वाइड-फील्ड माइक्रोस्कोप का उपयोग करके प्रकाशिकी सेक्शनिंग को रोकती है।^[4] फोकल प्लेन पर द्वि-आयामी प्रकाशिकी स्थानतारण प्रकार्य की गणना जेड-अक्ष के साथ 3डी प्रकाशिकी स्थानतारण प्रकार्य के एकीकरण द्वारा की जा सकती है। यद्यपि वाइड-फील्ड माइक्रोस्कोप (बी) का 3डी स्थानतारण प्रकार्य z ≠ 0 के लिए z-अक्ष पर शून्य है; इसका अभिन्न अंग, 2D प्रकाशिकी स्थानतारण , x = y = 0 पर अधिकतम तक पहुंचता है। यह केवल इसलिए संभव है क्योंकि 3D प्रकाशिकी स्थानतारण प्रकार्य मूल x = y = z = 0 पर विचलन करता है। प्रकार्य मान z-अक्ष के साथ होता है 3डी प्रकाशिकी स्थानतारण प्रकार्य डिराक डेल्टा प्रकार्य के अनुरूप होता है।

गणना

अधिकांश प्रकाशिकी लेंस प्रारूप में लेंस प्रारूप के प्रकाशिकी या प्रतिरुपण स्थानतारण प्रकार्य की गणना करने की कार्यक्षमता होती है। यहां दिए गए उदाहरणों में आदर्श प्रणालियों की गणना जूलिया (प्रोग्रामिंग भाषा), जीएनयू ऑक्टेव या मैटलैब जैसे सॉफ़्टवेयर का उपयोग करके सरलता से संख्यात्मक रूप से की जाती है, और कुछ विशिष्ट स्थितियों में विश्लेषणात्मक रूप से भी की जाती है। प्रकाशिकी स्थानतारण प्रकार्य की गणना निम्नलिखित दो दृष्टिकोणों से की जा सकती है:^[5]

असंगत बिंदु प्रसार प्रकार्य के फूरियर रूपांतरण के रूप में, या
प्रकाशिकी प्रणाली के पुतली प्रकार्य के ऑटो-सहसंबंध के रूप में

गणितीय रूप से दोनों दृष्टिकोण समतुल्य हैं। संख्यात्मक गणना सामान्यतः फूरियर रूपांतर के माध्यम से सबसे कुशलता से की जाती है; यद्यपि, ऑटो-सहसंबंध दृष्टिकोण का उपयोग करके विश्लेषणात्मक गणना अधिक सुव्यवस्थित हो सकती है।

उदाहरण

परिपत्र छिद्र् के साथ आदर्श लेंस प्रणाली

पुतली के कार्य का स्वत: सहसंबंध

चूंकि प्रकाशिकी स्थानतारण प्रकार्य पॉइंट स्प्रेड कार्य का फूरियर रूपांतरण है, और पॉइंट स्प्रेड प्रकार्य व्युत्क्रम फूरियर रूपांतरित पुतली कार्य का वर्ग निरपेक्ष है, प्रकाशिकी स्थानतारण प्रकार्य की गणना सीधे पुतली कार्य से भी की जा सकती है। कनवल्शन प्रमेय से यह देखा जा सकता है कि प्रकाशिकी स्थानतारण प्रकार्य वास्तव में पुतली प्रकार्य का स्वत: सहसंबंध है।^[5]

एक गोलाकार छिद्र् के साथ एक आदर्श प्रकाशिकी प्रणाली का पुतली कार्य इकाई त्रिज्या की एक डिस्क है। इस प्रकार ऐसी प्रणाली के प्रकाशिकी स्थानतारण प्रकार्य की गणना ज्यामितीय रूप से की दूरी पर दो समान डिस्क के बीच के अंतरविभाजक क्षेत्र से की जा सकती है। $2\nu$ , कहाँ $\nu$ उच्चतम संचरित आवृत्ति के लिए सामान्यीकृत स्थानिक आवृत्ति है।^[2] सामान्यतः प्रकाशिकी स्थानतारण प्रकार्य को एक के अधिकतम मान $\nu =0$ पर सामान्यीकृत किया जाता है, इसलिए परिणामी क्षेत्र $\pi$ को विभाजित किया जाना चाहिए

प्रतिच्छेदी क्षेत्र की गणना दो समान गोलाकार खंडों के क्षेत्रों के योग के रूप में की जा सकती है: $\theta /2-\sin(\theta )/2$ , कहाँ $\theta$ वृत्त खंड कोण है. प्रतिस्थापित करके $|\nu |=\cos(\theta /2)$ , और समानताओं का उपयोग करना $\sin(\theta )/2=\sin(\theta /2)\cos(\theta /2)$ और $1=\nu ^{2}+\sin(\arccos(|\nu |))^{2}$ , क्षेत्र के लिए समीकरण को इस प्रकार फिर से लिखा जा सकता है $\arccos(|\nu |)-|\nu |{\sqrt {1-\nu ^{2}}}$ . इसलिए सामान्यीकृत प्रकाशिकी स्थानतारण प्रकार्य इस प्रकार दिया गया है:

\operatorname {OTF} (\nu )={\frac {2}{\pi }}\left(\arccos(|\nu |)-|\nu |{\sqrt {1-\nu ^{2}}}\right).

अधिक विस्तृत चर्चा यहां पाई जा सकती है ^[5]।^[2]^{: 152–153}

संख्यात्मक मूल्यांकन

एक-आयामी प्रकाशिकी स्थानतारण प्रकार्य की गणना लाइन स्प्रेड प्रकार्य के असतत फूरियर रूपांतरण के रूप में की जा सकती है। यह डेटा स्थानिक आवृत्ति डेटा के विरुद्ध ग्राफ़ किया गया है। इस स्थिति में, प्रवृत्ति दिखाने के लिए छठे क्रम के बहुपद को एमटीएफ बनाम स्थानिक आवृत्ति वक्र पर फिट किया जाता है। 50% कटऑफ आवृत्ति संबंधित स्थानिक आवृत्ति प्राप्त करने के लिए निर्धारित की जाती है। इस प्रकार, परीक्षण के तहत इकाई के सर्वोत्तम फोकस की अनुमानित स्थिति इस डेटा से निर्धारित की जाती है।

लाइन स्प्रेड प्रकार्य (एलएसएफ) का फूरियर रूपांतरण निम्नलिखित समीकरणों द्वारा विश्लेषणात्मक रूप से निर्धारित नहीं किया जा सकता है:

\operatorname {MTF} ={\mathcal {F}}\left[\operatorname {LSF} \right]\qquad \qquad \operatorname {MTF} =\int f(x)e^{-i2\pi \,xs}\,dx

इसलिए, फूरियर ट्रांसफॉर्म को असतत फूरियर ट्रांसफॉर्म का उपयोग करके संख्यात्मक रूप से अनुमानित किया जाता है ${\mathcal {DFT}}$ .^[6]

\operatorname {MTF} ={\mathcal {DFT}}[\operatorname {LSF} ]=Y_{k}=\sum _{n=0}^{N-1}y_{n}e^{-ik{\frac {2\pi }{N}}n}\qquad k\in [0,N-1]

कहाँ

$Y_{k}\,$ = द $k^{\text{th}}$ एमटीएफ का मूल्य
$N\,$ = डेटा बिंदुओं की संख्या
$n\,$ = सूचकांक
$k\,$ = $k^{\text{th}}$ एलएसएफ डेटा की अवधि
$y_{n}\,$ = $n^{\text{th}}\,$ पिक्सेल स्थिति
$i={\sqrt {-1}}$

e^{\pm ia}=\cos(a)\,\pm \,i\sin(a)

\operatorname {MTF} ={\mathcal {DFT}}[\operatorname {LSF} ]=Y_{k}=\sum _{n=0}^{N-1}y_{n}\left[\cos \left(k{\frac {2\pi }{N}}n\right)-i\sin \left(k{\frac {2\pi }{N}}n\right)\right]\qquad k\in [0,N-1]

फिर एमटीएफ को स्थानिक आवृत्ति के विरुद्ध प्लॉट किया जाता है और इस परीक्षण से संबंधित सभी प्रासंगिक डेटा उस ग्राफ से निर्धारित किया जा सकता है।

वेक्टरियल स्थानतारण प्रकार्य

माइक्रोस्कोपी में पाए जाने वाले उच्च संख्यात्मक छिद्र् पर, प्रकाश ले जाने वाले क्षेत्रों की वेक्टर प्रकृति पर विचार करना महत्वपूर्ण है। कार्टेशियन अक्षों के अनुरूप तीन स्वतंत्र घटकों में तरंगों को विघटित करके, प्रत्येक घटक के लिए एक बिंदु प्रसार प्रकार्य की गणना की जा सकती है और एक वेक्टरियल बिंदु प्रसार प्रकार्य में जोड़ा जा सकता है। इसी प्रकार, एक वेक्टरियल प्रकाशिकी स्थानतारण प्रकार्य को निर्धारित किया जा सकता है।^[7]^[8]

मा

प्रकाशिकी स्थानतारण प्रकार्य न केवल प्रकाशिकी प्रणाली के प्रारूप के लिए उपयोगी है, बल्कि यह निर्मित प्रणाली को चिह्नित करने के लिए भी मूल्यवान है।

बिंदु प्रसार प्रकार्य से प्रारंभ

प्रकाशिकी स्थानतारण प्रकार्य को प्रकाशिकी प्रणाली की आवेग प्रतिक्रिया के फूरियर रूपांतरण के रूप में परिभाषित किया गया है, जिसे पॉइंट स्प्रेड प्रकार्य भी कहा जाता है। इस प्रकार प्रकाशिकी स्थानतारण प्रकार्य को पहले एक बिंदु स्रोत की प्रतिबिंबप्राप्त करके और नमूना प्रतिबिंबमें द्वि-आयामी असतत फूरियर ट्रांसफॉर्म को लागू करके आसानी से प्राप्त किया जाता है। ऐसा बिंदु-स्रोत, उदाहरण के लिए, एक पिन छेद वाली स्क्रीन के पीछे एक चमकदार रोशनी, एक फ्लोरोसेंट या धात्विक माइक्रोस्फीयर, या बस एक स्क्रीन पर चित्रित एक बिंदु हो सकता है। बिंदु प्रसार प्रकार्य के माध्यम से प्रकाशिकी स्थानतारण प्रकार्य की गणना बहुमुखी है क्योंकि यह बिंदु स्रोत के विभिन्न पदों और तरंग दैर्ध्य स्पेक्ट्रा के लिए प्रक्रिया को पुनरावर्तित स्थानिक भिन्नता और रंगीन विपथन के साथ प्रकाशिकी को पूरी तरह से चित्रित कर सकता है।

स्थानिक रूप से अपरिवर्तनीय प्रकाशिकी के लिए विस्तारित परीक्षण वस्तुओं का उपयोग करना

जब विपथन को स्थानिक रूप से अपरिवर्तनीय माना जा सकता है, तो वैकल्पिक पैटर्न का उपयोग लाइनों और किनारों जैसे प्रकाशिकी स्थानतारण प्रकार्य को निर्धारित करने के लिए किया जा सकता है। संबंधित स्थानांतरण प्रकार्य को क्रमशः लाइन-स्प्रेड प्रकार्य और एज-स्प्रेड प्रकार्य के रूप में जाना जाता है। ऐसी विस्तारित वस्तुएं प्रतिबिंबमें अधिक पिक्सेल को रोशन करती हैं, और बड़े सिग्नल-टू-शोर अनुपात के कारण माप सटीकता में सुधार कर सकती हैं। इस मामले में प्रकाशिकी स्थानतारण प्रकार्य की गणना प्रतिबिंब के द्वि-आयामी असतत फूरियर रूपांतरण के रूप में की जाती है और इसे विस्तारित ऑब्जेक्ट से विभाजित किया जाता है। सामान्यतः या तो एक रेखा या काले-सफ़ेद किनारे का उपयोग किया जाता है।

लाइन-स्प्रेड प्रकार्य

मूल के माध्यम से एक रेखा का द्वि-आयामी फूरियर रूपांतरण, इसके लिए और मूल के माध्यम से एक रेखा ओर्थोगोनल है। इस प्रकार विभाजक एक आयाम को छोड़कर सभी के लिए शून्य है, परिणामस्वरूप, प्रकाशिकी स्थानतारण प्रकार्य केवल एकल लाइन-स्प्रेड प्रकार्य (एलएसएफ) का उपयोग करके एकल आयाम के लिए निर्धारित किया जा सकता है। यदि आवश्यक हो, तो विभिन्न कोणों पर रेखाओं के साथ माप को दोहराकर द्वि-आयामी प्रकाशिकी स्थानांतरण प्रकार्य निर्धारित किया जा सकता है।

लाइन स्प्रेड प्रकार्य को दो अलग-अलग तरीकों का उपयोग करके पाया जा सकता है। इसे सीधे स्लिट परीक्षण लक्ष्य द्वारा प्रदान की गई एक आदर्श रेखा सन्निकटन से पाया जा सकता है या इसे एज स्प्रेड प्रकार्य से प्राप्त किया जा सकता है, जिसकी चर्चा अगले उप अनुभाग में की गई है।

एज-स्प्रेड प्रकार्य

एक किनारे का द्वि-आयामी फूरियर रूपांतरण भी केवल एक पंक्ति पर गैर-शून्य है, किनारे पर ऑर्थोगोनल है। इस प्रकार्य को कभी-कभी एज स्प्रेड प्रकार्य (ईएसएफ) के रूप में जाना जाता है।^[9]^[10] यद्यपि, इस रेखा पर मान मूल बिंदु से दूरी के व्युत्क्रमानुपाती होते हैं। यद्यपि इस तकनीक से प्राप्त माप छवियां कैमरे के एक बड़े क्षेत्र को रोशन करती हैं, इससे मुख्य रूप से कम स्थानिक आवृत्तियों पर सटीकता को लाभ होता है। लाइन स्प्रेड प्रकार्य की तरह, प्रत्येक माप प्रकाशिकी स्थानतारण प्रकार्य के केवल एक अक्ष को निर्धारित करता है, इसलिए बार-बार माप आवश्यक हैं यदि प्रकाशिकी प्रणाली को घूर्णी सममित नहीं माना जा सकता है।

जैसा कि दाहिने हाथ के चित्र में दिखाया गया है, एक ऑपरेटर एक बॉक्स क्षेत्र को परिभाषित करता है जो एक काले शरीर द्वारा चाकू-धार परीक्षण लक्ष्य प्रतिबिंबके किनारे को घेरता है। बॉक्स क्षेत्र को लगभग 10% परिभाषित किया गया हैकुल फ़्रेम क्षेत्र का. प्रतिबिंबपिक्सेल डेटा को दो-आयामी सरणी में अनुवादित किया जाता है। सरणी के भीतर प्रत्येक पंक्ति (वीडियो) का आयाम (पिक्सेल तीव्रता) सामान्यीकरण (सांख्यिकी) और औसत है। इससे एज स्प्रेड प्रकार्य प्राप्त होता है।

\operatorname {ESF} ={\frac {X-\mu }{\sigma }}\qquad \qquad \sigma \,={\sqrt {\frac {\sum _{i=0}^{n-1}(x_{i}-\mu \,)^{2}}{n}}}\qquad \qquad \mu \,={\frac {\sum _{i=0}^{n-1}x_{i}}{n}}

यहाँ

ईएसएफ = सामान्यीकृत पिक्सेल तीव्रता डेटा का आउटपुट सरणी
$X\,$ = पिक्सेल तीव्रता डेटा की इनपुट सरणी
$x_{i}\,$ = मैं^वेंका तत्व $X\,$
$\mu \,$ = पिक्सेल तीव्रता डेटा का औसत मूल्य
$\sigma \,$ = पिक्सेल तीव्रता डेटा का मानक विचलन
$n\,$ = औसत में प्रयुक्त पिक्सेल की संख्या

लाइन स्प्रेड प्रकार्य एज स्प्रेड प्रकार्य के व्युत्पन्न के समान है,^[11] जिसे संख्यात्मक विश्लेषण का उपयोग करके विभेदित किया जाता है। यदि एज स्प्रेड प्रकार्य को मापना अधिक व्यावहारिक है, तो कोई लाइन स्प्रेड प्रकार्य को निम्नानुसार निर्धारित कर सकता है:

\operatorname {LSF} ={\frac {d}{dx}}\operatorname {ESF} (x)

सामान्यतः ईएसएफ केवल अलग-अलग बिंदुओं पर ही जाना जाता है, इसलिए एलएसएफ को सीमित अंतर का उपयोग करके संख्यात्मक रूप से अनुमानित किया जाता है:

\operatorname {LSF} ={\frac {d}{dx}}\operatorname {ESF} (x)\approx {\frac {\Delta \operatorname {ESF} }{\Delta x}}

\operatorname {LSF} \approx {\frac {\operatorname {ESF} _{i+1}-\operatorname {ESF} _{i-1}}{2(x_{i+1}-x_{i})}}

यहाँ:

$i\,$ = सूचकांक $i=1,2,\dots ,n-1$
$x_{i}\,$ = $i^{\text{th}}\,$ की स्थिति $i^{\text{th}}\,$ पिक्सेल
$\operatorname {ESF} _{i}\,$ = का ईएसएफ $i^{\text{th}}\,$ पिक्सेल

काली और सफेद रेखाओं के ग्रिड का उपयोग करना

यद्यपि 'शार्पनेस का मूल्यांकन को प्रायः वैकल्पिक काली और सफेद रेखाओं के ग्रिड पैटर्न पर आंका जाता है, इसे काले से सफेद से साइन-वेव भिन्नता का उपयोग करके सख्ती से मापा जाना चाहिए। जहां एक वर्गाकार तरंग पैटर्न का उपयोग किया जाता है (सरल काली और सफेद रेखाएं) न केवल अलियासिंग का अधिक संकट होता है, बल्कि इस तथ्य को भी ध्यान में रखना चाहिए कि एक वर्गाकार तरंग का मूल घटक वर्गाकार तरंग के आयाम से अधिक होता है। इसलिए एक वर्ग तरंग परीक्षण चार्ट आशावादी परिणाम दिखाएगा वास्तव में प्राप्त की तुलना में उच्च स्थानिक आवृत्तियों का बेहतर विश्लेषण वर्ग तरंग परिणाम को कभी-कभी 'व्यतिरेक स्थानतारण प्रकार्य ' (सीटीएफ) के रूप में जाना जाता है।

सामान्य कैमरा प्रणाली में एमटीएफ को प्रभावित करने वाले कारक

सामान्यतः, कई कारकों के परिणामस्वरूप पुनरुत्पादित प्रतिबिंबकाफी हद तक धुंधली हो जाती है, जैसे कि नाइक्विस्ट दर के ठीक नीचे स्थानिक आवृत्ति वाले पैटर्न भी दिखाई नहीं दे सकते हैं, और बेहतरीन पैटर्न जो काले नहीं बल्कि भूरे रंग के रंगों के रूप में 'धुले हुए' दिखाई दे सकते हैं। सफ़ेद। एक प्रमुख कारक सामान्यतः सही 'ईंट की दीवार' प्रकाशिकी फिल्टर बनाने की असंभवता है। डिस्प्ले की नाइक्विस्ट दर से ऊपर स्थानिक आवृत्तियों को समाप्त करके अलियासिंग को कम करने के लिए ऐसा फ़िल्टर आवश्यक है।

प्रकाशिकी स्थानतारण प्रकार्य को बनाए रखने के लिए अधिप्रतिचयन और डाउनलोडसंस्करण

कैमरे जैसे डिजिटलप्रतिबिंब प्रणाली में संभव सैद्धांतिक तीक्ष्णता तक पहुंचने का एकमात्र नियम अंतिम प्रतिबिंबमें नमूनाकरण (सिग्नल प्रोसेसिंग) के सापेक्ष कैमरा सेंसर में अधिक पिक्सेल का उपयोग करना है, और विशेष का उपयोग करके 'डाउनकन्वर्ट' या 'इंटरपोलेट' करना है। डिजिटल प्रोसेसिंग जो अलियासिंग से बचने के लिए नाइक्विस्ट दर से ऊपर की उच्च आवृत्तियों को काट देती है और उस आवृत्ति तक यथोचित सपाट एमटीएफ बनाए रखती है। यह दृष्टिकोण पहली बार 1970 के दशक में अपनाया गया था जब फ्लाइंग स्पॉट स्कैनर, और बाद में चार्ज-युग्मित डिवाइस लाइन स्कैनर विकसित किए गए थे, जो आवश्यकता से अधिक पिक्सेल का नमूना लेते थे और फिर नीचे परिवर्तित हो जाते थे, यही कारण है कि टेलीविजन पर फिल्में सदैव अन्य सामग्रियों की तुलना में अधिक स्पष्ट दिखती हैं। एक वीडियो कैमरा. इंटरपोलेशन या डाउनकन्वर्ट करने का एकमात्र सैद्धांतिक रूप से सही तरीका एक खड़ी कम-पास स्थानिक फ़िल्टर का उपयोग है, जिसे दो-आयामी एक्स भार प्रकार्य के साथ संवलनीय द्वारा महसूस किया जाता है जिसके लिए शक्तिशाली प्रसंस्करण की आवश्यकता होती है। व्यवहार में, प्रसंस्करण आवश्यकता को कम करने के लिए इसके विभिन्न गणितीय अनुमानों का उपयोग किया जाता है। ये अनुमान अब वीडियो संपादन प्रणालियों और फोटोशॉप जैसे प्रतिबिंब प्रसंस्करण कार्यक्रमों में व्यापक रूप से लागू किए जाते हैं।

जिस तरह उच्च व्यतिरेक एमटीएफ के साथ मानक परिभाषा वीडियो केवल अधिप्रतिचयन के साथ संभव है, उसी तरह पूर्ण सैद्धांतिक तीक्ष्णता वाला एचडी टेलीविजन केवल ऐसे कैमरे से प्रारंभ करना संभव है जिसमें काफी अधिक विश्लेषण हो, उसके बाद डिजिटल फ़िल्टरिंग हो। अब फिल्में 4K विश्लेषण और यहां तक कि सिनेमा के लिए 8k वीडियो में शूट की जा रही हैं, हम एचडीटीवी पर केवल उच्च मानक पर शूट की गई फिल्मों या सामग्री से सर्वश्रेष्ठ तस्वीरें देखने की उम्मीद कर सकते हैं। हम कैमरों में उपयोग किए जाने वाले पिक्सेल की संख्या चाहे कितनी भी बढ़ा लें, एक संपूर्ण प्रकाशिकी स्थानिक फ़िल्टर के अभाव में यह हमेशा सत्य रहेगा। इसी प्रकार, 5-मेगापिक्सेल स्थिर कैमरे से प्राप्त 5-मेगापिक्सेल प्रतिबिंब कभी भी समान गुणवत्ता वाले 10-मेगापिक्सेल स्थिर कैमरे से डाउन-रूपांतरण के बाद प्राप्त 5-मेगापिक्सेल प्रतिबिंब से अधिक तेज नहीं हो सकती है। उच्च व्यतिरेक एमटीएफ को बनाए रखने की समस्या के कारण, बीबीसी जैसे प्रसारकों ने लंबे समय तक मानक परिभाषा टेलीविजन को बनाए रखने पर विचार किया, परंतु कई अधिक पिक्सेल के साथ शूटिंग और देखने के द्वारा इसकी गुणवत्ता में सुधार किया यद्यपि जैसा कि पहले उल्लेख किया गया है, ऐसी प्रणाली, यद्यपि प्रभावशाली है, अंततः बहुत बारीक विवरण का अभाव है, जो यद्यपि क्षीण हो गया है, वास्तविक एचडी देखने के प्रभाव को बढ़ाता है।

डिजिटल कैमरे और कैमकोर्डर में एक अन्य कारक लेंस विश्लेषण है। ऐसा कहा जा सकता है कि एक लेंस 1920 क्षैतिज रेखाओं को 'समाधान' करता है, लेकिन इसका मतलब यह नहीं है कि यह काले से सफेद तक पूर्ण प्रतिरुपण के साथ ऐसा करता है। 'मॉड्यूलेशन स्थानतारण प्रकार्य लेंस के प्रदर्शन का सही माप देता है, और स्थानिक आवृत्ति के विरुद्ध आयाम के ग्राफ द्वारा दर्शाया जाता है।

लेंस छिद्र् विवर्तन भी एमटीएफ को सीमित करता है। जबकि लेंस के छिद्र् को कम करने से सामान्यतः विपथन कम हो जाता है और इसलिए एमटीएफ की समतलता में सुधार होता है, किसी भी लेंस और प्रतिबिंबसेंसर आकार के लिए एक इष्टतम छिद्र् होता है, जिसके परे छोटे छिद्र् विवर्तन के कारण विश्लेषण को कम कर देते हैं, जो प्रतिबिंबसेंसर में प्रकाश फैलाता है। प्लेट कैमरों और यहां तक कि 35 मिमी फिल्म के दिनों में यह शायद ही कोई समस्या थी, लेकिन कुछ डिजिटल कैमरों और विशेष रूप से वीडियो कैमरों में उपयोग किए जाने वाले बहुत छोटे प्रारूप सेंसर के साथ यह एक दुर्गम सीमा बन गई है। पहली पीढ़ी के एचडी उपभोक्ता कैमकोर्डर में 1/4-इंच सेंसर का उपयोग किया जाता है, जिसके लिए एफ4 से छोटे छिद्र् विश्लेषण को सीमित करना प्रारंभ कर देते हैं। यहां तक कि पेशेवर वीडियो कैमरे भी ज्यादातर 2/3 इंच सेंसर का उपयोग करते हैं, जो एफ16 के आसपास छिद्र् के उपयोग को प्रतिबंधित करता है जिसे फिल्म प्रारूपों के लिए सामान्य माना जाता है। कुछ कैमरे जैसे पेंटाक्स K10D) में एमटीएफ स्वतः एक्सपोजर मोड की सुविधा होती है, जहां छिद्र् की पसंद को अधिकतम तीक्ष्णता के लिए अनुकूलित किया जाता है। सामान्यतः इसका अर्थ यह होता है यह छिद्र् रेंज के बीच में होता है।^[12]

बड़े प्रारूप वाले डीएसएलआर की ओर रुझान और बेहतर एमटीएफ क्षमता

हाल ही में कम रोशनी की संवेदनशीलता और क्षेत्र प्रभावों की संकीर्ण गहराई की आवश्यकता के कारण बड़े प्रतिबिंबप्रारूप वाले डिजिटल सिंगल-लेंस रिफ्लेक्स कैमरा के उपयोग की ओर बदलाव आया है। इसके कारण कुछ फिल्म और टेलीविजन कार्यक्रम निर्माताओं द्वारा पेशेवर एचडी वीडियो कैमरों के सापेक्ष ऐसे कैमरों को उनकी 'फिल्मी' क्षमता के कारण प्राथमिकता दी जाने लगी है। सिद्धांत रूप में, 16- और 21-मेगापिक्सेल सेंसर वाले कैमरों का उपयोग, अलियासिंग को खत्म करने के लिए डिजिटल फ़िल्टरिंग के साथ, कैमरे के भीतर डाउनकनवर्जन द्वारा लगभग पूर्ण तीक्ष्णता की संभावना प्रदान करता है। ऐसे कैमरे बहुत प्रभावशाली परिणाम देते हैं, और डिजिटल फ़िल्टरिंग के साथ बड़े-प्रारूप वाले डाउन-रूपांतरण की दिशा में वीडियो उत्पादन का मार्ग प्रशस्त करते हुए दिखाई देते हैं, जो अलियासिंग से वास्तविक स्वतंत्रता के साथ एक फ्लैट एमटीएफ की प्राप्ति के लिए मानक दृष्टिकोण बन गया है।

प्रकाशिकी स्थानतारण प्रकार्य का डिजिटल व्युत्क्रम

प्रकाशिकी प्रभावों के कारण व्यतिरेक उप-इष्टतम हो सकता है और डिस्प्ले के नाइक्विस्ट-शैनन सैंपलिंग प्रमेय तक पहुंचने से पहले शून्य तक पहुंच सकता है। प्रदर्शन या आगे की प्रक्रिया से पहले स्थानिक आवृत्तियों को डिजिटल रूप से बढ़ाकर प्रकाशिकी व्यतिरेक कमी को आंशिक रूप से विपरीत किया जा सकता है। यद्यपि अधिक उन्नत डिजिटल प्रतिबिंबपुनर्स्थापना प्रक्रियाएँ उपस्थित हैं, विजेता विखंडन कलन विधि का उपयोग प्रायः इसकी सादगी और दक्षता के लिए किया जाता है। चूँकि यह तकनीक प्रतिबिंबके स्थानिक वर्णक्रमीय घटकों को कई गुना बढ़ा देती है, यह उदाहरण के लिए शोर और त्रुटियों को भी बढ़ा देती है। इसलिए यह केवल पर्याप्त उच्च सिग्नल-टू-शोर अनुपात के साथ अच्छी गुणवत्ता वाली रिकॉर्डिंग पर प्रभावी है।

सीमाएँ

सामान्यतः, बिंदु प्रसार प्रकार्य, एक बिंदु स्रोत की प्रतिबिंब तरंग दैर्ध्य, और दृश्य कोण के क्षेत्र जैसे कारकों पर भी निर्भर करती है। जब ऐसी भिन्नता पर्याप्त रूप से क्रमिक होती है, तो प्रकाशिकी प्रणाली को प्रकाशिकी स्थानतारण कार्य के एक समुच्चय द्वारा चित्रित किया जा सकता है। यद्यपि, जब पार्श्व अनुवाद पर बिंदु स्रोत की प्रतिबिंबअचानक बदल जाती है, तो प्रकाशिकी स्थानतारण प्रकार्य प्रकाशिकी प्रणाली का सटीक वर्णन नहीं करता है।

यह भी देखें

बोकेह
गामा सुधार
न्यूनतम समाधान योग्य व्यतिरेक
न्यूनतम समाधान योग्य तापमान अंतर
प्रकाशिकी विश्लेषण
शोर अनुपात करने के लिए संकेत
सिग्नल स्थानतारण प्रकार्य
स्ट्रेहल अनुपात
स्थानांतरण प्रकार्य
वेवफ्रंट कोडिंग

संदर्भ

↑ The exact definition of resolution may vary and is often taken to be 1.22 times larger as defined by the Rayleigh criterion.
↑ ^2.0 ^2.1 ^2.2 Williams, Charles S. (2002). ऑप्टिकल ट्रांसफर फ़ंक्शन का परिचय. SPIE – The International Society for Optical Engineering. ISBN 0-8194-4336-0.
↑ "कंट्रास्ट ट्रांसफर फ़ंक्शन". Retrieved 16 November 2013.
↑ Macias-Garza, F.; Bovik, A.; Diller, K.; Aggarwal, S.; Aggarwal, J. (1988). "The missing cone problem and low-pass distortion in optical serial sectioning microscopy". ICASSP-88., International Conference on Acoustics, Speech, and Signal Processing. Vol. 2. pp. 890–893. doi:10.1109/ICASSP.1988.196731. S2CID 120191405.
↑ ^5.0 ^5.1 ^5.2 Goodman, Joseph (2005). फूरियर ऑप्टिक्स का परिचय (3rd ed.). Roberts & Co Publishers. ISBN 0-9747077-2-4.
↑ Chapra, S.C.; Canale, R.P. (2006). Numerical Methods for Engineers (5th ed.). New York, New York: McGraw-Hill
↑ Sheppard, C.J.R.; Larkin, K. (1997). "वेक्टरियल पुतली फ़ंक्शन और वेक्टरियल ट्रांसफर फ़ंक्शन" (PDF). Optik-Stuttgart. 107: 79–87.
↑ Arnison, M. R.; Sheppard, C. J. R. (2002). "A 3D vectorial optical transfer function suitable for arbitrary pupil functions". Optics Communications. 211 (1–6): 53–63. Bibcode:2002OptCo.211...53A. doi:10.1016/S0030-4018(02)01857-6.
↑ Holst, G.C. (1998). Testing and Evaluation of Infrared Imaging Systems (2nd ed.). Florida:JCD Publishing, Washington:SPIE.
↑ "Test and Measurement – Products – EOI". www.Electro-Optical.com. Archived from the original on 28 August 2008. Retrieved 2 January 2018.
↑ Mazzetta, J.A.; Scopatz, S.D. (2007). Automated Testing of Ultraviolet, Visible, and Infrared Sensors Using Shared Optics. Infrared Imaging Systems: Design Analysis, Modeling, and Testing XVIII, Vol. 6543, pp. 654313-1 654313-14
↑ "B2BVideoSource.com: Camera Terminology". www.B2BVideoSource.com. Retrieved 2 January 2018.

बाहरी संबंध

"Modulation transfer function", by Glenn D. Boreman on SPIE Optipedia.
"How to Measure MTF and other Properties of Lenses", by Optikos Corporation.

[1] The exact definition of resolution may vary and is often taken to be 1.22 times larger as defined by the Rayleigh criterion.

[Williams2002-2] 2.0 ^2.1 ^2.2 Williams, Charles S. (2002). ऑप्टिकल ट्रांसफर फ़ंक्शन का परिचय. SPIE – The International Society for Optical Engineering. ISBN 0-8194-4336-0.

[CTF-3] "कंट्रास्ट ट्रांसफर फ़ंक्शन". Retrieved 16 November 2013.

[MaciasGarza88-4] Macias-Garza, F.; Bovik, A.; Diller, K.; Aggarwal, S.; Aggarwal, J. (1988). "The missing cone problem and low-pass distortion in optical serial sectioning microscopy". ICASSP-88., International Conference on Acoustics, Speech, and Signal Processing. Vol. 2. pp. 890–893. doi:10.1109/ICASSP.1988.196731. S2CID 120191405.

[Goodman2005-5] 5.0 ^5.1 ^5.2 Goodman, Joseph (2005). फूरियर ऑप्टिक्स का परिचय (3rd ed.). Roberts & Co Publishers. ISBN 0-9747077-2-4.

[6] Chapra, S.C.; Canale, R.P. (2006). Numerical Methods for Engineers (5th ed.). New York, New York: McGraw-Hill

[Sheppard1997-7] Sheppard, C.J.R.; Larkin, K. (1997). "वेक्टरियल पुतली फ़ंक्शन और वेक्टरियल ट्रांसफर फ़ंक्शन" (PDF). Optik-Stuttgart. 107: 79–87.

[Arnison2002-8] Arnison, M. R.; Sheppard, C. J. R. (2002). "A 3D vectorial optical transfer function suitable for arbitrary pupil functions". Optics Communications. 211 (1–6): 53–63. Bibcode:2002OptCo.211...53A. doi:10.1016/S0030-4018(02)01857-6.

[9] Holst, G.C. (1998). Testing and Evaluation of Infrared Imaging Systems (2nd ed.). Florida:JCD Publishing, Washington:SPIE.

[ElectroOpticalTestLab-10] "Test and Measurement – Products – EOI". www.Electro-Optical.com. Archived from the original on 28 August 2008. Retrieved 2 January 2018.

[Mazzetta2007-11] Mazzetta, J.A.; Scopatz, S.D. (2007). Automated Testing of Ultraviolet, Visible, and Infrared Sensors Using Shared Optics. Infrared Imaging Systems: Design Analysis, Modeling, and Testing XVIII, Vol. 6543, pp. 654313-1 654313-14

[12] "B2BVideoSource.com: Camera Terminology". www.B2BVideoSource.com. Retrieved 2 January 2018.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

@@ Line 1: / Line 1: @@
-'''प्रकाशिकी [[स्थानांतरण प्रकार्य]]''' (ओटीएफ) एक दीप्रणली की तरह [[कैमरा]], [[माइक्रोस्कोप]], मानव आंख या [[छवि प्रोजेक्टर|प्रोजेक्टर]] जैसे प्रकाशिकी प्रणाली के बारे में बताता है कि विभिन्न स्थानिक आवृत्ति कैसे कैप्चर या प्रेषित की जाती है। यह प्रकाशिकी अभियंता द्वारा प्रयोग किया जाता है जिससे प्रकाशिकी किसी वस्तु या दृश्य से प्रकाश को फोटोग्राफिक फिल्म, छवि सेंसर, [[रेटिना]], स्क्रीन, या प्रका टीशिकी ट्रांसमिशन चेन के अगले विषय पर प्रोजेक्ट कैसे करते हैं। एक रूपांतर, प्रतिरुपण स्थानतारण प्रकार्य (एमटीएफ), फेज प्रभावों की उपेक्षा करता है, परंतु बहुत सी स्थितियों में ओटीएफ के समान होता है।
+'''प्रकाशिकी [[स्थानांतरण प्रकार्य]]''' (ओटीएफ) एक प्रकाशिकी प्रणाली जैसे कि [[कैमरा]], [[माइक्रोस्कोप]], मानव नेत्र, या [[छवि प्रोजेक्टर|प्रोजेक्टर]] को, यह निर्धारित करता है कि विभिन्न स्थानिक आवृत्ति कैसे कैप्चर किए जाते हैं या प्रेषित किए जाते हैं। यह प्रकाशिकी अभियंताओ द्वारा प्रयोग किया जाता है जिससे प्रकाशिकी किसी वस्तु या दृश्य से प्रकाश को फोटोग्राफिक फिल्म, प्रतिबिंबसेंसर, [[रेटिना]], स्क्रीन, या प्रकाशिकी ट्रांसमिशन चेन के अगले विषय पर प्रोजेक्ट कैसे करते हैं। एक रूपांतर, प्रतिरुपण स्थानतारण प्रकार्य (एमटीएफ), फेज प्रभावों की उपेक्षा करता है, परंतु बहुत सी स्थितियों में ओटीएफ के समान होता है।
-किसी भी स्थानतारण प्रकार्य, लेंस सिस्टम के माध्यम से गुजरने वाले एक आवृत्ति वाले साइन-वेव पैटर्न के प्रति उसकी स्थानिक प्रकाशिकी या अवधि और उसके दिशा के आधार पर प्रतिक्रिया को निर्दिष्ट करता है। औपचारिक रूप से, ओटीएफ को [[बिंदु प्रसार फ़ंक्शन|बिंदु प्रसार प्रकार्य]] (पीएसएफ), अर्थात प्रकाशिकी की [[आवेग प्रतिक्रिया]], एक बिंदु स्रोत की छवि के [[फूरियर रूपांतरण]] के रूप में परिभाषित किया गया है। फूरियर रूपांतरण के रूप में, ओटीएफ जटिल-मूल्यवान है; परंतु पीएसएफ के सामान्य विषय में इसका वास्तविक मूल्य होगा जो इसके केंद्र के बारे में सममित है। एमटीएफ को औपचारिक रूप से जटिल ओटीएफ के परिमाण (पूर्ण मूल्य) के रूप में परिभाषित किया गया है।
+किसी भी स्थानतारण प्रकार्य, लेंस प्रणाली के माध्यम से गुजरने वाले एक आवृत्ति वाले साइन-वेव पैटर्न के प्रति उसकी स्थानिक प्रकाशिकी या अवधि और उसके दिशा के आधार पर प्रतिक्रिया को निर्दिष्ट करता है। औपचारिक रूप से, ओटीएफ को [[बिंदु प्रसार फ़ंक्शन|बिंदु प्रसार प्रकार्य]] (पीएसएफ), अर्थात प्रकाशिकी की [[आवेग प्रतिक्रिया]], एक बिंदु स्रोत की प्रतिबिंबके [[फूरियर रूपांतरण]] के रूप में परिभाषित किया गया है। फूरियर रूपांतरण के रूप में, ओटीएफ जटिल-मूल्यवान है; परंतु पीएसएफ के सामान्य विषय में इसका वास्तविक मूल्य होगा जो इसके केंद्र के बारे में सममित है। एमटीएफ को औपचारिक रूप से जटिल ओटीएफ के परिमाण (पूर्ण मूल्य) के रूप में परिभाषित किया गया है।
-दाएं ओर की छवि में पैनल (ए) और (डी) में दो विभिन्न प्रकाशिकी प्रणाली के लिए प्रकाशिकी अंतरण प्रकार्य दिखाए गए हैं। पहला आदर्श, [[विवर्तन-सीमित प्रणाली]], इमेजिंग प्रणाली का है जिसमें एक गोल पुतली होता है। इसका स्थानांतरण कार्य स्थानिक आवृत्ति के साथ लगभग धीरे-धीरे कम हो जाता है जब तक कि यह विवर्तन-सीमा तक नहीं पहुंच जाता, इस स्थिति में 500 चक्र प्रति मिलीमीटर या 2 माइक्रोन की अवधि पर होता है, चूंकि इस अवधि जितनी छोटी आवधिक विशेषताएं इस इमेजिंग प्रणाली द्वारा कैप्चर की जाती हैं, इसलिए यह कहा जा सकता है कि इसका प्रस्ताव 2 माइक्रोन है।<ref>The exact definition of resolution may vary and is often taken to be 1.22 times larger as defined by the [[angular resolution|Rayleigh criterion]].</ref> पैनल (डी) एक प्रकाशिकी प्रणाली  दिखाता है जो फोकस से बाहर है। इससे विवर्तन-सीमित छवि प्रणाली के सापेक्ष व्यतिरेक में तेज कमी आती है। यह देखा जा सकता है कि व्यतिरेक 250 चक्र/मिमी, या 4 माइक्रोन की अवधि के आसपास शून्य है। यह बताता है कि आउट-ऑफ-फोकस प्रणाली  (ई, एफ) की छवियां विवर्तन-सीमित प्रणाली (बी, सी) के सापेक्ष अधिक धुंधली क्यों हैं। ध्यान दें कि यद्यपि आउट-ऑफ-फोकस प्रणाली में 250 चक्र/मिमी के आसपास स्थानिक आवृत्तियों पर बहुत कम व्यतिरेक है, 500 चक्र/मिमी की विवर्तन सीमा के पास स्थानिक आवृत्तियों पर व्यतिरेक विवर्तन-सीमित है। पैनल (एफ) में छवि का बारीकी से अवलोकन करने से पता चलता है कि स्पोक लक्ष्य के केंद्र के पास बड़े स्पोक घनत्व की छवि अपेक्षाकृत तेज है।
+दाएं ओर की प्रतिबिंबमें पैनल (ए) और (डी) में दो विभिन्न प्रकाशिकी प्रणाली के लिए प्रकाशिकी अंतरण प्रकार्य दिखाए गए हैं। पहला आदर्श, [[विवर्तन-सीमित प्रणाली]],प्रतिबिंब प्रणाली का है जिसमें एक गोल पुतली होता है। इसका स्थानांतरण कार्य स्थानिक आवृत्ति के साथ लगभग धीरे-धीरे कम हो जाता है जब तक कि यह विवर्तन-सीमा तक नहीं पहुंच जाता, इस स्थिति में 500 चक्र प्रति मिलीमीटर या 2 माइक्रोन की अवधि पर होता है, चूंकि इस अवधि जितनी छोटी आवधिक विशेषताएं इसप्रतिबिंब प्रणाली द्वारा कैप्चर की जाती हैं, इसलिए यह कहा जा सकता है कि इसका प्रस्ताव 2 माइक्रोन है।<ref>The exact definition of resolution may vary and is often taken to be 1.22 times larger as defined by the [[angular resolution|Rayleigh criterion]].</ref> पैनल (डी) एक प्रकाशिकी प्रणाली  दिखाता है जो फोकस से बाहर है। इससे विवर्तन-सीमित प्रतिबिंबप्रणाली के सापेक्ष व्यतिरेक में तेज कमी आती है। यह देखा जा सकता है कि व्यतिरेक 250 चक्र/मिमी, या 4 माइक्रोन की अवधि के आसपास शून्य है। यह बताता है कि आउट-ऑफ-फोकस प्रणाली  (ई, एफ) की छवियां विवर्तन-सीमित प्रणाली (बी, सी) के सापेक्ष अधिक धुंधली क्यों हैं। ध्यान दें कि यद्यपि आउट-ऑफ-फोकस प्रणाली में 250 चक्र/मिमी के आसपास स्थानिक आवृत्तियों पर बहुत कम व्यतिरेक है, 500 चक्र/मिमी की विवर्तन सीमा के पास स्थानिक आवृत्तियों पर व्यतिरेक विवर्तन-सीमित है। पैनल (एफ) में प्रतिबिंबका बारीकी से अवलोकन करने से पता चलता है कि स्पोक लक्ष्य के केंद्र के पास बड़े स्पोक घनत्व की प्रतिबिंबअपेक्षाकृत तेज है।
 ==परिभाषा और संबंधित अवधारणाएँ==
-प्रकाशिकी स्थानतारण प्रकार्य के बाद से<ref name=Williams2002>{{cite book |first=Charles S.|last=Williams|year=2002|title=ऑप्टिकल ट्रांसफर फ़ंक्शन का परिचय|publisher=SPIE – The International Society for Optical Engineering|isbn=0-8194-4336-0}}</ref> (ओटीएफ) को बिंदु-प्रसार प्रकार्य  (पीएसएफ) के फूरियर रूपांतरण के रूप में परिभाषित किया गया है, यह सामान्यतः स्थानिक आवृत्ति का एक जटिल मूल्य वाला प्रकार्य होता है। एक विशिष्ट आवधिक पैटर्न का प्रक्षेपण क्रमशः अनुमानित प्रक्षेपण के सापेक्ष विपरीत और अनुवाद के आनुपातिक पूर्ण मूल्य और [[जटिल तर्क]] के साथ एक जटिल संख्या द्वारा दर्शाया जाता है।
+प्रकाशिकी स्थानतारण प्रकार्य के बाद से<ref name=Williams2002>{{cite book |first=Charles S.|last=Williams|year=2002|title=ऑप्टिकल ट्रांसफर फ़ंक्शन का परिचय|publisher=SPIE – The International Society for Optical Engineering|isbn=0-8194-4336-0}}</ref> (ओटीएफ) को बिंदु-प्रसार प्रकार्य (पीएसएफ) के फूरियर रूपांतरण के रूप में परिभाषित किया गया है, यह सामान्यतः स्थानिक आवृत्ति का एक जटिल मूल्य वाला प्रकार्य होता है। एक विशिष्ट आवधिक पैटर्न का प्रक्षेपण क्रमशः अनुमानित प्रक्षेपण के सापेक्ष विपरीत और अनुवाद के आनुपातिक पूर्ण मूल्य और [[जटिल तर्क]] के साथ एक जटिल संख्या द्वारा दर्शाया जाता है।
-[[File:Definitions PSF OTF MTF PhTF.svg|right|thumb|400px|एक प्रकाशिकी प्रणाली  की विभिन्न बारीकी से संबंधित विशेषताएँ कोमा को प्रदर्शित करती हैं, एक विशिष्ट विपथन जो अक्ष से बाहर होता है। (ए) प्वाइंट-स्प्रेड प्रकार्य (पीएसएफ) एक बिंदु स्रोत की छवि है। (बी) एक रेखा की छवि को लाइन-स्प्रेड प्रकार्य  के रूप में संदर्भित किया जाता है, इस स्थिति में एक लंबवत रेखा लाइन-स्प्रेड प्रकार्य  बिंदु-स्प्रेड छवि के ऊर्ध्वाधर एकीकरण के सीधे आनुपातिक है। प्रकाशिकी-स्थानतारण  प्रकार्य  (ओटीएफ) को बिंदु-प्रसार प्रकार्य  के फूरियर रूपांतरण के रूप में परिभाषित किया गया है और इस प्रकार यह सामान्यतः एक दो-आयामी जटिल प्रकार्य  है। सामान्यतः केवल एक-आयामी स्लाइस दिखाया जाता है (सी), लाइन-स्प्रेड प्रकार्य  के फूरियर ट्रांसफॉर्म के अनुरूप। मोटी हरी रेखा प्रकार्य  के वास्तविक भाग को संकेत करती है, और पतली लाल रेखा काल्पनिक भाग को संकेत करती है। प्रायः    केवल जटिल प्रकार्य  का पूर्ण मान दिखाया जाता है, इससे द्वि-आयामी प्रकार्य  (डी) के दृश्य की अनुमति मिलती है; यद्यपि , सामान्यतः केवल एक-आयामी प्रकार्य दिखाया जाता है। उत्तरार्द्ध को सामान्यतः स्थानिक आवृत्ति शून्य पर सामान्यीकृत किया जाता है और इसे प्रतिरुपण स्थानतारण  प्रकार्य  (एमटीएफ) के रूप में जाना जाता है। पूर्णता के लिए, जटिल तर्क को कभी-कभी चरण स्थानांतरण प्रकार्य  (पीएचटीएफ) के रूप में प्रदान किया जाता है, जिसे पैनल (एफ) में दिखाया गया है।]]
+[[File:Definitions PSF OTF MTF PhTF.svg|right|thumb|400px|एक प्रकाशिकी प्रणाली  की विभिन्न बारीकी से संबंधित विशेषताएँ कोमा को प्रदर्शित करती हैं, एक विशिष्ट विपथन जो अक्ष से बाहर होता है। (ए) प्वाइंट-स्प्रेड प्रकार्य (पीएसएफ) एक बिंदु स्रोत की प्रतिबिंबहै। (बी) एक रेखा की प्रतिबिंबको लाइन-स्प्रेड प्रकार्य  के रूप में संदर्भित किया जाता है, इस स्थिति में एक लंबवत रेखा लाइन-स्प्रेड प्रकार्य  बिंदु-स्प्रेड प्रतिबिंबके ऊर्ध्वाधर एकीकरण के सीधे आनुपातिक है। प्रकाशिकी-स्थानतारण  प्रकार्य  (ओटीएफ) को बिंदु-प्रसार प्रकार्य  के फूरियर रूपांतरण के रूप में परिभाषित किया गया है और इस प्रकार यह सामान्यतः एक दो-आयामी जटिल प्रकार्य  है। सामान्यतः केवल एक-आयामी स्लाइस दिखाया जाता है (सी), लाइन-स्प्रेड प्रकार्य  के फूरियर ट्रांसफॉर्म के अनुरूप। मोटी हरी रेखा प्रकार्य  के वास्तविक भाग को संकेत करती है, और पतली लाल रेखा काल्पनिक भाग को संकेत करती है। प्रायः    केवल जटिल प्रकार्य  का पूर्ण मान दिखाया जाता है, इससे द्वि-आयामी प्रकार्य  (डी) के दृश्य की अनुमति मिलती है; यद्यपि , सामान्यतः केवल एक-आयामी प्रकार्य दिखाया जाता है। उत्तरार्द्ध को सामान्यतः स्थानिक आवृत्ति शून्य पर सामान्यीकृत किया जाता है और इसे प्रतिरुपण स्थानतारण  प्रकार्य  (एमटीएफ) के रूप में जाना जाता है। पूर्णता के लिए, जटिल तर्क को कभी-कभी चरण स्थानांतरण प्रकार्य  (पीएचटीएफ) के रूप में प्रदान किया जाता है, जिसे पैनल (एफ) में दिखाया गया है।]]
 {| class="wikitable floatright"
 |-
@@ Line 27: / Line 27: @@
 |3डी प्रकाशिकी -स्थानतारण प्रकार्य
 |}
-प्रायः व्यतिरेक में कमी सबसे अधिक रुचिकर होती है और पैटर्न के अनुवाद को नजरअंदाज किया जा सकता है। सापेक्ष व्यतिरेक प्रकाशिकी स्थानतारण प्रकार्य के पूर्ण मूल्य द्वारा दिया जाता है, एक प्रकार्य  जिसे सामान्यतः प्रतिरुपण स्थानतारण प्रकार्य (एमटीएफ) के रूप में जाना जाता है। इसके मान दर्शाते हैं कि स्थानिक आवृत्ति के कार्य के रूप में वस्तु का कितना व्यतिरेक छवि में कैप्चर किया गया है। स्थानिक आवृत्ति 1 से 0 बढ़ने के साथ एमटीएफ घटने लगता है; यद्यपि, प्रकार्य  प्रायः[[ एकरस | एक जैसा]] नहीं होता है। दूसरी ओर, जब पैटर्न अनुवाद भी महत्वपूर्ण होता है, तो प्रकाशिकी स्थानतारण प्रकार्य  के जटिल तर्क को दूसरे वास्तविक-मूल्य वाले प्रकार्य के रूप में दर्शाया जा सकता है, जिसे सामान्यतः  चरण स्थानतारण  प्रकार्य  (पीएचटीएफ) के रूप में जाना जाता है। जटिल-मूल्यवान प्रकाशिकी स्थानतारण  प्रकार्य  को इन दो वास्तविक-मूल्यवान कार्यों के संयोजन के रूप में देखा जा सकता है:
+प्रायः व्यतिरेक में कमी सबसे अधिक रुचिकर होती है और पैटर्न के अनुवाद को नजरअंदाज किया जा सकता है। सापेक्ष व्यतिरेक प्रकाशिकी स्थानतारण प्रकार्य के पूर्ण मूल्य द्वारा दिया जाता है, एक प्रकार्य  जिसे सामान्यतः प्रतिरुपण स्थानतारण प्रकार्य (एमटीएफ) के रूप में जाना जाता है। इसके मान दर्शाते हैं कि स्थानिक आवृत्ति के कार्य के रूप में वस्तु का कितना व्यतिरेक प्रतिबिंबमें कैप्चर किया गया है। स्थानिक आवृत्ति 1 से 0 बढ़ने के साथ एमटीएफ घटने लगता है; यद्यपि, प्रकार्य  प्रायः[[ एकरस | एक जैसा]] नहीं होता है। दूसरी ओर, जब पैटर्न अनुवाद भी महत्वपूर्ण होता है, तो प्रकाशिकी स्थानतारण प्रकार्य  के जटिल तर्क को दूसरे वास्तविक-मूल्य वाले प्रकार्य के रूप में दर्शाया जा सकता है, जिसे सामान्यतः चरण स्थानतारण  प्रकार्य (पीएचटीएफ) के रूप में जाना जाता है। जटिल-मूल्यवान प्रकाशिकी स्थानतारण प्रकार्य  को इन दो वास्तविक-मूल्यवान कार्यों के संयोजन के रूप में देखा जा सकता है:
 :<math>\mathrm{OTF}(\nu)=\mathrm{MTF}(\nu)e^{i\,\mathrm{PhTF}(\nu)}</math>
 यहाँ
@@ Line 38: / Line 38: @@
 स्थानांतरण फलन की परिभाषा के अनुरूप, <math>\mathrm{OTF}(0)=\mathrm{MTF}(0)</math> प्रकाश के उस अंश को इंगित करना चाहिए जो बिंदु स्रोत वस्तु से पता लगाया गया था। यद्यपि, सामान्यतः पता लगाए गए प्रकाश की कुल मात्रा के सापेक्ष व्यतिरेक सबसे महत्वपूर्ण है। इस प्रकार, प्रकाशिकी स्थानतारण प्रकार्य को ज्ञात तीव्रता तक सामान्य करना साधारण बात है, इसलिए <math>\mathrm{MTF}(0)\equiv 1</math>सामान्यतः अपनाया जाता है।
-प्रकाशिकी स्थानतारण प्रकार्य उत्सर्जित प्रकाश के वर्णक्रम और ध्रुवीकरण और बिंदु स्रोत की स्थिति जैसे कारकों पर निर्भर करता है। जैसे छवि व्यतिरेक और विश्लेषण सामान्यतः छवि के केंद्र में इष्टतम होते हैं, और दृश्य क्षेत्र के किनारों की ओर बिगड़ते हैं। जब महत्वपूर्ण भिन्नता होती है, तो प्रकाशिकी स्थानतारण प्रकार्य की गणना प्रतिनिधि स्थितियों या रंगों के एक समुच्चय के लिए की जा सकती है।
+प्रकाशिकी स्थानतारण प्रकार्य उत्सर्जित प्रकाश के वर्णक्रम और ध्रुवीकरण और बिंदु स्रोत की स्थिति जैसे कारकों पर निर्भर करता है। जैसे प्रतिबिंबव्यतिरेक और विश्लेषण सामान्यतः प्रतिबिंबके केंद्र में इष्टतम होते हैं, और दृश्य क्षेत्र के किनारों की ओर बिगड़ते हैं। जब महत्वपूर्ण भिन्नता होती है, तो प्रकाशिकी स्थानतारण प्रकार्य की गणना प्रतिनिधि स्थितियों या रंगों के एक समुच्चय के लिए की जा सकती है।
-कभी-कभी बाइनरी ब्लैक-व्हाइट स्ट्राइप पैटर्न के आधार पर स्थानांतरण कार्यों को परिभाषित करना अधिक व्यावहारिक होता है। समान-चौड़ाई वाले काले-सफ़ेद आवधिक पैटर्न के लिए स्थानांतरण प्रकार्य  को व्यतिरेक स्थानतारण प्रकार्य  (सी.टी.एफ) कहा जाता है।<ref name=CTF >{{cite web |title=कंट्रास्ट ट्रांसफर फ़ंक्शन|url=http://www.microscopyu.com/articles/optics/mtfintro.html|access-date=16 November 2013}}</ref>
+कभी-कभी बाइनरी ब्लैक-व्हाइट स्ट्राइप पैटर्न के आधार पर स्थानांतरण कार्यों को परिभाषित करना अधिक व्यावहारिक होता है। समान-चौड़ाई वाले काले-सफ़ेद आवधिक पैटर्न के लिए स्थानांतरण प्रकार्य  को व्यतिरेक स्थानतारण प्रकार्य (सी.टी.एफ) कहा जाता है।<ref name=CTF >{{cite web |title=कंट्रास्ट ट्रांसफर फ़ंक्शन|url=http://www.microscopyu.com/articles/optics/mtfintro.html|access-date=16 November 2013}}</ref>
@@ Line 46: / Line 46: @@
 ===एक आदर्श लेंस प्रणाली का ओटीएफ===
-एक आदर्श लेंस प्रणाली आवधिक पैटर्न को बदले बिना एक उच्च व्यतिरेक प्रक्षेपण प्रदान करेगी, इसलिए प्रकाशिकी स्थानतारण  प्रकार्य  प्रतिरुपण स्थानतारण प्रकार्य  के समान है। सामान्यतः प्रकाशिकी के विश्लेषण द्वारा परिभाषित बिंदु पर व्यतिरेक धीरे-धीरे शून्य की ओर कम हो जाएगा। उदाहरण के लिए, 500 एनएम की दृश्यमान तरंग दैर्ध्य पर उपयोग किए जाने वाले एक आदर्श, [[ऑप्टिकल विपथन|प्रकाशिकी विपथन]]|गैर-विपथन, एफ-नंबर एफ/4 प्रकाशिकी इमेजिंग प्रणाली में दाहिने हाथ की आकृति में दर्शाया गया प्रकाशिकी स्थानतारण प्रकार्य होगा।
+एक आदर्श लेंस प्रणाली आवधिक पैटर्न को बदले बिना एक उच्च व्यतिरेक प्रक्षेपण प्रदान करेगी, इसलिए प्रकाशिकी स्थानतारण  प्रकार्य  प्रतिरुपण स्थानतारण प्रकार्य  के समान है। सामान्यतः प्रकाशिकी के विश्लेषण द्वारा परिभाषित बिंदु पर व्यतिरेक धीरे-धीरे शून्य की ओर कम हो जाएगा। उदाहरण के लिए, 500 एनएम की दृश्यमान तरंग दैर्ध्य पर उपयोग किए जाने वाले एक आदर्श, [[ऑप्टिकल विपथन|प्रकाशिकी विपथन]] गैर-विपथन, एफ-नंबर एफ/4 प्रकाशिकी प्रतिबिंब प्रणाली में दाहिने हाथ की आकृति में दर्शाया गया प्रकाशिकी स्थानतारण प्रकार्य होगा।
 {{multiple image
@@ Line 55: / Line 55: @@
 }}
-कथानक से यह पढ़ा जा सकता है कि व्यतिरेक धीरे-धीरे कम हो जाता है और 500 चक्र प्रति मिलीमीटर की स्थानिक आवृत्ति पर शून्य तक पहुंच जाता है, दूसरे शब्दों में छवि प्रक्षेपण का प्रकाशिकी विश्लेषण 1/500 है एक मिलीमीटर, या 2 माइक्रोमीटर का होता है। तदनुसार, इस विशेष इमेजिंग डिवाइस के लिए, स्पोक केंद्र की ओर अधिक से अधिक धुंधले हो जाते हैं जब तक कि वे एक ग्रे, अनसुलझे, डिस्क में विलीन नहीं हो जाते। ध्यान दें कि कभी-कभी प्रकाशिकी स्थानतारण प्रकार्य ऑब्जेक्ट या नमूना स्थान की इकाइयों, अवलोकन कोण, आवरण की चौड़ाई, या सैद्धांतिक अधिकतम तक सामान्यीकृत किया जाता है। दोनों के बीच रूपांतरण सामान्यतः   गुणा या भाग की स्थिति है। जैसे एक माइक्रोस्कोप सामान्यतः हर वस्तु को 10 से 100 गुना तक बढ़ा देता है, और एक रिफ्लेक्स कैमरा सामान्यतः 5 मीटर की दूरी पर वस्तुओं को 100 से 200 गुना तक बढ़ा देता है।
+कथानक से यह पढ़ा जा सकता है कि व्यतिरेक धीरे-धीरे कम हो जाता है और 500 चक्र प्रति मिलीमीटर की स्थानिक आवृत्ति पर शून्य तक पहुंच जाता है, दूसरे शब्दों में प्रतिबिंबप्रक्षेपण का प्रकाशिकी विश्लेषण 1/500 है एक मिलीमीटर, या 2 माइक्रोमीटर का होता है। तदनुसार, इस विशेषप्रतिबिंब डिवाइस के लिए, स्पोक केंद्र की ओर अधिक से अधिक धुंधले हो जाते हैं जब तक कि वे एक ग्रे, अनसुलझे, डिस्क में विलीन नहीं हो जाते। ध्यान दें कि कभी-कभी प्रकाशिकी स्थानतारण प्रकार्य ऑब्जेक्ट या नमूना स्थान की इकाइयों, अवलोकन कोण, आवरण की चौड़ाई, या सैद्धांतिक अधिकतम तक सामान्यीकृत किया जाता है। दोनों के बीच रूपांतरण सामान्यतः गुणा या भाग की स्थिति है। जैसे एक माइक्रोस्कोप सामान्यतः हर वस्तु को 10 से 100 गुना तक बढ़ा देता है, और एक रिफ्लेक्स कैमरा सामान्यतः 5 मीटर की दूरी पर वस्तुओं को 100 से 200 गुना तक बढ़ा देता है।
-एक डिजिटल इमेजिंग डिवाइस का विश्लेषण न केवल प्रकाशिकी द्वारा सीमित होता है, बल्कि पिक्सेल की संख्या, विशेष रूप से उनकी पृथक्करण दूरी द्वारा भी सीमित होता है। जैसा कि नाइक्विस्ट-शैनन सैंपलिंग प्रमेय द्वारा समझाया गया है, दिए गए उदाहरण के प्रकाशिकी विश्लेषण से मेल खाने के लिए, प्रत्येक रंग चैनल के पिक्सल को 1 माइक्रोमीटर, प्रति मिलीमीटर 500 चक्र की आधी अवधि से अलग किया जाना चाहिए। समान सेंसर आकार पर पिक्सेल की अधिक संख्या बेहतर विवरण के विश्लेषण की अनुमति नहीं देगी। दूसरी ओर, जब पिक्सेल रिक्ति 1 माइक्रोमीटर से बड़ी होती है, तो विश्लेषण पिक्सेल के बीच पृथक्करण द्वारा सीमित होगा; इसके अतिरिक्त,[[अलियासिंग|एलियासिंग]] से छवि निष्ठा में और कमी आ सकती है।
+एक डिजिटल प्रतिबिंब डिवाइस का विश्लेषण न केवल प्रकाशिकी द्वारा सीमित होता है, बल्कि पिक्सेल की संख्या, विशेष रूप से उनकी पृथक्करण दूरी द्वारा भी सीमित होता है। जैसा कि नाइक्विस्ट-शैनन सैंपलिंग प्रमेय द्वारा समझाया गया है, दिए गए उदाहरण के प्रकाशिकी विश्लेषण से मेल खाने के लिए, प्रत्येक रंग चैनल के पिक्सल को 1 माइक्रोमीटर, प्रति मिलीमीटर 500 चक्र की आधी अवधि से अलग किया जाना चाहिए। समान सेंसर आकार पर पिक्सेल की अधिक संख्या बेहतर विवरण के विश्लेषण की अनुमति नहीं देगी। दूसरी ओर, जब पिक्सेल रिक्ति 1 माइक्रोमीटर से बड़ी होती है, तो विश्लेषण पिक्सेल के बीच पृथक्करण द्वारा सीमित होगा; इसके अतिरिक्त,[[अलियासिंग|एलियासिंग]] से प्रतिबिंबनिष्ठा में और कमी आ सकती है।
 ===अपूर्ण लेंस प्रणाली का ओटीएफ===
-एक अपूर्ण, प्रकाशिकी विपथन इमेजिंग प्रणाली में निम्नलिखित चित्र में दर्शाए गए प्रकाशिकी स्थानतारण प्रकार्य  हो सकते हैं।
+एक अपूर्ण, प्रकाशिकी विपथन प्रतिबिंब प्रणाली में निम्नलिखित चित्र में दर्शाए गए प्रकाशिकी स्थानतारण प्रकार्य  हो सकते हैं।
 {{multiple image|align=left|total_width=560
@@ Line 68: / Line 68: @@
 }}
-आदर्श लेंस प्रणाली के रूप में, 500 चक्र प्रति मिलीमीटर की स्थानिक आवृत्ति पर व्यतिरेक शून्य तक पहुंच जाता है। यद्यपि, कम स्थानिक आवृत्तियों पर व्यतिरेक पिछले उदाहरण में सही प्रणाली के सापेक्ष अत्यधिक कम है। वास्तव में, 500 चक्र प्रति मिलीमीटर से कम स्थानिक आवृत्तियों के लिए भी कई अवसरों पर व्यतिरेक शून्य हो जाता है। यह उपरोक्त चित्र में दिखाई गई स्पोक छवि में ग्रे गोलाकार बैंड की व्याख्या करता है। ग्रे बैंड के बीच में, तीलियाँ काले से सफेद और इसके विपरीत उलटी होती दिखाई देती हैं, इसे व्यतिरेक व्युत्क्रमण के रूप में जाना जाता है, जो सीधे प्रकाशिकी स्थानतारण  प्रकार्य  के वास्तविक भाग में साइन रिवर्सल से संबंधित है, और कुछ सामान्य आकृतियों के लिए यह आधे एक अवधि के साथ एक स्थानांतरण के रूप में प्रस्तुत होता है।
+आदर्श लेंस प्रणाली के रूप में, 500 चक्र प्रति मिलीमीटर की स्थानिक आवृत्ति पर व्यतिरेक शून्य तक पहुंच जाता है। यद्यपि, कम स्थानिक आवृत्तियों पर व्यतिरेक पिछले उदाहरण में सही प्रणाली के सापेक्ष अत्यधिक कम है। वास्तव में, 500 चक्र प्रति मिलीमीटर से कम स्थानिक आवृत्तियों के लिए भी कई अवसरों पर व्यतिरेक शून्य हो जाता है। यह उपरोक्त चित्र में दिखाई गई स्पोक प्रतिबिंब में ग्रे गोलाकार बैंड की व्याख्या करता है। ग्रे बैंड के बीच में, तीलियाँ काले से सफेद और इसके विपरीत उलटी होती दिखाई देती हैं, इसे व्यतिरेक व्युत्क्रमण के रूप में जाना जाता है, जो सीधे प्रकाशिकी स्थानतारण  प्रकार्य  के वास्तविक भाग में साइन रिवर्सल से संबंधित है, और कुछ सामान्य आकृतियों के लिए यह आधे एक अवधि के साथ एक स्थानांतरण के रूप में प्रस्तुत होता है।
-यद्यपि यह तर्क दिया जा सकता है कि आदर्श और अपूर्ण दोनों प्रणालियों का विश्लेषण 2 माइक्रोमीटर या 500 एलपी/मिमी है, यह स्पष्ट है कि बाद वाले उदाहरण की छवियां कम तेज हैं। विश्लेषण की एक परिभाषा जो कथित गुणवत्ता के अनुरूप है, इसके बजाय स्थानिक आवृत्ति का उपयोग करेगी जिस पर पहला शून्य होता है, 10 माइक्रोमीटर, या 100 एलपी/मिमी। संपूर्ण इमेजिंग प्रणाली  के लिए भी विश्लेषण की परिभाषाएँ व्यापक रूप से भिन्न होती हैं। प्रकाशिकी स्थानतारण  प्रकार्य  द्वारा एक अधिक संपूर्ण, स्पष्ट चित्र प्रदान किया जाता है।
+यद्यपि यह तर्क दिया जा सकता है कि आदर्श और अपूर्ण दोनों प्रणालियों का विश्लेषण 2 माइक्रोमीटर या 500 एलपी/मिमी है, यह स्पष्ट है कि बाद वाले उदाहरण की छवियां कम तेज हैं। विश्लेषण की एक परिभाषा जो कथित गुणवत्ता के अनुरूप है, इसके अतिरिक्त स्थानिक आवृत्ति का उपयोग करेगी जिस पर पहला शून्य होता है, 10 माइक्रोमीटर, या 100 एलपी/मिमी। संपूर्णप्रतिबिंब प्रणाली  के लिए भी विश्लेषण की परिभाषाएँ व्यापक रूप से भिन्न होती हैं। प्रकाशिकी स्थानतारण  प्रकार्य  द्वारा एक अधिक संपूर्ण, स्पष्ट चित्र प्रदान किया जाता है।
 [[Category:All articles with unsourced statements]]
@@ Line 84: / Line 84: @@
 ===गैर-घूर्णी सममित विपथन वाले प्रकाशिकी प्रणाली  का ओटीएफ===
-[[File:Trefoil aberration PSF OTF and example image.svg|right|thumb|600px|जब ट्रेफ़ोइल विपथन के साथ एक प्रकाशिकी प्रणाली  के माध्यम से देखा जाता है, तो एक बिंदु वस्तु की छवि तीन-बिंदु वाले तारे (ए) के रूप में दिखाई देगी। चूँकि बिंदु-प्रसार प्रकार्य  घूर्णी सममित नहीं है, केवल एक द्वि-आयामी प्रकाशिकी स्थानतारण  प्रकार्य  ही इसका अच्छी तरह से वर्णन कर सकता है (बी)। सतह प्लॉट की ऊंचाई निरपेक्ष मान को इंगित करती है और रंग प्रकार्य  के जटिल तर्क को इंगित करता है। ऐसे इमेजिंग उपकरण द्वारा चित्रित एक स्पोक लक्ष्य (सी) में सिमुलेशन द्वारा दिखाया गया है।]]प्रकाशिकी प्रणाली, और विशेष रूप से प्रकाशिकी विपथन सदैव पुनर्निर्देशनीय नहीं होते हैं। इसलिए, विभिन्न दिशा वाली आवृत्ति वाले आवर्तक पैटर्न्स को यदि उनकी आवृत्ति समान होती है, तो उनके विभिन्न बिना आवृत्ति चेतना के चित्रित किया जा सकता है। प्रकाशिकी स्थानतारण प्रकार्य या  प्रतिरुपण स्थानतारण प्रकार्य सामान्यतः द्वि-आयामी प्रकार्य  होते हैं। निम्नलिखित चित्र में पहले चर्चित आदर्श और अपूर्ण प्रणाली के द्वि-आयामी रूप के प्रकाशिकी प्रणाली के लिए इन दो-आयामी प्रकार्य का तुलनात्मक संकेत दिखाते हैं, जिसमें ट्रीफोइल, एक गैर-पुनर्निर्देशनीय विपथन, होता है।
+[[File:Trefoil aberration PSF OTF and example image.svg|right|thumb|600px|जब ट्रेफ़ोइल विपथन के साथ एक प्रकाशिकी प्रणाली  के माध्यम से देखा जाता है, तो एक बिंदु वस्तु की प्रतिबिंबतीन-बिंदु वाले तारे (ए) के रूप में दिखाई देगी। चूँकि बिंदु-प्रसार प्रकार्य  घूर्णी सममित नहीं है, केवल एक द्वि-आयामी प्रकाशिकी स्थानतारण  प्रकार्य  ही इसका अच्छी तरह से वर्णन कर सकता है (बी)। सतह प्लॉट की ऊंचाई निरपेक्ष मान को इंगित करती है और रंग प्रकार्य  के जटिल तर्क को इंगित करता है। ऐसेप्रतिबिंब उपकरण द्वारा चित्रित एक स्पोक लक्ष्य (सी) में सिमुलेशन द्वारा दिखाया गया है।]]प्रकाशिकी प्रणाली, और विशेष रूप से प्रकाशिकी विपथन सदैव पुनर्निर्देशनीय नहीं होते हैं। इसलिए, विभिन्न दिशा वाली आवृत्ति वाले आवर्तक पैटर्न्स को यदि उनकी आवृत्ति समान होती है, तो उनके विभिन्न बिना आवृत्ति चेतना के चित्रित किया जा सकता है। प्रकाशिकी स्थानतारण प्रकार्य या प्रतिरुपण स्थानतारण प्रकार्य सामान्यतः द्वि-आयामी प्रकार्य  होते हैं। निम्नलिखित चित्र में पहले चर्चित आदर्श और अपूर्ण प्रणाली के द्वि-आयामी रूप के प्रकाशिकी प्रणाली के लिए इन दो-आयामी प्रकार्य का तुलनात्मक संकेत दिखाते हैं, जिसमें ट्रीफोइल, एक गैर-पुनर्निर्देशनीय विपथन, होता है।
 प्रकाशिकी स्थानतारण प्रकार्य सदैव वास्तविक-मूल्यवान नहीं होते हैं। प्रणाली में विपथन के आधार पर, अवधि पैटर्न को किसी भी मात्रा में स्थानांतरित किया जा सकता है। यह सामान्यतः गैर-घूर्णी-सममित विपथन के स्थिति में होता है। उपरोक्त आकृति में सतह भूखंडों के रंगों का रंग चरण को दर्शाता है। यह देखा जा सकता है कि, जबकि घूर्णी सममित विपथन के लिए चरण या तो 0 या π है और इस प्रकार स्थानांतरण प्रकार्य वास्तविक मूल्य है, गैर-घूर्णी सममित विपथन के लिए स्थानांतरण प्रकार्य  में एक काल्पनिक घटक होता है और चरण लगातार बदलता रहता है।
 ===व्यावहारिक उदाहरण - उच्च परिभाषा वीडियो प्रणाली ===
-जबकि [[ऑप्टिकल रिज़ॉल्यूशन|प्रकाशिकी विश्लेषण]], जैसा कि सामान्यतः कैमरा प्रणाली  के संदर्भ में उपयोग किया जाता है, एक छवि में केवल पिक्सेल की संख्या का वर्णन करता है, और इसलिए बारीक विवरण दिखाने की क्षमता, स्थानांतरण प्रकार्य  प्रतिक्रिया में आसन्न पिक्सेल की काले से सफेद में बदलने की क्षमता का वर्णन करता है अलग-अलग स्थानिक आवृत्ति के पैटर्न, और इसलिए पूर्ण या कम व्यतिरेक के साथ, बारीक विवरण दिखाने की वास्तविक क्षमता। प्रकाशिकी स्थानतारण  प्रकार्य  के साथ पुनरुत्पादित एक छवि जो उच्च स्थानिक आवृत्तियों पर होता है, वो साधारण भाषा में 'ब्लर' या 'धुंधला' दिखाई देगी।
+जबकि [[ऑप्टिकल रिज़ॉल्यूशन|प्रकाशिकी विश्लेषण]], जैसा कि सामान्यतः कैमरा प्रणाली  के संदर्भ में उपयोग किया जाता है, एक प्रतिबिंबमें केवल पिक्सेल की संख्या का वर्णन करता है, और इसलिए बारीक विवरण दिखाने की क्षमता, स्थानांतरण प्रकार्य  प्रतिक्रिया में आसन्न पिक्सेल की काले से सफेद में बदलने की क्षमता का वर्णन करता है अलग-अलग स्थानिक आवृत्ति के पैटर्न, और इसलिए पूर्ण या कम व्यतिरेक के साथ, बारीक विवरण दिखाने की वास्तविक क्षमता। प्रकाशिकी स्थानतारण  प्रकार्य  के साथ पुनरुत्पादित एक प्रतिबिंब जो उच्च स्थानिक आवृत्तियों पर होता है, वो साधारण भाषा में 'ब्लर' या 'धुंधला' दिखाई देगी।
-वर्तमान- उच्च परिभाषा (एचडी) वीडियो प्रणाली  का उदाहरण लेते हुए, 1920 गुणा 1080 पिक्सल के साथ, नाइक्विस्ट-शैनन सैंपलिंग प्रमेय में कहा गया है कि एक आदर्श प्रणाली में, पूरी तरह से हल करना संभव होना चाहिए। कुल मिलाकर 1920 काली और सफेद वैकल्पिक रेखाएं, अन्यथा प्रति चित्र चौड़ाई 1920/2=960 रेखा जोड़े, या प्रति चित्र चौड़ाई 960 चक्र की स्थानिक आवृत्ति के रूप में संदर्भित की जाती हैं, संभव है परंतु कैमरे के साथ व्यवहार करते समय सामान्यतः कम स्पष्ट होता है और दूरबीन आदि के लिए अधिक उपयुक्त होता है।
+वर्तमान- उच्च परिभाषा (एचडी) वीडियो प्रणाली का उदाहरण लेते हुए, 1920 गुणा 1080 पिक्सल के साथ, नाइक्विस्ट-शैनन सैंपलिंग प्रमेय में कहा गया है कि एक आदर्श प्रणाली में, पूरी तरह से हल करना संभव होना चाहिए। कुल मिलाकर 1920 काली और सफेद वैकल्पिक रेखाएं, अन्यथा प्रति चित्र चौड़ाई 1920/2=960 रेखा जोड़े, या प्रति चित्र चौड़ाई 960 चक्र की स्थानिक आवृत्ति के रूप में संदर्भित की जाती हैं, संभव है परंतु कैमरे के साथ व्यवहार करते समय सामान्यतः कम स्पष्ट होता है और दूरबीन आदि के लिए अधिक उपयुक्त होता है।
 व्यवहारिक दृष्टिकोण से यह बिल्कुल नहीं होता है, और स्थानिक आवृत्तियाँ जो निक्विस्ट दर की ओर आती हैं, सामान्यतः घटते हुए गुणक से पुनर्प्रक्षेपित होंगी, इसलिए मामूली विवरण की चौड़ाई में कमी होती है, हालांकि यह देखा जा सकता है कि उसे दर्शाने की क्षमता है। इससे यह दिलचस्प दृष्टिकोण उत्पन्न होता है कि, उदाहरण के लिए, एक फ़िल्म स्कैनर का उपयोग करके प्राप्त किया गया एक मानक परिभाषा टेलीविजन चित्र एक ऐसे कैमरे से जो किसी खराब प्रतिरुपण र स्थानातरण प्रकार्य वाला होता है, शार्प दिख सकता है। इन दो चित्रों में एक दिलचस्प अंतर होता है, जो अक्सर छूट जाता है, पहले में एक निश्चित सीमा तक विवरण पर पूरा दर दिखाता है, फिर असल में कोई वाकई त्वचा विवरण नहीं होता है, जबकि दूसरे में दरार विवरण तो होता है, लेकिन इसमें दर को कम किया जाता है, जिससे कुल में अधीन होने के रूप में दिखाई देता है।
@@ Line 97: / Line 97: @@
 ==त्रि-आयामी प्रकाशिकी स्थानांतरण प्रकार्य ==
-[[File:3DPSF 3DMTF widefield confocal.png|right|thumb|600px|वाइड-फील्ड माइक्रोस्कोप (ए, बी) और कन्फोकल माइक्रोस्कोप (सी, डी) के त्रि-आयामी बिंदु प्रसार प्रकार्य  (ए, सी) और संबंधित प्रतिरुपण स्थानतारण  प्रकार्य  (बी, डी)। दोनों ही स्थिति में अभिदृश्यक का संख्यात्मक छिद्र 1.49 है और माध्यम का अपवर्तनांक 1.52 है। उत्सर्जित प्रकाश की तरंग दैर्ध्य 600 एनएम मानी जाती है और, कन्फोकल माइक्रोस्कोप के स्थिति में, गोलाकार ध्रुवीकरण के साथ उत्तेजना प्रकाश की तरंग दैर्ध्य 500 एनएम होती है। आंतरिक तीव्रता वितरण को देखने के लिए एक अनुभाग काटा जाता है। लघुगणकीय रंग पैमाने पर दिखाए गए रंग अधिकतम मान के लिए सामान्यीकृत विकिरण (ए,सी) और वर्णक्रमीय घनत्व (बी,डी) को दर्शाते हैं।]]यद्यपि     कोई सामान्यतः   किसी छवि को समतल या द्वि-आयामी मानता है, इमेजिंग प्रणाली छवि स्थान में त्रि-आयामी तीव्रता वितरण उत्पन्न करेगी जिसे सिद्धांत रूप से मापा जा सकता है। जैसे त्रि-आयामी तीव्रता वितरण को पकड़ने के लिए एक द्वि-आयामी सेंसर का अनुवाद किया जा सकता है। एक बिंदु स्रोत की छवि भी एक त्रि-आयामी (3डी) तीव्रता वितरण है जिसे 3डी बिंदु-प्रसार प्रकार्य  द्वारा दर्शाया जा सकता है। उदाहरण के तौर पर, दाईं ओर का चित्र एक वाइड-फील्ड माइक्रोस्कोप (ए) के ऑब्जेक्ट स्पेस में कन्फोकल माइक्रोस्कोप (सी) के साथ 3 डी पॉइंट-स्प्रेड प्रकार्य  दिखाता है। यद्यपि 1.49 के संख्यात्मक छिद्र्  के साथ एक ही माइक्रोस्कोप उद्देश्य का उपयोग किया जाता है, यह स्पष्ट है कि कन्फोकल पॉइंट स्प्रेड प्रकार्य पार्श्व आयाम (एक्स, वाई) और अक्षीय आयाम (जेड) दोनों में अधिक कॉम्पैक्ट है। कोई सही निष्कर्ष निकाल सकता है कि कन्फोकल माइक्रोस्कोप का विश्लेषण तीनों आयामों में वाइड-फील्ड माइक्रोस्कोप से बेहतर है।
+[[File:3DPSF 3DMTF widefield confocal.png|right|thumb|600px|वाइड-फील्ड माइक्रोस्कोप (ए, बी) और कन्फोकल माइक्रोस्कोप (सी, डी) के त्रि-आयामी बिंदु प्रसार प्रकार्य  (ए, सी) और संबंधित प्रतिरुपण स्थानतारण  प्रकार्य  (बी, डी)। दोनों ही स्थिति में अभिदृश्यक का संख्यात्मक छिद्र 1.49 है और माध्यम का अपवर्तनांक 1.52 है। उत्सर्जित प्रकाश की तरंग दैर्ध्य 600 एनएम मानी जाती है और, कन्फोकल माइक्रोस्कोप के स्थिति में, गोलाकार ध्रुवीकरण के साथ उत्तेजना प्रकाश की तरंग दैर्ध्य 500 एनएम होती है। आंतरिक तीव्रता वितरण को देखने के लिए एक अनुभाग काटा जाता है। लघुगणकीय रंग पैमाने पर दिखाए गए रंग अधिकतम मान के लिए सामान्यीकृत विकिरण (ए,सी) और वर्णक्रमीय घनत्व (बी,डी) को दर्शाते हैं।]]यद्यपि कोई सामान्यतः   किसी प्रतिबिंब को समतल या द्वि-आयामी मानता है,प्रतिबिंब प्रणाली प्रतिबिंब स्थान में त्रि-आयामी तीव्रता वितरण उत्पन्न करेगी जिसे सिद्धांत रूप से मापा जा सकता है। जैसे त्रि-आयामी तीव्रता वितरण को पकड़ने के लिए एक द्वि-आयामी सेंसर का अनुवाद किया जा सकता है। एक बिंदु स्रोत की प्रतिबिंब भी एक त्रि-आयामी (3डी) तीव्रता वितरण है जिसे 3डी बिंदु-प्रसार प्रकार्य  द्वारा दर्शाया जा सकता है। उदाहरण के तौर पर, दाईं ओर का चित्र एक वाइड-फील्ड माइक्रोस्कोप (ए) के ऑब्जेक्ट स्पेस में कन्फोकल माइक्रोस्कोप (सी) के साथ 3 डी पॉइंट-स्प्रेड प्रकार्य  दिखाता है। यद्यपि 1.49 के संख्यात्मक छिद्र्  के साथ एक ही माइक्रोस्कोप उद्देश्य का उपयोग किया जाता है, यह स्पष्ट है कि कन्फोकल पॉइंट स्प्रेड प्रकार्य पार्श्व आयाम (एक्स, वाई) और अक्षीय आयाम (जेड) दोनों में अधिक कॉम्पैक्ट है। कोई सही निष्कर्ष निकाल सकता है कि कन्फोकल माइक्रोस्कोप का विश्लेषण तीनों आयामों में वाइड-फील्ड माइक्रोस्कोप से बेहतर है।
 त्रि-आयामी प्रकाशिकी स्थानतारण प्रकार्य की गणना 3डी पॉइंट-स्प्रेड प्रकार्य के त्रि-आयामी फूरियर रूपांतरण के रूप में की जा सकती है। इसका रंग-कोडित परिमाण क्रमशः पैनल (ए) और (सी) में दिखाए गए बिंदु-प्रसार कार्यों के अनुरूप पैनल (बी) और (डी) में प्लॉट किया गया है। वाइड-फील्ड माइक्रोस्कोप के स्थानतारण  प्रकार्य  में एक [[समर्थन (गणित)]] होता है जो सभी तीन-आयामों में कन्फोकल माइक्रोस्कोप का आधा होता है, जो वाइड-फील्ड माइक्रोस्कोप के पहले नोट किए गए निचले विश्लेषण की पुष्टि करता है। ध्यान दें कि z-अक्ष के साथ, x = y = 0 के लिए, स्थानांतरण प्रकार्य  मूल को छोड़कर हर जगह शून्य है। यह गायब शंकु एक प्रसिद्ध समस्या है जो वाइड-फील्ड माइक्रोस्कोप का उपयोग करके प्रकाशिकी सेक्शनिंग को रोकती है।<ref name=MaciasGarza88>{{cite book |last1= Macias-Garza |first1= F. |last2= Bovik |first2= A. |last3= Diller |first3= K. |last4= Aggarwal |first4= S. |last5= Aggarwal |first5= J. |title= ICASSP-88., International Conference on Acoustics, Speech, and Signal Processing |chapter= The missing cone problem and low-pass distortion in optical serial sectioning microscopy <!-- unsupported parameter |conference= ICASSP-88., International Conference on Acoustics, Speech, and Signal Processing, Acoustics, Speech, and Signal Processing, 1988. ICASSP-88., 1988 International Conference on, Institute of Electrical & Electronics Engineers (IEEE) --> |pages= 890–893 |volume= 2 |year= 1988 |doi= 10.1109/ICASSP.1988.196731 |s2cid= 120191405 }}</ref>
-फोकल प्लेन पर द्वि-आयामी प्रकाशिकी स्थानतारण  प्रकार्य  की गणना जेड-अक्ष के साथ 3डी प्रकाशिकी स्थानतारण  प्रकार्य  के एकीकरण द्वारा की जा सकती है। यद्यपि वाइड-फील्ड माइक्रोस्कोप (बी) का 3डी स्थानतारण  प्रकार्य  z ≠ 0 के लिए z-अक्ष पर शून्य है; इसका अभिन्न अंग, 2D प्रकाशिकी स्थानतारण , x = y = 0 पर अधिकतम तक पहुंचता है। यह केवल इसलिए संभव है क्योंकि 3D प्रकाशिकी स्थानतारण  प्रकार्य  मूल x = y = z = 0 पर विचलन करता है। प्रकार्य  मान z-अक्ष के साथ होता है 3डी प्रकाशिकी स्थानतारण प्रकार्य  [[डिराक डेल्टा फ़ंक्शन|डिराक डेल्टा प्रकार्य]]  के अनुरूप होता है।
+फोकल प्लेन पर द्वि-आयामी प्रकाशिकी स्थानतारण  प्रकार्य  की गणना जेड-अक्ष के साथ 3डी प्रकाशिकी स्थानतारण  प्रकार्य  के एकीकरण द्वारा की जा सकती है। यद्यपि वाइड-फील्ड माइक्रोस्कोप (बी) का 3डी स्थानतारण  प्रकार्य  z ≠ 0 के लिए z-अक्ष पर शून्य है; इसका अभिन्न अंग, 2D प्रकाशिकी स्थानतारण , x = y = 0 पर अधिकतम तक पहुंचता है। यह केवल इसलिए संभव है क्योंकि 3D प्रकाशिकी स्थानतारण  प्रकार्य  मूल x = y = z = 0 पर विचलन करता है। प्रकार्य  मान z-अक्ष के साथ होता है 3डी प्रकाशिकी स्थानतारण प्रकार्य [[डिराक डेल्टा फ़ंक्शन|डिराक डेल्टा प्रकार्य]] के अनुरूप होता है।
 ==गणना==
@@ Line 125: / Line 125: @@
 एक-आयामी प्रकाशिकी स्थानतारण  प्रकार्य  की गणना लाइन स्प्रेड प्रकार्य  के [[असतत फूरियर रूपांतरण]] के रूप में की जा सकती है। यह डेटा स्थानिक आवृत्ति डेटा के विरुद्ध ग्राफ़ किया गया है। इस स्थिति में, प्रवृत्ति दिखाने के लिए छठे क्रम के बहुपद को एमटीएफ बनाम स्थानिक आवृत्ति वक्र पर फिट किया जाता है। 50% कटऑफ आवृत्ति संबंधित स्थानिक आवृत्ति प्राप्त करने के लिए निर्धारित की जाती है। इस प्रकार, परीक्षण के तहत इकाई के सर्वोत्तम फोकस की अनुमानित स्थिति इस डेटा से निर्धारित की जाती है।
-लाइन स्प्रेड प्रकार्य  (एलएसएफ) का फूरियर रूपांतरण निम्नलिखित समीकरणों द्वारा विश्लेषणात्मक रूप से निर्धारित नहीं किया जा सकता है:
+लाइन स्प्रेड प्रकार्य (एलएसएफ) का फूरियर रूपांतरण निम्नलिखित समीकरणों द्वारा विश्लेषणात्मक रूप से निर्धारित नहीं किया जा सकता है:
 :<math>\operatorname{MTF} = \mathcal{F} \left[ \operatorname{LSF}\right] \qquad \qquad \operatorname{MTF}= \int f(x) e^{-i 2 \pi\, x s}\, dx</math>
 इसलिए, फूरियर ट्रांसफॉर्म को असतत फूरियर ट्रांसफॉर्म का उपयोग करके संख्यात्मक रूप से अनुमानित किया जाता है <math>\mathcal{DFT}</math>.<ref>Chapra, S.C.; Canale, R.P. (2006). ''Numerical Methods for Engineers (5th ed.). New York, New York: McGraw-Hill</ref>
@@ Line 141: / Line 141: @@
 ===वेक्टरियल स्थानतारण  प्रकार्य ===
-माइक्रोस्कोपी में पाए जाने वाले उच्च संख्यात्मक छिद्र्  पर, प्रकाश ले जाने वाले क्षेत्रों की वेक्टर प्रकृति पर विचार करना महत्वपूर्ण है। कार्टेशियन अक्षों के अनुरूप तीन स्वतंत्र घटकों में तरंगों को विघटित करके, प्रत्येक घटक के लिए एक बिंदु प्रसार प्रकार्य  की गणना की जा सकती है और एक वेक्टरियल बिंदु प्रसार प्रकार्य  में जोड़ा जा सकता है। इसी प्रकार, एक वेक्टरियल प्रकाशिकी स्थानतारण  प्रकार्य  को निर्धारित किया जा सकता है।<ref name=Sheppard1997>{{cite journal |last1= Sheppard |first1= C.J.R. |last2= Larkin |first2= K. |title= वेक्टरियल पुतली फ़ंक्शन और वेक्टरियल ट्रांसफर फ़ंक्शन|journal= Optik-Stuttgart |volume= 107 |pages= 79–87 |year= 1997 |url= http://www.nontrivialzeros.net/KGL_Papers/28_Vectorial_OTF_Optik_1997.pdf}}</ref><ref name=Arnison2002>{{cite journal |last1= Arnison |first1= M. R. |last2= Sheppard |first2= C. J. R. |doi= 10.1016/S0030-4018(02)01857-6 |title= A 3D vectorial optical transfer function suitable for arbitrary pupil functions |journal= Optics Communications |volume= 211 |issue= 1–6 |pages= 53–63 |year= 2002 |url= http://www.purplebark.net/mra/research/votf/|bibcode= 2002OptCo.211...53A}}</ref>
+माइक्रोस्कोपी में पाए जाने वाले उच्च संख्यात्मक छिद्र्  पर, प्रकाश ले जाने वाले क्षेत्रों की वेक्टर प्रकृति पर विचार करना महत्वपूर्ण है। कार्टेशियन अक्षों के अनुरूप तीन स्वतंत्र घटकों में तरंगों को विघटित करके, प्रत्येक घटक के लिए एक बिंदु प्रसार प्रकार्य  की गणना की जा सकती है और एक वेक्टरियल बिंदु प्रसार प्रकार्य  में जोड़ा जा सकता है। इसी प्रकार, एक वेक्टरियल प्रकाशिकी स्थानतारण प्रकार्य  को निर्धारित किया जा सकता है।<ref name=Sheppard1997>{{cite journal |last1= Sheppard |first1= C.J.R. |last2= Larkin |first2= K. |title= वेक्टरियल पुतली फ़ंक्शन और वेक्टरियल ट्रांसफर फ़ंक्शन|journal= Optik-Stuttgart |volume= 107 |pages= 79–87 |year= 1997 |url= http://www.nontrivialzeros.net/KGL_Papers/28_Vectorial_OTF_Optik_1997.pdf}}</ref><ref name=Arnison2002>{{cite journal |last1= Arnison |first1= M. R. |last2= Sheppard |first2= C. J. R. |doi= 10.1016/S0030-4018(02)01857-6 |title= A 3D vectorial optical transfer function suitable for arbitrary pupil functions |journal= Optics Communications |volume= 211 |issue= 1–6 |pages= 53–63 |year= 2002 |url= http://www.purplebark.net/mra/research/votf/|bibcode= 2002OptCo.211...53A}}</ref>
 ==मा==
-प्रकाशिकी स्थानतारण  प्रकार्य  न केवल प्रकाशिकी प्रणाली  के डिजाइन के लिए उपयोगी है, बल्कि यह निर्मित प्रणाली  को चिह्नित करने के लिए भी मूल्यवान है।
+प्रकाशिकी स्थानतारण  प्रकार्य  न केवल प्रकाशिकी प्रणाली के प्रारूप के लिए उपयोगी है, बल्कि यह निर्मित प्रणाली को चिह्नित करने के लिए भी मूल्यवान है।
 ===बिंदु प्रसार प्रकार्य  से प्रारंभ===
-प्रकाशिकी स्थानतारण  प्रकार्य  को प्रकाशिकी प्रणाली  की आवेग प्रतिक्रिया के फूरियर रूपांतरण के रूप में परिभाषित किया गया है, जिसे पॉइंट स्प्रेड प्रकार्य  भी कहा जाता है। इस प्रकार प्रकाशिकी स्थानतारण  प्रकार्य  को पहले एक बिंदु स्रोत की छवि प्राप्त करके और नमूना छवि में द्वि-आयामी असतत फूरियर ट्रांसफॉर्म को लागू करके आसानी से प्राप्त किया जाता है। ऐसा बिंदु-स्रोत, उदाहरण के लिए, एक पिन छेद वाली स्क्रीन के पीछे एक चमकदार रोशनी, एक फ्लोरोसेंट या धात्विक [[माइक्रोस्फीयर]], या बस एक स्क्रीन पर चित्रित एक बिंदु हो सकता है। बिंदु प्रसार प्रकार्य  के माध्यम से प्रकाशिकी स्थानतारण  प्रकार्य  की गणना बहुमुखी है क्योंकि यह बिंदु स्रोत के विभिन्न पदों और तरंग दैर्ध्य स्पेक्ट्रा के लिए प्रक्रिया को दोहराकर स्थानिक भिन्नता और रंगीन विपथन के साथ प्रकाशिकी को पूरी तरह से चित्रित कर सकता है।
+प्रकाशिकी स्थानतारण  प्रकार्य  को प्रकाशिकी प्रणाली की आवेग प्रतिक्रिया के फूरियर रूपांतरण के रूप में परिभाषित किया गया है, जिसे पॉइंट स्प्रेड प्रकार्य भी कहा जाता है। इस प्रकार प्रकाशिकी स्थानतारण  प्रकार्य  को पहले एक बिंदु स्रोत की प्रतिबिंबप्राप्त करके और नमूना प्रतिबिंबमें द्वि-आयामी असतत फूरियर ट्रांसफॉर्म को लागू करके आसानी से प्राप्त किया जाता है। ऐसा बिंदु-स्रोत, उदाहरण के लिए, एक पिन छेद वाली स्क्रीन के पीछे एक चमकदार रोशनी, एक फ्लोरोसेंट या धात्विक [[माइक्रोस्फीयर]], या बस एक स्क्रीन पर चित्रित एक बिंदु हो सकता है। बिंदु प्रसार प्रकार्य के माध्यम से प्रकाशिकी स्थानतारण  प्रकार्य  की गणना बहुमुखी है क्योंकि यह बिंदु स्रोत के विभिन्न पदों और तरंग दैर्ध्य स्पेक्ट्रा के लिए प्रक्रिया को पुनरावर्तित स्थानिक भिन्नता और रंगीन विपथन के साथ प्रकाशिकी को पूरी तरह से चित्रित कर सकता है।
 ===स्थानिक रूप से अपरिवर्तनीय प्रकाशिकी के लिए विस्तारित परीक्षण वस्तुओं का उपयोग करना===
-जब विपथन को स्थानिक रूप से अपरिवर्तनीय माना जा सकता है, तो वैकल्पिक पैटर्न का उपयोग लाइनों और किनारों जैसे प्रकाशिकी स्थानतारण  प्रकार्य  को निर्धारित करने के लिए किया जा सकता है। संबंधित स्थानांतरण प्रकार्य  को क्रमशः लाइन-स्प्रेड प्रकार्य  और एज-स्प्रेड प्रकार्य  के रूप में जाना जाता है। ऐसी विस्तारित वस्तुएं छवि में अधिक पिक्सेल को रोशन करती हैं, और बड़े सिग्नल-टू-शोर अनुपात के कारण माप सटीकता में सुधार कर सकती हैं। इस मामले में प्रकाशिकी स्थानतारण  प्रकार्य  की गणना छवि के द्वि-आयामी असतत फूरियर रूपांतरण के रूप में की जाती है और इसे विस्तारित ऑब्जेक्ट से विभाजित किया जाता है। सामान्यतः   या तो एक रेखा या काले-सफ़ेद किनारे का उपयोग किया जाता है।
+जब विपथन को स्थानिक रूप से अपरिवर्तनीय माना जा सकता है, तो वैकल्पिक पैटर्न का उपयोग लाइनों और किनारों जैसे प्रकाशिकी स्थानतारण  प्रकार्य  को निर्धारित करने के लिए किया जा सकता है। संबंधित स्थानांतरण प्रकार्य  को क्रमशः लाइन-स्प्रेड प्रकार्य  और एज-स्प्रेड प्रकार्य  के रूप में जाना जाता है। ऐसी विस्तारित वस्तुएं प्रतिबिंबमें अधिक पिक्सेल को रोशन करती हैं, और बड़े सिग्नल-टू-शोर अनुपात के कारण माप सटीकता में सुधार कर सकती हैं। इस मामले में प्रकाशिकी स्थानतारण प्रकार्य की गणना प्रतिबिंब के द्वि-आयामी असतत फूरियर रूपांतरण के रूप में की जाती है और इसे विस्तारित ऑब्जेक्ट से विभाजित किया जाता है। सामान्यतः या तो एक रेखा या काले-सफ़ेद किनारे का उपयोग किया जाता है।
 ====लाइन-स्प्रेड प्रकार्य ====
@@ Line 158: / Line 158: @@
 ====एज-स्प्रेड प्रकार्य ====
-एक किनारे का द्वि-आयामी फूरियर रूपांतरण भी केवल एक पंक्ति पर गैर-शून्य है, किनारे पर ऑर्थोगोनल है। इस प्रकार्य  को कभी-कभी एज स्प्रेड प्रकार्य  (ईएसएफ) के रूप में जाना जाता है।<ref>Holst, G.C. (1998). ''Testing and Evaluation of Infrared Imaging Systems'' (2nd ed.). Florida:JCD Publishing, Washington:SPIE.</ref><ref name="ElectroOpticalTestLab">{{cite web|url=http://www.electro-optical.com/html/toplevel/educationref.asp|title=Test and Measurement – Products – EOI|website=www.Electro-Optical.com|access-date=2 January 2018|archive-url=https://web.archive.org/web/20080828124035/http://www.electro-optical.com/html/toplevel/educationref.asp|archive-date=28 August 2008|url-status=dead}}</ref> यद्यपि    , इस रेखा पर मान मूल बिंदु से दूरी के व्युत्क्रमानुपाती होते हैं। यद्यपि इस तकनीक से प्राप्त माप छवियां कैमरे के एक बड़े क्षेत्र को रोशन करती हैं, इससे मुख्य रूप से कम स्थानिक आवृत्तियों पर सटीकता को लाभ होता है। लाइन स्प्रेड प्रकार्य  की तरह, प्रत्येक माप प्रकाशिकी स्थानतारण  प्रकार्य  के केवल एक अक्ष को निर्धारित करता है, इसलिए बार-बार माप आवश्यक हैं यदि प्रकाशिकी प्रणाली  को घूर्णी सममित नहीं माना जा सकता है।
+एक किनारे का द्वि-आयामी फूरियर रूपांतरण भी केवल एक पंक्ति पर गैर-शून्य है, किनारे पर ऑर्थोगोनल है। इस प्रकार्य  को कभी-कभी एज स्प्रेड प्रकार्य  (ईएसएफ) के रूप में जाना जाता है।<ref>Holst, G.C. (1998). ''Testing and Evaluation of Infrared Imaging Systems'' (2nd ed.). Florida:JCD Publishing, Washington:SPIE.</ref><ref name="ElectroOpticalTestLab">{{cite web|url=http://www.electro-optical.com/html/toplevel/educationref.asp|title=Test and Measurement – Products – EOI|website=www.Electro-Optical.com|access-date=2 January 2018|archive-url=https://web.archive.org/web/20080828124035/http://www.electro-optical.com/html/toplevel/educationref.asp|archive-date=28 August 2008|url-status=dead}}</ref> यद्यपि, इस रेखा पर मान मूल बिंदु से दूरी के व्युत्क्रमानुपाती होते हैं। यद्यपि इस तकनीक से प्राप्त माप छवियां कैमरे के एक बड़े क्षेत्र को रोशन करती हैं, इससे मुख्य रूप से कम स्थानिक आवृत्तियों पर सटीकता को लाभ होता है। लाइन स्प्रेड प्रकार्य  की तरह, प्रत्येक माप प्रकाशिकी स्थानतारण  प्रकार्य  के केवल एक अक्ष को निर्धारित करता है, इसलिए बार-बार माप आवश्यक हैं यदि प्रकाशिकी प्रणाली  को घूर्णी सममित नहीं माना जा सकता है।
-जैसा कि दाहिने हाथ के चित्र में दिखाया गया है, एक ऑपरेटर एक बॉक्स क्षेत्र को परिभाषित करता है जो एक काले शरीर द्वारा चाकू-धार परीक्षण लक्ष्य छवि के किनारे को घेरता है। बॉक्स क्षेत्र को लगभग 10% परिभाषित किया गया हैकुल फ़्रेम क्षेत्र का. छवि [[पिक्सेल]] डेटा को दो-आयामी सरणी में अनुवादित किया जाता है। सरणी के भीतर प्रत्येक पंक्ति (वीडियो) का आयाम (पिक्सेल तीव्रता) [[सामान्यीकरण (सांख्यिकी)]] और औसत है। इससे एज स्प्रेड प्रकार्य  प्राप्त होता है।
+जैसा कि दाहिने हाथ के चित्र में दिखाया गया है, एक ऑपरेटर एक बॉक्स क्षेत्र को परिभाषित करता है जो एक काले शरीर द्वारा चाकू-धार परीक्षण लक्ष्य प्रतिबिंबके किनारे को घेरता है। बॉक्स क्षेत्र को लगभग 10% परिभाषित किया गया हैकुल फ़्रेम क्षेत्र का. प्रतिबिंब[[पिक्सेल]] डेटा को दो-आयामी सरणी में अनुवादित किया जाता है। सरणी के भीतर प्रत्येक पंक्ति (वीडियो) का आयाम (पिक्सेल तीव्रता) [[सामान्यीकरण (सांख्यिकी)]] और औसत है। इससे एज स्प्रेड प्रकार्य  प्राप्त होता है।
 :<math>\operatorname{ESF} = \frac{X - \mu}{\sigma} \qquad \qquad \sigma\, = \sqrt{\frac{\sum_{i=0}^{n-1} (x_i-\mu\,)^2}{n}} \qquad \qquad \mu\, = \frac{\sum_{i=0}^{n-1} x_i}{n} </math>
 यहाँ
@@ Line 184: / Line 184: @@
 ==सामान्य कैमरा प्रणाली  में एमटीएफ को प्रभावित करने वाले कारक==
-सामान्यतः, कई कारकों के परिणामस्वरूप पुनरुत्पादित छवि काफी हद तक धुंधली हो जाती है, जैसे कि नाइक्विस्ट दर के ठीक नीचे स्थानिक आवृत्ति वाले पैटर्न भी दिखाई नहीं दे सकते हैं, और बेहतरीन पैटर्न जो काले नहीं बल्कि भूरे रंग के रंगों के रूप में 'धुले हुए' दिखाई दे सकते हैं। सफ़ेद। एक प्रमुख कारक सामान्यतः सही 'ईंट की दीवार' प्रकाशिकी फिल्टर  बनाने की असंभवता है। डिस्प्ले की नाइक्विस्ट दर से ऊपर स्थानिक आवृत्तियों को समाप्त करके अलियासिंग को कम करने के लिए ऐसा फ़िल्टर आवश्यक है।
+सामान्यतः, कई कारकों के परिणामस्वरूप पुनरुत्पादित प्रतिबिंबकाफी हद तक धुंधली हो जाती है, जैसे कि नाइक्विस्ट दर के ठीक नीचे स्थानिक आवृत्ति वाले पैटर्न भी दिखाई नहीं दे सकते हैं, और बेहतरीन पैटर्न जो काले नहीं बल्कि भूरे रंग के रंगों के रूप में 'धुले हुए' दिखाई दे सकते हैं। सफ़ेद। एक प्रमुख कारक सामान्यतः सही 'ईंट की दीवार' प्रकाशिकी फिल्टर  बनाने की असंभवता है। डिस्प्ले की नाइक्विस्ट दर से ऊपर स्थानिक आवृत्तियों को समाप्त करके अलियासिंग को कम करने के लिए ऐसा फ़िल्टर आवश्यक है।
 ===प्रकाशिकी स्थानतारण  प्रकार्य  को बनाए रखने के लिए अधिप्रतिचयन और डाउनलोडसंस्करण===
-कैमरे जैसे डिजिटल इमेजिंग प्रणाली में संभव सैद्धांतिक तीक्ष्णता तक पहुंचने का एकमात्र नियम अंतिम छवि में [[नमूनाकरण (सिग्नल प्रोसेसिंग)]] के सापेक्ष कैमरा सेंसर में अधिक पिक्सेल का उपयोग करना है, और विशेष का उपयोग करके 'डाउनकन्वर्ट' या 'इंटरपोलेट' करना है। डिजिटल प्रोसेसिंग जो अलियासिंग से बचने के लिए नाइक्विस्ट दर से ऊपर की उच्च आवृत्तियों को काट देती है और उस आवृत्ति तक यथोचित सपाट एमटीएफ बनाए रखती है। यह दृष्टिकोण पहली बार 1970 के दशक में अपनाया गया था जब फ्लाइंग स्पॉट स्कैनर, और बाद में चार्ज-युग्मित डिवाइस लाइन स्कैनर विकसित किए गए थे, जो आवश्यकता से अधिक पिक्सेल का नमूना लेते थे और फिर नीचे परिवर्तित हो जाते थे, यही कारण है कि टेलीविजन पर फिल्में सदैव अन्य सामग्रियों की तुलना में अधिक स्पष्ट दिखती हैं। एक वीडियो कैमरा. इंटरपोलेशन या डाउनकन्वर्ट करने का एकमात्र सैद्धांतिक रूप से सही तरीका एक खड़ी कम-पास स्थानिक फ़िल्टर का उपयोग है, जिसे दो-आयामी एक्स [[ भार ]]प्रकार्य के साथ संवलनीय द्वारा महसूस किया जाता है जिसके लिए शक्तिशाली प्रसंस्करण की आवश्यकता होती है। व्यवहार में, प्रसंस्करण आवश्यकता को कम करने के लिए इसके विभिन्न गणितीय अनुमानों का उपयोग किया जाता है। ये अनुमान अब वीडियो संपादन प्रणालियों और [[फोटोशॉप]] जैसे छवि प्रसंस्करण कार्यक्रमों में व्यापक रूप से लागू किए जाते हैं।
+कैमरे जैसे डिजिटलप्रतिबिंब प्रणाली में संभव सैद्धांतिक तीक्ष्णता तक पहुंचने का एकमात्र नियम अंतिम प्रतिबिंबमें [[नमूनाकरण (सिग्नल प्रोसेसिंग)]] के सापेक्ष कैमरा सेंसर में अधिक पिक्सेल का उपयोग करना है, और विशेष का उपयोग करके 'डाउनकन्वर्ट' या 'इंटरपोलेट' करना है। डिजिटल प्रोसेसिंग जो अलियासिंग से बचने के लिए नाइक्विस्ट दर से ऊपर की उच्च आवृत्तियों को काट देती है और उस आवृत्ति तक यथोचित सपाट एमटीएफ बनाए रखती है। यह दृष्टिकोण पहली बार 1970 के दशक में अपनाया गया था जब फ्लाइंग स्पॉट स्कैनर, और बाद में चार्ज-युग्मित डिवाइस लाइन स्कैनर विकसित किए गए थे, जो आवश्यकता से अधिक पिक्सेल का नमूना लेते थे और फिर नीचे परिवर्तित हो जाते थे, यही कारण है कि टेलीविजन पर फिल्में सदैव अन्य सामग्रियों की तुलना में अधिक स्पष्ट दिखती हैं। एक वीडियो कैमरा. इंटरपोलेशन या डाउनकन्वर्ट करने का एकमात्र सैद्धांतिक रूप से सही तरीका एक खड़ी कम-पास स्थानिक फ़िल्टर का उपयोग है, जिसे दो-आयामी एक्स [[ भार |भार]] प्रकार्य के साथ संवलनीय द्वारा महसूस किया जाता है जिसके लिए शक्तिशाली प्रसंस्करण की आवश्यकता होती है। व्यवहार में, प्रसंस्करण आवश्यकता को कम करने के लिए इसके विभिन्न गणितीय अनुमानों का उपयोग किया जाता है। ये अनुमान अब वीडियो संपादन प्रणालियों और [[फोटोशॉप]] जैसे प्रतिबिंब प्रसंस्करण कार्यक्रमों में व्यापक रूप से लागू किए जाते हैं।
-जिस तरह उच्च व्यतिरेक एमटीएफ के साथ मानक परिभाषा वीडियो केवल अधिप्रतिचयन के साथ संभव है, उसी तरह पूर्ण सैद्धांतिक तीक्ष्णता वाला एचडी टेलीविजन केवल ऐसे कैमरे से प्रारंभ करना संभव है जिसमें काफी अधिक विश्लेषण हो, उसके बाद डिजिटल फ़िल्टरिंग हो। अब फिल्में 4K विश्लेषण और यहां तक कि सिनेमा के लिए 8k वीडियो में शूट की जा रही हैं, हम एचडीटीवी पर केवल उच्च मानक पर शूट की गई फिल्मों या सामग्री से सर्वश्रेष्ठ तस्वीरें देखने की उम्मीद कर सकते हैं। हम कैमरों में उपयोग किए जाने वाले पिक्सेल की संख्या चाहे कितनी भी बढ़ा लें, एक संपूर्ण प्रकाशिकी स्थानिक फ़िल्टर के अभाव में यह हमेशा सत्य रहेगा। इसी प्रकार, 5-मेगापिक्सेल स्थिर कैमरे से प्राप्त 5-मेगापिक्सेल छवि कभी भी समान गुणवत्ता वाले 10-मेगापिक्सेल स्थिर कैमरे से डाउन-रूपांतरण के बाद प्राप्त 5-मेगापिक्सेल छवि से अधिक तेज नहीं हो सकती है। उच्च व्यतिरेक एमटीएफ को बनाए रखने की समस्या के कारण, [[बीबीसी]] जैसे प्रसारकों ने लंबे समय तक मानक परिभाषा टेलीविजन को बनाए रखने पर विचार किया, परंतु कई अधिक पिक्सेल के साथ शूटिंग और देखने के द्वारा इसकी गुणवत्ता में सुधार किया यद्यपि  जैसा कि पहले उल्लेख किया गया है, ऐसी प्रणाली, यद्यपि प्रभावशाली है, अंततः बहुत बारीक विवरण का अभाव है, जो यद्यपि क्षीण हो गया है, वास्तविक एचडी देखने के प्रभाव को बढ़ाता है।
+जिस तरह उच्च व्यतिरेक एमटीएफ के साथ मानक परिभाषा वीडियो केवल अधिप्रतिचयन के साथ संभव है, उसी तरह पूर्ण सैद्धांतिक तीक्ष्णता वाला एचडी टेलीविजन केवल ऐसे कैमरे से प्रारंभ करना संभव है जिसमें काफी अधिक विश्लेषण हो, उसके बाद डिजिटल फ़िल्टरिंग हो। अब फिल्में 4K विश्लेषण और यहां तक कि सिनेमा के लिए 8k वीडियो में शूट की जा रही हैं, हम एचडीटीवी पर केवल उच्च मानक पर शूट की गई फिल्मों या सामग्री से सर्वश्रेष्ठ तस्वीरें देखने की उम्मीद कर सकते हैं। हम कैमरों में उपयोग किए जाने वाले पिक्सेल की संख्या चाहे कितनी भी बढ़ा लें, एक संपूर्ण प्रकाशिकी स्थानिक फ़िल्टर के अभाव में यह हमेशा सत्य रहेगा। इसी प्रकार, 5-मेगापिक्सेल स्थिर कैमरे से प्राप्त 5-मेगापिक्सेल प्रतिबिंब कभी भी समान गुणवत्ता वाले 10-मेगापिक्सेल स्थिर कैमरे से डाउन-रूपांतरण के बाद प्राप्त 5-मेगापिक्सेल प्रतिबिंब से अधिक तेज नहीं हो सकती है। उच्च व्यतिरेक एमटीएफ को बनाए रखने की समस्या के कारण, [[बीबीसी]] जैसे प्रसारकों ने लंबे समय तक मानक परिभाषा टेलीविजन को बनाए रखने पर विचार किया, परंतु कई अधिक पिक्सेल के साथ शूटिंग और देखने के द्वारा इसकी गुणवत्ता में सुधार किया यद्यपि  जैसा कि पहले उल्लेख किया गया है, ऐसी प्रणाली, यद्यपि प्रभावशाली है, अंततः बहुत बारीक विवरण का अभाव है, जो यद्यपि क्षीण हो गया है, वास्तविक एचडी देखने के प्रभाव को बढ़ाता है।
 डिजिटल कैमरे और कैमकोर्डर में एक अन्य कारक लेंस विश्लेषण है। ऐसा कहा जा सकता है कि एक लेंस 1920 क्षैतिज रेखाओं को 'समाधान' करता है, लेकिन इसका मतलब यह नहीं है कि यह काले से सफेद तक पूर्ण प्रतिरुपण के साथ ऐसा करता है। 'मॉड्यूलेशन स्थानतारण  प्रकार्य  लेंस के प्रदर्शन का सही माप देता है, और स्थानिक आवृत्ति के विरुद्ध आयाम के ग्राफ द्वारा दर्शाया जाता है।
-लेंस छिद्र्  विवर्तन भी एमटीएफ को सीमित करता है। जबकि लेंस के छिद्र्  को कम करने से सामान्यतः विपथन कम हो जाता है और इसलिए एमटीएफ की समतलता में सुधार होता है, किसी भी लेंस और छवि सेंसर आकार के लिए एक इष्टतम छिद्र्  होता है, जिसके परे छोटे छिद्र् विवर्तन के कारण विश्लेषण को कम कर देते हैं, जो छवि सेंसर में प्रकाश फैलाता है। प्लेट कैमरों और यहां तक कि 35 मिमी फिल्म के दिनों में यह शायद ही कोई समस्या थी, लेकिन कुछ डिजिटल कैमरों और विशेष रूप से वीडियो कैमरों में उपयोग किए जाने वाले बहुत छोटे प्रारूप सेंसर के साथ यह एक दुर्गम सीमा बन गई है। पहली पीढ़ी के एचडी उपभोक्ता कैमकोर्डर में 1/4-इंच सेंसर का उपयोग किया जाता है, जिसके लिए एफ4 से छोटे छिद्र्  विश्लेषण को सीमित करना प्रारंभ कर देते हैं। यहां तक कि पेशेवर वीडियो कैमरे भी ज्यादातर 2/3 इंच सेंसर का उपयोग करते हैं, जो एफ16 के आसपास छिद्र्  के उपयोग को प्रतिबंधित करता है जिसे फिल्म प्रारूपों के लिए सामान्य माना जाता है। कुछ कैमरे जैसे [[पेंटाक्स K10D]]) में एमटीएफ स्वतः एक्सपोजर मोड की सुविधा होती है, जहां छिद्र्  की पसंद को अधिकतम तीक्ष्णता के लिए अनुकूलित किया जाता है। सामान्यतः इसका अर्थ यह होता है यह छिद्र् रेंज के बीच में होता है।<ref>{{cite web|url=http://www.b2bvideosource.com/mm5/merchant.mvc?Screen=CAMERA_TERMINOLOGY&Store_Code=BVS|title=B2BVideoSource.com: Camera Terminology|website=www.B2BVideoSource.com|access-date=2 January 2018}}</ref>
+लेंस छिद्र्  विवर्तन भी एमटीएफ को सीमित करता है। जबकि लेंस के छिद्र्  को कम करने से सामान्यतः विपथन कम हो जाता है और इसलिए एमटीएफ की समतलता में सुधार होता है, किसी भी लेंस और प्रतिबिंबसेंसर आकार के लिए एक इष्टतम छिद्र्  होता है, जिसके परे छोटे छिद्र् विवर्तन के कारण विश्लेषण को कम कर देते हैं, जो प्रतिबिंबसेंसर में प्रकाश फैलाता है। प्लेट कैमरों और यहां तक कि 35 मिमी फिल्म के दिनों में यह शायद ही कोई समस्या थी, लेकिन कुछ डिजिटल कैमरों और विशेष रूप से वीडियो कैमरों में उपयोग किए जाने वाले बहुत छोटे प्रारूप सेंसर के साथ यह एक दुर्गम सीमा बन गई है। पहली पीढ़ी के एचडी उपभोक्ता कैमकोर्डर में 1/4-इंच सेंसर का उपयोग किया जाता है, जिसके लिए एफ4 से छोटे छिद्र्  विश्लेषण को सीमित करना प्रारंभ कर देते हैं। यहां तक कि पेशेवर वीडियो कैमरे भी ज्यादातर 2/3 इंच सेंसर का उपयोग करते हैं, जो एफ16 के आसपास छिद्र्  के उपयोग को प्रतिबंधित करता है जिसे फिल्म प्रारूपों के लिए सामान्य माना जाता है। कुछ कैमरे जैसे [[पेंटाक्स K10D]]) में एमटीएफ स्वतः एक्सपोजर मोड की सुविधा होती है, जहां छिद्र्  की पसंद को अधिकतम तीक्ष्णता के लिए अनुकूलित किया जाता है। सामान्यतः इसका अर्थ यह होता है यह छिद्र् रेंज के बीच में होता है।<ref>{{cite web|url=http://www.b2bvideosource.com/mm5/merchant.mvc?Screen=CAMERA_TERMINOLOGY&Store_Code=BVS|title=B2BVideoSource.com: Camera Terminology|website=www.B2BVideoSource.com|access-date=2 January 2018}}</ref>
 ===बड़े प्रारूप वाले डीएसएलआर की ओर रुझान और बेहतर एमटीएफ क्षमता===
-हाल ही में कम रोशनी की संवेदनशीलता और क्षेत्र प्रभावों की संकीर्ण गहराई की आवश्यकता के कारण बड़े छवि प्रारूप वाले [[डिजिटल सिंगल-लेंस रिफ्लेक्स कैमरा]] के उपयोग की ओर बदलाव आया है। इसके कारण कुछ फिल्म और टेलीविजन कार्यक्रम निर्माताओं द्वारा पेशेवर एचडी वीडियो कैमरों के सापेक्ष ऐसे कैमरों को उनकी 'फिल्मी' क्षमता के कारण प्राथमिकता दी जाने लगी है। सिद्धांत रूप में, 16- और 21-मेगापिक्सेल सेंसर वाले कैमरों का उपयोग, अलियासिंग को खत्म करने के लिए डिजिटल फ़िल्टरिंग के साथ, कैमरे के भीतर डाउनकनवर्जन द्वारा लगभग पूर्ण तीक्ष्णता की संभावना प्रदान करता है। ऐसे कैमरे बहुत प्रभावशाली परिणाम देते हैं, और डिजिटल फ़िल्टरिंग के साथ बड़े-प्रारूप वाले डाउन-रूपांतरण की दिशा में वीडियो उत्पादन का मार्ग प्रशस्त करते हुए दिखाई देते हैं, जो अलियासिंग से वास्तविक स्वतंत्रता के साथ एक फ्लैट एमटीएफ की प्राप्ति के लिए मानक दृष्टिकोण बन गया है।
+हाल ही में कम रोशनी की संवेदनशीलता और क्षेत्र प्रभावों की संकीर्ण गहराई की आवश्यकता के कारण बड़े प्रतिबिंबप्रारूप वाले [[डिजिटल सिंगल-लेंस रिफ्लेक्स कैमरा]] के उपयोग की ओर बदलाव आया है। इसके कारण कुछ फिल्म और टेलीविजन कार्यक्रम निर्माताओं द्वारा पेशेवर एचडी वीडियो कैमरों के सापेक्ष ऐसे कैमरों को उनकी 'फिल्मी' क्षमता के कारण प्राथमिकता दी जाने लगी है। सिद्धांत रूप में, 16- और 21-मेगापिक्सेल सेंसर वाले कैमरों का उपयोग, अलियासिंग को खत्म करने के लिए डिजिटल फ़िल्टरिंग के साथ, कैमरे के भीतर डाउनकनवर्जन द्वारा लगभग पूर्ण तीक्ष्णता की संभावना प्रदान करता है। ऐसे कैमरे बहुत प्रभावशाली परिणाम देते हैं, और डिजिटल फ़िल्टरिंग के साथ बड़े-प्रारूप वाले डाउन-रूपांतरण की दिशा में वीडियो उत्पादन का मार्ग प्रशस्त करते हुए दिखाई देते हैं, जो अलियासिंग से वास्तविक स्वतंत्रता के साथ एक फ्लैट एमटीएफ की प्राप्ति के लिए मानक दृष्टिकोण बन गया है।
 ==प्रकाशिकी स्थानतारण  प्रकार्य  का डिजिटल व्युत्क्रम==
-प्रकाशिकी प्रभावों के कारण व्यतिरेक उप-इष्टतम हो सकता है और डिस्प्ले के नाइक्विस्ट-शैनन सैंपलिंग प्रमेय तक पहुंचने से पहले शून्य तक पहुंच सकता है। प्रदर्शन या आगे की प्रक्रिया से पहले स्थानिक आवृत्तियों को डिजिटल रूप से बढ़ाकर प्रकाशिकी व्यतिरेक कमी को आंशिक रूप से विपरीत किया जा सकता है। यद्यपि अधिक उन्नत डिजिटल छवि पुनर्स्थापना प्रक्रियाएँ उपस्थित हैं, [[वीनर डिकोनवोल्यूशन|विजेता विखंडन]] कलन विधि  का उपयोग प्रायः इसकी सादगी और दक्षता के लिए किया जाता है। चूँकि यह तकनीक छवि के स्थानिक वर्णक्रमीय घटकों को कई गुना बढ़ा देती है, यह उदाहरण के लिए शोर और त्रुटियों को भी बढ़ा देती है। इसलिए यह केवल पर्याप्त उच्च सिग्नल-टू-शोर अनुपात के साथ अच्छी गुणवत्ता वाली रिकॉर्डिंग पर प्रभावी है।
+प्रकाशिकी प्रभावों के कारण व्यतिरेक उप-इष्टतम हो सकता है और डिस्प्ले के नाइक्विस्ट-शैनन सैंपलिंग प्रमेय तक पहुंचने से पहले शून्य तक पहुंच सकता है। प्रदर्शन या आगे की प्रक्रिया से पहले स्थानिक आवृत्तियों को डिजिटल रूप से बढ़ाकर प्रकाशिकी व्यतिरेक कमी को आंशिक रूप से विपरीत किया जा सकता है। यद्यपि अधिक उन्नत डिजिटल प्रतिबिंबपुनर्स्थापना प्रक्रियाएँ उपस्थित हैं, [[वीनर डिकोनवोल्यूशन|विजेता विखंडन]] कलन विधि  का उपयोग प्रायः इसकी सादगी और दक्षता के लिए किया जाता है। चूँकि यह तकनीक प्रतिबिंबके स्थानिक वर्णक्रमीय घटकों को कई गुना बढ़ा देती है, यह उदाहरण के लिए शोर और त्रुटियों को भी बढ़ा देती है। इसलिए यह केवल पर्याप्त उच्च सिग्नल-टू-शोर अनुपात के साथ अच्छी गुणवत्ता वाली रिकॉर्डिंग पर प्रभावी है।
 ==सीमाएँ==
-सामान्य तौर पर, बिंदु प्रसार प्रकार्य , एक बिंदु स्रोत की छवि [[तरंग दैर्ध्य]], और दृश्य कोण के क्षेत्र जैसे कारकों पर भी निर्भर करती है। जब ऐसी भिन्नता पर्याप्त रूप से क्रमिक होती है, तो प्रकाशिकी प्रणाली को प्रकाशिकी स्थानतारण कार्य के एक समुच्चय द्वारा चित्रित किया जा सकता है। यद्यपि, जब पार्श्व अनुवाद पर बिंदु स्रोत की छवि अचानक बदल जाती है, तो प्रकाशिकी स्थानतारण प्रकार्य प्रकाशिकी प्रणाली का सटीक वर्णन नहीं करता है।
+सामान्यतः, बिंदु प्रसार प्रकार्य, एक बिंदु स्रोत की प्रतिबिंब [[तरंग दैर्ध्य]], और दृश्य कोण के क्षेत्र जैसे कारकों पर भी निर्भर करती है। जब ऐसी भिन्नता पर्याप्त रूप से क्रमिक होती है, तो प्रकाशिकी प्रणाली को प्रकाशिकी स्थानतारण कार्य के एक समुच्चय द्वारा चित्रित किया जा सकता है। यद्यपि, जब पार्श्व अनुवाद पर बिंदु स्रोत की प्रतिबिंबअचानक बदल जाती है, तो प्रकाशिकी स्थानतारण प्रकार्य प्रकाशिकी प्रणाली का सटीक वर्णन नहीं करता है।
 ==यह भी देखें==

Anonymous

Search

प्रकाशिकी अंतरण प्रकार्य: Difference between revisions

Namespaces

More

Page actions

Revision as of 12:25, 29 September 2023

Contents

परिभाषा और संबंधित अवधारणाएँ