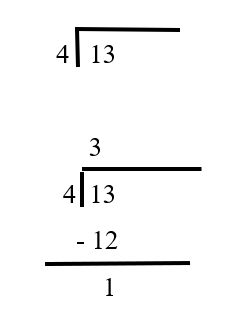Parikarmāṣṭaka - Fundamental Operations

Introduction

Arithmetic deals with calculations using numbers. Pāṭīgaṇita is the Samskrit word for arithmetic and geometry .Pāṭīgaṇita

Mathematical Operations

is formed by combining the words Pāṭī (slate) and gaṇita (mathematics). Since gaṇita was done using a board of a slate , it was called Pāṭīgaṇita. For all transactions using numbers will require the basic operations of addition, subtraction, multiplication, division, squaring etc. Ancient Indian Mathematicians mentioned eight fundamental operations together called as Parikarmāṣṭaka.

Definition

Parikarma means arithmetic operations and aṣṭaka means group of eight. Parikarmāṣṭaka signifies eight basic operations.

The eight fundamental operations are  :

1. Saṅkalanam (addition)
2. Vyavakalanam (subtraction)
3. Guṇana (multiplication)
4. Bhājana (division)
5. Varga (squaring)
6. Varga-mūla (square root)
7. Ghana (cubing) and
8. Gana-mūla (cube root)

Addition and subtraction form the basis of all calculations. Bhāskara I mentions in the below shloka

संयोगभेदा गुणनागतानि शुद्धेश्च भागो गतमूलमुक्तम् ।

व्याप्तं समीक्ष्योपचयक्षयाभ्यां विद्यादिदं द्व्यात्मकमेव शास्त्रम् ॥ (Āryabhaṭīya-bhāṣya in Gaṇitapāda, p.43)

"All arithmetical operations resolve into two categories though usually considered to be four. The two main categories are increase and decrease. Addition is increase and subtraction is decrease. These two varieties of operations permeate the whole of mathematics. Multiplication and evolution ( square etc,) are particular kinds of addition; and division and involution( square root etc) are particular kinds of subtraction. Indeed every mathematical operation will be recognised to consist of increase or decrease. Hence the whole of this science should be known as consisting truly of these two only."

Saṅkalana and Vyavakalana (Addition and Subtraction)

Addition

Addition is the first fundamental operation in mathematics. Subtraction is the reverse of addition.

Āryabhaṭa II (950) defines addition as " The making into one of several numbers is addition".

Āryabhaṭa II (950) defines subtraction as " The taking out (of some number) from the sarvadhana (total) is subtraction. What remains is called śeṣa (remainder) ".

Bhāskara II has mentioned about these operations in his work on Līlavatī.

कार्यः क्रमादुत्क्रमतोऽथवाऽङ्कयोगो यथास्थानकमन्तरं वा ॥ (Līlavatī , vs.12, p.12)

"The addition or subtraction (of digits in the given numbers) is to be done place wise right to left or left to right."

Write the given numbers one below the other so that the digits are aligned to their place value. Then starting with the units place add or subtract the digits, later move to tens and so on.

Samskrita names for Addition - yoga (addition), saṃyoga (sum), saṃyojana (joining together) , saṃyuti (sum), saṃyuti (sum), saṇkalana (making together).

Samskrita names for Subtraction - vyutkalita(made apart), vyutkalana(making apart), śodhana (clearing), pātana (causing to fall), viyoga (separation) , śeṣa (residue) and anatara (difference) have been used for the remainder.

Guṇana (Multiplication)

The multiplication of whole numbers is repeated addition. For example :

$2\quad X\quad 4=2+2+2+2=8$

Samskrita names for Multiplication - āhati (multiplication), ghāta (product), [guṇana , hanana, hati, vadha] (multiplication).

2	X	4	=	8
↑		↑		↑
guṇya (multiplicand)		guṇaka (multiplier)		guṇana-phala (Result of Multiplication)

Methods of Multiplication :

• Rūpa-guṇana - Direct Method
• Khaṇḍa-guṇana - Split Method
• Bhakta-guṇana - Factor Method
• Sthāna-vibhāga-guṇana - Place wise multiplication
• Iṣṭonayug-guṇana (Adding or subtracting a desired number)

Rūpa-guṇana - Direct method :

Here the tables of multiplier should be known. Multiplier is taken as a whole.Each digit of multiplicand is multiplied by the multiplier to get the product. In this method, the multiplier is taken a whole since it is small.

Example: 234 X 5 =

(1) (2)

2 3 4

x 5 =

1 1 7 0

Khaṇḍa-guṇana - Split Method :

Here the multiplier is split into sum of two numbers . This is represented as below.

a X b = a X (c + d) = (a X c) + (a X d) where b = c + d.

This is the distributive property of multiplication over addition.

Example: 234 X 16 = 234 X (10 + 6 ) = (234 X 10) + (234 X 6) = 2340 + 1404 = 3744

Bhakta-guṇana - Factor Method :

Here the multiplier is split into product of two numbers. This is represented as below.

a X b = a X (c X d) = (a X c) X d where b = c X d

Example: 234 X 16 = 234 X (8 X 2) = (234 X 8) X 2 = 1872 X 2 = 3744

Sthāna-vibhāga-guṇana - Place wise multiplication :

Multiplication

Multiply the multiplicand by each digit of the multiplier separately. Place them appropriately one below the other . Add those numbers. This method is the standard method of doing multiplication.

Example: 234 X 16

2 3 4

X 1 6 =

1 4 0 4

+ 2 3 4 =

3 7 4 4

Iṣṭonayug-guṇana (Adding or subtracting a desired number) :

The Samskrit word Iṣṭonayug is a compound word consisting of iṣṭa , ūna , yuk which means respectively 'desired, minus and plus'.

इष्टोनयुक्तेन गुणेन निघ्नोऽभीष्टघ्नगुण्यान्वितवर्जितो वा । (Līlāvatī, vs.16, p.15)

"Add or subtract any convenient number to the multiplier and multiply it. Then multiply by the added or subtracted number and subtract or add this product from the previous one."

Add any desired number to the multiplier to get a convenient round figure. Then multiply the multiplicand with the round figure and the added number. Then subtract the products to get the final answer.

or

Subtract any desired number from the multiplier to get a convenient round figure. Then multiply the multiplicand with the round figure and the subtracted number. Then add the products to get the final answer.

Example:

234 X 16 = 234 X (20 - 4) = (234 X 20) - (234 X 4) = 4680 - 936 = 3744

234 X 16 = 234 X (10 + 6) = (234 x 10) + (234 x 6) = 2340 + 1404 = 3744

Tatstha-guṇana

Ancient Indian Mathematicians enhanced the several methods for multiplication to perform multiplication more efficiently and easily. Tatstha-guṇana is one of those methods making multiplication involving three or more digits faster. Indian Mathematicians like Śrīdhara, Mahāvīra, Śripati have mentioned this method. Tatstha-guṇana is also known as vajrābhyāsa.

Gaṇeśa (c.1545) explains Tatstha-guṇana as "That method of multiplication in which the numbers stand in the same place is called Tatstha-guṇana. It is as follows: after setting the multiplier under the multiplicand multiply unit by unit and the note the result underneath. Then as in vajrābhyāsa multiply unit by ten and ten by unit, add together and set down the result in the line. Next multiply unit by hundred, hundred by unit and ten by ten, add together and set down the result as before; and so on with the rest of the digits. This being done, the line of results is the product.".

This method was known to the Hindu scholars of the 8th century, or earlier. The method seems to have travelled to Arabia and thence was transmitted to Europe, where it occurs in Pacioli's Suma and is stated to be "more fantastic and ingenious than the others."

Gaṇeśa has also remarked that "this (method) is very fantastic and cannot be learnt by the dull without the traditional oral instructions."

Example : Multiply 234 and 15

2 3 5

0 1 5 X

Hundreds	Tens	Unit
2	3	4
0	1	5

1. Multiply unit digit by unit digit. 4 X 5 = 20
2. Multiply the unit digit by tens digit and tens digit by unit digit and add them. (3 X 5) + (4 X 1) = 15 + 4 = 19
3. Multiply unit digit by hundreds digit, hundreds digit by unit digit and tens digits by tens digit and add them. (2 x 5) + (4 X 0) + (3 X 1) = 10 + 0 + 3 = 13
4. Multiply hundreds digit by tens digit and tens digit by hundreds digit and add them. (2 X 1) + (3 X 0) = 2 + 0 = 2 = 02
5. Multiply hundred digit by hundreds digit. 2 X 0 = 0 = 00
6. Place the results of each step as shown and add.

1.					2	0
2.				1	9
3.			1	3
4.		0	2
5.	0	0
	0	0	3	5	1	0

The result is 3510.

Bhājana (Division)

Division

Division is considered as the inverse of multiplication.

Samskrita names for Division - bhāgahāra (divide) , bhājana (break), harana (take away), chedana (cut).

The dividend is termed as bhājya or hārya, the divisor is called bhājaka, bhāgahara or hara. The quotient is called labhdi (the obtained) or labdha .Bhāskara II has mentioned the rule for division as:

भाज्याद्धरः शुद्ध्यति यद्गुणः स्यादन्त्यात्फलं तत्खलु भागहारे। समेन केनाप्यपवर्त्य हारभाज्यौ भवेद्वा सति सम्भवे तु ॥ (Līlāvatī, vs.18,p.18)

"Starting from the last digit of the divided, the (maximum) number of times by which divisor can be subtracted,that indeed is the quotient (result of division). If possible, divide after cancelling some common factor in the divisor and the dividend."

Bhāskara II mentioned along with the regular method of division, he has described the method of removing the common factors of the divisor and dividend to obtain the result.

Example ${\frac {748}{108}}={\frac {748/4}{108/4}}={\frac {187}{27}}={\frac {Bhajya}{Bhajaka}}=Labdhi(6)$

Varga (Square)

Samskrita name for square - varga or kṛti . The word varga means "rows" or bunch of similar things. But in Mathematics it denotes the square power and also the square figure or its area. Aryabhaṭa I says : "A square figure of four equal sides and the (number representing its) area called varga. The product of two equal quantities is also varga."

Bhāskara I has given a method for finding square as follows:

"According to the rule of squaring, square the last digit (leftmost), multiply by twice the last digit all the remaining digits, repeat the process by shifting one digit to the right (till the first digit is arrived)." Example : Square of 6387= 40793769

After step 4.1 add the numbers on each column. wherever there are two digits. unit digit to be retained. digit at tenth place to be carried to next column on the left side and added . Here also unit digit to be retained. digit at tenth place to be carried to next column on the left side and added ...... so on.

		40	7	9	3	7	6	9
Step		39	15	27	23	7	6	9
4.1	72						4	9
3.2	2 x 8 x 7				1	1	2
3.1	82				6	4
2.3	2 x 3 x 7				4	2
2.2	2 x 3 x 8			4	8
2.1	32			9
1.4	2 x 6 x 7			8	4
1.3	2 x 6 x 8		9	6
1.2	2 x 6 x 3	3	6
1.1	62	36
1	Given Number	6	3	8	7
2	Shift Number to the right		6	3	8	7
3	Shift Number to the right			6	3	8	7
4	Shift Number to the right				6	3	8	7

Varga-mūla (Square Root)

Square and Square root

Samskrita name for Square root is Varga-mūla. mūla , pada means root in Hindu terminology. The word karanī is found in the Śulbasūtras as a term for the square root.

In Āryabhaṭīya the method of finding the square root is given as " Always divide the even place by twice the square-root (upto the preceding odd place); after having subtracted from the odd place the square (of the quotient) , the quotient put down at the next place (in the line of the root) gives the root "

Example : Square root of 956484 = 978

		Avarga	Varga	Avarga	Varga	Avarga	Varga
		9	5	6	4	8	4
Subtract by the square = 92		8	1					Root = 9
Divide by twice the root = 2 x 9 =18	18	1	4	6	7			Root = 97
		1	2	6
			2	0	4
Subtract by square of the quotient = 72 = 49				4	9
Divide by twice the root = 2 x 97 = 194	194		1	5	5	8	8	Root = 978
			1	5	5	2
						6	4
Subtract by square of the quotient = 82 = 64	64					6	4
							0

Ghana (Cube)

Samskrita name for Cube is ghana, vṛnda.

Cube - Cube Root

Bhāskara II mentioned a rule for find the cube of a number as " Set down the cube of the last; then the square of the last multiplied by three times the succeeding; then the square of the succeeding multiplied by three times the last and then the cube of the succeeding; these placed so that there is difference of a place between one result and the next, and added give the cube. The given number is distributed into portions according to places, one of which is taken for the last and the next as the first and in like manner repeatedly (if there be occasion). Or the same process may be begun from the first place of figures for finding the cube."

Example: Cube of 1234 has four places as shown below. Initially we take the last digit 1 and succeeding digit 2 i.e 12 and apply the method of cubing

1

2

3

4

			1	2
Cube of last digit			1
Thrice the square of the last digit (3 x 12) muliplied by the succeding digit (2) is 2 x 3 x 12 and placing at the next place				6
Thrice the square of the succeding digit (2)multiplied by the last digit is 3 x 22 x 1 and placing at the next place				1	2
Cube of succeeding digit (23)						8
Cube of 12 = sum of the above digits			1	7	2	8

Next we will take the next digit 3 i.e the number is 123. Here 12 is the last digit and 3 is succeeding digit. The method continues thus.

			12	3
Cube of last digit -12 (already obtained)	1	7	2	8
Thrice the square of the last digit (3 x 122) muliplied by the succeding digit (3) is 3 x 3 x 122 and placing at the next place		1	2	9	6
Thrice the square of the succeding digit (3)multiplied by the last digit is 3 x 32 x 12 and placing at the next place				3	2	4
Cube of succeeding digit (33)						2	7
Cube of 123 = sum of the above digits	1	8	6	0	8	6	7

Now the remaining digit 4 is taken so that the number is 1234 of which 123 is the last digit and 4 is the succeeding digit. The method continues thus.

			123	4
Cube of last digit -123 (already obtained)	1	8	6	0	8	6	7
Thrice the square of the last digit (3 x 1232) muliplied by the succeding digit (4) is 4 x 3 x 1232 and placing at the next place			1	8	1	5	4	8
Thrice the square of the succeeding digit (4)multiplied by the last digit is 3 x 42 x 123 and placing at the next place						5	9	0	4
Cube of succeeding digit (43)									6	4
Cube of 1234 = sum of the above digits	1	8	7	9	0	8	0	9	0	4

Ghana-mūla (Cube Root)

Samskrita name for Cube root is ghana-mūla , ghana-pada.

In Āryabhaṭīya the description of the operation of the cube-root is given as "Divide the second aghana place by thrice the square of the cube-root; subtract from the first aghana place the square of the quotient multiplied by thrice the preceding cube-root); and (subtract) the cube (of the quotient) from the ghana place; (the quotient put down at the next place (in the line of the root) gives the root)" . Cube root of 2628072 is 138

		Ghana	Aghana	Aghana	Ghana	Aghana	Aghana	Ghana		Root
		2	6	2	8	0	7	2
Subtract 13		1								1
Divide by 3 x 12	3	1	6	3 - Quotient						13
			9
			7	2
Subtract 3 x 1 x 32			2	7
			4	5	8
Subtract 33				2	7
Divide by 3 x 132	507		4	3	1	0	8 -Quotient			138
			4	0	5	6
				2	5	4	7
Subrract 3 x 13 x 82				2	4	9	6
						5	1	2
Subtract 83						5	1	2
								0

See also

परिकर्माष्टक- मूल संक्रिया

External Links

• Patiganita
• Aryabhatiya