सामान्यीकृत वितरण नियम: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
सामान्यीकृत वितरण | सामान्यीकृत वितरण नियम (जीडीएल) वितरण गुण का एक ऐसा सामान्यीकरण है जो सामान्य [[संदेश देना]] एल्गोरिदम को जन्म देता है।<ref name=GenDistLaw>{{cite journal|last=Aji|first=S.M.|author2=McEliece, R.J.|title=सामान्यीकृत वितरणात्मक कानून|journal=IEEE Transactions on Information Theory|date=Mar 2000|volume=46|issue=2|pages=325–343|doi=10.1109/18.825794|url=https://authors.library.caltech.edu/1541/1/AJIieeetit00.pdf}}</ref> यह [[सूचना सिद्धांत]], [[डिजिटल संचार]], [[ संकेत आगे बढ़ाना |संकेत आगे बढ़ाना]] , सांख्यिकी और कृत्रिम बुद्धिमत्ता समुदायों में कई लेखकों के कार्य का संश्लेषण है। नियम और एल्गोरिदम को इसी शीर्षक के साथ श्रीनिवास एम. अजी और रॉबर्ट जे. मैकएलीस द्वारा अर्ध-ट्यूटोरियल में प्रस्तुत किया गया था।<ref name=GenDistLaw /> | ||
==परिचय== | ==परिचय== | ||
''गणित में वितरणात्मक | ''गणित में वितरणात्मक नियम गुणा और जोड़ की संक्रियाओं से संबंधित नियम है, जिसे प्रतीकात्मक रूप से कहा गया है, <math> a*(b + c) = a*b + a*c</math>; अर्थात, एकपदी गुणनखंड <math>a</math> द्विपद गुणनखंड <math> b + c </math> के प्रत्येक पद पर वितरित किया जाता है, या अलग से लागू किया जाता है, जिसके परिणामस्वरूप उत्पाद <math> a*b + a*c </math>- होता है" - ब्रिटानिका''<ref name="Britannica">{{cite encyclopedia|title=वितरणात्मक कानून|url=http://www.britannica.com/EBchecked/topic/166204/distributive-law|encyclopedia=Encyclopædia Britannica. Encyclopædia Britannica Online|publisher=Encyclopædia Britannica Inc|accessdate=1 May 2012}}</ref> | ||
जैसा कि परिभाषा से देखा जा सकता है, | जैसा कि परिभाषा से देखा जा सकता है, अंकगणितीय अभिव्यक्ति में वितरणात्मक नियम को लागू करने से इसमें संक्रियाओं की संख्या कम हो जाती है। पूर्व उदाहरण में संक्रियाओं की कुल संख्या तीन <math> a*b + a*c </math>) में दो गुणा और एक जोड़) से घटकर दो हो गई <math> a*(b + c) </math>में एक गुणा और एक जोड़)। वितरणात्मक नियम के सामान्यीकरण से [[तेज़ एल्गोरिदम|तीव्र एल्गोरिदम]] का बड़ा वर्ग तैयार होता है। इसमें [[फास्ट फूरियर ट्रांसफॉर्म]] और [[विटर्बी एल्गोरिदम]] सम्मिलित हैं। | ||
इसे नीचे दिए गए उदाहरण में अधिक औपचारिक | इसे नीचे दिए गए उदाहरण में अधिक औपचारिक विधि से समझाया गया है: | ||
<math>\alpha(a,\, b) \stackrel{\mathrm{def}}{=} \displaystyle\sum \limits_{c,d,e \in A} f(a, \, c, \, b) \, g(a, \, d, \, e) </math> कहाँ <math>f(\cdot)</math> और <math>g(\cdot)</math> वास्तविक-मूल्यवान कार्य हैं, <math>a,b,c,d,e \in A</math> और <math>|A|=q</math> (कहना) | <math>\alpha(a,\, b) \stackrel{\mathrm{def}}{=} \displaystyle\sum \limits_{c,d,e \in A} f(a, \, c, \, b) \, g(a, \, d, \, e) </math> कहाँ <math>f(\cdot)</math> और <math>g(\cdot)</math> वास्तविक-मूल्यवान कार्य हैं, <math>a,b,c,d,e \in A</math> और <math>|A|=q</math> (कहना) | ||
यहां हम स्वतंत्र चरों को हाशिए पर रख रहे हैं (<math>c</math>, <math>d</math>, और <math>e</math>) परिणाम प्राप्त करने के लिए. जब हम कम्प्यूटेशनल जटिलता की गणना कर रहे हैं, तो हम इसे प्रत्येक के लिए देख सकते हैं <math>q^{2}</math> के जोड़े <math>(a,b)</math>, वहाँ हैं <math>q^{3}</math> त्रिक के कारण शर्तें <math>(c,d,e)</math> जिसके मूल्यांकन में भाग लेने की आवश्यकता है <math>\alpha(a,\, b)</math> प्रत्येक चरण में | यहां हम स्वतंत्र चरों को हाशिए पर रख रहे हैं (<math>c</math>, <math>d</math>, और <math>e</math>) परिणाम प्राप्त करने के लिए. जब हम कम्प्यूटेशनल जटिलता की गणना कर रहे हैं, तो हम इसे प्रत्येक के लिए देख सकते हैं <math>q^{2}</math> के जोड़े <math>(a,b)</math>, वहाँ हैं <math>q^{3}</math> त्रिक के कारण शर्तें <math>(c,d,e)</math> जिसके मूल्यांकन में भाग लेने की आवश्यकता है <math>\alpha(a,\, b)</math> प्रत्येक चरण में जोड़ और गुणा होता है। इसलिए, आवश्यक गणनाओं की कुल संख्या है <math>2\cdot q^2 \cdot q^3 = 2q^5</math>. इसलिए उपरोक्त फ़ंक्शन की स्पर्शोन्मुख जटिलता है <math>O(n^5)</math>. | ||
यदि हम वितरण नियम को समीकरण के आरएचएस पर लागू करते हैं, तो हमें निम्नलिखित मिलता है: | यदि हम वितरण नियम को समीकरण के आरएचएस पर लागू करते हैं, तो हमें निम्नलिखित मिलता है: | ||
: <math>\alpha(a, \, b) \stackrel{\mathrm{def}}{=} \displaystyle\sum\limits_{c \in A} f(a, \, c, \, b ) \cdot \sum _{d,\,e \in A} g(a,\,d,\,e) </math> | : <math>\alpha(a, \, b) \stackrel{\mathrm{def}}{=} \displaystyle\sum\limits_{c \in A} f(a, \, c, \, b ) \cdot \sum _{d,\,e \in A} g(a,\,d,\,e) </math> | ||
इसका अर्थ यह है कि <math>\alpha(a, \, b)</math> | इसका अर्थ यह है कि <math>\alpha(a, \, b)</math> उत्पाद के रूप में वर्णित किया जा सकता है <math>\alpha_{1}(a,\, b) \cdot \alpha_{2}(a)</math> कहाँ <math> \alpha_{1}(a,b) \stackrel{\mathrm{def}}{=} \displaystyle\sum\limits_{c \in A} f(a, \, c, \, b )</math> और <math>\alpha_{2}(a) \stackrel{\mathrm{def}}{=} \displaystyle\sum\limits_{d,\,e \in A} g(a,\, d, \,e )</math> | ||
अब, जब हम कम्प्यूटेशनल जटिलता की गणना कर रहे हैं, तो हम देख सकते हैं कि वहाँ हैं <math>q^{3}</math> में परिवर्धन <math>\alpha_{1}(a,\, b)</math> और <math>\alpha_{2}(a)</math> प्रत्येक और वहाँ हैं <math>q^2</math> जब हम उत्पाद का उपयोग कर रहे होते हैं तो गुणन <math>\alpha_{1}(a,\, b) \cdot \alpha_{2}(a)</math> मूल्यांकन करना <math>\alpha(a, \, b)</math>. इसलिए, आवश्यक गणनाओं की कुल संख्या है <math>q^3 + q^3 + q^2 = 2q^3 + q^2</math>. इसलिए गणना की स्पर्शोन्मुख जटिलता <math>\alpha(a,b)</math> तक कम कर देता है <math>O(n^{3})</math> से <math>O(n^{5})</math>. यह | अब, जब हम कम्प्यूटेशनल जटिलता की गणना कर रहे हैं, तो हम देख सकते हैं कि वहाँ हैं <math>q^{3}</math> में परिवर्धन <math>\alpha_{1}(a,\, b)</math> और <math>\alpha_{2}(a)</math> प्रत्येक और वहाँ हैं <math>q^2</math> जब हम उत्पाद का उपयोग कर रहे होते हैं तो गुणन <math>\alpha_{1}(a,\, b) \cdot \alpha_{2}(a)</math> मूल्यांकन करना <math>\alpha(a, \, b)</math>. इसलिए, आवश्यक गणनाओं की कुल संख्या है <math>q^3 + q^3 + q^2 = 2q^3 + q^2</math>. इसलिए गणना की स्पर्शोन्मुख जटिलता <math>\alpha(a,b)</math> तक कम कर देता है <math>O(n^{3})</math> से <math>O(n^{5})</math>. यह उदाहरण से पता चलता है कि वितरण नियम लागू करने से कम्प्यूटेशनल जटिलता कम हो जाती है जो कि तीव्र एल्गोरिदम की अच्छी विशेषताओं में से है। | ||
==इतिहास== | ==इतिहास== | ||
कुछ समस्याएँ जिन्हें हल करने के लिए वितरणात्मक | कुछ समस्याएँ जिन्हें हल करने के लिए वितरणात्मक नियम का उपयोग किया गया, उन्हें निम्नानुसार समूहीकृत किया जा सकता है | ||
1. डिकोडिंग एल्गोरिदम<br> | 1. डिकोडिंग एल्गोरिदम<br> | ||
कम घनत्व समता-जांच कोड को डिकोड करने के लिए गैलेजर द्वारा | कम घनत्व समता-जांच कोड को डिकोड करने के लिए गैलेजर द्वारा जीडीएल जैसे एल्गोरिदम का उपयोग किया गया था। गैलागर के कार्य के आधार पर टान्नर ने [[टान्नर ग्राफ]] प्रस्तुत किया और गैलागर के कार्य को संदेश पासिंग फॉर्म में व्यक्त किया। टेनर्स ग्राफ़ ने विटरबी एल्गोरिथम को समझाने में भी मदद की। | ||
फ़ॉर्नी द्वारा यह देखा गया है कि विटर्बी के [[कन्वेन्शनल कोड]] की अधिकतम संभावना डिकोडिंग में जीडीएल जैसी व्यापकता के एल्गोरिदम का भी उपयोग किया जाता है। | फ़ॉर्नी द्वारा यह देखा गया है कि विटर्बी के [[कन्वेन्शनल कोड]] की अधिकतम संभावना डिकोडिंग में जीडीएल जैसी व्यापकता के एल्गोरिदम का भी उपयोग किया जाता है। | ||
2. [[फॉरवर्ड-बैकवर्ड एल्गोरिथम]]<br> | 2. [[फॉरवर्ड-बैकवर्ड एल्गोरिथम]]<br> | ||
फॉरवर्ड बैकवर्ड एल्गोरिदम ने [[मार्कोव श्रृंखला]] में राज्यों को ट्रैक करने के लिए | फॉरवर्ड बैकवर्ड एल्गोरिदम ने [[मार्कोव श्रृंखला]] में राज्यों को ट्रैक करने के लिए एल्गोरिदम के रूप में मदद की। और इसमें भी सामान्यता की तरह जीडीएल के एल्गोरिदम का उपयोग किया गया था | ||
3. कृत्रिम बुद्धिमत्ता<br> | 3. कृत्रिम बुद्धिमत्ता<br> | ||
| Line 34: | Line 34: | ||
==एमपीएफ समस्या== | ==एमपीएफ समस्या== | ||
एमपीएफ या उत्पाद फ़ंक्शन को हाशिए पर रखना | एमपीएफ या उत्पाद फ़ंक्शन को हाशिए पर रखना सामान्य कम्प्यूटेशनल समस्या है जिसमें विशेष मामले में कई शास्त्रीय समस्याएं सम्मिलित हैं जैसे कि असतत [[हैडामर्ड परिवर्तन]] की गणना, मेमोरी-कम [[चैनल (संचार)]] पर [[रैखिक कोड]] की [[अधिकतम संभावना डिकोडिंग]], और [[मैट्रिक्स श्रृंखला गुणन]]। जीडीएल की शक्ति इस तथ्य में निहित है कि यह उन स्थितियों पर लागू होता है जिनमें जोड़ और गुणा को सामान्यीकृत किया जाता है। | ||
इस व्यवहार को समझाने के लिए | इस व्यवहार को समझाने के लिए [[क्रमविनिमेय सेमीरिंग]] अच्छा ढाँचा है। इसे सेट पर परिभाषित किया गया है <math>K</math> ऑपरेटरों के साथ<math>+</math>और<math>.</math>कहाँ <math>(K,\, +)</math> और <math>(K,\, .)</math> [[क्रमविनिमेय मोनोइड]] हैं और वितरणात्मक नियम कायम है। | ||
होने देना <math>p_1, \ldots, p_n</math> ऐसे परिवर्तनशील बनें <math>p_1 \in A_1, \ldots, p_n \in A_{n}</math> कहाँ <math>A </math> | होने देना <math>p_1, \ldots, p_n</math> ऐसे परिवर्तनशील बनें <math>p_1 \in A_1, \ldots, p_n \in A_{n}</math> कहाँ <math>A </math> परिमित समुच्चय है और <math>|A_i| = q_i</math>. यहाँ <math>i = 1,\ldots, n</math>. अगर <math>S = \{i_{1}, \ldots, i_{r}\}</math> और <math>S \, \subset \{1,\ldots, n\}</math>, होने देना | ||
<math> A_{S} = A_{i_1} \times \cdots \times A_{i_r} </math>, | <math> A_{S} = A_{i_1} \times \cdots \times A_{i_r} </math>, | ||
<math> p_{S} = (p_{i_1},\ldots, p_{i_r})</math>, | <math> p_{S} = (p_{i_1},\ldots, p_{i_r})</math>, | ||
| Line 45: | Line 45: | ||
<math>\mathbf p = \{p_{1}, \ldots, p_{n}\}</math> | <math>\mathbf p = \{p_{1}, \ldots, p_{n}\}</math> | ||
होने देना <math>S = \{S_{j}\}_{j=1}^M </math> कहाँ <math>S_{j} \subset \{1, ...\,,n\}</math>. मान लीजिए किसी फ़ंक्शन को इस प्रकार परिभाषित किया गया है <math>\alpha_{i}: A_{S_{i}} \rightarrow R</math>, कहाँ <math>R</math> | होने देना <math>S = \{S_{j}\}_{j=1}^M </math> कहाँ <math>S_{j} \subset \{1, ...\,,n\}</math>. मान लीजिए किसी फ़ंक्शन को इस प्रकार परिभाषित किया गया है <math>\alpha_{i}: A_{S_{i}} \rightarrow R</math>, कहाँ <math>R</math> क्रमविनिमेय सेमीरिंग है। भी, <math> p_{S_{i}}</math> स्थानीय डोमेन नाम दिए गए हैं और <math>\alpha_{i}</math> स्थानीय गुठली के रूप में. | ||
अब वैश्विक कर्नेल <math>\beta : \mathbf A \rightarrow R</math> परिभाषित किया जाता है : | अब वैश्विक कर्नेल <math>\beta : \mathbf A \rightarrow R</math> परिभाषित किया जाता है : | ||
<math> \beta(p_{1}, ...\,, p_{n}) = \prod_{i=1}^M \alpha(p_{S_{i}})</math> | <math> \beta(p_{1}, ...\,, p_{n}) = \prod_{i=1}^M \alpha(p_{S_{i}})</math> | ||
एमपीएफ समस्या की परिभाषा: | एमपीएफ समस्या की परिभाषा: या अधिक सूचकांकों के लिए <math>i = 1, ...\,, M</math>, के मानों की तालिका की गणना करें <math>S_{i}</math>-वैश्विक कर्नेल का हाशियाकरण <math>\beta</math>, जो कि कार्य है <math>\beta_{i}:A_{S_{i}} \rightarrow R</math> के रूप में परिभाषित <math>\beta_{i}(p_{S_{i}}) \, = \displaystyle\sum\limits_{p_{S_{i}^c} \in A_{S_{i}^c}} \beta(p)</math> | ||
यहाँ <math>S_{i}^c</math> का पूरक है <math>S_{i}</math> इसके संबंध में <math>\mathbf \{1,...\,,n\}</math> और यह <math>\beta_i(p_{S_i})</math> कहा जाता है <math>i^{th}</math> वस्तुनिष्ठ फलन, या वस्तुनिष्ठ फलन <math>S_i</math>. यह देखा जा सकता है कि की गणना <math>i^{th}</math> स्पष्ट | यहाँ <math>S_{i}^c</math> का पूरक है <math>S_{i}</math> इसके संबंध में <math>\mathbf \{1,...\,,n\}</math> और यह <math>\beta_i(p_{S_i})</math> कहा जाता है <math>i^{th}</math> वस्तुनिष्ठ फलन, या वस्तुनिष्ठ फलन <math>S_i</math>. यह देखा जा सकता है कि की गणना <math>i^{th}</math> स्पष्ट विधि से वस्तुनिष्ठ कार्य की आवश्यकता है <math>Mq_1 q_2 q_3\cdots q_{n}</math> परिचालन. ऐसा इसलिए है क्योंकि वहाँ हैं <math>q_1 q_2\cdots q_n</math> अतिरिक्त और <math>(M-1)q_1 q_2...q_n</math> की गणना में आवश्यक गुणन <math>i^\text{th}</math> उद्देश्य समारोह। जीडीएल एल्गोरिदम जिसे अगले भाग में समझाया गया है, इस कम्प्यूटेशनल जटिलता को कम कर सकता है। | ||
निम्नलिखित एमपीएफ समस्या का | निम्नलिखित एमपीएफ समस्या का उदाहरण है। | ||
होने देना <math>p_{1},\,p_{2},\,p_{3},\,p_{4},</math> और <math>p_{5}</math> ऐसे परिवर्तनशील बनें <math>p_{1} \in A_{1}, p_{2} \in A_{2}, p_{3} \in A_{3}, p_{4} \in A_{4}, </math> और <math>p_{5} \in A_{5}</math>. यहाँ <math>M=4</math> और <math>S = \{\{1,2,5\},\{2,4\},\{1,4\}, \{2\}\}</math>. इन वेरिएबल्स का उपयोग करके दिए गए फ़ंक्शन हैं <math>f(p_{1},p_{2},p_{5})</math> और <math>g(p_{3},p_{4})</math> और हमें गणना करने की आवश्यकता है <math>\alpha(p_{1}, \, p_{4})</math> और <math>\beta(p_{2})</math> के रूप में परिभाषित: | होने देना <math>p_{1},\,p_{2},\,p_{3},\,p_{4},</math> और <math>p_{5}</math> ऐसे परिवर्तनशील बनें <math>p_{1} \in A_{1}, p_{2} \in A_{2}, p_{3} \in A_{3}, p_{4} \in A_{4}, </math> और <math>p_{5} \in A_{5}</math>. यहाँ <math>M=4</math> और <math>S = \{\{1,2,5\},\{2,4\},\{1,4\}, \{2\}\}</math>. इन वेरिएबल्स का उपयोग करके दिए गए फ़ंक्शन हैं <math>f(p_{1},p_{2},p_{5})</math> और <math>g(p_{3},p_{4})</math> और हमें गणना करने की आवश्यकता है <math>\alpha(p_{1}, \, p_{4})</math> और <math>\beta(p_{2})</math> के रूप में परिभाषित: | ||
| Line 72: | Line 72: | ||
कहाँ <math>\alpha(p_{1}, p_{4})</math> है <math>3^{rd}</math> वस्तुनिष्ठ कार्य और <math>\beta(p_{2})</math> है <math>4^{th}</math> उद्देश्य समारोह। | कहाँ <math>\alpha(p_{1}, p_{4})</math> है <math>3^{rd}</math> वस्तुनिष्ठ कार्य और <math>\beta(p_{2})</math> है <math>4^{th}</math> उद्देश्य समारोह। | ||
एक और उदाहरण पर विचार करें जहां <math>p_{1},p_{2},p_{3},p_{4},r_{1},r_{2},r_{3},r_{4} \in \{0,1\}</math> और <math>f(r_{1},r_{2},r_{3},r_{4})</math> | एक और उदाहरण पर विचार करें जहां <math>p_{1},p_{2},p_{3},p_{4},r_{1},r_{2},r_{3},r_{4} \in \{0,1\}</math> और <math>f(r_{1},r_{2},r_{3},r_{4})</math> वास्तविक मूल्यवान कार्य है। अब, हम एमपीएफ समस्या पर विचार करेंगे जहां क्रमविनिमेय सेमीरिंग को सामान्य जोड़ और गुणा के साथ वास्तविक संख्याओं के सेट के रूप में परिभाषित किया गया है और स्थानीय डोमेन और स्थानीय कर्नेल को निम्नानुसार परिभाषित किया गया है: | ||
{| | {| | ||
| Line 96: | Line 96: | ||
: <math>F(p_1, p_2, p_3,p_4) = \displaystyle\sum \limits_{r_1,r_2,r_3,r_4} f(r_1,r_2,r_3,r_4) \cdot(-1)^{p_1r_1 + p_2r_2 + p_3r_3 + p_4r_4}.</math> | : <math>F(p_1, p_2, p_3,p_4) = \displaystyle\sum \limits_{r_1,r_2,r_3,r_4} f(r_1,r_2,r_3,r_4) \cdot(-1)^{p_1r_1 + p_2r_2 + p_3r_3 + p_4r_4}.</math> | ||
यह फ़ंक्शन का Hadamard रूपांतरण है <math>f(\cdot)</math>. इसलिए हम देख सकते हैं कि हैडामर्ड ट्रांसफॉर्म की गणना एमपीएफ समस्या का | यह फ़ंक्शन का Hadamard रूपांतरण है <math>f(\cdot)</math>. इसलिए हम देख सकते हैं कि हैडामर्ड ट्रांसफॉर्म की गणना एमपीएफ समस्या का विशेष मामला है। यह साबित करने के लिए और अधिक उदाहरण प्रदर्शित किए जा सकते हैं कि एमपीएफ समस्या कई शास्त्रीय समस्याओं के विशेष मामले बनाती है जैसा कि ऊपर बताया गया है जिनका विवरण यहां पाया जा सकता है<ref name=GenDistLaw /> | ||
== जीडीएल: एमपीएफ समस्या को हल करने के लिए | == जीडीएल: एमपीएफ समस्या को हल करने के लिए एल्गोरिदम == | ||
यदि कोई किसी दिए गए सेट के तत्वों के बीच | यदि कोई किसी दिए गए सेट के तत्वों के बीच संबंध पा सकता है <math>S</math>, तो कोई विश्वास प्रसार की धारणा के आधार पर एमपीएफ समस्या को हल कर सकता है जो संदेश भेजने की तकनीक का विशेष उपयोग है। आवश्यक संबंध यह है कि स्थानीय डोमेन के दिए गए सेट को जंक्शन ट्री में व्यवस्थित किया जा सकता है। दूसरे शब्दों में, हम के तत्वों के साथ ग्राफ सैद्धांतिक वृक्ष बनाते हैं <math>S</math> पेड़ के शीर्ष के रूप में (ग्राफ सिद्धांत) <math>T</math>, जैसे कि किन्हीं दो मनमाने शीर्षों के लिए कहें <math>v_{i}</math> और <math>v_{j}</math> कहाँ <math>i \neq j</math> और इन दो शीर्षों के बीच किनारा मौजूद है, फिर संबंधित लेबलों का प्रतिच्छेदन, अर्थात <math>S_{i}\cap S_{j}</math>, से अद्वितीय पथ पर प्रत्येक शीर्ष पर लेबल का उपसमूह है <math>v_{i}</math> को <math>v_{j}</math>. | ||
उदाहरण के लिए, | उदाहरण के लिए, | ||
| Line 116: | Line 116: | ||
ऊपर दिए गए स्थानीय डोमेन के सेट के लिए, कोई उन्हें जंक्शन ट्री में व्यवस्थित कर सकता है जैसा कि नीचे दिखाया गया है: | ऊपर दिए गए स्थानीय डोमेन के सेट के लिए, कोई उन्हें जंक्शन ट्री में व्यवस्थित कर सकता है जैसा कि नीचे दिखाया गया है: | ||
[[File:An example of a junction tree on a given set.png|center|पेड़ के जंक्शन का | [[File:An example of a junction tree on a given set.png|center|पेड़ के जंक्शन का उदाहरण]]इसी प्रकार यदि निम्नलिखित जैसा और सेट दिया गया है | ||
उदाहरण 2: निम्नलिखित चार स्थानीय डोमेन पर विचार करें: | उदाहरण 2: निम्नलिखित चार स्थानीय डोमेन पर विचार करें: | ||
| Line 129: | Line 129: | ||
6.<math>\{p_{2},p_{3}</math>,<math>p_{4}\}</math> | 6.<math>\{p_{2},p_{3}</math>,<math>p_{4}\}</math> | ||
इसी प्रकार डोमेन के इन सेट के लिए, जंक्शन ट्री नीचे दिखाए गए जैसा दिखता है: | इसी प्रकार डोमेन के इन सेट के लिए, जंक्शन ट्री नीचे दिखाए गए जैसा दिखता है: | ||
[[File:Example of junction tree.png|center|जंक्शन वृक्ष का | [[File:Example of junction tree.png|center|जंक्शन वृक्ष का और उदाहरण]] | ||
===सामान्यीकृत वितरण | ===सामान्यीकृत वितरण नियम (जीडीएल) एल्गोरिदम=== | ||
इनपुट: स्थानीय डोमेन का | इनपुट: स्थानीय डोमेन का सेट।<br /> | ||
आउटपुट: डोमेन के दिए गए सेट के लिए, समस्या को हल करने के लिए आवश्यक न्यूनतम संख्या में ऑपरेशन की गणना की जाती है। <br/> | आउटपुट: डोमेन के दिए गए सेट के लिए, समस्या को हल करने के लिए आवश्यक न्यूनतम संख्या में ऑपरेशन की गणना की जाती है। <br/> | ||
तो यदि <math>v_{i}</math> और <math>v_{j}</math> जंक्शन ट्री में | तो यदि <math>v_{i}</math> और <math>v_{j}</math> जंक्शन ट्री में किनारे से जुड़े होते हैं, फिर संदेश से <math>v_{i}</math> को <math>v_{j}</math> किसी फ़ंक्शन द्वारा दिए गए मानों का सेट/तालिका है: <math>\mu_{i,j}</math>:<math>A_{S_{i}\cap S_{j}} \rightarrow R</math>. सभी कार्यों के साथ आरंभ करने के लिए अर्थात सभी संयोजनों के लिए <math>i</math> और <math>j</math> दिए गए पेड़ में, <math>\mu_{i,j}</math> को समान रूप से परिभाषित किया गया है <math>1</math> और जब कोई विशेष संदेश अद्यतन किया जाता है, तो यह नीचे दिए गए समीकरण का पालन करता है। | ||
: <math>\mu_{i,j}(p_{S_{i}\cap S_{j}})</math> = <math>\sum_{p_{S_{i}\setminus S_{j}}\in A_{S_{i} \setminus S_{j}}} \alpha _{i} (p_{S_{i}}) \prod_{{v_k \operatorname{adj} v_i},{k \neq j}} \mu_{k,j}(p_{S_k\cap S_i})(1) | : <math>\mu_{i,j}(p_{S_{i}\cap S_{j}})</math> = <math>\sum_{p_{S_{i}\setminus S_{j}}\in A_{S_{i} \setminus S_{j}}} \alpha _{i} (p_{S_{i}}) \prod_{{v_k \operatorname{adj} v_i},{k \neq j}} \mu_{k,j}(p_{S_k\cap S_i})(1) | ||
| Line 140: | Line 140: | ||
कहाँ <math>v_k \operatorname{adj} v_i</math> मतलब कि <math>v_{k}</math> का निकटवर्ती शीर्ष है <math>v_{i}</math> पेड़ में. | कहाँ <math>v_k \operatorname{adj} v_i</math> मतलब कि <math>v_{k}</math> का निकटवर्ती शीर्ष है <math>v_{i}</math> पेड़ में. | ||
इसी प्रकार प्रत्येक शीर्ष पर | इसी प्रकार प्रत्येक शीर्ष पर स्थिति होती है जिसे फ़ंक्शन के मानों वाली तालिका के रूप में परिभाषित किया जाता है <math>\sigma_{i}: A_{S_{i}} \rightarrow R </math>, बिल्कुल वैसे ही जैसे संदेश 1 से प्रारंभ होते हैं, ठीक उसी तरह, की स्थिति <math>v_{i}</math> स्थानीय कर्नेल के रूप में परिभाषित किया गया है <math>\alpha(p_{S_{i}})</math>, लेकिन जब भी <math>\sigma_{i}</math> अद्यतन हो जाता है, यह निम्नलिखित समीकरण का पालन करता है: | ||
: <math>\sigma(p_{S_i}) = \alpha_i(p_{S_i}) \prod_{v_k \operatorname{adj} v_i} \mu_{k,j}(p_{S_k\cap S_i})(2).</math> | : <math>\sigma(p_{S_i}) = \alpha_i(p_{S_i}) \prod_{v_k \operatorname{adj} v_i} \mu_{k,j}(p_{S_k\cap S_i})(2).</math> | ||
===एल्गोरिदम का मूल कार्य=== | ===एल्गोरिदम का मूल कार्य=== | ||
इनपुट के रूप में स्थानीय डोमेन के दिए गए सेट के लिए, हम यह पता लगाते हैं कि क्या हम जंक्शन ट्री बना सकते हैं, या तो सीधे सेट का उपयोग करके या पहले सेट में डमी डोमेन जोड़कर और फिर जंक्शन ट्री बनाकर, यदि निर्माण जंक्शन संभव नहीं है तो एल्गोरिदम आउटपुट देता है कि दिए गए समीकरण समस्या की गणना करने के लिए चरणों की संख्या को कम करने का कोई तरीका नहीं है, लेकिन | इनपुट के रूप में स्थानीय डोमेन के दिए गए सेट के लिए, हम यह पता लगाते हैं कि क्या हम जंक्शन ट्री बना सकते हैं, या तो सीधे सेट का उपयोग करके या पहले सेट में डमी डोमेन जोड़कर और फिर जंक्शन ट्री बनाकर, यदि निर्माण जंक्शन संभव नहीं है तो एल्गोरिदम आउटपुट देता है कि दिए गए समीकरण समस्या की गणना करने के लिए चरणों की संख्या को कम करने का कोई तरीका नहीं है, लेकिन बार जब हमारे पास जंक्शन ट्री होता है, तो एल्गोरिदम को संदेशों को शेड्यूल करना होगा और राज्यों की गणना करनी होगी, ऐसा करने से हम जान सकते हैं कि चरणों को कहां कम किया जा सकता है, इसलिए इस पर नीचे चर्चा की जाएगी। | ||
== संदेश भेजने का शेड्यूल और स्थिति की गणना == | == संदेश भेजने का शेड्यूल और स्थिति की गणना == | ||
ऐसे दो विशेष मामले हैं जिनके बारे में हम यहां बात करने जा रहे हैं, अर्थात् सिंगल वर्टेक्स समस्या जिसमें उद्देश्य फ़ंक्शन की गणना केवल | ऐसे दो विशेष मामले हैं जिनके बारे में हम यहां बात करने जा रहे हैं, अर्थात् सिंगल वर्टेक्स समस्या जिसमें उद्देश्य फ़ंक्शन की गणना केवल शीर्ष पर की जाती है। <math>v_{0}</math> और दूसरा ऑल वर्टिसेस समस्या है जहां लक्ष्य सभी शीर्षों पर वस्तुनिष्ठ फ़ंक्शन की गणना करना है। | ||
आइए 'सिंगल-वर्टेक्स समस्या' से शुरुआत करें, जीडीएल प्रत्येक किनारे को लक्षित शीर्ष की ओर निर्देशित करके शुरू करेगा <math>v_0</math>. यहां संदेश केवल लक्षित शीर्ष की दिशा में ही भेजे जाते हैं। ध्यान दें कि सभी निर्देशित संदेश केवल | आइए 'सिंगल-वर्टेक्स समस्या' से शुरुआत करें, जीडीएल प्रत्येक किनारे को लक्षित शीर्ष की ओर निर्देशित करके शुरू करेगा <math>v_0</math>. यहां संदेश केवल लक्षित शीर्ष की दिशा में ही भेजे जाते हैं। ध्यान दें कि सभी निर्देशित संदेश केवल बार भेजे जाते हैं। संदेश लीफ नोड्स (जहां डिग्री 1 है) से शुरू होकर लक्ष्य शीर्ष की ओर बढ़ते हैं <math>v_0</math>. संदेश पत्तियों से उसके माता-पिता तक और फिर वहां से उनके माता-पिता तक और इसी तरह तब तक चलता रहता है जब तक कि वह लक्ष्य शीर्ष तक नहीं पहुंच जाता <math>v_0</math>. लक्ष्य शिखर <math>v_0</math> अपनी स्थिति की गणना तभी करेगा जब उसे अपने सभी पड़ोसियों से सभी संदेश प्राप्त होंगे। बार जब हमें स्थिति मिल जाती है, तो हमें उत्तर मिल जाता है और इसलिए एल्गोरिथम समाप्त हो जाता है। | ||
उदाहरण के लिए, आइए ऊपर दिए गए स्थानीय डोमेन के सेट से निर्मित | उदाहरण के लिए, आइए ऊपर दिए गए स्थानीय डोमेन के सेट से निर्मित जंक्शन ट्री पर विचार करें, यानी उदाहरण 1 से सेट, <br />अब इन डोमेन के लिए शेड्यूलिंग तालिका है (जहां लक्ष्य शीर्ष है) <math>p_2</math>). | ||
<math>\text{Round Message or State Computation} </math><br/> | <math>\text{Round Message or State Computation} </math><br/> | ||
| Line 171: | Line 171: | ||
<math>d(v)</math> की [[डिग्री (ग्राफ सिद्धांत)]] है <math>v</math> (अर्थात् v के निकटवर्ती शीर्षों की संख्या)। | <math>d(v)</math> की [[डिग्री (ग्राफ सिद्धांत)]] है <math>v</math> (अर्थात् v के निकटवर्ती शीर्षों की संख्या)। | ||
ऑल-वर्टिसेस समस्या को हल करने के लिए, हम जीडीएल को कई तरीकों से शेड्यूल कर सकते हैं, उनमें से कुछ समानांतर कार्यान्वयन हैं जहां प्रत्येक दौर में, प्रत्येक राज्य को अपडेट किया जाता है और प्रत्येक संदेश की गणना और | ऑल-वर्टिसेस समस्या को हल करने के लिए, हम जीडीएल को कई तरीकों से शेड्यूल कर सकते हैं, उनमें से कुछ समानांतर कार्यान्वयन हैं जहां प्रत्येक दौर में, प्रत्येक राज्य को अपडेट किया जाता है और प्रत्येक संदेश की गणना और ही समय में प्रसारित किया जाता है। इस प्रकार के कार्यान्वयन में अवस्थाएं और संदेश अधिक से अधिक संख्या में चक्कर लगाने के बाद स्थिर हो जाएंगे जो कि पेड़ के व्यास के बराबर है। इस बिंदु पर शीर्षों की सभी अवस्थाएँ वांछित उद्देश्य फ़ंक्शन के बराबर होंगी। | ||
इस समस्या के लिए जीडीएल को शेड्यूल करने का दूसरा तरीका क्रमिक कार्यान्वयन है जहां यह सिंगल वर्टेक्स समस्या के समान है, सिवाय इसके कि हम एल्गोरिदम को तब तक नहीं रोकते हैं जब तक कि आवश्यक सेट के सभी शीर्षों को अपने सभी पड़ोसियों से सभी संदेश नहीं मिल जाते हैं और उनकी गणना नहीं कर लेते हैं राज्य। <br/> | इस समस्या के लिए जीडीएल को शेड्यूल करने का दूसरा तरीका क्रमिक कार्यान्वयन है जहां यह सिंगल वर्टेक्स समस्या के समान है, सिवाय इसके कि हम एल्गोरिदम को तब तक नहीं रोकते हैं जब तक कि आवश्यक सेट के सभी शीर्षों को अपने सभी पड़ोसियों से सभी संदेश नहीं मिल जाते हैं और उनकी गणना नहीं कर लेते हैं राज्य। <br/> | ||
| Line 178: | Line 178: | ||
==जंक्शन ट्री का निर्माण== | ==जंक्शन ट्री का निर्माण== | ||
जंक्शन ट्री बनाने की कुंजी स्थानीय डोमेन ग्राफ़ में निहित है <math>G_{LD}</math>, जो | जंक्शन ट्री बनाने की कुंजी स्थानीय डोमेन ग्राफ़ में निहित है <math>G_{LD}</math>, जो भारित पूर्ण ग्राफ़ है <math>M</math> कोने <math>v_1,v_2,v_3,\ldots ,v_M</math> यानी प्रत्येक स्थानीय डोमेन के लिए एक, जिसमें किनारे का भार होता है <math>e_{i,j} : v_i \leftrightarrow v_j</math> <br /> द्वारा परिभाषित | ||
<math>\omega_{i,j} = |S_{i} \cap S_{j}|</math>.<br /> | <math>\omega_{i,j} = |S_{i} \cap S_{j}|</math>.<br /> | ||
अगर <math>x_{k} \in S_{i} \cap S_{j}</math>, तो हम कहते हैं <math>x_{k}</math> में निहित है<math>e_{i,j}</math>. द्वारा चिह्नित <math>\omega_{max}</math> (अधिकतम वजन वाले फैले हुए पेड़ का वजन <math>G_{LD}</math>), जिसे परिभाषित किया गया है | अगर <math>x_{k} \in S_{i} \cap S_{j}</math>, तो हम कहते हैं <math>x_{k}</math> में निहित है<math>e_{i,j}</math>. द्वारा चिह्नित <math>\omega_{max}</math> (अधिकतम वजन वाले फैले हुए पेड़ का वजन <math>G_{LD}</math>), जिसे परिभाषित किया गया है | ||
| Line 186: | Line 186: | ||
== शेड्यूलिंग प्रमेय == | == शेड्यूलिंग प्रमेय == | ||
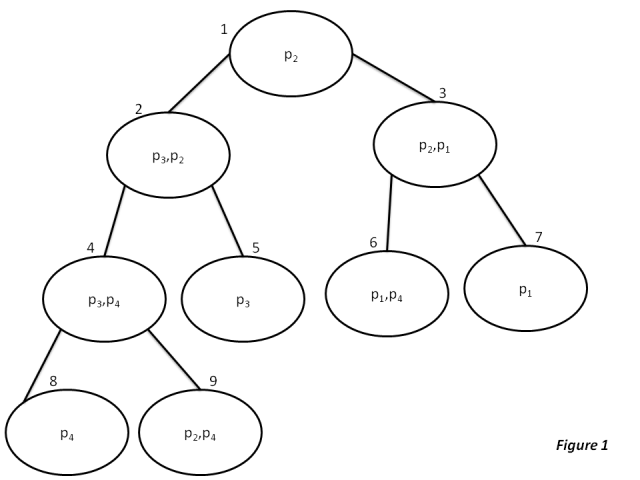
होने देना <math>'T'</math> वर्टेक्स सेट के साथ | होने देना <math>'T'</math> वर्टेक्स सेट के साथ जंक्शन ट्री बनें <math>'V'</math> और किनारा सेट <math>'E'</math>. इस एल्गोरिथ्म में, संदेश किसी भी किनारे पर दोनों दिशाओं में भेजे जाते हैं, इसलिए हम किनारे के सेट E को शीर्षों के क्रमित जोड़े के सेट के रूप में कह/मान सकते हैं। उदाहरण के लिए, चित्र 1 से <math>'E'</math> निम्नानुसार परिभाषित किया जा सकता है | ||
: <math>E = \{(1,2),(2,1),(1,3),(3,1),(4,2),(2,4),(5,2),(2,5),(6,3),(3,6),(7,3),(3,7),(8,4),(4,8),(9,4),(4,9)\}</math> | : <math>E = \{(1,2),(2,1),(1,3),(3,1),(4,2),(2,4),(5,2),(2,5),(6,3),(3,6),(7,3),(3,7),(8,4),(4,8),(9,4),(4,9)\}</math> | ||
टिप्पणी:<math>E</math> उपरोक्त आपको वे सभी संभावित दिशा-निर्देश देता है जिनसे | टिप्पणी:<math>E</math> उपरोक्त आपको वे सभी संभावित दिशा-निर्देश देता है जिनसे संदेश पेड़ में फैल सकता है। | ||
जीडीएल के लिए शेड्यूल को सबसेट के | जीडीएल के लिए शेड्यूल को सबसेट के सीमित अनुक्रम के रूप में परिभाषित किया गया है<math>E</math>. जिसका सामान्यतः प्रतिनिधित्व किया जाता है | ||
<math>\mathcal{E} =</math>{<math>E_{1},E_{2},E_{3},\ldots, E_{N}</math>}, कहाँ <math>E_{N}</math> के दौरान अद्यतन किए गए संदेशों का सेट है <math>N^{th}</math> एल्गोरिदम चलाने का दौर। | <math>\mathcal{E} =</math>{<math>E_{1},E_{2},E_{3},\ldots, E_{N}</math>}, कहाँ <math>E_{N}</math> के दौरान अद्यतन किए गए संदेशों का सेट है <math>N^{th}</math> एल्गोरिदम चलाने का दौर। | ||
कुछ नोटेशनों को परिभाषित/देखने के बाद, हम देखेंगे कि प्रमेय कहता है, | कुछ नोटेशनों को परिभाषित/देखने के बाद, हम देखेंगे कि प्रमेय कहता है, | ||
जब हमें | जब हमें शेड्यूल दिया जाता है <math>\mathcal{E} =\{ E_1,E_2,E_3,\ldots, E_N\}</math>, वर्टेक्स सेट के साथ परिमित निर्देशित ग्राफ के रूप में संबंधित [[ सलाखें (ग्राफ) |सलाखें (ग्राफ)]] । <math>V \times \{0,1,2,3,\ldots, N\}</math>, जिसमें विशिष्ट तत्व को निरूपित किया जाता है <math>v_{i}(t)</math> के लिए <math>t \in \{0,1,2,3,\ldots,N\}</math>, फिर संदेश पारित होने के पूरा होने के बाद, शीर्ष पर बताएं <math>v_{j}</math> यह होंगे <math>j^\text{th}</math> उद्देश्य परिभाषित | ||
: <math>\sigma(p_{S_i}) = \alpha_i(p_{S_i}) \prod_{v_k \operatorname{adj} v_i} \mu_{k,j}(p_{S_{k}\cap S_{i}})</math> | : <math>\sigma(p_{S_i}) = \alpha_i(p_{S_i}) \prod_{v_k \operatorname{adj} v_i} \mu_{k,j}(p_{S_{k}\cap S_{i}})</math> | ||
और <nowiki>iff</nowiki> से | और <nowiki>iff</nowiki> से रास्ता है <math>v_i(0)</math> को <math>v_j(N)</math> | ||
== कम्प्यूटेशनल जटिलता == | == कम्प्यूटेशनल जटिलता == | ||
यहां हम गणना के लिए आवश्यक गणितीय संक्रियाओं की संख्या के संदर्भ में एमपीएफ समस्या को हल करने की जटिलता को समझाने का प्रयास करते हैं। यानी हम सामान्य विधि का उपयोग करके गणना करते समय आवश्यक संचालन की संख्या की तुलना करते हैं (यहां सामान्य विधि से हमारा मतलब उन तरीकों से है जो संदेश पासिंग या जंक्शन पेड़ों का उपयोग नहीं करते हैं जो संक्षिप्त तरीकों में जीडीएल की अवधारणाओं का उपयोग नहीं करते हैं) और उपयोग करने वाले संचालन की संख्या की तुलना करते हैं सामान्यीकृत वितरणात्मक | यहां हम गणना के लिए आवश्यक गणितीय संक्रियाओं की संख्या के संदर्भ में एमपीएफ समस्या को हल करने की जटिलता को समझाने का प्रयास करते हैं। यानी हम सामान्य विधि का उपयोग करके गणना करते समय आवश्यक संचालन की संख्या की तुलना करते हैं (यहां सामान्य विधि से हमारा मतलब उन तरीकों से है जो संदेश पासिंग या जंक्शन पेड़ों का उपयोग नहीं करते हैं जो संक्षिप्त तरीकों में जीडीएल की अवधारणाओं का उपयोग नहीं करते हैं) और उपयोग करने वाले संचालन की संख्या की तुलना करते हैं सामान्यीकृत वितरणात्मक नियम. | ||
उदाहरण: सबसे सरल मामले पर विचार करें जहां हमें निम्नलिखित अभिव्यक्ति की गणना करने की आवश्यकता है <math>ab+ac</math>. | उदाहरण: सबसे सरल मामले पर विचार करें जहां हमें निम्नलिखित अभिव्यक्ति की गणना करने की आवश्यकता है <math>ab+ac</math>. | ||
इस अभिव्यक्ति का मूल्यांकन करने के लिए दो गुणा और | इस अभिव्यक्ति का मूल्यांकन करने के लिए दो गुणा और जोड़ की आवश्यकता होती है। अभिव्यक्ति जब वितरणात्मक नियम का उपयोग करके व्यक्त की जाती है तो उसे इस प्रकार लिखा जा सकता है <math>a(b+c)</math> सरल अनुकूलन जो संचालन की संख्या को जोड़ और गुणा तक कम कर देता है। | ||
ऊपर बताए गए उदाहरण के समान हम जीडीएल लागू करके यथासंभव कम ऑपरेशन करने के लिए समीकरणों को विभिन्न रूपों में व्यक्त करेंगे। | ऊपर बताए गए उदाहरण के समान हम जीडीएल लागू करके यथासंभव कम ऑपरेशन करने के लिए समीकरणों को विभिन्न रूपों में व्यक्त करेंगे। | ||
जैसा कि | जैसा कि पूर्व अनुभागों में बताया गया है, हम जंक्शन पेड़ों की अवधारणा का उपयोग करके समस्या का समाधान करते हैं। इन पेड़ों के उपयोग से प्राप्त अनुकूलन पेड़ों पर अर्ध समूह समस्या को हल करके प्राप्त अनुकूलन के बराबर है। उदाहरण के लिए, संख्याओं के समूह का न्यूनतम ज्ञात करने के लिए हम यह देख सकते हैं कि यदि हमारे पास पेड़ है और सभी तत्व पेड़ के नीचे हैं, तो हम समानांतर में दो वस्तुओं के न्यूनतम की तुलना कर सकते हैं और परिणामी न्यूनतम होगा माता-पिता को लिखा गया। जब यह प्रक्रिया पेड़ तक फैलती है तो जड़ में तत्वों का न्यूनतम समूह पाया जाएगा। | ||
संदेश पासिंग का उपयोग करके जंक्शन ट्री को हल करने की जटिलता निम्नलिखित है | संदेश पासिंग का उपयोग करके जंक्शन ट्री को हल करने की जटिलता निम्नलिखित है | ||
| Line 221: | Line 221: | ||
: <math>\sigma_v(p_v) = \alpha_v (p_v) \prod_{u \operatorname{adj} v} \mu _{v,w} (p _{v \cap w}) </math> | : <math>\sigma_v(p_v) = \alpha_v (p_v) \prod_{u \operatorname{adj} v} \mu _{v,w} (p _{v \cap w}) </math> | ||
हम पहले एकल-शीर्ष समस्या का विश्लेषण करेंगे और मान लेंगे कि लक्ष्य शीर्ष है <math>v_0</math> और इसलिए हमारे पास | हम पहले एकल-शीर्ष समस्या का विश्लेषण करेंगे और मान लेंगे कि लक्ष्य शीर्ष है <math>v_0</math> और इसलिए हमारे पास किनारा है <math>v</math> को <math>v _{0}</math>. | ||
मान लीजिए हमारे पास बढ़त है <math>(v,w)</math> हम संदेश समीकरण का उपयोग करके संदेश की गणना करते हैं। की गणना करना <math>p _{u \cap v}</math> आवश्यक है | मान लीजिए हमारे पास बढ़त है <math>(v,w)</math> हम संदेश समीकरण का उपयोग करके संदेश की गणना करते हैं। की गणना करना <math>p _{u \cap v}</math> आवश्यक है | ||
| Line 261: | Line 261: | ||
: <math> \chi (T) = \sum _{v \in V} d(v)q _{v} - \sum _{e \in E} q _{e}</math> ----<math>(1)</math> | : <math> \chi (T) = \sum _{v \in V} d(v)q _{v} - \sum _{e \in E} q _{e}</math> ----<math>(1)</math> | ||
कहाँ <math>e = (v,w)</math> | कहाँ <math>e = (v,w)</math> किनारा है और इसका आकार इससे परिभाषित होता है <math>q _{v \cap w}</math> | ||
उपरोक्त सूत्र हमें ऊपरी सीमा देता है। | उपरोक्त सूत्र हमें ऊपरी सीमा देता है। | ||
| Line 287: | Line 287: | ||
<math>b_1 = a_1, b_2= b_1 \cdot a_2 = a_1 \cdot a _2, b _{d-1} = b _{d-2} \cdot a_{d-1} = a_1 a_2 \cdots a_{d-1}</math> और <math>c_d = a_d, c_{d-1} = a_{d-1} c_d = a _{d-1} \cdot a_d, \ldots , c_2 = a _2 \cdot c_3 = a _2 a_3 \cdots a_d</math> यह लेता है <math> 2 (d-2)</math> गुणन. तो अगर <math> m_j</math> सभी के उत्पाद को दर्शाता है <math> a_i</math> के अलावा <math> a_j</math> हमारे पास है <math> m_1 = c_2, m_2 = b_1 \cdot c_3</math> और इसी तरह दूसरे की आवश्यकता होगी <math>d-2</math> गुणन से कुल बनता है <math> 3 (d-2)</math> | <math>b_1 = a_1, b_2= b_1 \cdot a_2 = a_1 \cdot a _2, b _{d-1} = b _{d-2} \cdot a_{d-1} = a_1 a_2 \cdots a_{d-1}</math> और <math>c_d = a_d, c_{d-1} = a_{d-1} c_d = a _{d-1} \cdot a_d, \ldots , c_2 = a _2 \cdot c_3 = a _2 a_3 \cdots a_d</math> यह लेता है <math> 2 (d-2)</math> गुणन. तो अगर <math> m_j</math> सभी के उत्पाद को दर्शाता है <math> a_i</math> के अलावा <math> a_j</math> हमारे पास है <math> m_1 = c_2, m_2 = b_1 \cdot c_3</math> और इसी तरह दूसरे की आवश्यकता होगी <math>d-2</math> गुणन से कुल बनता है <math> 3 (d-2)</math> | ||
जब जंक्शन ट्री के निर्माण की बात आती है तो हम बहुत कुछ नहीं कर सकते हैं, सिवाय इसके कि हमारे पास कई अधिकतम वजन वाले स्पैनिंग ट्री हो सकते हैं और हमें सबसे कम वजन वाले स्पैनिंग ट्री का चयन करना चाहिए। <math>\chi(T)</math> और कभी-कभी इसका मतलब जंक्शन ट्री जटिलता को कम करने के लिए | जब जंक्शन ट्री के निर्माण की बात आती है तो हम बहुत कुछ नहीं कर सकते हैं, सिवाय इसके कि हमारे पास कई अधिकतम वजन वाले स्पैनिंग ट्री हो सकते हैं और हमें सबसे कम वजन वाले स्पैनिंग ट्री का चयन करना चाहिए। <math>\chi(T)</math> और कभी-कभी इसका मतलब जंक्शन ट्री जटिलता को कम करने के लिए स्थानीय डोमेन जोड़ना हो सकता है। | ||
ऐसा लग सकता है कि GDL तभी सही है जब स्थानीय डोमेन को जंक्शन ट्री के रूप में व्यक्त किया जा सकता है। लेकिन ऐसे मामलों में भी जहां चक्र और कई पुनरावृत्तियां हैं, संदेश लगभग उद्देश्य फ़ंक्शन के बराबर होंगे। कम घनत्व समता-जांच कोड के लिए गैलेजर-टान्नर-वाइबर्ग एल्गोरिदम पर प्रयोग इस दावे का समर्थन करते थे। | ऐसा लग सकता है कि GDL तभी सही है जब स्थानीय डोमेन को जंक्शन ट्री के रूप में व्यक्त किया जा सकता है। लेकिन ऐसे मामलों में भी जहां चक्र और कई पुनरावृत्तियां हैं, संदेश लगभग उद्देश्य फ़ंक्शन के बराबर होंगे। कम घनत्व समता-जांच कोड के लिए गैलेजर-टान्नर-वाइबर्ग एल्गोरिदम पर प्रयोग इस दावे का समर्थन करते थे। | ||
Revision as of 16:23, 23 November 2023
सामान्यीकृत वितरण नियम (जीडीएल) वितरण गुण का एक ऐसा सामान्यीकरण है जो सामान्य संदेश देना एल्गोरिदम को जन्म देता है।[1] यह सूचना सिद्धांत, डिजिटल संचार, संकेत आगे बढ़ाना , सांख्यिकी और कृत्रिम बुद्धिमत्ता समुदायों में कई लेखकों के कार्य का संश्लेषण है। नियम और एल्गोरिदम को इसी शीर्षक के साथ श्रीनिवास एम. अजी और रॉबर्ट जे. मैकएलीस द्वारा अर्ध-ट्यूटोरियल में प्रस्तुत किया गया था।[1]
परिचय
गणित में वितरणात्मक नियम गुणा और जोड़ की संक्रियाओं से संबंधित नियम है, जिसे प्रतीकात्मक रूप से कहा गया है, ; अर्थात, एकपदी गुणनखंड द्विपद गुणनखंड के प्रत्येक पद पर वितरित किया जाता है, या अलग से लागू किया जाता है, जिसके परिणामस्वरूप उत्पाद - होता है" - ब्रिटानिका[2]
जैसा कि परिभाषा से देखा जा सकता है, अंकगणितीय अभिव्यक्ति में वितरणात्मक नियम को लागू करने से इसमें संक्रियाओं की संख्या कम हो जाती है। पूर्व उदाहरण में संक्रियाओं की कुल संख्या तीन ) में दो गुणा और एक जोड़) से घटकर दो हो गई में एक गुणा और एक जोड़)। वितरणात्मक नियम के सामान्यीकरण से तीव्र एल्गोरिदम का बड़ा वर्ग तैयार होता है। इसमें फास्ट फूरियर ट्रांसफॉर्म और विटर्बी एल्गोरिदम सम्मिलित हैं।
इसे नीचे दिए गए उदाहरण में अधिक औपचारिक विधि से समझाया गया है:
कहाँ और वास्तविक-मूल्यवान कार्य हैं, और (कहना)
यहां हम स्वतंत्र चरों को हाशिए पर रख रहे हैं (, , और ) परिणाम प्राप्त करने के लिए. जब हम कम्प्यूटेशनल जटिलता की गणना कर रहे हैं, तो हम इसे प्रत्येक के लिए देख सकते हैं के जोड़े , वहाँ हैं त्रिक के कारण शर्तें जिसके मूल्यांकन में भाग लेने की आवश्यकता है प्रत्येक चरण में जोड़ और गुणा होता है। इसलिए, आवश्यक गणनाओं की कुल संख्या है . इसलिए उपरोक्त फ़ंक्शन की स्पर्शोन्मुख जटिलता है .
यदि हम वितरण नियम को समीकरण के आरएचएस पर लागू करते हैं, तो हमें निम्नलिखित मिलता है:
इसका अर्थ यह है कि उत्पाद के रूप में वर्णित किया जा सकता है कहाँ और अब, जब हम कम्प्यूटेशनल जटिलता की गणना कर रहे हैं, तो हम देख सकते हैं कि वहाँ हैं में परिवर्धन और प्रत्येक और वहाँ हैं जब हम उत्पाद का उपयोग कर रहे होते हैं तो गुणन मूल्यांकन करना . इसलिए, आवश्यक गणनाओं की कुल संख्या है . इसलिए गणना की स्पर्शोन्मुख जटिलता तक कम कर देता है से . यह उदाहरण से पता चलता है कि वितरण नियम लागू करने से कम्प्यूटेशनल जटिलता कम हो जाती है जो कि तीव्र एल्गोरिदम की अच्छी विशेषताओं में से है।
इतिहास
कुछ समस्याएँ जिन्हें हल करने के लिए वितरणात्मक नियम का उपयोग किया गया, उन्हें निम्नानुसार समूहीकृत किया जा सकता है
1. डिकोडिंग एल्गोरिदम
कम घनत्व समता-जांच कोड को डिकोड करने के लिए गैलेजर द्वारा जीडीएल जैसे एल्गोरिदम का उपयोग किया गया था। गैलागर के कार्य के आधार पर टान्नर ने टान्नर ग्राफ प्रस्तुत किया और गैलागर के कार्य को संदेश पासिंग फॉर्म में व्यक्त किया। टेनर्स ग्राफ़ ने विटरबी एल्गोरिथम को समझाने में भी मदद की।
फ़ॉर्नी द्वारा यह देखा गया है कि विटर्बी के कन्वेन्शनल कोड की अधिकतम संभावना डिकोडिंग में जीडीएल जैसी व्यापकता के एल्गोरिदम का भी उपयोग किया जाता है।
2. फॉरवर्ड-बैकवर्ड एल्गोरिथम
फॉरवर्ड बैकवर्ड एल्गोरिदम ने मार्कोव श्रृंखला में राज्यों को ट्रैक करने के लिए एल्गोरिदम के रूप में मदद की। और इसमें भी सामान्यता की तरह जीडीएल के एल्गोरिदम का उपयोग किया गया था
3. कृत्रिम बुद्धिमत्ता
एआई में कई समस्याओं को हल करने के लिए जंक्शन पेड़ों की अवधारणा का उपयोग किया गया है। इसके अलावा बाल्टी उन्मूलन की अवधारणा में कई अवधारणाओं का उपयोग किया गया।
एमपीएफ समस्या
एमपीएफ या उत्पाद फ़ंक्शन को हाशिए पर रखना सामान्य कम्प्यूटेशनल समस्या है जिसमें विशेष मामले में कई शास्त्रीय समस्याएं सम्मिलित हैं जैसे कि असतत हैडामर्ड परिवर्तन की गणना, मेमोरी-कम चैनल (संचार) पर रैखिक कोड की अधिकतम संभावना डिकोडिंग, और मैट्रिक्स श्रृंखला गुणन। जीडीएल की शक्ति इस तथ्य में निहित है कि यह उन स्थितियों पर लागू होता है जिनमें जोड़ और गुणा को सामान्यीकृत किया जाता है। इस व्यवहार को समझाने के लिए क्रमविनिमेय सेमीरिंग अच्छा ढाँचा है। इसे सेट पर परिभाषित किया गया है ऑपरेटरों के साथऔरकहाँ और क्रमविनिमेय मोनोइड हैं और वितरणात्मक नियम कायम है।
होने देना ऐसे परिवर्तनशील बनें कहाँ परिमित समुच्चय है और . यहाँ . अगर और , होने देना , ,
, , और
होने देना कहाँ . मान लीजिए किसी फ़ंक्शन को इस प्रकार परिभाषित किया गया है , कहाँ क्रमविनिमेय सेमीरिंग है। भी, स्थानीय डोमेन नाम दिए गए हैं और स्थानीय गुठली के रूप में.
अब वैश्विक कर्नेल परिभाषित किया जाता है : एमपीएफ समस्या की परिभाषा: या अधिक सूचकांकों के लिए , के मानों की तालिका की गणना करें -वैश्विक कर्नेल का हाशियाकरण , जो कि कार्य है के रूप में परिभाषित यहाँ का पूरक है इसके संबंध में और यह कहा जाता है वस्तुनिष्ठ फलन, या वस्तुनिष्ठ फलन . यह देखा जा सकता है कि की गणना स्पष्ट विधि से वस्तुनिष्ठ कार्य की आवश्यकता है परिचालन. ऐसा इसलिए है क्योंकि वहाँ हैं अतिरिक्त और की गणना में आवश्यक गुणन उद्देश्य समारोह। जीडीएल एल्गोरिदम जिसे अगले भाग में समझाया गया है, इस कम्प्यूटेशनल जटिलता को कम कर सकता है।
निम्नलिखित एमपीएफ समस्या का उदाहरण है। होने देना और ऐसे परिवर्तनशील बनें और . यहाँ और . इन वेरिएबल्स का उपयोग करके दिए गए फ़ंक्शन हैं और और हमें गणना करने की आवश्यकता है और के रूप में परिभाषित:
यहां स्थानीय डोमेन और स्थानीय कर्नेल को इस प्रकार परिभाषित किया गया है:
| local domains | local kernels |
|---|---|
कहाँ है वस्तुनिष्ठ कार्य और है उद्देश्य समारोह।
एक और उदाहरण पर विचार करें जहां और वास्तविक मूल्यवान कार्य है। अब, हम एमपीएफ समस्या पर विचार करेंगे जहां क्रमविनिमेय सेमीरिंग को सामान्य जोड़ और गुणा के साथ वास्तविक संख्याओं के सेट के रूप में परिभाषित किया गया है और स्थानीय डोमेन और स्थानीय कर्नेल को निम्नानुसार परिभाषित किया गया है:
| local domains | local kernels |
|---|---|
अब चूंकि वैश्विक कर्नेल को स्थानीय कर्नेल के उत्पाद के रूप में परिभाषित किया गया है, यह है
और स्थानीय डोमेन पर उद्देश्य फ़ंक्शन है
यह फ़ंक्शन का Hadamard रूपांतरण है . इसलिए हम देख सकते हैं कि हैडामर्ड ट्रांसफॉर्म की गणना एमपीएफ समस्या का विशेष मामला है। यह साबित करने के लिए और अधिक उदाहरण प्रदर्शित किए जा सकते हैं कि एमपीएफ समस्या कई शास्त्रीय समस्याओं के विशेष मामले बनाती है जैसा कि ऊपर बताया गया है जिनका विवरण यहां पाया जा सकता है[1]
जीडीएल: एमपीएफ समस्या को हल करने के लिए एल्गोरिदम
यदि कोई किसी दिए गए सेट के तत्वों के बीच संबंध पा सकता है , तो कोई विश्वास प्रसार की धारणा के आधार पर एमपीएफ समस्या को हल कर सकता है जो संदेश भेजने की तकनीक का विशेष उपयोग है। आवश्यक संबंध यह है कि स्थानीय डोमेन के दिए गए सेट को जंक्शन ट्री में व्यवस्थित किया जा सकता है। दूसरे शब्दों में, हम के तत्वों के साथ ग्राफ सैद्धांतिक वृक्ष बनाते हैं पेड़ के शीर्ष के रूप में (ग्राफ सिद्धांत) , जैसे कि किन्हीं दो मनमाने शीर्षों के लिए कहें और कहाँ और इन दो शीर्षों के बीच किनारा मौजूद है, फिर संबंधित लेबलों का प्रतिच्छेदन, अर्थात , से अद्वितीय पथ पर प्रत्येक शीर्ष पर लेबल का उपसमूह है को .
उदाहरण के लिए,
उदाहरण 1: निम्नलिखित नौ स्थानीय डोमेन पर विचार करें:
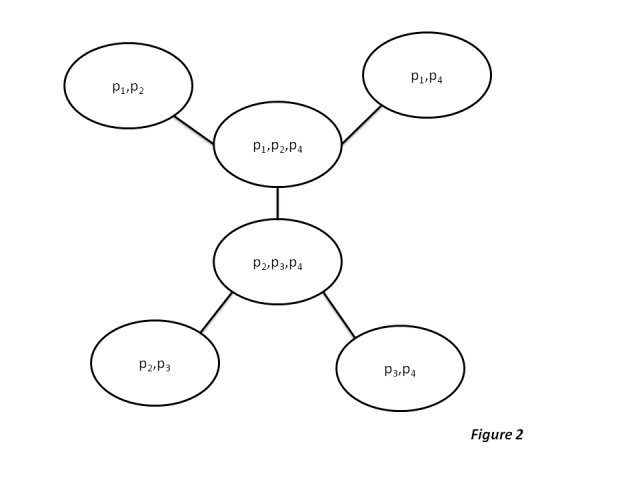
ऊपर दिए गए स्थानीय डोमेन के सेट के लिए, कोई उन्हें जंक्शन ट्री में व्यवस्थित कर सकता है जैसा कि नीचे दिखाया गया है:
इसी प्रकार यदि निम्नलिखित जैसा और सेट दिया गया है
उदाहरण 2: निम्नलिखित चार स्थानीय डोमेन पर विचार करें:
फिर केवल इन स्थानीय डोमेन के साथ पेड़ का निर्माण संभव नहीं है क्योंकि मूल्यों के इस सेट में कोई सामान्य डोमेन नहीं है जिसे उपरोक्त सेट के किन्हीं दो मानों के बीच रखा जा सके। लेकिन हालाँकि, यदि नीचे दिखाए गए अनुसार दो डमी डोमेन जोड़ें तो अद्यतन सेट को जंक्शन ट्री में व्यवस्थित करना संभव और आसान भी होगा।
5.,
6.,
इसी प्रकार डोमेन के इन सेट के लिए, जंक्शन ट्री नीचे दिखाए गए जैसा दिखता है:
सामान्यीकृत वितरण नियम (जीडीएल) एल्गोरिदम
इनपुट: स्थानीय डोमेन का सेट।
आउटपुट: डोमेन के दिए गए सेट के लिए, समस्या को हल करने के लिए आवश्यक न्यूनतम संख्या में ऑपरेशन की गणना की जाती है।
तो यदि और जंक्शन ट्री में किनारे से जुड़े होते हैं, फिर संदेश से को किसी फ़ंक्शन द्वारा दिए गए मानों का सेट/तालिका है: :. सभी कार्यों के साथ आरंभ करने के लिए अर्थात सभी संयोजनों के लिए और दिए गए पेड़ में, को समान रूप से परिभाषित किया गया है और जब कोई विशेष संदेश अद्यतन किया जाता है, तो यह नीचे दिए गए समीकरण का पालन करता है।
- =
कहाँ मतलब कि का निकटवर्ती शीर्ष है पेड़ में.
इसी प्रकार प्रत्येक शीर्ष पर स्थिति होती है जिसे फ़ंक्शन के मानों वाली तालिका के रूप में परिभाषित किया जाता है , बिल्कुल वैसे ही जैसे संदेश 1 से प्रारंभ होते हैं, ठीक उसी तरह, की स्थिति स्थानीय कर्नेल के रूप में परिभाषित किया गया है , लेकिन जब भी अद्यतन हो जाता है, यह निम्नलिखित समीकरण का पालन करता है:
एल्गोरिदम का मूल कार्य
इनपुट के रूप में स्थानीय डोमेन के दिए गए सेट के लिए, हम यह पता लगाते हैं कि क्या हम जंक्शन ट्री बना सकते हैं, या तो सीधे सेट का उपयोग करके या पहले सेट में डमी डोमेन जोड़कर और फिर जंक्शन ट्री बनाकर, यदि निर्माण जंक्शन संभव नहीं है तो एल्गोरिदम आउटपुट देता है कि दिए गए समीकरण समस्या की गणना करने के लिए चरणों की संख्या को कम करने का कोई तरीका नहीं है, लेकिन बार जब हमारे पास जंक्शन ट्री होता है, तो एल्गोरिदम को संदेशों को शेड्यूल करना होगा और राज्यों की गणना करनी होगी, ऐसा करने से हम जान सकते हैं कि चरणों को कहां कम किया जा सकता है, इसलिए इस पर नीचे चर्चा की जाएगी।
संदेश भेजने का शेड्यूल और स्थिति की गणना
ऐसे दो विशेष मामले हैं जिनके बारे में हम यहां बात करने जा रहे हैं, अर्थात् सिंगल वर्टेक्स समस्या जिसमें उद्देश्य फ़ंक्शन की गणना केवल शीर्ष पर की जाती है। और दूसरा ऑल वर्टिसेस समस्या है जहां लक्ष्य सभी शीर्षों पर वस्तुनिष्ठ फ़ंक्शन की गणना करना है।
आइए 'सिंगल-वर्टेक्स समस्या' से शुरुआत करें, जीडीएल प्रत्येक किनारे को लक्षित शीर्ष की ओर निर्देशित करके शुरू करेगा . यहां संदेश केवल लक्षित शीर्ष की दिशा में ही भेजे जाते हैं। ध्यान दें कि सभी निर्देशित संदेश केवल बार भेजे जाते हैं। संदेश लीफ नोड्स (जहां डिग्री 1 है) से शुरू होकर लक्ष्य शीर्ष की ओर बढ़ते हैं . संदेश पत्तियों से उसके माता-पिता तक और फिर वहां से उनके माता-पिता तक और इसी तरह तब तक चलता रहता है जब तक कि वह लक्ष्य शीर्ष तक नहीं पहुंच जाता . लक्ष्य शिखर अपनी स्थिति की गणना तभी करेगा जब उसे अपने सभी पड़ोसियों से सभी संदेश प्राप्त होंगे। बार जब हमें स्थिति मिल जाती है, तो हमें उत्तर मिल जाता है और इसलिए एल्गोरिथम समाप्त हो जाता है।
उदाहरण के लिए, आइए ऊपर दिए गए स्थानीय डोमेन के सेट से निर्मित जंक्शन ट्री पर विचार करें, यानी उदाहरण 1 से सेट,
अब इन डोमेन के लिए शेड्यूलिंग तालिका है (जहां लक्ष्य शीर्ष है) ).
इस प्रकार सिंगल वर्टेक्स जीडीएल की जटिलता को इस प्रकार दिखाया जा सकता है
अंकगणितीय संक्रियाएँ
कहां (नोट: उपरोक्त समीकरण का स्पष्टीकरण लेख में बाद में बताया गया है)
का लेबल है .
की डिग्री (ग्राफ सिद्धांत) है (अर्थात् v के निकटवर्ती शीर्षों की संख्या)।
ऑल-वर्टिसेस समस्या को हल करने के लिए, हम जीडीएल को कई तरीकों से शेड्यूल कर सकते हैं, उनमें से कुछ समानांतर कार्यान्वयन हैं जहां प्रत्येक दौर में, प्रत्येक राज्य को अपडेट किया जाता है और प्रत्येक संदेश की गणना और ही समय में प्रसारित किया जाता है। इस प्रकार के कार्यान्वयन में अवस्थाएं और संदेश अधिक से अधिक संख्या में चक्कर लगाने के बाद स्थिर हो जाएंगे जो कि पेड़ के व्यास के बराबर है। इस बिंदु पर शीर्षों की सभी अवस्थाएँ वांछित उद्देश्य फ़ंक्शन के बराबर होंगी।
इस समस्या के लिए जीडीएल को शेड्यूल करने का दूसरा तरीका क्रमिक कार्यान्वयन है जहां यह सिंगल वर्टेक्स समस्या के समान है, सिवाय इसके कि हम एल्गोरिदम को तब तक नहीं रोकते हैं जब तक कि आवश्यक सेट के सभी शीर्षों को अपने सभी पड़ोसियों से सभी संदेश नहीं मिल जाते हैं और उनकी गणना नहीं कर लेते हैं राज्य।
इस प्रकार इस कार्यान्वयन के लिए आवश्यक अंकगणित की संख्या अधिकतम है अंकगणितीय आपरेशनस।
जंक्शन ट्री का निर्माण
जंक्शन ट्री बनाने की कुंजी स्थानीय डोमेन ग्राफ़ में निहित है , जो भारित पूर्ण ग्राफ़ है कोने यानी प्रत्येक स्थानीय डोमेन के लिए एक, जिसमें किनारे का भार होता है
द्वारा परिभाषित
.
अगर , तो हम कहते हैं में निहित है. द्वारा चिह्नित (अधिकतम वजन वाले फैले हुए पेड़ का वजन ), जिसे परिभाषित किया गया है
जहाँ n उस सेट में तत्वों की संख्या है। अधिक स्पष्टता और विवरण के लिए, कृपया इन्हें देखें।[3][4]
शेड्यूलिंग प्रमेय
होने देना वर्टेक्स सेट के साथ जंक्शन ट्री बनें और किनारा सेट . इस एल्गोरिथ्म में, संदेश किसी भी किनारे पर दोनों दिशाओं में भेजे जाते हैं, इसलिए हम किनारे के सेट E को शीर्षों के क्रमित जोड़े के सेट के रूप में कह/मान सकते हैं। उदाहरण के लिए, चित्र 1 से निम्नानुसार परिभाषित किया जा सकता है
टिप्पणी: उपरोक्त आपको वे सभी संभावित दिशा-निर्देश देता है जिनसे संदेश पेड़ में फैल सकता है।
जीडीएल के लिए शेड्यूल को सबसेट के सीमित अनुक्रम के रूप में परिभाषित किया गया है. जिसका सामान्यतः प्रतिनिधित्व किया जाता है
{}, कहाँ के दौरान अद्यतन किए गए संदेशों का सेट है एल्गोरिदम चलाने का दौर।
कुछ नोटेशनों को परिभाषित/देखने के बाद, हम देखेंगे कि प्रमेय कहता है, जब हमें शेड्यूल दिया जाता है , वर्टेक्स सेट के साथ परिमित निर्देशित ग्राफ के रूप में संबंधित सलाखें (ग्राफ) । , जिसमें विशिष्ट तत्व को निरूपित किया जाता है के लिए , फिर संदेश पारित होने के पूरा होने के बाद, शीर्ष पर बताएं यह होंगे उद्देश्य परिभाषित
और iff से रास्ता है को
कम्प्यूटेशनल जटिलता
यहां हम गणना के लिए आवश्यक गणितीय संक्रियाओं की संख्या के संदर्भ में एमपीएफ समस्या को हल करने की जटिलता को समझाने का प्रयास करते हैं। यानी हम सामान्य विधि का उपयोग करके गणना करते समय आवश्यक संचालन की संख्या की तुलना करते हैं (यहां सामान्य विधि से हमारा मतलब उन तरीकों से है जो संदेश पासिंग या जंक्शन पेड़ों का उपयोग नहीं करते हैं जो संक्षिप्त तरीकों में जीडीएल की अवधारणाओं का उपयोग नहीं करते हैं) और उपयोग करने वाले संचालन की संख्या की तुलना करते हैं सामान्यीकृत वितरणात्मक नियम.
उदाहरण: सबसे सरल मामले पर विचार करें जहां हमें निम्नलिखित अभिव्यक्ति की गणना करने की आवश्यकता है .
इस अभिव्यक्ति का मूल्यांकन करने के लिए दो गुणा और जोड़ की आवश्यकता होती है। अभिव्यक्ति जब वितरणात्मक नियम का उपयोग करके व्यक्त की जाती है तो उसे इस प्रकार लिखा जा सकता है सरल अनुकूलन जो संचालन की संख्या को जोड़ और गुणा तक कम कर देता है।
ऊपर बताए गए उदाहरण के समान हम जीडीएल लागू करके यथासंभव कम ऑपरेशन करने के लिए समीकरणों को विभिन्न रूपों में व्यक्त करेंगे।
जैसा कि पूर्व अनुभागों में बताया गया है, हम जंक्शन पेड़ों की अवधारणा का उपयोग करके समस्या का समाधान करते हैं। इन पेड़ों के उपयोग से प्राप्त अनुकूलन पेड़ों पर अर्ध समूह समस्या को हल करके प्राप्त अनुकूलन के बराबर है। उदाहरण के लिए, संख्याओं के समूह का न्यूनतम ज्ञात करने के लिए हम यह देख सकते हैं कि यदि हमारे पास पेड़ है और सभी तत्व पेड़ के नीचे हैं, तो हम समानांतर में दो वस्तुओं के न्यूनतम की तुलना कर सकते हैं और परिणामी न्यूनतम होगा माता-पिता को लिखा गया। जब यह प्रक्रिया पेड़ तक फैलती है तो जड़ में तत्वों का न्यूनतम समूह पाया जाएगा।
संदेश पासिंग का उपयोग करके जंक्शन ट्री को हल करने की जटिलता निम्नलिखित है
हम पहले इस्तेमाल किए गए फॉर्मूले को निम्नलिखित फॉर्म में फिर से लिखते हैं। यह शीर्ष v से w तक भेजे जाने वाले संदेश का समीकरण है
- ----संदेश समीकरण
इसी प्रकार हम शीर्ष v की स्थिति की गणना के लिए समीकरण को निम्नानुसार फिर से लिखते हैं
हम पहले एकल-शीर्ष समस्या का विश्लेषण करेंगे और मान लेंगे कि लक्ष्य शीर्ष है और इसलिए हमारे पास किनारा है को . मान लीजिए हमारे पास बढ़त है हम संदेश समीकरण का उपयोग करके संदेश की गणना करते हैं। की गणना करना आवश्यक है
अतिरिक्त और
गुणन.
(हम इसका प्रतिनिधित्व करते हैं जैसा .)
लेकिन इसके लिए कई संभावनाएं होंगी इसलिए
के लिए संभावनाएं .
इस प्रकार पूरे संदेश की आवश्यकता होगी
अतिरिक्त और
गुणा
एक संदेश भेजने के लिए आवश्यक अंकगणितीय संक्रियाओं की कुल संख्या पेड़ के किनारों के साथ होगा
अतिरिक्त और
गुणन.
एक बार जब सभी संदेश प्रसारित हो जाते हैं तो एल्गोरिदम स्थिति की गणना के साथ समाप्त हो जाता है राज्य गणना की आवश्यकता है अधिक गुणन. राज्य की गणना के लिए आवश्यक गणनाओं की संख्या नीचे दी गई है
अतिरिक्त और
गुणा
इस प्रकार गणनाओं की संख्या का कुल योग है
- ----
कहाँ किनारा है और इसका आकार इससे परिभाषित होता है उपरोक्त सूत्र हमें ऊपरी सीमा देता है।
यदि हम किनारे की जटिलता को परिभाषित करते हैं जैसा
इसलिए, के रूप में लिखा जा सकता है
अब हम चित्र 1 में परिभाषित समस्या के लिए किनारे की जटिलता की गणना निम्नानुसार करते हैं
पूरी जटिलता होगी जो प्रत्यक्ष विधि की तुलना में काफी कम है। (यहां प्रत्यक्ष विधि से हमारा मतलब उन तरीकों से है जो संदेश भेजने का उपयोग नहीं करते हैं। प्रत्यक्ष विधि का उपयोग करने में लगने वाला समय प्रत्येक नोड पर संदेश की गणना करने और प्रत्येक नोड की स्थिति की गणना करने के समय के बराबर होगा।)
अब हम ऑल-वर्टेक्स समस्या पर विचार करते हैं जहां संदेश को दोनों दिशाओं में भेजना होगा और दोनों शीर्षों पर स्थिति की गणना करनी होगी। ये लगेगा लेकिन प्रीकंप्यूटिंग द्वारा हम गुणन की संख्या को कम कर सकते हैं . यहाँ शीर्ष की डिग्री है. उदाहरणार्थ: यदि कोई समुच्चय है साथ नंबर. के सभी d उत्पादों की गणना करना संभव है की अधिक से अधिक के साथ स्पष्ट के बजाय गुणा . हम मात्राओं की पूर्व-गणना करके ऐसा करते हैं
और यह लेता है गुणन. तो अगर सभी के उत्पाद को दर्शाता है के अलावा हमारे पास है और इसी तरह दूसरे की आवश्यकता होगी गुणन से कुल बनता है
जब जंक्शन ट्री के निर्माण की बात आती है तो हम बहुत कुछ नहीं कर सकते हैं, सिवाय इसके कि हमारे पास कई अधिकतम वजन वाले स्पैनिंग ट्री हो सकते हैं और हमें सबसे कम वजन वाले स्पैनिंग ट्री का चयन करना चाहिए। और कभी-कभी इसका मतलब जंक्शन ट्री जटिलता को कम करने के लिए स्थानीय डोमेन जोड़ना हो सकता है।
ऐसा लग सकता है कि GDL तभी सही है जब स्थानीय डोमेन को जंक्शन ट्री के रूप में व्यक्त किया जा सकता है। लेकिन ऐसे मामलों में भी जहां चक्र और कई पुनरावृत्तियां हैं, संदेश लगभग उद्देश्य फ़ंक्शन के बराबर होंगे। कम घनत्व समता-जांच कोड के लिए गैलेजर-टान्नर-वाइबर्ग एल्गोरिदम पर प्रयोग इस दावे का समर्थन करते थे।
संदर्भ
- ↑ 1.0 1.1 1.2 Aji, S.M.; McEliece, R.J. (Mar 2000). "सामान्यीकृत वितरणात्मक कानून" (PDF). IEEE Transactions on Information Theory. 46 (2): 325–343. doi:10.1109/18.825794.
- ↑ "वितरणात्मक कानून". Encyclopædia Britannica. Encyclopædia Britannica Online. Encyclopædia Britannica Inc. Retrieved 1 May 2012.
- ↑ "संग्रहीत प्रति" (PDF). Archived from the original (PDF) on 2015-03-19. Retrieved 2015-03-19. The Junction Tree Algorithms
- ↑ http://www-anw.cs.umass.edu/~cs691t/SS02/lectures/week7.PDF Archived 2012-05-26 at the Wayback Machine The Junction Tree Algorithm