आठ-शीर्ष प्रारूप: Difference between revisions
(Created page with "{{short description|Generalization of the ice-type (six-vertex) models}} सांख्यिकीय यांत्रिकी में, आठ-शीर्ष म...") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{short description|Generalization of the ice-type (six-vertex) models}} | {{short description|Generalization of the ice-type (six-vertex) models}} | ||
[[सांख्यिकीय यांत्रिकी]] में, आठ-शीर्ष मॉडल बर्फ-प्रकार मॉडल का | [[सांख्यिकीय यांत्रिकी]] में, आठ-शीर्ष मॉडल बर्फ-प्रकार मॉडल का सामान्यीकरण है|बर्फ-प्रकार (छह-शीर्ष) मॉडल; इसकी चर्चा सदरलैंड ने की थी,<ref>{{cite journal | last=Sutherland | first=Bill | title=Two‐Dimensional Hydrogen Bonded Crystals without the Ice Rule | journal=Journal of Mathematical Physics | publisher=AIP Publishing | volume=11 | issue=11 | year=1970 | issn=0022-2488 | doi=10.1063/1.1665111 | pages=3183–3186| bibcode=1970JMP....11.3183S }}</ref> और फैन और वू,<ref>{{cite journal | last1=Fan | first1=Chungpeng | last2=Wu | first2=F. Y. | title=चरण संक्रमण का सामान्य जाली मॉडल| journal=Physical Review B | publisher=American Physical Society (APS) | volume=2 | issue=3 | date=1970-08-01 | issn=0556-2805 | doi=10.1103/physrevb.2.723 | pages=723–733| bibcode=1970PhRvB...2..723F }}</ref> और शून्य-क्षेत्र मामले में [[रॉडने बैक्सटर]] द्वारा हल किया गया।<ref>{{cite journal | last=Baxter | first=R. J. | title=जाली सांख्यिकी में आठ-वर्टेक्स मॉडल| journal=Physical Review Letters | publisher=American Physical Society (APS) | volume=26 | issue=14 | date=1971-04-05 | issn=0031-9007 | doi=10.1103/physrevlett.26.832 | pages=832–833| bibcode=1971PhRvL..26..832B }}</ref> | ||
== विवरण == | |||
बर्फ-प्रकार के मॉडल की तरह, आठ-शीर्ष मॉडल वर्गाकार [[जाली (समूह)]] है, जहां प्रत्येक राज्य शीर्ष पर तीरों का विन्यास है। अनुमत शीर्षों में शीर्ष की ओर इंगित करने वाले तीरों की संख्या सम है; इनमें बर्फ-प्रकार के मॉडल (1-6), और सिंक और स्रोत (7, 8) से विरासत में मिले छह शामिल हैं। | |||
[[File:Eightvertex2.png|thumb|आठवर्टेक्स2]]हम पर विचार करते हैं <math>N\times N</math> जाली, के साथ <math>N^2</math> शिखर और <math>2N^2</math> किनारों. आवधिक सीमा शर्तों को लागू करने के लिए आवश्यक है कि राज्य 7 और 8 समान रूप से बार-बार घटित हों, जैसा कि राज्य 5 और 6 में होता है, और इस प्रकार इसे समान ऊर्जा के रूप में लिया जा सकता है। शून्य-क्षेत्र मामले के लिए राज्यों के दो अन्य युग्मों के लिए भी यही सच है। प्रत्येक शिखर <math>j</math> संबद्ध ऊर्जा है <math>\epsilon_j</math> और [[बोल्ट्ज़मान कारक]] <math>w_j=e^{-\frac{\epsilon_j}{kT}}</math>, जाली के ऊपर [[विभाजन फ़ंक्शन (सांख्यिकीय यांत्रिकी)]] दे रहा है | |||
[[File:Eightvertex2.png|thumb|आठवर्टेक्स2]]हम | |||
:<math> | :<math> | ||
Z=\sum \exp\left(-\frac{\sum_j n_j\epsilon_j}{kT}\right) | Z=\sum \exp\left(-\frac{\sum_j n_j\epsilon_j}{kT}\right) | ||
| Line 24: | Line 22: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
समाधान इस अवलोकन पर आधारित है कि [[स्थानांतरण मैट्रिक्स विधि]] में पंक्तियाँ इन चार बोल्ट्ज़मान भारों के | समाधान इस अवलोकन पर आधारित है कि [[स्थानांतरण मैट्रिक्स विधि]] में पंक्तियाँ इन चार बोल्ट्ज़मान भारों के निश्चित पैरामीट्रिज़ेशन के लिए परिवर्तित होती हैं। यह [[छह-शीर्ष मॉडल]] के लिए वैकल्पिक समाधान के संशोधन के रूप में आया; यह [[जैकोबी थीटा फ़ंक्शन]] का उपयोग करता है। | ||
===कम्यूटिंग ट्रांसफर मैट्रिसेस=== | ===कम्यूटिंग ट्रांसफर मैट्रिसेस=== | ||
| Line 46: | Line 44: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
और <math>H(u)</math> और <math>\Theta(u)</math> मापांक के थीटा फलन हैं <math>k</math>. संबद्ध स्थानांतरण मैट्रिक्स <math>T</math> इस प्रकार का | और <math>H(u)</math> और <math>\Theta(u)</math> मापांक के थीटा फलन हैं <math>k</math>. संबद्ध स्थानांतरण मैट्रिक्स <math>T</math> इस प्रकार का कार्य है <math>u</math> अकेला; सभी के लिए <math>u</math>, <math>v</math> | ||
:<math> | :<math> | ||
T(u)T(v)=T(v)T(u). | T(u)T(v)=T(v)T(u). | ||
</math> | </math> | ||
'''मैट्रिक्स फ़ंक्शन <math>Q(u)</math>''' | |||
समाधान का अन्य महत्वपूर्ण हिस्सा गैर-विलक्षण मैट्रिक्स-मूल्य फ़ंक्शन का अस्तित्व है <math>Q</math>, जैसे कि सभी जटिल के लिए <math>u</math> मैट्रिक्स <math>Q(u), Q(u')</math> -दूसरे के साथ आवागमन करें और स्थानांतरण मैट्रिसेस करें, और संतुष्ट हों | |||
समाधान का अन्य महत्वपूर्ण हिस्सा | |||
{{NumBlk|:|<math> \zeta(u)T(u)Q(u)=\phi(u-\eta)Q(u+2\eta)+\phi(u+\eta)Q(u-2\eta)</math>|{{EquationRef|1}}}} | {{NumBlk|:|<math> \zeta(u)T(u)Q(u)=\phi(u-\eta)Q(u+2\eta)+\phi(u+\eta)Q(u-2\eta)</math>|{{EquationRef|1}}}} | ||
जहाँ | |||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 63: | Line 60: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
ऐसे फ़ंक्शन के अस्तित्व और रूपान्तरण संबंधों को छह-वर्टेक्स मॉडल के समान तरीके से, | ऐसे फ़ंक्शन के अस्तित्व और रूपान्तरण संबंधों को छह-वर्टेक्स मॉडल के समान तरीके से, शीर्ष के माध्यम से जोड़ी प्रसार और थीटा कार्यों की आवधिकता संबंधों पर विचार करके प्रदर्शित किया जाता है। | ||
===स्पष्ट समाधान=== | ===स्पष्ट समाधान=== | ||
| Line 81: | Line 78: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
जहाँ <math>K</math> और <math>K'</math> मॉड्यूलि के पूर्ण अण्डाकार अभिन्न अंग हैं <math>k</math> और <math>k'</math>. | |||
आठ वर्टेक्स मॉडल को भी [[quasicrystals]] में हल किया गया था। | आठ वर्टेक्स मॉडल को भी [[quasicrystals]] में हल किया गया था। | ||
==आइज़िंग मॉडल के साथ समतुल्यता== | ==आइज़िंग मॉडल के साथ समतुल्यता== | ||
आठ-वर्टेक्स मॉडल और [[आइसिंग मॉडल]] के बीच 2-स्पिन और 4-स्पिन निकटतम पड़ोसी इंटरैक्शन के बीच | आठ-वर्टेक्स मॉडल और [[आइसिंग मॉडल]] के बीच 2-स्पिन और 4-स्पिन निकटतम पड़ोसी इंटरैक्शन के बीच प्राकृतिक पत्राचार है। इस मॉडल की अवस्थाएँ स्पिन हैं <math>\sigma=\pm 1</math> वर्गाकार जाली के फलकों पर. आठ-शीर्ष मॉडल में 'किनारों' का एनालॉग आसन्न चेहरों पर स्पिन के उत्पाद हैं: | ||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 100: | Line 97: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
जहाँ <math>J_h</math>, <math>J_v</math>, <math>J</math>, <math>J'</math> क्षैतिज, ऊर्ध्वाधर और दो विकर्ण 2-स्पिन इंटरैक्शन का वर्णन करें, और <math>J''</math> शीर्ष पर चार चेहरों के बीच 4-स्पिन इंटरैक्शन का वर्णन करता है; योग पूरी जाली से अधिक है। | |||
[[File:Isinginteractions.png|Isingबातचीत]]हम आठ-शीर्ष मॉडल में क्षैतिज और ऊर्ध्वाधर स्पिन (किनारों पर तीर) को दर्शाते हैं <math>\mu</math>, <math>\alpha</math> क्रमशः, और ऊपर और दाएं को सकारात्मक दिशाओं के रूप में परिभाषित करें। शीर्ष स्थिति पर प्रतिबंध यह है कि | [[File:Isinginteractions.png|Isingबातचीत]]हम आठ-शीर्ष मॉडल में क्षैतिज और ऊर्ध्वाधर स्पिन (किनारों पर तीर) को दर्शाते हैं <math>\mu</math>, <math>\alpha</math> क्रमशः, और ऊपर और दाएं को सकारात्मक दिशाओं के रूप में परिभाषित करें। शीर्ष स्थिति पर प्रतिबंध यह है कि शीर्ष पर चार किनारों का गुणनफल 1 है; यह स्वचालित रूप से आइसिंग 'किनारों' के लिए मान्य है। प्रत्येक <math>\sigma</math> कॉन्फ़िगरेशन तब अद्वितीय से मेल खाता है <math>\mu</math>, <math>\alpha</math> कॉन्फ़िगरेशन, जबकि प्रत्येक <math>\mu</math>, <math>\alpha</math> कॉन्फ़िगरेशन दो विकल्प देता है <math>\sigma</math> विन्यास। | ||
प्रत्येक शीर्ष के लिए बोल्ट्ज़मान भार का समीकरण सामान्य रूप <math>j</math>, के बीच निम्नलिखित संबंध <math>\epsilon_j</math> और <math>J_h</math>, <math>J_v</math>, <math>J</math>, <math>J'</math>, <math>J''</math> जाली मॉडल के बीच पत्राचार को परिभाषित करें: | प्रत्येक शीर्ष के लिए बोल्ट्ज़मान भार का समीकरण सामान्य रूप <math>j</math>, के बीच निम्नलिखित संबंध <math>\epsilon_j</math> और <math>J_h</math>, <math>J_v</math>, <math>J</math>, <math>J'</math>, <math>J''</math> जाली मॉडल के बीच पत्राचार को परिभाषित करें: | ||
:<math> | :<math> | ||
| Line 114: | Line 111: | ||
यह इस प्रकार है कि आठ-शीर्ष मॉडल के शून्य-क्षेत्र मामले में, संबंधित आइसिंग मॉडल में क्षैतिज और ऊर्ध्वाधर इंटरैक्शन गायब हो जाते हैं। | यह इस प्रकार है कि आठ-शीर्ष मॉडल के शून्य-क्षेत्र मामले में, संबंधित आइसिंग मॉडल में क्षैतिज और ऊर्ध्वाधर इंटरैक्शन गायब हो जाते हैं। | ||
ये संबंध समतुल्यता प्रदान करते हैं <math>Z_I=2Z_{8V}</math> आठ-वर्टेक्स मॉडल और 2,4-स्पिन आइसिंग मॉडल के विभाजन कार्यों के बीच। परिणामस्वरूप किसी भी मॉडल में | ये संबंध समतुल्यता प्रदान करते हैं <math>Z_I=2Z_{8V}</math> आठ-वर्टेक्स मॉडल और 2,4-स्पिन आइसिंग मॉडल के विभाजन कार्यों के बीच। परिणामस्वरूप किसी भी मॉडल में समाधान तुरंत दूसरे मॉडल में समाधान की ओर ले जाएगा। | ||
==यह भी देखें== | ==यह भी देखें== | ||
| Line 124: | Line 121: | ||
{{Reflist}} | {{Reflist}} | ||
== संदर्भ == | |||
==संदर्भ== | |||
*{{Citation | last1=Baxter | first1=Rodney J. | title=Exactly solved models in statistical mechanics | url=http://physics.anu.edu.au/theophys/_files/Exactly.pdf | publisher=Academic Press Inc. [Harcourt Brace Jovanovich Publishers] | location=London | isbn=978-0-12-083180-7 | mr=690578 | year=1982 | access-date=2012-08-12 | archive-date=2021-04-14 | archive-url=https://web.archive.org/web/20210414063635/https://physics.anu.edu.au/theophys/_files/Exactly.pdf | url-status=dead }} | *{{Citation | last1=Baxter | first1=Rodney J. | title=Exactly solved models in statistical mechanics | url=http://physics.anu.edu.au/theophys/_files/Exactly.pdf | publisher=Academic Press Inc. [Harcourt Brace Jovanovich Publishers] | location=London | isbn=978-0-12-083180-7 | mr=690578 | year=1982 | access-date=2012-08-12 | archive-date=2021-04-14 | archive-url=https://web.archive.org/web/20210414063635/https://physics.anu.edu.au/theophys/_files/Exactly.pdf | url-status=dead }} | ||
[[Category: बिल्कुल हल करने योग्य मॉडल]] [[Category: सांख्यिकीय यांत्रिकी]] [[Category: जाली मॉडल]] | [[Category: बिल्कुल हल करने योग्य मॉडल]] [[Category: सांख्यिकीय यांत्रिकी]] [[Category: जाली मॉडल]] | ||
Revision as of 19:50, 4 December 2023
सांख्यिकीय यांत्रिकी में, आठ-शीर्ष मॉडल बर्फ-प्रकार मॉडल का सामान्यीकरण है|बर्फ-प्रकार (छह-शीर्ष) मॉडल; इसकी चर्चा सदरलैंड ने की थी,[1] और फैन और वू,[2] और शून्य-क्षेत्र मामले में रॉडने बैक्सटर द्वारा हल किया गया।[3]
विवरण
बर्फ-प्रकार के मॉडल की तरह, आठ-शीर्ष मॉडल वर्गाकार जाली (समूह) है, जहां प्रत्येक राज्य शीर्ष पर तीरों का विन्यास है। अनुमत शीर्षों में शीर्ष की ओर इंगित करने वाले तीरों की संख्या सम है; इनमें बर्फ-प्रकार के मॉडल (1-6), और सिंक और स्रोत (7, 8) से विरासत में मिले छह शामिल हैं।
हम पर विचार करते हैं जाली, के साथ शिखर और किनारों. आवधिक सीमा शर्तों को लागू करने के लिए आवश्यक है कि राज्य 7 और 8 समान रूप से बार-बार घटित हों, जैसा कि राज्य 5 और 6 में होता है, और इस प्रकार इसे समान ऊर्जा के रूप में लिया जा सकता है। शून्य-क्षेत्र मामले के लिए राज्यों के दो अन्य युग्मों के लिए भी यही सच है। प्रत्येक शिखर संबद्ध ऊर्जा है और बोल्ट्ज़मान कारक , जाली के ऊपर विभाजन फ़ंक्शन (सांख्यिकीय यांत्रिकी) दे रहा है
जहां जालक में शीर्षों के सभी अनुमत विन्यासों का योग है। इस सामान्य रूप में विभाजन फ़ंक्शन अनसुलझा रहता है।
शून्य-क्षेत्र मामले में समाधान
मॉडल का शून्य-क्षेत्र मामला भौतिक रूप से बाहरी विद्युत क्षेत्रों की अनुपस्थिति से मेल खाता है। इसलिए, सभी तीरों के उलटने पर भी मॉडल अपरिवर्तित रहता है; परिणामस्वरूप अवस्थाएँ 1 और 2, और 3 और 4, जोड़े के रूप में घटित होनी चाहिए। शीर्षों को मनमाना भार सौंपा जा सकता है
समाधान इस अवलोकन पर आधारित है कि स्थानांतरण मैट्रिक्स विधि में पंक्तियाँ इन चार बोल्ट्ज़मान भारों के निश्चित पैरामीट्रिज़ेशन के लिए परिवर्तित होती हैं। यह छह-शीर्ष मॉडल के लिए वैकल्पिक समाधान के संशोधन के रूप में आया; यह जैकोबी थीटा फ़ंक्शन का उपयोग करता है।
कम्यूटिंग ट्रांसफर मैट्रिसेस
प्रमाण इस तथ्य पर निर्भर करता है कि कब और , मात्राओं के लिए
स्थानांतरण मैट्रिक्स और (वजन से जुड़ा हुआ , , , और , , , ) आना-जाना। स्टार-त्रिकोण संबंध का उपयोग करते हुए, बैक्सटर ने इस स्थिति को दिए गए भारों के पैरामीट्रिजेशन के बराबर के रूप में पुन: तैयार किया
निश्चित मापांक के लिए और और परिवर्तनशील . यहाँ snh, sn का अतिशयोक्तिपूर्ण एनालॉग है, जो कि दिया गया है
और और मापांक के थीटा फलन हैं . संबद्ध स्थानांतरण मैट्रिक्स इस प्रकार का कार्य है अकेला; सभी के लिए ,
मैट्रिक्स फ़ंक्शन
समाधान का अन्य महत्वपूर्ण हिस्सा गैर-विलक्षण मैट्रिक्स-मूल्य फ़ंक्शन का अस्तित्व है , जैसे कि सभी जटिल के लिए मैट्रिक्स -दूसरे के साथ आवागमन करें और स्थानांतरण मैट्रिसेस करें, और संतुष्ट हों
-
(1)
जहाँ
ऐसे फ़ंक्शन के अस्तित्व और रूपान्तरण संबंधों को छह-वर्टेक्स मॉडल के समान तरीके से, शीर्ष के माध्यम से जोड़ी प्रसार और थीटा कार्यों की आवधिकता संबंधों पर विचार करके प्रदर्शित किया जाता है।
स्पष्ट समाधान
(में मैट्रिक्स का रूपान्तरण1) उन्हें विकर्णीय मैट्रिक्स होने की अनुमति दें, और इस प्रकार eigenvalues पाया जा सकता है। विभाजन फ़ंक्शन की गणना अधिकतम eigenvalue से की जाती है, जिसके परिणामस्वरूप प्रति साइट थर्मोडायनामिक मुक्त ऊर्जा प्राप्त होती है
के लिए
जहाँ और मॉड्यूलि के पूर्ण अण्डाकार अभिन्न अंग हैं और . आठ वर्टेक्स मॉडल को भी quasicrystals में हल किया गया था।
आइज़िंग मॉडल के साथ समतुल्यता
आठ-वर्टेक्स मॉडल और आइसिंग मॉडल के बीच 2-स्पिन और 4-स्पिन निकटतम पड़ोसी इंटरैक्शन के बीच प्राकृतिक पत्राचार है। इस मॉडल की अवस्थाएँ स्पिन हैं वर्गाकार जाली के फलकों पर. आठ-शीर्ष मॉडल में 'किनारों' का एनालॉग आसन्न चेहरों पर स्पिन के उत्पाद हैं:
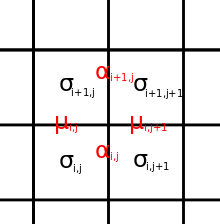 इस मॉडल के लिए ऊर्जा का सबसे सामान्य रूप है
इस मॉडल के लिए ऊर्जा का सबसे सामान्य रूप है
जहाँ , , , क्षैतिज, ऊर्ध्वाधर और दो विकर्ण 2-स्पिन इंटरैक्शन का वर्णन करें, और शीर्ष पर चार चेहरों के बीच 4-स्पिन इंटरैक्शन का वर्णन करता है; योग पूरी जाली से अधिक है।
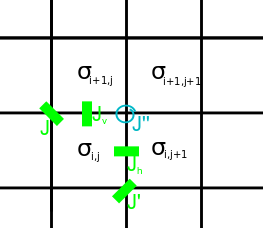 हम आठ-शीर्ष मॉडल में क्षैतिज और ऊर्ध्वाधर स्पिन (किनारों पर तीर) को दर्शाते हैं , क्रमशः, और ऊपर और दाएं को सकारात्मक दिशाओं के रूप में परिभाषित करें। शीर्ष स्थिति पर प्रतिबंध यह है कि शीर्ष पर चार किनारों का गुणनफल 1 है; यह स्वचालित रूप से आइसिंग 'किनारों' के लिए मान्य है। प्रत्येक कॉन्फ़िगरेशन तब अद्वितीय से मेल खाता है , कॉन्फ़िगरेशन, जबकि प्रत्येक , कॉन्फ़िगरेशन दो विकल्प देता है विन्यास।
प्रत्येक शीर्ष के लिए बोल्ट्ज़मान भार का समीकरण सामान्य रूप , के बीच निम्नलिखित संबंध और , , , , जाली मॉडल के बीच पत्राचार को परिभाषित करें:
हम आठ-शीर्ष मॉडल में क्षैतिज और ऊर्ध्वाधर स्पिन (किनारों पर तीर) को दर्शाते हैं , क्रमशः, और ऊपर और दाएं को सकारात्मक दिशाओं के रूप में परिभाषित करें। शीर्ष स्थिति पर प्रतिबंध यह है कि शीर्ष पर चार किनारों का गुणनफल 1 है; यह स्वचालित रूप से आइसिंग 'किनारों' के लिए मान्य है। प्रत्येक कॉन्फ़िगरेशन तब अद्वितीय से मेल खाता है , कॉन्फ़िगरेशन, जबकि प्रत्येक , कॉन्फ़िगरेशन दो विकल्प देता है विन्यास।
प्रत्येक शीर्ष के लिए बोल्ट्ज़मान भार का समीकरण सामान्य रूप , के बीच निम्नलिखित संबंध और , , , , जाली मॉडल के बीच पत्राचार को परिभाषित करें:
यह इस प्रकार है कि आठ-शीर्ष मॉडल के शून्य-क्षेत्र मामले में, संबंधित आइसिंग मॉडल में क्षैतिज और ऊर्ध्वाधर इंटरैक्शन गायब हो जाते हैं।
ये संबंध समतुल्यता प्रदान करते हैं आठ-वर्टेक्स मॉडल और 2,4-स्पिन आइसिंग मॉडल के विभाजन कार्यों के बीच। परिणामस्वरूप किसी भी मॉडल में समाधान तुरंत दूसरे मॉडल में समाधान की ओर ले जाएगा।
यह भी देखें
- सिक्स-वर्टेक्स मॉडल
- स्थानांतरण-मैट्रिक्स विधि
- आइज़िंग मॉडल
टिप्पणियाँ
- ↑ Sutherland, Bill (1970). "Two‐Dimensional Hydrogen Bonded Crystals without the Ice Rule". Journal of Mathematical Physics. AIP Publishing. 11 (11): 3183–3186. Bibcode:1970JMP....11.3183S. doi:10.1063/1.1665111. ISSN 0022-2488.
- ↑ Fan, Chungpeng; Wu, F. Y. (1970-08-01). "चरण संक्रमण का सामान्य जाली मॉडल". Physical Review B. American Physical Society (APS). 2 (3): 723–733. Bibcode:1970PhRvB...2..723F. doi:10.1103/physrevb.2.723. ISSN 0556-2805.
- ↑ Baxter, R. J. (1971-04-05). "जाली सांख्यिकी में आठ-वर्टेक्स मॉडल". Physical Review Letters. American Physical Society (APS). 26 (14): 832–833. Bibcode:1971PhRvL..26..832B. doi:10.1103/physrevlett.26.832. ISSN 0031-9007.
संदर्भ
- Baxter, Rodney J. (1982), Exactly solved models in statistical mechanics (PDF), London: Academic Press Inc. [Harcourt Brace Jovanovich Publishers], ISBN 978-0-12-083180-7, MR 0690578, archived from the original (PDF) on 2021-04-14, retrieved 2012-08-12
