घातीय प्रकार: Difference between revisions
(Created page with "{{Short description|Type of complex function with growth bounded by an exponential function}} {{for|exponential types in type theory and programming languages|Function type}}...") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Type of complex function with growth bounded by an exponential function}} | {{Short description|Type of complex function with growth bounded by an exponential function}} | ||
{{for| | {{for|प्ररूप सिद्धांत और प्रोग्रामिंग भाषाओं में घातीय प्रकार|फलन प्ररूप }} | ||
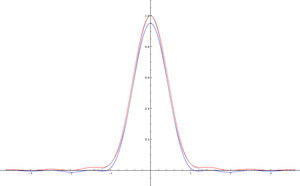
[[File:ExtremeGaussian.png|thumb| | [[File:ExtremeGaussian.png|thumb|<math>e^{-\pi z^{2}}</math> फलन का ग्राफ ग्रे रंग में है, गाऊसी वास्तविक अक्ष तक ही सीमित है। फिर गॉसियन में घातीय प्ररूप नहीं होता है, किन्तु लाल और नीले रंग में कार्य एक तरफा सन्निकटन होते हैं जिनमें घातांक प्रकार <math>2\pi</math> होता है.]][[जटिल विश्लेषण|सम्मिश्र विश्लेषण]] में, गणित की एक शाखा, एक [[होलोमोर्फिक फ़ंक्शन|होलोमोर्फिक]] फलन को घातीय प्ररूप C का कहा जाता है यदि इसकी वृद्धि घातीय फलन <math>e^{C|z|}</math> द्वारा सीमित होती है किसी [[वास्तविक संख्या]] के लिए वास्तविक-मान स्थिरांक <math>C</math> जैसा <math>|z|\to\infty</math>. जब कोई फलन इस तरह से घिरा होता है, तो इसे अन्य सम्मिश्र फलन की श्रृंखला पर कुछ प्रकार के अभिसरण योगों के रूप में व्यक्त करना संभव होता है, साथ ही यह समझना भी संभव होता है कि [[बोरेल योग]] जैसी तकनीकों को क्रियान्वित करना कब संभव है, या, उदाहरण के लिए , [[ मध्य परिवर्तन |मेलिन परिवर्तन]] को क्रियान्वित करने के लिए, या यूलर-मैकलॉरिन फॉर्मूला का उपयोग करके सन्निकटन करने के लिए। सामान्य स्थितियों को नचबिन के प्रमेय द्वारा नियंत्रित किया जाता है,जो <math>e^z</math> के विपरीत एक सामान्य फलन <math>\Psi(z)</math> के लिए <math>\Psi</math>-प्रकार की अनुरूप धारणा को परिभाषित करता है।. | ||
== | ==मूल विचार== | ||
एक | [[जटिल विश्लेषण|सम्मिश्र]] तल पर परिभाषित एक फलन <math>f(z)</math> को घातीय प्रकार का कहा जाता है यदि वास्तविक-मान वाले स्थिरांक <math>M</math> और <math>\tau</math> उपस्तिथ हों जैसे कि | ||
:<math>\left|f\left(re^{i\theta}\right)\right| \le Me^{\tau r}</math> | :<math>\left|f\left(re^{i\theta}\right)\right| \le Me^{\tau r}</math> | ||
<math>r\to\infty</math> की सीमा में. यहाँ, [[जटिल चर|सम्मिश्र चर]] <math>z</math> को <math>z=re^{i\theta}</math> रूप में लिखा गया था जिससे कि इस बात पर ज़ोर देना कि सीमा सभी दिशाओं में <math>\theta</math> को बनाए रखना चाहिए। ऐसे सभी <math>\tau</math> के न्यूनतम के लिए <math>\tau</math> स्थित रहें <math>\tau</math>, तो कोई कहता है कि फलन <math>f</math> घातीय प्ररूप <math>\tau</math> का है . | |||
उदाहरण के लिए, चलो <math>f(z)=\sin(\pi z)</math>. फिर कोई कहता है <math>\sin(\pi z)</math> घातीय | उदाहरण के लिए, चलो <math>f(z)=\sin(\pi z)</math>. फिर कोई कहता है <math>\sin(\pi z)</math> घातीय प्ररूप <math>\pi</math> का है, क्योंकि <math>\pi</math> वह सबसे छोटी संख्या है जो काल्पनिक अक्ष के साथ <math>\sin(\pi z)</math> को सीमित करती है. इसलिए, इस उदाहरण के लिए, कार्लसन का प्रमेय क्रियान्वित नहीं हो सकता, क्योंकि इसके लिए इससे कम घातीय प्ररूप <math>\pi</math> के फलनों की आवश्यकता होती है. इसी तरह, यूलर-मैकलॉरिन फॉर्मूला भी क्रियान्वित नहीं किया जा सकता है, क्योंकि यह भी एक प्रमेय को व्यक्त करता है जो अंततः [[परिमित अंतर]] के सिद्धांत में निहित है। | ||
==औपचारिक परिभाषा== | ==औपचारिक परिभाषा== | ||
होलोमोर्फिक फलन <math>F(z)</math> घातीय प्ररूप <math>\sigma>0</math> का कहा जाता है यदि प्रत्येक <math>\varepsilon>0</math> के लिए वहाँ एक वास्तविक-मान स्थिरांक <math>A_\varepsilon </math> उपस्तिथ है ऐसा है कि | |||
:<math>|F(z)|\leq A_\varepsilon e^{(\sigma+\varepsilon)|z|}</math> | :<math>|F(z)|\leq A_\varepsilon e^{(\sigma+\varepsilon)|z|}</math> | ||
<math>|z|\to\infty</math> के लिए जहाँ <math>z\in\mathbb{C}</math>. हम कहते हैं <math>F(z)</math> यदि घातीय प्ररूप का है यदि <math>F(z)</math> कुछ <math>\sigma>0</math> घातीय प्ररूप <math>\sigma</math> का है. जो संख्या | |||
हम कहते हैं <math>F(z)</math> यदि घातीय | |||
:<math>\tau(F)=\sigma=\displaystyle\limsup_{|z|\rightarrow\infty}|z|^{-1}\log|F(z)|</math> | :<math>\tau(F)=\sigma=\displaystyle\limsup_{|z|\rightarrow\infty}|z|^{-1}\log|F(z)|</math> | ||
<math>F(z)</math> का घातीय प्ररूप है. यहां श्रेष्ठ सीमा का कारण किसी दिए गए त्रिज्या के बाहर अनुपात के सर्वोच्च की सीमा है क्योंकि त्रिज्या अनंत तक जाती है। यह किसी दिए गए त्रिज्या पर अनुपात के अधिकतम से श्रेष्ठ सीमा भी है क्योंकि त्रिज्या अनंत तक जाती है। उच्चतम सीमा त्रिज्या पर अधिकतम होने पर भी उपस्तिथ हो सकती है <math>r </math> जैसी कोई सीमा नहीं है <math>r </math> अनंत तक जाता है. उदाहरण के लिए, फलन के लिए | |||
:<math>F(z)=\sum_{n=1}^\infty\frac{z^{10^{n!}}}{(10^{n!})!}</math> | :<math>F(z)=\sum_{n=1}^\infty\frac{z^{10^{n!}}}{(10^{n!})!}</math> | ||
| Line 33: | Line 32: | ||
&\sim(\log 10)(n!-1-(n-1)!)/10^{n!-1-(n-1)!}\\ | &\sim(\log 10)(n!-1-(n-1)!)/10^{n!-1-(n-1)!}\\ | ||
\end{align}</math> | \end{align}</math> | ||
और यह शून्य हो जाता है <math>n</math> अनंत तक जाता है,<ref>In fact, even <math>(\max_{|z|=r}\log \log|F(z)|) /(\log r)</math> goes to zero at <math>r=10^{n!-1}</math> as | और यह शून्य हो जाता है <math>n </math> अनंत तक जाता है,<ref>In fact, even <math>(\max_{|z|=r}\log \log|F(z)|) /(\log r)</math> goes to zero at <math>r=10^{n!-1}</math> as | ||
<math>n</math> goes to infinity.</ref> | <math>n</math> goes to infinity.</ref> किन्तु <math>F(z)</math> फिर भी यह घातीय प्ररूप 1 का है, जैसा कि बिंदुओं <math>z=10^{n!}</math> को देखकर देखा जा सकता है. | ||
==सममित उत्तल पिंड के संबंध में घातीय | ==सममित उत्तल पिंड के संबंध में घातीय प्ररूप== | ||
{{harvtxt|Stein|1957}} ने [[कई जटिल चर]] | {{harvtxt|Stein|1957}} ने [[कई जटिल चर|कई सम्मिश्र चर]] के [[संपूर्ण कार्य|संपूर्ण फलन]] के लिए घातीय प्ररूप का सामान्यीकरण दिया है। मान लीजिए <math>K </math> एक उत्तल समुच्चय, [[सघन तत्व]] और [[सममित]] उपसमुच्चय <math>\mathbb{R}^n</math> है. यह ज्ञात है कि हर ऐसे के लिए <math>K</math> एक संबद्ध मानदंड <math>\|\cdot\|_K</math> है (गणित) उस गुण के साथ | ||
:<math> K=\{x\in\mathbb{R}^n : \|x\|_K \leq1\}. </math> | :<math> K=\{x\in\mathbb{R}^n : \|x\|_K \leq1\}. </math> | ||
दूसरे शब्दों में, <math>K</math> में यूनिट बॉल | दूसरे शब्दों में, <math>K</math> में यूनिट बॉल <math>\mathbb{R}^{n}</math> है इसके संबंध में समुच्चय <math>\|\cdot\|_K</math>. | ||
:<math>K^{*}=\{y\in\mathbb{R}^{n}:x\cdot y \leq 1 \text{ for all }x\in{K}\}</math> | :<math>K^{*}=\{y\in\mathbb{R}^{n}:x\cdot y \leq 1 \text{ for all }x\in{K}\}</math> | ||
ध्रुवीय समुच्चय कहा जाता है और यह उत्तल समुच्चय, सघन तत्व और सममित उपसमुच्चय भी है | <math>\mathbb{R}^n</math> को ध्रुवीय समुच्चय कहा जाता है और यह उत्तल समुच्चय, सघन तत्व और सममित उपसमुच्चय भी है. इसके अतिरिक्त, हम लिख सकते हैं | ||
:<math>\|x\|_K = \displaystyle\sup_{y\in K^{*}}|x\cdot y|.</math> | :<math>\|x\|_K = \displaystyle\sup_{y\in K^{*}}|x\cdot y|.</math> | ||
| Line 51: | Line 49: | ||
:<math>\|z\|_K = \displaystyle\sup_{y\in K^{*}}|z\cdot y|.</math> | :<math>\|z\|_K = \displaystyle\sup_{y\in K^{*}}|z\cdot y|.</math> | ||
एक संपूर्ण | एक संपूर्ण फलन <math>F(z) </math> का <math>n </math>-सम्मिश्र चर को घातीय प्ररूप <math>K </math> का कहा जाता है यदि प्रत्येक के लिए <math>\varepsilon>0</math> वहाँ एक वास्तविक-मान स्थिरांक उपस्तिथ <math>A_\varepsilon </math> है ऐसा है कि | ||
:<math>|F(z)|<A_\varepsilon e^{2\pi(1+\varepsilon)\|z\|_K}</math> | :<math>|F(z)|<A_\varepsilon e^{2\pi(1+\varepsilon)\|z\|_K}</math> | ||
सभी के लिए <math>z\in\mathbb{C}^{n}</math>. | सभी के लिए <math>z\in\mathbb{C}^{n}</math>. | ||
==फ्रेचेट | ==फ्रेचेट समष्टि== | ||
घातीय | घातीय प्ररूप के फलनों का संग्रह <math>\tau</math> मानदंड (गणित) के गणनीय वर्ग द्वारा प्रेरित [[टोपोलॉजिकल स्पेस|टोपोलॉजिकल समष्टि]] द्वारा एक पूर्ण [[टोपोलॉजिकल स्पेस|समष्टि]], समान समष्टि, अर्थात् फ़्रेचेट समष्टि, बना सकता है | ||
: <math> \|f\|_n = \sup_{z \in \mathbb{C}} \exp \left[-\left(\tau + \frac{1}{n}\right)|z|\right]|f(z)|. </math> | : <math> \|f\|_n = \sup_{z \in \mathbb{C}} \exp \left[-\left(\tau + \frac{1}{n}\right)|z|\right]|f(z)|. </math> | ||
| Line 64: | Line 62: | ||
==यह भी देखें== | ==यह भी देखें== | ||
*पेली-वीनर प्रमेय | *पेली-वीनर प्रमेय | ||
*पेली-वीनर | *पेली-वीनर समष्टि | ||
== संदर्भ == | == संदर्भ == | ||
{{Reflist}} | {{Reflist}} | ||
Revision as of 09:28, 12 December 2023
सम्मिश्र विश्लेषण में, गणित की एक शाखा, एक होलोमोर्फिक फलन को घातीय प्ररूप C का कहा जाता है यदि इसकी वृद्धि घातीय फलन द्वारा सीमित होती है किसी वास्तविक संख्या के लिए वास्तविक-मान स्थिरांक जैसा . जब कोई फलन इस तरह से घिरा होता है, तो इसे अन्य सम्मिश्र फलन की श्रृंखला पर कुछ प्रकार के अभिसरण योगों के रूप में व्यक्त करना संभव होता है, साथ ही यह समझना भी संभव होता है कि बोरेल योग जैसी तकनीकों को क्रियान्वित करना कब संभव है, या, उदाहरण के लिए , मेलिन परिवर्तन को क्रियान्वित करने के लिए, या यूलर-मैकलॉरिन फॉर्मूला का उपयोग करके सन्निकटन करने के लिए। सामान्य स्थितियों को नचबिन के प्रमेय द्वारा नियंत्रित किया जाता है,जो के विपरीत एक सामान्य फलन के लिए -प्रकार की अनुरूप धारणा को परिभाषित करता है।.
मूल विचार
सम्मिश्र तल पर परिभाषित एक फलन को घातीय प्रकार का कहा जाता है यदि वास्तविक-मान वाले स्थिरांक और उपस्तिथ हों जैसे कि
की सीमा में. यहाँ, सम्मिश्र चर को रूप में लिखा गया था जिससे कि इस बात पर ज़ोर देना कि सीमा सभी दिशाओं में को बनाए रखना चाहिए। ऐसे सभी के न्यूनतम के लिए स्थित रहें , तो कोई कहता है कि फलन घातीय प्ररूप का है .
उदाहरण के लिए, चलो . फिर कोई कहता है घातीय प्ररूप का है, क्योंकि वह सबसे छोटी संख्या है जो काल्पनिक अक्ष के साथ को सीमित करती है. इसलिए, इस उदाहरण के लिए, कार्लसन का प्रमेय क्रियान्वित नहीं हो सकता, क्योंकि इसके लिए इससे कम घातीय प्ररूप के फलनों की आवश्यकता होती है. इसी तरह, यूलर-मैकलॉरिन फॉर्मूला भी क्रियान्वित नहीं किया जा सकता है, क्योंकि यह भी एक प्रमेय को व्यक्त करता है जो अंततः परिमित अंतर के सिद्धांत में निहित है।
औपचारिक परिभाषा
होलोमोर्फिक फलन घातीय प्ररूप का कहा जाता है यदि प्रत्येक के लिए वहाँ एक वास्तविक-मान स्थिरांक उपस्तिथ है ऐसा है कि
के लिए जहाँ . हम कहते हैं यदि घातीय प्ररूप का है यदि कुछ घातीय प्ररूप का है. जो संख्या
का घातीय प्ररूप है. यहां श्रेष्ठ सीमा का कारण किसी दिए गए त्रिज्या के बाहर अनुपात के सर्वोच्च की सीमा है क्योंकि त्रिज्या अनंत तक जाती है। यह किसी दिए गए त्रिज्या पर अनुपात के अधिकतम से श्रेष्ठ सीमा भी है क्योंकि त्रिज्या अनंत तक जाती है। उच्चतम सीमा त्रिज्या पर अधिकतम होने पर भी उपस्तिथ हो सकती है जैसी कोई सीमा नहीं है अनंत तक जाता है. उदाहरण के लिए, फलन के लिए
का मान है
पर का प्रभुत्व है शब्द इसलिए हमारे पास स्पर्शोन्मुख अभिव्यक्तियाँ हैं:
और यह शून्य हो जाता है अनंत तक जाता है,[1] किन्तु फिर भी यह घातीय प्ररूप 1 का है, जैसा कि बिंदुओं को देखकर देखा जा सकता है.
सममित उत्तल पिंड के संबंध में घातीय प्ररूप
Stein (1957) ने कई सम्मिश्र चर के संपूर्ण फलन के लिए घातीय प्ररूप का सामान्यीकरण दिया है। मान लीजिए एक उत्तल समुच्चय, सघन तत्व और सममित उपसमुच्चय है. यह ज्ञात है कि हर ऐसे के लिए एक संबद्ध मानदंड है (गणित) उस गुण के साथ
दूसरे शब्दों में, में यूनिट बॉल है इसके संबंध में समुच्चय .
को ध्रुवीय समुच्चय कहा जाता है और यह उत्तल समुच्चय, सघन तत्व और सममित उपसमुच्चय भी है. इसके अतिरिक्त, हम लिख सकते हैं
हम विस्तार करते हैं से को द्वारा
एक संपूर्ण फलन का -सम्मिश्र चर को घातीय प्ररूप का कहा जाता है यदि प्रत्येक के लिए वहाँ एक वास्तविक-मान स्थिरांक उपस्तिथ है ऐसा है कि
सभी के लिए .
फ्रेचेट समष्टि
घातीय प्ररूप के फलनों का संग्रह मानदंड (गणित) के गणनीय वर्ग द्वारा प्रेरित टोपोलॉजिकल समष्टि द्वारा एक पूर्ण समष्टि, समान समष्टि, अर्थात् फ़्रेचेट समष्टि, बना सकता है
यह भी देखें
- पेली-वीनर प्रमेय
- पेली-वीनर समष्टि
संदर्भ
- ↑ In fact, even goes to zero at as goes to infinity.
- Stein, E.M. (1957), "Functions of exponential type", Ann. of Math., 2, 65: 582–592, doi:10.2307/1970066, JSTOR 1970066, MR 0085342