फेयरनेस (मशीन लर्निंग): Difference between revisions
m (added Category:Vigyan Ready using HotCat) |
m (7 revisions imported from alpha:फेयरनेस_(मशीन_लर्निंग)) |
(No difference)
| |
Latest revision as of 22:22, 18 December 2023
यंत्र अधिगम में निष्पक्षता यंत्र अधिगम प्रतिरूप के आधार पर स्वचालित निर्णय प्रक्रियाओं में कलनविधि पूर्वाग्रह को सही करने के विभिन्न प्रयासों को संदर्भित करता है। यंत्र अधिगम प्रक्रिया के बाद कंप्यूटर द्वारा लिए गए निर्णय अनुचित माने जा सकते हैं यदि वे संवेदनशील माने जाने वाले चर पर आधारित है। इस प्रकार के चर के उदाहरणों में लिंग, जातीयता, लैंगिक अभिविन्यास, विकलांगता और बहुत कुछ सम्मिलित हैं। जैसा कि कई नैतिक अवधारणाओं का प्रकरण है, निष्पक्षता और पूर्वाग्रह की परिभाषाएँ हमेशा विवादास्पद होती हैं। सामान्य रूप में, निष्पक्षता और पूर्वाग्रह तब प्रासंगिक माने जाते हैं जब निर्णय प्रक्रिया लोगों के जीवन को प्रभावित करती है। यंत्र अधिगम में, कलनविधि पूर्वाग्रह की समस्या सर्वविदित है और इसका अच्छी तरह से अध्ययन किया गया है। कई कारकों के कारण परिणाम विषम हो सकते हैं और इस प्रकार इन्हें कुछ समूहों या व्यक्तियों के संबंध में अनुचित माना जा सकता है। इसका एक उदाहरण प्रकार होगा जिससे सामाजिक मीडिया साइटें उपभोक्ताओं को वैयक्तिकृत समाचार प्रदान करती हैं।
सन्दर्भ
यंत्र अधिगम में निष्पक्षता के बारे में परिचर्चा अपेक्षाकृत आधुनिक विषय है। 2016 के बाद से इस विषय पर अनुसंधान में तेजी से वृद्धि हुई है।[1] इस वृद्धि को आंशिक रूप से प्रोपब्लिका की एक प्रभावशाली प्रतिवेदन के कारण माना जा सकता है जिसमें दावा किया गया था कि कॉम्पास (सॉफ़्टवेयर) सॉफ़्टवेयर, जिसका व्यापक रूप से अमेरिकी अदालतों में पुनरावृत्ति की भविष्यवाणी करने के लिए उपयोग किया जाता था, जातीयता के आधार पर पक्षपाती था।[2] अनुसंधान और परिचर्चा का एक विषय निष्पक्षता की परिभाषा है, क्योंकि इसकी कोई सार्वभौमिक परिभाषा नहीं है, और विभिन्न परिभाषाएँ एक-दूसरे के साथ विरोधाभास में हो सकती हैं, जिससे यंत्र अधिगम प्रतिरूप का न्याय करना कठिन हो सकता है।[3] अन्य अनुसंधान विषयों में पूर्वाग्रह की उत्पत्ति, पूर्वाग्रह के प्रकार और पूर्वाग्रह को कम करने के प्रकार सम्मिलित हैं।[4]
आधुनिक वर्षों में तकनीकी कंपनियों ने यंत्र अधिगम में पूर्वाग्रह का पता लगाने और उसे कम करने के प्रकार पर उपकरण और नियमावली बनाते हैं। आईबीएम के पास सॉफ्टवेयर पूर्वाग्रह को कम करने और इसकी निष्पक्षता बढ़ाने के लिए कई कलनविधि के साथ पायथन (प्रोग्रामिंग भाषा) और R (प्रोग्रामिंग भाषा) के लिए उपकरण हैं।[5][6] गूगल ने यंत्र अधिगम में पूर्वाग्रह का अध्ययन करने और उससे प्रतिरोध के लिए दिशानिर्देश और उपकरण प्रकाशित किए हैं।[7][8] फेसबुक ने अपनी एआई में पूर्वाग्रह का पता लगाने के लिए एक टूल, निष्पक्षता प्रवाह के उपयोग की सूचना दी है।[9] हालाँकि, आलोचकों ने तर्क दिया है कि कंपनी के प्रयास अपर्याप्त हैं, कर्मचारियों द्वारा टूल के बहुत कम उपयोग की सूचना दी गई है क्योंकि इसका उपयोग उनके सभी कार्यक्रमों के लिए नहीं किया जा सकता है और जब यह संभव हो, तब भी उपकरण का उपयोग वैकल्पिक है।[10]
यह ध्यान रखना महत्वपूर्ण है कि निर्णय लेने में निष्पक्षता और अन्यायपूर्ण भेदभाव का परीक्षण करने के मात्रात्मक प्रकार के बारे में परिचर्चा यंत्र अधिगम में निष्पक्षता पर आधुनिक तर्क वितर्क से कई दशकों पहले हुई थी।[11] वास्तव में, वैज्ञानिक समुदाय द्वारा इस विषय पर एक सजीव परिचर्चा 1960 और 1970 के दशक के मध्य में उन्नतिशील, जो ज्यादातर अमेरिकी नागरिक अधिकार आंदोलन और विशेष रूप से, 1964 के अमेरिकी नागरिक अधिकार अधिनियम के अनुच्छेद परिणामस्वरूप हुई है। हालाँकि, 1970 के दशक के अंत तक, तर्क वितर्क व्यापक रुप से लुप्त हो गए, क्योंकि निष्पक्षता की अलग-अलग और कभी-कभी प्रतिस्पर्धी धारणाओं ने स्पष्टता के लिए बहुत कम जगह छोड़ी कि कब निष्पक्षता की एक धारणा दूसरे के लिए श्रेष्ठ हो सकती है।
विवाद
कानूनी प्रणाली में कलनविधि निर्णय लेने का उपयोग अनुसंधान के अंतर्गत उपयोग का एक उल्लेखनीय क्षेत्र रहा है। 2014 में, तत्कालीन संयुक्त राज्य अमेरिका के अटॉर्नी सार्वजनिक एरिक होल्डर ने चिंता जताई कि "जोखिम निर्धारण" के प्रकार उन कारकों पर अनुचित ध्यान केंद्रित कर सकते हैं जो प्रतिवादी के नियंत्रण में नहीं हैं, जैसे कि उनकी शिक्षा का स्तर या सामाजिक-आर्थिक पृष्ठभूमि हैं।[12] कम्पास (सॉफ्टवेयर) पर प्रोपब्लिका की 2016 की प्रतिवेदन में दावा किया गया है कि काले प्रतिवादियों को सफेद प्रतिवादियों की तुलना में गलत प्रकार से उच्च जोखिम के रूप में लेबल किए जाने की संभावना लगभग दोगुनी थी, जबकि सफेद प्रतिवादियों के साथ विपरीत गलती हुई थी।[2] कम्पास (सॉफ्टवेयर) के निर्माता, नॉर्थपॉइंट इंक ने प्रतिवेदन का खंडन करते हुए दावा किया कि उनका उपकरण निष्पक्ष है और प्रोपब्लिका ने सांख्यिकीय त्रुटियां की हैं,[13] जिसे बाद में प्रोपब्लिका द्वारा फिर से खंडन कर दिया गया हैं।[14]
प्रतिबिंब पहचान कलनविधि में प्रजातीय और लिंग पूर्वाग्रह भी विख्यात किया गया है। कैमरों में चेहरे और गतिविधि का पता लगाने से गैर-श्वेत विषयों के चेहरे के भावों को अनदेखा या गलत लेबल करना पाया गया है।[15] 2015 में, फ़्लिकर और गूगल फ़ोटो दोनों में स्वचालित टैगिंग सुविधा काले लोगों को "जानवर" और "गोरिल्ला" जैसे टैग के साथ लेबल करने के लिए पाई गई थी।[16] एआई कलनविधि द्वारा निर्णय ली गई 2016 की एक अंतर्राष्ट्रीय सौंदर्य प्रतियोगिता को हल्की त्वचा वाले व्यक्तियों के प्रति पक्षपाती पाया गया, संभवतः प्रशिक्षण डेटा में पूर्वाग्रह के कारण पाया गया है। [17] 2018 में तीन व्यावसायिक लिंग वर्गीकरण कलनविधि के एक अध्ययन में पाया गया कि सभी तीन कलनविधि सामान्यतः गोरी त्वचा वाले पुरुषों को वर्गीकृत करते समय सबसे यथार्थ थे और गहरे रंग की महिलाओं को वर्गीकृत करते समय सबसे निकृष्टतम थे।[18] 2020 में, ट्विटर के एक प्रतिबिंब क्रॉपिंग टूल में पतले त्वचा वाले चेहरों को प्राथमिकता देते हुए दिखाया गया था।[19] DALL-E, एक यंत्र अधिगम टेक्स्ट-टू-प्रतिबिंब प्रतिरूप, जिसे 2021 में जारी किया गया था, जातिवादी और लिंग भेद प्रतिबिंब बनाने के लिए प्रवृत्त रहा है जो सामाजिक रूढ़िवादिता को मजबूत करता है, जिसे इसके रचनाकारों ने स्वीकार किया है।[20]
अन्य क्षेत्र जहां यंत्र अधिगम कलनविधि का उपयोग किया जाता है, उन्हें पक्षपातपूर्ण दिखाया गया है, उनमें नौकरी और ऋण आवेदन सम्मिलित हैं। अमेज़ॅन (कंपनी) ने ऐसे नौकरी आवेदनों की समीक्षा करने के लिए सॉफ़्टवेयर का उपयोग किया है जो लैंगिक भेदभाव वाले थे, उदाहरण के लिए उन बायोडाटा को दंडित करके जिनमें महिला शब्द सम्मिलित था।[21] 2019 में, अपने नए एप्पल कार्ड के लिए क्रेडिट कार्ड की सीमा निर्धारित करने के लिए ऐप्पल इंक के कलनविधि ने महिलाओं की तुलना में पुरुषों को बहुत अधिक सीमाएं दीं हैं, यहां तक कि उन जोड़ों के लिए भी जो अपने वित्त को साझा करते हैं।[22] 2021 में द मार्कअप की एक प्रतिवेदन के अनुसार अमेरिका में उपयोग में आने वाले बंधक-अनुमोदन कलनविधि में गैर-श्वेत आवेदकों को अस्वीकार करने की अधिक संभावना दिखाई गई है।[23]
सीमाएँ
आधुनिक कार्य यंत्र अधिगम में निष्पक्षता के वर्तमान परिदृश्य में कई सीमाओं की उपस्थिति को रेखांकित करते हैं, विशेष रुप से जब बात आती है कि एआई के लगातार बढ़ते वास्तविक दुनिया अनुप्रयोगों में इस संबंध में वास्तविक रूप से क्या प्राप्त किया जा सकता है। [24][25] उदाहरण के लिए, निष्पक्षता को औपचारिक बनाने के लिए गणितीय और मात्रात्मक दृष्टिकोण, और संबंधित "डी-बायसिंग" दृष्टिकोण, बहुत सरल और आसानी से उपेक्षित की जाने वाली धारणाओं पर भरोसा किया जा सकता है, जैसे कि व्यक्तियों को पूर्व-परिभाषित सामाजिक समूहों में वर्गीकृत करना है। अन्य कमज़ोर पहलू हैं, उदाहरण के लिए, कई उचित विशेषताओं के मध्य परस्पर क्रिया,[18]और गैर-भेदभाव की स्पष्ट और साझा दार्शनिक और/या कानूनी धारणा का अभाव है।
समूह निष्पक्षता मानदंड
वर्गीकरण समस्याओं में, एक कलनविधि ज्ञात विशेषताओं से एक अलग विशेषता , लक्ष्य चर की भविष्यवाणी करने के लिए एक फलन सीखता है। हम को एक अलग यादृच्छिक चर के रूप में प्रतिरूप करते हैं जो में निहित या अंतर्निहित रूप से कूटलिखित की गई कुछ विशेषताओं को कूटलेखन करना है जिन्हें हम संवेदनशील विशेषताओं (लिंग, जातीयता, लैंगिक अभिविन्यास, इत्यादि) के रूप में मानते हैं। हम अंततः वर्गीकरण की भविष्यवाणी को द्वारा निरूपित करते हैं। अब मूल्यांकन करने के लिए तीन मुख्य मानदंडों को परिभाषित करें कि क्या कोई दिया गया वर्गीकरण निष्पक्ष है, अर्थात् इसकी भविष्यवाणियां इनमें से कुछ संवेदनशील चर से प्रभावित नहीं हैं।[26]
स्वतंत्रता
हम कहते हैं कि यादृच्छिक चर स्वतंत्रता को संतुष्ट करते हैं यदि संवेदनशील विशेषताएं भविष्यवाणी से सांख्यिकीय रूप से स्वतंत्र हैं, और हम लिखते हैं
फिर भी स्वतंत्रता के लिए एक और समकक्ष अभिव्यक्ति यादृच्छिक चर के मध्य पारस्परिक जानकारी की अवधारणा का उपयोग करके दी जा सकती है, जिसे इस प्रकार परिभाषित किया गया है
स्वतंत्रता की परिभाषा में संभावित छूट (अनुमान) में एक धनात्मक स्लैक प्रस्तावित करना सम्मिलित है और सूत्र द्वारा दिया गया है:
पृथक्करण
हम कहते हैं कि यादृच्छिक चर पृथक्करण को संतुष्ट करते हैं यदि संवेदनशील विशेषताएं लक्ष्य मान दिए जाने पर भविष्यवाणी से सांख्यिकीय रूप से स्वतंत्र हैं, और हम लिखते है
द्विआधारी लक्ष्य दर के विषय में एक और समतुल्य अभिव्यक्ति यह है कि संवेदनशील विशेषताओं के प्रत्येक मूल्य के लिए यथार्त धनात्मक दर और मिथ्या धनात्मक दर समान होती है (और इसलिए आभासी धनात्मक दर और वास्तविक धनात्मक दर समान होती है):
कुछ क्षेत्रों में भ्रम आव्यूह में पृथक्करण (पृथक्करण गुणांक) अनुमानित संचयी प्रतिशत ऋणात्मक और अनुमानित संचयी प्रतिशत धनात्मक के मध्य की दूरी (संभावना अंक के दिए गए स्तर पर) का एक माप है।
किसी दिए गए अंक मान पर यह पृथक्करण गुणांक जितना अधिक होगा, प्रतिरूप एक विशेष प्रायिकता कट-ऑफ पर धनात्मक और ऋणात्मक के समुच्चय के मध्य अंतर करने में उतना ही अधिक प्रभावी होता है। मेयस के अनुसार:[27] "क्रेडिट उद्योग में प्रायः यह देखा जाता है कि यथार्तापन उपायों का चयन प्रतिरूपण दृष्टिकोण पर निर्भर करता है। उदाहरण के लिए, यदि प्रतिरूपण प्रक्रिया प्राचलिक या अर्ध-प्राचलिक है, तो दो-प्रतिदर्श K-S परीक्षण प्रायः उपयोग करते है। यदि प्रतिरूप अनुमानी या पुनरावृत्तीय खोज विधियों द्वारा प्राप्त किया गया है, तो प्रतिरूप प्रदर्शन का माप सामान्यतः अपसरण होता है। तीसरा विकल्प पृथक्करण का गुणांक है... अन्य दो प्रकार की तुलना में पृथक्करण का गुणांक, प्रतिरूप प्रदर्शन के माप के रूप में सबसे उचित प्रतीत होता है क्योंकि यह एक प्रतिरूप के पृथक्करण रूप को दर्शाता है।"
पर्याप्तता
हम कहते हैं कि यादृच्छिक चर पर्याप्तता को संतुष्ट करता हैं यदि संवेदनशील विशेषताएं भविष्यवाणी को देखते हुए लक्ष्य मूल्य से सांख्यिकीय रूप से स्वतंत्र हैं, और हम लिखते हैं
परिभाषाओं के मध्य संबंध
अंत में, हम कुछ मुख्य परिणामों का सारांश देते हैं जो ऊपर दी गई तीन परिभाषाओं से संबंधित हैं:
- यह मानते हुए कि द्विआधारी है, यदि और सांख्यिकीय रूप से स्वतंत्र नहीं हैं, और और भी सांख्यिकीय रूप से स्वतंत्र नहीं हैं, तो अलंकारिक प्रकरण को छोड़कर स्वतंत्रता और पृथक्करण दोनों सम्मिलित नहीं रह सकते हैं।
- यदि संयुक्त वितरण के रूप में के सभी संभावित मूल्यों के लिए धनात्मक प्रायिकता सिद्धांत है और और सांख्यिकीय रूप से स्वतंत्र नहीं हैं, तो अलंकारिक प्रकरण को छोड़कर पृथक्करण और पर्याप्तता दोनों सम्मिलित नहीं रह सकते हैं।
इसे पूर्ण निष्पक्षता कहा जाता है जब स्वतंत्रता, पृथक्करण और पर्याप्तता सभी एक साथ संतुष्ट होते हैं।[28] हालाँकि, विशिष्ट अलंकारिक प्रकरण के अलावा पूर्ण निष्पक्षता प्राप्त करना संभव नहीं है। [29]
समूह निष्पक्षता परिभाषाओं का गणितीय सूत्रीकरण
प्रारंभिक परिभाषाएँ
This section may require cleanup to meet Wikipedia's quality standards. The specific problem is: अनावश्यक और अत्यधिक विशिष्ट जानकारी, भ्रम आव्यूह लेख का लिंक इस उपधारा की अधिकांश विषय सूची के लिए पर्याप्त है. (नवंबर 2023) (Learn how and when to remove this template message) |
निष्पक्षता के अधिकांश सांख्यिकीय उपाय विभिन्न मापन विज्ञान पर निर्भर करते हैं, इसलिए हम उन्हें परिभाषित करके प्रारंभ करते हैं। द्विआधारी वर्गीकारक के साथ काम करते समय, अनुमानित और वास्तविक वर्ग दोनों दो मान ले सकते हैं: धनात्मक और ऋणात्मक। अब हम पूर्वानुमानित और वास्तविक परिणाम के मध्य विभिन्न संभावित संबंधों को समझाना प्रारंभ करें:[30]
- यथार्त धनात्मक (टीपी): वह प्रकरण जहां पूर्वानुमानित और वास्तविक परिणाम दोनों धनात्मक वर्ग में हैं।
- यथार्त ऋणात्मक (टीएन): वह प्रकरण जहां अनुमानित परिणाम और वास्तविक परिणाम दोनों को ऋणात्मक वर्ग को निर्दिष्ट किया गया है।
- मिथ्या धनात्मक (एफपी): जिस प्रकरण के वास्तविक परिणाम में निर्दिष्ट धनात्मक वर्ग में आने की भविष्यवाणी की गई है, वह ऋणात्मक है।
- मिथ्या ऋणात्मक (एफएन): जिस प्रकरण के ऋणात्मक वर्ग में होने की भविष्यवाणी की गई है, उसका वास्तविक परिणाम धनात्मक है।
इन संबंधों को आसानी से एक भ्रम आव्यूह के साथ दर्शाया जा सकता है, एक सूची जो वर्गीकरण प्रतिरूप की यथार्थता का वर्णन करती है। इस आव्यूह में, कॉलम और पंक्तियाँ क्रमशः अनुमानित और वास्तविक प्रकरण के उदाहरणों का प्रतिनिधित्व करती हैं।
इन संबंधों का उपयोग करके, हम कई मेट्रिक्स को परिभाषित कर सकते हैं जिनका उपयोग बाद में कलनविधि की निष्पक्षता को मापने के लिए किया जा सकता है:
- धनात्मक पूर्वानुमानित मूल्य (पीपीवी): धनात्मक प्रकरण का वह भिन्न जिसकी सभी धनात्मक भविष्यवाणियों में से सही भविष्यवाणी की गई थी। इसे सामान्यतः परिशुद्धता के रूप में जाना जाता है, और यह एक सही धनात्मक भविष्यवाणी की संभावना का प्रतिनिधित्व करता है। इसे निम्नलिखित सूत्र द्वारा दिया गया है:
- मिथ्या खोज दर (एफडीआर): धनात्मक भविष्यवाणियों का वह भिन्न जो वास्तव में सभी धनात्मक भविष्यवाणियों में से ऋणात्मक था। यह एक अशुद्ध धनात्मक भविष्यवाणी की संभावना का प्रतिनिधित्व करता है, और इसे निम्नलिखित सूत्र द्वारा दिया गया है:
- ऋणात्मक अनुमानित मूल्य (एनपीवी): ऋणात्मक प्रकरण का वह भिन्न जिसकी सभी ऋणात्मक भविष्यवाणियों में से सही भविष्यवाणी की गई थी। यह एक सही ऋणात्मक भविष्यवाणी की संभावना का प्रतिनिधित्व करता है, और इसे निम्नलिखित सूत्र द्वारा दिया गया है:
- मिथ्या लोप दर (FOR): ऋणात्मक भविष्यवाणियों का वह भिन्न जो वास्तव में सभी ऋणात्मक भविष्यवाणियों में से धनात्मक है। यह एक मिथ्या ऋणात्मक भविष्यवाणी की संभावना का प्रतिनिधित्व करता है, और इसे निम्नलिखित सूत्र द्वारा दिया गया है:
- यथार्त धनात्मक दर (टीपीआर): सभी धनात्मक प्रकरण में से धनात्मक प्रकरण का वह भिन्न जिसकी सही भविष्यवाणी की गई थी। इसे सामान्यतः संवेदनशीलता या प्रत्याह्वान के रूप में संदर्भित किया जाता है, और यह धनात्मक विषयों को इस तरह सही प्रकार से र्गीकृत किए जाने की संभावना का प्रतिनिधित्व करता है। यह सूत्र द्वारा दिया गया है:
- मिथ्या ऋणात्मक दर (एफएनआर): धनात्मक प्रकरण का वह भिन्न जिसके सभी धनात्मक प्रकरण में से ऋणात्मक होने की गलत भविष्यवाणी की गई थी। यह धनात्मक विषयों को गलत प्रकार से ऋणात्मक के रूप में वर्गीकृत किए जाने की संभावना को दर्शाता है, और यह सूत्र द्वारा दिया गया है:
- यथार्त ऋणात्मक दर (टीएनआर): सभी ऋणात्मक प्रकरण में से ऋणात्मक प्रकरण का वह भिन्न जिसकी सही भविष्यवाणी की गई थी। यह ऋणात्मक विषयों को सही प्रकार से वर्गीकृत किए जाने की संभावना को दर्शाता है, और यह सूत्र द्वारा दिया गया है:
- मिथ्या धनात्मक दर (एफपीआर): ऋणात्मक प्रकरण का वह भिन्न जिसके सभी ऋणात्मक प्रकरण में से धनात्मक होने की गलत भविष्यवाणी की गई थी। यह ऋणात्मक विषयों को गलत प्रकार से धनात्मक के रूप में वर्गीकृत किए जाने की संभावना को दर्शाता है, और यह सूत्र द्वारा दिया गया है:
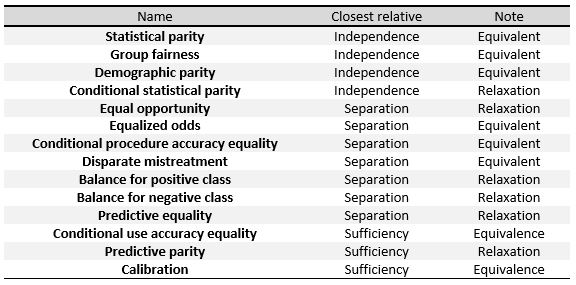
निम्नलिखित मानदंडों को इस खंड के आरंभ में दी गई तीन सामान्य परिभाषा, अर्थात् स्वतंत्रता, पृथक्करण और पर्याप्तता के उपायों के रूप में समझा जा सकता है।[26] दाईं ओर, हम उनके मध्य संबंध देख सकते हैं।
इन उपायों को विशेष रूप से परिभाषित करने के लिए, हम उन्हें तीन बड़े समूहों में विभाजित करेंगे जैसा कि वर्मा एट अल में किया गया है:[30] पूर्वानुमानित परिणाम पर आधारित परिभाषाएँ, पूर्वानुमानित और वास्तविक परिणामों पर, और पूर्वानुमानित संभावनाओं और वास्तविक परिणाम पर आधारित परिभाषाएँ है।
हम एक द्विआधारी वर्गीकारक और निम्नलिखित नोटेशन के साथ काम करेंगे: वर्गीकारक द्वारा दिए गए अंक को संदर्भित करता है, जो एक निश्चित विषय के धनात्मक या ऋणात्मक वर्ग में होने की संभावना है। कलनविधि द्वारा अनुमानित अंतिम वर्गीकरण का प्रतिनिधित्व करता है, और इसका मूल्य सामान्यतः से प्राप्त होता है, उदाहरण के लिए धनात्मक होगा जब एक निश्चित सीमा से ऊपर है। वास्तविक परिणाम का प्रतिनिधित्व करता है, अर्थात, व्यक्ति का वास्तविक वर्गीकरण और अंततः, विषयों की संवेदनशील विशेषताओं को दर्शाता है।
पूर्वानुमानित परिणाम पर आधारित परिभाषाएँ
इस खंड की परिभाषाएँ विषयों के विभिन्न वितरणों के लिए अनुमानित परिणाम पर ध्यान केंद्रित करता हैं। वे निष्पक्षता की सबसे सरल और सबसे सहज धारणाएँ हैं।
- जनसांख्यिकीय समता, जिसे सांख्यिकीय समता, स्वीकृति दर समता और बेंचमार्किंग भी कहा जाता है। एक वर्गीकारक इस परिभाषा को संतुष्ट करता है यदि संरक्षित और असंरक्षित समूहों के विषयों को धनात्मक पूर्वानुमानित वर्ग को नियुक्त के समान संभावना है। ऐसा तब होता है, जब निम्नलिखित सूत्र संतुष्ट होता है:
- सशर्त सांख्यिकीय समता, मूल रूप से उपरोक्त परिभाषा में सम्मिलित है, लेकिन केवल उदाहरणों के उपसमुच्चय तक ही सीमित है। गणितीय संकेतन में यह होगा:
पूर्वानुमानित और वास्तविक परिणामों पर आधारित परिभाषाएँ
ये परिभाषाएँ नहीं केवल पूर्वानुमानित परिणाम पर विचार करता हैं लेकिन इसकी तुलना वास्तविक परिणाम से भी होती हैं।
- पूर्वानुमानित समता, जिसे परिणाम परीक्षण भी कहा जाता है। यदि संरक्षित और असंरक्षित समूहों के विषयों में समान पीपीवी है तो एक वर्गीकारक इस परिभाषा को संतुष्ट करता है। ऐसा तब होता है, जब निम्नलिखित सूत्र संतुष्ट होता है:
- गणितीय रूप से, यदि किसी वर्गीकारक के पास दोनों समूहों के लिए समान पीपीवी है, तो उसके पास समान एफडीआर भी होगा, जो सूत्र को संतुष्ट करता है:
- मिथ्या धनात्मक त्रुटि दर संतुलन, जिसे पूर्वानुमानित समानता भी कहा जाता है। यदि संरक्षित और असंरक्षित समूहों के विषयों में समान एफपीआर है तो एक वर्गीकारक इस परिभाषा को संतुष्ट करता है। ऐसा तब होता है, जब निम्नलिखित सूत्र संतुष्ट होता है:
- गणितीय रूप से, यदि किसी वर्गीकारक में दोनों समूहों के लिए समान एफपीआर है, तो इसका टीएनआर भी समान होगा, जो सूत्र को संतुष्ट करता है:
- मिथ्या ऋणात्मक त्रुटि दर संतुलन, जिसे समान अवसर भी कहा जाता है। यदि संरक्षित और असंरक्षित समूहों में विषयों का एफएनआर समान है तो एक वर्गीकारक इस परिभाषा को संतुष्ट करता है। ऐसा तब होता है, जब निम्नलिखित सूत्र संतुष्ट होता है:
- गणितीय रूप से, यदि किसी वर्गीकारक के पास दोनों समूहों के लिए समान एफएनआर है, तो उसके पास समान टीपीआर भी होगा, जो सूत्र को संतुष्ट करता है:
- समान अंतर, जिसे सशर्त प्रक्रिया यथार्थता समानता और असमान दुर्व्यवहार भी कहा जाता है। एक वर्गीकारक इस परिभाषा को संतुष्ट करता है यदि संरक्षित और असंरक्षित समूहों के विषयों में समान टीपीआर और समान एफपीआर है, जो सूत्र को संतुष्ट करता है:
- सशर्त उपयोग यथार्थता समानता एक वर्गीकारक इस परिभाषा को संतुष्ट करता है यदि संरक्षित और असंरक्षित समूहों के विषयों में समान पीपीवी और समान एनपीवी है, जो सूत्र को संतुष्ट करता है:
- समग्र यथार्थता समानता एक वर्गीकारक इस परिभाषा को संतुष्ट करता है यदि संरक्षित और असंरक्षित समूहों में विषय की भविष्यवाणी यथार्थता समान है, अर्थात, एक वर्ग से किसी विषय को नियुक्त की संभावना है। यदि यह निम्नलिखित सूत्र को संतुष्ट करता है:
- अभिक्रिया समानता एक वर्गीकारक इस परिभाषा को संतुष्ट करता है यदि संरक्षित और असंरक्षित समूहों के विषयों में एफएन और एफपी का समान अनुपात है, जो सूत्र को संतुष्ट करता है:
पूर्वानुमानित संभावनाओं और वास्तविक परिणाम पर आधारित परिभाषाएँ
ये परिभाषाएँ वास्तविक परिणाम और अनुमानित प्रायिकता अंक पर आधारित हैं।
- परीक्षण-निष्पक्षता, जिसे अंशांकन या सशर्त आवृत्तियों के मिलान के रूप में भी जाना जाता है। एक वर्गीकारक इस परिभाषा को संतुष्ट करता है यदि समान पूर्वानुमानित प्रायिकता अंक वाले व्यक्तियों को धनात्मक वर्ग में वर्गीकृत होने के समान संभावना होती है जब वे संरक्षित या असंरक्षित समूह से संबंधित होते हैं:
- अनुकूल-अंशांकन पूर्व परिभाषा का विस्तार है। इसमें कहा गया है कि जब संरक्षित समूह के आंतरिक या बाहरी व्यक्तियों के पास समान पूर्वानुमानित प्रायिकता अंक होता है, तो उनके पास धनात्मक वर्ग में वर्गीकृत होने की समान संभावना होनी चाहिए, और यह प्रायिकता के समान होनी चाहिए:
- धनात्मक वर्ग के लिए संतुलन एक वर्गीकारक इस परिभाषा को संतुष्ट करता है यदि संरक्षित और असंरक्षित दोनों समूहों से धनात्मक वर्ग का गठन करने वाले विषयों का औसत अनुमानित प्रायिकता अंक समान है। इसका अर्थ यह है कि धनात्मक वास्तविक परिणाम के साथ संरक्षित और असंरक्षित समूहों के लिए प्रायिकता अंक का अपेक्षित मूल्य समान है, जो सूत्र को संतुष्ट करता है:
- ऋणात्मक वर्ग के लिए संतुलन एक वर्गीकारक इस परिभाषा को संतुष्ट करता है यदि संरक्षित और असंरक्षित दोनों समूहों के ऋणात्मक वर्ग का गठन करने वाले विषयों का औसत अनुमानित प्रायिकता अंक समान है। इसका अर्थ यह है कि ऋणात्मक वास्तविक परिणाम वाले संरक्षित और असंरक्षित समूहों के लिए प्रायिकता अंक का अपेक्षित मूल्य समान है, जो सूत्र को संतुष्ट करता है:
समान भ्रम निष्पक्षता
भ्रम आव्यूह के संबंध में, स्वतंत्रता, पृथक्करण और पर्याप्तता के लिए नीचे सूचीबद्ध संबंधित मात्राओं की आवश्यकता होती है ताकि संवेदनशील विशेषताओं में सांख्यिकीय रूप से महत्वपूर्ण अंतर नहीं है।
- स्वतंत्रता: (टीपी + एफपी) / (टीपी + एफपी + एफएन + टीएन) (अर्थात, )।
- पृथक्करण: टीएन / (टीएन + एफपी) और टीपी / (टीपी + एफएन) (अर्थात, विशिष्टता और याद करें )।
- पर्याप्तता: टीपी / (टीपी + एफपी) और टीएन / (टीएन + एफएन) (अर्थात, परिशुद्धता और ऋणात्मक पूर्वानुमानित मूल्य )।
समान भ्रम निष्पक्षता की धारणा[31] के लिए किसी दिए गए निर्णय प्रणाली के भ्रम आव्यूह को समान वितरण की आवश्यकता होती है, जब सभी संवेदनशील विशेषताओं पर स्तरीकृत गणना होती है।
समाज कल्याण कार्य
कुछ विद्वानों ने सामाजिक कल्याण कार्य के संदर्भ में कलनविधि निष्पक्षता को परिभाषित करने का प्रस्ताव दिया है। उनका तर्क है कि सामाजिक कल्याण फलन का उपयोग एक कलनविधि अभिकल्पक को कलनविधि से प्रभावित लोगों को उनके लाभों के संदर्भ में निष्पक्षता और पूर्वानुमान यथार्थता पर विचार करने में सक्षम बनाता है। यह डिजाइनर को सैद्धांतिक प्रकार से दक्षता और समता का आदान-प्रदान करने की भी अनुमति देता है।[32] सेंथिल मुलैनाथन ने कहा है कि कलनविधि अभिकल्पक को वंचित समूहों के लिए पूर्ण लाभ की पहचान करने के लिए सामाजिक कल्याण कार्यों का उपयोग करना चाहिए। उदाहरण के लिए, एक अध्ययन में पाया गया कि शुद्ध मानव निर्णय के बदले पूर्व परीक्षण सुधार में निर्णय लेने वाले कलनविधि का उपयोग करने से सुधार दर को स्थिर रखते हुए भी कुल मिलाकर अश्वेतों, हिस्पैनिक और नस्लीय अल्पसंख्यकों के लिए अपराध दर कम हो गई है।[33]
व्यक्तिगत निष्पक्षता मानदंड
निष्पक्षता परिभाषाओं के मध्य एक महत्वपूर्ण अंतर समूह और व्यक्तिगत धारणाओं के मध्य है।[34][35][30][36] स्थूलतः कहें तो, जबकि समूह निष्पक्षता मानदंड समूह स्तर पर मात्राओं की तुलना करते हैं, सामान्यतः संवेदनशील विशेषताओं (जैसे लिंग, जातीयता, आयु, आदि ...) द्वारा पहचाने जाते हैं, व्यक्तिगत मानदंड व्यक्तियों की तुलना करते हैं। शब्दों में, व्यक्तिगत निष्पक्षता इस सिद्धांत का अनुकरण करते है कि समान व्यक्तियों को समान अभिक्रिया प्राप्त होना चाहिए।
निष्पक्षता के लिए एक बहुत ही सहज दृष्टिकोण है, जिसे सामान्यतः अनभिज्ञता के माध्यम से निष्पक्षता (एफटीयू), या दृष्टिहीनता के नाम से जाना जाता है, जो (स्वचालित) निर्णय लेते समय स्पष्ट रूप से संवेदनशील विशेषताओं को स्पष्ट रूप से नियोजित नहीं करने का निर्देश देता है। यह प्रभावी रूप से व्यक्तिगत निष्पक्षता की धारणा है, क्योंकि दो व्यक्ति केवल अपनी संवेदनशील विशेषताओं के मूल्य के लिए भिन्न होते हैं, उन्हें एक ही परिणाम प्राप्त होता है।
हालाँकि, सामान्य रूप में, एफटीयू में कई कमियाँ हैं, मुख्य बात यह है कि यह निर्णय लेने की प्रक्रिया में नियोजित संवेदनशील विशेषताओं और गैर-संवेदनशील विशेषताओं के मध्य संभावित सहसंबंधों को ध्यान में नहीं रखता है। उदाहरण के लिए, लिंग के आधार पर भेदभाव करने के (घातक) अभिप्राय एक कर्ता प्रतिरूप में लिंग के लिए एक प्रतिनिधि चर प्रस्तावित कर सकता है (अर्थात लिंग के साथ अत्यधिक सहसंबंधित चर) और एफटीयू औषधयोजन के अनुरूप होने के साथ-साथ लिंग संबंधी जानकारी का प्रभावकारी रूप से उपयोग कर सकता है।
संवेदनशील चर से संबंधित कौन से चर निर्णय लेने की प्रक्रिया में एक प्रतिरूप द्वारा पूरी तरह से रोजगार योग्य हैं, यह समस्या एक महत्वपूर्ण, और समूह अवधारणाओं के लिए भी प्रासंगिक है: स्वतंत्रता मेट्रिक्स के लिए संवेदनशील जानकारी को पूरी तरह से अलग करने की आवश्यकता होती है, जबकि पृथक्करण-आधारित मेट्रिक्स सहसंबंध की अनुमति देते हैं, लेकिन केवल तब तक जहां तक लेबल किए गए लक्ष्य चर उन्हें "उचित" ठहराते हैं।
व्यक्तिगत निष्पक्षता की सबसे सामान्य अवधारणा को 2012 में सिंथिया डवर्क और सहयोगियों द्वारा अग्रणी कार्य में प्रस्तावित किया गया था[37] और इसे इस सिद्धांत के गणितीय अनुवाद के रूप में सोचा जा सकता है कि निवेश के रूप में सुविधाओं को इस तरह बनाया जाना चाहिए कि यह "समान व्यक्तियों को समान रूप से मानचित्रित करें", जिसे प्रतिरूप मानचित्र पर लिप्सचिट्ज़ निरंतरता के रूप में व्यक्त किया गया है। वे इस दृष्टिकोण को जानकारी के माध्यम से निष्पक्षता (एफटीए) कहते हैं, जो कि एफटीयू के विपरीत है, क्योंकि वे यह आकलन करने के लिए उपयुक्त लक्ष्य-संबंधित दूरी मीट्रिक चयन करने के महत्व को रेखांकित करते हैं कि कौन से व्यक्ति विशिष्ट परिस्थितियों में समान हैं। फिर, यह समस्या ऊपर उठाए गए बिंदु से बहुत संबंधित है कि विशेष संदर्भों में किन चरों को "उचित" रूप में देखा जा सकता है।
कार्य-कारण-आधारित मेट्रिक्स
कारण निष्पक्षता उस आवृत्ति को मापती है जिसके साथ दो लगभग समान उपयोगकर्ता या अनुप्रयोग जो केवल विशेषताओं के एक समुच्चय में भिन्न होते हैं जिसके संबंध में संसाधन आवंटन उचित होना चाहिए, समान अभिक्रिया प्राप्त करते हैं।[38][dubious ]
निष्पक्षता मेट्रिक्स पर अकादमिक अनुसंधान की एक पूरी शाखा यंत्र अधिगम प्रतिरूप में पूर्वाग्रह का आकलन करने के लिए कारण प्रतिरूप का लाभ उठाने के लिए समर्पित है। यह दृष्टिकोण सामान्यतः इस तथ्य से उचित है कि डेटा का एक ही अवलोकन वितरण खेल में चर के मध्य अलग-अलग कारण संबंधों को गुप्त रखता है, संभवतः अलग-अलग व्याख्याओं के साथ कि परिणाम किसी प्रकार के पूर्वाग्रह से प्रभावित होते हैं या नहीं होते हैं।[26]
कुस्नर एट अल.[39] प्रतितथ्यात्मक को नियोजित करने का प्रस्ताव, और निर्णय लेने की प्रक्रिया को प्रतितथ्यात्मक रूप से निष्पक्ष रूप से परिभाषित करते है, यदि किसी भी व्यक्ति के लिए, प्रतितथ्यात्मक परिदृश्य में परिणाम नहीं बदलता है जहां संवेदनशील गुण बदल जाता हैं। गणितीय सूत्रीकरण पढ़ता है:
अर्थात्: संवेदनशील विशेषता और अन्य विशेषताओं के साथ एक यादृच्छिक व्यक्ति लिया गया और उसी व्यक्ति के पास यदि है, तो उन्हें स्वीकार किए जाने की समान संभावना होनी चाहिए। प्रतीक उस परिदृश्य में प्रतितथ्यात्मक यादृच्छिक चर का प्रतिनिधित्व करता है जहां संवेदनशील विशेषता को पर तय किया गया है। पर प्रतिबंधन का अर्थ है कि यह आवश्यकता व्यक्तिगत स्तर पर है, जिसमें हम एक ही अवलोकन की पहचान करने वाले सभी चर पर प्रतिबंधन कर रहे हैं।
यंत्र अधिगम प्रतिरूप को प्रायः डेटा पर प्रशिक्षित किया जाता है जहां परिणाम उस समय लिए गए निर्णय पर निर्भर करता है।[40] उदाहरण के लिए, यदि यंत्र अधिगम प्रतिरूप को यह निर्धारित करना है कि क्या कोई कैदी दोबारा अपराध करेगा या नहीं और यह निर्धारित करेगा कि क्या कैदी को जल्दी विमुक्त किया जाना चाहिए, तो परिणाम इस पर निर्भर हो सकता है कि कैदी को जल्दी विमुक्त किया गया था या नहीं किया गया था। मिशलर एट अल.[41] प्रतितथ्यात्मक समान बाधाओं के लिए एक सूत्र प्रस्तावित करता है:
जहां एक यादृच्छिक चर है, उस परिणाम को दर्शाता है जो निर्णय लिया गया था, और एक संवेदनशील विशेषता हैं।
प्लेको और बरेइनबोइम[42] निष्पक्षता के कारणात्मक विश्लेषण से समझौते के लिए एक एकीकृत संरचना का प्रस्ताव हैं। वे एक मानक निष्पक्षता प्रतिरूप के उपयोग का सुझाव देते हैं, जिसमें 4 प्रकार के चर के साथ एक कारण आरेख सम्मिलित है:
- संवेदनशील गुण (),
- लक्ष्य चर (),
- और के मध्य मध्यस्थ (), परिणाम पर संवेदनशील विशेषताओं के संभावित अप्रत्यक्ष प्रभावों का प्रतिनिधित्व करता हैं,
- चर संभवतः () के साथ एक सामान्य कारण साझा करते हैं, जो परिणाम पर संवेदनशील विशेषताओं के संभावित मिथ्या (अर्थात, गैर-कारण) प्रभावों का प्रतिनिधित्व करते है।
इस रूपरेखा के अंतर्गत, प्लेको और बरेइनबोइम[42] उन संभावित प्रभावों को वर्गीकृत करने में सक्षम हैं जो संवेदनशील विशेषताओं के परिणाम पर हो सकते हैं। इसके अलावा, वह ग्रैन्युलैरिटी जिस पर इन प्रभावों को मापा जाता है - अर्थात्, प्रभाव को औसत करने के लिए उपयोग किए जाने वाले प्रतिबंधन चर - निष्पक्षता मूल्यांकन के "व्यक्तिगत बनाम समूह" दृष्टिकोण से सीधे जुड़े हुए हैं।
पूर्वाग्रह न्यूनीकरण योजना
यंत्र अधिगम कलनविधि पर निष्पक्षता को तीन अलग-अलग प्रकार से उपयोजित किया जा सकता है: डेटा पूर्वसंस्करण, सॉफ्टवेयर प्रशिक्षण के समय गणितीय अनुकूलन, या कलनविधि के प्रसंस्करण के बाद परिणाम से उपयोजित किया जा सकता है।
पूर्वसंस्करण
सामान्यतः, वर्गीकारक ही एकमात्र समस्या नहीं है; डाटासमुच्चय भी पक्षपाती हैं। समूह के संबंध में डेटासमुच्चय का भेदभाव निम्नानुसार परिभाषित किया जा सकता है:
पूर्वसंस्करण में पूर्वाग्रह को सही करने वाले कलनविधि डेटासमुच्चय चर के बारे में जानकारी अलग कर देते हैं जिसके परिणामस्वरूप अनुचित निर्णय हो सकते हैं, जबकि जितना संभव हो उतना कम बदलाव करने का प्रयत्न किया जाता है। यह केवल संवेदनशील चर को अलग करने जितना आसान नहीं है, क्योंकि अन्य विशेषताओं को संरक्षित चर से सहसंबद्ध किया जा सकता है।
ऐसा करने का एक प्रकार प्रारंभिक डेटासमुच्चय में प्रत्येक व्यक्ति को एक मध्यवर्ती प्रतिनिधित्व के लिए मानचित्र करना है जिसमें यथासंभव अधिक जानकारी बनाए रखते हुए यह पहचानना असंभव है कि यह किसी विशेष संरक्षित समूह से संबंधित है या नहीं है। फिर, कलनविधि में अधिकतम यथार्थता प्राप्त करने के लिए डेटा के नए प्रतिनिधित्व को समायोजित किया जाता है।
इस तरह, व्यक्तियों को एक नए बहुपरिवर्तनीय प्रतिनिधित्व में मानचित्र किया जाता है जहां संरक्षित समूह के किसी भी सदस्य को नए प्रतिनिधित्व में एक निश्चित मूल्य पर मानचित्र किए जाने की संभावना उस व्यक्ति की संभावना के समान होती है जो संरक्षित समूह से संबंधित नहीं है। फिर, प्रारंभिक डेटा के बदले, इस प्रतिनिधित्व का उपयोग व्यक्ति के लिए भविष्यवाणी प्राप्त करने के लिए किया जाता है। मध्यवर्ती प्रतिनिधित्व का निर्माण संरक्षित समूह के आंतरिक या बाहरी के व्यक्तियों को समान संभावना देते हुए किया गया है, इसलिए यह विशेषता वर्गीकरणकर्ता के लिए गुप्त है।
ज़ेमेल एट अल में एक उदाहरण समझाया गया है।[43] जहां एक बहुपद यादृच्छिक चर का उपयोग मध्यवर्ती प्रतिनिधित्व के रूप में किया जाता है। इस प्रक्रिया में, व्यवस्था को उन सूचनाओं को छोड़कर सभी सूचनाओं को संरक्षित करने के लिए प्रोत्साहित किया जाता है जो पक्षपातपूर्ण निर्णय ले सकती हैं, और यथासंभव यथार्थ भविष्यवाणी प्राप्त करने के लिए प्रोत्साहित हो सकती हैं।
एक ओर, इस प्रक्रिया का लाभ यह है कि पूर्व-संसाधित डेटा का उपयोग किसी भी यंत्र अधिगम कार्य के लिए किया जा सकता है। इसके अलावा, वर्गीकारक को संशोधित करने की आवश्यकता नहीं है, क्योंकि प्रसंस्करण से पहले सुधार को डेटा समुच्चय पर उपयोजित किया जाता है। दूसरी ओर, अन्य विधियाँ यथार्थता और निष्पक्षता में श्रेष्ठतर परिणाम प्राप्त करती हैं।[44]
पुनःभारण
पुनःभारण करना पूर्वसंस्करण कलनविधि का एक उदाहरण है। विचार यह है कि प्रत्येक डेटासमुच्चय बिंदु को एक भार दिया जाए ताकि निर्दिष्ट समूह के संबंध में भारित भेदभाव 0 हैं।[45]
यदि डेटासमुच्चय निष्पक्ष था तो संवेदनशील चर और लक्ष्य चर सांख्यिकीय रूप से स्वतंत्र हैं और संयुक्त वितरण की संभावना निम्नानुसार संभावनाओं का उत्पाद होगा:
प्रसंस्करण में
दूसरा प्रकार प्रशिक्षण के समय पूर्वाग्रह को सही करना है। यह कलनविधि के अनुकूलन उद्देश्य में बाधाएँ जोड़कर किया जा सकता है।[46] ये बाधाएं कलनविधि को संरक्षित समूह और अन्य व्यक्तियों के लिए कुछ उपायों की समान दरें रखकर, निष्पक्षता में सुधार करने के लिए बलपूर्वक हैं। उदाहरण के लिए, हम कलनविधि के उद्देश्य में यह प्रतिबंध जोड़ सकते हैं कि मिथ्या धनात्मक दर संरक्षित समूह के व्यक्तियों और संरक्षित समूह के बाहर के व्यक्तियों के लिए समान है।
इस दृष्टिकोण में उपयोग किए जाने वाले मुख्य उपाय मिथ्या धनात्मक दर, गलत ऋणात्मक दर और समग्र गलत वर्गीकरण दर हैं। कलनविधि के उद्देश्य में इनमें से केवल एक या कई बाधाओं को जोड़ना संभव है। ध्यान दें कि गलत ऋणात्मक दरों की समानता का तात्पर्य वास्तविक धनात्मक दरों की समानता से है, इसलिए इसका तात्पर्य अवसर की समानता से है। प्रतिबंध जोड़ने के बाद समस्या प्रचण्ड हो सकती है, इसलिए उन पर छूट की आवश्यकता हो सकती है।
यह तकनीक उच्च यथार्थता बनाए रखते हुए निष्पक्षता में सुधार लाने में अच्छे परिणाम प्राप्त करती है और प्रोग्रामर को सुधार के लिए निष्पक्षता उपायों को चयन करने की सुविधा देती है। हालाँकि, प्रत्येक यंत्र अधिगम कार्य को उपयोजित करने के लिए एक अलग विधि की आवश्यकता हो सकती है और वर्गीकारक में कोड को संशोधित करने की आवश्यकता होती है, जो हमेशा संभव नहीं होती है।[44]
विरोधात्मक तर्क वितर्क
हम कुछ प्रवणता-आधारित विधि (जैसे: प्रवणता अवरोहण) के माध्यम से एक ही समय में दो सांख्यिकीय को प्रशिक्षित करते हैं। पहला, भविष्यवक्ता कुछ हानि फलन को कम करने के लिए अपने भार को संशोधित करके, निवेश दिए गए लक्ष्य चर की भविष्यवाणी करने का कार्य पूरा करने का प्रयास करता है। दूसरा, प्रतिद्वंद्वी कुछ हानि फलन को कम करने के लिए अपने भार को संशोधित करके दिए गए संवेदनशील चर की भविष्यवाणी करने का कार्य पूरा करने का प्रयास करता है।[47][48]
यहां एक महत्वपूर्ण बिंदु यह है कि, सही प्रकार से प्रचारित करने के लिए, उपरोक्त को वर्गीकारक के असंसाधित निर्गत को संदर्भित करना चाहिए, असतत भविष्यवाणी नहीं; उदाहरण के लिए, एक कृत्रिम तंत्रिका नेटवर्क और एक वर्गीकरण समस्या के साथ, सॉफ्टमैक्स स्तर के निर्गत को संदर्भित कर सकता है।
फिर हम प्रवणता के अनुसार प्रत्येक प्रशिक्षण स्तर में को कम करने के लिए को अद्यनीकृत करते हैं और हम अभिव्यक्ति के अनुसार को संशोधित करते हैं:
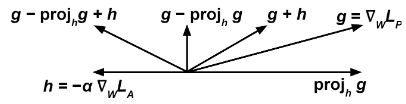
सहज विचार यह है कि हम चाहते हैं कि भविष्यवक्ता को कम करने का प्रयास करे (इसलिए शब्द , जबकि, एक ही समय में, को अधिकतम करें (इसलिए शब्द ), ताकि प्रतिद्वंद्वी से संवेदनशील चर की भविष्यवाणी करने में विफल है)।
शब्द भविष्यवक्ता को उस दिशा में जाने से रोकता है जो प्रतिद्वंद्वी को उसके ह्रास के फलन को कम करने में सहायता करता है।
यह दिखाया जा सकता है कि इस कलनविधि के साथ एक भविष्यवक्ता वर्गीकरण प्रतिरूप को प्रशिक्षित करने से प्रतिद्वंद्वी के बिना इसे प्रशिक्षित करने के संबंध में जनसांख्यिकीय समानता में सुधार होता है।
पश्चप्रसंस्करण
अंतिम विधि निष्पक्षता प्राप्त करने के लिए वर्गीकारक के परिणामों को सही करने का प्रयास करती है। इस पद्धति में, हमारे पास एक वर्गीकारक है जो प्रत्येक व्यक्ति के लिए एक अंक लौटाता है और हमें उनके लिए एक द्विआधारी भविष्यवाणी करने की आवश्यकता होती है। उच्च अंक प्राप्त करने पर धनात्मक परिणाम मिलने की संभावना है, जबकि कम अंक प्राप्त करने पर ऋणात्मक परिणाम मिलने की संभावना है, लेकिन हम इच्छानुसार हाँ में उत्तर कब देना है यह निर्धारित करने के लिए सीमा को समायोजित कर सकते हैं। ध्यान दें कि सीमा मूल्य में भिन्नता वास्तविक धनात्मक और वास्तविक ऋणात्मक दरों के मध्य व्यापार-बंद को प्रभावित करता है।
यदि अंक फलन इस अर्थ में उचित है कि यह संरक्षित विशेषता से स्वतंत्र है, तो सीमा का कोई भी विकल्प उचित होगा, लेकिन इस प्रकार के वर्गीकारक पक्षपातपूर्ण होते हैं, इसलिए निष्पक्षता प्राप्त करने के लिए प्रत्येक संरक्षित समूह के लिए एक अलग सीमा की आवश्यकता हो सकती है। [49]ऐसा करने का एक प्रकार विभिन्न प्रभावसीमा विन्यास (इसे आरओसी वक्र कहा जाता है) पर मिथ्या ऋणात्मक दर के विरुद्ध वास्तविक धनात्मक दर की आलेखन रचना है और एक सीमा खोजें जहां संरक्षित समूह और अन्य व्यक्तियों के लिए दरें समान हैं।[49]
पश्चप्रसंस्करण के लाभ में यह सम्मिलित है कि तकनीक को किसी भी वर्गीकारक के बाद बिना संशोधित किए उपयोजित किया जा सकता है, और निष्पक्षता उपायों में इसका प्रदर्शन अच्छा है। विपक्ष में परीक्षण के समय संरक्षित विशेषता तक पहुंचने की आवश्यकता और यथार्थता और निष्पक्षता के मध्य संतुलन में विकल्प की कमी सम्मिलित है।[44]
विकल्प आधारित वर्गीकरण को अस्वीकार करें
एक वर्गीकारक को देखते हुए मान लीजिए कि वर्गीकारक द्वारा गणना की जाने वाली प्रायिकता है, इस प्रायिकता के रूप में कि उदाहरण धनात्मक वर्ग + से संबंधित है। जब 1 या 0 के पास है, तो उदाहरण को क्रमशः वर्ग + या - से संबंधित उच्च निश्चितता के साथ निर्दिष्ट किया जाता है। हालाँकि, जब 0.5 के पास होता है तो वर्गीकरण अधिक अस्पष्ट होता है।[50]
हम कहते हैं कि एक "अस्वीकृत उदाहरण" है यदि एक निश्चित के साथ ऐसा है कि है।
"आरओसी" के कलनविधि में उपरोक्त नियम का पालन करते हुए गैर-अस्वीकृत उदाहरणों और अस्वीकृत उदाहरणों को निम्नानुसार वर्गीकृत करना सम्मिलित है: यदि उदाहरण वंचित समूह () का उदाहरण है तो इसे धनात्मक के रूप में लेबल करें, अन्यथा, इसे ऋणात्मक के रूप में लेबल करते है।
हम प्रत्येक समस्या के लिए इष्टतम खोजने और विशेषाधिकार प्राप्त समूह के विरूद्व भेदभावपूर्ण बनने से बचने के लिए के फलानो के रूप में भेदभाव के विभिन्न उपायों (लिंक) को अनुकूलित कर सकते हैं।[50]
यह भी देखें
- कलनविधि पूर्वाग्रह
- यंत्र अधिगम
संदर्भ
- ↑ Caton, Simon; Haas, Christian (2020-10-04). "Fairness in Machine Learning: A Survey". arXiv:2010.04053 [cs.LG].
- ↑ 2.0 2.1 Mattu, Julia Angwin,Jeff Larson,Lauren Kirchner,Surya. "मशीन पूर्वाग्रह". ProPublica (in English). Retrieved 2022-04-16.
{{cite web}}: CS1 maint: multiple names: authors list (link) - ↑ Friedler, Sorelle A.; Scheidegger, Carlos; Venkatasubramanian, Suresh (April 2021). "The (Im)possibility of fairness: different value systems require different mechanisms for fair decision making". Communications of the ACM (in English). 64 (4): 136–143. doi:10.1145/3433949. ISSN 0001-0782. S2CID 1769114.
- ↑ Mehrabi, Ninareh; Morstatter, Fred; Saxena, Nripsuta; Lerman, Kristina; Galstyan, Aram (2021-07-13). "मशीन लर्निंग में पूर्वाग्रह और निष्पक्षता पर एक सर्वेक्षण". ACM Computing Surveys. 54 (6): 115:1–115:35. arXiv:1908.09635. doi:10.1145/3457607. ISSN 0360-0300. S2CID 201666566.
- ↑ "AI Fairness 360". aif360.mybluemix.net. Retrieved 2022-11-18.
- ↑ "IBM AI Fairness 360 open source toolkit adds new functionalities". Tech Republic. 4 June 2020.
- ↑ "जिम्मेदार एआई अभ्यास". Google AI (in English). Retrieved 2022-11-18.
- ↑ Fairness Indicators, tensorflow, 2022-11-10, retrieved 2022-11-18
- ↑ "हम एआई बनाने में मदद के लिए फेयरनेस फ्लो का उपयोग कैसे कर रहे हैं जो सभी के लिए बेहतर काम करता है". ai.facebook.com (in English). Retrieved 2022-11-18.
- ↑ "एआई विशेषज्ञों ने चेतावनी दी है कि फेसबुक का पूर्वाग्रह-विरोधी उपकरण 'पूरी तरह से अपर्याप्त' है". VentureBeat (in English). 2021-03-31. Retrieved 2022-11-18.
- ↑ Hutchinson, Ben; Mitchell, Margaret (2019-01-29). 50 Years of Test (Un)fairness. New York, NY, USA: ACM FAT*'19. doi:10.1145/3287560.3287600.
- ↑ "Attorney General Eric Holder Speaks at the National Association of Criminal Defense Lawyers 57th Annual Meeting and 13th State Criminal Justice Network Conference". www.justice.gov (in English). 2014-08-01. Retrieved 2022-04-16.
- ↑ Dieterich, William; Mendoza, Christina; Brennan, Tim (2016). "COMPAS Risk Scales: Demonstrating Accuracy Equity and Predictive Parity" (PDF). Northpointe Inc.
- ↑ Angwin, Jeff Larson,Julia (29 July 2016). "नॉर्थपॉइंट को तकनीकी प्रतिक्रिया". ProPublica (in English). Retrieved 2022-11-18.
{{cite web}}: CS1 maint: multiple names: authors list (link) - ↑ Rose, Adam (2010-01-22). "Are face-detection cameras racist?". Time (in English). ISSN 0040-781X. Retrieved 2022-11-18.
- ↑ "Google ने फोटो ऐप में नस्लवादी ऑटो-टैग के लिए खेद जताया है". The Guardian (in English). 2015-07-01. Retrieved 2022-04-16.
- ↑ "एक सौंदर्य प्रतियोगिता का मूल्यांकन एआई द्वारा किया गया और रोबोटों को सांवली त्वचा पसंद नहीं आई". The Guardian (in English). 2016-09-08. Retrieved 2022-04-16.
- ↑ 18.0 18.1 Buolamwini, Joy; Gebru, Timnit (February 2018). Gender Shades: Intersectional Accuracy Disparities in Commercial Gender Classification (PDF). Conference on Fairness, Accountability and Transparency. New York, NY, USA. pp. 77–91.
- ↑ "छात्र ने ट्विटर एल्गोरिदम को हल्के, पतले, युवा चेहरों के प्रति 'पूर्वाग्रह' साबित किया". The Guardian (in English). 2021-08-10. Retrieved 2022-11-18.
- ↑ openai/dalle-2-preview, OpenAI, 2022-11-17, retrieved 2022-11-18
- ↑ "अमेज़ॅन ने गुप्त एआई भर्ती उपकरण को रद्द कर दिया जो महिलाओं के खिलाफ पूर्वाग्रह दिखाता था". Reuters (in English). 2018-10-10. Retrieved 2022-11-18.
- ↑ "एप्पल कार्ड एल्गोरिदम ने गोल्डमैन सैक्स के खिलाफ लैंगिक भेदभाव के आरोपों को जन्म दिया". Washington Post (in English). ISSN 0190-8286. Retrieved 2022-11-18.
- ↑ Martinez, Emmanuel; Kirchner, Lauren (25 August 2021). "The Secret Bias Hidden in Mortgage-Approval Algorithms – The Markup". themarkup.org (in English). Retrieved 2022-11-18.
- ↑ Buyl, Maarten; De Bie, Tijl. "एआई निष्पक्षता की अंतर्निहित सीमाएँ". arXiv. arXiv. doi:10.48550/ARXIV.2212.06495. Retrieved 2023-11-25.
- ↑ Castelnovo, Alessandro; Inverardi, Nicole; Nanino, Gabriele; Penco, Ilaria Giuseppina; Regoli, Daniele. "Fair Enough? A map of the current limitations of the requirements to have "fair algorithms". arXiv. doi:10.48550/ARXIV.2311.12435. Retrieved 2023-11-25.
- ↑ 26.0 26.1 26.2 26.3 Solon Barocas; Moritz Hardt; Arvind Narayanan, Fairness and Machine Learning. Retrieved 15 December 2019.
- ↑ Mayes, Elizabeth (2001). क्रेडिट स्कोरिंग की हैंडबुक (in English). NY, NY, USA: Glenlake Publishing. p. 282. ISBN 0-8144-0619-X.
- ↑ Berk, Richard; Heidari, Hoda; Jabbari, Shahin; Kearns, Michael; Roth, Aaron (February 2021). "Fairness in Criminal Justice Risk Assessments: The State of the Art". Sociological Methods & Research (in English). 50 (1): 3–44. arXiv:1703.09207. doi:10.1177/0049124118782533. ISSN 0049-1241. S2CID 12924416.
- ↑ Räz, Tim (2021-03-03). "Group Fairness: Independence Revisited". निष्पक्षता, जवाबदेही और पारदर्शिता पर 2021 एसीएम सम्मेलन की कार्यवाही (in English). ACM. pp. 129–137. arXiv:2101.02968. doi:10.1145/3442188.3445876. ISBN 978-1-4503-8309-7. S2CID 231667399.
- ↑ 30.0 30.1 30.2 वर्मा, साहिल, और जूलिया रुबिन। निष्पक्षता की परिभाषाएँ समझाई गईं। 2018 में सॉफ्टवेयर निष्पक्षता (फेयरवेयर) पर आईईईई/एसीएम अंतर्राष्ट्रीय कार्यशाला, पीपी 1-7। आईईईई, 2018।
- ↑ Gursoy, Furkan; Kakadiaris, Ioannis A. (November 2022). "Equal Confusion Fairness: Measuring Group-Based Disparities in Automated Decision Systems". 2022 IEEE International Conference on Data Mining Workshops (ICDMW). IEEE. pp. 137–146. arXiv:2307.00472. doi:10.1109/ICDMW58026.2022.00027. ISBN 979-8-3503-4609-1. S2CID 256669476.
- ↑ Chen, Violet (Xinying); Hooker, J. N. (2021). "अनुकूलन के माध्यम से कल्याण-आधारित निष्पक्षता". arXiv:2102.00311 [cs.AI].
- ↑ Mullainathan, Sendhil (June 19, 2018). एल्गोरिथम निष्पक्षता और सामाजिक कल्याण कार्य. Keynote at the 19th ACM Conference on Economics and Computation (EC'18). YouTube. 48 minutes in.
In other words, if you have a social welfare function where what you care about is harm, and you care about harm to the African Americans, there you go: 12 percent less African Americans in jail overnight.... Before we get into the minutiae of relative harm, the welfare function is defined in absolute harm, so we should actually calculate the absolute harm first.
- ↑ Mitchell, Shira; Potash, Eric; Barocas, Solon; d'Amour, Alexander; Lum, Kristian (2021). "Algorithmic Fairness: Choices, Assumptions, and Definitions". Annual Review of Statistics and Its Application. 8 (1): 141–163. Bibcode:2021AnRSA...8..141M. doi:10.1146/annurev-statistics-042720-125902. S2CID 228893833.
- ↑ Castelnovo, Alessandro; Crupi, Riccardo; Greco, Greta; Regoli, Daniele; Penco, Ilaria Giuseppina; Cosentini, Andrea Claudio (2022). "निष्पक्षता मेट्रिक्स परिदृश्य में बारीकियों का स्पष्टीकरण". Scientific Reports. 12 (1): 4209. arXiv:2106.00467. Bibcode:2022NatSR..12.4209C. doi:10.1038/s41598-022-07939-1. PMC 8913820. PMID 35273279.
- ↑ Mehrabi, Ninareh, Fred Morstatter, Nripsuta Saxena, Kristina Lerman, and Aram Galstyan. "A survey on bias and fairness in machine learning." ACM Computing Surveys (CSUR) 54, no. 6 (2021): 1-35.
- ↑ Dwork, Cynthia; Hardt, Moritz; Pitassi, Toniann; Reingold, Omer; Zemel, Richard (2012). "Fairness through awareness". Proceedings of the 3rd Innovations in Theoretical Computer Science Conference on - ITCS '12. pp. 214–226. doi:10.1145/2090236.2090255. ISBN 9781450311151. S2CID 13496699.
- ↑ Galhotra, Sainyam; Brun, Yuriy; Meliou, Alexandra (2017). "Fairness testing: Testing software for discrimination". Proceedings of the 2017 11th Joint Meeting on Foundations of Software Engineering. pp. 498–510. arXiv:1709.03221. doi:10.1145/3106237.3106277. ISBN 9781450351058. S2CID 6324652.
- ↑ Kusner, M. J., Loftus, J., Russell, C., & Silva, R. (2017). Counterfactual fairness. Advances in neural information processing systems, 30.
- ↑ Coston, Amanda; Mishler, Alan; Kennedy, Edward H.; Chouldechova, Alexandra (2020-01-27). "Counterfactual risk assessments, evaluation, and fairness". Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency. FAT* '20. New York, NY, USA: Association for Computing Machinery. pp. 582–593. doi:10.1145/3351095.3372851. ISBN 978-1-4503-6936-7. S2CID 202539649.
- ↑ Mishler, Alan; Kennedy, Edward H.; Chouldechova, Alexandra (2021-03-01). "Fairness in Risk Assessment Instruments". Proceedings of the 2021 ACM Conference on Fairness, Accountability, and Transparency. FAccT '21. New York, NY, USA: Association for Computing Machinery. pp. 386–400. doi:10.1145/3442188.3445902. ISBN 978-1-4503-8309-7. S2CID 221516412.
- ↑ 42.0 42.1 Plecko, Drago; Bareinboim, Elias. "कारण निष्पक्षता विश्लेषण". arXiv. doi:10.48550/ARXIV.2207.11385. Retrieved 2023-11-25.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Richard Zemel; Yu (Ledell) Wu; Kevin Swersky; Toniann Pitassi; Cyntia Dwork, Learning Fair Representations. Retrieved 1 December 2019
- ↑ 44.0 44.1 44.2 Ziyuan Zhong, Tutorial on Fairness in Machine Learning. Retrieved 1 December 2019
- ↑ Faisal Kamiran; Toon Calders, Data preprocessing techniques for classification without discrimination. Retrieved 17 December 2019
- ↑ Muhammad Bilal Zafar; Isabel Valera; Manuel Gómez Rodríguez; Krishna P. Gummadi, Fairness Beyond Disparate Treatment & Disparate Impact: Learning Classification without Disparate Mistreatment. Retrieved 1 December 2019
- ↑ 47.0 47.1 Brian Hu Zhang; Blake Lemoine; Margaret Mitchell, Mitigating Unwanted Biases with Adversarial Learning. Retrieved 17 December 2019
- ↑ Joyce Xu, Algorithmic Solutions to Algorithmic Bias: A Technical Guide. Retrieved 17 December 2019
- ↑ 49.0 49.1 Moritz Hardt; Eric Price; Nathan Srebro, Equality of Opportunity in Supervised Learning. Retrieved 1 December 2019
- ↑ 50.0 50.1 Faisal Kamiran; Asim Karim; Xiangliang Zhang, Decision Theory for Discrimination-aware Classification. Retrieved 17 December 2019
