आईईईई 754-1985: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{short description|First edition of the IEEE 754 floating-point standard}} | {{short description|First edition of the IEEE 754 floating-point standard}} | ||
{{See also|आईईईई 754}} | {{See also|आईईईई 754}} | ||
'''आईईईई 754-1985'''<ref>{{Cite book|title=बाइनरी फ़्लोटिंग-पॉइंट अंकगणित के लिए आईईईई मानक|year=1985|doi=10.1109/IEEESTD.1985.82928|isbn=0-7381-1165-1}}</ref> [[कंप्यूटर]] में [[ तैरनेवाला स्थल |फ्लोटिंग-पॉइंट]] | '''आईईईई 754-1985'''<ref>{{Cite book|title=बाइनरी फ़्लोटिंग-पॉइंट अंकगणित के लिए आईईईई मानक|year=1985|doi=10.1109/IEEESTD.1985.82928|isbn=0-7381-1165-1}}</ref> [[कंप्यूटर]] में [[ तैरनेवाला स्थल |फ्लोटिंग-पॉइंट]] नंबर्स को रिप्रेजेंट करने के लिए इंडस्ट्री [[तकनीकी मानक|स्टैण्डर्ड]] था, जिसे सामान्यतः 1985 में स्वीकार किया गया था और 2008 में [[IEEE 754-2008|आईईईई 754-2008]] द्वारा प्रतिस्थापित किया गया था, और फिर 2019 में माइनर वर्ज़न [[IEEE 754-2019|आईईईई 754-2019]] द्वारा प्रतिस्थापित किया गया था।<ref>{{Cite web|url=http://754r.ucbtest.org/background/|title=ANSI/IEEE Std 754-2019|website=754r.ucbtest.org|access-date=2019-08-06}}</ref> अपने 23 वर्षों के समय में, यह फ़्लोटिंग-पॉइंट कैलकुलेशन के लिए सबसे वाइड रूप से उपयोग किया जाने वाला प्रारूप था। इसे सॉफ़्टवेयर में, फ़्लोटिंग-पॉइंट [[ पुस्तकालय (कंप्यूटिंग) |लाइब्रेरीज़]] के रूप में, और हार्डवेयर में, कई [[ CPU |सीपीयू]] और [[फ़्लोटिंग-पॉइंट इकाई|एफपीयू]] के [[निर्देश (कंप्यूटर विज्ञान)|इंस्ट्रक्शन]] में इम्प्लीमेंट किया गया था। आईईईई 754-1985 बनने वाले ड्राफ्ट को इम्प्लीमेंट करने वाला प्रथम इंटीग्रेटेड सर्किट [[इंटेल 8087]] था। | ||
आईईईई 754-1985 बाइनरी में | आईईईई 754-1985 बाइनरी में नंबर्स को रिप्रेजेंट करता है, जो एक्यूरेसी के चार लेवल्स की परिभाषा प्रदान करता है, जिनमें से दो सबसे अधिक उपयोग किए जाते हैं: | ||
{| class="wikitable" | {| class="wikitable" | ||
| Line 9: | Line 9: | ||
!लेवल | !लेवल | ||
!विड्थ | !विड्थ | ||
!पूर्ण | !पूर्ण एक्यूरेसी से रेंज करें | ||
! | !एक्यूरेसी{{efn|Precision: The number of decimal digits precision is calculated via number_of_mantissa_bits * Log<sub>10</sub>(2). Thus ~7.2 and ~15.9 for single and double precision respectively.}} | ||
|- | |- | ||
| | |सिंगल एक्यूरेसी | ||
|32 bits | |32 bits | ||
|±1.18{{e|-38}} to ±3.4{{e|38}} | |±1.18{{e|-38}} to ±3.4{{e|38}} | ||
|लगभग 7 दशमलव अंक | |लगभग 7 दशमलव अंक | ||
|- | |- | ||
| | |डबल एक्यूरेसी | ||
|64 bits | |64 bits | ||
|±2.23{{e|-308}} to ±1.80{{e|308}} | |±2.23{{e|-308}} to ±1.80{{e|308}} | ||
|लगभग 16 दशमलव अंक | |लगभग 16 दशमलव अंक | ||
|} | |} | ||
स्टैण्डर्ड पॉजिटिव और नेगेटिव इनफाइनाइट के लिए रिप्रेजेंट को भी परिभाषित करता है, [[नकारात्मक शून्य|नेगेटिव शून्य]], [[शून्य से विभाजन]] जैसे अमान्य परिणामों को सुरक्षित करने के लिए पांच एक्सेप्शन, उन एक्सेप्शन्स का रिप्रेजेंट करने के लिए विशेष मान जिन्हें [[NaN]] कहा जाता है, ऊपर दिखाए गए छोटी नंबर्स का रिप्रेजेंट करने के लिए [[असामान्य संख्या|डिनॉर्मल नंबर्स]], और चार गोल मोड है। | |||
== | ==नंबर्स का रिप्रेजेंट== | ||
[[Image:IEEE 754 Single Floating Point Format.svg|right|frame|संख्या 0.15625 को | [[Image:IEEE 754 Single Floating Point Format.svg|right|frame|संख्या 0.15625 को सिंगल-त्रुटिहीन आईईईई 754-1985 फ़्लोटिंग-पॉइंट संख्या के रूप में दर्शाया गया है। स्पष्टीकरण के लिए टेक्स्ट देखें। ]] | ||
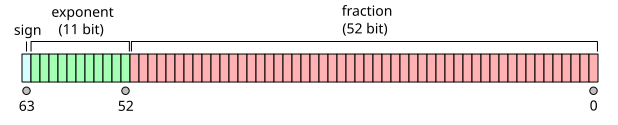
[[Image:IEEE 754 Double Floating Point Format.svg|right|frame|64 बिट आईईईई 754 में तीन क्षेत्र फ़्लोट होते हैं।]]आईईईई 754 प्रारूप में फ़्लोटिंग-पॉइंट नंबरों में तीन क्षेत्र होते हैं: [[साइन बिट]], बायस्ड घातांक और अंश। निम्नलिखित उदाहरण प्रत्येक का अर्थ बताता है। | [[Image:IEEE 754 Double Floating Point Format.svg|right|frame|64 बिट आईईईई 754 में तीन क्षेत्र फ़्लोट होते हैं।]]आईईईई 754 प्रारूप में फ़्लोटिंग-पॉइंट नंबरों में तीन क्षेत्र होते हैं: [[साइन बिट]], बायस्ड घातांक और अंश। निम्नलिखित उदाहरण प्रत्येक का अर्थ बताता है। | ||
दशमलव संख्या 0.15625<sub>10</sub> बाइनरी में 0.00101<sub>2</sub> (अर्थात् 1/8 + 1/32) प्रदर्शित किया गया है। (अंकाक्षर संख्या [[मूलांक]] प्रदर्शित करते हैं।) [[वैज्ञानिक संकेतन]] के अनुरूप, जहां | दशमलव संख्या 0.15625<sub>10</sub> बाइनरी में 0.00101<sub>2</sub> (अर्थात् 1/8 + 1/32) प्रदर्शित किया गया है। (अंकाक्षर संख्या [[मूलांक]] प्रदर्शित करते हैं।) [[वैज्ञानिक संकेतन]] के अनुरूप, जहां नंबर्स को दशमलव बिंदु के बाईं ओर अन्य-शून्य अंक के रूप में लिखा जाता है, हम इस संख्या को पुनः लिखते हैं जिससे कि इसमें बाइनरी बिंदु के बाईं ओर सिंगल 1 बिट होता है। हम तीन स्थितियों द्वारा त्यागे गए बिट्स के स्थानांतरण की पूर्ति के लिए 2 की उचित शक्ति से गुणा करते हैं: | ||
: <math>0.00101_2 = 1.01_2 \times 2^{-3}</math> | : <math>0.00101_2 = 1.01_2 \times 2^{-3}</math> | ||
अब हम भिन्न और घातांक को पढ़ सकते हैं: भिन्न .01<sub>2</sub> है और घातांक −3 है। | अब हम भिन्न और घातांक को पढ़ सकते हैं: भिन्न .01<sub>2</sub> है और घातांक −3 है। | ||
जैसा कि चित्रों में प्रदर्शित किया गया है, आईईईई 754 में इस संख्या का | जैसा कि चित्रों में प्रदर्शित किया गया है, आईईईई 754 में इस संख्या का रिप्रेजेंट करने वाले तीन क्षेत्र हैं: | ||
: चिन्ह = 0, क्योंकि संख्या | : चिन्ह = 0, क्योंकि संख्या पॉजिटिव है (1 नेगेटिव प्रदर्शित करता है।)। | ||
: बायस्ड घातांक = −3 + बायस है। ' | : बायस्ड घातांक = −3 + बायस है। 'सिंगल एक्यूरेसी' में, बायस '127' है, इसलिए इस उदाहरण में बायस्ड घातांक 124 है; 'डबल प्रिसिजन' में, बायस '1023' है, इसलिए इस उदाहरण में बायस्ड घातांक 1020 है। | ||
: अपूर्णांक = .01000…<sub>2</sub>. | : अपूर्णांक = .01000…<sub>2</sub>. | ||
आईईईई 754 घातांक में [[ऑफसेट बाइनरी]] जोड़ता है जिससे कि कई स्थितियों में | आईईईई 754 घातांक में [[ऑफसेट बाइनरी]] जोड़ता है जिससे कि कई स्थितियों में नंबर्स की अपेक्षा उसी हार्डवेयर द्वारा सरलता से की जा सके जो हस्ताक्षरित 2-पूरक पूर्णांकों की अपेक्षा करता है। बायस्ड घातांक का उपयोग करते हुए, दो पॉजिटिव फ़्लोटिंग-पॉइंट नंबर्स में से छोटी संख्या चिह्न और परिमाण पूर्णांक के समान क्रम के पश्चात बड़ी संख्या से कम निकलती है। यदि दो फ़्लोटिंग-पॉइंट नंबर्स के भिन्न-भिन्न चिह्न हैं, तो चिह्न-और-परिमाण अपेक्षा बायस्ड घातांक के साथ भी कार्य करती है। चूँकि, यदि दोनों बायस्ड-घातांक फ़्लोटिंग-पॉइंट नंबर्स नेगेटिव हैं, तो क्रम को विपरीत कर दिया जाना चाहिए। यदि घातांक को, मान लीजिए, 2-पूरक संख्या के रूप में प्रदर्शित किया जाता है, तो यह देखने के लिए अपेक्षा करना कि दो नंबर्स में से कौन सी बड़ी है, सुविधाजनक नहीं होता है। | ||
अग्रणी 1 बिट को विस्थापित कर दिया गया है क्योंकि शून्य को त्यागकर सभी | अग्रणी 1 बिट को विस्थापित कर दिया गया है क्योंकि शून्य को त्यागकर सभी नंबर्स अग्रणी 1 से प्रारंभ होती हैं; अग्रणी 1 अंतर्निहित है और वास्तव में इसे संग्रहीत करने की आवश्यकता नहीं है जो मुफ़्त में अतिरिक्त एक्यूरेसी प्रदान करता है। | ||
=== शून्य === | === शून्य === | ||
| Line 48: | Line 48: | ||
शून्य संख्या को विशेष रूप से प्रदर्शित किया गया है: | शून्य संख्या को विशेष रूप से प्रदर्शित किया गया है: | ||
: | : पॉजिटिव शून्य के लिए चिह्न = 0, नेगेटिव शून्य के लिए 1 है। | ||
: बायस्ड घातांक = 0 है। | : बायस्ड घातांक = 0 है। | ||
: अपूर्णांक = 0 है। | : अपूर्णांक = 0 है। | ||
=== असामान्यीकृत | === असामान्यीकृत नंबर्स === | ||
ऊपर वर्णित संख्या निरूपण को सामान्यीकृत कहा जाता है, जिसका अर्थ है कि अंतर्निहित अग्रणी बाइनरी अंक 1 है। अंडरफ्लो होने पर | ऊपर वर्णित संख्या निरूपण को सामान्यीकृत कहा जाता है, जिसका अर्थ है कि अंतर्निहित अग्रणी बाइनरी अंक 1 है। अंडरफ्लो होने पर एक्यूरेसी की हानि को कम करने के लिए, आईईईई 754 में सामान्यीकृत रिप्रेजेंट में संभव से छोटे अंशों का रिप्रेजेंट करने की क्षमता सम्मिलित है। अंतर्निहित अग्रणी अंक 0 बनाता है। ऐसी नंबर्स को असामान्य नंबर्स कहा जाता है। उनमें सामान्यीकृत संख्या के रूप में कई [[महत्वपूर्ण अंक]] सम्मिलित नहीं होते हैं, किन्तु जब किसी ऑपरेशन का परिणाम शून्य नहीं होता है, किन्तु सामान्यीकृत संख्या द्वारा प्रदर्शित किये जाने के लिए शून्य के अधिक निकट होता है, तो वे एक्यूरेसी की क्रमिक हानि को सक्षम करते हैं। | ||
असामान्य संख्या को सभी 0 बिट्स के बायस्ड घातांक के साथ प्रदर्शित किया जाता है, जो | असामान्य संख्या को सभी 0 बिट्स के बायस्ड घातांक के साथ प्रदर्शित किया जाता है, जो सिंगल एक्यूरेसी में −126 के घातांक का रिप्रेजेंट करता है (−127 नहीं), या दोहरी एक्यूरेसी में −1022 (−1023 नहीं) का रिप्रेजेंट करता है।<ref>{{cite book|last=Hennessy|title=कंप्यूटर संगठन और डिज़ाइन|year=2009|url=https://archive.org/details/computerorganiza00patt_779|url-access=limited|publisher=Morgan Kaufmann|page=[https://archive.org/details/computerorganiza00patt_779/page/n291 270]|isbn=9780123744937 }}</ref> इसके विपरीत, सामान्य संख्या का रिप्रेजेंट करने वाला सबसे छोटा बायस्ड घातांक 1 है (नीचे उदाहरण देखें)। | ||
==गैर- | ==गैर-नंबर्स का रिप्रेजेंट == | ||
किसी | किसी कैलकुलेशन की अनंतता या अमान्य परिणाम को प्रदर्शित करने के लिए बायस्ड-घातांक क्षेत्र सभी 1 बिट्स से पूर्ण है। | ||
=== | === पॉजिटिव और नेगेटिव इनफाइनाइट === | ||
[[विस्तारित वास्तविक रेखा| | [[विस्तारित वास्तविक रेखा|पॉजिटिव और नेगेटिव इनफाइनाइट]] को इस प्रकार प्रदर्शित किया गया है: | ||
: | : पॉजिटिव इनफाइनाइट के लिए चिह्न = 0, नेगेटिव इनफाइनाइट के लिए 1 है। | ||
: बायस्ड घातांक = सभी 1 बिट्स है। | : बायस्ड घातांक = सभी 1 बिट्स है। | ||
: अपूर्णांक = सभी 0 बिट्स है। | : अपूर्णांक = सभी 0 बिट्स है। | ||
| Line 72: | Line 72: | ||
=== NaN === | === NaN === | ||
फ़्लोटिंग-पॉइंट अंकगणित के कुछ ऑपरेशन अमान्य हैं, जैसे | फ़्लोटिंग-पॉइंट अंकगणित के कुछ ऑपरेशन अमान्य हैं, जैसे नेगेटिव संख्या का वर्गमूल लेता है। किसी अमान्य परिणाम तक पहुंचने की क्रिया को फ़्लोटिंग-पॉइंट अपवाद कहा जाता है। असाधारण परिणाम को "नॉट ए नंबर" के लिए NaN नामक विशेष कोड द्वारा प्रदर्शित किया जाता है। आईईईई 754-1985 में सभी NaN का प्रारूप यह है: | ||
: चिह्न = या तो 0 या 1 होता है। | : चिह्न = या तो 0 या 1 होता है। | ||
: बायस्ड घातांक = सभी 1 बिट्स है। | : बायस्ड घातांक = सभी 1 बिट्स है। | ||
: अपूर्णांक = सभी 0 बिट्स को त्यागकर कुछ भी होता है (क्योंकि सभी 0 बिट्स | : अपूर्णांक = सभी 0 बिट्स को त्यागकर कुछ भी होता है (क्योंकि सभी 0 बिट्स इनफाइनाइट का रिप्रेजेंट करते हैं)। | ||
== श्रेणी और | == श्रेणी और एक्यूरेसी == | ||
[[File:IEEE 754 relative precision.svg|thumb|महत्वपूर्ण अंकों की निश्चित संख्या का उपयोग करके दशमलव | [[File:IEEE 754 relative precision.svg|thumb|महत्वपूर्ण अंकों की निश्चित संख्या का उपयोग करके दशमलव रिप्रेजेंट की अपेक्षा में सिंगल (बाइनरी 32) और डबल त्रुटिहीन (बाइनरी 64) नंबर्स की सापेक्ष एक्यूरेसी है। सापेक्ष एक्यूरेसी को यहां ulp(x)/x के रूप में परिभाषित किया गया है, जहां ulp(x) x के रिप्रेजेंट में [[अंतिम स्थान पर इकाई]] है, अर्थात x और अगले रिप्रेजेंट योग्य संख्या के मध्य का अंतर है।]]एक्यूरेसी को दो क्रमिक मंटिसा अभ्यावेदन के मध्य न्यूनतम अंतर के रूप में परिभाषित किया गया है; इस प्रकार यह केवल मंटिसा में फंक्शन है; जबकि अंतर को दो क्रमिक नंबर्स के मध्य के अंतर के रूप में परिभाषित किया गया है।<ref>{{citation |title=Computer Arithmetic |author1=Hossam A. H. Fahmy |author2=Shlomo Waser |author3=Michael J. Flynn |url=http://arith.stanford.edu/~hfahmy/webpages/arith_class/arith.pdf |access-date=2011-01-02 |url-status=dead |archive-url=https://web.archive.org/web/20101008203307/http://arith.stanford.edu/~hfahmy/webpages/arith_class/arith.pdf |archive-date=2010-10-08}}</ref> | ||
[[एकल परिशुद्धता|''' | [[एकल परिशुद्धता|'''सिंगल एक्यूरेसी''']] | ||
सिंगल-त्रुटिहीन नंबर्स 32 बिट्स पर व्याप्त हैं। सिंगल एक्यूरेसी में: | |||
* शून्य के निकटतम | * शून्य के निकटतम पॉजिटिव और नेगेटिव नंबर्स (घातक क्षेत्र में सभी 0 के साथ असामान्य मान और अपूर्णांक क्षेत्र में बाइनरी मान 1 द्वारा प्रदर्शित की जाती हैं) हैं: | ||
*: ±2<sup>−23</sup>×2<sup>−126</sup> ≈ ±1.40130{{e|−45}} | *: ±2<sup>−23</sup>×2<sup>−126</sup> ≈ ±1.40130{{e|−45}} | ||
* शून्य के निकटतम | * शून्य के निकटतम पॉजिटिव और नेगेटिव सामान्यीकृत नंबर्स (घातक क्षेत्र में बाइनरी मान 1 और अपूर्णांक क्षेत्र में 0 के साथ प्रदर्शित की जाती हैं) हैं: | ||
*: ±1 × 2<sup>−126</sup> ≈ ±1.17549{{e|−38}} | *: ±1 × 2<sup>−126</sup> ≈ ±1.17549{{e|−38}} | ||
* शून्य से सबसे दूर की परिमित | * शून्य से सबसे दूर की परिमित पॉजिटिव और परिमित नेगेटिव नंबर्स (घातक क्षेत्र में 254 और अपूर्णांक क्षेत्र में सभी 1 के साथ मान द्वारा प्रदर्शित की गई) हैं: | ||
*: ±(2−2<sup>−23</sup>) × 2<sup>127</sup><ref name="Kahan">{{Cite document | *: ±(2−2<sup>−23</sup>) × 2<sup>127</sup><ref name="Kahan">{{Cite document | ||
| author = William Kahan |author-link=William Kahan | | author = William Kahan |author-link=William Kahan | ||
| Line 97: | Line 97: | ||
| access-date = 2007-04-12 }}</ref> ≈ ±3.40282{{e|38}} | | access-date = 2007-04-12 }}</ref> ≈ ±3.40282{{e|38}} | ||
सिंगल एक्यूरेसी में दिए गए घातांक के लिए कुछ उदाहरण सीमा और अंतराल मान है: | |||
{| class="wikitable" style="text-align:right;" | {| class="wikitable" style="text-align:right;" | ||
| Line 161: | Line 161: | ||
| ≈ 2.02824e31 | | ≈ 2.02824e31 | ||
|} | |} | ||
उदाहरण के लिए, 16,777,217 को 32-बिट फ़्लोट के रूप में एन्कोड नहीं किया जा सकता क्योंकि इसे 16,777,216 पर पूर्णांकित किया जाएगा। इससे ज्ञात होता है कि फ़्लोटिंग पॉइंट अंकगणित लेखांकन सॉफ़्टवेयर के लिए अनुपयुक्त क्यों है। चूँकि, | उदाहरण के लिए, 16,777,217 को 32-बिट फ़्लोट के रूप में एन्कोड नहीं किया जा सकता क्योंकि इसे 16,777,216 पर पूर्णांकित किया जाएगा। इससे ज्ञात होता है कि फ़्लोटिंग पॉइंट अंकगणित लेखांकन सॉफ़्टवेयर के लिए अनुपयुक्त क्यों है। चूँकि, रिप्रेजेंट योग्य सीमा के अंदर सभी पूर्णांक जो 2 की शक्ति हैं, उन्हें बिना गोलाई के 32-बिट फ़्लोट में संग्रहीत किया जा सकता है। | ||
=== दोहरी | === दोहरी एक्यूरेसी === | ||
डबल-त्रुटिहीन | डबल-त्रुटिहीन नंबर्स 64 बिट्स पर व्याप्त हैं। दोहरी एक्यूरेसी में: | ||
* शून्य के निकटतम | * शून्य के निकटतम पॉजिटिव और नेगेटिव नंबर्स (एक्सप क्षेत्र में सभी 0 के साथ असामान्य मान और अपूर्णांक क्षेत्र में बाइनरी मान 1 द्वारा प्रदर्शित की जाती हैं) हैं | ||
*: ±2<sup>−52</sup>×2<sup>−1022</sup> ≈ ±4.94066{{e|−324}} | *: ±2<sup>−52</sup>×2<sup>−1022</sup> ≈ ±4.94066{{e|−324}} | ||
* शून्य के निकटतम | * शून्य के निकटतम पॉजिटिव और नेगेटिव सामान्यीकृत नंबर्स (एक्सप क्षेत्र में बाइनरी मान 1 और अपूर्णांक क्षेत्र में 0 के साथ प्रदर्शित की जाती हैं) हैं: | ||
*: ±1 × 2<sup>−1022</sup> ≈ ±2.22507{{e|−308}} | *: ±1 × 2<sup>−1022</sup> ≈ ±2.22507{{e|−308}} | ||
* शून्य से सबसे दूर की परिमित | * शून्य से सबसे दूर की परिमित पॉजिटिव और परिमित नेगेटिव नंबर्स (एक्सप क्षेत्र में 2046 और अपूर्णांक क्षेत्र में सभी 1 के साथ मान द्वारा प्रदर्शित की गई) हैं: | ||
*: ±(2−2<sup>−52</sup>)×2<sup>1023</sup><ref name="Kahan" />≈ ±1.79769{{e|308}} | *: ±(2−2<sup>−52</sup>)×2<sup>1023</sup><ref name="Kahan" />≈ ±1.79769{{e|308}} | ||
दोहरी | दोहरी एक्यूरेसी में दिए गए घातांक के लिए कुछ उदाहरण सीमा और अंतराल मान है: | ||
{| class="wikitable" style="text-align:right;" | {| class="wikitable" style="text-align:right;" | ||
| Line 240: | Line 240: | ||
'''विस्तारित प्रारूप''' | '''विस्तारित प्रारूप''' | ||
स्टैण्डर्ड राउंड-ऑफ त्रुटियों को कम करने के लिए, अंतिम परिणाम के लिए आवश्यक उच्च एक्यूरेसी पर आंतरिक कैलकुलेशन करने के लिए विस्तारित प्रारूप का उपयोग करने का अनुरोध करता है: स्टैण्डर्ड केवल ऐसे प्रारूपों के लिए न्यूनतम एक्यूरेसी और घातांक आवश्यकताओं को निर्दिष्ट करता है। [[x87]] 80-बिट विस्तारित प्रारूप सबसे अधिक कार्यान्वित विस्तारित प्रारूप है जो इन आवश्यकताओं को पूर्ण करता है। | |||
== उदाहरण == | == उदाहरण == | ||
यहां | यहां सिंगल-त्रुटिहीन आईईईई 754 अभ्यावेदन के कुछ उदाहरण दिए गए हैं: | ||
{| class="wikitable" | {| class="wikitable" | ||
| Line 264: | Line 264: | ||
| 0.0 | | 0.0 | ||
|- | |- | ||
| [[Negative zero| | | [[Negative zero|नेगेटिव शून्य]] | ||
| style="text-align:center;"| 1 | | style="text-align:center;"| 1 | ||
| −126 | | −126 | ||
| Line 328: | Line 328: | ||
| ±(2−2<sup>−23</sup>) × 2<sup>127</sup> ≈ ±3.4{{e|38}} | | ±(2−2<sup>−23</sup>) × 2<sup>127</sup> ≈ ±3.4{{e|38}} | ||
|- | |- | ||
| | | पॉजिटिव अनन्तता | ||
| style="text-align:center;"| 0 | | style="text-align:center;"| 0 | ||
| 128 | | 128 | ||
| Line 336: | Line 336: | ||
| +∞ | | +∞ | ||
|- | |- | ||
| | | नेगेटिव अनन्तता | ||
| style="text-align:center;"| 1 | | style="text-align:center;"| 1 | ||
| 128 | | 128 | ||
| Line 355: | Line 355: | ||
|} | |} | ||
== फ़्लोटिंग-पॉइंट | == फ़्लोटिंग-पॉइंट नंबर्स की अपेक्षा करना == | ||
नेगेटिव शून्य और पॉजिटिव शून्य के लिए बिट्स के दो संयोजनों को त्यागकर, प्रत्येक संभावित बिट संयोजन या तो NaN है या संबद्ध क्रम के साथ एफ़िनली विस्तारित वास्तविक संख्या प्रणाली में अद्वितीय मान वाला नंबर है, जिस पर कभी-कभी विशेष ध्यान देने की आवश्यकता होती है (नीचे देखें)। बाइनरी रिप्रेजेंट में विशेष गुण होता है कि, NaN को त्यागकर, किसी भी दो नंबर्स की अपेक्षा चिह्न और परिमाण पूर्णांक के रूप में की जा सकती है ([[endianness|एंडियननेस]] उद्देश्य इम्प्लीमेंट होते हैं)। 2 के पूरक पूर्णांकों के रूप में अपेक्षा करते समय: यदि साइन बिट भिन्न होते हैं, तो नेगेटिव संख्या पॉजिटिव संख्या से पूर्व होती है, इसलिए 2 का पूरक सही परिणाम देता है (इसके अतिरिक्त कि नेगेटिव शून्य और पॉजिटिव शून्य को समान माना जाना चाहिए)। यदि दोनों मान पॉजिटिव हैं, तो 2 की पूरक अपेक्षा पुनः उचित परिणाम देती है। अन्यथा (दो नेगेटिव नंबर्स), उचित एफपी क्रम 2 के पूरक क्रम के विपरीत है। | |||
फ़्लोटिंग पॉइंट गणनाओं में निहित राउंडिंग त्रुटियाँ परिणामों की त्रुटिहीन समानता के परीक्षण के लिए अपेक्षाओं के उपयोग को सीमित कर सकती हैं। स्वीकार्य सीमा का चयन करना समष्टि विषय है। सामान्य तकनीक अनुमानित अपेक्षा करने के लिए अपेक्षात्मक ईपीएसलॉन मान का उपयोग करना है।<ref>{{cite web|url=https://github.com/godotengine/godot/blob/master/core/math/math_funcs.h#L302|title=Godot math_funcs.h|website=GitHub.com|date=30 July 2022 }}</ref> अपेक्षाएँ कितनी उदार हैं, इस पर निर्भर करते हुए, सामान्य मूल्यों में | फ़्लोटिंग पॉइंट गणनाओं में निहित राउंडिंग त्रुटियाँ परिणामों की त्रुटिहीन समानता के परीक्षण के लिए अपेक्षाओं के उपयोग को सीमित कर सकती हैं। स्वीकार्य सीमा का चयन करना समष्टि विषय है। सामान्य तकनीक अनुमानित अपेक्षा करने के लिए अपेक्षात्मक ईपीएसलॉन मान का उपयोग करना है।<ref>{{cite web|url=https://github.com/godotengine/godot/blob/master/core/math/math_funcs.h#L302|title=Godot math_funcs.h|website=GitHub.com|date=30 July 2022 }}</ref> अपेक्षाएँ कितनी उदार हैं, इस पर निर्भर करते हुए, सामान्य मूल्यों में सिंगल-एक्यूरेसी के लिए <code>1e-6</code> या <code>1e-5</code>और दोहरी एक्यूरेसी के लिए <code>1e-14</code> सम्मिलित हैं।<ref>{{cite web|url=https://github.com/godotengine/godot/blob/master/core/math/math_defs.h#L34|title=Godot math_defs.h|website=GitHub.com|date=30 July 2022 }}</ref><ref>{{cite web|url=https://github.com/godotengine/godot/blob/master/modules/mono/glue/Managed/Files/MathfEx.cs#L18|title=गोडोट MathfEx.cs|website=GitHub.com}}</ref> अन्य सामान्य तकनीक यूएलपी है, जो यह परीक्षण करती है कि अंतिम स्थान के अंकों में क्या अंतर है, प्रभावी रूप से यह परीक्षण करती है कि दोनों मान कितने दूर हैं।<ref>{{cite web|url=https://randomascii.wordpress.com/2012/02/25/comparing-floating-point-numbers-2012-edition/|title=Comparing Floating Point Numbers, 2012 Edition|website=randomascii.wordpress.com|date=26 February 2012 }}</ref> | ||
चूँकि अपेक्षात्मक उद्देश्यों के लिए | चूँकि अपेक्षात्मक उद्देश्यों के लिए नेगेटिव शून्य और पॉजिटिव शून्य को सामान्यतः समान माना जाता है, कुछ [[प्रोग्रामिंग भाषा|प्रोग्रामिंग लैंग्वेज]] [[रिलेशनल ऑपरेटर]] और समान निर्माण उन्हें भिन्न मानते हैं। [[जावा (प्रोग्रामिंग भाषा)|जावा]] लैंग्वेज विशिष्टता के अनुसार,<ref>{{cite web|url=http://java.sun.com/docs/books/jls/|title=जावा भाषा और वर्चुअल मशीन विशिष्टताएँ|website=Java Documentation}}</ref> अपेक्षा और समानता संचालक उन्हें समान मानते हैं, किन्तु <code>Math.min()</code> और <code>Math.max()</code> उन्हें भिन्न करते हैं (सामान्यतः जावा संस्करण 1.1 से प्रारंभ करते हैं किन्तु वास्तव में 1.1.1 के साथ), जैसा कि अपेक्षा विधियां <code>Float</code> और <code>Double</code> कक्षाओं का <code>equals()</code>, <code>compareTo()</code> और यहां तक कि <code>compare()</code> भी हैं। | ||
==फ़्लोटिंग-पॉइंट | ==फ़्लोटिंग-पॉइंट नंबर्स को पूर्णांकित करना== | ||
आईईईई | आईईईई स्टैण्डर्ड में चार भिन्न-भिन्न राउंडिंग मोड हैं; प्रथम डिफ़ॉल्ट है; अन्य को [[निर्देशित गोलाई]] कहा जाता है। | ||
* '''<nowiki/>'राउंड टू नियरेस्ट'''' - निकटतम मान तक राउंड; यदि संख्या मध्य में गिरती है तो इसे सम (शून्य) कम से कम महत्वपूर्ण बिट के साथ निकटतम मान तक पूर्णांकित किया जाता है, जिसका अर्थ है कि इसे 50% समय तक पूर्णांकित किया जाता है (आईईईई 754-2008 में इस मोड को दूसरे से अलग करने के लिए राउंडटीज़टूईवन कहा जाता है) -से-निकटतम मोड)। | * '''<nowiki/>'राउंड टू नियरेस्ट'''' - निकटतम मान तक राउंड; यदि संख्या मध्य में गिरती है तो इसे सम (शून्य) कम से कम महत्वपूर्ण बिट के साथ निकटतम मान तक पूर्णांकित किया जाता है, जिसका अर्थ है कि इसे 50% समय तक पूर्णांकित किया जाता है (आईईईई 754-2008 में इस मोड को दूसरे से अलग करने के लिए राउंडटीज़टूईवन कहा जाता है) -से-निकटतम मोड)। | ||
* '''<nowiki/>'राउंड टुवर्ड 0'''' - शून्य की ओर निर्देशित गोलाई। | * '''<nowiki/>'राउंड टुवर्ड 0'''' - शून्य की ओर निर्देशित गोलाई। | ||
* '''<nowiki/>'राउंड टुवर्ड +∞'''' - | * '''<nowiki/>'राउंड टुवर्ड +∞'''' - पॉजिटिव इनफाइनाइट की ओर निर्देशित गोलाई। | ||
* '''<nowiki/>'राउंड टुवर्ड -∞'''' - | * '''<nowiki/>'राउंड टुवर्ड -∞'''' - नेगेटिव इनफाइनाइट की ओर निर्देशित गोलाई। | ||
==वास्तविक | ==वास्तविक नंबर्स का विस्तार== | ||
आईईईई | आईईईई स्टैण्डर्ड भिन्न-भिन्न पॉजिटिव और नेगेटिव अनन्तताओं के साथ, पूर्ण रूप से विस्तारित वास्तविक संख्या प्रणाली को नियोजित (और विस्तारित) करता है। प्रारूपण के समय, प्रोग्रामर को मोड चयन विकल्प प्रदान करके, सिंगल अहस्ताक्षरित इनफाइनाइट के साथ प्रोजेक्टिवली विस्तारित वास्तविक संख्या प्रणाली को सम्मिलित करने के लिए स्टैण्डर्ड का प्रस्ताव था। चूँकि, अंतिम स्टैण्डर्ड की समष्टिता को कम करने के हित में, प्रोजेक्टिव मोड को विस्थापित कर दिया गया था। इंटेल 8087 और [[Intel 80287|इंटेल 80287]] फ़्लोटिंग पॉइंट सह-प्रोसेसर दोनों इस प्रोजेक्टिव मोड का समर्थन करते हैं।<ref>{{cite journal|journal=ACM Transactions on Programming Languages and Systems|volume=18|issue=2|date=March 1996|format=PDF|url=http://www.jhauser.us/publications/1996_Hauser_FloatingPointExceptions.html|author=John R. Hauser|title=संख्यात्मक कार्यक्रमों में फ़्लोटिंग-पॉइंट अपवादों को संभालना|doi=10.1145/227699.227701|pages=139–174|s2cid=9820157}}</ref><ref>{{cite journal|title=IEEE Task P754: A proposed standard for binary floating-point arithmetic|date=March 1981|journal=IEEE Computer|volume=14|issue=3|pages=51–62|author=David Stevenson|doi=10.1109/C-M.1981.220377|s2cid=15523399 }}</ref><ref>{{cite journal|author= William Kahan and John Palmer|year=1979|title=प्रस्तावित फ़्लोटिंग-पॉइंट मानक पर|journal=SIGNUM Newsletter|volume=14|issue=Special|pages=13–21|doi= 10.1145/1057520.1057522|s2cid=16981715}}</ref> | ||
== फंक्शन्स और प्रेडिकेट्स == | == फंक्शन्स और प्रेडिकेट्स == | ||
=== | ===स्टैण्डर्ड संचालन=== | ||
निम्नलिखित कार्य प्रदान किए जाने चाहिए: | निम्नलिखित कार्य प्रदान किए जाने चाहिए: | ||
*जोड़ें, घटाएं, गुणा करें, भाग करें। | *जोड़ें, घटाएं, गुणा करें, भाग करें। | ||
*[[वर्गमूल]] | *[[वर्गमूल]] | ||
*फ़्लोटिंग पॉइंट शेष यह सामान्य [[मॉड्यूलो ऑपरेशन]] के जैसे नहीं है, यह दो | *फ़्लोटिंग पॉइंट शेष यह सामान्य [[मॉड्यूलो ऑपरेशन]] के जैसे नहीं है, यह दो पॉजिटिव नंबर्स के लिए नेगेटिव हो सकता है। यह {{math|x–(round(x/y)·y)}} का त्रुटिहीन मान प्रदान करता है। | ||
* [[पूर्णांक तक पूर्णांकन|निकटतम पूर्णांक तक पूर्णांकन]] अप्रत्यक्ष पूर्णांकन के लिए जब दो पूर्णांकों के मध्य आधा हो तो सम पूर्णांक चयन किया जाता है। | * [[पूर्णांक तक पूर्णांकन|निकटतम पूर्णांक तक पूर्णांकन]] अप्रत्यक्ष पूर्णांकन के लिए जब दो पूर्णांकों के मध्य आधा हो तो सम पूर्णांक चयन किया जाता है। | ||
*अपेक्षा संचालन. अधिक स्पष्ट परिणामों के अतिरिक्त, आईईईई 754 परिभाषित करता है कि −∞ = −∞, +∞ = +∞ और <var>x</var> ≠<code>NaN</code> किसी भी <var>x</var> के लिए (सहित) <code>NaN</code>) होता है। | *अपेक्षा संचालन. अधिक स्पष्ट परिणामों के अतिरिक्त, आईईईई 754 परिभाषित करता है कि −∞ = −∞, +∞ = +∞ और <var>x</var> ≠<code>NaN</code> किसी भी <var>x</var> के लिए (सहित) <code>NaN</code>) होता है। | ||
===अनुशंसित फंक्शन्स और प्रेडिकेट्स === | ===अनुशंसित फंक्शन्स और प्रेडिकेट्स === | ||
* <code>copysign(x,y)</code> y के चिह्न के साथ x प्रदान करता है, इसलिए <code>abs(x)</code> <code>copysign(x,1.0)</code> के समान होती है। यह उन कुछ ऑपरेशनों में से है जो अंकगणित के समान NaN पर संचालित होता है। फ़ंक्शन <code>copysign</code> C99 | * <code>copysign(x,y)</code> y के चिह्न के साथ x प्रदान करता है, इसलिए <code>abs(x)</code> <code>copysign(x,1.0)</code> के समान होती है। यह उन कुछ ऑपरेशनों में से है जो अंकगणित के समान NaN पर संचालित होता है। फ़ंक्शन <code>copysign</code> C99 स्टैण्डर्ड में नया है। | ||
* −x, विपरीत चिह्न के साथ x प्रदान करता है। यह कुछ स्थितियों में 0−x से भिन्न है, विशेष रूप से जब x 0 है। तो −(0) −0 है, किन्तु 0−0 का चिह्न पूर्णांकन मोड पर निर्भर करता है। | * −x, विपरीत चिह्न के साथ x प्रदान करता है। यह कुछ स्थितियों में 0−x से भिन्न है, विशेष रूप से जब x 0 है। तो −(0) −0 है, किन्तु 0−0 का चिह्न पूर्णांकन मोड पर निर्भर करता है। | ||
* <code>scalb(y, N)</code> | * <code>scalb(y, N)</code> | ||
| Line 393: | Line 393: | ||
* <code>unordered(x, y)</code> सत्य है जब x, y के साथ अव्यवस्थित है, अर्थात, x या y NaN है। | * <code>unordered(x, y)</code> सत्य है जब x, y के साथ अव्यवस्थित है, अर्थात, x या y NaN है। | ||
* <code>class(x)</code> | * <code>class(x)</code> | ||
* <code>nextafter(x,y)</code> x से y की दिशा में अगला | * <code>nextafter(x,y)</code> x से y की दिशा में अगला रिप्रेजेंट योग्य मान प्रदान करता है। | ||
==इतिहास== | ==इतिहास== | ||
1976 में, [[इंटेल]] फ्लोटिंग-पॉइंट[[ सह प्रोसेसर | कोप्रोसेसर]] का विकास प्रारंभ कर रहा था।<ref name="Intel_2016_Case"/><ref name="Kahan_1998_Story"/> इंटेल को अपेक्षा थी कि वह व्यापक रूप से भिन्न गणित सॉफ्टवेयर लाइब्रेरी में पाए जाने वाले सभी ऑपरेशनों के उत्तम कार्यान्वयन वाली चिप विक्रय में सक्षम होगी।<ref name="Intel_2016_Case"/><ref name="Woehr_1997_Kahan"/> | 1976 में, [[इंटेल]] फ्लोटिंग-पॉइंट[[ सह प्रोसेसर | कोप्रोसेसर]] का विकास प्रारंभ कर रहा था।<ref name="Intel_2016_Case"/><ref name="Kahan_1998_Story"/> इंटेल को अपेक्षा थी कि वह व्यापक रूप से भिन्न गणित सॉफ्टवेयर लाइब्रेरी में पाए जाने वाले सभी ऑपरेशनों के उत्तम कार्यान्वयन वाली चिप विक्रय में सक्षम होगी।<ref name="Intel_2016_Case"/><ref name="Woehr_1997_Kahan"/> | ||
जॉन पामर, जिन्होंने इस परियोजना का प्रबंधन किया था, इसका मानना था कि इस प्रयास को भिन्न-भिन्न प्रोसेसरों में | जॉन पामर, जिन्होंने इस परियोजना का प्रबंधन किया था, इसका मानना था कि इस प्रयास को भिन्न-भिन्न प्रोसेसरों में स्टैण्डर्ड एकीकृत फ़्लोटिंग पॉइंट संचालन द्वारा समर्थित किया जाना चाहिए। उन्होंने [[कैलिफोर्निया विश्वविद्यालय]] के [[विलियम कहाँ|विलियम काहन]] से संपर्क किया, जिन्होंने[[ हेवलेट पैकर्ड ]]के कैलकुलेटर की एक्यूरेसी में सुधार करने में सहायता की थी। काहन ने सुझाव दिया कि इंटेल[[ डिजिटल उपकरण निगम | डिजिटल इक्विपमेंट कॉर्पोरेशन]] (डीईसी) वैक्स के फ्लोटिंग पॉइंट का उपयोग करता है। प्रथम वैक्स, वैक्स-11/780 1977 के अंत में सामने आया था, और इसके फ्लोटिंग पॉइंट को अत्यधिक महत्व दिया गया था। चूँकि, अपनी चिप को व्यापक मार्केट में विक्रय के लिए, इंटेल सर्वोत्तम फ़्लोटिंग पॉइंट चाहता था, और काहन ने विशिष्टताओं को प्रस्तुत किया था।<ref name="Intel_2016_Case"/> काहन ने प्रारंभ में अनुरोध किया था कि फ़्लोटिंग पॉइंट बेस दशमलव हो<ref>W. Kahan 2003, pers. comm. to [[Mike Cowlishaw]] and others after an IEEE 754 meeting</ref>{{unreliable source?|date=October 2016}} किन्तु कोप्रोसेसर का हार्डवेयर डिज़ाइन उस परिवर्तन को करने के लिए अधिक दूर था। | ||
इंटेल के अंदर कार्य ने अन्य विक्रेताओं को चिंतित कर दिया, जिन्होंने समान संयोग सुनिश्चित करने के लिए मानकीकरण प्रयास स्थापित किया था। काहन ने नवंबर 1977 में आयोजित दूसरी आईईईई 754 | इंटेल के अंदर कार्य ने अन्य विक्रेताओं को चिंतित कर दिया, जिन्होंने समान संयोग सुनिश्चित करने के लिए मानकीकरण प्रयास स्थापित किया था। काहन ने नवंबर 1977 में आयोजित दूसरी आईईईई 754 स्टैण्डर्ड कार्य समूह की बैठक में भाग लिया था। अंत में उन्हें इंटेल से उनके कोप्रोसेसर के लिए उनके कार्य के आधार पर ड्राफ्ट प्रस्ताव प्रस्तुत करने की अनुमति प्राप्त हुई; उन्हें प्रारूप के विवरण और उसके औचित्य को समझाने की अनुमति प्रदान की गई थी, किन्तु इंटेल के कार्यान्वयन वास्तुकला से संबंधित कुछ भी नहीं था। ड्राफ्ट जेरोम कूनन और हेरोल्ड स्टोन के साथ सह-लिखित था, और प्रारंभ में इसे काहन-कूनन-स्टोन प्रस्ताव या के-सी-एस प्रारूप के रूप में जाना जाता था।<ref name="Intel_2016_Case"/><ref name="Kahan_1998_Story"/><ref name="Woehr_1997_Kahan"/><ref name="Chuck_Kahan_Interview"/> | ||
चूंकि 8-बिट घातांक दोहरे- | चूंकि 8-बिट घातांक दोहरे-एक्यूरेसी नंबर्स के लिए वांछित कुछ परिचालनों के लिए पर्याप्त चौड़ा नहीं था, उदाहरण के लिए दो 32-बिट नंबर्स के उत्पाद को संग्रहीत करने के लिए,<ref name="Microsoft_2006_KB35826"/> काहन के प्रस्ताव और डीईसी के प्रति-प्रस्ताव दोनों में 11 बिट्स का उपयोग किया गया था, जैसे कि 1965 से [[सीडीसी 6600]] के समय-परीक्षणित 60-बिट फ़्लोटिंग-पॉइंट प्रारूप था।<ref name="Kahan_1998_Story"/><ref name="Chuck_Kahan_Interview"/><ref name="Thornton_1970_CDC6600"/> काहन के प्रस्ताव में अनन्तताओं का भी प्रावधान किया गया है, जो विभाजन-दर-शून्य स्थितियों के निवारण में उपयोगी होते हैं; नॉट-ए-नंबर मान, जो अमान्य संचालन के निवारण में उपयोगी होते हैं; [[असामान्य संख्या|असामान्य नंबर्स,]] जो अंडरफ्लो के कारण होने वाली समस्याओं को कम करने में सहायता करती हैं;<ref name="Chuck_Kahan_Interview"/><ref name="Kahan_Why"/><ref name="Kahan_Java"/> और उत्तम संतुलित घातांक पूर्वाग्रह, जो किसी संख्या का व्युत्क्रम लेते समय अतिप्रवाह और अल्पप्रवाह से विक्रय में सहायता कर सकता है।<ref name="Turner_2013"/><ref name="Kahan_Names"/> | ||
अनुमोदित होने से पूर्व ही, ड्राफ्ट | अनुमोदित होने से पूर्व ही, ड्राफ्ट स्टैण्डर्ड को कई निर्माताओं द्वारा इम्प्लीमेंट किया गया था।<ref>{{cite web|url=http://www.eecs.berkeley.edu/~wkahan/ieee754status/754story.html|title=फ़्लोटिंग-प्वाइंट के बूढ़े आदमी के साथ एक साक्षात्कार| author=Charles Severance |author-link=Charles Severance (computer scientist) |date=20 February 1998}}</ref><ref>{{cite web|publisher=Connexions |url=http://cnx.org/content/m32770/latest/ |title=आईईईई फ़्लोटिंग-पॉइंट प्रारूप का इतिहास|author=Charles Severance |author-link=Charles Severance (computer scientist) |archive-url=https://web.archive.org/web/20091120095507/http://cnx.org/content/m32770/latest/ |archive-date=2009-11-20 |url-status=dead}}</ref> इंटेल 8087, जिसे 1980 में घोषित किया गया था, जो ड्राफ्ट स्टैण्डर्ड को इम्प्लीमेंट करने वाली प्रथम चिप थी। | ||
[[File:Intel C8087.jpg|thumb|left|इंटेल 8087 फ्लोटिंग-पॉइंट कोप्रोसेसर]]1980 में, इंटेल 8087 चिप पहले ही | [[File:Intel C8087.jpg|thumb|left|इंटेल 8087 फ्लोटिंग-पॉइंट कोप्रोसेसर]]1980 में, इंटेल 8087 चिप पहले ही इम्प्लीमेंट हो चुकी थी,<ref name="Olympus_MIC-D"/> किन्तु प्रदर्शन संबंधी चिंताओं के कारण डीईसी विशेष रूप से असामान्य नंबर्स का विरोध करता रहा और चूंकि इससे डीईसी को डीईसी के प्रारूप पर मानकीकरण करने के लिए प्रतिस्पर्धात्मक लाभ मिलता है। | ||
क्रमिक अंडरफ़्लो पर विचार 1981 तक चला जब इसका आकलन करने के लिए डीईसी द्वारा नियुक्त विशेषज्ञ ने असंतुष्टों का पक्ष लिया था। डीईसी ने यह प्रदर्शित करने के लिए अध्ययन करवाया था कि क्रमिक अंडरफ़्लो बुरा विचार था, किन्तु अध्ययन का निष्कर्ष विपरीत था, और डीईसी ने हार मान ली थी। 1985 में, | क्रमिक अंडरफ़्लो पर विचार 1981 तक चला जब इसका आकलन करने के लिए डीईसी द्वारा नियुक्त विशेषज्ञ ने असंतुष्टों का पक्ष लिया था। डीईसी ने यह प्रदर्शित करने के लिए अध्ययन करवाया था कि क्रमिक अंडरफ़्लो बुरा विचार था, किन्तु अध्ययन का निष्कर्ष विपरीत था, और डीईसी ने हार मान ली थी। 1985 में, स्टैण्डर्ड की पुष्टि की गई थी, किन्तु यह एक वर्ष पूर्व ही वास्तविक स्टैण्डर्ड बन गया था, जिसे कई निर्माताओं द्वारा कार्यान्वित किया गया था।<ref name="Kahan_1998_Story"/><ref name="Chuck_Kahan_Interview"/><ref name="Kahan"/> | ||
==यह भी देखें== | ==यह भी देखें== | ||
*[[आईईईई 754]] | *[[आईईईई 754]] | ||
Revision as of 12:16, 15 September 2023
आईईईई 754-1985[1] कंप्यूटर में फ्लोटिंग-पॉइंट नंबर्स को रिप्रेजेंट करने के लिए इंडस्ट्री स्टैण्डर्ड था, जिसे सामान्यतः 1985 में स्वीकार किया गया था और 2008 में आईईईई 754-2008 द्वारा प्रतिस्थापित किया गया था, और फिर 2019 में माइनर वर्ज़न आईईईई 754-2019 द्वारा प्रतिस्थापित किया गया था।[2] अपने 23 वर्षों के समय में, यह फ़्लोटिंग-पॉइंट कैलकुलेशन के लिए सबसे वाइड रूप से उपयोग किया जाने वाला प्रारूप था। इसे सॉफ़्टवेयर में, फ़्लोटिंग-पॉइंट लाइब्रेरीज़ के रूप में, और हार्डवेयर में, कई सीपीयू और एफपीयू के इंस्ट्रक्शन में इम्प्लीमेंट किया गया था। आईईईई 754-1985 बनने वाले ड्राफ्ट को इम्प्लीमेंट करने वाला प्रथम इंटीग्रेटेड सर्किट इंटेल 8087 था।
आईईईई 754-1985 बाइनरी में नंबर्स को रिप्रेजेंट करता है, जो एक्यूरेसी के चार लेवल्स की परिभाषा प्रदान करता है, जिनमें से दो सबसे अधिक उपयोग किए जाते हैं:
| लेवल | विड्थ | पूर्ण एक्यूरेसी से रेंज करें | एक्यूरेसी[lower-alpha 1] |
|---|---|---|---|
| सिंगल एक्यूरेसी | 32 bits | ±1.18×10−38 to ±3.4×1038 | लगभग 7 दशमलव अंक |
| डबल एक्यूरेसी | 64 bits | ±2.23×10−308 to ±1.80×10308 | लगभग 16 दशमलव अंक |
स्टैण्डर्ड पॉजिटिव और नेगेटिव इनफाइनाइट के लिए रिप्रेजेंट को भी परिभाषित करता है, नेगेटिव शून्य, शून्य से विभाजन जैसे अमान्य परिणामों को सुरक्षित करने के लिए पांच एक्सेप्शन, उन एक्सेप्शन्स का रिप्रेजेंट करने के लिए विशेष मान जिन्हें NaN कहा जाता है, ऊपर दिखाए गए छोटी नंबर्स का रिप्रेजेंट करने के लिए डिनॉर्मल नंबर्स, और चार गोल मोड है।
नंबर्स का रिप्रेजेंट
आईईईई 754 प्रारूप में फ़्लोटिंग-पॉइंट नंबरों में तीन क्षेत्र होते हैं: साइन बिट, बायस्ड घातांक और अंश। निम्नलिखित उदाहरण प्रत्येक का अर्थ बताता है।
दशमलव संख्या 0.1562510 बाइनरी में 0.001012 (अर्थात् 1/8 + 1/32) प्रदर्शित किया गया है। (अंकाक्षर संख्या मूलांक प्रदर्शित करते हैं।) वैज्ञानिक संकेतन के अनुरूप, जहां नंबर्स को दशमलव बिंदु के बाईं ओर अन्य-शून्य अंक के रूप में लिखा जाता है, हम इस संख्या को पुनः लिखते हैं जिससे कि इसमें बाइनरी बिंदु के बाईं ओर सिंगल 1 बिट होता है। हम तीन स्थितियों द्वारा त्यागे गए बिट्स के स्थानांतरण की पूर्ति के लिए 2 की उचित शक्ति से गुणा करते हैं:
अब हम भिन्न और घातांक को पढ़ सकते हैं: भिन्न .012 है और घातांक −3 है।
जैसा कि चित्रों में प्रदर्शित किया गया है, आईईईई 754 में इस संख्या का रिप्रेजेंट करने वाले तीन क्षेत्र हैं:
- चिन्ह = 0, क्योंकि संख्या पॉजिटिव है (1 नेगेटिव प्रदर्शित करता है।)।
- बायस्ड घातांक = −3 + बायस है। 'सिंगल एक्यूरेसी' में, बायस '127' है, इसलिए इस उदाहरण में बायस्ड घातांक 124 है; 'डबल प्रिसिजन' में, बायस '1023' है, इसलिए इस उदाहरण में बायस्ड घातांक 1020 है।
- अपूर्णांक = .01000…2.
आईईईई 754 घातांक में ऑफसेट बाइनरी जोड़ता है जिससे कि कई स्थितियों में नंबर्स की अपेक्षा उसी हार्डवेयर द्वारा सरलता से की जा सके जो हस्ताक्षरित 2-पूरक पूर्णांकों की अपेक्षा करता है। बायस्ड घातांक का उपयोग करते हुए, दो पॉजिटिव फ़्लोटिंग-पॉइंट नंबर्स में से छोटी संख्या चिह्न और परिमाण पूर्णांक के समान क्रम के पश्चात बड़ी संख्या से कम निकलती है। यदि दो फ़्लोटिंग-पॉइंट नंबर्स के भिन्न-भिन्न चिह्न हैं, तो चिह्न-और-परिमाण अपेक्षा बायस्ड घातांक के साथ भी कार्य करती है। चूँकि, यदि दोनों बायस्ड-घातांक फ़्लोटिंग-पॉइंट नंबर्स नेगेटिव हैं, तो क्रम को विपरीत कर दिया जाना चाहिए। यदि घातांक को, मान लीजिए, 2-पूरक संख्या के रूप में प्रदर्शित किया जाता है, तो यह देखने के लिए अपेक्षा करना कि दो नंबर्स में से कौन सी बड़ी है, सुविधाजनक नहीं होता है।
अग्रणी 1 बिट को विस्थापित कर दिया गया है क्योंकि शून्य को त्यागकर सभी नंबर्स अग्रणी 1 से प्रारंभ होती हैं; अग्रणी 1 अंतर्निहित है और वास्तव में इसे संग्रहीत करने की आवश्यकता नहीं है जो मुफ़्त में अतिरिक्त एक्यूरेसी प्रदान करता है।
शून्य
शून्य संख्या को विशेष रूप से प्रदर्शित किया गया है:
- पॉजिटिव शून्य के लिए चिह्न = 0, नेगेटिव शून्य के लिए 1 है।
- बायस्ड घातांक = 0 है।
- अपूर्णांक = 0 है।
असामान्यीकृत नंबर्स
ऊपर वर्णित संख्या निरूपण को सामान्यीकृत कहा जाता है, जिसका अर्थ है कि अंतर्निहित अग्रणी बाइनरी अंक 1 है। अंडरफ्लो होने पर एक्यूरेसी की हानि को कम करने के लिए, आईईईई 754 में सामान्यीकृत रिप्रेजेंट में संभव से छोटे अंशों का रिप्रेजेंट करने की क्षमता सम्मिलित है। अंतर्निहित अग्रणी अंक 0 बनाता है। ऐसी नंबर्स को असामान्य नंबर्स कहा जाता है। उनमें सामान्यीकृत संख्या के रूप में कई महत्वपूर्ण अंक सम्मिलित नहीं होते हैं, किन्तु जब किसी ऑपरेशन का परिणाम शून्य नहीं होता है, किन्तु सामान्यीकृत संख्या द्वारा प्रदर्शित किये जाने के लिए शून्य के अधिक निकट होता है, तो वे एक्यूरेसी की क्रमिक हानि को सक्षम करते हैं।
असामान्य संख्या को सभी 0 बिट्स के बायस्ड घातांक के साथ प्रदर्शित किया जाता है, जो सिंगल एक्यूरेसी में −126 के घातांक का रिप्रेजेंट करता है (−127 नहीं), या दोहरी एक्यूरेसी में −1022 (−1023 नहीं) का रिप्रेजेंट करता है।[3] इसके विपरीत, सामान्य संख्या का रिप्रेजेंट करने वाला सबसे छोटा बायस्ड घातांक 1 है (नीचे उदाहरण देखें)।
गैर-नंबर्स का रिप्रेजेंट
किसी कैलकुलेशन की अनंतता या अमान्य परिणाम को प्रदर्शित करने के लिए बायस्ड-घातांक क्षेत्र सभी 1 बिट्स से पूर्ण है।
पॉजिटिव और नेगेटिव इनफाइनाइट
पॉजिटिव और नेगेटिव इनफाइनाइट को इस प्रकार प्रदर्शित किया गया है:
- पॉजिटिव इनफाइनाइट के लिए चिह्न = 0, नेगेटिव इनफाइनाइट के लिए 1 है।
- बायस्ड घातांक = सभी 1 बिट्स है।
- अपूर्णांक = सभी 0 बिट्स है।
NaN
फ़्लोटिंग-पॉइंट अंकगणित के कुछ ऑपरेशन अमान्य हैं, जैसे नेगेटिव संख्या का वर्गमूल लेता है। किसी अमान्य परिणाम तक पहुंचने की क्रिया को फ़्लोटिंग-पॉइंट अपवाद कहा जाता है। असाधारण परिणाम को "नॉट ए नंबर" के लिए NaN नामक विशेष कोड द्वारा प्रदर्शित किया जाता है। आईईईई 754-1985 में सभी NaN का प्रारूप यह है:
- चिह्न = या तो 0 या 1 होता है।
- बायस्ड घातांक = सभी 1 बिट्स है।
- अपूर्णांक = सभी 0 बिट्स को त्यागकर कुछ भी होता है (क्योंकि सभी 0 बिट्स इनफाइनाइट का रिप्रेजेंट करते हैं)।
श्रेणी और एक्यूरेसी

एक्यूरेसी को दो क्रमिक मंटिसा अभ्यावेदन के मध्य न्यूनतम अंतर के रूप में परिभाषित किया गया है; इस प्रकार यह केवल मंटिसा में फंक्शन है; जबकि अंतर को दो क्रमिक नंबर्स के मध्य के अंतर के रूप में परिभाषित किया गया है।[4]
सिंगल-त्रुटिहीन नंबर्स 32 बिट्स पर व्याप्त हैं। सिंगल एक्यूरेसी में:
- शून्य के निकटतम पॉजिटिव और नेगेटिव नंबर्स (घातक क्षेत्र में सभी 0 के साथ असामान्य मान और अपूर्णांक क्षेत्र में बाइनरी मान 1 द्वारा प्रदर्शित की जाती हैं) हैं:
- ±2−23×2−126 ≈ ±1.40130×10−45
- शून्य के निकटतम पॉजिटिव और नेगेटिव सामान्यीकृत नंबर्स (घातक क्षेत्र में बाइनरी मान 1 और अपूर्णांक क्षेत्र में 0 के साथ प्रदर्शित की जाती हैं) हैं:
- ±1 × 2−126 ≈ ±1.17549×10−38
- शून्य से सबसे दूर की परिमित पॉजिटिव और परिमित नेगेटिव नंबर्स (घातक क्षेत्र में 254 और अपूर्णांक क्षेत्र में सभी 1 के साथ मान द्वारा प्रदर्शित की गई) हैं:
- ±(2−2−23) × 2127[5] ≈ ±3.40282×1038
सिंगल एक्यूरेसी में दिए गए घातांक के लिए कुछ उदाहरण सीमा और अंतराल मान है:
| वास्तविक घातांक (अनबायस्ड) | घातांक (बायस्ड) | न्यूनतम | अधिकतम | गैप |
|---|---|---|---|---|
| −1 | 126 | 0.5 | ≈ 0.999999940395 | ≈ 5.96046e-8 |
| 0 | 127 | 1 | ≈ 1.999999880791 | ≈ 1.19209e-7 |
| 1 | 128 | 2 | ≈ 3.999999761581 | ≈ 2.38419e-7 |
| 2 | 129 | 4 | ≈ 7.999999523163 | ≈ 4.76837e-7 |
| 10 | 137 | 1024 | ≈ 2047.999877930 | ≈ 1.22070e-4 |
| 11 | 138 | 2048 | ≈ 4095.999755859 | ≈ 2.44141e-4 |
| 23 | 150 | 8388608 | 16777215 | 1 |
| 24 | 151 | 16777216 | 33554430 | 2 |
| 127 | 254 | ≈ 1.70141e38 | ≈ 3.40282e38 | ≈ 2.02824e31 |
उदाहरण के लिए, 16,777,217 को 32-बिट फ़्लोट के रूप में एन्कोड नहीं किया जा सकता क्योंकि इसे 16,777,216 पर पूर्णांकित किया जाएगा। इससे ज्ञात होता है कि फ़्लोटिंग पॉइंट अंकगणित लेखांकन सॉफ़्टवेयर के लिए अनुपयुक्त क्यों है। चूँकि, रिप्रेजेंट योग्य सीमा के अंदर सभी पूर्णांक जो 2 की शक्ति हैं, उन्हें बिना गोलाई के 32-बिट फ़्लोट में संग्रहीत किया जा सकता है।
दोहरी एक्यूरेसी
डबल-त्रुटिहीन नंबर्स 64 बिट्स पर व्याप्त हैं। दोहरी एक्यूरेसी में:
- शून्य के निकटतम पॉजिटिव और नेगेटिव नंबर्स (एक्सप क्षेत्र में सभी 0 के साथ असामान्य मान और अपूर्णांक क्षेत्र में बाइनरी मान 1 द्वारा प्रदर्शित की जाती हैं) हैं
- ±2−52×2−1022 ≈ ±4.94066×10−324
- शून्य के निकटतम पॉजिटिव और नेगेटिव सामान्यीकृत नंबर्स (एक्सप क्षेत्र में बाइनरी मान 1 और अपूर्णांक क्षेत्र में 0 के साथ प्रदर्शित की जाती हैं) हैं:
- ±1 × 2−1022 ≈ ±2.22507×10−308
- शून्य से सबसे दूर की परिमित पॉजिटिव और परिमित नेगेटिव नंबर्स (एक्सप क्षेत्र में 2046 और अपूर्णांक क्षेत्र में सभी 1 के साथ मान द्वारा प्रदर्शित की गई) हैं:
- ±(2−2−52)×21023[5]≈ ±1.79769×10308
दोहरी एक्यूरेसी में दिए गए घातांक के लिए कुछ उदाहरण सीमा और अंतराल मान है:
| वास्तविक घातांक (अनबायस्ड) | घातांक (बायस्ड) | न्यूनतम | अधिकतम | गैप |
|---|---|---|---|---|
| −1 | 1022 | 0.5 | ≈ 0.999999999999999888978 | ≈ 1.11022e-16 |
| 0 | 1023 | 1 | ≈ 1.999999999999999777955 | ≈ 2.22045e-16 |
| 1 | 1024 | 2 | ≈ 3.999999999999999555911 | ≈ 4.44089e-16 |
| 2 | 1025 | 4 | ≈ 7.999999999999999111822 | ≈ 8.88178e-16 |
| 10 | 1033 | 1024 | ≈ 2047.999999999999772626 | ≈ 2.27374e-13 |
| 11 | 1034 | 2048 | ≈ 4095.999999999999545253 | ≈ 4.54747e-13 |
| 52 | 1075 | 4503599627370496 | 9007199254740991 | 1 |
| 53 | 1076 | 9007199254740992 | 18014398509481982 | 2 |
| 1023 | 2046 | ≈ 8.98847e307 | ≈ 1.79769e308 | ≈ 1.99584e292 |
विस्तारित प्रारूप
स्टैण्डर्ड राउंड-ऑफ त्रुटियों को कम करने के लिए, अंतिम परिणाम के लिए आवश्यक उच्च एक्यूरेसी पर आंतरिक कैलकुलेशन करने के लिए विस्तारित प्रारूप का उपयोग करने का अनुरोध करता है: स्टैण्डर्ड केवल ऐसे प्रारूपों के लिए न्यूनतम एक्यूरेसी और घातांक आवश्यकताओं को निर्दिष्ट करता है। x87 80-बिट विस्तारित प्रारूप सबसे अधिक कार्यान्वित विस्तारित प्रारूप है जो इन आवश्यकताओं को पूर्ण करता है।
उदाहरण
यहां सिंगल-त्रुटिहीन आईईईई 754 अभ्यावेदन के कुछ उदाहरण दिए गए हैं:
| प्रकार | चिह्न | वास्तविक घातांक | घातांक (बायस्ड) | घातांक क्षेत्र | अपूर्णांक क्षेत्र | मान |
|---|---|---|---|---|---|---|
| शून्य | 0 | −126 | 0 | 0000 0000 | 000 0000 0000 0000 0000 0000 | 0.0 |
| नेगेटिव शून्य | 1 | −126 | 0 | 0000 0000 | 000 0000 0000 0000 0000 0000 | −0.0 |
| एक | 0 | 0 | 127 | 0111 1111 | 000 0000 0000 0000 0000 0000 | 1.0 |
| शून्य से एक कम | 1 | 0 | 127 | 0111 1111 | 000 0000 0000 0000 0000 0000 | −1.0 |
| सबसे छोटी असामान्यीकृत संख्या | * | −126 | 0 | 0000 0000 | 000 0000 0000 0000 0000 0001 | ±2−23 × 2−126 = ±2−149 ≈ ±1.4×10−45 |
| "मध्य" असामान्यीकृत संख्या | * | −126 | 0 | 0000 0000 | 100 0000 0000 0000 0000 0000 | ±2−1 × 2−126 = ±2−127 ≈ ±5.88×10−39 |
| सबसे बड़ी असामान्यीकृत संख्या | * | −126 | 0 | 0000 0000 | 111 1111 1111 1111 1111 1111 | ±(1−2−23) × 2−126 ≈ ±1.18×10−38 |
| सबसे छोटी सामान्यीकृत संख्या | * | −126 | 1 | 0000 0001 | 000 0000 0000 0000 0000 0000 | ±2−126 ≈ ±1.18×10−38 |
| सबसे बड़ी सामान्यीकृत संख्या | * | 127 | 254 | 1111 1110 | 111 1111 1111 1111 1111 1111 | ±(2−2−23) × 2127 ≈ ±3.4×1038 |
| पॉजिटिव अनन्तता | 0 | 128 | 255 | 1111 1111 | 000 0000 0000 0000 0000 0000 | +∞ |
| नेगेटिव अनन्तता | 1 | 128 | 255 | 1111 1111 | 000 0000 0000 0000 0000 0000 | −∞ |
| कोई संख्या नहीं | * | 128 | 255 | 1111 1111 | गैर शून्य | NaN |
| * साइन बिट 0 या 1 हो सकता है। | ||||||
फ़्लोटिंग-पॉइंट नंबर्स की अपेक्षा करना
नेगेटिव शून्य और पॉजिटिव शून्य के लिए बिट्स के दो संयोजनों को त्यागकर, प्रत्येक संभावित बिट संयोजन या तो NaN है या संबद्ध क्रम के साथ एफ़िनली विस्तारित वास्तविक संख्या प्रणाली में अद्वितीय मान वाला नंबर है, जिस पर कभी-कभी विशेष ध्यान देने की आवश्यकता होती है (नीचे देखें)। बाइनरी रिप्रेजेंट में विशेष गुण होता है कि, NaN को त्यागकर, किसी भी दो नंबर्स की अपेक्षा चिह्न और परिमाण पूर्णांक के रूप में की जा सकती है (एंडियननेस उद्देश्य इम्प्लीमेंट होते हैं)। 2 के पूरक पूर्णांकों के रूप में अपेक्षा करते समय: यदि साइन बिट भिन्न होते हैं, तो नेगेटिव संख्या पॉजिटिव संख्या से पूर्व होती है, इसलिए 2 का पूरक सही परिणाम देता है (इसके अतिरिक्त कि नेगेटिव शून्य और पॉजिटिव शून्य को समान माना जाना चाहिए)। यदि दोनों मान पॉजिटिव हैं, तो 2 की पूरक अपेक्षा पुनः उचित परिणाम देती है। अन्यथा (दो नेगेटिव नंबर्स), उचित एफपी क्रम 2 के पूरक क्रम के विपरीत है।
फ़्लोटिंग पॉइंट गणनाओं में निहित राउंडिंग त्रुटियाँ परिणामों की त्रुटिहीन समानता के परीक्षण के लिए अपेक्षाओं के उपयोग को सीमित कर सकती हैं। स्वीकार्य सीमा का चयन करना समष्टि विषय है। सामान्य तकनीक अनुमानित अपेक्षा करने के लिए अपेक्षात्मक ईपीएसलॉन मान का उपयोग करना है।[6] अपेक्षाएँ कितनी उदार हैं, इस पर निर्भर करते हुए, सामान्य मूल्यों में सिंगल-एक्यूरेसी के लिए 1e-6 या 1e-5और दोहरी एक्यूरेसी के लिए 1e-14 सम्मिलित हैं।[7][8] अन्य सामान्य तकनीक यूएलपी है, जो यह परीक्षण करती है कि अंतिम स्थान के अंकों में क्या अंतर है, प्रभावी रूप से यह परीक्षण करती है कि दोनों मान कितने दूर हैं।[9]
चूँकि अपेक्षात्मक उद्देश्यों के लिए नेगेटिव शून्य और पॉजिटिव शून्य को सामान्यतः समान माना जाता है, कुछ प्रोग्रामिंग लैंग्वेज रिलेशनल ऑपरेटर और समान निर्माण उन्हें भिन्न मानते हैं। जावा लैंग्वेज विशिष्टता के अनुसार,[10] अपेक्षा और समानता संचालक उन्हें समान मानते हैं, किन्तु Math.min() और Math.max() उन्हें भिन्न करते हैं (सामान्यतः जावा संस्करण 1.1 से प्रारंभ करते हैं किन्तु वास्तव में 1.1.1 के साथ), जैसा कि अपेक्षा विधियां Float और Double कक्षाओं का equals(), compareTo() और यहां तक कि compare() भी हैं।
फ़्लोटिंग-पॉइंट नंबर्स को पूर्णांकित करना
आईईईई स्टैण्डर्ड में चार भिन्न-भिन्न राउंडिंग मोड हैं; प्रथम डिफ़ॉल्ट है; अन्य को निर्देशित गोलाई कहा जाता है।
- 'राउंड टू नियरेस्ट' - निकटतम मान तक राउंड; यदि संख्या मध्य में गिरती है तो इसे सम (शून्य) कम से कम महत्वपूर्ण बिट के साथ निकटतम मान तक पूर्णांकित किया जाता है, जिसका अर्थ है कि इसे 50% समय तक पूर्णांकित किया जाता है (आईईईई 754-2008 में इस मोड को दूसरे से अलग करने के लिए राउंडटीज़टूईवन कहा जाता है) -से-निकटतम मोड)।
- 'राउंड टुवर्ड 0' - शून्य की ओर निर्देशित गोलाई।
- 'राउंड टुवर्ड +∞' - पॉजिटिव इनफाइनाइट की ओर निर्देशित गोलाई।
- 'राउंड टुवर्ड -∞' - नेगेटिव इनफाइनाइट की ओर निर्देशित गोलाई।
वास्तविक नंबर्स का विस्तार
आईईईई स्टैण्डर्ड भिन्न-भिन्न पॉजिटिव और नेगेटिव अनन्तताओं के साथ, पूर्ण रूप से विस्तारित वास्तविक संख्या प्रणाली को नियोजित (और विस्तारित) करता है। प्रारूपण के समय, प्रोग्रामर को मोड चयन विकल्प प्रदान करके, सिंगल अहस्ताक्षरित इनफाइनाइट के साथ प्रोजेक्टिवली विस्तारित वास्तविक संख्या प्रणाली को सम्मिलित करने के लिए स्टैण्डर्ड का प्रस्ताव था। चूँकि, अंतिम स्टैण्डर्ड की समष्टिता को कम करने के हित में, प्रोजेक्टिव मोड को विस्थापित कर दिया गया था। इंटेल 8087 और इंटेल 80287 फ़्लोटिंग पॉइंट सह-प्रोसेसर दोनों इस प्रोजेक्टिव मोड का समर्थन करते हैं।[11][12][13]
फंक्शन्स और प्रेडिकेट्स
स्टैण्डर्ड संचालन
निम्नलिखित कार्य प्रदान किए जाने चाहिए:
- जोड़ें, घटाएं, गुणा करें, भाग करें।
- वर्गमूल
- फ़्लोटिंग पॉइंट शेष यह सामान्य मॉड्यूलो ऑपरेशन के जैसे नहीं है, यह दो पॉजिटिव नंबर्स के लिए नेगेटिव हो सकता है। यह x–(round(x/y)·y) का त्रुटिहीन मान प्रदान करता है।
- निकटतम पूर्णांक तक पूर्णांकन अप्रत्यक्ष पूर्णांकन के लिए जब दो पूर्णांकों के मध्य आधा हो तो सम पूर्णांक चयन किया जाता है।
- अपेक्षा संचालन. अधिक स्पष्ट परिणामों के अतिरिक्त, आईईईई 754 परिभाषित करता है कि −∞ = −∞, +∞ = +∞ और x ≠
NaNकिसी भी x के लिए (सहित)NaN) होता है।
अनुशंसित फंक्शन्स और प्रेडिकेट्स
copysign(x,y)y के चिह्न के साथ x प्रदान करता है, इसलिएabs(x)copysign(x,1.0)के समान होती है। यह उन कुछ ऑपरेशनों में से है जो अंकगणित के समान NaN पर संचालित होता है। फ़ंक्शनcopysignC99 स्टैण्डर्ड में नया है।- −x, विपरीत चिह्न के साथ x प्रदान करता है। यह कुछ स्थितियों में 0−x से भिन्न है, विशेष रूप से जब x 0 है। तो −(0) −0 है, किन्तु 0−0 का चिह्न पूर्णांकन मोड पर निर्भर करता है।
scalb(y, N)logb(x)finite(x)x के लिए प्रेडीकेट परिमित मान है, जो −Inf < x < Inf के समान है।isnan(x)x के लिए प्रेडीकेट NaN है, जो x ≠ x के समान है।x <> y, जिसका व्यवहार NaN के कारण NOT(x = y) से भिन्न होता है।unordered(x, y)सत्य है जब x, y के साथ अव्यवस्थित है, अर्थात, x या y NaN है।class(x)nextafter(x,y)x से y की दिशा में अगला रिप्रेजेंट योग्य मान प्रदान करता है।
इतिहास
1976 में, इंटेल फ्लोटिंग-पॉइंट कोप्रोसेसर का विकास प्रारंभ कर रहा था।[14][15] इंटेल को अपेक्षा थी कि वह व्यापक रूप से भिन्न गणित सॉफ्टवेयर लाइब्रेरी में पाए जाने वाले सभी ऑपरेशनों के उत्तम कार्यान्वयन वाली चिप विक्रय में सक्षम होगी।[14][16]
जॉन पामर, जिन्होंने इस परियोजना का प्रबंधन किया था, इसका मानना था कि इस प्रयास को भिन्न-भिन्न प्रोसेसरों में स्टैण्डर्ड एकीकृत फ़्लोटिंग पॉइंट संचालन द्वारा समर्थित किया जाना चाहिए। उन्होंने कैलिफोर्निया विश्वविद्यालय के विलियम काहन से संपर्क किया, जिन्होंनेहेवलेट पैकर्ड के कैलकुलेटर की एक्यूरेसी में सुधार करने में सहायता की थी। काहन ने सुझाव दिया कि इंटेल डिजिटल इक्विपमेंट कॉर्पोरेशन (डीईसी) वैक्स के फ्लोटिंग पॉइंट का उपयोग करता है। प्रथम वैक्स, वैक्स-11/780 1977 के अंत में सामने आया था, और इसके फ्लोटिंग पॉइंट को अत्यधिक महत्व दिया गया था। चूँकि, अपनी चिप को व्यापक मार्केट में विक्रय के लिए, इंटेल सर्वोत्तम फ़्लोटिंग पॉइंट चाहता था, और काहन ने विशिष्टताओं को प्रस्तुत किया था।[14] काहन ने प्रारंभ में अनुरोध किया था कि फ़्लोटिंग पॉइंट बेस दशमलव हो[17][unreliable source?] किन्तु कोप्रोसेसर का हार्डवेयर डिज़ाइन उस परिवर्तन को करने के लिए अधिक दूर था।
इंटेल के अंदर कार्य ने अन्य विक्रेताओं को चिंतित कर दिया, जिन्होंने समान संयोग सुनिश्चित करने के लिए मानकीकरण प्रयास स्थापित किया था। काहन ने नवंबर 1977 में आयोजित दूसरी आईईईई 754 स्टैण्डर्ड कार्य समूह की बैठक में भाग लिया था। अंत में उन्हें इंटेल से उनके कोप्रोसेसर के लिए उनके कार्य के आधार पर ड्राफ्ट प्रस्ताव प्रस्तुत करने की अनुमति प्राप्त हुई; उन्हें प्रारूप के विवरण और उसके औचित्य को समझाने की अनुमति प्रदान की गई थी, किन्तु इंटेल के कार्यान्वयन वास्तुकला से संबंधित कुछ भी नहीं था। ड्राफ्ट जेरोम कूनन और हेरोल्ड स्टोन के साथ सह-लिखित था, और प्रारंभ में इसे काहन-कूनन-स्टोन प्रस्ताव या के-सी-एस प्रारूप के रूप में जाना जाता था।[14][15][16][18]
चूंकि 8-बिट घातांक दोहरे-एक्यूरेसी नंबर्स के लिए वांछित कुछ परिचालनों के लिए पर्याप्त चौड़ा नहीं था, उदाहरण के लिए दो 32-बिट नंबर्स के उत्पाद को संग्रहीत करने के लिए,[19] काहन के प्रस्ताव और डीईसी के प्रति-प्रस्ताव दोनों में 11 बिट्स का उपयोग किया गया था, जैसे कि 1965 से सीडीसी 6600 के समय-परीक्षणित 60-बिट फ़्लोटिंग-पॉइंट प्रारूप था।[15][18][20] काहन के प्रस्ताव में अनन्तताओं का भी प्रावधान किया गया है, जो विभाजन-दर-शून्य स्थितियों के निवारण में उपयोगी होते हैं; नॉट-ए-नंबर मान, जो अमान्य संचालन के निवारण में उपयोगी होते हैं; असामान्य नंबर्स, जो अंडरफ्लो के कारण होने वाली समस्याओं को कम करने में सहायता करती हैं;[18][21][22] और उत्तम संतुलित घातांक पूर्वाग्रह, जो किसी संख्या का व्युत्क्रम लेते समय अतिप्रवाह और अल्पप्रवाह से विक्रय में सहायता कर सकता है।[23][24]
अनुमोदित होने से पूर्व ही, ड्राफ्ट स्टैण्डर्ड को कई निर्माताओं द्वारा इम्प्लीमेंट किया गया था।[25][26] इंटेल 8087, जिसे 1980 में घोषित किया गया था, जो ड्राफ्ट स्टैण्डर्ड को इम्प्लीमेंट करने वाली प्रथम चिप थी।
1980 में, इंटेल 8087 चिप पहले ही इम्प्लीमेंट हो चुकी थी,[27] किन्तु प्रदर्शन संबंधी चिंताओं के कारण डीईसी विशेष रूप से असामान्य नंबर्स का विरोध करता रहा और चूंकि इससे डीईसी को डीईसी के प्रारूप पर मानकीकरण करने के लिए प्रतिस्पर्धात्मक लाभ मिलता है।
क्रमिक अंडरफ़्लो पर विचार 1981 तक चला जब इसका आकलन करने के लिए डीईसी द्वारा नियुक्त विशेषज्ञ ने असंतुष्टों का पक्ष लिया था। डीईसी ने यह प्रदर्शित करने के लिए अध्ययन करवाया था कि क्रमिक अंडरफ़्लो बुरा विचार था, किन्तु अध्ययन का निष्कर्ष विपरीत था, और डीईसी ने हार मान ली थी। 1985 में, स्टैण्डर्ड की पुष्टि की गई थी, किन्तु यह एक वर्ष पूर्व ही वास्तविक स्टैण्डर्ड बन गया था, जिसे कई निर्माताओं द्वारा कार्यान्वित किया गया था।[15][18][5]
यह भी देखें
- आईईईई 754
- आईईईई 754 फ़्लोटिंग पॉइंट नंबरों के गुणों के सरल उदाहरणों के लिए मिनीफ्लोट
- निश्चित-बिंदु अंकगणित
टिप्पणियाँ
- ↑ Precision: The number of decimal digits precision is calculated via number_of_mantissa_bits * Log10(2). Thus ~7.2 and ~15.9 for single and double precision respectively.
संदर्भ
- ↑ बाइनरी फ़्लोटिंग-पॉइंट अंकगणित के लिए आईईईई मानक. 1985. doi:10.1109/IEEESTD.1985.82928. ISBN 0-7381-1165-1.
- ↑ "ANSI/IEEE Std 754-2019". 754r.ucbtest.org. Retrieved 2019-08-06.
- ↑ Hennessy (2009). कंप्यूटर संगठन और डिज़ाइन. Morgan Kaufmann. p. 270. ISBN 9780123744937.
- ↑ Hossam A. H. Fahmy; Shlomo Waser; Michael J. Flynn, Computer Arithmetic (PDF), archived from the original (PDF) on 2010-10-08, retrieved 2011-01-02
- ↑ 5.0 5.1 5.2 William Kahan (October 1, 1997). "Lecture Notes on the Status of IEEE 754" (PDF). University of California, Berkeley. Retrieved 2007-04-12.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ "Godot math_funcs.h". GitHub.com. 30 July 2022.
- ↑ "Godot math_defs.h". GitHub.com. 30 July 2022.
- ↑ "गोडोट MathfEx.cs". GitHub.com.
- ↑ "Comparing Floating Point Numbers, 2012 Edition". randomascii.wordpress.com. 26 February 2012.
- ↑ "जावा भाषा और वर्चुअल मशीन विशिष्टताएँ". Java Documentation.
- ↑ John R. Hauser (March 1996). "संख्यात्मक कार्यक्रमों में फ़्लोटिंग-पॉइंट अपवादों को संभालना" (PDF). ACM Transactions on Programming Languages and Systems. 18 (2): 139–174. doi:10.1145/227699.227701. S2CID 9820157.
- ↑ David Stevenson (March 1981). "IEEE Task P754: A proposed standard for binary floating-point arithmetic". IEEE Computer. 14 (3): 51–62. doi:10.1109/C-M.1981.220377. S2CID 15523399.
- ↑ William Kahan and John Palmer (1979). "प्रस्तावित फ़्लोटिंग-पॉइंट मानक पर". SIGNUM Newsletter. 14 (Special): 13–21. doi:10.1145/1057520.1057522. S2CID 16981715.
- ↑ 14.0 14.1 14.2 14.3 "Intel and Floating-Point - Updating One of the Industry's Most Successful Standards - The Technology Vision for the Floating-Point Standard" (PDF). Intel. 2016. Archived from the original (PDF) on 2016-03-04. Retrieved 2016-05-30. (11 pages)
- ↑ 15.0 15.1 15.2 15.3 "An Interview with the Old Man of Floating-Point". cs.berkeley.edu. 1998-02-20. Retrieved 2016-05-30.
- ↑ 16.0 16.1 Woehr, Jack, ed. (1997-11-01). "A Conversation with William Kahan". Dr. Dobb's. drdobbs.com. Retrieved 2016-05-30.
- ↑ W. Kahan 2003, pers. comm. to Mike Cowlishaw and others after an IEEE 754 meeting
- ↑ 18.0 18.1 18.2 18.3 "IEEE 754: An Interview with William Kahan" (PDF). dr-chuck.com. Retrieved 2016-06-02.
- ↑ "IEEE vs. Microsoft Binary Format; Rounding Issues (Complete)". Microsoft Support. Microsoft. 2006-11-21. Article ID KB35826, Q35826. Archived from the original on 2020-08-28. Retrieved 2010-02-24.
- ↑ Thornton, James E. (1970). Written at Advanced Design Laboratory, Control Data Corporation. Design of a Computer: The Control Data 6600 (PDF) (1 ed.). Glenview, Illinois, USA: Scott, Foresman and Company. LCCN 74-96462. Archived (PDF) from the original on 2020-08-28. Retrieved 2016-06-02. (1+13+181+2+2 pages)
- ↑ Kahan, William Morton. "Why do we need a floating-point arithmetic standard?" (PDF). cs.berkeley.edu. Retrieved 2016-06-02.
- ↑ Kahan, William Morton; Darcy, Joseph D. "How Java's Floating-Point Hurts Everyone Everywhere" (PDF). cs.berkeley.edu. Retrieved 2016-06-02.
- ↑ Turner, Peter R. (2013-12-21). Numerical Analysis and Parallel Processing: Lectures given at The Lancaster …. Springer. ISBN 978-3-66239812-8. Retrieved 2016-05-30.
- ↑ "Names for Standardized Floating-Point Formats" (PDF). cs.berkeley.edu. Retrieved 2016-06-02.
- ↑ Charles Severance (20 February 1998). "फ़्लोटिंग-प्वाइंट के बूढ़े आदमी के साथ एक साक्षात्कार".
- ↑ Charles Severance. "आईईईई फ़्लोटिंग-पॉइंट प्रारूप का इतिहास". Connexions. Archived from the original on 2009-11-20.
- ↑ "Molecular Expressions: Science, Optics & You - Olympus MIC-D: Integrated Circuit Gallery - Intel 8087 Math Coprocessor". micro.magnet.fsu.edu. Retrieved 2016-05-30.
अग्रिम पठन
- Charles Severance (March 1998). "IEEE 754: An Interview with William Kahan" (PDF). IEEE Computer. 31 (3): 114–115. doi:10.1109/MC.1998.660194. S2CID 33291145. Archived from the original (PDF) on 2009-08-23. Retrieved 2008-04-28.
- David Goldberg (March 1991). "What Every Computer Scientist Should Know About Floating-Point Arithmetic" (PDF). ACM Computing Surveys. 23 (1): 5–48. doi:10.1145/103162.103163. S2CID 222008826. Retrieved 2008-04-28.
- Chris Hecker (February 1996). "Let's Get To The (Floating) Point" (PDF). Game Developer Magazine: 19–24. ISSN 1073-922X. Archived from the original (PDF) on 2007-02-03.
- David Monniaux (May 2008). "The pitfalls of verifying floating-point computations". ACM Transactions on Programming Languages and Systems. 30 (3): 1–41. arXiv:cs/0701192. doi:10.1145/1353445.1353446. ISSN 0164-0925. S2CID 218578808.: A compendium of non-intuitive behaviours of floating-point on popular architectures, with implications for program verification and testing.