कर्नेल (छवि प्रसंस्करण): Difference between revisions
m (added Category:Vigyan Ready using HotCat) |
m (14 revisions imported from alpha:कर्नेल_(छवि_प्रसंस्करण)) |
(No difference)
| |
Latest revision as of 22:19, 2 February 2024
इमेज प्रोसेसिंग में, कर्नेल, कन्वोल्यूशन मैट्रिक्स, या मास्क स्मॉल मैट्रिक्स है जिसका उपयोग ब्लर्रिंग, शार्पनिंग, एम्बॉसिंग, एज डिटेक्शन के लिए किया जाता है। यह कर्नेल और बिटमैप इमेज के मध्य कनवल्शन करके पूर्ण किया जाता है। या अधिक सरलता से, जब आउटपुट इमेज में प्रत्येक पिक्सेल इनपुट इमेज में पास के पिक्सेल का फंक्शन होता है, तो कर्नेल वह फंक्शन होता है।
विवरण
कनवल्शन की सामान्य अभिव्यक्ति है:
जहाँ फ़िल्टर की गई इमेज है, मूल इमेज है, फ़िल्टर कर्नेल है, फ़िल्टर कर्नेल के प्रत्येक एलिमेंट पर विचार किया जाता है और .
एलिमेंट वैल्यूज के आधार पर, कर्नेल कई प्रकार के प्रभाव उत्पन्न कर सकता है:
| आपरेशन | कर्नेल ω | इमेज रिजल्ट g(x,y) |
|---|---|---|
| आइडेंटिटी | 
| |
| रिज या एज डिटेक्शन | 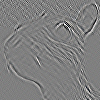
| |

| ||
| शार्पन | 
| |
| बॉक्स ब्लर (सामान्यीकृत)) |

| |
| गॉसियन ब्लर्रिंग 3 × 3 (अनुमान) |

| |
| गाऊसी ब्लर्रिंग 5 × 5 (अनुमान) |

| |
| अनशार्प मास्किंग 5 × 5 गॉसियन ब्लर पर आधारित 1 और के रूप में अमाउंट के साथ सीमा 0 के रूप में |
|

|
उपरोक्त कर्नेल और इमेजे को संयोजित करके प्राप्त किए जाने वाले प्रभावों के कुछ उदाहरण हैं।
ओरिजिन
मूल कर्नेल की स्थिति है, जो वर्तमान आउटपुट पिक्सेल से ऊपर (वैचारिक रूप से) है। यह रियल कर्नेल के बाहर हो सकता है, चूंकि सामान्यतः यह कर्नेल एलिमेंट्स में से एक के समान है। सिमेट्रिक कर्नेल के लिए, मूल सामान्यतः केंद्र एलिमेंट होता है।
कनवल्शन
कनवल्शन इमेज के प्रत्येक एलिमेंट को उसके लोकल नेबर के साथ जोड़ने की प्रक्रिया है, जिसे कर्नेल द्वारा वेट किया जाता है। यह कन्वोल्यूशन के रूप से संबंधित है। * द्वारा निरूपित होने के पश्चात भी डेनोटे किया जा रहा मैट्रिक्स ऑपरेशन - कन्वोल्यूशन - मैट्रिक्स मल्टिप्लिकेशन नहीं है।
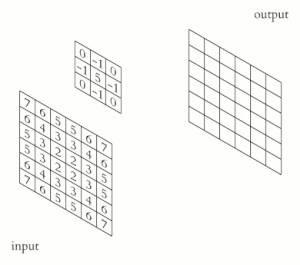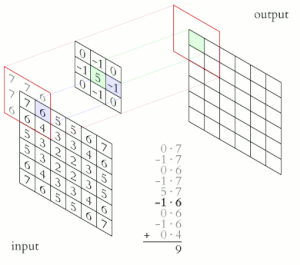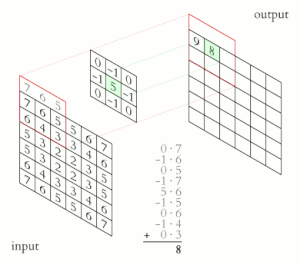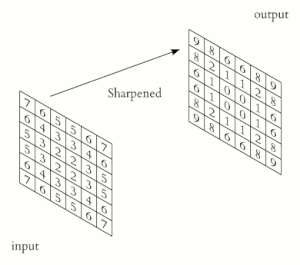
उदाहरण के लिए, यदि हमारे पास दो थ्री-बाय-थ्री मैट्रिक्स हैं, प्रथम कर्नेल, और दूसरा इमेज अंश, कनवल्शन कर्नेल की दोनों रोस और कॉलम्स को फ़्लिप करने और लोकली समान एंट्रीज और योग को गुणा करने की प्रक्रिया है। परिणामी इमेज के कोऑर्डिनेट्स [2, 2] (अर्थात, सेंट्रल एलिमेंट) पर एलिमेंट इमेज मैट्रिक्स की सभी एंट्रीज का वेट संयोजन होगा, जिसमें कर्नेल द्वारा दिए गए वजन होंगे:
आउटपुट इमेज में दिए गए पिक्सेल के वैल्यूज की गणना प्रत्येक कर्नेल वैल्यू को संबंधित इनपुट इमेज पिक्सेल वैल्यूज से गुणा करके की जाती है। इसे निम्नलिखित सूडो कोड के साथ एल्गोरिदमिक रूप से डिस्क्राइब किया जा सकता है:
for each image row in input image:
for each pixel in image row:
set accumulator to zero
for each kernel row in kernel:
for each element in kernel row:
if element position corresponding* to pixel position then
multiply element value corresponding* to pixel value
add result to accumulator
endif
set output image pixel to accumulator
- *संबंधित इनपुट इमेज पिक्सेल कर्नेल की उत्पत्ति के सापेक्ष पाए जाते हैं।
यदि कर्नेल सिमेट्रिक है, तो कर्नेल के केंद्र (मूल) को वर्तमान पिक्सेल पर रखें। कर्नेल मूल के आस-पास के पड़ोसी पिक्सेल को ओवरलैप करेगा। प्रत्येक कर्नेल एलिमेंट को उस पिक्सेल वैल्यू से गुणा किया जाना चाहिए जिसके साथ यह ओवरलैप होता है और सभी प्राप्त वैल्यूज का योग किया जाना चाहिए। यह परिणामी योग वर्तमान में कर्नेल के केंद्र के साथ ओवरलैप किए गए वर्तमान पिक्सेल के लिए नया वैल्यू होगा।
यदि कर्नेल सिमेट्रिक नहीं है, तो उपरोक्त के अनुसार कनवल्शन की गणना करने से पूर्व इसे क्षैतिज और ऊर्ध्वाधर अक्ष के चारों ओर फ़्लिप करना होगा।[1]
मैट्रिक्स कनवल्शन का सामान्य रूप है:
कर्नेल कनवल्शन के लिए सामान्यतः इमेज सीमाओं के बाहर पिक्सेल से वैल्यू की आवश्यकता होती है। इमेज इमेज को संभालने के लिए कई प्रकार की विधियाँ हैं।
- एक्सटेंड
- कनवल्शन के लिए वैल्यू प्रदान करने के लिए निकटतम सीमा पिक्सेल को जहाँ तक आवश्यक हो बढ़ाया जाता है। कॉर्नर पिक्सल को 90° वेजेज में बढ़ाया गया है। अन्य एज वाले पिक्सेल लाइनों में विस्तारित हैं।
- व्रैप
- इमेज वैचारिक रूप से धारण की गई है (या टाइल की गई है) और वैल्यू विपरीत एज या कोने से लिए गए हैं।
- मिरर
- इमेज वैचारिक रूप से इमेज पर प्रतिबिंबित होती है। उदाहरण के लिए, एज के बाहर पिक्सेल 3 यूनिट्स को लर्निंग का प्रयत्न करने पर इसके अतिरिक्त एज के अंदर 3 यूनिट्स को पढ़ता है।
- क्रॉप करें/ओवरलैप से बचें
- आउटपुट इमेज में कोई भी पिक्सेल जिसे एज से बियॉन्ड वैल्यूज की आवश्यकता होती है, उसे त्याग दिया जाता है। इस विधि के परिणामस्वरूप आउटपुट इमेज स्मॉल हो सकती है, इमेज को क्रॉप कर दिया गया है। कर्नेल को स्थानांतरित करें जिससे इमेज के बाहर से वैल्यूज की आवश्यकता न हो। मशीन लर्निंग मुख्य रूप से इस एप्रोच का उपयोग करती है। उदाहरण: कर्नेल आकार 10x10, इमेज आकार 32x32, परिणाम इमेज 23x23 है।
- कर्नेल क्रॉप
- कर्नेल में कोई भी पिक्सेल जो इनपुट इमेज से आगे बढ़ता है, उसका उपयोग नहीं किया जाता है और कम्पनसेट करने के लिए नॉर्मलाइजेशन को समायोजित किया जाता है।
- कांस्टेंट
- इमेज के बाहर पिक्सेल के लिए कांस्टेंट वैल्यू का उपयोग करें। सामान्यतः काले या कभी-कभी भूरे रंग का प्रयोग किया जाता है। सामान्यतः यह एप्लीकेशन पर निर्भर करता है।
नॉर्मलाइजेशन
नॉर्मलाइजेशन को सभी कर्नेल एलिमेंट्स के योग द्वारा कर्नेल में प्रत्येक एलिमेंट के विभाजन के रूप में परिभाषित किया गया है, जिससे सामान्यीकृत कर्नेल के एलिमेंट्स का योग यूनिटी हो। यह सुनिश्चित करेगा कि मॉडिफाइड इमेज में औसत पिक्सेल मूल इमेज में औसत पिक्सेल जितना ब्राइट हो।
ऑप्टिमिसेशन
तीव्र कनवल्शन एल्गोरिदम में सम्मिलित हैं:[2]
- सेपरेबल कनवल्शन
सेपरेबल कनवल्शन
M × N कर्नेल के साथ 2D कनवल्शन के लिए प्रत्येक नमूने (पिक्सेल) के लिए M × N मल्टिप्लिकेशन की आवश्यकता होती है। यदि कर्नेल सेपरेबल है, तो गणना को M + N मल्टिप्लिकेशन तक कम किया जा सकता है। भिन्न-भिन्न कनवल्शन का उपयोग करने से 2D कनवल्शन के अतिरिक्त दो बार 1D कनवल्शन करके गणना में अत्यधिक कमी आ सकती है।[3]
इम्प्लीमेंटेशन
यहां जीएलएसएल शेडिंग लैंग्वेज शेडिंग लैंग्वेज के साथ ठोस कनवल्शन इम्प्लीमेंटेशन किया गया है:
// author : csblo
// Work made just by consulting :
// https://en.wikipedia.org/wiki/Kernel_(image_processing)
// Define kernels
#define identity mat3(0, 0, 0, 0, 1, 0, 0, 0, 0)
#define edge0 mat3(1, 0, -1, 0, 0, 0, -1, 0, 1)
#define edge1 mat3(0, 1, 0, 1, -4, 1, 0, 1, 0)
#define edge2 mat3(-1, -1, -1, -1, 8, -1, -1, -1, -1)
#define sharpen mat3(0, -1, 0, -1, 5, -1, 0, -1, 0)
#define box_blur mat3(1, 1, 1, 1, 1, 1, 1, 1, 1) * 0.1111
#define gaussian_blur mat3(1, 2, 1, 2, 4, 2, 1, 2, 1) * 0.0625
#define emboss mat3(-2, -1, 0, -1, 1, 1, 0, 1, 2)
// Find coordinate of matrix element from index
vec2 kpos(int index)
{
return vec2[9] (
vec2(-1, -1), vec2(0, -1), vec2(1, -1),
vec2(-1, 0), vec2(0, 0), vec2(1, 0),
vec2(-1, 1), vec2(0, 1), vec2(1, 1)
)[index] / iResolution.xy;
}
// Extract region of dimension 3x3 from sampler centered in uv
// sampler : texture sampler
// uv : current coordinates on sampler
// return : an array of mat3, each index corresponding with a color channel
mat3[3] region3x3(sampler2D sampler, vec2 uv)
{
// Create each pixels for region
vec4[9] region;
for (int i = 0; i < 9; i++)
region[i] = texture(sampler, uv + kpos(i));
// Create 3x3 region with 3 color channels (red, green, blue)
mat3[3] mRegion;
for (int i = 0; i < 3; i++)
mRegion[i] = mat3(
region[0][i], region[1][i], region[2][i],
region[3][i], region[4][i], region[5][i],
region[6][i], region[7][i], region[8][i]
);
return mRegion;
}
// Convolve a texture with kernel
// kernel : kernel used for convolution
// sampler : texture sampler
// uv : current coordinates on sampler
vec3 convolution(mat3 kernel, sampler2D sampler, vec2 uv)
{
vec3 fragment;
// Extract a 3x3 region centered in uv
mat3[3] region = region3x3(sampler, uv);
// for each color channel of region
for (int i = 0; i < 3; i++)
{
// get region channel
mat3 rc = region[i];
// component wise multiplication of kernel by region channel
mat3 c = matrixCompMult(kernel, rc);
// add each component of matrix
float r = c[0][0] + c[1][0] + c[2][0]
+ c[0][1] + c[1][1] + c[2][1]
+ c[0][2] + c[1][2] + c[2][2];
// for fragment at channel i, set result
fragment[i] = r;
}
return fragment;
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
// Normalized pixel coordinates (from 0 to 1)
vec2 uv = fragCoord/iResolution.xy;
// Convolve kernel with texture
vec3 col = convolution(emboss, iChannel0, uv);
// Output to screen
fragColor = vec4(col, 1.0);
}
संदर्भ
- Ludwig, Jamie (n.d.). Image Convolution (PDF).
{{cite book}}:|work=ignored (help) - Lecarme, Olivier; Delvare, Karine (January 2013). The Book of GIMP: A Complete Guide to Nearly Everything. p. 429. ISBN 978-1593273835.
{{cite book}}:|work=ignored (help) - Gumster, Jason van; Shimonski, Robert (March 2012). GIMP Bible. pp. 438–442. ISBN 978-0470523971.
{{cite book}}:|work=ignored (help) - Shapiro, Linda G.; Stockman, George C. (February 2001). Computer Vision. pp. 53–54. ISBN 978-0130307965.
{{cite book}}:|work=ignored (help)