फोइल विधि: Difference between revisions
m (9 revisions imported from alpha:फोइल_विधि) |
No edit summary |
||
| Line 131: | Line 131: | ||
* {{cite book |first1=Ray |last1=Steege |first2=Kerry |last2=Bailey |title=Schaum's Outline of Theory and Problems of Intermediate Algebra |year=1997 |publisher=McGraw–Hill |place=New York |series=Schaum's Outline Series |isbn=978-0-07-060839-9 }} | * {{cite book |first1=Ray |last1=Steege |first2=Kerry |last2=Bailey |title=Schaum's Outline of Theory and Problems of Intermediate Algebra |year=1997 |publisher=McGraw–Hill |place=New York |series=Schaum's Outline Series |isbn=978-0-07-060839-9 }} | ||
{{DEFAULTSORT:Foil Method}} | {{DEFAULTSORT:Foil Method}} | ||
[[Category:Articles with hatnote templates targeting a nonexistent page|Foil Method]] | |||
[[Category:CS1 English-language sources (en)]] | |||
[[Category: | [[Category:Created On 03/02/2023|Foil Method]] | ||
[[Category:Created On 03/02/2023]] | [[Category:Lua-based templates|Foil Method]] | ||
[[Category:Vigyan Ready]] | [[Category:Machine Translated Page|Foil Method]] | ||
[[Category:Pages with script errors|Foil Method]] | |||
[[Category:Short description with empty Wikidata description|Foil Method]] | |||
[[Category:Templates Vigyan Ready|Foil Method]] | |||
[[Category:Templates that add a tracking category|Foil Method]] | |||
[[Category:Templates that generate short descriptions|Foil Method]] | |||
[[Category:Templates using TemplateData|Foil Method]] | |||
[[Category:गुणा|Foil Method]] | |||
[[Category:प्राथमिक बीजगणित|Foil Method]] | |||
[[Category:मेनेमोनिक संक्षिप्त नाम|Foil Method]] | |||
[[Category:विज्ञान -विज्ञान|Foil Method]] | |||
Latest revision as of 19:55, 9 February 2023
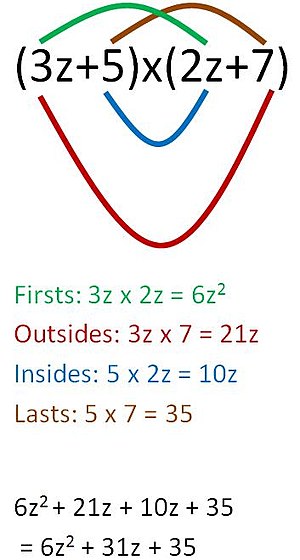 A visual representation of the FOIL rule. Each colored line represents two terms that must be multiplied. | |
| Type | Method |
|---|---|
| Field | Elementary algebra, elementary arithmetic |
| Statement | A technique for multiplying two binomials in an algebraic expression using distributive law. |
| First stated by | William Betz |
| First stated in | 1929 |
माध्यमिक विद्यालय में, फोइल दो द्विपदों को गुणा करने की मानक विधि के लिए एक स्मरक है [1] इसलिए विधि को फोइल विधि के रूप में संदर्भित किया जा सकता है। शब्द फोइल शब्द उत्पाद के चार शब्दों का संक्षिप्त रूप है:
- प्रथम ("प्रथम" प्रत्येक द्विपद के पदों को एक साथ गुणा किया जाता है)
- बाहरी ("बाहर" शब्दों को गुणा किया जाता है - अर्थात, पहले द्विपद का पहला पद और दूसरे का दूसरा पद)
- आंतरिक ("अंदर" शब्दों को गुणा किया जाता है - पहले द्विपद का दूसरा पद और दूसरे का पहला पद)
- अंतिम ("प्रत्येक द्विपद के अंतिम" शब्द गुणा किए जाते हैं)
सामान्य रूप है
ध्यान दें कि a एक पहला शब्द और बाहरी शब्द दोनों है; b दोनों एक अंतिम और आंतरिक शब्द है, और आगे। योग में चार शब्दों का क्रम महत्वपूर्ण नहीं है और फोइल शब्द के अक्षरों के क्रम से मेल खाना आवश्यक नहीं है।
इतिहास
फोइल विधिविधि वितरण कानून का उपयोग करके बीजगणितीय अभिव्यक्तियों को गुणा करने के लिए अधिक सामान्य विधि का एक विशेष स्थितियों है। फोइल शब्द मूल रूप से बीजगणित सीखने वाले हाई-स्कूल के छात्रों के लिए एक स्मरक के रूप में अभिप्रेत था। यह शब्द विलियम बेट्ज़ के 1929 के पाठ अलजेब्रा फॉर टुडे में दिखाई देता है, जहां वह कहता है :[2]
... पहला पद, बाहरी पद, भीतरी पद, अंतिम पद। (उपर्युक्त नियम को फोइल शब्द से भी याद किया जा सकता है, जो पहले, बाहरी, आंतरिक, अंतिम शब्दों के पहले अक्षरों द्वारा सुझाया गया है।
विलियम बेट्ज़ उस समय संयुक्त राज्य अमेरिका में गणित में सुधार के आंदोलन में सक्रिय थे, उन्होंने प्राथमिक गणित विषयों पर कई ग्रंथ लिखे थे और "गणित शिक्षा के सुधार के लिए अपना जीवन समर्पित कर दिया था"। [3] विलियम बेट्ज़ उस समय संयुक्त राज्य अमेरिका में गणित में सुधार के आंदोलन में सक्रिय थे, उन्होंने प्राथमिक गणित विषयों पर कई ग्रंथ लिखे थे और "गणित शिक्षा के सुधार के लिए अपना जीवन समर्पित कर दिया था"।[4]
उदाहरण
रैखिक द्विपदों को गुणा करने के लिए विधि का सबसे अधिक उपयोग किया जाता है। उदाहरण के लिए,
यदि किसी भी द्विपद में घटाव सम्मलित है, तो संबंधित शर्तों को अस्वीकार किया जाना चाहिए। उदाहरण के लिए,
वितरण कानून
फोइल विधि वितरण कानून से जुड़ी दो-चरणीय प्रक्रिया के बराबर है: [5]
पहले चरण में, c + d) को पहले द्विपद में जोड़ पर वितरित किया जाता है। दूसरे चरण में, वितरण नियम का उपयोग दो शब्दों में से प्रत्येक को सरल बनाने के लिए किया जाता है। ध्यान दें कि इस प्रक्रिया में वितरण संपत्ति के कुल तीन अनुप्रयोग सम्मलित हैं। विधि के विपरीत, वितरण का उपयोग करने वाली विधि को उत्पादों पर आसानी से लागू किया जा सकता है जैसे ट्रिनोमियल और उच्चतर।
रिवर्स फोइल
फोइल नियम दो द्विपदों के गुणनफल को चार (या कम, यदि समान पद संयुक्त हों तो) एकपदी के योग में परिवर्तित करता है।[6] रिवर्स प्रक्रिया को फैक्टरिंग या फैक्टराइजेशन कहा जाता है। विशेष रूप से, यदि उपरोक्त प्रमाण को उल्टा पढ़ा जाता है तो यह समूहीकरण द्वारा फैक्टरिंग नामक तकनीक को दर्शाता है।
फोइल के विकल्प के रूप में तालिका
एक विज़ुअल मेमोरी टूल बहुपदों की एक जोड़ी के लिए फोइल स्मरक को किसी भी संख्या में शब्दों के साथ बदल सकता है। पहले बहुपद के पदों को बाएँ किनारे पर और दूसरे बहुपद के पदों को शीर्ष किनारे पर रखते हुए एक तालिका बनाएँ, फिर तालिका को गुणा के गुणनफल से भरें। फोइल नियम के समतुल्य तालिका इस तरह दिखती है:
इस स्थितियों में कि ये बहुपद हैं,(ax + b)(cx + d),दी गई डिग्री की शर्तों को प्रतिविषम के साथ जोड़कर पाया जाता है:
इसलिए
(a + b + c)(w + x + y + z),को गुणा करने के लिए तालिका इस प्रकार होगी:
तालिका प्रविष्टियों का योग बहुपदों का उत्पाद है। इस प्रकार:
इसी प्रकार, गुणा करने के लिए (ax2 + bx + c)(dx3 + ex2 + fx + g), एक ही तालिका लिखती है:
और प्रतिविषम के साथ रकम::
सामान्यीकरण
फोइल नियम को दो से अधिक बहुभाजित संक्रिया या दो से अधिक योग वाले बहुभाजित संक्रिया वाले विस्तारित उत्पादों पर सीधे लागू नहीं किया जा सकता है। सम्मलित, साहचर्य कानून और पुनरावर्ती फ़ॉइलिंग को लागू करने से ऐसे उत्पादों का विस्तार करने की अनुमति मिलती है। उदाहरण के लिए:
वितरण पर आधारित वैकल्पिक विधि फोइल नियम के उपयोग को छोड़ देते हैं, किन्तु याद रखना और लागू करना आसान हो सकता है। उदाहरण के लिए:
यह भी देखें
- द्विपद प्रमेय
- फैक्टराइजेशन
संदर्भ
- ↑ "Simplifying using the FOIL Method Lessons". Retrieved 10 May 2018.
- ↑ Betz, William (1929), Algebra for Today (vol. 1), Ginn and Company, p. 291.
- ↑ W. D. R. (November 1937), "Review of Algebra for Today : First Year", The Mathematics Teacher, National Council for the Teaching of Mathematics, 30 (7): 348.
- ↑ McCrea, Emma (2019-05-01). Making Every Maths Lesson Count: Six principles to support great maths teaching (Making Every Lesson Count series) (in English). Crown House Publishing Ltd. ISBN 978-1-78583-421-9.
- ↑ Khare, Apoorva; Lachowska, Anna (2015). Beautiful, Simple, Exact, Crazy: Mathematics in the Real World (in English). Yale University Press. p. 3. ISBN 978-0-300-19089-2.
This is sometimes called the "FOIL" method – essentially, it is simply the distributive law applied twice
. - ↑ Kirkland, Carla C.; Cleveland, Chan (2020-01-29). Praxis Core For Dummies with Online Practice Tests (in English). John Wiley & Sons. p. 78. ISBN 978-1-119-62047-1.
...reverse FOIL can take you in the opposite direction from one expression to two-term expressions times each other. It's a form of factoring.
अग्रिम पठन
- Steege, Ray; Bailey, Kerry (1997). Schaum's Outline of Theory and Problems of Intermediate Algebra. Schaum's Outline Series. New York: McGraw–Hill. ISBN 978-0-07-060839-9.