उत्तल अनुकूलन

उत्तल अनुकूलन गणितीय अनुकूलन का एक उपक्षेत्र है। जो उत्तल सेटों पर उत्तल कार्यों को कम करने की समस्या का अध्ययन करता है (या समकक्ष उत्तल सेटों पर अवतल कार्यों को अधिकतम करना)। उत्तल अनुकूलन समस्याओं के कई वर्ग बहुपद-काल एल्गोरिदम को स्वीकार करते हैं। जबकि गणितीय अनुकूलन सामान्य रूप से एनपी कठिन है।उत्तल अनुकूलन में व्यापक श्रेणी के अनुशासन हैं। जैसे स्वचालित नियंत्रण प्रणाली, अनुमान और संकेत आगे बढ़ाना, संचार और नेटवर्क, इलेक्ट्रॉनिक सर्किट डिज़ाइन, डेटा विश्लेषण और मॉडलिंग, वित्त, सांख्यिकी (इष्टतम डिजाइन) और संरचनात्मक अनुकूलन, जहां सन्निकटन अवधारणा कुशल प्रमाणित हुई है। कंप्यूटिंग और गणितीय अनुकूलन कम्प्यूटेशनल अनुकूलन तकनीकों की प्रगति के साथ उत्तल प्रोग्रामिंग लगभग रैखिक प्रोग्रामिंग के रूप में सीधी है।

परिभाषा

उत्तल अनुकूलन समस्या एक अनुकूलन समस्या है। जिसमें उद्देश्य फलन उत्तल फलन होता है और साध्य क्षेत्र उत्तल समुच्चय होता है। एक समारोह $f$ के कुछ उपसमुच्चय का मानचित्रण करना $\mathbb {R} ^{n}$में $\mathbb {R} \cup \{\pm \infty \}$ उत्तल है। यदि इसका डोमेन उत्तल है और सभी के लिए $\theta \in [0,1]$ और सभी $x,y$ इसके डोमेन में निम्नलिखित नियम रखती है: $f(\theta x+(1-\theta )y)\leq \theta f(x)+(1-\theta )f(y)$। सभी सदस्यों के लिए एक सेट S उत्तल है। $x,y\in S$ और सभी $\theta \in [0,1]$ हमारे पास वह है। $\theta x+(1-\theta )y\in S$

वस्तुतः एक उत्तल अनुकूलन समस्या कुछ खोजने की समस्या है। $\mathbf {x^{\ast }} \in C$ को प्राप्त

$\inf\{f(\mathbf {x} ):\mathbf {x} \in C\}$,

जहां उद्देश्य समारोह $f:{\mathcal {D}}\subseteq \mathbb {R} ^{n}\to \mathbb {R}$ उत्तल है। जैसा कि संभव सेट $C$ है। यदि ऐसा कोई बिंदु उपस्थित है। तो इसे एक इष्टतम बिंदु या समाधान कहा जाता है। सभी इष्टतम बिंदुओं के समुच्चय को इष्टतम समुच्चय कहा जाता है। जो $f$ नीचे असीमित है। $C$ या न्यूनतम प्राप्त नहीं हुआ है। तो अनुकूलन समस्या को अबाधित कहा जाता है। नहीं तो $C$ रिक्त समुच्चय है। तो समस्या असाध्य कहलाती है।

मानक रूप

उत्तल अनुकूलन समस्या मानक रूप में होती है। यदि इसे इस रूप में लिखा जाए

${\begin{aligned}&{\underset {\mathbf {x} }{\operatorname {minimize} }}&&f(\mathbf {x} )\\&\operatorname {subject\ to} &&g_{i}(\mathbf {x} )\leq 0,\quad i=1,\dots ,m\\&&&h_{i}(\mathbf {x} )=0,\quad i=1,\dots ,p,\end{aligned}}$

जहाँ:

• $\mathbf {x} \in \mathbb {R} ^{n}$ अनुकूलन चर है;
• उद्देश्य समारोह $f:{\mathcal {D}}\subseteq \mathbb {R} ^{n}\to \mathbb {R}$ एक उत्तल कार्य है;
• असमानता बाधा कार्य करती है $g_{i}:\mathbb {R} ^{n}\to \mathbb {R}$, $i=1,\ldots ,m$, उत्तल कार्य हैं;
• समानता बाधा कार्य करती है $h_{i}:\mathbb {R} ^{n}\to \mathbb {R}$, $i=1,\ldots ,p$, एक ठीक परिवर्तन हैं। अर्थात् इस रूप का $h_{i}(\mathbf {x} )=\mathbf {a_{i}} \cdot \mathbf {x} -b_{i}$, जहाँ $\mathbf {a_{i}}$ एक वेक्टर है और $b_{i}$ एक अदिश राशि है।

यह संकेतन खोजने की समस्या का वर्णन करता है। $\mathbf {x} \in \mathbb {R} ^{n}$ जो कम करता है। $f(\mathbf {x} )$ इन सब में $\mathbf {x}$ संतुष्टि देने वाला $g_{i}(\mathbf {x} )\leq 0$, $i=1,\ldots ,m$ और $h_{i}(\mathbf {x} )=0$, $i=1,\ldots ,p$. कार्यक्रम $f$ समस्या का उद्देश्य कार्य है और कार्य $g_{i}$ और $h_{i}$ बाधा कार्य हैं।

व्यवहार्य सेट $C$ अनुकूलन समस्या में सभी बिंदु सम्मिलित हैं और $\mathbf {x} \in {\mathcal {D}}$ बाधाओं को संतुष्ट करना है। यह सेट उत्तल है क्योंकि ${\mathcal {D}}$ उत्तल है। उत्तल कार्यों के सबलेवल सेट उत्तल हैं। अफीन सेट उत्तल हैं और उत्तल सेट का प्रतिच्छेदन उत्तल है। उत्तल अनुकूलन समस्या का समाधान कोई बिंदु $\mathbf {x} \in C$ को प्राप्त $\inf\{f(\mathbf {x} ):\mathbf {x} \in C\}$ है। सामान्यतः उत्तल अनुकूलन समस्या में शून्य, एक या कई समाधान हो सकते हैं। इस मानक रूप में कई अनुकूलन समस्याओं को समान रूप से तैयार किया जा सकता है। उदाहरण के लिए अवतल कार्य को अधिकतम करने की समस्या $f$ उत्तल कार्य को कम करने की समस्या के रूप में समान रूप से पुन: तैयार किया जा सकता है। $-f$ उत्तल सेट पर अवतल कार्य को अधिकतम करने की समस्या को सामान्यतः उत्तल अनुकूलन समस्या कहा जाता है।

गुण

उत्तल अनुकूलन समस्याओं के उपयोगी गुण निम्नलिखित हैं:

• प्रत्येक स्थानीय न्यूनतम एक वैश्विक न्यूनतम है;
• इष्टतम सेट उत्तल है;
• यदि उद्देश्य फ़ंक्शन सख्ती से उत्तल है। तो समस्या में अधिकतम एक इष्टतम बिंदु होता है।

इन परिणामों का उपयोग कार्यात्मक विश्लेषण (हिल्बर्ट रिक्त स्थान में) जैसे हिल्बर्ट प्रक्षेपण प्रमेय अलग करने वाले हाइपरप्लेन प्रमेय और फ़ार्कस लेम्मा से ज्यामितीय धारणाओं के साथ-साथ उत्तल न्यूनीकरण के सिद्धांत द्वारा किया जाता है।

अनुप्रयोग

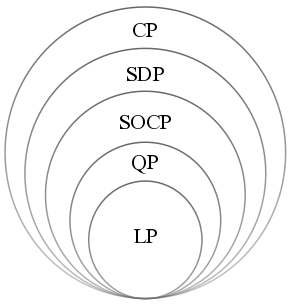
निम्नलिखित समस्या वर्ग सभी उत्तल अनुकूलन समस्याएँ हैं, या सरल परिवर्तनों के माध्यम से उत्तल अनुकूलन समस्याओं को कम किया जा सकता है:

उत्तल अनुकूलन समस्याओं का एक पदानुक्रम। (एलपी: लीनियर प्रोग्राम, क्यूपी: क्वाड्रैटिक प्रोग्राम, एसओसीपी सेकंड-ऑर्डर कोन प्रोग्राम, एसडीपी: सेमिडेफिनिट प्रोग्राम, सीपी: कोन प्रोग्राम।)

*कम से कम वर्गों

• रैखिक प्रोग्रामिंग
• रैखिक बाधाओं के साथ उत्तल द्विघात प्रोग्रामिंग
• द्विघात रूप से विवश द्विघात प्रोग्रामिंग
• शंकु अनुकूलन
• ज्यामितीय प्रोग्रामिंग
• दूसरा क्रम शंकु प्रोग्रामिंग
• अर्ध-परिमित प्रोग्रामिंग
• उपयुक्त बाधाओं के साथ एंट्रॉपी अधिकतमकरण

उत्तल अनुकूलन में निम्नलिखित के लिए व्यावहारिक अनुप्रयोग हैं।

• पोर्टफोलियो अनुकूलन।
• सबसे खराब स्थिति जोखिम विश्लेषण।* इष्टतम विज्ञापन।* प्रतिगमन विश्लेषण के बदलाव (नियमन (गणित) और मात्रात्मक प्रतिगमन सहित)।* मॉडल फिटिंग(विशेष रूप से मल्टीक्लास वर्गीकरण).
• बिजली उत्पादन अनुकूलन।* संयुक्त अनुकूलन।* अनिश्चितता का गैर-संभाव्य मॉडलिंग।
• वायरलेस सिग्नल का उपयोग करके स्थानीयकरण

लैग्रेंज गुणक

लागत फलन द्वारा मानक रूप में दी गई उत्तल न्यूनीकरण समस्या पर विचार करें $f(x)$ और असमानता की बाधाएं $g_{i}(x)\leq 0$ के लिए $1\leq i\leq m$. फिर डोमेन ${\mathcal {X}}$ है:

${\mathcal {X}}=\left\{x\in X\vert g_{1}(x),\ldots ,g_{m}(x)\leq 0\right\}.$

समस्या के लिए Lagrangian समारोह है

$L(x,\lambda _{0},\lambda _{1},\ldots ,\lambda _{m})=\lambda _{0}f(x)+\lambda _{1}g_{1}(x)+\cdots +\lambda _{m}g_{m}(x).$

प्रत्येक बिंदु के लिए $x$ में $X$ जो कम करता है $f$ ऊपर $X$, वास्तविक संख्याएँ उपस्थित हैं $\lambda _{0},\lambda _{1},\ldots ,\lambda _{m},$ लैग्रेंज गुणक कहलाते हैं, जो इन नियमों को एक साथ पूरा करते हैं:

1. $x$ कम करता है $L(y,\lambda _{0},\lambda _{1},\ldots ,\lambda _{m})$ कुल मिलाकर $y\in X,$
2. $\lambda _{0},\lambda _{1},\ldots ,\lambda _{m}\geq 0,$ कम से कम एक के साथ $\lambda _{k}>0,$
3. $\lambda _{1}g_{1}(x)=\cdots =\lambda _{m}g_{m}(x)=0$ (पूरक शिथिलता)।

अगर कोई पूरी तरह से संभव बिंदु उपस्थित है, यानी, एक बिंदु $z$ संतुष्टि देने वाला

$g_{1}(z),\ldots ,g_{m}(z)<0,$

तो उपरोक्त कथन को उसकी आवश्यकता के लिए मजबूत किया जा सकता है $\lambda _{0}=1$.

इसके विपरीत यदि कुछ $x$ में $X$ संतुष्ट करता है (1)–(3) स्केलर (गणित) के लिए $\lambda _{0},\ldots ,\lambda _{m}$ साथ $\lambda _{0}=1$ तब $x$ कम करना निश्चित है $f$ ऊपर $X$.

एल्गोरिदम

अप्रतिबंधित उत्तल अनुकूलन को आसानी से ढतला हुआ वंश (स्टीपेस्ट डिसेंट की विधि का एक विशेष मामला) या अनुकूलन में न्यूटन की विधि के साथ हल किया जा सकता है। न्यूटन की विधि, एक उपयुक्त चरण आकार के लिए लाइन खोज के साथ संयुक्त; इन्हें गणितीय रूप से शीघ्रता से अभिसरण करने के लिए सिद्ध किया जा सकता है, विशेष रूप से बाद वाली विधि। रैखिक समानता बाधाओं के साथ उत्तल अनुकूलन को केकेटी मैट्रिक्स तकनीकों का उपयोग करके भी हल किया जा सकता है यदि उद्देश्य फ़ंक्शन एक द्विघात फ़ंक्शन है (जो न्यूटन की विधि की भिन्नता के लिए सामान्य है, जो काम करता है भले ही आरंभीकरण बिंदु बाधाओं को पूरा नहीं करता है), लेकिन यह भी कर सकता है आम तौर पर रैखिक बीजगणित के साथ समानता की बाधाओं को दूर करके या दोहरी समस्या को हल करके हल किया जा सकता है।अंत में, रैखिक समानता बाधाओं और उत्तल असमानता बाधाओं दोनों के साथ उत्तल अनुकूलन को ऑब्जेक्टिव फ़ंक्शन प्लस लॉगरिदमिक बैरियर फ़ंक्शन नियमों के लिए एक अप्रतिबंधित उत्तल अनुकूलन तकनीक लागू करके हल किया जा सकता है।(जब प्रारंभिक बिंदु संभव नहीं है - अर्थात, बाधाओं को संतुष्ट करना - यह तथाकथित चरण I विधियों से पहले होता है, जो या तो एक व्यवहार्य बिंदु ढूंढते हैं या दिखाते हैं कि कोई भी अस्तित्व में नहीं है। चरण I विधियों में आम तौर पर प्रश्न में खोज को कम करना सम्मिलित है। अभी तक एक और उत्तल अनुकूलन समस्या के लिए। उत्तल अनुकूलन समस्याओं को निम्नलिखित समकालीन तरीकों से भी हल किया जा सकता है:

• सबग्रेडिएंट मेथड # सबग्रेडिएंट-प्रोजेक्शन एंड बंडल मेथड्स (वोल्फ, लेमारेचल, किवील), और
• सबग्रेडिएंट मेथड # सबग्रेडिएंट-प्रोजेक्शन एंड बंडल मेथड्स मेथड्स (पॉलीक),
• आंतरिक बिंदु तरीके,जो स्व-समन्वय फलन | स्व-समन्वय अवरोधक प्रकार्यों का उपयोग करते हैं और स्व-नियमित बाधा कार्य।
• कटिंग-प्लेन तरीके
• दीर्घवृत्त विधि
• सबग्रेडिएंट विधि
• ड्रिफ्ट प्लस पेनल्टी|डुअल सबग्रेडिएंट्स और ड्रिफ्ट-प्लस-पेनल्टी विधि

सबग्रेडिएंट विधियों को आसानी से लागू किया जा सकता है और इसलिए व्यापक रूप से उपयोग किया जाता है। दोहरी सबग्रेडिएंट विधियाँ एक द्वैत (अनुकूलन) पर लागू सबग्रेडिएंट विधियाँ हैं। ड्रिफ्ट प्लस पेनल्टी | ड्रिफ्ट-प्लस-पेनल्टी विधि दोहरी सबग्रेडिएंट विधि के समान है, लेकिन प्रारंभिक चर का समय औसत लेती है।

कार्यान्वयन

उत्तल अनुकूलन और संबंधित एल्गोरिदम को निम्नलिखित सॉफ्टवेयर प्रोग्रामों में लागू किया गया है:

Program	Language	Description	FOSS?	Ref
CVX	MATLAB	Interfaces with SeDuMi and SDPT3 solvers; designed to only express convex optimization problems.	Yes
CVXMOD	Python	Interfaces with the CVXOPT solver.	Yes
CVXPY	Python
Convex.jl	Julia	Disciplined convex programming, supports many solvers.	Yes
CVXR	R		Yes
YALMIP	MATLAB, Octave	Interfaces with CPLEX, GUROBI, MOSEK, SDPT3, SEDUMI, CSDP, SDPA, PENNON solvers; also supports integer and nonlinear optimization, and some nonconvex optimization. Can perform robust optimization with uncertainty in LP/SOCP/SDP constraints.	Yes
LMI lab	MATLAB	Expresses and solves semidefinite programming problems (called "linear matrix inequalities")	No
LMIlab translator		Transforms LMI lab problems into SDP problems.	Yes
xLMI	MATLAB	Similar to LMI lab, but uses the SeDuMi solver.	Yes
AIMMS		Can do robust optimization on linear programming (with MOSEK to solve second-order cone programming) and mixed integer linear programming. Modeling package for LP + SDP and robust versions.	No
ROME		Modeling system for robust optimization. Supports distributionally robust optimization and uncertainty sets.	Yes
GloptiPoly 3	MATLAB, Octave	Modeling system for polynomial optimization.	Yes
SOSTOOLS		Modeling system for polynomial optimization. Uses SDPT3 and SeDuMi. Requires Symbolic Computation Toolbox.	Yes
SparsePOP		Modeling system for polynomial optimization. Uses the SDPA or SeDuMi solvers.	Yes
CPLEX		Supports primal-dual methods for LP + SOCP. Can solve LP, QP, SOCP, and mixed integer linear programming problems.	No
CSDP	C	Supports primal-dual methods for LP + SDP. Interfaces available for MATLAB, R, and Python. Parallel version available. SDP solver.	Yes
CVXOPT	Python	Supports primal-dual methods for LP + SOCP + SDP. Uses Nesterov-Todd scaling. Interfaces to MOSEK and DSDP.	Yes
MOSEK		Supports primal-dual methods for LP + SOCP.	No
SeDuMi	MATLAB, Octave, MEX	Solves LP + SOCP + SDP. Supports primal-dual methods for LP + SOCP + SDP.	Yes
SDPA	C++	Solves LP + SDP. Supports primal-dual methods for LP + SDP. Parallelized and extended precision versions are available.	Yes
SDPT3	MATLAB, Octave, MEX	Solves LP + SOCP + SDP. Supports primal-dual methods for LP + SOCP + SDP.	Yes
ConicBundle		Supports general-purpose codes for LP + SOCP + SDP. Uses a bundle method. Special support for SDP and SOCP constraints.	Yes
DSDP		Supports general-purpose codes for LP + SDP. Uses a dual interior point method.	Yes
LOQO		Supports general-purpose codes for SOCP, which it treats as a nonlinear programming problem.	No
PENNON		Supports general-purpose codes. Uses an augmented Lagrangian method, especially for problems with SDP constraints.	No
SDPLR		Supports general-purpose codes. Uses low-rank factorization with an augmented Lagrangian method.	Yes
GAMS		Modeling system for linear, nonlinear, mixed integer linear/nonlinear, and second-order cone programming problems.	No
Optimization Services		XML standard for encoding optimization problems and solutions.

एक्सटेंशन

उत्तल अनुकूलन के विस्तार में उभयोत्तल अनुकूलन, छद्म-उत्तल कार्य|छद्म-उत्तल, और अर्ध-उत्तल कार्यों का अनुकूलन सम्मिलित है। उत्तल विश्लेषण के सिद्धांत के विस्तार और लगभग गैर-उत्तल न्यूनीकरण समस्याओं को हल करने के लिए पुनरावृत्त तरीके उत्तलता (गणित) के क्षेत्र में होते हैं # उत्तलता के लिए सामान्यीकरण और विस्तार, जिसे अमूर्त उत्तल विश्लेषण भी कहा जाता है।

यह भी देखें

• द्वैत (अनुकूलन)
• करुश-कुह्न-टकर की स्थिति
• अनुकूलन समस्या
• समीपस्थ ढाल विधि

संदर्भ

• Bertsekas, Dimitri P.; Nedic, Angelia; Ozdaglar, Asuman (2003). Convex Analysis and Optimization. Belmont, MA.: Athena Scientific. ISBN 978-1-886529-45-8.
• Bertsekas, Dimitri P. (2009). Convex Optimization Theory. Belmont, MA.: Athena Scientific. ISBN 978-1-886529-31-1.
• Bertsekas, Dimitri P. (2015). Convex Optimization Algorithms. Belmont, MA.: Athena Scientific. ISBN 978-1-886529-28-1.
• Borwein, Jonathan; Lewis, Adrian (2000). Convex Analysis and Nonlinear Optimization: Theory and Examples, Second Edition (PDF). Springer. Retrieved 12 Apr 2021.{{cite book}}: CS1 maint: url-status (link)
• Christensen, Peter W.; Anders Klarbring (2008). An introduction to structural optimization. Vol. 153. Springer Science & Business Media. ISBN 9781402086663.

• Hiriart-Urruty, Jean-Baptiste, and Lemaréchal, Claude. (2004). Fundamentals of Convex analysis. Berlin: Springer.
• Hiriart-Urruty, Jean-Baptiste; Lemaréchal, Claude (1993). Convex analysis and minimization algorithms, Volume I: Fundamentals. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. Vol. 305. Berlin: Springer-Verlag. pp. xviii+417. ISBN 978-3-540-56850-6. MR 1261420.
• Hiriart-Urruty, Jean-Baptiste; Lemaréchal, Claude (1993). Convex analysis and minimization algorithms, Volume II: Advanced theory and bundle methods. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. Vol. 306. Berlin: Springer-Verlag. pp. xviii+346. ISBN 978-3-540-56852-0. MR 1295240.
• Kiwiel, Krzysztof C. (1985). Methods of Descent for Nondifferentiable Optimization. Lecture Notes in Mathematics. New York: Springer-Verlag. ISBN 978-3-540-15642-0.
• Lemaréchal, Claude (2001). "Lagrangian relaxation". In Michael Jünger and Denis Naddef (ed.). Computational combinatorial optimization: Papers from the Spring School held in Schloß Dagstuhl, May 15–19, 2000. Lecture Notes in Computer Science. Vol. 2241. Berlin: Springer-Verlag. pp. 112–156. doi:10.1007/3-540-45586-8_4. ISBN 978-3-540-42877-0. MR 1900016. S2CID 9048698.
• Nesterov, Yurii; Nemirovskii, Arkadii (1994). Interior Point Polynomial Methods in Convex Programming. SIAM.
• Nesterov, Yurii. (2004). Introductory Lectures on Convex Optimization, Kluwer Academic Publishers
• Rockafellar, R. T. (1970). Convex analysis. Princeton: Princeton University Press.

• Ruszczyński, Andrzej (2006). Nonlinear Optimization. Princeton University Press.
• Schmit, L.A.; Fleury, C. 1980: Structural synthesis by combining approximation concepts and dual methods. J. Amer. Inst. Aeronaut. Astronaut 18, 1252-1260

बाहरी संबंध

• EE364a: Convex Optimization I and EE364b: Convex Optimization II, Stanford course homepages
• 6.253: Convex Analysis and Optimization, an MIT OCW course homepage
• Brian Borchers, An overview of software for convex optimization
• Convex Optimization Book by Lieven Vandenberghe and Stephen P. Boyd

| group5 = Metaheuristics | abbr5 = heuristic | list5 =

• Evolutionary algorithm
• Hill climbing
• Local search
• Simulated annealing
• Tabu search

| below =

• Software

}} | group5 =Metaheuuristic |abbr5 = heuristic | list5 =*विकासवादी एल्गोरिथ्म

• पहाड़ी की चढ़ाई
• स्थानीय खोज
• तैयार किए हुयी धातु पे पानी चढाने की कला
• तब्बू खोज

| below =* सॉफ्टवेयर

}}