विसंगति (भौतिकी)

From Vigyanwiki
Quantum field theory
Feynmann Diagram Gluon Radiation.svg
Feynman diagram
History
Background
Symmetries
Tools
Equations
Standard Model
Incomplete theories
Scientists
Not to be confused with विसंगति (प्राकृतिक विज्ञान).

क्वांटम भौतिकी में एक विसंगति या क्वांटम विसंगति सिद्धांत की मौलिक क्रिया (भौतिकी) की समरूपता की पूर्ण क्वांटम सिद्धांत के किसी भी नियमितीकरण (भौतिकी) की समरूपता की विफलता है।[1][2] मौलिक भौतिकी में, एक मौलिक विसंगति उस सीमा में समरूपता को बहाल करने में विफलता होती है जिसमें समरूपता- विभंजन वाला पैरामीटर शून्य हो जाता है। संभवतः पहली ज्ञात विसंगति विघटनकारी विसंगति थी[3] विक्षोभ में: समय-प्रतिवर्तीता लुप्त होती स्थिरता की सीमा पर (और ऊर्जा अपव्यय दर परिमित) रहती है।

क्वांटम सिद्धांत में, खोजी गई पहली विसंगति एडलर-बेल-जैकिव विसंगति थी, जिसमें चिराल एनोमली को बिजली का गतिविज्ञान की मौलिक समरूपता के रूप में संरक्षित किया जाता है, लेकिन परिमाणित सिद्धांत द्वारा इसे तोड़ दिया जाता है। अतियाह-सिंगर इंडेक्स प्रमेय से इस विसंगति का संबंध सिद्धांत की प्रसिद्ध उपलब्धियों में से एक था। तकनीकी रूप से, क्वांटम सिद्धांत में एक विषम समरूपता क्रिया (भौतिकी) की एक समरूपता है, लेकिन माप (भौतिकी) की नहीं, और इसलिए संपूर्ण रूप से विभाजन कार्य (क्वांटम क्षेत्र सिद्धांत) की नहीं।

वैश्विक विसंगतियाँ

वैश्विक विसंगति एक वैश्विक समरूपता वर्तमान संरक्षण का क्वांटम उल्लंघन है। एक वैश्विक विसंगति का अर्थ यह भी हो सकता है कि एक गैर-परेशान वैश्विक विसंगति को एक लूप या किसी लूप पर्टुरबेटिव फेनमैन आरेख गणना द्वारा कैप्चर नहीं किया जा सकता है - उदाहरणों में Witten विसंगति और वैंग-वेन-Witten विसंगति सम्मलित हैं। Witten विसंगति और वांग-वेन-Witten विसंगति .

स्केलिंग और रीनॉर्मलाइजेशन

भौतिकी में सबसे प्रचलित वैश्विक विसंगति क्वांटम सुधारों द्वारा स्केल इनवेरियन के उल्लंघन से जुड़ी है, जो कि पुनर्सामान्यीकरण में परिमाणित है। चूंकि नियामक सामान्यतः एक दूरी के पैमाने का परिचय देते हैं, मौलिक पैमाने-अपरिवर्तनीय सिद्धांत पुनर्सामान्यीकरण समूह प्रवाह के अधीन होते हैं, अर्थात, ऊर्जा पैमाने के साथ बदलते व्यवहार। उदाहरण के लिए, मजबूत परमाणु बल की बड़ी ताकत एक ऐसे सिद्धांत से उत्पन्न होती है जो इस पैमाने की विसंगति के कारण लंबी दूरी पर एक मजबूत युग्मित सिद्धांत के लिए कम दूरी पर कमजोर रूप से युग्मित होता है।

कठोर समरूपता

विनिमेय वैश्विक समरूपता में विसंगतियाँ क्वांटम क्षेत्र सिद्धांत में कोई समस्या नहीं पैदा करती हैं, और अक्सर सामने आती हैं (चिरल विसंगति का उदाहरण देखें)। विशेष रूप से पथ अभिन्न सूत्रीकरण की सीमा स्थितियों को ठीक करके संबंधित विषम समरूपता को ठीक किया जा सकता है।

बड़े गेज परिवर्तन

चूँकि, समरूपता में वैश्विक विसंगतियाँ, जो पहचान को पर्याप्त रूप से अनंत तक पहुँचाती हैं, समस्याएँ पैदा करती हैं। ज्ञात उदाहरणों में ऐसी समरूपता गेज समरूपता के डिस्कनेक्ट किए गए घटकों के अनुरूप होती है। उदाहरण के लिए, इस तरह की समरूपता और संभावित विसंगतियाँ उत्पन्न होती हैं, उदाहरण के लिए, 4k + 2 आयामों में गुरुत्वाकर्षण के साथ मिलकर चिराल फ़र्मियन या स्व-दोहरी विभेदक रूपों वाले सिद्धांतों में, और एक सामान्य 4-आयामी SU(2) गेज सिद्धांत में #Witten विसंगति में भी।

चूंकि ये समरूपता अनंतता पर गायब हो जाती है, इसलिए उन्हें सीमा शर्तों से विवश नहीं किया जा सकता है और इसलिए उन्हें अभिन्न पथ में अभिव्यक्त किया जाना चाहिए। किसी राज्य की गेज कक्षा का योग उन चरणों का योग है जो U(1) का एक उपसमूह बनाते हैं। जैसा कि एक विसंगति है, ये सभी चरण समान नहीं हैं, इसलिए यह पहचान उपसमूह नहीं है। यू (1) के हर दूसरे उपसमूह में चरणों का योग शून्य के बराबर है, और इस तरह की विसंगति होने पर और सिद्धांत मौजूद नहीं होने पर सभी पथ इंटीग्रल शून्य के बराबर होते हैं।

एक अपवाद तब हो सकता है जब कॉन्फ़िगरेशन का स्थान स्वयं डिस्कनेक्ट हो जाता है, उस स्थिति में किसी को किसी भी पर एकीकृत करने के लिए चुनने की स्वतंत्रता हो सकती है घटकों का सबसेट। यदि डिस्कनेक्टेड गेज समरूपता डिस्कनेक्टेड कॉन्फ़िगरेशन के बीच सिस्टम को मैप करती है, तो सामान्य रूप से एक सिद्धांत का एक सुसंगत ट्रंकेशन होता है जिसमें कोई केवल उन जुड़े घटकों पर एकीकृत होता है जो बड़े गेज परिवर्तनों से संबंधित नहीं होते हैं। इस मामले में बड़े गेज परिवर्तन प्रणाली पर कार्य नहीं करते हैं और पथ अभिन्न को गायब होने का कारण नहीं बनाते हैं।

विटेन एनोमली और वैंग-वेन-विट एनोमली

SU(2) गेज सिद्धांत में 4 आयामी मिन्कोव्स्की अंतरिक्ष में, एक गेज परिवर्तन अंतरिक्ष-समय में प्रत्येक बिंदु पर विशेष एकात्मक समूह SU(2) के एक तत्व की विकल्प से मेल खाता है। ऐसे गेज परिवर्तनों का समूह समाहित हुआ होता है।

चूँकि, अगर हम केवल गेज परिवर्तनों के उपसमूह में रुचि रखते हैं जो अनंत पर गायब हो जाते हैं, तो हम अनंत पर 3-गोले को एक बिंदु मान सकते हैं, क्योंकि गेज परिवर्तन वैसे भी गायब हो जाते हैं। यदि अनंत पर 3-गोले की पहचान एक बिंदु से की जाती है, तो हमारे मिन्कोवस्की स्थान की पहचान 4-गोले के साथ की जाती है। इस प्रकार हम देखते हैं कि मिन्कोवस्की अंतरिक्ष में अनंत पर गायब होने वाले गेज परिवर्तनों का समूह 4-गोले पर सभी गेज परिवर्तनों के समूह के लिए आइसोमोर्फिक है।

यह वह समूह है जिसमें 4-गोले पर प्रत्येक बिंदु के लिए SU(2) में गेज परिवर्तन की निरंतर विकल्प होती है। दूसरे शब्दों में, गेज समरूपता 4-गोले से 3-गोले के नक्शे के साथ एक-से-एक पत्राचार में हैं, जो SU(2) का समूह कई गुना है। ऐसे नक्शों का स्थान जुड़ा नहीं है, इसके बजाय जुड़े हुए घटकों को 3-गोले के चौथे समरूप समूह द्वारा वर्गीकृत किया जाता है जो क्रम दो का चक्रीय समूह है। विशेष रूप से, दो जुड़े घटक हैं। एक में पहचान होती है और इसे पहचान घटक कहा जाता है, दूसरे को डिस्कनेक्ट किया गया घटक कहा जाता है।

जब किसी सिद्धांत में चिराल फ़र्मियन के स्वादों की विषम संख्या होती है, तो पहचान घटक में गेज समरूपता की क्रियाएं और भौतिक अवस्था पर गेज समूह के डिस्कनेक्ट किए गए घटक एक संकेत से भिन्न होते हैं। इस प्रकार जब कोई कार्यात्मक एकीकरण में सभी भौतिक विन्यासों पर योग करता है, तो वह पाता है कि योगदान विपरीत संकेतों वाले जोड़े में आते हैं। नतीजतन, सभी पथ अभिन्न गायब हो जाते हैं और एक सिद्धांत मौजूद नहीं होता है।

वैश्विक विसंगति का उपरोक्त विवरण SU(2) गेज सिद्धांत के लिए है जो 4 स्पेसटाइम आयामों में विषम संख्या (आइसो-) स्पिन-1/2 वेइल फर्मियन से जुड़ा है। इसे Witten SU(2) विसंगति के रूप में जाना जाता है।[4] 2018 में, वैंग, वेन और विट्टन द्वारा यह पाया गया कि SU(2) गेज सिद्धांत 4 स्पेसटाइम आयामों में विषम संख्या (आइसो-) स्पिन-3/2 वेइल फर्मियन के साथ मिलकर एक और सूक्ष्म गैर-परेशान वैश्विक विसंगति है। स्पिन संरचना के बिना कुछ गैर-स्पिन मैनिफोल्ड पर पता लगाने योग्य।[5] इस नई विसंगति को नई एसयू(2) विसंगति कहा जाता है। दोनों प्रकार की विसंगतियाँ[4] [5]डायनेमिक गेज सिद्धांतों के लिए (1) डायनेमिक गेज विसंगतियों और (2) वैश्विक समरूपता के 'टी हूफ्ट विसंगतियों' के अनुरूप हैं। इसके अलावा, दोनों प्रकार की विसंगतियाँ mod 2 वर्ग हैं (वर्गीकरण के संदर्भ में, वे दोनों परिमित समूह Z हैं2 2 वर्गों के क्रम में), और 4 और 5 स्पेसटाइम आयामों में अनुरूप हैं।[5] अधिक सामान्यतः, किसी भी प्राकृतिक पूर्णांक एन के लिए, यह दिखाया जा सकता है कि (आईएसओ) -स्पिन 2N+1/2 के निरूपण में फ़र्मियन मल्टीप्लेट्स की एक विषम संख्या में SU(2) विसंगति हो सकती है; (आइसो)-स्पिन 4N+3/2 के अभ्यावेदन में फ़र्मियन मल्टीप्लेट्स की एक विषम संख्या में नई SU(2) विसंगति हो सकती है।[5] अर्ध-पूर्णांक स्पिन प्रतिनिधित्व में फ़र्मियन के लिए, यह दिखाया गया है कि केवल दो प्रकार की SU(2) विसंगतियाँ हैं और इन दो विसंगतियों के रैखिक संयोजन हैं; ये सभी वैश्विक SU(2) विसंगतियों को वर्गीकृत करते हैं।[5]यह नया एसयू(2) विसंगति एसओ(10) भव्य एकीकृत सिद्धांत की निरंतरता की पुष्टि के लिए एक महत्वपूर्ण नियम भी निभाता है, जिसमें स्पिन(10) गेज समूह और गैर-स्पिन मैनिफोल्ड्स पर परिभाषित 16-आयामी स्पिनर अभ्यावेदन में चिरल फ़र्मियन सम्मलित हैं। .[5][6]

उच्च विसंगतियों में उच्च वैश्विक समरूपता सम्मलित है: उदाहरण के रूप में शुद्ध यांग-मिल्स गेज सिद्धांत

वैश्विक समरूपता की अवधारणा को उच्च वैश्विक समरूपता के लिए सामान्यीकृत किया जा सकता है,[7] जैसे कि साधारण 0-रूप समरूपता के लिए आवेशित वस्तु एक कण है, जबकि n-रूप समरूपता के लिए आवेशित वस्तु एक n-आयामी विस्तारित संचालिका है। यह पाया गया है कि 4 आयामी शुद्ध यांग-मिल्स सिद्धांत केवल SU(2) गेज क्षेत्रों के साथ एक स्थलीय थीटा शब्द के साथ 0-फॉर्म टाइम-रिवर्सल समरूपता और 1-फॉर्म Z के बीच मिश्रित उच्च 'टी हूफ्ट विसंगति हो सकती है2 केंद्र समरूपता।[8] 4 आयामी शुद्ध यांग-मिल्स सिद्धांत के 'टी हूफ्ट विसंगति को 5 आयामी व्युत्क्रमणीय स्थलीय क्षेत्र सिद्धांत या गणितीय रूप से 5 आयामी बोर्डिज्म इनवेरिएंट के रूप में लिखा जा सकता है, जो इस Z2 वर्ग के विसंगति प्रवाह चित्र को सामान्य करता है।[9] दूसरे शब्दों में, हम 4 आयामी शुद्ध यांग-मिल्स सिद्धांत को एक सामयिक थीटा शब्द के साथ मान सकते हैं आयामी सीमा पर उनकी उच्च विसंगतियों से मेल खाने के क्रम में, एक निश्चित Z2 वर्ग उलटा स्थलीय क्षेत्र सिद्धांत की एक सीमा स्थिति के रूप में रहते हैं। [9]

गेज विसंगतियाँ

Main article: गेज विसंगति

गेज समरूपता में विसंगतियां एक असंगतता का कारण बनती हैं, क्योंकि एक नकारात्मक मानदंड (जैसे कि समय दिशा में ध्रुवीकृत फोटॉन) के साथ स्वतंत्रता की गैर-भौतिक डिग्री को रद्द करने के लिए गेज समरूपता की आवश्यकता होती है। उन्हें रद्द करने का प्रयास - यानी, गेज समरूपता के अनुरूप सिद्धांतों का निर्माण करने के लिए - अक्सर सिद्धांतों पर अतिरिक्त बाधाओं की ओर जाता है (जैसे कि कण भौतिकी के मानक मॉडल में गेज विसंगति की स्थितियों है)। गेज सिद्धांतों में विसंगतियों का गेज समूह की टोपोलॉजी और ज्यामिति से महत्वपूर्ण संबंध है।

गेज समरूपता में विसंगतियों की गणना बिल्कुल एक-लूप स्तर पर की जा सकती है। वृक्ष स्तर (शून्य लूप) पर, एक मौलिक सिद्धांत को पुन: उत्पन्न करता है। एक से अधिक लूप वाले फेनमैन आरेखों में हमेशा आंतरिक बोसॉन प्रचारक होते हैं। जैसा कि बोसॉन को हमेशा गेज इनवेरियन को तोड़े बिना द्रव्यमान दिया जा सकता है, समरूपता को संरक्षित करते हुए ऐसे आरेखों का एक पाउली-विलार्स नियमितीकरण संभव है। जब भी आरेख का नियमितीकरण किसी दिए गए समरूपता के अनुरूप होता है, तो वह आरेख समरूपता के संबंध में एक विसंगति उत्पन्न नहीं करता है।

वेक्टर गेज विसंगतियाँ हमेशा चिरल विसंगति होती हैं। एक अन्य प्रकार की गेज विसंगति गुरुत्वाकर्षण विसंगति है।

विभिन्न ऊर्जा पैमानों पर

Main article: विसंगति मिलान की स्थिति

पुनर्सामान्यीकरण की प्रक्रिया के माध्यम से क्वांटम विसंगतियों की खोज की गई, जब कुछ पराबैंगनी विचलन को इस तरह से नियमितीकरण (भौतिकी) नहीं किया जा सकता है, कि सभी समरूपता साथ संरक्षित हैं। यह उच्च ऊर्जा भौतिकी से संबंधित है। चूँकि, जेरार्ड 'टी हूफ्ट की विसंगति मिलान की स्थिति के कारण, किसी भी चिरल विसंगति को या तो स्वतंत्रता की यूवी डिग्री (उच्च ऊर्जा पर प्रासंगिक) या आईआर स्वतंत्रता की डिग्री (कम ऊर्जा पर प्रासंगिक) द्वारा वर्णित किया जा सकता है। इस प्रकार एक सिद्धांत के एक यूवी पूरा होने से एक विसंगति को रद्द नहीं किया जा सकता है - एक विषम समरूपता सिद्धांत की समरूपता नहीं है, भले ही शास्त्रीय रूप से ऐसा प्रतीत होता है।

विसंगति रद्दीकरण

Triangle diagram.svg

चूंकि विसंगतियों को रद्द करना गेज सिद्धांतों की निरंतरता के लिए आवश्यक है, ऐसे रद्दीकरण मानक मॉडल की फ़र्मियन सामग्री को बाधित करने में केंद्रीय महत्व के हैं, जो कि चिरल गेज सिद्धांत है।

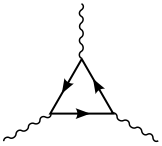
उदाहरण के लिए, दो SU(2) जेनरेटर और एक U(1) हाइपरचार्ज से जुड़ी मिश्रित विसंगति के गायब होने से फ़र्मियन पीढ़ी में सभी चार्ज शून्य तक जुड़ जाते हैं,[10][11] और इस तरह तय होता है कि योग का योग प्रोटॉन प्लस इलेक्ट्रॉन का योग लुप्त हो जाता है: क्वार्क और लेप्टान के आवेश समानुपाती होने चाहिए। विशेष रूप से, त्रिभुज आरेख के शीर्ष पर दो बाहरी गेज फ़ील्ड Wa, Wb और एक हाइपरचार्ज B के लिए, त्रिभुज को रद्द करने की आवश्यकता होती हैआवश्यकता है

इसलिए, प्रत्येक पीढ़ी के लिए, लेप्टान और क्वार्क के आवेश संतुलित होते हैं, , जहां से Qp + Qe = 0[citation needed].

एस.एम. में विसंगति निरसन का उपयोग तीसरी पीढ़ी, शीर्ष क्वार्क से एक क्वार्क की भविष्यवाणी करने के लिए भी किया गया था। [12]

इसके अलावा इस तरह के तंत्र में सम्मलित हैं:

  • एक्सियन
  • चेर्न-सीमन्स
  • ग्रीन-श्वार्ज तंत्र
  • लिउविल क्रिया

विसंगतियाँ और सहवाद

कोबोर्डिज्म सिद्धांत द्वारा वर्गीकृत विसंगतियों के आधुनिक विवरण में,[13] फेनमैन-डायसन ग्राफ़ केवल पूर्ण भाग के रूप में ज्ञात पूर्णांक Z वर्गों द्वारा वर्गीकृत विचलित करने वाली स्थानीय विसंगतियों को पकड़ता है। चक्रीय समूह Z/nZ वर्गों द्वारा वर्गीकृत गैर-विवादास्पद वैश्विक विसंगतियाँ मौजूद हैं जिन्हें आघूर्ण बल वाले भाग के रूप में भी जाना जाता है।

20वीं शताब्दी के अंत में यह व्यापक रूप से ज्ञात और जांचा गया था कि मानक मॉडल और चिराल गेज सिद्धांत परेशान करने वाली स्थानीय विसंगतियों (फेनमैन आरेख द्वारा कब्जा कर लिया गया) से मुक्त हैं। चूँकि,यह पूरी तरह से स्पष्ट नहीं है कि मानक मॉडल और चिराल गेज सिद्धांतों के लिए कोई गैर-विवादास्पद वैश्विक विसंगतियां हैं या नहीं। हाल के घटनाक्रम [14][15][16] सह-बोर्डिज्म सिद्धांत पर आधारित इस समस्या की जांच करते हैं, और कई अतिरिक्त गैर-तुच्छ वैश्विक विसंगतियां पाई जाती हैं जो इन गेज सिद्धांतों को और बाधित कर सकती हैं। अतियाह, पटोदी, और सिंगर [17][18] और एक उच्च आयाम के संदर्भ में अपरिवर्तनीय प्रवाह के संदर्भ में गड़बड़ी के स्थानीय और गैर-विक्षुब्ध वैश्विक विवरण दोनों का एक सूत्रीकरण भी है। जब भी परेशान करने वाली स्थानीय विसंगतियाँ गायब हो जाती हैं, तो यह और अपरिवर्तनीय कोबोरिज्म इनवेरिएंट होता है। [19]

उदाहरण

यह भी देखें

  • विसंगतियां, 1980 के दशक में कुछ बहस का विषय, कुछ उच्च-ऊर्जा भौतिकी प्रयोगों के परिणामों में विसंगतियां पाई गईं, जो पदार्थ की असामान्य रूप से अत्यधिक संवादात्मक अवस्थाओं के अस्तित्व की ओर इशारा करती थीं। विषय अपने पूरे इतिहास में विवादास्पद था।

संदर्भ

Citations
  1. ↑ Bardeen, William (1969). "Anomalous Ward identities in spinor field theories". Physical Review. 184 (5): 1848–1859. Bibcode:1969PhRv..184.1848B. doi:10.1103/physrev.184.1848.
  2. ↑ Cheng, T.P.; Li, L.F. (1984). प्राथमिक कण भौतिकी का गेज सिद्धांत. Oxford Science Publications.
  3. ↑ "एकल यूलर प्रवाह में विघटनकारी विसंगतियाँ" (PDF).
  4. ↑ 4.0 4.1 Witten, Edward (November 1982). "An SU(2) Anomaly". Phys. Lett. B. 117 (5): 324. Bibcode:1982PhLB..117..324W. doi:10.1016/0370-2693(82)90728-6.
  5. ↑ 5.0 5.1 5.2 5.3 5.4 5.5 Wang, Juven; Wen, Xiao-Gang; Witten, Edward (May 2019). "A New SU(2) Anomaly". Journal of Mathematical Physics. 60 (5): 052301. arXiv:1810.00844. Bibcode:2019JMP....60e2301W. doi:10.1063/1.5082852. ISSN 1089-7658. S2CID 85543591.
  6. ↑ Wang, Juven; Wen, Xiao-Gang (1 June 2020). "मानक मॉडल की गैर-अनुस्पर्धी परिभाषा". Physical Review Research. 2 (2): 023356. arXiv:1809.11171. Bibcode:2018arXiv180911171W. doi:10.1103/PhysRevResearch.2.023356. ISSN 2469-9896. S2CID 53346597.
  7. ↑ Gaiotto, Davide; Kapustin, Anton; Seiberg, Nathan; Willett, Brian (February 2015). "सामान्यीकृत वैश्विक समरूपता". JHEP. 2015 (2): 172. arXiv:1412.5148. Bibcode:2015JHEP...02..172G. doi:10.1007/JHEP02(2015)172. ISSN 1029-8479. S2CID 37178277.
  8. ↑ Gaiotto, Davide; Kapustin, Anton; Komargodski, Zohar; Seiberg, Nathan (May 2017). "Theta, Time Reversal, and Temperature". JHEP. 2017 (5): 91. arXiv:1412.5148. Bibcode:2017JHEP...05..091G. doi:10.1007/JHEP05(2017)091. ISSN 1029-8479. S2CID 119528151.
  9. ↑ 9.0 9.1 Wan, Zheyan; Wang, Juven; Zheng, Yunqin (October 2019). "Quantum 4d Yang-Mills Theory and Time-Reversal Symmetric 5d Higher-Gauge Topological Field Theory". Physical Review D. 100 (8): 085012. arXiv:1904.00994. Bibcode:2019PhRvD.100h5012W. doi:10.1103/PhysRevD.100.085012. ISSN 2470-0029. S2CID 201305547.
  10. ↑ Bouchiat, Cl, Iliopoulos, J, and Meyer, Ph (1972) . "An anomaly-free version of Weinberg's model." Physics Letters B38, 519-523.
  11. ↑ Minahan, J. A.; Ramond, P.; Warner, R. C. (1990). "मानक मॉडल में विसंगति रद्दीकरण पर टिप्पणी करें". Phys. Rev. D. 41 (2): 715–716. Bibcode:1990PhRvD..41..715M. doi:10.1103/PhysRevD.41.715. PMID 10012386.
  12. ↑ Conlon, Joseph (2016-08-19). Why String Theory? (in English) (1 ed.). CRC Press. p. 81. doi:10.1201/9781315272368. ISBN 978-1-315-27236-8.
  13. ↑ Freed, Daniel S.; Hopkins, Michael J. (2021). "Reflection positivity and invertible topological phases". Geometry & Topology. 25 (3): 1165–1330. arXiv:1604.06527. Bibcode:2016arXiv160406527F. doi:10.2140/gt.2021.25.1165. ISSN 1465-3060. S2CID 119139835.
  14. ↑ García-Etxebarria, Iñaki; Montero, Miguel (August 2019). "कण भौतिकी में दाई-मुक्त विसंगतियाँ". JHEP. 2019 (8): 3. arXiv:1808.00009. Bibcode:2019JHEP...08..003G. doi:10.1007/JHEP08(2019)003. ISSN 1029-8479. S2CID 73719463.
  15. ↑ Davighi, Joe; Gripaios, Ben; Lohitsiri, Nakarin (July 2020). "मानक मॉडल (नों) और परे में वैश्विक विसंगतियाँ". JHEP. 2020 (7): 232. arXiv:1910.11277. Bibcode:2020JHEP...07..232D. doi:10.1007/JHEP07(2020)232. ISSN 1029-8479. S2CID 204852053.
  16. ↑ Wan, Zheyan; Wang, Juven (July 2020). "Beyond Standard Models and Grand Unifications: Anomalies, Topological Terms, and Dynamical Constraints via Cobordisms". JHEP. 2020 (7): 62. arXiv:1910.14668. Bibcode:2020JHEP...07..062W. doi:10.1007/JHEP07(2020)062. ISSN 1029-8479. S2CID 207800450.
  17. ↑ Atiyah, Michael Francis; Patodi, V. K.; Singer, I. M. (1973), "Spectral asymmetry and Riemannian geometry", The Bulletin of the London Mathematical Society, 5 (2): 229–234, CiteSeerX 10.1.1.597.6432, doi:10.1112/blms/5.2.229, ISSN 0024-6093, MR 0331443
  18. ↑ Atiyah, Michael Francis; Patodi, V. K.; Singer, I. M. (1975), "Spectral asymmetry and Riemannian geometry. I", Mathematical Proceedings of the Cambridge Philosophical Society, 77 (1): 43–69, Bibcode:1975MPCPS..77...43A, doi:10.1017/S0305004100049410, ISSN 0305-0041, MR 0397797, S2CID 17638224
  19. ↑ Witten, Edward; Yonekura, Kazuya (2019). "विसंगति प्रवाह और ईटा-इनवेरिएंट". arXiv:1909.08775. {{cite journal}}: Cite journal requires |journal= (help)
General
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=विसंगति_(भौतिकी)&oldid=117679’