एरलांग वितरण

This article is about गणितीय / सांख्यिकीय वितरण अवधारणा. For other uses, see एरलांग.

Erlang

Probability density function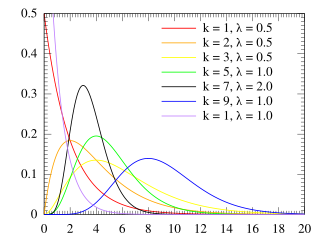
Cumulative distribution function
Parameters	$k\in \{1,2,3,\ldots \},$ shape $\lambda \in (0,\infty ),$ rate alt.: $\beta =1/\lambda ,$ scale
Support	$x\in [0,\infty )$
PDF	${\frac {\lambda ^{k}x^{k-1}e^{-\lambda x}}{(k-1)!}}$
CDF	$P(k,\lambda x)={\frac {\gamma (k,\lambda x)}{(k-1)!}}=1-\sum _{n=0}^{k-1}{\frac {1}{n!}}e^{-\lambda x}(\lambda x)^{n}$
Mean	${\frac {k}{\lambda }}$
Median	No simple closed form
Mode	${\frac {1}{\lambda }}(k-1)$
Variance	${\frac {k}{\lambda ^{2}}}$
Skewness	${\frac {2}{\sqrt {k}}}$
Ex. kurtosis	${\frac {6}{k}}$
Entropy	$(1-k)\psi (k)+\ln \left[{\frac {\Gamma (k)}{\lambda }}\right]+k$
MGF	$\left(1-{\frac {t}{\lambda }}\right)^{-k}$ for $t<\lambda$
CF	$\left(1-{\frac {it}{\lambda }}\right)^{-k}$

एरलांग वितरण समर्थन (गणित) $x\in [0,\infty )$ के साथ निरंतर प्रायिकता वितरण का दो-पैरामीटर परिवार है। दो पैरामीटर हैं:

• एक सकारात्मक पूर्णांक $k,$ आकार, और
• एक सकारात्मक वास्तविक संख्या $\lambda ,$ ''दर'' । "स्केल", $\beta ,$ दर का पारस्परिक, कभी-कभी इसके बदले प्रयोग किया जाता है।

एरलांग वितरण प्रत्येक $1/\lambda$ माध्य के साथ $k$ स्वतंत्रत घातीय चर के योग का वितरण है। समतुल्य रूप से, यह $\lambda$ की दर के साथ प्वाइजन प्रक्रिया की k वीं घटना तक के समय का वितरण है। एरलांग और प्वाइजन वितरण पूरक हैं, जबकि प्वाइजन वितरण निश्चित समय में होने वाली घटनाओं की संख्या की गणना करता है, एरलांग वितरण घटनाओं की एक निश्चित संख्या की घटना तक समय की मात्रा की गणना करता है। कब $k=1$, वितरण घातीय वितरण के लिए सरल हो जाता है। एरलांग वितरण गामा वितरण का एक विशेष प्रकरण है जिसमें वितरण का आकार अलग-अलग होता है।

एरलांग वितरण को A. K. एरलांग द्वारा विकसित किया गया था ताकि स्विचिंग स्टेशनों के संचालक को एक ही समय में किए जाने वाले टेलीफोन कॉल की संख्या की जांच की जा सके। सामान्यतः क्यूइंग प्रणाली में प्रतीक्षा समय पर विचार करने के लिए टेलीफोन ट्रैफ़िक अभियांत्रिकी पर यह काम विस्तारित किया गया है। वितरण का उपयोग प्रसंभाव्य प्रक्रम के क्षेत्र में भी किया जाता है।

विशेषता

प्रायिकता घनत्व फलन

एरलांग वितरण का प्रायिकता घनत्व फलन है

$f(x;k,\lambda )={\lambda ^{k}x^{k-1}e^{-\lambda x} \over (k-1)!}\quad {\mbox{for }}x,\lambda \geq 0,$

पैरामीटर k को आकार पैरामीटर और पैरामीटर कहा जाता है $\lambda$ को दर पैरामीटर कहा जाता है।

एक वैकल्पिक, लेकिन समतुल्य, प्राचलीकरण स्केल पैरामीटर $\beta$ का उपयोग करता है, जो दर पैरामीटर का पारस्परिक है (अर्थात, $\beta =1/\lambda$):

$f(x;k,\beta )={\frac {x^{k-1}e^{-{\frac {x}{\beta }}}}{\beta ^{k}(k-1)!}}\quad {\mbox{for }}x,\beta \geq 0.$

जब स्केल पैरामीटर $\beta$ 2 के समान है, तो वितरण 2k डिग्री स्वतंत्रता के साथ ची-वर्ग वितरण को सरल करता है। इसलिए इसे स्वतंत्रता की डिग्री की सम संख्याओं के लिए सामान्यीकृत ची-वर्ग वितरण के रूप में माना जा सकता है।

संचयी वितरण फलन (सीडीएफ)

एरलांग वितरण का संचयी वितरण फलन है

$F(x;k,\lambda )=P(k,\lambda x)={\frac {\gamma (k,\lambda x)}{\Gamma (k)}}={\frac {\gamma (k,\lambda x)}{(k-1)!}},$

जहाँ $\gamma$ निम्न अपूर्ण गामा फलन है और $P$ निम्न नियमित गामा फलन है। सीडीएफ को भी व्यक्त किया जा सकता है

$F(x;k,\lambda )=1-\sum _{n=0}^{k-1}{\frac {1}{n!}}e^{-\lambda x}(\lambda x)^{n}.$

एरलांग-k

एरलांग-k वितरण (जहाँ k एक सकारात्मक पूर्णांक है) $E_{k}(\lambda )$ को एरलांग वितरण के पीडीएफ में k समायोजन करके परिभाषित किया गया है। उदाहरण के लिए, एरलांग-2 वितरण $E_{2}(\lambda )={\lambda ^{2}x}e^{-\lambda x}\quad {\mbox{for }}x,\lambda \geq 0$ है, जो $f(x;2,\lambda )$ समान हैं।

मध्य

एरलांग वितरण के माध्यिका के लिए एक स्पर्शोन्मुख विस्तार जाना जाता है, जिसके लिए गुणांकों की गणना की जा सकती है और सीमाएं ज्ञात हैं। एक सन्निकटन ${\frac {k}{\lambda }}\left(1-{\dfrac {1}{3k+0.2}}\right)$है, अर्थात माध्य ${\frac {k}{\lambda }}.$ से नीचे।

एरलांग-वितरित यादृच्छिक चर उत्पन्न करना

निम्नलिखित सूत्र का उपयोग करके समान रूप से वितरित यादृच्छिक संख्याओं ($U\in [0,1]$) से एरलांग-वितरित यादृच्छिक चर उत्पन्न किए जा सकते हैं:

$E(k,\lambda )=-{\frac {1}{\lambda }}\ln \prod _{i=1}^{k}U_{i}=-{\frac {1}{\lambda }}\sum _{i=1}^{k}\ln U_{i}$

अनुप्रयोग

प्रतीक्षा काल

कुछ औसत दर के साथ स्वतंत्र रूप से घटित होने वाली घटनाओं को एक पॉइसन प्रक्रिया के साथ प्रतिरूपित किया जाता है। घटना की k घटनाओं के मध्य प्रतीक्षा काल एरलांग वितरित किया जाता है। (किसी दिए गए काल में घटनाओं की संख्या से संबंधित प्रश्न प्वाइजन वितरण द्वारा वर्णित है।)

एरलांग वितरण, जो इनकमिंग कॉल के मध्य के समय को मापता है, का उपयोग इनकमिंग कॉल की अपेक्षित अवधि के साथ संयोजन में किया जा सकता है ताकि एरलांग में मापे गए ट्रैफ़िक भार के बारे में जानकारी प्राप्त की जा सके। इसका उपयोग पैकेट के नुकसान या देरी की संभावना को निर्धारित करने के लिए किया जा सकता है, इस बारे में की गई विभिन्न धारणाओं के अनुसार कि क्या ब्लॉक किए गए कॉल निरस्त किए गए हैं (एरलांग B सूत्र) या कतारबद्ध जब तक सेवा नहीं दी गई है (एरलांग C सूत्र)। कॉल केंद्रो के डिज़ाइन जैसे अनुप्रयोगों के लिए ट्रैफ़िक मॉडलिंग के लिए एरलांग-B और C सूत्र अभी भी दैनिक के उपयोग में हैं।

अन्य अनुप्रयोग

कैंसर रोग की घटनाओं का आयु वितरण प्रायः एरलांग वितरण का अनुसरण करता है, जबकि आकार और पैमाने के पैरामीटर क्रमशः चालक घटनाओं की संख्या और उनके मध्य समय अंतराल की भविष्यवाणी करते हैं। अधिक सामान्यतः, बहुचरण मॉडल के परिणाम के रूप में, एरलांग वितरण को सेल चक्र समय वितरण के अच्छे अनुमान के रूप में सुझाया गया है।

इंटरपरचेज समय का वर्णन करने के लिए इसका उपयोग व्यावसायिक अर्थशास्त्र में भी किया गया है।

गुण

• अगर $X\sim \operatorname {Erlang} (k,\lambda )$ तो $a\cdot X\sim \operatorname {Erlang} \left(k,{\frac {\lambda }{a}}\right)$ साथ में $a\in \mathbb {R}$
• अगर $X\sim \operatorname {Erlang} (k_{1},\lambda )$ और $Y\sim \operatorname {Erlang} (k_{2},\lambda )$ तो $X+Y\sim \operatorname {Erlang} (k_{1}+k_{2},\lambda )$ अगर $X,Y$ स्वतंत्र हैं

संबंधित वितरण

• एरलांग वितरण k स्वतंत्र और समान रूप से वितरित यादृच्छिक चर के योग का वितरण है, प्रत्येक में एक घातीय वितरण है। दीर्घकालिक दर जिस पर घटनाएं घटित होती हैं, वह $X$ की अपेक्षा का पारस्परिक है, अर्थात $\lambda /k$। एरलांग वितरण की (आयु विशिष्ट घटना) दर, $k>1$ के लिए, $x$ में एकदिष्‍ट है, 0 से $x=0$ पर बढ़ रही है, $\lambda$ के रूप में $x$ अनंत की ओर जाता है।
• अर्थात्: अगर $X_{i}\sim \operatorname {Exponential} (\lambda ),$ तब
  $$\sum _{i=1}^{k}{X_{i}}\sim \operatorname {Erlang} (k,\lambda )$$
• पीडीएफ और सीडीएफ के भाजक में क्रमगुणित फलन के कारण, एरलांग वितरण केवल तभी परिभाषित होता है जब पैरामीटर k एक सकारात्मक पूर्णांक होता है। वास्तव में, इस वितरण को कभी-कभी एरलांग-k वितरण कहा जाता है (उदाहरण के लिए, एरलांग -2 वितरण $k=2$ के साथ एरलांग वितरण है)। गामा वितरण क्रमगुणित फलन के बदले गामा फलन का उपयोग करके, किसी भी सकारात्मक वास्तविक संख्या होने की अनुमति देकर एरलांग वितरण को सामान्यीकृत करता है।
  • अर्थात्: यदि k एक पूर्णांक है और $X\sim \operatorname {Gamma} (k,\lambda ),$ तब $X\sim \operatorname {Erlang} (k,\lambda )$
• अगर $U\sim \operatorname {Exponential} (\lambda )$ और $V\sim \operatorname {Erlang} (n,\lambda )$ तब ${\frac {U}{V}}+1\sim \operatorname {Pareto} (1,n)$
• एरलांग वितरण पियर्सन प्रकार III वितरण का एक विशेष प्रकरण है
• एरलांग वितरण ची-वर्ग वितरण से संबंधित है। अगर $X\sim \operatorname {Erlang} (k,\lambda ),$ तब $2\lambda X\sim \chi _{2k}^{2}$
• एरलांग वितरण प्वाइजन प्रक्रिया द्वारा प्वाइजन वितरण से संबंधित है: यदि $S_{n}=\sum _{i=1}^{n}X_{i}$ ऐसा है कि $X_{i}\sim \operatorname {Exponential} (\lambda ),$ तब
  $$S_{n}\sim \operatorname {Erlang} (n,\lambda )$$
  और
  $$\operatorname {Pr} (N(x)\leq n-1)=\operatorname {Pr} (S_{n}>x)=1-F_{X}(x;n,\lambda )=\sum _{k=0}^{n-1}{\frac {1}{k!}}e^{-\lambda x}(\lambda x)^{k}.$$
  $n$ पर अंतर लेने से प्वाइजन वितरण प्राप्त होता है।

यह भी देखें

• कॉक्सियन वितरण
• एंगसेट गणना
• एरलांग बी सूत्र
• एरलांग इकाई
• चरण-प्रकार वितरण
• ट्रैफ़िक उत्पादन मॉडल

संदर्भ

• Ian Angus "An Introduction to एरलांग B and एरलांग C", Telemanagement #187 (PDF Document - Has terms and formulae plus short biography)
• Stuart Harris "एरलांग Calculations vs. Simulation"

बाहरी संबंध

• एरलांग Distribution
• Resource Dimensioning Using एरलांग-B and एरलांग-C