मोत्ज़किन संख्या
| Named after | थियोडोर मोत्जकिन |
|---|---|
| Publication year | 1948 |
| Author of publication | थियोडोर मोत्जकिन |
| No. of known terms | अनंत |
| Formula | गुण देखा जाता हैं |
| First terms | 1, 1, 2, 4, 9, 21, 51 |
| OEIS index |
|
गणित में, nवें मोत्जकिन संख्या एक वृत्त पर n बिंदु (आवश्यक नहीं कि प्रत्येक बिंदु को जीवा से स्पर्श किया जाता हैं) के बीच अप्रतिछेदी जीवा खींचने के विभिन्न प्रकारो की संख्या है। मोत्जकिन संख्याओं का नाम थिओडोर मोत्ज़किन के नाम पर रखा गया है और ज्यामिति, साहचर्य और संख्या सिद्धांत में इसके विविध अनुप्रयोग हैं।
मोत्ज़किन संख्याएँ के लिए अनुक्रम बनाया जाता हैं:
उदाहरण
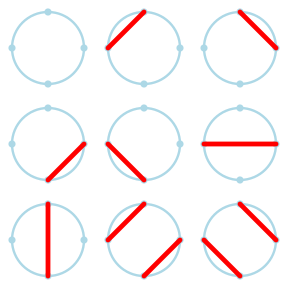
निम्नलिखित चित्र वृत्त (M4 = 9) पर 4 बिंदुओं के बीच अप्रतिछेदी जीवाएँ खींचने के 9 प्रकारो को दिखाता है:
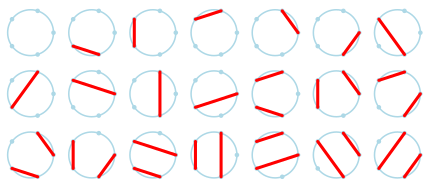
 निम्नलिखित चित्र वृत्त M5 = 21 पर 5 बिंदुओं के बीच अप्रतिछेदी जीवाएँ खींचने के 21 प्रकारो को दिखाता है:
निम्नलिखित चित्र वृत्त M5 = 21 पर 5 बिंदुओं के बीच अप्रतिछेदी जीवाएँ खींचने के 21 प्रकारो को दिखाता है:
गुण
मोत्ज़किन संख्याएँ पुनरावृत्ति सम्बन्धो को संतुष्ट करती हैं
मोत्ज़किन संख्याओं को द्विपद गुणांक और कैटलन संख्याओं के रूप में व्यक्त किया जा सकता है:
और इसके विपरीत,[1]
यह देता है
जनक फलन को मोत्ज़किन संख्याएँ संतुष्ट करती हैं
और स्पष्ट रूप से व्यक्त किया गया है
मोत्ज़किन संख्याओं का अभिन्न प्रतिनिधित्व किया गया है
- .
उनका व्यवहार अनन्तस्पर्शी है
- .
मोत्ज़किन अभाज्य एक मोत्ज़किन संख्या है जो अभाज्य संख्या है। As of 2019[update], केवल चार ऐसे अभाज्य ज्ञात हैं:
संयोगिक व्याख्याएँ
n के लिए मोत्जकिन संख्या n − 1 लंबाई के धनात्मक पूर्णांक अनुक्रमों की संख्या भी है जिसमें प्रारंभिक और अंतिम अवयव या तो 1 या 2 हैं, और किन्हीं दो क्रमागत अवयवों के बीच का अंतर −1, 0 या 1 है। समान रूप से, n मोत्ज़किन संख्या n + 1 लंबाई के धनात्मक पूर्णांक अनुक्रमों की संख्या है जिसमें प्रारंभिक और अंतिम अवयव 1 हैं, और किन्हीं दो क्रमागत अवयवों के बीच का अंतर −1, 0 या 1 है।
इसके अतिरिक्त, n के लिए मोत्जकिन संख्या n चरण में निर्देशांक (0, 0) से निर्देशांक (n, 0) तक ग्रिड के ऊपरी दाएं चतुर्थांश पर मार्गों की संख्या देता है यदि किसी को प्रत्येक चरण पर केवल दाईं ओर (ऊपर, नीचे या सीधे) जाने की अनुमति है लेकिन नीचे y = 0 अक्ष पर नहीं जाने दिया जाता हैं।
उदाहरण के लिए, निम्नलिखित चित्र (0, 0) से (4, 0) तक 9 वैध मोत्ज़किन पथ दिखाता है:
 जैसा कि गणना की गई है, गणित की विभिन्न शाखाओं में मोत्ज़किन संख्याओं की कम से कम चौदह अलग-अलग अभिव्यक्तियाँ हैं जो मोत्ज़किन संख्याओं के अपने सर्वेक्षण में डोनाघे & शापिरो (1977) द्वारा प्रागणित किया गया हैं।
जैसा कि गणना की गई है, गणित की विभिन्न शाखाओं में मोत्ज़किन संख्याओं की कम से कम चौदह अलग-अलग अभिव्यक्तियाँ हैं जो मोत्ज़किन संख्याओं के अपने सर्वेक्षण में डोनाघे & शापिरो (1977) द्वारा प्रागणित किया गया हैं।
गुइबर्ट, पर्गोला & पिंजानि (2001) ने दिखाया कि वेक्सिलरी प्रत्यावर्तन की गणना मोत्ज़किन संख्याओं द्वारा की जाती है।
यह भी देखें
- टेलीफोन संख्या जो प्रतिच्छेदन की अनुमति होने पर जीवाएँ बनाने के प्रकारो की संख्या को दर्शाता है
- डेलानॉय संख्या
- नारायण संख्या
- श्रोडर संख्या
संदर्भ
- ↑ Yi Wang and Zhi-Hai Zhang (2015). "सामान्यीकृत मोट्ज़किन संख्याओं का संयोजन" (PDF). Journal of Integer Sequences (18).
- Bernhart, Frank R. (1999), "Catalan, Motzkin, and Riordan numbers", Discrete Mathematics, 204 (1–3): 73–112, doi:10.1016/S0012-365X(99)00054-0
- Donaghey, R.; Shapiro, L. W. (1977), "Motzkin numbers", Journal of Combinatorial Theory, Series A, 23 (3): 291–301, doi:10.1016/0097-3165(77)90020-6, MR 0505544
- Guibert, O.; Pergola, E.; Pinzani, R. (2001), "Vexillary involutions are enumerated by Motzkin numbers", Annals of Combinatorics, 5 (2): 153–174, doi:10.1007/PL00001297, ISSN 0218-0006, MR 1904383, S2CID 123053532
- Motzkin, T. S. (1948), "Relations between hypersurface cross ratios, and a combinatorial formula for partitions of a polygon, for permanent preponderance, and for non-associative products", Bulletin of the American Mathematical Society, 54 (4): 352–360, doi:10.1090/S0002-9904-1948-09002-4