Theory of Machines

Definition

Theory of Machines is a branch of science dealing with the study of relative motion between the various parts of a machine and forces which act on them. Theory of Machines has two sub branches namely Kinematics and Dynamics.

Kinematics deals with the study of relative motion between the various parts of a machine. The force which act on them would be static in nature.

Dynamics deals with the study of relative motion between the various parts of a machine. The force which act on them would be static or dynamic in nature. Dynamics has two sub branches namely Kinetics and Statics.

Kinetics is a branch of theory of machine which deals with various forces when the body is moving whereas Statics is a branch of theory of machine which deals with various forces when the body is stationary.

Mechanism

Mechanism is a combination of rigid or restraining bodies which are so shaped and connected that they move upon each other with definite relative motion.

Machine

A machine may be defined as an assemblage of resistant bodies whose relative motions are successfully constrained so that some form of natural energy may be modified or transmitted to do some special kind of work.

A machine is a mechanism or a combination of mechanisms which not only imparts definite motions to the parts but also transmits and modifies the available mechanical energy into some kind of useful energy. This useful energy may be in the shape of some kind of desired work. The slider-crank mechanism will become a machine when it is being used in automobile engine by adding valve mechanism. Here it will convert the available energy which is force on the piston into desired energy which is torque on the crankshaft. This torque will enable the movement of the vehicle.

Link

A link is defined as a member or combination of members, connecting other members and having motion relative to them. A slider crank mechanism consists of the following four links. 1. Frame , 2.Crank, 3. Connecting rod , 4. Slider

Kinematic Pair

Fig 1. Slider Crank Mechanism

Kinematic pair is defined as the two links or elements of a machine when in contact with each other are said to form a pair. If the relative motion between them is completely or successfully constrained in a definite direction, the pair is known as the Kinematic pair.

In a slider crank mechanism shown in fig 1. here are the Kinematic pairs .

• Link 2 rotates relative to link 1 and hence link 1 and 2 is a Kinematic pair.
• Link 2 is having motion relative to link 3 and hence link 2 and link 3 is a Kinematic pair
• Link 3 is having motion relative to link 4
• Link 4 is having motion relative to link 1. Hence links 3,4 and 4 , 1 constitute Kinematic Pairs.

Classification of Kinematic Pairs

1. According to nature of contact between the links.
   • Lower Pair - Two links has surface contact or area contact between them. Example: Shaft rotating in a bearing, Nut rotating on a screw.
   • Higher Pair - Two links has a point or line of contact between them. Example: Wheel rolling on a surface and Cam & follower
2. According to the type of relative motion between the two links
   • Sliding pair - Kinematic pair where the two links have a sliding motion relative to each other. Example : rectangle rod in a rectangular hole as shown in the fig 2 .
     

     Fig 2. Sliding Pair
   • Turning pair - Kinematic pair where one link has a turning motion relative to the other. In fig 1. link 2 is having a turning motion relative to link 1, hence links 2 and 1 constitutes turning pair. Similarly links 3 & 4 and 2 & 3 forms turning pair.
   • Rolling pair - Kinematic pair where one link has a rolling motion relative to the other. Example: A rolling wheel on a flat surface forms a rolling pair. In a ball bearing , the ball and bearing forms one rolling pair and other rolling pair is ball and the shaft.
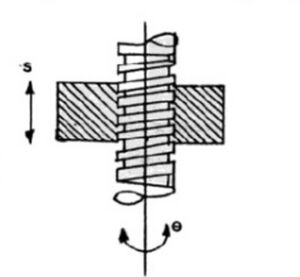
   • Screw pair ( Helical pair) - Kinematic pair where the two links have a turning as well
     

     Fig 3. Screw Pair
     as sliding motion between them. The lead screw and the nut of a lathe is a screw pair. Fig 3 shows screw pair.
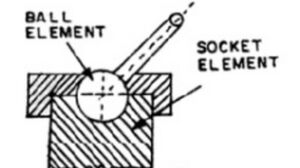
   • Spherical pair - Kinematic pair where one link in the form of sphere turns inside a fixed link. Ball and socket joint shown in fig 4. is a spherical pair.
     

     Fig 4. Ball & Socket Joint
3. According to the nature of mechanical constraint between two links
   • Closed pair - Two elements of the pair are held together mechanically
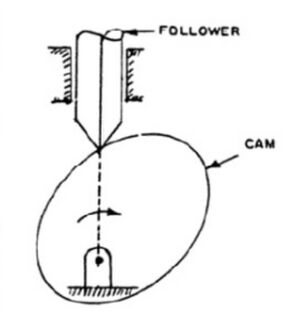
   • Unclosed pair - Two elements of the pair are in contact due to force of gravity or due to some spring action . Example Cam and the follower in fig. 5 as it is kept in contact by the forces exerted by spring and gravity.
     

     Fig 5. Cam & Follower

Degrees of Freedom

The number of independent motion (translation and rotational) a body can have is known as Degrees of freedom.

Fig 6. Degrees of Freedom

Fig 6. shows a rigid body in a space. If there is no constraint on the body then the following independent motion can be described.

1. Translation motion along x, y and z axes
2. Rotational motion about x, y and z axes.

Hence the body can have six independent motions. This body is said to have six degrees of freedom.

Degrees of freedom = 6 - number of constraints

if number of constraints are four then degrees of freedom = 6 - 4 = 2

Kinematic Chain

A Kinematic chain is defined as the combination of kinematic pairs, joined in such a way that each link forms a part of two pairs and the motion of each relative to other is definite. Or when the kinematic pairs are coupled in such a way that the last link is joined to the first link to transmit definite motion , it is called a kinematic chain.

In Fig 1. Slider crank mechanism link 1 is connected to link 2 and also to link 4. Links 1 and 2 is kinematic pair also links 1 and 4 is a kinematic pair. Hence link 1 forms part of two kinematic pairs. Similarly link 2 forms a part of two pairs ( kinematic pair of links 2 & 1 and kinematic pairs of links 2 & 3 ). Similarly links 3 and 4 each forms a part of two pairs. Hence in a slider crank mechanism each link forms a part of two pairs and motion of each relative to other is definite. So the total combination of these links is a kinematic chain.

The relation between the number of pairs (p) and number of links (L) in a four link kinematic chain is mentioned by

$L=2p-4$ ..................... (1.1)

The relation between the number of links (L) and number of joints (j) forming a four link kinematic chain is given by

$j={\frac {3}{2}}L-2$ .................... (1.2)

The equations (1.1) and (1.2) are applied only to kinematic chains having lower pairs. If they are applied to kinematic chains having

L.H.S = R.H.S then chain is constrainedhigher pairs, then each higher pair must be taken equivalent to two lower pairs and an additional link. In equations (1.1) and (1.2) if

L.H.S > R.H.S then chain is locked

L.H.S < R.H.S then chain is unconstrained

External Links

Fundamental_of_Kinematics_&_Mechanism

Theory-of-Machines

See Also

यंत्र के सिद्धांत