समन्वय वंश
समन्वय वंश अनुकूलन कलनविधि है जो किसी फलन के न्यूनतम को खोजने के लिए क्रमिक रूप से समन्वयित दिशाओं को कम करता है। प्रत्येक पुनरावृत्ति पर, कलनविधि समन्वय प्रणाली को निर्धारित करता है या समन्वय चयन नियम के माध्यम से समन्वय ब्लॉक करता है, फिर अन्य सभी निर्देशांक या समन्वय ब्लॉकों को ठीक करते समय संबंधित समन्वय हाइपरप्लेन पर ठीक या अनुचित विधि से कम करता है। उपयुक्त चरण आकार निर्धारित करने के लिए समन्वय प्रणाली दिशा के साथ लाइन खोज वर्तमान पुनरावृति पर की जा सकती है। समन्वय अवरोहण अलग-अलग और व्युत्पन्न-मुक्त दोनों संदर्भों में प्रयुक्त होता है।
विवरण
समन्वय वंश इस विचार पर आधारित है कि बहुभिन्नरूपी कार्य का न्यूनीकरण इसे एक समय में एक दिशा में कम से कम करके प्राप्त किया जा सकता है, अर्थात, लूप में अविभाज्य (या कम से कम बहुत सरल) अनुकूलन समस्याओं का समाधान करना।[1] चक्रीय समन्वय अवतरण के सबसे सरल स्थिति में, एक समय में एक दिशा के माध्यम से चक्रीय रूप से पुनरावृत्ति करता है, समय में प्रत्येक समन्वय दिशा के संबंध में उद्देश्य समारोह को कम करता है। यही है, प्रारंभिक चर मानों से प्रारंभ करना
- ,
गोल , से को एकल चर अनुकूलन समस्याओं को क्रमिक रूप से समाधान करके परिभाषित करता है
प्रत्येक चर का के लिए, 1 से .
इस प्रकार, प्रारंभिक अनुमान के साथ प्रारंभ होता है स्थानीय न्यूनतम के लिए , और अनुक्रम पुनरावृत्त रूप से प्राप्त करता है
प्रत्येक पुनरावृत्ति में लाइन खोज करने से, स्वचालित रूप से होता है
यह दिखाया जा सकता है कि इस अनुक्रम में समान अभिसरण गुण हैं जैसे कि सबसे तेज वंश। समन्वय दिशाओं के साथ लाइन खोज के चक्र के बाद कोई संशोधन नहीं होने का अर्थ है कि स्थिर बिंदु तक पहुंच गया है।
यह प्रक्रिया नीचे सचित्र है।
अलग स्थिति
निरंतर भिन्न कार्य F के स्थिति में, समन्वय वंश कलनविधि को इस रूप में स्केच किया जा सकता है:[1]
- प्रारंभिक पैरामीटर सदिश चुनें x.
- जब तक अभिसरण नहीं हो जाता, या पुनरावृत्तियों की कुछ निश्चित संख्या के लिए:
- एक सूचकांक चुनें i से 1 को n.
- कदम का आकार चुनें α.
- अद्यतन xi को xi − α∂F/∂xi(x).
चरण आकार को विभिन्न विधियों से चुना जा सकता है, उदाहरण के लिए, स्पष्ट न्यूनतम के लिए समाधान करके f(xi) = F(x) (अर्थात, F लेकिन सभी चर के साथ xi फ़िक्स्ड), या पारंपरिक लाइन खोज मानदंड द्वारा।[1]
सीमाएं
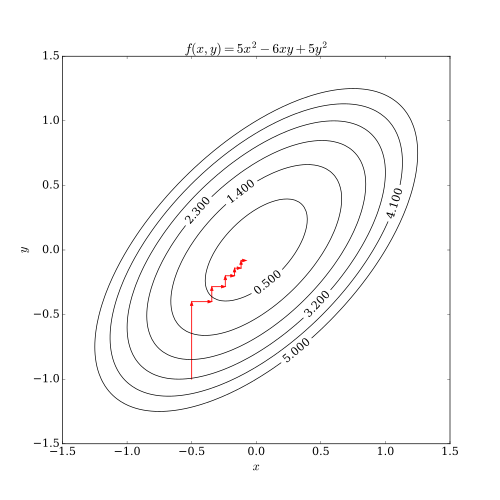
समन्वय वंश में दो समस्याएं हैं। उनमें से गैर-चिकनापन बहुभिन्नरूपी कार्य कर रहा है। निम्नलिखित चित्र से पता चलता है कि यदि किसी फलन के स्तर वक्र सुचारू नहीं हैं, तो समन्वय वंश पुनरावृत्ति गैर-स्थिर बिंदु पर अटक सकती है। मान लीजिए कि कलनविधि बिंदु (-2, -2) पर है; फिर दो अक्ष-संरेखित दिशाएँ हैं जिन पर वह कदम उठाने के लिए विचार कर सकता है, जो लाल तीरों द्वारा इंगित किया गया है। चूँकि, इन दो दिशाओं के साथ हर कदम उद्देश्य समारोह के मूल्य में वृद्धि करेगा (न्यूनतमकरण समस्या मानते हुए), इसलिए कलनविधि कोई कदम नहीं उठाएगा, तथापि दोनों कदम एक साथ कलनविधि को इष्टतम के निकट लाएंगे। चूँकि इस उदाहरण से पता चलता है कि समन्वय वंश आवश्यक रूप से इष्टतम के लिए अभिसरण नहीं है, उचित परिस्थितियों में औपचारिक अभिसरण दिखाना संभव है।[3]
दूसरी समस्या, समांतरता में कठिनाई है। चूंकि समन्वय वंश की प्रकृति दिशाओं के माध्यम से चक्रित करना है और प्रत्येक समन्वय दिशा के संबंध में वस्तुनिष्ठ कार्य को कम करना है, इसलिए समन्वय वंश बड़े पैमाने पर समानता के लिए स्पष्ट प्रत्याशी नहीं है। हाल के शोध कार्यों से पता चला है कि बड़े पैमाने पर समानता प्रत्येक समन्वय दिशा के संबंध में वस्तुनिष्ठ कार्य के परिवर्तन को सुविधा से समन्वयित करने के लिए प्रयुक्त होती है।[4][5][6]
अनुप्रयोग
समन्वय वंश कलनविधि अपनी सरलता के कारण चिकित्सकों के बीच लोकप्रिय हैं, लेकिन इसी गुण ने अनुकूलन शोधकर्ताओं को अधिक रोचक (जटिल) विधियों के पक्ष में बड़े पैमाने पर उनकी उपेक्षा करने के लिए प्रेरित किया है।[1] परिकलित टोमोग्राफी के क्षेत्र में समन्वय वंश अनुकूलन का प्रारंभिक अनुप्रयोग था[7] जहां यह शीघ्रता से अभिसरण पाया गया है[8] और बाद में नैदानिक बहु-स्लाइस हेलिकल स्कैन सीटी पुनर्निर्माण के लिए उपयोग किया गया।[9] प्रोटीन संरचना भविष्यवाणी में चक्रीय समन्वय वंश कलनविधि (सीसीडी) प्रयुक्त किया गया है।[10] इसके अतिरिक्त, मशीन सीखने में बड़े पैमाने पर समस्याओं के आगमन के साथ समन्वय वंश के उपयोग में रुचि बढ़ गई है, जहां रैखिक समर्थन सदिश यंत्र को प्रशिक्षित करने जैसी समस्याओं पर प्रयुक्त होने पर समन्वय वंश को अन्य विधियों के लिए प्रतिस्पर्धी दिखाया गया है।[11] (लिब्लिनियर और गैर-नकारात्मक आव्यूह गुणनखंडन देखें)।[12] वे उन समस्याओं के लिए आकर्षक हैं जहां प्रवणता की गणना करना संभव नहीं है, संभवतया इसलिए कि ऐसा करने के लिए आवश्यक डेटा कंप्यूटर नेटवर्क में वितरित किया जाता है।[13]
यह भी देखें
- अनुकूली समन्वय वंश
- संयुग्म ढाल
- ढतला हुआ वंश
- रेखा खोज
- गणितीय अनुकूलन
- अनुकूलन में न्यूटन की विधि | न्यूटन की विधि
- स्टोचैस्टिक प्रवणता डिसेंट - समन्वय के अतिरिक्त एक समय में एक उदाहरण का उपयोग करता है
संदर्भ
- ↑ 1.0 1.1 1.2 1.3 Wright, Stephen J. (2015). "Coordinate descent algorithms". Mathematical Programming. 151 (1): 3–34. arXiv:1502.04759. doi:10.1007/s10107-015-0892-3. S2CID 15284973.
- ↑ https://www.cs.cmu.edu/~ggordon/10725-F12/slides/25-coord-desc.pdf[bare URL PDF]
- ↑ Spall, J. C. (2012). "Cyclic Seesaw Process for Optimization and Identification". Journal of Optimization Theory and Applications. 154 (1): 187–208. doi:10.1007/s10957-012-0001-1. S2CID 7795605.
- ↑ Zheng, J.; Saquib, S. S.; Sauer, K.; Bouman, C. A. (2000-10-01). "Parallelizable Bayesian tomography algorithms with rapid, guaranteed convergence". IEEE Transactions on Image Processing. 9 (10): 1745–1759. Bibcode:2000ITIP....9.1745Z. CiteSeerX 10.1.1.34.4282. doi:10.1109/83.869186. ISSN 1057-7149. PMID 18262913.
- ↑ Fessler, J. A.; Ficaro, E. P.; Clinthorne, N. H.; Lange, K. (1997-04-01). "Grouped-coordinate ascent algorithms for penalized-likelihood transmission image reconstruction". IEEE Transactions on Medical Imaging. 16 (2): 166–175. doi:10.1109/42.563662. hdl:2027.42/86021. ISSN 0278-0062. PMID 9101326. S2CID 1523517.
- ↑ Wang, Xiao; Sabne, Amit; Kisner, Sherman; Raghunathan, Anand; Bouman, Charles; Midkiff, Samuel (2016-01-01). High Performance Model Based Image Reconstruction. pp. 2:1–2:12. doi:10.1145/2851141.2851163. ISBN 9781450340922. S2CID 16569156.
{{cite book}}:|journal=ignored (help) - ↑ Sauer, Ken; Bouman, Charles (February 1993). "A Local Update Strategy for Iterative Reconstruction from Projections" (PDF). IEEE Transactions on Signal Processing. 41 (2): 534–548. Bibcode:1993ITSP...41..534S. CiteSeerX 10.1.1.135.6045. doi:10.1109/78.193196.
- ↑ Yu, Zhou; Thibault, Jean-Baptiste; Bouman, Charles; Sauer, Ken; Hsieh, Jiang (January 2011). "Fast Model-Based X-ray CT Reconstruction Using Spatially Non-Homogeneous ICD Optimization" (PDF). IEEE Transactions on Image Processing. 20 (1): 161–175. Bibcode:2011ITIP...20..161Y. doi:10.1109/TIP.2010.2058811. PMID 20643609. S2CID 9315957.
- ↑ Thibault, Jean-Baptiste; Sauer, Ken; Bouman, Charles; Hsieh, Jiang (November 2007). "A Three-Dimensional Statistical Approach to Improved Image Quality for Multi-Slice Helical CT" (PDF). Medical Physics. 34 (11): 4526–4544. Bibcode:2007MedPh..34.4526T. doi:10.1118/1.2789499. PMID 18072519.
- ↑ Canutescu, AA; Dunbrack, RL (2003). "Cyclic coordinate descent: A robotics algorithm for protein loop closure". Protein Science. 12 (5): 963–72. doi:10.1110/ps.0242703. PMC 2323867. PMID 12717019.
- ↑ Hsieh, C. J.; Chang, K. W.; Lin, C. J.; Keerthi, S. S.; Sundararajan, S. (2008). "A dual coordinate descent method for large-scale linear SVM" (PDF). Proceedings of the 25th international conference on Machine learning - ICML '08. p. 408. doi:10.1145/1390156.1390208. ISBN 9781605582054. S2CID 7880266.
- ↑ Hsieh, C. J.; Dhillon, I. S. (2011). Fast coordinate descent methods with variable selection for non-negative matrix factorization (PDF). Proceedings of the 17th ACM SIGKDD international conference on Knowledge discovery and data mining - KDD '11. p. 1064. doi:10.1145/2020408.2020577. ISBN 9781450308137.
- ↑ Nesterov, Yurii (2012). "Efficiency of coordinate descent methods on huge-scale optimization problems" (PDF). SIAM J. Optim. 22 (2): 341–362. CiteSeerX 10.1.1.332.3336. doi:10.1137/100802001.
- Bezdek, J. C.; Hathaway, R. J.; Howard, R. E.; Wilson, C. A.; Windham, M. P. (1987), "Local convergence analysis of a grouped variable version of coordinate descent", Journal of Optimization Theory and Applications, Kluwer Academic/Plenum Publishers, vol. 54, no. 3, pp. 471–477, doi:10.1007/BF00940196, S2CID 120052975
- Bertsekas, Dimitri P. (1999). Nonlinear Programming, Second Edition Athena Scientific, Belmont, Massachusetts. ISBN 1-886529-00-0.
- Luo, Zhiquan; Tseng, P. (1992), "On the convergence of the coordinate descent method for convex differentiable minimization", Journal of Optimization Theory and Applications, Kluwer Academic/Plenum Publishers, vol. 72, no. 1, pp. 7–35, doi:10.1007/BF00939948, hdl:1721.1/3164, S2CID 121091844.
- Wu, TongTong; Lange, Kenneth (2008), "Coordinate descent algorithms for Lasso penalized regression", The Annals of Applied Statistics, Institute of Mathematical Statistics, vol. 2, no. 1, pp. 224–244, arXiv:0803.3876, doi:10.1214/07-AOAS147, S2CID 16350311.
- Richtarik, Peter; Takac, Martin (April 2011), "Iteration complexity of randomized block-coordinate descent methods for minimizing a composite function", Mathematical Programming, Springer, vol. 144, no. 1–2, pp. 1–38, arXiv:1107.2848, doi:10.1007/s10107-012-0614-z, S2CID 16816638.
- Richtarik, Peter; Takac, Martin (December 2012), "Parallel coordinate descent methods for big data optimization", ArXiv:1212.0873, arXiv:1212.0873.
| group5 = Metaheuristics | abbr5 = heuristic | list5 =
| below =
}} | group5 =Metaheuuristic |abbr5 = heuristic | list5 =*विकासवादी एल्गोरिथ्म
| below =* सॉफ्टवेयर
}}