स्टेटिक सिंगल-असाइनमेंट फॉर्म

कंपाइलर डिज़ाइन में, स्थिर एकल असाइनमेंट फॉर्म (अक्सर एसएसए फॉर्म या बस एसएसए के रूप में संक्षिप्त) एक मध्यवर्ती प्रतिनिधित्व (आईआर) की एक गुण है जिसके लिए प्रत्येक चर को एक बार निर्दिष्ट करने और उपयोग किए जाने से पहले परिभाषित करने की आवश्यकता होती है। मूल आईआर में मौजूदा चर संस्करणों में विभाजित हैं, नए चर आमतौर पर पाठ्यपुस्तकों में एक उपलेख के साथ मूल नाम से संकेतित होते हैं, ताकि हर परिभाषा को अपना संस्करण मिल जाए। एसएसए फॉर्म में, यूज़-डेफ चेन स्पष्ट हैं और प्रत्येक में एक तत्व होता है।

एसएसए का प्रस्ताव 1988 में बैरी के. रोसेन, मार्क एन. वेगमैन और एफ. केनेथ ज़ेडेक ने दिया था।^[1] रॉन साइट्रॉन, जेनी फेरेंटे और आईबीएम के पिछले तीन शोधकर्ताओं ने एक एल्गोरिद्म विकसित किया जो एसएसए फॉर्म की कुशलता से गणना कर सकता है।Cite error: Closing </ref> missing for <ref> tag

फोरट्रान, सी, सी ++, [3] या जावा (एंड्रॉइड रनटाइम) के लिए एक कंपाइलर में एसएसए खोजने की उम्मीद कर सकते हैं; जबकि कार्यात्मक भाषा संकलक में, जैसे कि योजना और एमएल के लिए, निरंतरता-गुजरने वाली शैली (सीपीएस) का आमतौर पर उपयोग किया जाता है। एसएसए औपचारिक रूप से गैर-स्थानीय नियंत्रण प्रवाह को छोड़कर सीपीएस के एक अच्छे व्यवहार वाले सबसेट के बराबर है, जो तब नहीं होता जब सीपीएस को मध्यवर्ती प्रतिनिधित्व के रूप में उपयोग किया जाता है।^[2] इसलिए एक के संदर्भ में तैयार किए गए अनुकूलन और परिवर्तन दूसरे पर तुरंत लागू होते हैं।

लाभ

एसएसए की प्राथमिक उपयोगिता इस बात से आती है कि कैसे यह एक साथ चर के गुणों को सरल बनाकर विभिन्न प्रकार के कंपाइलर अनुकूलन के परिणामों को सरल और बेहतर बनाता है। उदाहरण के लिए, कोड के इस भाग पर विचार करें:

y := 1

y := 2

x := y

मनुष्य देख सकते हैं कि पहला असाइनमेंट अनावश्यक है और तीसरी लाइन में इस्तेमाल होने वाले y का मान y के दूसरे असाइनमेंट से आता है। इसे निर्धारित करने के लिए एक कार्यक्रम को एक परिभाषा विश्लेषण करना होगा। लेकिन यदि कार्यक्रम सर्व शिक्षा अभियान के रूप में है, तो ये दोनों तत्काल हैं:

y₁ := 1

y₂ := 2

x₁ := y₂

कंपाइलर ऑप्टिमाइज़ेशन एल्गोरिदम जो या तो सक्षम हैं या एसएसए के उपयोग से दृढ़ता से बढ़ाए गए हैं:

निरंतर प्रसार - रनटाइम से संकलन समय तक की गणना का रूपांतरण, उदा। निर्देश a=3*4+5;का उपयोग करें; जैसे की a=17; था;।
मूल्य सीमा प्रसार ^[3] - संभावित सीमाओं को पूर्वनिर्धारित करें, एक गणना हो सकती है, जो अग्रिम में शाखा भविष्यवाणियों के निर्माण के लिए अनुमति देता है।
विरल सशर्त निरंतर प्रसार -विरल सशर्त निरंतर प्रसार - कुछ मूल्यों की जाँच करें, सबसे अधिक संभावना शाखा की भविष्यवाणी करने के लिए परीक्षणों की अनुमति मिलती है।
डेड-कोड उन्मूलन - ऐसे कोड को हटा दें जिसका परिणामों पर कोई प्रभाव नहीं पड़ेगा।
वैश्विक मूल्य अंकन - एक ही परिणाम का उत्पादन करने वाले प्रतिलिपि गणना को बदलें।
आंशिक अतिरेक उन्मूलन - प्रोग्राम की कुछ शाखाओं में पहले किए गए प्रतिलिपि गणना को हटाना।
सामर्थ्य में कमी - कम खर्चीले लेकिन समकक्ष के साथ महंगे संचालन की जगह, उदाहरण पूर्णांक को गुणा करें या संभावित रूप से कम महंगी पारी के साथ 2 की शक्तियों से विभाजित करें या बाएं (गुणा के लिए) या बदलाव दाएं (विभाजन के लिए) के साथ।
रजिस्टर आवंटन - अनुकूलन करें कि गणना के लिए सीमित मशीन रजिस्टर की सीमित संख्या का उपयोग कैसे किया जा सकता है।

एसएसए में परिवर्तित

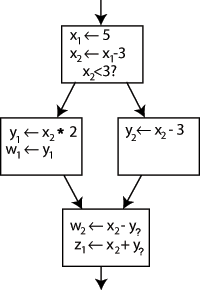
सामान्य कोड को एसएसए फॉर्म में परिवर्तित करना मुख्य रूप से प्रत्येक असाइनमेंट के लक्ष्य को एक नए चर के साथ बदलने का मामला है, और उस बिंदु तक पहुंचने वाले चर के "संस्करण" के साथ एक चर के प्रत्येक उपयोग को बदलना है। उदाहरण के लिए, निम्न नियंत्रण-प्रवाह ग्राफ़ पर विचार करें:

x ← x - 3 के बायीं ओर नाम बदलने और x के निम्नलिखित उपयोगों को उस नए नाम में बदलने से प्रोग्राम अपरिवर्तित रहेगा। एसएसए में दो नए वेरिएबल: x₁ और x₂ बनाकर इसका उपयोग किया जा सकता है, जिनमें से प्रत्येक को केवल एक बार असाइन किया गया है। इसी तरह, अन्य सभी वेरिएबल्स को अलग-अलग सबस्क्रिप्ट देने से उपज मिलती है:

एक मामले को छोड़कर, यह स्पष्ट है कि प्रत्येक उपयोग किस परिभाषा का उल्लेख कर रहा है: बॉटम ब्लॉक में y के दोनों उपयोग या तो y₁ या y₂ को संदर्भित कर सकते हैं, यह इस बात पर निर्भर करता है कि नियंत्रण प्रवाह किस पथ पर गया था।

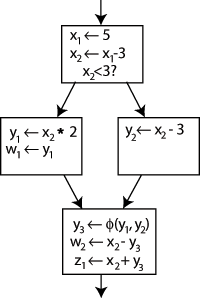
इसे हल करने के लिए, एक विशेष कथन अंतिम ब्लॉक में डाला जाता है, जिसे Φ (Phi) फ़ंक्शन कहा जाता है। यह कथन अतीत में नियंत्रण प्रवाह के आधार पर y₁ या y₂ को "चुनकर" y₃ नामक y की एक नई परिभाषा उत्पन्न करेगा।

अब, अंतिम ब्लॉक केवल y₃ का उपयोग कर सकता है, और सही मान किसी भी तरह से प्राप्त होगा। x के लिए Φ फ़ंक्शन की आवश्यकता नहीं है: x का केवल एक संस्करण, अर्थात् x₂ इस स्थान पर पहुंच रहा है, इसलिए कोई समस्या नहीं है (दूसरे शब्दों में, Φ(x₂,x₂)=x₂)।

एक मनमाना नियंत्रण-प्रवाह ग्राफ दिया गया है, यह बताना मुश्किल हो सकता है कि Φ फ़ंक्शंस कहाँ सम्मिलित करें, और किन चरों के लिए। इस सामान्य प्रश्न का एक कुशल समाधान है जिसे एक अवधारणा का उपयोग करके गणना की जा सकती है जिसे प्रभुत्व सीमाएँ कहा जाता है (नीचे देखें)।

एक कंपाइलर प्रत्येक पूर्ववर्ती ब्लॉक के अंत में "मूव" संचालन सम्मिलित करके Φ फ़ंक्शन को कार्यान्वित कर सकता है। ऊपर दिए गए उदाहरण में, कंपाइलर मध्य-बाएँ ब्लॉक के अंत में y₁ से y₃ तक और मध्य-दाएँ ब्लॉक के अंत में y₂ से y₃ तक एक चाल सम्मिलित कर सकता है। हो सकता है कि ये मूव ऑपरेशंस कंपाइलर के रजिस्टर आवंटन प्रक्रिया के आधार पर अंतिम कोड में समाप्त न हो। हालांकि, यह दृष्टिकोण तब काम नहीं कर सकता है जब एक साथ संचालन अनुमानित रूप से Φ फ़ंक्शन के इनपुट का उत्पादन कर रहे हों, जैसा कि व्यापक-अंक वाली मशीनों पर हो सकता है। आमतौर पर, एक वाइड-इश्यू मशीन में Φ फ़ंक्शन को लागू करने के लिए कंपाइलर द्वारा ऐसी स्थितियों में उपयोग किए जाने वाले चयन निर्देश होते हैं।

केनी ज़ेडेक के अनुसार,^[4] Φ कार्यों को मूल रूप से नकली कार्यों के रूप में जाना जाता था, जबकि 1980 के दशक में एसएसए को आईबीएम रिसर्च में विकसित किया जा रहा था। एक Φ फ़ंक्शन का औपचारिक नाम केवल तभी अपनाया गया था जब काम पहली बार अकादमिक पेपर में प्रकाशित हुआ था।

प्रमुख सीमाओं का उपयोग करते हुए न्यूनतम एसएसए की गणना करना

एक नियंत्रण-प्रवाह ग्राफ में, नोड A को एक अलग नोड B पर सख्ती से प्रभावित होने के लिए कहा जाता है, अगर पहले A से गुजरे बिना B तक पहुंचना असंभव है। दूसरे शब्दों में, यदि नोड B तक पहुँच जाता है, तो यह माना जा सकता है कि A चल चुका है। A को B पर हावी होना कहा जाता है (या B को A द्वारा हावी होना कहा जाता है) यदि A सख्ती से B या A = B पर प्रभावित होता है।

नोड जो नियंत्रण को नोड A पर स्थानांतरित करता है, उसे A का तत्काल पूर्ववर्ती कहा जाता है।

नोड A का प्रभुत्व सीमा नोड B का सेट है जहां A B पर कड़ाई से प्रभावित नहीं होता है, लेकिन B के कुछ तत्काल पूर्ववर्ती पर हावी होता है। ये वे बिंदु हैं जिन पर कई नियंत्रण पथ एक साथ एक पथ में वापस मिल जाते हैं।

उदाहरण के लिए निम्न कोड में:

[1] x = random()

if x < 0.5

[2] result = "heads"

else

[3] result = "tails"

end

[4] print(result)

नोड 1 सख्ती से 2, 3, और 4 पर हावी है, और नोड 4 के तत्काल पूर्ववर्ती नोड 2 और 3 हैं।

प्रमुख सीमाएँ उन बिंदुओं को परिभाषित करती हैं जिन पर Φ प्रकार्यों की आवश्यकता होती है। उपरोक्त उदाहरण में, जब नियंत्रण को नोड 4 पर पारित किया जाता है, तो प्रयुक्त परिणाम की परिभाषा इस बात पर निर्भर करती है कि नियंत्रण नोड 2 या 3 से पारित किया गया था या नहीं। डोमिनेटर में परिभाषित वेरिएबल्स के लिए Φ फ़ंक्शंस की आवश्यकता नहीं है, क्योंकि केवल एक ही संभव परिभाषा है जो लागू हो सकती है।

प्रत्येक नोड के प्रभुत्व सीमाओं को खोजने के लिए एक कुशल एल्गोरिदम है। इस एल्गोरिथ्म को मूल रूप से 1991 में रॉन साइट्रॉन, जीन फेरेंटे, एट अल द्वारा "कुशलतापूर्वक कम्प्यूटिंग स्टेटिक सिंगल असाइनमेंट फॉर्म और कंट्रोल ग्राफ" में वर्णित किया गया था।^[5]

कीथ डी. कूपर, टिमोथी जे. हार्वे, और राइस विश्वविद्यालय के केन कैनेडी ने अपने पेपर में एक सरल, तेज प्रभुत्व एल्गोरिथम नामक एक एल्गोरिद्म का वर्णन किया है:^[6] लाइव-वैरिएबल जानकारी कंप्यूटिंग की अपेक्षाकृत उच्च लागत के बिना Φ कार्यों की संख्या को कम करने का प्रयास है। यह निम्नलिखित अवलोकन पर आधारित है: यदि एक मूल ब्लॉक में प्रवेश पर एक चर कभी भी जीवित नहीं होता है, तो उसे कभी भी Φ फ़ंक्शन की आवश्यकता नहीं होती है। एसएसए निर्माण के दौरान, किसी भी ब्लॉक-स्थानीय चर के लिए Φ फ़ंक्शन छोड़े जाते हैं।

ब्लॉक-लोकल वेरिएबल्स के सेट की गणना पूर्ण लाइव-वैरिएबल विश्लेषण की तुलना में एक सरल और तेज प्रक्रिया है, जो सेमी-प्रून किए गए एसएसए फॉर्म को कम एसएसए फॉर्म की तुलना में गणना करने के लिए अधिक कुशल बनाता है। दूसरी ओर, सेमी-प्रून्ड एसएसए फॉर्म में अधिक Φ फंक्शन होंगे।

ब्लॉक तर्क

ब्लॉक तर्क Φ कार्यों का एक विकल्प है जो प्रतिनिधित्वात्मक रूप से समान है लेकिन व्यवहार में अनुकूलन के दौरान अधिक सुविधाजनक हो सकता है। ब्लॉक का नाम दिया गया है और फ़ंक्शन पैरामीटर के रूप में नोट किए गए ब्लॉक तर्कों की एक सूची लें। ब्लॉक को कॉल करते समय ब्लॉक तर्क निर्दिष्ट मानों से बंधे होते हैं। स्विफ्ट और एलएलवीएम का बहु-स्तरीय मध्यवर्ती प्रतिनिधित्व ब्लॉक तर्कों का उपयोग करता है।^[7]

एसएसए फॉर्म से कनवर्ट करना

एसएसए फॉर्म का आमतौर पर प्रत्यक्ष निष्पादन के लिए उपयोग नहीं किया जाता है (हालांकि एसएसए की व्याख्या करना संभव है)^[8], और इसे अक्सर "एक और आईआर के शीर्ष पर" उपयोग किया जाता है जिसके साथ यह सीधे पत्राचार में रहता है। इसे मौजूदा आईआर (बुनियादी ब्लॉक, निर्देश, ऑपरेंड, आदि) और इसके एसएसए समकक्ष के हिस्सों के बीच मैप करने वाले कार्यों के एक सेट के रूप में "निर्माण" करके पूरा किया जा सकता है। जब एसएसए फॉर्म की अब आवश्यकता नहीं है, केवल अब-अनुकूलित आईआर को छोड़कर इन मैपिंग कार्यों को छोड़ दिया जा सकता है, ।

एक्सटेंशन

एसएसए फॉर्म के एक्सटेंशन को दो श्रेणियों में बांटा जा सकता है।

नाम बदलने की योजना के विस्तार से नाम बदलने की कसौटी बदल जाती है। याद रखें कि एसएसए फॉर्म प्रत्येक वेरिएबल का नाम बदल देता है जब इसे मान निर्दिष्ट किया जाता है। वैकल्पिक योजनाओं में स्टैटिक सिंगल-यूज़ फॉर्म (जो उपयोग किए जाने पर प्रत्येक स्टेटमेंट पर प्रत्येक वेरिएबल का नाम बदलता है) और स्टैटिक सिंगल इंफॉर्मेशन फॉर्म (जो प्रत्येक वेरिएबल का नाम बदल देता है जब उसे मान दिया जाता है, और पोस्ट-डोमिनेंस फ्रंटियर पर) शामिल होता है।

फ़ीचर-विशिष्ट एक्सटेंशन चर के लिए एकल असाइनमेंट प्रॉपर्टी को बनाए रखते हैं लेकिन अतिरिक्त सुविधाओं को मॉडल करने के लिए नए सिमेंटिक्स को शामिल करते हैं। कुछ फीचर-विशिष्ट एक्सटेंशन उच्च-स्तरीय प्रोग्रामिंग भाषाओं को मॉडल करते हैं, जैसे सरणियाँ, ऑब्जेक्ट और अलियास पॉइंटर्स। अन्य फीचर-विशिष्ट एक्सटेंशन मॉडल निम्न-स्तरीय वास्तुशिल्प सुविधाओं जैसे अनुमान और भविष्यवाणी आदि।

एसएसए फॉर्म का उपयोग करने वाले कंपाइलर्स

एसएसए फॉर्म कंपाइलर समुदाय में एक अपेक्षाकृत हालिया विकास है। जैसे, कई पुराने संकलक संकलन या अनुकूलन प्रक्रिया के कुछ भाग के लिए केवल एसएसए फॉर्म का उपयोग करते हैं, लेकिन अधिकांश इस पर भरोसा नहीं करते हैं। एसएसए फॉर्म पर भारी निर्भर करने वाले कंपाइलर्स के उदाहरणों में शामिल हैं:

ईटीएच ओबेरोन -2 कंपाइलर "जीएसए" को शामिल करने वाली पहली सार्वजनिक परियोजनाओं में से एक था, जो एसएसए का एक प्रकार है।
एलएलवीएम कंपाइलर इन्फ्रास्ट्रक्चर अपने प्राथमिक कोड प्रतिनिधित्व में सभी स्केलर रजिस्टर वैल्यू (मेमोरी को छोड़कर सब कुछ) के लिए एसएसए फॉर्म का उपयोग करता है। एसएसए फॉर्म केवल तभी समाप्त हो जाता है जब पंजीकरण आवंटन होता है, संकलन प्रक्रिया में देर से (अक्सर लिंक समय पर)।
ओपन64 (Open64) कंपाइलर अपने वैश्विक स्केलर ऑप्टिमाइज़र में एसएसए फॉर्म का उपयोग करता है, हालाँकि कोड को पहले एसएसए फॉर्म में लाया जाता है और बाद में एसएसए फॉर्म से बाहर कर दिया जाता है। ओपन64 एसएसए फॉर्म में एक्सटेंशन का उपयोग एसएसए फॉर्म के साथ-साथ स्केलर वैल्यू में मेमोरी का प्रतिनिधित्व करने के लिए करता है।
संस्करण 4 (अप्रैल 2005 में जारी) जीसीसी के अनुसार, जीएनयू कंपाइलर संग्रह एसएसए का व्यापक उपयोग करता है। दृश्यपटल "सामान्य" कोड उत्पन्न करता है जिसे बाद में "जिम्पलिफायर" द्वारा "गिम्पल" कोड में परिवर्तित किया जाता है। उच्च-स्तरीय अनुकूलन तब "गिम्पल" के एसएसए फॉर्म पर लागू होते हैं। परिणामी अनुकूलित इंटरमीडिएट कोड को तब आरटीएल में अनुवादित किया जाता है, जिस पर निम्न-स्तरीय अनुकूलन लागू होते हैं। आर्किटेक्चर-विशिष्ट बैकएंड अंततः आरटीएल को असेंबली भाषा में बदल देते हैं।
आईबीएम का ओपन सोर्स एडेप्टिव जावा वर्चुअल मशीन, जैक्स आरवीएम, विस्तारित एरे एसएसए का उपयोग करता है, जो एसएसए का एक विस्तार है जो एक एकीकृत ढांचे में स्केलर, एरे और ऑब्जेक्ट फील्ड के विश्लेषण की अनुमति देता है। विस्तारित ऐरे एसएसए विश्लेषण केवल अधिकतम अनुकूलन स्तर पर सक्षम है, जो कोड के सबसे अधिक बार निष्पादित भागों पर लागू होता है।
2002 में, शोधकर्ताओं ने मानक जावा बाइटकोड और टाइपसेफ एसएसए (सेफटीएसए) बाईटकोड क्लास फाइलों को चलाने के लिए आईबीएम के जाइक्सआरवीएम (उस समय जलपीनो नाम) को संशोधित किया और एसएसए बाइटकोड का उपयोग करने के लिए महत्वपूर्ण प्रदर्शन लाभ प्रदर्शित किए।
ओरेकल की हॉटस्पॉट जावा वर्चुअल मशीन अपने जेआईटी कंपाइलर में एसएसए -आधारित मध्यवर्ती भाषा का उपयोग करती है।^[9]
माइक्रोसॉफ्ट विजुअल स्टूडियो 2015 अपडेट 3 में उपलब्ध माइक्रोसॉफ्ट विजुअल सी ++ कंपाइलर बैकएंड एसएसए का उपयोग करता है।^[10]
मोनो अपने जेआईटी कंपाइलर में मिनी नामक एसएसए का उपयोग करता है।
जैकअकादमिक निर्देश सेट जैकल 3.0 के लिए एक ओपन-सोर्स कंपाइलर है। यह अपने मध्यवर्ती प्रतिनिधित्व के लिए एसएसए के साथ एक साधारण 3-ऑपरेंड कोड का उपयोग करता है। एक दिलचस्प संस्करण के रूप में, यह Φ कार्यों को एक तथाकथित समान निर्देश के साथ बदल देता है, जो रजिस्टर एलोकेटर को दो लाइव रेंज को एक ही भौतिक रजिस्टर में रखने का निर्देश देता है।
हालांकि एक कंपाइलर नहीं है, [1]डीकंपाइलर अपने आंतरिक प्रतिनिधित्व में एसएसए फॉर्म का उपयोग करता है। एसएसए का उपयोग अभिव्यक्ति प्रसार को सरल बनाने, मापदंडों और रिटर्न की पहचान करने, संरक्षण विश्लेषण और बहुत कुछ करने के लिए किया जाता है।
पोर्टेबल.नेट अपने जेआईटी कंपाइलर में एसएसए का उपयोग करता है।
लिबफर्म कम्पाइलरों के लिए एक पूर्ण ग्राफ-आधारित एसएसए मध्यवर्ती प्रतिनिधित्व। लिबफर्म एसएसए-जागरूक रजिस्टर आवंटक के उपयोग से कोड जनरेशन तक सभी स्केलर रजिस्टर मानों के लिए एसएसए फॉर्म का उपयोग करता है।
इलिनोइस कॉन्सर्ट कंपाइलर लगभग 1994^[11] ने एसएसए के एक प्रकार का उपयोग किया जिसे एसएसयू (स्टेटिक सिंगल यूज़) कहा जाता है जो प्रत्येक चर का नाम बदल देता है जब उसे एक मान दिया जाता है, और प्रत्येक सशर्त संदर्भ में जिसमें उस चर का उपयोग किया जाता है; अनिवार्य रूप से ऊपर उल्लिखित स्थिर एकल सूचना प्रपत्र। एसएसयू फॉर्म को जॉन प्लेव्याक की पीएचडी थीसिस में प्रलेखित किया गया है।
कॉइंस कंपाइलर एसएसए फॉर्म अनुकूलन का उपयोग करता है जैसा कि यहाँ बताया गया है।
मोज़िला फ़ायरफ़ॉक्स स्पाइडरमोन्की जावास्क्रिप्ट इंजन एसएसए-आधारित आईआर का उपयोग करता है।^[12]
दिसंबर 2010 में घोषित क्रोमियम V8 जावास्क्रिप्ट इंजन अपने क्रैंकशाफ्ट कंपाइलर इंफ्रास्ट्रक्चर में एसएसए को लागू करता है
पाईपाई अपने जेआईटी कंपाइलर में निशान के लिए एक रैखिक एसएसए प्रतिनिधित्व का उपयोग करता है।

एंड्रॉइड (Android) रनटाइम के लिए एंड्रॉइड का नया अनुकूलन कंपाइलर अपने आईआर के लिए एसएसए का उपयोग करता है।
मानक एमएल कंपाइलर एमएलटन अपनी मध्यवर्ती भाषाओं में से एक में एसएसए का उपयोग करता है।
लुआजिट एसएसए-आधारित अनुकूलन का भारी उपयोग करता है।^[13]
पीएचपी (PHP) और हैक कंपाइलर एचएचवीएम (HHVM) अपने आईआर में एसएसए का उपयोग करता है।^[14]
जलाशय लैब्स का आर-स्ट्रीम कंपाइलर गैर-एसएसए (क्वाड लिस्ट), एसएसए और एसएसआई (स्टेटिक सिंगल इंफॉर्मेशन^[15]) रूपों का समर्थन करता है।^[16]
जाओ (1.7: केवल x86-64 आर्किटेक्चर के लिए; 1.8: सभी समर्थित आर्किटेक्चर के लिए)।^[17]^[18]
एसपीआईआर-वी, वल्कन ग्राफिक्स एपीआई के लिए छायांकन भाषा मानक और ओपनसीएल कंप्यूट एपीआई के लिए कर्नेल भाषा, एक एसएसए प्रतिनिधित्व है।^[19]
एनआईआर के माध्यम से विभिन्न मेसा चालक, छायांकन भाषाओं के लिए एक एसएसए प्रतिनिधित्व।^[20]
वेबकिट अपने जेआईटी कम्पाइलरों में एसएसए का उपयोग करता है।^[21]^[22]
स्विफ्ट एलएलवीएम आईआर के ऊपर अपने स्वयं के एसएसए फॉर्म को परिभाषित करता है, जिसे एसआईएल (स्विफ्ट इंटरमीडिएट लैंग्वेज) कहा जाता है।^[23]^[24]
एरलांग ने ओटीपी 22.0 में अपने कंपाइलर को "स्टेटिक सिंगल असाइनमेंट (एसएसए) पर आधारित एक मध्यवर्ती प्रतिनिधित्व का आंतरिक रूप से उपयोग करने के लिए" फिर से लिखा। भविष्य के रिलीज में एसएसए के शीर्ष पर निर्मित और अनुकूलन की योजनाओं के साथ।^[25]

संदर्भ

↑ Barry Rosen; Mark N. Wegman; F. Kenneth Zadeck (1988). "Global value numbers and redundant computations" (PDF). Proceedings of the 15th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages.
↑ Kelsey, Richard A. (1995). "A Correspondence between Continuation Passing Style and Static Single Assignment Form" (PDF). Papers from the 1995 ACM SIGPLAN Workshop on Intermediate Representations: 13–22. doi:10.1145/202529.202532. ISBN 0897917545. S2CID 6207179.
↑ value range propagation
↑ see page 43 ["The Origin of Ф-Functions and the Name"] of Zadeck, F. Kenneth, Presentation on the History of SSA at the SSA'09 Seminar, Autrans, France, April 2009
↑ Cytron, Ron; Ferrante, Jeanne; Rosen, Barry K.; Wegman, Mark N.; Zadeck, F. Kenneth (1 October 1991). "Efficiently computing static single assignment form and the control dependence graph". ACM Transactions on Programming Languages and Systems. 13 (4): 451–490. doi:10.1145/115372.115320. S2CID 13243943.
↑
Cooper, Keith D.; Harvey, Timothy J.; Kennedy, Ken (2001). "एक सरल, तेज प्रभुत्व एल्गोरिथम" (PDF). Archived from the original (PDF) on 2022-03-26. {{cite journal}}: Cite journal requires |journal= (help)</रेफरी> प्रत्येक नोड के लिए बी प्रभुत्व_फ्रंटियर (बी) := {} प्रत्येक नोड के लिए बी यदि बी ≥ 2 के तत्काल पूर्ववर्तियों की संख्या बी के तत्काल पूर्ववर्तियों में प्रत्येक पी के लिए धावक := प जबकि धावक ≠ मुहावरा (बी) प्रभुत्व_फ्रंटियर (धावक) := प्रभुत्व_फ्रंटियर (धावक) ∪ { बी } धावक := इडोम (धावक) उपरोक्त कोड में, idom(b) हैimmediate dominatorb का, अद्वितीय नोड जो सख्ती से b पर हावी होता है लेकिन किसी अन्य नोड पर कड़ाई से हावी नहीं होता है जो सख्ती से b पर हावी होता है।
वेरिएशंस जो Φ फंक्शन्स की संख्या को कम करते हैं
```
न्यूनतम एसएसए यह सुनिश्चित करने के लिए आवश्यक Φ कार्यों की न्यूनतम संख्या सम्मिलित करता है कि प्रत्येक नाम को एक बार एक मान निर्दिष्ट किया गया है और मूल कार्यक्रम में एक नाम का प्रत्येक संदर्भ (उपयोग) अभी भी एक अद्वितीय नाम का उल्लेख कर सकता है। (बाद की आवश्यकता यह सुनिश्चित करने के लिए आवश्यक है कि संकलक प्रत्येक ऑपरेशन में प्रत्येक ऑपरेंड के लिए एक नाम लिख सके।)
```
हालाँकि, इनमें से कुछ Φ फ़ंक्शंस मृत कोड उन्मूलन हो सकते हैं। इस कारण से, न्यूनतम एसएसए आवश्यक रूप से सबसे कम Φ कार्यों का उत्पादन नहीं करता है जो एक विशिष्ट प्रक्रिया के लिए आवश्यक हैं। कुछ प्रकार के विश्लेषणों के लिए, ये Φ कार्य अनावश्यक हैं और विश्लेषण को कम कुशलता से चलाने का कारण बन सकते हैं।

छंटनी एसएसए

प्रून्ड एसएसए फॉर्म एक साधारण अवलोकन पर आधारित है: Φ फ़ंक्शन केवल वेरिएबल्स के लिए आवश्यक हैं जो Φ फ़ंक्शन के बाद लाइव हैं। (यहां, लाइव का अर्थ है कि मान का उपयोग किसी ऐसे पथ के साथ किया जाता है जो प्रश्न में Φ फ़ंक्शन से शुरू होता है।) यदि कोई चर लाइव नहीं है, तो Φ फ़ंक्शन का परिणाम उपयोग नहीं किया जा सकता है और Φ फ़ंक्शन द्वारा असाइनमेंट समाप्त हो गया है।
छंटे हुए एसएसए फॉर्म का निर्माण लाइव-वैरिएबल विश्लेषण का उपयोग करता है। यह तय करने के लिए Φ फ़ंक्शन सम्मिलन चरण में लाइव-वैरिएबल जानकारी दी गई है कि किसी दिए गए Φ फ़ंक्शन की आवश्यकता है या नहीं। यदि मूल चर नाम Φ फ़ंक्शन सम्मिलन बिंदु पर लाइव नहीं है, तो Φ फ़ंक्शन सम्मिलित नहीं किया गया है।
एक अन्य संभावना यह है कि छंटाई को डेड-कोड एलिमिनेशन समस्या के रूप में देखा जाए। फिर, एक Φ फ़ंक्शन केवल तभी लाइव होता है जब इनपुट प्रोग्राम में कोई उपयोग इसे फिर से लिखा जाएगा, या यदि इसे किसी अन्य Φ फ़ंक्शन में तर्क के रूप में उपयोग किया जाएगा। एसएसए फॉर्म में प्रवेश करते समय, प्रत्येक उपयोग को उस पर हावी होने वाली निकटतम परिभाषा में फिर से लिखा जाता है। एक Φ फ़ंक्शन को तब तक लाइव माना जाएगा जब तक कि यह निकटतम परिभाषा है जो कम से कम एक उपयोग पर हावी है, या लाइव Φ का कम से कम एक तर्क है।

सेमी-प्रूनेड एसएसए

सेमी-प्रून एसएसए फॉर्म<ref>Briggs, Preston; Cooper, Keith D.; Harvey, Timothy J.; Simpson, L. Taylor (1998). "Practical Improvements to the Construction and Destruction of Static Single Assignment Form" (PDF). Archived from the original (PDF) on 2010-06-07. {{cite journal}}: Cite journal requires |journal= (help)
↑ "Block Arguments vs PHI nodes - MLIR Rationale". mlir.llvm.org. Retrieved 4 March 2022.
↑ von Ronne, Jeffery; Ning Wang; Michael Franz (2004). "Interpreting programs in static single assignment form". Proceedings of the 2004 workshop on Interpreters, virtual machines and emulators - IVME '04. p. 23. doi:10.1145/1059579.1059585. ISBN 1581139098. S2CID 451410.
↑ "The Java HotSpot Performance Engine Architecture". Oracle Corporation.
↑ "Introducing a new, advanced Visual C++ code optimizer". 4 May 2016.
↑ "Illinois Concert Project".
↑ "IonMonkey Overview".,
↑ "Bytecode Optimizations". the LuaJIT project.
↑ "HipHop Intermediate Representation (HHIR)". GitHub. 30 October 2021.
↑ Ananian, C. Scott; Rinard, Martin (1999). "Static Single Information Form". CiteSeerX 10.1.1.1.9976. {{cite journal}}: Cite journal requires |journal= (help)
↑ Encyclopedia of Parallel Computing.
↑ "Go 1.7 Release Notes - The Go Programming Language". golang.org. Retrieved 2016-08-17.
↑ "Go 1.8 Release Notes - The Go Programming Language". golang.org. Retrieved 2017-02-17.
↑ "SPIR-V spec" (PDF).
↑ Ekstrand, Jason. "Reintroducing NIR, a new IR for mesa".
↑ "Introducing the WebKit FTL JIT". 13 May 2014.
↑ "Introducing the B3 JIT Compiler". 15 February 2016.
↑ "Swift Intermediate Language (GitHub)". GitHub. 30 October 2021.
↑ "Swift's High-Level IR: A Case Study of Complementing LLVM IR with Language-Specific Optimization, LLVM Developers Meetup 10/2015". YouTube. Archived from the original on 2021-12-21.
↑ "OTP 22.0 Release Notes".

सामान्य संदर्भ

Appel, Andrew W. (1999). एमएल में आधुनिक संकलक कार्यान्वयन. Cambridge University Press. ISBN 978-0-521-58274-2. जावा (प्रोग्रामिंग भाषा) में भी उपलब्ध (ISBN 0-521-82060-X, 2002) और सी (प्रोग्रामिंग भाषा) (ISBN 0-521-60765-5, 1998) संस्करण।
Cooper, Keith D. & Torczon, Linda (2003). इंजीनियरिंग एक संकलक. Morgan Kaufmann. ISBN 978-1-55860-698-2.
Muchnick, Steven S. (1997). उन्नत संकलक डिजाइन और कार्यान्वयन. Morgan Kaufmann. ISBN 978-1-55860-320-2.
Kelsey, Richard A. (March 1995). "कंटीन्यूएशन पासिंग स्टाइल और स्टेटिक सिंगल असाइनमेंट फॉर्म के बीच एक पत्राचार". ACM SIGPLAN Notices. 30 (3): 13–22. doi:10.1145/202530.202532.
Appel, Andrew W. (April 1998). "एसएसए कार्यात्मक प्रोग्रामिंग है". ACM SIGPLAN Notices. 33 (4): 17–20. doi:10.1145/278283.278285. S2CID 207227209.
Pop, Sebastian (2006). "एसएसए प्रतिनिधित्व ढांचा: शब्दार्थ, विश्लेषण और जीसीसी कार्यान्वयन" (PDF). {{cite journal}}: Cite journal requires |journal= (help)
Matthias Braun; Sebastian Buchwald; Sebastian Hack; Roland Leißa; Christoph Mallon; Andreas Zwinkau (2013), "Simple and Efficient Construction of Static Single Assignment Form", Compiler Construction, Lecture Notes in Computer Science, vol. 7791, Springer Berlin Heidelberg, pp. 102–122, doi:10.1007/978-3-642-37051-9_6, ISBN 978-3-642-37050-2, retrieved 24 March 2013

बाहरी संबंध

Bosscher, Steven; and Novillo, Diego. GCC gets a new Optimizer Framework. An article about GCC's use of SSA and how it improves over older IRs.
The SSA Bibliography. Extensive catalogue of SSA research papers.
Zadeck, F. Kenneth. "The Development of Static Single Assignment Form", December 2007 talk on the origins of SSA.
VV.AA. "SSA-based Compiler Design" (2014)

[original-1] Barry Rosen; Mark N. Wegman; F. Kenneth Zadeck (1988). "Global value numbers and redundant computations" (PDF). Proceedings of the 15th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages.

[Kelsey-2] Kelsey, Richard A. (1995). "A Correspondence between Continuation Passing Style and Static Single Assignment Form" (PDF). Papers from the 1995 ACM SIGPLAN Workshop on Intermediate Representations: 13–22. doi:10.1145/202529.202532. ISBN 0897917545. S2CID 6207179.

[3] value range propagation

[4] see page 43 ["The Origin of Ф-Functions and the Name"] of Zadeck, F. Kenneth, Presentation on the History of SSA at the SSA'09 Seminar, Autrans, France, April 2009

[5] Cytron, Ron; Ferrante, Jeanne; Rosen, Barry K.; Wegman, Mark N.; Zadeck, F. Kenneth (1 October 1991). "Efficiently computing static single assignment form and the control dependence graph". ACM Transactions on Programming Languages and Systems. 13 (4): 451–490. doi:10.1145/115372.115320. S2CID 13243943.

[Cooper_2001-6] Cooper, Keith D.; Harvey, Timothy J.; Kennedy, Ken (2001). "एक सरल, तेज प्रभुत्व एल्गोरिथम" (PDF). Archived from the original (PDF) on 2022-03-26. {{cite journal}}: Cite journal requires |journal= (help)</रेफरी> प्रत्येक नोड के लिए बी प्रभुत्व_फ्रंटियर (बी) := {} प्रत्येक नोड के लिए बी यदि बी ≥ 2 के तत्काल पूर्ववर्तियों की संख्या बी के तत्काल पूर्ववर्तियों में प्रत्येक पी के लिए धावक := प जबकि धावक ≠ मुहावरा (बी) प्रभुत्व_फ्रंटियर (धावक) := प्रभुत्व_फ्रंटियर (धावक) ∪ { बी } धावक := इडोम (धावक) उपरोक्त कोड में, idom(b) हैimmediate dominatorb का, अद्वितीय नोड जो सख्ती से b पर हावी होता है लेकिन किसी अन्य नोड पर कड़ाई से हावी नहीं होता है जो सख्ती से b पर हावी होता है।
वेरिएशंस जो Φ फंक्शन्स की संख्या को कम करते हैं

न्यूनतम एसएसए यह सुनिश्चित करने के लिए आवश्यक Φ कार्यों की न्यूनतम संख्या सम्मिलित करता है कि प्रत्येक नाम को एक बार एक मान निर्दिष्ट किया गया है और मूल कार्यक्रम में एक नाम का प्रत्येक संदर्भ (उपयोग) अभी भी एक अद्वितीय नाम का उल्लेख कर सकता है। (बाद की आवश्यकता यह सुनिश्चित करने के लिए आवश्यक है कि संकलक प्रत्येक ऑपरेशन में प्रत्येक ऑपरेंड के लिए एक नाम लिख सके।)

हालाँकि, इनमें से कुछ Φ फ़ंक्शंस मृत कोड उन्मूलन हो सकते हैं। इस कारण से, न्यूनतम एसएसए आवश्यक रूप से सबसे कम Φ कार्यों का उत्पादन नहीं करता है जो एक विशिष्ट प्रक्रिया के लिए आवश्यक हैं। कुछ प्रकार के विश्लेषणों के लिए, ये Φ कार्य अनावश्यक हैं और विश्लेषण को कम कुशलता से चलाने का कारण बन सकते हैं।

छंटनी एसएसए

प्रून्ड एसएसए फॉर्म एक साधारण अवलोकन पर आधारित है: Φ फ़ंक्शन केवल वेरिएबल्स के लिए आवश्यक हैं जो Φ फ़ंक्शन के बाद लाइव हैं। (यहां, लाइव का अर्थ है कि मान का उपयोग किसी ऐसे पथ के साथ किया जाता है जो प्रश्न में Φ फ़ंक्शन से शुरू होता है।) यदि कोई चर लाइव नहीं है, तो Φ फ़ंक्शन का परिणाम उपयोग नहीं किया जा सकता है और Φ फ़ंक्शन द्वारा असाइनमेंट समाप्त हो गया है।
छंटे हुए एसएसए फॉर्म का निर्माण लाइव-वैरिएबल विश्लेषण का उपयोग करता है। यह तय करने के लिए Φ फ़ंक्शन सम्मिलन चरण में लाइव-वैरिएबल जानकारी दी गई है कि किसी दिए गए Φ फ़ंक्शन की आवश्यकता है या नहीं। यदि मूल चर नाम Φ फ़ंक्शन सम्मिलन बिंदु पर लाइव नहीं है, तो Φ फ़ंक्शन सम्मिलित नहीं किया गया है।
एक अन्य संभावना यह है कि छंटाई को डेड-कोड एलिमिनेशन समस्या के रूप में देखा जाए। फिर, एक Φ फ़ंक्शन केवल तभी लाइव होता है जब इनपुट प्रोग्राम में कोई उपयोग इसे फिर से लिखा जाएगा, या यदि इसे किसी अन्य Φ फ़ंक्शन में तर्क के रूप में उपयोग किया जाएगा। एसएसए फॉर्म में प्रवेश करते समय, प्रत्येक उपयोग को उस पर हावी होने वाली निकटतम परिभाषा में फिर से लिखा जाता है। एक Φ फ़ंक्शन को तब तक लाइव माना जाएगा जब तक कि यह निकटतम परिभाषा है जो कम से कम एक उपयोग पर हावी है, या लाइव Φ का कम से कम एक तर्क है।

सेमी-प्रूनेड एसएसए

सेमी-प्रून एसएसए फॉर्म<ref>Briggs, Preston; Cooper, Keith D.; Harvey, Timothy J.; Simpson, L. Taylor (1998). "Practical Improvements to the Construction and Destruction of Static Single Assignment Form" (PDF). Archived from the original (PDF) on 2010-06-07. {{cite journal}}: Cite journal requires |journal= (help)

[7] "Block Arguments vs PHI nodes - MLIR Rationale". mlir.llvm.org. Retrieved 4 March 2022.

[8] von Ronne, Jeffery; Ning Wang; Michael Franz (2004). "Interpreting programs in static single assignment form". Proceedings of the 2004 workshop on Interpreters, virtual machines and emulators - IVME '04. p. 23. doi:10.1145/1059579.1059585. ISBN 1581139098. S2CID 451410.

[9] "The Java HotSpot Performance Engine Architecture". Oracle Corporation.

[10] "Introducing a new, advanced Visual C++ code optimizer". 4 May 2016.

[11] "Illinois Concert Project".

[12] "IonMonkey Overview".,

[13] "Bytecode Optimizations". the LuaJIT project.

[14] "HipHop Intermediate Representation (HHIR)". GitHub. 30 October 2021.

[15] Ananian, C. Scott; Rinard, Martin (1999). "Static Single Information Form". CiteSeerX 10.1.1.1.9976. {{cite journal}}: Cite journal requires |journal= (help)

[16] Encyclopedia of Parallel Computing.

[17] "Go 1.7 Release Notes - The Go Programming Language". golang.org. Retrieved 2016-08-17.

[18] "Go 1.8 Release Notes - The Go Programming Language". golang.org. Retrieved 2017-02-17.

[19] "SPIR-V spec" (PDF).

[20] Ekstrand, Jason. "Reintroducing NIR, a new IR for mesa".

[21] "Introducing the WebKit FTL JIT". 13 May 2014.

[22] "Introducing the B3 JIT Compiler". 15 February 2016.

[23] "Swift Intermediate Language (GitHub)". GitHub. 30 October 2021.

[24] "Swift's High-Level IR: A Case Study of Complementing LLVM IR with Language-Specific Optimization, LLVM Developers Meetup 10/2015". YouTube. Archived from the original on 2021-12-21.

[25] "OTP 22.0 Release Notes".

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

Anonymous

Search

स्टेटिक सिंगल-असाइनमेंट फॉर्म

Namespaces

More

Page actions

Contents