अलेक्जेंडर बहुपद

गणित में, अलेक्जेंडर बहुपद एक गाँठ अपरिवर्तनीय है जो प्रत्येक गाँठ प्रकार के लिए पूर्णांक गुणांक वाले बहुपद को निर्दिष्ट करता है। जेम्स वैडेल अलेक्जेंडर II ने 1923 में, पहली गांठ बहुपद की खोज की। 1969 में, जॉन हॉर्टन कॉनवे ने इस बहुपद का एक संस्करण दिखाया, जिसे अब अलेक्जेंडर-कॉनवे बहुपद कहा जाता है, इसकी गणना एक स्केन संबंध का उपयोग करके की जा सकती है, हालांकि इसका महत्व महसूस नहीं किया गया था। 1984 में जोन्स बहुपद की खोज तक। कॉनवे द्वारा अलेक्जेंडर बहुपद पर फिर से काम करने के तुरंत बाद, यह महसूस किया गया कि एक समान स्कीन संबंध अलेक्जेंडर के पेपर में उनके बहुपद पर प्रदर्शित किया गया था।

परिभाषा

बता दें कि K 3-गोले में एक गाँठ (गणित) है। एक्स को के के गाँठ पूरक के अनंत अंतरिक्ष को कवर करना होने दें। इस कवरिंग को के की सीफर्ट सतह के साथ गाँठ के पूरक को काटकर प्राप्त किया जा सकता है और एक चक्रीय तरीके से सीमा के साथ परिणामी कई गुनाओं की असीम रूप से कई प्रतियों को एक साथ जोड़कर प्राप्त किया जा सकता है। एक्स पर अभिनय करने वाला एक डेक परिवर्तन टी है। एक्स के पहले समरूपता (पूर्णांक गुणांक के साथ) पर विचार करें, निरूपित $H_{1}(X)$. परिवर्तन टी समरूपता पर कार्य करता है और इसलिए हम विचार कर सकते हैं $H_{1}(X)$ लॉरेंट बहुपदों की अंगूठी पर एक मॉड्यूल (गणित)। $\mathbb {Z} [t,t^{-1}]$. इसे अलेक्जेंडर इनवेरिएंट या अलेक्जेंडर मॉड्यूल कहा जाता है।

मॉड्यूल पूरी तरह से प्रस्तुत करने योग्य है; इस मॉड्यूल के लिए एक प्रस्तुति मैट्रिक्स को अलेक्जेंडर मैट्रिक्स कहा जाता है। यदि जनरेटर की संख्या, $r$, संबंधों की संख्या से कम या उसके बराबर है, $s$ , तब हम सभी द्वारा उत्पन्न आदर्श पर विचार करते हैं $r\times r$ मैट्रिक्स के नाबालिग; यह जीरोथ फिटिंग आदर्श या अलेक्जेंडर आदर्श है और प्रस्तुति मैट्रिक्स की पसंद पर निर्भर नहीं करता है। अगर $r>s$, आदर्श को 0 के बराबर सेट करें। यदि अलेक्जेंडर आदर्श आदर्श आदर्श है, तो एक जनरेटर लें; इसे गाँठ का अलेक्जेंडर बहुपद कहा जाता है। चूंकि यह लॉरेंट मोनोमियल द्वारा गुणा करने के लिए केवल अद्वितीय है $\pm t^{n}$, अक्सर एक विशेष अद्वितीय रूप को ठीक करता है। अलेक्जेंडर की सामान्यीकरण की पसंद बहुपद को सकारात्मक स्थिर शब्द बनाने के लिए है।

सिकंदर ने साबित किया कि सिकंदर का आदर्श शून्य नहीं है और हमेशा प्रमुख है। इस प्रकार एक अलेक्जेंडर बहुपद हमेशा मौजूद होता है, और स्पष्ट रूप से एक गाँठ अपरिवर्तनीय होता है, जिसे निरूपित किया जाता है $\Delta _{K}(t)$. यह पता चला है कि गाँठ का अलेक्जेंडर बहुपद एक लॉरेंट बहुपद है $t^{2}$ और यह मिरर इमेज नॉट के लिए समान बहुपद है। दूसरे शब्दों में, यह एक गाँठ और उसकी दर्पण छवि के बीच अंतर नहीं कर सकता।

बहुपद की गणना

अलेक्जेंडर बहुपद की गणना के लिए निम्नलिखित प्रक्रिया जे डब्ल्यू अलेक्जेंडर द्वारा अपने पेपर में दी गई थी। के साथ गाँठ का उन्मुख चित्र लें $n$ क्रॉसिंग; वहाँ हैं $n+2$ गाँठ आरेख के क्षेत्र। अलेक्जेंडर बहुपद निकालने के लिए, पहले आकार का एक घटना मैट्रिक्स बनाना होगा $(n,n+2)$. $n$ h> पंक्तियाँ इसके अनुरूप हैं $n$ क्रॉसिंग, और $n+2$ क्षेत्रों के लिए कॉलम। मैट्रिक्स प्रविष्टियों के मान या तो हैं $0,1,-1,t,-t$.

किसी विशेष क्षेत्र और क्रॉसिंग से संबंधित प्रविष्टि पर विचार करें। यदि क्षेत्र क्रॉसिंग के समीप नहीं है, तो प्रवेश 0 है। यदि क्षेत्र क्रॉसिंग के समीप है, तो प्रवेश उसके स्थान पर निर्भर करता है। निम्न तालिका आने वाली अंडरक्रॉसिंग लाइन के परिप्रेक्ष्य से क्रॉसिंग पर क्षेत्र के स्थान द्वारा निर्धारित प्रविष्टि देती है।

अंडरक्रॉसिंग से पहले बाईं ओर: $-t$

अंडरक्रॉसिंग से पहले दाईं ओर: $1$ : बायीं ओर अंडरक्रॉसिंग के बाद: $t$

अंडरक्रॉसिंग के बाद दाईं ओर: $-1$

मैट्रिक्स से आसन्न क्षेत्रों से संबंधित दो कॉलम निकालें, और नए के निर्धारक का काम करें $n\times n$ आव्यूह। हटाए गए कॉलम के आधार पर, उत्तर गुणा द्वारा भिन्न होगा $\pm t^{n}$, जहां की शक्ति $n$ जरूरी नहीं कि गाँठ में क्रॉसिंग की संख्या हो। इस अस्पष्टता को हल करने के लिए, की सबसे बड़ी संभावित शक्ति को विभाजित करें $t$ और गुणा करें $-1$ यदि आवश्यक हो, ताकि स्थिर शब्द धनात्मक हो। यह अलेक्जेंडर बहुपद देता है।

अलेक्जेंडर बहुपद की गणना सीफर्ट मैट्रिक्स से भी की जा सकती है।

जे. डब्ल्यू अलेक्जेंडर के काम के बाद, राल्फ फॉक्स ने गाँठ समूह का एक प्रतिरूपण माना $\pi _{1}(S^{3}\backslash K)$, और गैर-कम्यूटेटिव डिफरेंशियल कैलकुलस पेश किया Fox (1961), जो किसी को गणना करने की अनुमति भी देता है $\Delta _{K}(t)$. पुस्तक में उच्चतर अलेक्जेंडर बहुपदों के बारे में इस दृष्टिकोण का विस्तृत विवरण पाया जा सकता है Crowell & Fox (1963).

बहुपद के मूल गुण

अलेक्जेंडर बहुपद सममित है: $\Delta _{K}(t^{-1})=\Delta _{K}(t)$ सभी गांठों के लिए के.

परिभाषा के दृष्टिकोण से, यह पोंकारे द्वैत की अभिव्यक्ति है | पोंकारे द्वैत समरूपतावाद ${\overline {H_{1}X}}\simeq \mathrm {Hom} _{\mathbb {Z} [t,t^{-1}]}(H_{1}X,G)$ कहाँ $G$ के अंशों के क्षेत्र का भागफल है $\mathbb {Z} [t,t^{-1}]$ द्वारा $\mathbb {Z} [t,t^{-1}]$, के रूप में माना जाता है $\mathbb {Z} [t,t^{-1}]$-मॉड्यूल, और कहाँ ${\overline {H_{1}X}}$ संयुग्मी है $\mathbb {Z} [t,t^{-1}]$-मॉड्यूल करने के लिए $H_{1}X$ यानी: एक एबेलियन समूह के रूप में यह समान है $H_{1}X$ लेकिन आवरण परिवर्तन $t$ द्वारा कार्य करता है $t^{-1}$.

इसके अलावा, अलेक्जेंडर बहुपद 1 पर एक इकाई का मूल्यांकन करता है: $\Delta _{K}(1)=\pm 1$.

परिभाषा के दृष्टिकोण से, यह इस तथ्य की अभिव्यक्ति है कि गाँठ पूरक एक समरूपता चक्र है, जो आवरण परिवर्तन द्वारा उत्पन्न होता है $t$. अधिक आम तौर पर अगर $M$ एक 3-कई गुना ऐसा है कि $rank(H_{1}M)=1$ इसमें एक अलेक्जेंडर बहुपद है $\Delta _{M}(t)$ इसके अनंत-चक्रीय आवरण वाले स्थान के आदेश आदर्श के रूप में परिभाषित किया गया है। इस मामले में $\Delta _{M}(1)$ के मरोड़ उपसमूह के क्रम के बराबर, ऊपर हस्ताक्षर करने के लिए है $H_{1}M$.

यह ज्ञात है कि प्रत्येक अभिन्न लॉरेंट बहुपद जो सममित है और 1 पर एक इकाई के लिए मूल्यांकन करता है, एक गाँठ का अलेक्जेंडर बहुपद है (कावौची 1996)।

बहुपद का ज्यामितीय महत्व

चूँकि सिकंदर का आदर्श प्रधान है, $\Delta _{K}(t)=1$ अगर और केवल अगर गाँठ समूह का कम्यूटेटर उपसमूह सही समूह है (अर्थात अपने स्वयं के कम्यूटेटर उपसमूह के बराबर)।

टोपोलॉजिकल स्लाइस नॉट के लिए, अलेक्जेंडर बहुपद फॉक्स-मिल्नोर स्थिति को संतुष्ट करता है $\Delta _{K}(t)=f(t)f(t^{-1})$ कहाँ $f(t)$ कुछ अन्य अभिन्न लॉरेंट बहुपद है।

सिकंदर बहुपद की डिग्री से सीफ़र्ट की सतह का दो गुना नीचे घिरा हुआ है।

माइकल फ्रीडमैन ने साबित किया कि 3-गोले में एक गाँठ स्थलाकृतिक रूप से कटी हुई है; यानी, 4-बॉल में एक स्थानीय-फ्लैट टोपोलॉजिकल डिस्क को बांधता है, अगर गाँठ का अलेक्जेंडर बहुपद तुच्छ है (फ्रीडमैन और क्विन, 1990)।

कौफमैन भौतिक मॉडल से प्राप्त राज्य योगों के माध्यम से अलेक्जेंडर बहुपद के पहले निर्माण का वर्णन करता है। इन विषयों का एक सर्वेक्षण और भौतिकी के साथ अन्य संबंध में दिए गए हैं।

सतहों और चिकनी 4-आयामी टोपोलॉजी के साथ अन्य संबंध भी हैं। उदाहरण के लिए, कुछ धारणाओं के तहत, एक सर्जरी सिद्धांत को निष्पादित करके एक चिकनी 4-कई गुना को संशोधित करने का एक तरीका है जिसमें दो-आयामी टोरस के पड़ोस को हटाने और इसे एस के साथ क्रॉस किए गए गाँठ पूरक के साथ बदलना शामिल है।^{1</उप>। परिणाम मूल के लिए एक चिकनी 4-कई गुना होमियोमॉर्फिक है, हालांकि अब सीबर्ग-विटेन इनवेरिएंट को गाँठ के अलेक्जेंडर बहुपद के साथ गुणा करके संशोधित किया गया है। समरूपता वाले नॉट्स प्रतिबंधित अलेक्जेंडर बहुपदों के लिए जाने जाते हैं। (कावौची 1996) में समरूपता अनुभाग देखें। बहरहाल, अलेक्जेंडर बहुपद कुछ समरूपता का पता लगाने में विफल हो सकता है, जैसे कि मजबूत उलटापन।}

यदि गांठ सर्कल के ऊपर तंतुओं का पूरक है, तो गाँठ के अलेक्जेंडर बहुपद को मोनिक के रूप में जाना जाता है (उच्चतम और निम्नतम क्रम के गुणांक बराबर हैं $\pm 1$). वास्तव में, अगर $S\to C_{K}\to S^{1}$ एक फाइबर बंडल है जहां $C_{K}$ गाँठ पूरक है, चलो $g:S\to S$ मोनोड्रोमी का प्रतिनिधित्व करते हैं, फिर $\Delta _{K}(t)={\rm {Det}}(tI-g_{*})$ कहाँ $g_{*}\colon H_{1}S\to H_{1}S$ अनुरूपता पर प्रेरित नक्शा है।

उपग्रह संचालन से संबंध

अगर गांठ $K$ पैटर्न नॉट के साथ एक उपग्रह गाँठ है $K'$ (एक एम्बेडिंग मौजूद है $f:S^{1}\times D^{2}\to S^{3}$ ऐसा है कि $K=f(K')$, कहाँ $S^{1}\times D^{2}\subset S^{3}$ एक अनकॉटेड सॉलिड टॉरस युक्त है $K'$), तब $\Delta _{K}(t)=\Delta _{f(S^{1}\times \{0\})}(t^{a})\Delta _{K'}(t)$, कहाँ $a\in \mathbb {Z}$ वह पूर्णांक है जो दर्शाता है $K'\subset S^{1}\times D^{2}$ में $H_{1}(S^{1}\times D^{2})=\mathbb {Z}$.

उदाहरण: कनेक्ट-योग के लिए $\Delta _{K_{1}\#K_{2}}(t)=\Delta _{K_{1}}(t)\Delta _{K_{2}}(t)$. अगर $K$ एक अनट्विस्टेड सैटेलाइट नॉट है, फिर $\Delta _{K}(t)=\pm 1$.

अलेक्जेंडर-कॉनवे बहुपद

सिकंदर ने सिद्ध किया कि सिकंदर बहुपद एक स्कीन संबंध को संतुष्ट करता है। जॉन होर्टन कॉनवे ने बाद में इसे एक अलग रूप में फिर से खोजा और दिखाया कि स्केन संबंध एक साथ अननॉट पर मूल्य के विकल्प के साथ बहुपद को निर्धारित करने के लिए पर्याप्त था। कॉनवे का संस्करण पूर्णांक गुणांकों के साथ z में एक बहुपद है, जिसे निरूपित किया गया है $\nabla (z)$ और अलेक्जेंडर-कॉनवे बहुपद (जिसे कॉनवे बहुपद या कॉनवे-अलेक्जेंडर बहुपद के रूप में भी जाना जाता है) कहा जाता है।

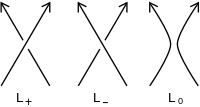
मान लीजिए कि हमें एक ओरिएंटेड लिंक आरेख दिया गया है, जहां $L_{+},L_{-},L_{0}$ are link diagrams resulting from crossing and smoothing changes on a local region of a specified crossing of the diagram, as indicated in the figure.

यहाँ कॉनवे के स्कीन संबंध हैं:

• $\nabla (O)=1$ (जहाँ O अननोट का कोई आरेख है)
• $\nabla (L_{+})-\nabla (L_{-})=z\nabla (L_{0})$

मानक अलेक्जेंडर बहुपद से संबंध किसके द्वारा दिया गया है $\Delta _{L}(t^{2})=\nabla _{L}(t-t^{-1})$. यहाँ $\Delta _{L}$ उचित रूप से सामान्यीकृत किया जाना चाहिए (के गुणन द्वारा $\pm t^{n/2}$) स्कीन संबंध को संतुष्ट करने के लिए $\Delta (L_{+})-\Delta (L_{-})=(t^{1/2}-t^{-1/2})\Delta (L_{0})$. ध्यान दें कि यह संबंध टी में लॉरेंट बहुपद देता है^1/2.

ट्रेफिल के कॉनवे बहुपद की गणना के उदाहरण के लिए गाँठ सिद्धांत देखें।

फ़्लोर होमोलॉजी से संबंध

छद्म-होलोमोर्फिक वक्रों का उपयोग करना, और गांठों के प्रत्येक समस्थानिक वर्ग के लिए नॉट फ्लोर होमोलॉजी कहे जाने वाले एक बड़े ग्रेडेड एबेलियन समूह से जुड़ा हुआ है। नॉट फ्लोर होमोलॉजी की वर्गीकृत यूलर विशेषता अलेक्जेंडर बहुपद है। जबकि अलेक्जेंडर बहुपद गाँठ के जीनस पर एक निचली सीमा देता है, ने दिखाया कि नॉट फ़्लोर होमोलॉजी जीनस का पता लगाती है। इसी तरह, जबकि अलेक्जेंडर बहुपद सर्कल के ऊपर फाइबरिंग के पूरक गाँठ के लिए एक बाधा देता है, ने दिखाया कि नॉट फ्लोर होमोलॉजी पूरी तरह से निर्धारित करती है कि कब एक गांठ सर्कल के ऊपर फाइबर को पूरक करती है। नॉट फ़्लोर होमोलॉजी समूह, इनवेरिएंट्स के हीगार्ड फ़्लोर होमोलॉजी परिवार का हिस्सा हैं; आगे की चर्चा के लिए फ़्लोर होमोलॉजी देखें।

संदर्भ

• Adams, Colin C. (2004) [1994]. The Knot Book: An elementary introduction to the mathematical theory of knots. American Mathematical Society. ISBN 978-0-8218-3678-1. (accessible introduction utilizing a skein relation approach)
• Alexander, J. W. (1928). "Topological invariants of knots and links". Transactions of the American Mathematical Society. 30 (2): 275–306. doi:10.2307/1989123. JSTOR 1989123.
• Crowell, Richard; Fox, Ralph (1963). Introduction to Knot Theory. Ginn and Co. after 1977 Springer Verlag.
• Fox, Ralph (1961). "A quick trip through knot theory". In Fort, M.K. (ed.). Proceedings of the University of Georgia Topology Institute. Englewood Cliffs. N. J.: Prentice-Hall. pp. 120–167. OCLC 73203715.
• Freedman, Michael H.; Quinn, Frank (1990). Topology of 4-manifolds. Princeton Mathematical Series. Vol. 39. Princeton University Press. ISBN 978-0-691-08577-7.
• Kauffman, Louis (2006) [1983]. Formal Knot Theory. Courier. ISBN 978-0-486-45052-0.
• Kauffman, Louis (2012). Knots and Physics (4th ed.). World Scientific Publishing Company. ISBN 978-981-4383-00-4.
• Kawauchi, Akio (2012) [1996]. A Survey of Knot Theory. Birkhäuser. ISBN 978-3-0348-9227-8. (covers several different approaches, explains relations between different versions of the Alexander polynomial)
• Ozsváth, Peter; Szabó, Zoltán (2004). "Holomorphic disks and knot invariants". Advances in Mathematics. 186 (1): 58–116. arXiv:math/0209056. Bibcode:2002math......9056O. doi:10.1016/j.aim.2003.05.001. S2CID 11246611.
• Ozsváth, Peter; Szabó, Zoltán (2004b). "Holomorphic disks and genus bounds". Geometry and Topology. 8 (2004): 311–334. arXiv:math/0311496. doi:10.2140/gt.2004.8.311. S2CID 11374897.
• Ni, Yi (2007). "Knot Floer homology detects fibred knots". Inventiones Mathematicae. Invent. Math. 170 (3): 577–608. arXiv:math/0607156. Bibcode:2007InMat.170..577N. doi:10.1007/s00222-007-0075-9. S2CID 119159648.
• Rasmussen, Jacob (2003). Floer homology and knot complements (Thesis). Harvard University. p. 6378. arXiv:math/0306378. Bibcode:2003math......6378R.
• Rolfsen, Dale (1990). Knots and Links (2nd ed.). Publish or Perish. ISBN 978-0-914098-16-4. (explains classical approach using the Alexander invariant; knot and link table with Alexander polynomials)

बाहरी संबंध

• "Alexander invariants", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• "Main Page" and "The Alexander-Conway Polynomial", The Knot Atlas. – knot and link tables with computed Alexander and Conway polynomials