केल्विन-वोइगट सामग्री

केल्विन-वोइग्ट सामग्री, जिसे वोइग्ट सामग्री भी कहा जाता है, सबसे सरल मॉडल viscoelastic सामग्री है जो विशिष्ट रबड़ जैसी गुण दिखाती है। यह लंबे समय के पैमाने (धीमी विरूपण) पर विशुद्ध रूप से लोचदार है, लेकिन तेजी से विरूपण के लिए अतिरिक्त प्रतिरोध दिखाता है। इसका नाम ब्रिटिश भौतिक विज्ञानी और इंजीनियर विलियम थॉमसन, प्रथम बैरन केल्विन और जर्मन भौतिक विज्ञानी वोल्डेमर वोइगट के नाम पर रखा गया है।

परिभाषा

केल्विन-वोइग्ट मॉडल, जिसे वोइग्ट मॉडल भी कहा जाता है, चित्र में दिखाए गए अनुसार विशुद्ध रूप से चिपचिपाहट स्पंज और विशुद्ध रूप से लोच (भौतिकी) वसंत द्वारा समानांतर में जुड़ा हुआ है।

केल्विन-वोइग मॉडल का योजनाबद्ध प्रतिनिधित्व।

यदि, इसके बजाय, हम इन दो तत्वों को श्रृंखला में जोड़ते हैं, तो हमें मैक्सवेल सामग्री का एक मॉडल मिलता है।

चूंकि मॉडल के दो घटक समानांतर में व्यवस्थित होते हैं, प्रत्येक घटक में उपभेद समान होते हैं:

$\varepsilon _{\text{Total}}=\varepsilon _{S}=\varepsilon _{D}.$

जहां सबस्क्रिप्ट डी डम्पर में तनाव-तनाव को इंगित करता है और सबस्क्रिप्ट एस वसंत में तनाव-तनाव को इंगित करता है। इसी तरह, कुल तनाव प्रत्येक घटक में तनाव का योग होगा:

$\sigma _{\text{Total}}=\sigma _{S}+\sigma _{D}.$

इन समीकरणों से हम पाते हैं कि एक केल्विन-वाॅइट सामग्री में, तनाव (भौतिकी) σ, तनाव (सामग्री विज्ञान) ε और समय टी के संबंध में परिवर्तन की उनकी दरें फॉर्म के समीकरणों द्वारा नियंत्रित होती हैं:

$\sigma (t)=E\varepsilon (t)+\eta {\frac {d\varepsilon (t)}{dt}},$

या, डॉट नोटेशन में:

$\sigma =E\varepsilon +\eta {\dot {\varepsilon }},$

जहां ई लोच का एक मापांक है और $\eta$ चिपचिपापन है। समीकरण या तो कतरनी तनाव या किसी सामग्री के सामान्य तनाव पर लागू किया जा सकता है।

अचानक तनाव का प्रभाव

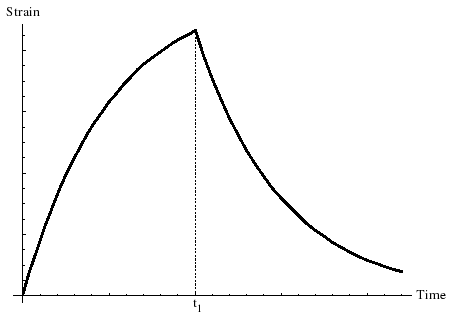
अगर हम अचानक कुछ निरंतर तनाव लागू करते हैं $\sigma _{0}$ केल्विन-वोइग सामग्री के लिए, तब विकृति शुद्ध लोचदार सामग्री के लिए विरूपण के करीब पहुंच जाएगी $\sigma _{0}/E$ अंतर तेजी से घटने के साथ:

$\varepsilon (t)={\frac {\sigma _{0}}{E}}(1-e^{-t/\tau _{R}}),$

जहां टी समय है और $\tau _{R}={\frac {\eta }{E}}$ मंदता का समय है।

अगर हम समय पर सामग्री मुक्त कर देंगे $t_{1}$, तो लोचदार तत्व सामग्री को तब तक पीछे छोड़ देगा जब तक कि विरूपण शून्य न हो जाए। मंदता निम्नलिखित समीकरण का पालन करती है:

$\varepsilon (t>t_{1})=\varepsilon (t_{1})e^{-(t-t_{1})/\tau _{R}}.$

चित्र आयाम रहित विरूपण की निर्भरता को दर्शाता है ${\frac {E\varepsilon (t)}{\sigma _{0}}}$ आयाम रहित समय पर $t/\tau _{R}$. तस्वीर में सामग्री पर तनाव समय पर लोड होता है $t=0$, और बाद के आयाम रहित समय पर जारी किया गया $t_{1}^{*}=t_{1}/\tau _{R}$.

आयाम रहित विरूपण की निर्भरता निरंतर तनाव के तहत आयामहीन समय पर

चूंकि सभी विरूपण उत्क्रमणीय हैं (हालांकि अचानक नहीं) केल्विन-वोइग सामग्री एक ठोस है।

वोइग्ट मॉडल मैक्सवेल मॉडल की तुलना में अधिक वास्तविक रूप से रेंगने की भविष्यवाणी करता है, क्योंकि अनंत समय सीमा में तनाव स्थिर रहता है:

$\lim _{t\to \infty }\varepsilon ={\frac {\sigma _{0}}{E}},$

जबकि मैक्सवेल मॉडल तनाव और समय के बीच एक रैखिक संबंध की भविष्यवाणी करता है, जो अक्सर ऐसा नहीं होता है। यद्यपि केल्विन-वोइगट मॉडल रेंगने की भविष्यवाणी करने के लिए प्रभावी है, तनाव भार हटा दिए जाने के बाद विश्राम व्यवहार का वर्णन करने में यह अच्छा नहीं है।

गतिशील मापांक

केल्विन-वोइग सामग्री का जटिल गतिशील मापांक निम्न द्वारा दिया गया है:

$E^{\star }(\omega )=E+i\eta \omega .$

इस प्रकार, गतिशील मापांक के वास्तविक और काल्पनिक घटक हैं:

$E_{1}=\Re [E(\omega )]=E,$

$E_{2}=\Im [E(\omega )]=\eta \omega .$

ध्यान दें कि $E_{1}$ स्थिर है, जबकि $E_{2}$ आवृत्ति के सीधे आनुपातिक है (जहां स्पष्ट चिपचिपाहट, $\eta$, आनुपातिकता का स्थिरांक है)।

संदर्भ

• Meyers and Chawla (1999): Section 13.11 of Mechanical Behaviors of Materials, Mechanical behavior of Materials, 570–580. Prentice Hall, Inc.
• http://stellar.mit.edu/S/course/3/fa06/3.032/index.html

यह भी देखें

• बर्गर सामग्री
• सामान्यीकृत मैक्सवेल मॉडल
• मैक्सवेल सामग्री
• मानक रैखिक ठोस मॉडल

श्रेणी:गैर-न्यूटोनियन तरल पदार्थ श्रेणी:पदार्थ विज्ञान श्रेणी:विलियम थॉमसन, प्रथम बैरन केल्विन