एकवचन समरूपता

Not to be confused with सार बीजगणितीय विविधताओं की एकवचन समरूपता.

बीजगणितीय सांस्थितिकी में, एकवचन समरूपता एक सांस्थितिक समष्टि 'x' के बीजगणितीय अचर के एक निश्चित समुच्चय के अध्ययन को संदर्भित करता है, तथाकथित समरूपता समूह $H_{n}(X).$ है। सहज रूप से, एकवचन गृहविज्ञान मायने रखता है, प्रत्येक आयाम n के लिए, अंतरिक्ष के n-आयामी छिद्र। एकवचन समरूपता एक समरूपता सिद्धांत का एक विशेष उदाहरण है, जो अब सिद्धांतों का एक व्यापक संग्रह बन गया है। विभिन्न सिद्धांतों में से, यह समझने के लिए शायद सबसे सरल सिद्धांतों में से एक है, काफी ठोस निर्माणों पर बनाया जा रहा है (संबंधित सिद्धांत सरल समरूपता भी देखें)।

संक्षेप में, एकवचन समरूपता का निर्माण प्रसमुच्चय | मानक n-प्रसमुच्चय के मानचित्रों सांस्थितिक समष्टि की श्रेणी में ले जाकर किया जाता है, और उन्हें फ्री एबेलियन ग्रुप # इंटेगर फ़ंक्शंस और औपचारिक योग में कंपोज़ किया जाता है, जिसे 'एकवचन श्रृंखला' कहा जाता है। सीमा संचालन - प्रत्येक n-विमीय प्रसमुच्चय को उसके (n-1) -विमीय सीमा संचालक से प्रतिचित्रण करना - एकवचन श्रृंखला समष्टि को प्रेरित करता है। एकवचन समरूपता तब श्रृंखला समष्टि की समरूपता (गणित) है। परिणामी समरूपता समूह सभी समस्थेयता # समस्थेयता समतुल्यता और अशक्त-समस्थेयता रिक्त स्थान के लिए समान हैं, जो उनके अध्ययन का कारण है। इन निर्माणों को सभी सांस्थितिक रिक्त स्थान पर अनुप्रयुक्त किया जा सकता है, और इसलिए एकवचन समरूपता को सांस्थितिक रिक्त स्थान की श्रेणी से ग्रेडेड एबेलियन समूहों की श्रेणी के रूप में अभिव्यक्त किया जा सकता है।

एकल सरल

मानक 2-प्रसमुच्चय Δ² R में^3</उप>

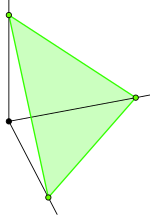
एक सांस्थितिक समष्टि में एक एकवचन n-प्रसमुच्चय | एकवचन n-प्रसमुच्चय एक सांतत्य फलन है (जिसे मानचित्र भी कहा जाता है) $\sigma$ मानक संकेतन से $\Delta ^{n}$ x के लिए, लिखा $\sigma :\Delta ^{n}\to X.$ इस मानचित्र को इंजेक्शन की आवश्यकता नहीं है, और x में समान छवि के साथ गैर-समकक्ष एकवचन सरल हो सकते हैं।

$\sigma ,$ की सीमा, इस रूप $\partial _{n}\sigma ,$ में घोषित किया गया एकवचन (n − 1) के औपचारिक योग के रूप में परिभाषित किया गया है - के प्रतिबंध द्वारा दर्शाए गए सरलीकरण $\sigma$ मानक n-प्रसमुच्चय के पार्श्व पर, उन्मुखीकरण को ध्यान में रखने के लिए एक वैकल्पिक संकेत के साथ। (औपचारिक योग सरलता पर मुक्त एबेलियन समूह का एक तत्व है। समूह के लिए आधार सभी संभावित एकवचन सरलताओं का अनंत समुच्चय है। समूह संचालन अतिरिक्त है और प्रसमुच्चय बी के साथ प्रसमुच्चय ए का योग सामान्यतः बस नामित किया जाता है। + b, परन्तु a + a = 2a और इसी तरह। प्रत्येक प्रसमुच्चय ए में नकारात्मक -ए है।) इस प्रकार, यदि हम नामित $\sigma$ इसके शिखर द्वारा

$[p_{0},p_{1},\ldots ,p_{n}]=[\sigma (e_{0}),\sigma (e_{1}),\ldots ,\sigma (e_{n})]$

शिखरों के अनुरूप $e_{k}$ मानक n-प्रसमुच्चय का $\Delta ^{n}$ (जो निश्चित रूप से निर्मित एकवचन प्रसमुच्चय को पूर्णतया से निर्दिष्ट नहीं करता है $\sigma$), तब

$\partial _{n}\sigma =\partial _{n}[p_{0},p_{1},\ldots ,p_{n}]=\sum _{k=0}^{n}(-1)^{k}[p_{0},\ldots ,p_{k-1},p_{k+1},\ldots ,p_{n}]=\sum _{k=0}^{n}(-1)^{k}\sigma \mid _{e_{0},\ldots ,e_{k-1},e_{k+1},\ldots ,e_{n}}$

एक विशिष्ट तरीके से निर्दिष्ट प्रसमुच्चय छवि के पार्श्व का एक औपचारिक योग है। (अर्थात, किसी विशेष पार्श्व का प्रतिबंध होना चाहिए $\sigma$ के एक पार्श्व के लिए $\Delta ^{n}$ जो उस क्रम पर निर्भर करता है जिसके शीर्ष सूचीबद्ध हैं।) इस प्रकार, उदाहरण के लिए, की सीमा $\sigma =[p_{0},p_{1}]$ (एक वक्र से जा रहा है $p_{0}$ को $p_{1}$) औपचारिक योग (या औपचारिक अंतर) है $[p_{1}]-[p_{0}]$.

एकवचन श्रृंखला समष्टि

सरलता के औपचारिक योगों को परिभाषित करके एकवचन समरूपता का सामान्य निर्माण आगे बढ़ता है, जिसे एक मुक्त एबेलियन समूह के तत्वों के रूप में समझा जा सकता है, और फिर दर्शा रहा है कि हम एक निश्चित समूह को परिभाषित कर सकते हैं, सांस्थितिक समष्टि का समरूपता समूह, जिसमें सीमा संचालक सम्मिलित है। .

पहले सभी संभव एकवचन n-सरलताओं के समुच्चय पर विचार करें $\sigma _{n}(X)$ एक सांस्थितिक समष्टि x पर। इस समुच्चय का उपयोग एक मुक्त एबेलियन समूह के आधार के रूप में किया जा सकता है, ताकि प्रत्येक एकवचन n-प्रसमुच्चय समूह का जनक हो। जनक का यह समुच्चय निश्चित रूप से अनंत है, प्रायः बेशुमार होता है, क्योंकि एक विशिष्ट सांस्थितिक समष्टि में एक प्रसमुच्चय को प्रतिचित्रण करने के कई तरीके हैं। इस आधार से उत्पन्न मुक्त आबेली समूह को सामान्य रूप से निरूपित किया जाता है $C_{n}(X)$. घटक $C_{n}(X)$ एकवचन n-श्रृंखला कहलाते हैं; वे पूर्णांक गुणांक वाले एकवचन सरलीकरण के औपचारिक योग हैं।

सीमा संचालक $\partial$ एकवचन n-श्रृंखला पर कार्य करने के लिए सरलता से बढ़ाया जाता है। विस्तार, जिसे सीमा संचालक कहा जाता है, के रूप में लिखा गया है

$\partial _{n}:C_{n}\to C_{n-1},$

समूहों का एक समरूपता है। सीमा संचालक, साथ में $C_{n}$, एबेलियन समूहों का एक श्रृंखला समष्टि बनाते हैं, जिसे एकवचन समष्टि कहा जाता है। इसे प्रायः के रूप में दर्शाया जाता है $(C_{\bullet }(X),\partial _{\bullet })$ या अधिक सरलता से $C_{\bullet }(X)$.

सीमा संचालक का कर्नेल है $Z_{n}(X)=\ker(\partial _{n})$, और एकवचन n-चक्रों का समूह कहलाता है। सीमा संचालक की छवि है $B_{n}(X)=\operatorname {im} (\partial _{n+1})$, और एकवचन n-सीमाओं का समूह कहलाता है।

यह भी दर्शाया जा सकता है $\partial _{n}\circ \partial _{n+1}=0$, तात्पर्य $B_{n}(X)\subseteq Z_{n}(X)$. $n$वें>-वें समरूपता समूह $X$ फिर कारक समूह के रूप में परिभाषित किया गया है

$H_{n}(X)=Z_{n}(X)/B_{n}(X).$

के तत्व $H_{n}(X)$ समरूपता वर्ग कहलाते हैं।

समस्थेयता निश्चरता

यदि X और Y एक ही समस्थेयता प्रकार के साथ दो सांस्थितिक समष्टि हैं (अर्थात समस्थेयता समतुल्य हैं), तो

$H_{n}(X)\cong H_{n}(Y)\,$

सभी n ≥ 0 के लिए। इसका तात्पर्य है कि समरूपता समूह समस्थेयता अचर हैं, और इसलिए सांस्थितिक अचर हैं।

विशेष रूप से, यदि X एक जुड़ा हुआ अनुबंधित स्थान है, तो इसके सभी समरूपता समूह 0 हैं, अतिरिक्त $H_{0}(X)\cong \mathbb {Z}$.

एकवचन समरूपता समूहों के समस्थेयता निश्चरता के लिए एक प्रमाण को निम्नानुसार आलिखित किया जा सकता है। एक सतत प्रतिचित्र f: X → Y एक समरूपता को प्रेरित करता है

$f_{\sharp }:C_{n}(X)\rightarrow C_{n}(Y).$

इसे तुरंत सत्यापित किया जा सकता है

$\partial f_{\sharp }=f_{\sharp }\partial ,$

अर्थात एफ_# एक श्रृंखला समष्टि # श्रृंखला प्रतिचित्रण है, जो समरूपता पर समरूपता तक उतरता है

$f_{*}:H_{n}(X)\rightarrow H_{n}(Y).$

अब हम दिखाते हैं कि यदि f और g समस्थानिक रूप से समतुल्य हैं, तो f_* = जी_*. इससे यह पता चलता है कि यदि f एक समस्थेयता तुल्यता है, तो f_* एक समरूपता है।

मान लीजिए F : X × [0, 1] → Y एक समरूपता है जो f को g में ले जाती है। श्रृंखला के स्तर पर, समाकारिता को परिभाषित कीजिए

$P:C_{n}(X)\rightarrow C_{n+1}(Y)$

वह, ज्यामितीय रूप से बोलते हुए, आधार तत्व σ: Δ लेता हैⁿ → C का X_n(x) प्रिज्म पी (σ) के लिए: Δⁿ × I → Y. P(σ) की सीमा को इस प्रकार व्यक्त किया जा सकता है

$\partial P(\sigma )=f_{\sharp }(\sigma )-g_{\sharp }(\sigma )-P(\partial \sigma ).$

तो अगर α मेंC_n(X) एक n-चक्र है, फिर f_#(α ) और g_#(α) एक सीमा से भिन्न होता है:

$f_{\sharp }(\alpha )-g_{\sharp }(\alpha )=\partial P(\alpha ),$

अर्थात वे समरूप हैं। यह अनुरोध सिद्ध करता है।

कॉमन समष्टि के समरूपता समूह

नीचे दी गई तालिका k-वें समरूपता समूहों को दर्शाती है $H_{k}(X)$ n-विमीय वास्तविक प्रक्षेपीय समष्टि Rपीⁿ, जटिल प्रक्षेप्य स्थान, 'CP'ⁿ, एक बिंदु, गोले Sⁿ($n\geq 1$), और एक 3-टोरस टी³ पूर्णांक गुणांकों के साथ।

Space	Homotopy type
RPn	$\mathbf {Z}$	k = 0 और k = n विषम
	$\mathbf {Z} /2\mathbf {Z}$	k विषम, 0 < k < n
	0	अन्यथा
CPn	$\mathbf {Z}$	k = 0,2,4,...,2n
	0	अन्यथा
बिंदु	$\mathbf {Z}$	k = 0
	0	अन्यथा
Sn	$\mathbf {Z}$	k = 0,n
	0	अन्यथा
T3	$\mathbf {Z}$	k = 0,3
	$\mathbf {Z}$3	k = 1,2
	0	अन्यथा

कार्यात्मकता

उपरोक्त निर्माण को किसी भी सामयिक स्थान के लिए परिभाषित किया जा सकता है, और निरंतर मानचित्रों की क्रिया द्वारा संरक्षित किया जाता है। इस व्यापकता का तात्पर्य है कि एकवचन समरूपता सिद्धांत को श्रेणी सिद्धांत की भाषा में पुनर्गठित किया जा सकता है। विशेष रूप से, समरूपता समूह को सांस्थितिक रिक्त स्थान की श्रेणी से एबेलियन समूह एब की श्रेणी के लिए एक मज़ेदार समझा जा सकता है।

पहले उस पर विचार करें $X\mapsto C_{n}(X)$ सांस्थितिक समष्टि से मुक्त एबेलियन समूहों का एक प्रतिचित्र है। इससे पता चलता है $C_{n}(X)$ एक functor के रूप में लिया जा सकता है, बशर्ते कोई शीर्ष के आकारिता पर अपनी कार्रवाई को समझ सके। अब, शीर्ष के आकारिता सांतत्य फलन हैं, इसलिए यदि $f:X\to Y$ सांस्थितिक समष्टि का एक सतत प्रतिचित्र है, इसे समूहों के समरूपता तक बढ़ाया जा सकता है

$f_{*}:C_{n}(X)\to C_{n}(Y)\,$

परिभाषित करके

$f_{*}\left(\sum _{i}a_{i}\sigma _{i}\right)=\sum _{i}a_{i}(f\circ \sigma _{i})$

कहाँ $\sigma _{i}:\Delta ^{n}\to X$ एक विलक्षण प्रसमुच्चय है, और $\sum _{i}a_{i}\sigma _{i}\,$ एक विलक्षण n-श्रृंखला है, जो कि एक तत्व है $C_{n}(X)$. इससे पता चलता है कि $C_{n}$ यह एक प्रकार्यक है

$C_{n}:\mathbf {Top} \to \mathbf {Ab}$

सांस्थितिक समष्टि की श्रेणी से एबेलियन समूहों की श्रेणी तक।

सीमा संचालक निरंतर मानचित्रों के साथ आवागमन करता है, ताकि $\partial _{n}f_{*}=f_{*}\partial _{n}$. यह संपूर्ण श्रृंखला समष्टि को एक मज़ेदार के रूप में माना जाने की अनुमति देता है। विशेष रूप से, यह दर्शाता है कि map $X\mapsto H_{n}(X)$ यह एक प्रकार्यक है

$H_{n}:\mathbf {Top} \to \mathbf {Ab}$

सांस्थितिक समष्टि की श्रेणी से एबेलियन समूहों की श्रेणी तक। समस्थेयता स्वयंसिद्ध द्वारा, किसी के पास वह है $H_{n}$ एक प्रकार्यक भी है, जिसे समरूपता प्रकार्यक कहा जाता है, hTop पर अभिनय करता है, भागफल समस्थेयता श्रेणी:

$H_{n}:\mathbf {hTop} \to \mathbf {Ab} .$

यह एकवचन समरूपता को अन्य समरूपता सिद्धांतों से अलग करता है, जिसमें $H_{n}$ अभी भी एक मज़ेदार है, परन्तु यह आवश्यक नहीं है कि सभी शीर्ष पर परिभाषित किया गया हो। कुछ अर्थों में, एकवचन समरूपता सबसे बड़ा समरूपता सिद्धांत है, जिसमें शीर्ष के एक उपश्रेणी पर हर समरूपता सिद्धांत उस उपश्रेणी पर एकवचन समरूपता से सहमत है। दूसरी ओर, एकवचन समरूपता में सबसे साफ श्रेणीबद्ध गुण नहीं होते हैं; इस तरह की सफाई अन्य समरूपता सिद्धांतों जैसे सेलुलर समरूपता के विकास को प्रेरित करती है।

अधिक सामान्यतः, समरूपता प्रकार्यक को स्वयंसिद्ध रूप से परिभाषित किया जाता है, एक एबेलियन श्रेणी पर प्रकार्यक के रूप में, या, वैकल्पिक रूप से, श्रृंखला समष्टिों पर एक प्रकार्यक के रूप में, संतोषजनक स्वयंसिद्धों के लिए एक सीमा आकारिकी की आवश्यकता होती है जो छोटे सटीक अनुक्रमों को लंबे सटीक अनुक्रमों में परिवर्तित कर देती है। एकवचन समरूपता के मामले में, समरूपता प्रकार्यक को दो टुकड़ों में विभाजित किया जा सकता है, एक सांस्थितिक खंड और एक बीजगणितीय खंड। सांस्थितिक खंड द्वारा दिया गया है

$C_{\bullet }:\mathbf {Top} \to \mathbf {Comp}$

जो सांस्थितिक समष्टि को प्रतिचित्रण करता है $X\mapsto (C_{\bullet }(X),\partial _{\bullet })$ और सांतत्य फलन करता है $f\mapsto f_{*}$. यहाँ तो, $C_{\bullet }$ एकवचन श्रृंखला प्रकार्यक समझा जाता है, जो सांस्थितिक समष्टि को श्रृंखला समष्टि कॉम्प (या कॉम) की श्रेणी में प्रतिचित्रण करता है। श्रृंखला समष्टिों की श्रेणी में इसकी वस्तु (श्रेणी सिद्धांत) के रूप में श्रृंखला समष्टि हैं, और श्रृंखला मानचित्र इसके आकारिकी के रूप में हैं।

दूसरा, बीजगणितीय भाग समरूपता प्रकार्यक है

$H_{n}:\mathbf {Comp} \to \mathbf {Ab}$

कौन सा मानचित्र

$C_{\bullet }\mapsto H_{n}(C_{\bullet })=Z_{n}(C_{\bullet })/B_{n}(C_{\bullet })$

और श्रृंखला मानचित्रों को एबेलियन समूहों के मानचित्रों तक ले जाता है। यह समरूपता प्रकार्यक है जिसे स्वयंसिद्ध रूप से परिभाषित किया जा सकता है, ताकि यह श्रृंखला समष्टिों की श्रेणी पर एक प्रकार्यक के रूप में स्वयं खड़ा हो।

समस्थेयता प्रतिचित्रण्स समरूप रूप से समतुल्य श्रृंखला प्रतिचित्रण्स को परिभाषित करके चित्र में फिर से प्रवेश करते हैं। इस प्रकार, कोई भागफल श्रेणी hComp या K को परिभाषित कर सकता है, श्रृंखला समष्टिों की समस्थेयता श्रेणी।

R में गुणांक

किसी भी एकात्मक वलय (गणित) R को देखते हुए, एक सांस्थितिक समष्टि पर एकवचन n-सिम्पलिस के समुच्चय को फ्री मापांक के जनक के रूप में लिया जा सकता है। फ्री R-मापांक। अर्थात्, उपरोक्त निर्माणों को मुक्त एबेलियन समूहों के प्रारंभिक बिंदु से करने के बजाय, उनके स्थान पर मुफ्त R-मापांक का उपयोग करता है। सभी निर्माण बहुत कम या बिना किसी परिवर्तित कराव के होते हैं। इसका परिणाम है

$H_{n}(X;R)\$

जो अब एक मापांक (गणित) है | R-मापांक। बेशक, यह सामान्यतः एक मुफ्त मापांक नहीं है। सामान्य समरूपता समूह को ध्यान में रखते हुए पुनः प्राप्त किया जाता है

$H_{n}(X;\mathbb {Z} )=H_{n}(X)$

जब कोई वलय को पूर्णांकों का वलय मानता है। संकेतन एच_n(x; R) को लगभग समान अंकन एच के साथ भ्रमित नहीं होना चाहिए_n(x, ए), जो रिश्तेदार समरूपता (नीचे) को दर्शाता है।

सार्वभौमिक गुणांक प्रमेय लघु सटीक अनुक्रम का उपयोग करते हुए सामान्य पूर्णांक गुणांक वाले समरूपता के संदर्भ में R गुणांकों के साथ समरूपता की गणना करने के लिए एक तंत्र प्रदान करता है।

$0\to H_{n}(X;\mathbb {Z} )\otimes R\to H_{n}(X;R)\to Tor(H_{n-1}(X;\mathbb {Z} ),R)\to 0.$

जहाँ Tor, Tor functor है। ध्यान दें, यदि R मरोड़-मुक्त है, तो किसी भी G के लिए Tor(G, R) = 0 है, इसलिए उपरोक्त लघु सटीक अनुक्रम एक समरूपता के मध्य कम हो जाता है $H_{n}(X;\mathbb {Z} )\otimes R$ और $H_{n}(X;R).$

रिलेटिव समरूपता

Main article: Relative homology

उपक्षेत्र के लिए $A\subset X$, रिश्तेदार समरूपता एच_n(x, ए) को श्रृंखला समष्टिों के भागफल के समरूपता के रूप में समझा जाता है, अर्थात

$H_{n}(X,A)=H_{n}(C_{\bullet }(X)/C_{\bullet }(A))$

जहां शृंखला संकुलों का भागफल लघु सटीक अनुक्रम द्वारा दिया जाता है

$0\to C_{\bullet }(A)\to C_{\bullet }(X)\to C_{\bullet }(X)/C_{\bullet }(A)\to 0.$

कम समरूपता

Main article: Reduced homology

समष्टि x की घटी हुई समरूपता, के रूप में nोटेट की गई ${\tilde {H}}_{n}(X)$ सामान्य समरूपता के लिए एक साधारण संशोधन है जो कुछ रिश्तों की अभिव्यक्ति को सरल करता है और इस बात को पूर्ण करता है कि एक बिंदु के सभी समरूपता समूह शून्य होने चाहिए।

श्रृंखला समष्टि पर परिभाषित सामान्य समरूपता के लिए:

$\dotsb {\overset {\partial _{n+1}}{\longrightarrow \,}}C_{n}{\overset {\partial _{n}}{\longrightarrow \,}}C_{n-1}{\overset {\partial _{n-1}}{\longrightarrow \,}}\dotsb {\overset {\partial _{2}}{\longrightarrow \,}}C_{1}{\overset {\partial _{1}}{\longrightarrow \,}}C_{0}{\overset {\partial _{0}}{\longrightarrow \,}}0$

घटी हुई समरूपता को परिभाषित करने के लिए, हम श्रृंखला समष्टि को एक अतिरिक्त के साथ बढ़ाते हैं $\mathbb {Z}$ मध्य में $C_{0}$ और शून्य:

$\dotsb {\overset {\partial _{n+1}}{\longrightarrow \,}}C_{n}{\overset {\partial _{n}}{\longrightarrow \,}}C_{n-1}{\overset {\partial _{n-1}}{\longrightarrow \,}}\dotsb {\overset {\partial _{2}}{\longrightarrow \,}}C_{1}{\overset {\partial _{1}}{\longrightarrow \,}}C_{0}{\overset {\epsilon }{\longrightarrow \,}}\mathbb {Z} \to 0$ कहाँ $\epsilon \left(\sum _{i}n_{i}\sigma _{i}\right)=\sum _{i}n_{i}$. खाली समुच्चय को (-1)-simplex के रूप में व्याख्या करके इसे उचित ठहराया जा सकता है, जिसका अर्थ है $C_{-1}\simeq \mathbb {Z}$.

घटे हुए समरूपता समूहों को अब परिभाषित किया गया है ${\tilde {H}}_{n}(X)=\ker(\partial _{n})/\mathrm {im} (\partial _{n+1})$ सकारात्मक n और के लिए ${\tilde {H}}_{0}(X)=\ker(\epsilon )/\mathrm {im} (\partial _{1})$. n > 0 के लिए, $H_{n}(X)={\tilde {H}}_{n}(X)$, जबकि n = 0 के लिए, $H_{0}(X)={\tilde {H}}_{0}(X)\oplus \mathbb {Z} .$

सह समरूपता

Main article: सह समरूपता

समरूपता श्रृंखला समष्टि को दोहराकर (अर्थात प्रकार्यक होम (-, R), R को कोई भी वलय अनुप्रयुक्त करते हुए) हम कोबाउंड्री प्रतिचित्रण के साथ एक कोश्रृंखला समष्टि प्राप्त करते हैं $\delta$. X के सह समरूपता समूहों को इस समष्टि के समरूपता समूहों के रूप में परिभाषित किया गया है; एक चुटकी में, सह समरूपता सह [द्वैत समष्टि] की समरूपता है।

कोसमरूपता समूहों में समरूपता समूहों की तुलना में अधिक समृद्ध, या कम से कम अधिक परिचित, बीजगणितीय संरचना होती है। सबसे पहले, वे निम्नानुसार एक अवकलन ग्रेडेड बीजगणित बनाते हैं:

• समूहों का श्रेणीबद्ध समूह एक श्रेणीबद्ध R-मापांक (गणित) बनाता है;
• इसे कप उत्पाद का उपयोग करके एक श्रेणीबद्ध R-बीजगणित (अंगूठी सिद्धांत) की संरचना दी जा सकती है;
• बॉकस्टीन समरूपता β एक अंतर देता है।

अतिरिक्त सह समरूपता संचालन हैं, और सह समरूपता बीजगणित में अतिरिक्त संरचना मॉड पी है (पहले की तरह, मॉड पी सह समरूपता मॉड पी कोश्रृंखला समष्टि का सह समरूपता है, न कि मॉड पी सह समरूपता की कमी), विशेष रूप से स्टीनरोड बीजगणित संरचना।

बेट्टी समरूपता और सह समरूपता

चूंकि समरूपता सिद्धांतों की संख्या बड़ी हो गई है (देखें: श्रेणी: समरूपता सिद्धांत), 'बेट्टी समरूपता' और 'बेटी सह समरूपता' शब्द कभी-कभी एकवचन सिद्धांत पर अनुप्रयुक्त होते हैं (विशेष रूप से बीजगणितीय ज्यामिति पर लिखने वाले लेखकों द्वारा), सरल समष्टिों और बंद मैनिफोल्ड्स जैसे सबसे परिचित स्थानों की बेट्टी संख्या को जन्म देने के रूप में।

असाधारण समरूपता

Main article: असाधारण समरूपता सिद्धांत

यदि कोई समरूपता सिद्धांत को स्वैच्छिक रूप से परिभाषित करता है (एलेनबर्ग-स्टीनरोड xिओम्स के माध्यम से), और फिर xिओम्स (आयाम स्वयंसिद्ध) में से एक को Rाम देता है, तो एक सामान्यीकृत सिद्धांत प्राप्त होता है, जिसे असाधारण समरूपता सिद्धांत कहा जाता है। ये मूल रूप से असाधारण सह समरूपता सिद्धांतों के रूप में उत्पन्न हुए, अर्थात् के-सिद्धांत और कोबर्डिज्म सिद्धांत। इस संदर्भ में, एकवचन समरूपता को 'साधारण समरूपता' कहा जाता है।

यह भी देखें

• व्युत्पन्न श्रेणी
• उच्छेदन प्रमेय
• ह्यूरेविक्ज़ प्रमेय
• सरल समरूपता
• कोष्ठात्मक समरूपता

संदर्भ

• Allen Hatcher, Algebraic topology. Cambridge University Press, ISBN 0-521-79160-X and ISBN 0-521-79540-0
• J.P. May, A Concise Course in Algebraic Topology, Chicago University Press ISBN 0-226-51183-9
• Joseph J. Rotman, An Introduction to Algebraic Topology, Springer-Verlag, ISBN 0-387-96678-1