आइसोगोनल संयुग्म

__नोटोक__

कोण समद्विभाजक (केन्द्र I पर संगत)

  Lines from each vertex to P

कोण समद्विभाजकों के बारे में परिलक्षित P की रेखाएँ (P * पर समवर्ती, P का समकोणीय संयुग्म)

त्रिभुज के अंदर बिंदुओं पर समकोणीय संयुग्म परिवर्तन।

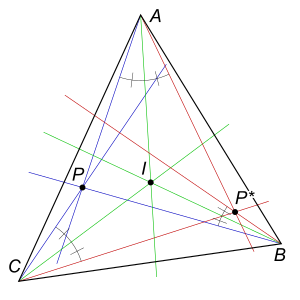
ज्यामिति में, एक बिंदु (ज्यामिति) के समकोणीय संयुग्म P त्रिभुज के संबंध में △ABC का निर्माण रेखाओं के परावर्तन (गणित) द्वारा किया जाता है PA, PB, PC के कोण द्विभाजक के बारे में A, B, C क्रमश। ये तीन परावर्तित रेखाएँ P समकोणिक संयुग्म पर समवर्ती रेखाएँ हैं (यह परिभाषा केवल उन बिंदुओं पर प्रयुक्त होती है जो त्रिभुज △ABC की विस्तारित भुजा पर नहीं हैं ) यह सेवा के प्रमेय के त्रिकोणमितीय रूप का प्रत्यक्ष परिणाम है।

एक बिंदु का समकोणीय संयुग्म P को कभी-कभी P* द्वारा निरूपित किया जाता है P* का समकोणीय संयुग्म P है P.

अंतःकेंद्र I का समकोणीय संयुग्म I ही है। लम्बकेन्द्र H का समकोणीय संयुग्म H परिकेन्द्र O है O. केन्द्रक G का समकोणीय संयुग्म G (परिभाषा के अनुसार) सिम्मेडियन बिंदु K है K. फर्मेट बिंदु के समकोणीय कॉन्जुगेट्स आइसोडायनामिक बिंदु ्स हैं और इसके विपरीत। ब्रोकार्ड बिंदु एक दूसरे के समकोणीय संयुग्म हैं।

ट्रिलिनियर निर्देशांक में, यदि $X=x:y:z$ त्रिभुज △ABC की भुजा पर नहीं एक बिंदु है △ABC, तो इसका समद्विबाहु संयुग्म है ${\tfrac {1}{x}}:{\tfrac {1}{y}}:{\tfrac {1}{z}}.$ इस कारण X से, का समकोणीय संयुग्म X को कभी-कभी निरूपित किया जाता है X ^–1. सेट (गणित) {{mvar|S}त्रिरेखीय गुणनफल के अंतर्गत त्रिभुज केंद्रों के }, द्वारा परिभाषित किया गया है

$(p:q:r)*(u:v:w)=pu:qv:rw,$

क्रमविनिमेय समूह है, और S प्रत्येक X का व्युत्क्रमX ^–1 है X में S है X ^–1.

जैसा कि समकोणीय संयुग्मन एक फलन (गणित) है, यह बिंदुओं के सेट, जैसे कि रेखाओं और वृत्तों के समकोणीय संयुग्मन के बारे में बात करने के लिए समझ में आता है। उदाहरण के लिए, एक रेखा का समकोणीय संयुग्म एक सर्कमोनिक और प्रतिष्ठित है; विशेष रूप से, एक दीर्घवृत्त, परवलय या अतिपरवलय के अनुसार रेखा परिवृत्त को 0, 1, या 2 बिंदुओं में काटती है। परिवृत्त का समकोणीय संयुग्म अनंत पर रेखा है। कई प्रसिद्ध क्यूबिक समतल वक्र (जैसे, थॉमसन क्यूबिक, डार्बौक्स क्यूबिक, न्युबर्ग क्यूबिक ) स्व-समकोणीय-संयुग्मी हैं, इस अर्थ में कि यदि X क्यूबिक पर है, तो X ^–1 क्यूबिक पर भी है।

== एक बिंदु == के समकोणीय संयुग्म के लिए एक और निर्माण

समकोणीय संयुग्म की दूसरी परिभाषा

त्रिभुज △ABC के तल में △ABCकिसी दिए गए बिंदु P के लिए P त्रिभुज के तल में △ABC,माना की भुजाओं BC, CA, AB में Pका प्रतिबिंबP_a, P_b, P_c है। प्रतिबिंब चलो P पार्श्व में BC, CA, AB होना P_a, P_b, P_c. तब वृत्त का केंद्र 〇P_aP_bP_c, P का समकोणीय संयुग्म है P.

यह भी देखें

• समस्थानिक संयुग्म
• सेंट्रल लाइन (ज्यामिति)
• त्रिकोण केंद्र

बाहरी संबंध

• Interactive Java Applet illustrating isogonal conjugate and its properties
• MathWorld
• Pedal Triangle and Isogonal Conjugacy