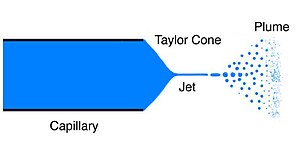
टेलर कोन

इलेक्ट्रोस्पिनिंग की प्रक्रिया द्वारा टेलर कोन से खींचे गए फाइबर को दिखाते हुए जलीय घोल में पॉलीविनाइल अल्कोहल के एक मेनिस्कस की तस्वीर।

एक टेलर कोन इलेक्ट्रोस्पिनिंग, इलेक्ट्रोस्प्रेइंग और हाइड्रोडायनेमिक स्प्रे प्रक्रियाओं में देखे गए शंकु को संदर्भित करता है, जिसमें से आवेशित कणों का एक जेट एक थ्रेशोल्ड वोल्टेज से ऊपर निकलता है। मास स्पेक्ट्रोमेट्री में इलेक्ट्रोस्प्रे आयनीकरण के अलावा, टेलर शंकु क्षेत्र-उत्सर्जन विद्युत प्रणोदन (FEEP) और कोलाइड थ्रस्टर्स में महत्वपूर्ण नियंत्रण और उच्च दक्षता (कम शक्ति) अंतरिक्ष यान के जोर में उपयोग किया जाता है।

इतिहास

इलेक्ट्रोस्प्रे की खोज से पहले 1964 में सर जेफ्री इनग्राम टेलर द्वारा इस शंकु का वर्णन किया गया था। यह काम जॉन ज़ेलेनी के काम के बाद हुआ जिन्होंने एक मजबूत विद्युत क्षेत्र में ग्लिसरीन के एक शंकु-जेट और कई अन्य लोगों के काम की तस्वीर ली: विल्सन और टेलर (1925), नोलन (1926) और मैकी (1931)। टेलर मुख्य रूप से तेज बिजली के क्षेत्रों में पानी की बूंदों के व्यवहार में रुचि रखते थे, जैसे कि गरज के साथ।

गठन

टेलर कोन, जेट और प्लूम को दर्शाने वाला इलेक्ट्रोस्प्रे डायग्राम

जब विद्युत प्रवाहकीय तरल की एक छोटी मात्रा एक विद्युत क्षेत्र के संपर्क में आती है, तो तरल का आकार केवल सतह तनाव के कारण होने वाले आकार से ख़राब होने लगता है। जैसे ही वोल्टेज बढ़ता है विद्युत क्षेत्र का प्रभाव अधिक प्रमुख हो जाता है। जैसे ही विद्युत क्षेत्र का यह प्रभाव छोटी बूंद पर बल के समान परिमाण को लागू करना शुरू करता है, जैसा कि सतह तनाव करता है, एक शंकु आकार उत्तल पक्षों और एक गोल टिप के साथ बनना शुरू होता है। यह 98.6° के पूरे कोण (चौड़ाई) के साथ एक शंकु (ज्यामिति) के आकार तक पहुंचता है।जब एक निश्चित थ्रेसहोल्ड वोल्टेज थोड़ा गोलाकार टिप तक पहुंच जाता है और तरल के एक जेट का उत्सर्जन करता है। इसे कोन-जेट कहा जाता है और यह इलेक्ट्रोस्प्रेइंग प्रक्रिया की शुरुआत है जिसमें आयनों को गैस चरण में स्थानांतरित किया जा सकता है। यह आम तौर पर पाया जाता है कि स्थिर शंकु-जेट प्राप्त करने के लिए थ्रेसहोल्ड वोल्टेज से थोड़ा अधिक उपयोग किया जाना चाहिए। जैसे ही वोल्टेज और भी अधिक बढ़ जाता है, छोटी बूंदों के विघटन के अन्य तरीके पाए जाते हैं। टेलर कोन शब्द विशेष रूप से पूर्वानुमानित कोण के पूर्ण शंकु की सैद्धांतिक सीमा को संदर्भित कर सकता है या आम तौर पर विद्युतप्रसार प्रक्रिया शुरू होने के बाद शंकु-जेट के लगभग शंक्वाकार भाग को संदर्भित करता है।

सिद्धांत

1964 में सर जेफ्री इनग्राम टेलर ने इस घटना का वर्णन किया, सैद्धांतिक रूप से सामान्य धारणाओं के आधार पर व्युत्पन्न किया गया था कि ऐसी परिस्थितियों में एक पूर्ण शंकु बनाने की आवश्यकताओं के लिए 49.3 डिग्री (98.6 डिग्री का एक पूर्ण कोण) के अर्ध-ऊर्ध्वाधर कोण की आवश्यकता होती है और यह प्रदर्शित करता है कि आकार जेट बनने से ठीक पहले इस तरह के शंकु ने सैद्धांतिक आकार लिया। इस कोण को टेलर कोण के नाम से जाना जाता है। यह कोण अधिक सटीक है $\pi -\theta _{0}\,$ कहाँ $\theta _{0}\,$ का प्रथम शून्य है $P_{1/2}(\cos \theta _{0})\,$ (आदेश 1/2 का लेजेंड्रे समारोह)।

टेलर की व्युत्पत्ति दो धारणाओं पर आधारित है: (1) कि शंकु की सतह एक समविभव सतह है और (2) कि शंकु स्थिर अवस्था संतुलन में मौजूद है। इन दोनों मानदंडों को पूरा करने के लिए विद्युत क्षेत्र में दिगंश समरूपता होनी चाहिए और होनी चाहिए ${\sqrt {R}}\,$ शंकु का उत्पादन करने के लिए सतह के तनाव का मुकाबला करने की निर्भरता। इस समस्या का समाधान है:

$V=V_{0}+AR^{1/2}P_{1/2}(\cos \theta _{0})\,$

कहाँ $V=V_{0}\,$ (समविभव सतह) के मान पर मौजूद है $\theta _{0}$ (आर की परवाह किए बिना) एक समविभव शंकु का उत्पादन करता है। के लिए आवश्यक कोण $V=V_{0}\,$ सभी के लिए R एक शून्य है $P_{1/2}(\cos \theta _{0})\,$ 0 और के बीच $\pi \,$ जो 130.7099° पर केवल एक है। इस कोण का पूरक टेलर कोण है।