वैन एम्डे बोस ट्री
This article's tone or style may not reflect the encyclopedic tone used on Wikipedia. (May 2021) (Learn how and when to remove this template message) |
| van Emde Boas tree | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | Non-binary tree | |||||||||||||||
| Invented | 1975 | |||||||||||||||
| Invented by | Peter van Emde Boas | |||||||||||||||
| Time complexity in big O notation | ||||||||||||||||
| ||||||||||||||||
एक वैन एम्डे बोस कदम (Dutch pronunciation: [vɑn ˈɛmdə ˈboːɑs]), जिसे वीईबी ट्री या वैन एम्डे बोस प्राथमिकता कतार के रूप में भी जाना जाता है, एक ट्री डेटा संरचना है जो एक सहयोगी सरणी को लागू करती है m-बिट पूर्णांक कुंजियाँ। इसका आविष्कार 1975 में डच कंप्यूटर वैज्ञानिक पीटर वैन एम्डे बोस के नेतृत्व वाली एक टीम ने किया था।[1] यह सभी कार्य निष्पादित करता है O(log m) समय (यह मानते हुए कि a m बिट ऑपरेशन निरंतर समय में किया जा सकता है), या समकक्ष में O(log log M) समय, कहाँ M = 2m पेड़ में संग्रहित किया जा सकने वाला सबसे बड़ा तत्व है। पैरामीटर M को पेड़ में संग्रहीत तत्वों की वास्तविक संख्या के साथ भ्रमित नहीं होना चाहिए, जिसके द्वारा अन्य पेड़ डेटा-संरचनाओं का प्रदर्शन अक्सर मापा जाता है।
वीईबी वृक्ष की अंतरिक्ष दक्षता ख़राब है। उदाहरण के लिए, 32-बिट पूर्णांक संग्रहीत करने के लिए (अर्थात्, कब m=32), उसकी आवश्यकता हैं M=232 भंडारण के टुकड़े। हालाँकि, समान रूप से अच्छी समय दक्षता और स्थान के साथ समान डेटा संरचनाएँ O(n) अस्तित्व में है, कहाँ n संग्रहीत तत्वों की संख्या है।
समर्थित संचालन
एक वीईबी एक ऑर्डर किए गए एसोसिएटिव ऐरे के संचालन का समर्थन करता है, जिसमें सामान्य एसोसिएटिव ऐरे ऑपरेशंस के साथ-साथ दो और ऑर्डर ऑपरेशंस, फाइंडनेक्स्ट और फाइंडप्रिवियस शामिल हैं:[2]
- सम्मिलित करें: एक के साथ एक कुंजी/मूल्य युग्म सम्मिलित करें m-बिट कुंजी
- हटाएँ: किसी दी गई कुंजी से कुंजी/मान युग्म को हटाएँ
- लुकअप: किसी दी गई कुंजी से संबद्ध मान ज्ञात करें
- अगला खोजें: सबसे छोटी कुंजी के साथ कुंजी/मान जोड़ी ढूंढें जो दी गई कुंजी से बड़ी हो k
- पिछला खोजें: सबसे बड़ी कुंजी के साथ कुंजी/मूल्य जोड़ी ढूंढें जो दी गई कुंजी से छोटी है k
एक वीईबी ट्री न्यूनतम और अधिकतम संचालन का भी समर्थन करता है, जो क्रमशः ट्री में संग्रहीत न्यूनतम और अधिकतम तत्व लौटाता है।[3] ये दोनों अंदर भागते हैं O(1) समय, चूंकि न्यूनतम और अधिकतम तत्व प्रत्येक पेड़ में विशेषताओं के रूप में संग्रहीत होते हैं।
फ़ंक्शन
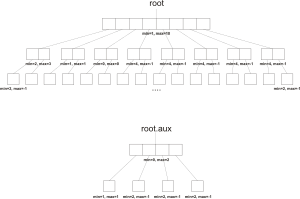
सरलता के लिए, चलो log2 m = k कुछ पूर्णांक k के लिए। परिभाषित करना M = 2m. एक वीईबी पेड़ T ब्रह्मांड पर {0, ..., M−1} में एक रूट नोड है जो एक सरणी संग्रहीत करता है T.children लंबाई का √M. T.children[i] एक वीईबी वृक्ष का सूचक है जो मूल्यों के लिए जिम्मेदार है {i√M, ..., (i+1)√M−1}. इसके अतिरिक्त, T दो मान संग्रहीत करता है T.min और T.max साथ ही एक सहायक वीईबी वृक्ष T.aux.
डेटा को वीईबी ट्री में निम्नानुसार संग्रहीत किया जाता है: वर्तमान में ट्री में सबसे छोटा मान संग्रहीत किया जाता है T.min और सबसे बड़ा मान संग्रहीत किया जाता है T.max. ध्यान दें कि T.min को vEB ट्री में कहीं और संग्रहीत नहीं किया गया है, जबकि T.max है। यदि T खाली है तो हम उस परिपाटी का उपयोग करते हैं T.max=−1 और T.min=M. कोई अन्य मान x उपवृक्ष में संग्रहीत है T.children[i] कहाँ i = ⌊x/√M⌋. सहायक वृक्ष T.auxइस बात पर नज़र रखता है कि कौन से बच्चे खाली नहीं हैं, इसलिए T.aux में मान j यदि और केवल यदि शामिल है T.children[j] गैर-रिक्त है.
अगला खोजें
संचालन FindNext(T, x) जो वीईबी ट्री में किसी तत्व x के उत्तराधिकारी की खोज करता है वह निम्नानुसार आगे बढ़ता है: यदि x<T.min तो खोज पूरी हो गई है, और उत्तर है T.min. अगर x≥T.max तो अगला तत्व मौजूद नहीं है, एम लौटें। अन्यथा, चलो i = ⌊x/√M⌋. अगर x<T.children[i].max तो खोजा जा रहा मान इसमें समाहित है T.children[i] इसलिए खोज पुनरावर्ती रूप से आगे बढ़ती है T.children[i]. अन्यथा, हम i मान के उत्तराधिकारी की खोज करते हैं T.aux. यह हमें पहले उपवृक्ष का सूचकांक j देता है जिसमें x से बड़ा तत्व होता है। एल्गोरिथ्म फिर वापस आता है T.children[j].min. बच्चों के स्तर पर पाए जाने वाले तत्व को एक संपूर्ण अगला तत्व बनाने के लिए उच्च बिट्स के साथ बनाने की आवश्यकता होती है।
फ़ंक्शन फाइंडनेक्स्ट(टी, एक्स)
यदि x < T.min तो
वापसी टी.मिनट
यदि x ≥ T.max तो // कोई अगला तत्व नहीं
वापसी एम
मैं = मंजिल(x/√M)
लो = एक्स मॉड √M
यदि lo < T.children[i].max तो
वापस करना (√M i) + FindNext(T.children[i], lo)
जे = फाइंडनेक्स्ट(टी.ऑक्स, आई)
वापस करना (√M जे) + टी.चिल्ड्रन[जे].मिन
अंत
ध्यान दें कि, किसी भी स्थिति में, एल्गोरिदम कार्य करता है O(1) काम करता है और फिर संभवतः आकार के ब्रह्मांड में एक उपवृक्ष पर पुनरावृत्ति करता है M1/2 (एक m/2 बिट ब्रह्मांड). यह के चलने के समय की पुनरावृत्ति देता है , जो हल करता है O(log m) = O(log log M).
सम्मिलित करें
कॉल insert(T, x) जो एक मान डालता है x एक वीईबी पेड़ में T निम्नानुसार संचालित होता है:
- यदि T खाली है तो हम सेट करते हैं T.min = T.max = x और हमारा काम हो गया.
- अन्यथा, यदि x<T.min फिर हम डालते हैं T.min उपवृक्ष में i के लिए जिम्मेदार T.min और फिर सेट करें T.min = x. अगर T.children[i] पहले खाली था, फिर हम भी डालते हैं i में T.aux
- अन्यथा, यदि x>T.max फिर हम डालते हैं x उपवृक्ष में i के लिए जिम्मेदार x और फिर सेट करें T.max = x. अगर T.children[i] पहले खाली था, फिर हम भी डालते हैं i में T.aux
- अन्यथा, T.min< x < T.max तो हम सम्मिलित करते हैं x उपवृक्ष में i के लिए जिम्मेदार x. अगर T.children[i] पहले खाली था, फिर हम भी डालते हैं i में T.aux.
कोड में:
फ़ंक्शन सम्मिलित करें (टी, एक्स)
यदि T.min > T.max है तो // T खाली है
टी.मिनट = टी.मैक्स = एक्स;
वापस करना
यदि x < T.min तो
स्वैप(एक्स, टी.मिनट)
यदि x > T.max तो
टी.मैक्स = एक्स
मैं = मंजिल(x / √M)
लो = एक्स मॉड √M
सम्मिलित करें(टी.बच्चे[i], लो)
यदि T.children[i].min == T.children[i].max तब
सम्मिलित करें(T.aux, i)
अंत
इस प्रक्रिया की दक्षता की कुंजी यह है कि एक खाली वीईबी पेड़ में एक तत्व डालने में समय लगता है O(1) समय। इसलिए, भले ही एल्गोरिदम कभी-कभी दो पुनरावर्ती कॉल करता है, यह केवल तब होता है जब पहली पुनरावर्ती कॉल एक खाली सबट्री में थी। इससे उसी रनिंग टाइम की पुनरावृत्ति होती है पहले जैसा।
हटाएं
वीईबी पेड़ों को हटाना सबसे मुश्किल ऑपरेशन है। कॉल Delete(T, x) जो वीईबी ट्री से एक मान x हटाता है T निम्नानुसार संचालित होता है:
- अगर T.min = T.max = x तो x पेड़ में संग्रहीत एकमात्र तत्व है और हम सेट करते हैं T.min = M और T.max = −1 यह इंगित करने के लिए कि पेड़ खाली है।
- अन्यथा, यदि x == T.min फिर हमें वीईबी ट्री में दूसरा सबसे छोटा मान y ढूंढना होगा, इसे इसके वर्तमान स्थान से हटाना होगा, और सेट करना होगा T.min=y. दूसरा सबसे छोटा मान y है T.children[T.aux.min].min, इसलिए इसे पाया जा सकता है O(1) समय। हम y को उस उपवृक्ष से हटा देते हैं जिसमें यह शामिल है।
- अगर x≠T.min और x≠T.max फिर हम सबट्री से x हटाते हैं T.children[i] जिसमें x शामिल है।
- अगर x == T.max तो हमें वीईबी ट्री और सेट में दूसरा सबसे बड़ा मान y ढूंढना होगा T.max=y. हम पिछले मामले की तरह x को हटाकर शुरुआत करते हैं। तब मान y या तो है T.min या T.children[T.aux.max].max, इसलिए इसे पाया जा सकता है O(1) समय।
- उपरोक्त किसी भी मामले में, यदि हम किसी उपवृक्ष से अंतिम तत्व x या y हटाते हैं T.children[i] फिर हम i को भी हटा देते हैं T.aux.
कोड में:
फ़ंक्शन हटाएं(टी, एक्स)
यदि T.min == T.max == x तो
टी.मिन = एम
टी.मैक्स = −1
वापस करना
यदि x == T.min तो
नमस्ते = T.aux.min * √M
जे = टी.ऑक्स.मिन
टी.मिनट = एक्स = हाय + टी.चिल्ड्रेन[जे].मिनट
मैं = मंजिल(x / √M)
लो = एक्स मॉड √M
हटाएं(टी.बच्चे[i], लो)
यदि T.children[i] तब खाली है
हटाएँ(T.aux, i)
यदि x == T.max तो
यदि T.aux खाली है तो
टी.मैक्स = टी.मिनट
अन्य
हाय = टी.ऑक्स.मैक्स * √M
जे = टी.ऑक्स.मैक्स
टी.मैक्स = हाय + टी.चिल्ड्रेन[जे].मैक्स
अंत
फिर, इस प्रक्रिया की दक्षता इस तथ्य पर निर्भर करती है कि केवल एक तत्व वाले वीईबी पेड़ को हटाने में केवल निरंतर समय लगता है। विशेष रूप से, दूसरा डिलीट कॉल केवल तभी निष्पादित होता है जब x एकमात्र तत्व था T.children[i] हटाने से पहले.
चर्चा
यह धारणा log m एक पूर्णांक अनावश्यक है. संचालन और केवल उच्च-क्रम लेकर प्रतिस्थापित किया जा सकता है ⌈m/2⌉ और निचला क्रम ⌊m/2⌋ का x, क्रमश। किसी भी मौजूदा मशीन पर, यह विभाजन या शेष गणना से अधिक कुशल है।
व्यावहारिक कार्यान्वयन में, विशेष रूप से शिफ्ट-बाय-के वाली मशीनों पर और पहले शून्य निर्देश ढूंढने पर, एक बार बिट सरणी पर स्विच करके प्रदर्शन में और सुधार किया जा सकता है m शब्द के बराबर (डेटा प्रकार) (या उसका एक छोटा गुणक) तक पहुंच जाता है। चूँकि एक ही शब्द पर सभी ऑपरेशन निरंतर समय के होते हैं, यह एसिम्प्टोटिक प्रदर्शन को प्रभावित नहीं करता है, लेकिन यह अधिकांश पॉइंटर स्टोरेज और कई पॉइंटर डेरेफ़रेंस से बचता है, इस ट्रिक के साथ समय और स्थान में महत्वपूर्ण व्यावहारिक बचत प्राप्त करता है।
वीईबी वृक्षों का एक स्पष्ट अनुकूलन खाली उपवृक्षों को त्यागना है। यह वीईबी पेड़ों को काफी कॉम्पैक्ट बनाता है जब उनमें कई तत्व होते हैं, क्योंकि जब तक उनमें कुछ जोड़ने की आवश्यकता नहीं होती तब तक कोई उप-पेड़ नहीं बनाया जाता है। प्रारंभ में, जोड़ा गया प्रत्येक तत्व लगभग बनाता है log(m) नए पेड़ों के बारे में m/2 सूचक सभी एक साथ। जैसे-जैसे पेड़ बढ़ता है, अधिक से अधिक उप-वृक्षों का पुन: उपयोग किया जाता है, विशेषकर बड़े पेड़ों का। के एक पूर्ण वृक्ष में Mतत्व, केवल O(M) स्थान का उपयोग किया जाता है. इसके अलावा, बाइनरी सर्च ट्री के विपरीत, इस स्थान का अधिकांश उपयोग डेटा संग्रहीत करने के लिए किया जा रहा है: यहां तक कि अरबों तत्वों के लिए, पूर्ण वीईबी ट्री में पॉइंटर्स की संख्या हजारों में होती है।
ऊपर वर्णित कार्यान्वयन पॉइंटर्स का उपयोग करता है और कुल स्थान घेरता है O(M) = O(2m), प्रमुख ब्रह्मांड के आकार के समानुपाती। इस प्रकार इसे देखा जा सकता है। पुनरावृत्ति है . उसका समाधान करने से यह होगा . सौभाग्य से, कोई इसे दिखा भी सकता है S(M) = M−2 प्रेरण द्वारा.[4]
== समान संरचनाएं == O(M)}') वीईबी पेड़ों का अंतरिक्ष उपयोग एक बहुत बड़ा ओवरहेड है जब तक कि चाबियों के ब्रह्मांड का एक बड़ा हिस्सा संग्रहीत नहीं किया जा रहा हो। यही एक कारण है कि वीईबी पेड़ व्यवहार में लोकप्रिय नहीं हैं। बच्चों को किसी अन्य डेटा संरचना में संग्रहीत करने के लिए उपयोग की जाने वाली सरणी को बदलकर इस सीमा को संबोधित किया जा सकता है। एक संभावना यह है कि प्रति स्तर केवल एक निश्चित संख्या में बिट्स का उपयोग किया जाए, जिसके परिणामस्वरूप एक प्रयास होता है। वैकल्पिक रूप से, प्रत्येक सरणी को हैश तालिका द्वारा प्रतिस्थापित किया जा सकता है, जिससे स्थान कम हो जाता है O(n log log M) (कहाँ n डेटा संरचना को यादृच्छिक बनाने की कीमत पर डेटा संरचना में संग्रहीत तत्वों की संख्या है)।
एक्स-फास्ट ट्राई और अधिक जटिल वाई-फास्ट प्रयास में वीईबी पेड़ों के लिए तुलनीय अद्यतन और क्वेरी समय होता है और उपयोग किए गए स्थान को कम करने के लिए यादृच्छिक हैश तालिकाओं का उपयोग किया जाता है। एक्स-फास्ट का उपयोग करने की कोशिश करता है O(n log M) स्थान जबकि y-fast उपयोग करने का प्रयास करता है O(n) अंतरिक्ष।
कार्यान्वयन
इसाबेल (प्रमाण सहायक) में एक सत्यापित कार्यान्वयन है।[5] कार्यात्मक शुद्धता और समय सीमा दोनों सिद्ध हैं। कुशल अनिवार्य मानक एमएल कोड उत्पन्न किया जा सकता है।
यह भी देखें
संदर्भ
- ↑ Peter van Emde Boas: Preserving order in a forest in less than logarithmic time (Proceedings of the 16th Annual Symposium on Foundations of Computer Science 10: 75-84, 1975)
- ↑ Gudmund Skovbjerg Frandsen: Dynamic algorithms: Course notes on van Emde Boas trees (PDF) (University of Aarhus, Department of Computer Science)
- ↑ Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Third Edition. MIT Press, 2009. ISBN 978-0-262-53305-8. Chapter 20: The van Emde Boas tree, pp. 531–560.
- ↑ Rex, A. "वैन एम्डे बोस पेड़ों की अंतरिक्ष जटिलता का निर्धारण". Retrieved 2011-05-27.
- ↑ Ammer, Thomas; Lammich, Peter. "एम्डे बोस पेड़ों की". Archive of Formal Proofs. Retrieved 26 November 2021.
अग्रिम पठन
- Erik Demaine, Sam Fingeret, Shravas Rao, Paul Christiano. Massachusetts Institute of Technology. 6.851: Advanced Data Structures (Spring 2012). Lecture 11 notes. March 22, 2012.
- van Emde Boas, P.; Kaas, R.; Zijlstra, E. (1976). "Design and implementation of an efficient priority queue". Mathematical Systems Theory. 10: 99–127. doi:10.1007/BF01683268.