निरंतर समान वितरण

${\mathbf {\text{Continuous uniform distribution}}}$${\mathbf {{\text{with parameters }}{\mathcal {a}}{\text{ and }}{\mathcal {b}}}}$

Probability density function 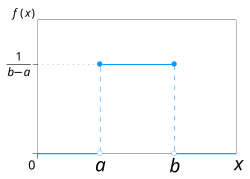Using maximum convention
Cumulative distribution function
Notation	${\mathcal {U}}_{[a,b]}$
Parameters	$-\infty <a<b<\infty$
Support	$[a,b]$
PDF	${\begin{cases}{\frac {1}{b-a}}&{\text{for }}x\in [a,b]\\0&{\text{otherwise}}\end{cases}}$
CDF	${\begin{cases}0&{\text{for }}x<a\\{\frac {x-a}{b-a}}&{\text{for }}x\in [a,b]\\1&{\text{for }}x>b\end{cases}}$
Mean	${\tfrac {1}{2}}(a+b)$
Median	${\tfrac {1}{2}}(a+b)$
Mode	${\text{any value in }}(a,b)$
Variance	${\tfrac {1}{12}}(b-a)^{2}$
MAD	${\tfrac {1}{4}}(b-a)$
Skewness	$0$
Ex. kurtosis	$-{\tfrac {6}{5}}$
Entropy	$\ln(b-a)$
MGF	${\begin{cases}{\frac {\mathrm {e} ^{tb}-\mathrm {e} ^{ta}}{t(b-a)}}&{\text{for }}t\neq 0\\1&{\text{for }}t=0\end{cases}}$
CF	${\begin{cases}{\frac {\mathrm {e} ^{\mathrm {i} tb}-\mathrm {e} ^{\mathrm {i} ta}}{\mathrm {i} t(b-a)}}&{\text{for }}t\neq 0\\1&{\text{for }}t=0\end{cases}}$

संभाव्यता सिद्धांत और सांख्यिकी में, निरंतर समान वितरण या आयताकार वितरण सममित वितरण संभाव्यता वितरण का एक परिवार है। ऐसा वितरण एक प्रयोग का वर्णन करता है जहां एक मनमाना परिणाम होता है जो कुछ सीमाओं के बीच होता है। सीमाएं मापदंडों द्वारा परिभाषित की जाती हैं, $a$ और $b,$ जो न्यूनतम और अधिकतम मान हैं। अंतराल या तो बंद अंतराल हो सकता है (यानी) $[a,b]$) या खुला अंतराल (अर्थात् $(a,b)$). इसलिए, वितरण अक्सर संक्षिप्त किया जाता है $U(a,b),$ कहाँ $U$ समान वितरण के लिए खड़ा है।सीमाओं के बीच का अंतर अंतराल की लंबाई को परिभाषित करता है; वितरण के समर्थन (गणित) पर समान लंबाई के सभी अंतराल (गणित) समान रूप से संभावित हैं। यह एक यादृच्छिक चर के लिए अधिकतम एन्ट्रापी संभाव्यता वितरण है $X$ इसके अलावा किसी अन्य बाधा के तहत यह वितरण के समर्थन में शामिल नहीं है।

परिभाषाएँ

संभाव्यता घनत्व फ़ंक्शन

सतत समान वितरण का संभाव्यता घनत्व कार्य है:

$f(x)={\begin{cases}{\frac {1}{b-a}}&{\text{for }}a\leq x\leq b,\\[8pt]0&{\text{for }}x<a\ {\text{ or }}\ x>b.\end{cases}}$

के मूल्य $f(x)$ दो सीमाओं पर $a$ और $b$ आमतौर पर महत्वहीन होते हैं, क्योंकि वे के मूल्य में परिवर्तन नहीं करते हैं ${\textstyle \int _{c}^{d}f(x)dx}$ किसी भी अंतराल पर $[c,d],$ न ही का ${\textstyle \int _{a}^{b}xf(x)dx,}$ न ही किसी उच्चतर क्षण का. कभी-कभी उन्हें शून्य होना चुना जाता है, और कभी-कभी शून्य होना चुना जाता है ${\tfrac {1}{b-a}}.$ उत्तरार्द्ध अधिकतम संभावना की विधि द्वारा अनुमान के संदर्भ में उपयुक्त है। फूरियर विश्लेषण के संदर्भ में, कोई इसका मूल्य ले सकता है $f(a)$ या $f(b)$ होना ${\tfrac {1}{2(b-a)}},$ क्योंकि तब इस समान फ़ंक्शन के कई अभिन्न परिवर्तनों का व्युत्क्रम परिवर्तन फ़ंक्शन को वापस लाएगा, न कि एक फ़ंक्शन जो लगभग हर जगह समान है, अर्थात शून्य माप सिद्धांत वाले बिंदुओं के एक सेट को छोड़कर। साथ ही, यह साइन फ़ंक्शन के अनुरूप है, जिसमें ऐसी कोई अस्पष्टता नहीं है।

कोई भी संभाव्यता घनत्व फ़ंक्शन एकीकृत होता है $1,$ इसलिए निरंतर समान वितरण की संभाव्यता घनत्व फ़ंक्शन को ग्राफ़िक रूप से एक आयत के रूप में चित्रित किया गया है $b-a$ आधार लंबाई है और ${\tfrac {1}{b-a}}$ ऊंचाई है. जैसे-जैसे आधार की लंबाई बढ़ती है, ऊंचाई (वितरण सीमाओं के भीतर किसी विशेष मूल्य पर घनत्व) कम हो जाती है। माध्य की दृष्टि से $\mu$ और विचरण $\sigma ^{2},$ निरंतर समान वितरण की संभाव्यता घनत्व फ़ंक्शन है:

$f(x)={\begin{cases}{\frac {1}{2\sigma {\sqrt {3}}}}&{\text{for }}-\sigma {\sqrt {3}}\leq x-\mu \leq \sigma {\sqrt {3}},\\0&{\text{otherwise}}.\end{cases}}$

संचयी वितरण फ़ंक्शन

सतत समान वितरण का संचयी वितरण कार्य है:

$F(x)={\begin{cases}0&{\text{for }}x<a,\\[8pt]{\frac {x-a}{b-a}}&{\text{for }}a\leq x\leq b,\\[8pt]1&{\text{for }}x>b.\end{cases}}$

इसका उलटा है:

$F^{-1}(p)=a+p(b-a)\quad {\text{ for }}0<p<1.$

माध्य की दृष्टि से $\mu$ और विचरण $\sigma ^{2},$ सतत समान वितरण का संचयी वितरण कार्य है:

$F(x)={\begin{cases}0&{\text{for }}x-\mu <-\sigma {\sqrt {3}},\\{\frac {1}{2}}\left({\frac {x-\mu }{\sigma {\sqrt {3}}}}+1\right)&{\text{for }}-\sigma {\sqrt {3}}\leq x-\mu <\sigma {\sqrt {3}},\\1&{\text{for }}x-\mu \geq \sigma {\sqrt {3}};\end{cases}}$

इसका व्युत्क्रम है:

$F^{-1}(p)=\sigma {\sqrt {3}}(2p-1)+\mu \quad {\text{ for }}0\leq p\leq 1.$

उदाहरण 1. सतत ​​समान वितरण फ़ंक्शन का उपयोग करना

एक यादृच्छिक चर के लिए $X\sim U(0,23),$ पाना $P(2<X<18):$

$P(2<X<18)=(18-2)\cdot {\frac {1}{23-0}}={\frac {16}{23}}.$

निरंतर समान वितरण फ़ंक्शन के चित्रमय प्रतिनिधित्व में $[f(x){\text{ vs }}x],$ निर्दिष्ट सीमा के भीतर वक्र के नीचे का क्षेत्र, संभाव्यता प्रदर्शित करते हुए, एक आयत है। उपरोक्त विशिष्ट उदाहरण के लिए, आधार होगा $16,$ और ऊंचाई होगी ${\tfrac {1}{23}}.$

उदाहरण 2. निरंतर समान वितरण फ़ंक्शन (सशर्त) का उपयोग करना

एक यादृच्छिक चर के लिए $X\sim U(0,23),$ पाना $P(X>12\ |\ X>8):$

$P(X>12\ |\ X>8)=(23-12)\cdot {\frac {1}{23-8}}={\frac {11}{15}}.$

उपरोक्त उदाहरण निरंतर समान वितरण के लिए एक सशर्त संभाव्यता मामला है: यह देखते हुए $X>8$ सत्य है, इसकी क्या प्रायिकता है $X>12?$ सशर्त संभाव्यता नमूना स्थान को बदल देती है, इसलिए एक नई अंतराल लंबाई $b-a'$ की गणना करनी होगी, कहां $b=23$ और $a'=8.$ग्राफिकल प्रतिनिधित्व अभी भी उदाहरण 1 का अनुसरण करेगा, जहां निर्दिष्ट सीमा के भीतर वक्र के नीचे का क्षेत्र संभाव्यता प्रदर्शित करता है; आयत का आधार होगा $11,$ और ऊंचाई होगी ${\tfrac {1}{15}}.$

कार्य उत्पन्न करना

क्षण उत्पन्न करने वाला कार्य

सतत एकसमान वितरण का क्षण-उत्पादक कार्य है:

$M_{X}=\mathrm {E} (\mathrm {e} ^{tX})=\int _{a}^{b}\mathrm {e} ^{tx}{\frac {dx}{b-a}}={\frac {\mathrm {e} ^{tb}-\mathrm {e} ^{ta}}{t(b-a)}}={\frac {B^{t}-A^{t}}{t(b-a)}},$

जिससे हम कच्चे क्षणों की गणना कर सकते हैं $m_{k}:$

$m_{1}={\frac {a+b}{2}},$

$m_{2}={\frac {a^{2}+ab+b^{2}}{3}},$

$m_{k}={\frac {\sum _{i=0}^{k}a^{i}b^{k-i}}{k+1}}.$

निरंतर समान वितरण के बाद एक यादृच्छिक चर के लिए, अपेक्षित मूल्य है $m_{1}={\tfrac {a+b}{2}},$ और भिन्नता है $m_{2}-m_{1}^{2}={\tfrac {(b-a)^{2}}{12}}.$ विशेष मामले के लिए $a=-b,$ निरंतर समान वितरण की संभाव्यता घनत्व फ़ंक्शन है:

$f(x)={\begin{cases}{\frac {1}{2b}}&{\text{for }}-b\leq x\leq b,\\[8pt]0&{\text{otherwise}};\end{cases}}$

क्षण-उत्पन्न करने वाला कार्य सरल रूप में कम हो जाता है:

$M_{X}={\frac {\sinh bt}{bt}}.$

क्यूमुलेंट-जनरेटिंग फ़ंक्शन

के लिए $n\geq 2,$ द $n$अंतराल पर निरंतर समान वितरण का -वाँ संचयी $[-{\tfrac {1}{2}},{\tfrac {1}{2}}]$ है ${\tfrac {B_{n}}{n}},$ कहाँ $B_{n}$ है $n$-वां बर्नौली संख्या ।

मानक समान वितरण

मापदंडों के साथ निरंतर समान वितरण $a=0$ और $b=1,$ अर्थात। $U(0,1),$ मानक समान वितरण कहलाता है।

मानक समान वितरण की एक दिलचस्प संपत्ति यह है कि यदि $u_{1}$ एक मानक समान वितरण है, तो ऐसा ही होता है $1-u_{1}.$ इस संपत्ति का उपयोग अन्य चीजों के अलावा, विपरीत भिन्नताएँ उत्पन्न करने के लिए किया जा सकता है। दूसरे शब्दों में, इस संपत्ति को उलटा विधि के रूप में जाना जाता है जहां निरंतर मानक समान वितरण का उपयोग किसी अन्य निरंतर वितरण के लिए सांख्यिकीय यादृच्छिकता उत्पन्न करने के लिए किया जा सकता है।अगर $u_{1}$ मानक समान वितरण के साथ एक समान यादृच्छिक संख्या है, अर्थात $U(0,1),$ तब $x=F^{-1}(u_{1})$ एक यादृच्छिक संख्या उत्पन्न करता है $x$ निर्दिष्ट संचयी वितरण फ़ंक्शन के साथ किसी भी निरंतर वितरण से $F.$

अन्य कार्यों से संबंध

जब तक संक्रमण बिंदुओं पर समान परंपराओं का पालन किया जाता है, तब तक निरंतर समान वितरण की संभाव्यता घनत्व फ़ंक्शन को हेविसाइड चरण फ़ंक्शन के संदर्भ में भी व्यक्त किया जा सकता है:

$f(x)={\frac {\operatorname {H} (x-a)-\operatorname {H} (x-b)}{b-a}},$

या आयत फ़ंक्शन के संदर्भ में:

$f(x)={\frac {1}{b-a}}\ \operatorname {rect} \left({\frac {x-{\frac {a+b}{2}}}{b-a}}\right).$

साइन फ़ंक्शन के संक्रमण बिंदु पर कोई अस्पष्टता नहीं है। संक्रमण बिंदुओं पर अर्ध-अधिकतम परिपाटी का उपयोग करते हुए, निरंतर समान वितरण को साइन फ़ंक्शन के संदर्भ में इस प्रकार व्यक्त किया जा सकता है:

$f(x)={\frac {\operatorname {sgn} {(x-a)}-\operatorname {sgn} {(x-b)}}{2(b-a)}}.$

गुण

क्षण

सतत एकसमान वितरण का माध्य (पहला कच्चा क्षण (गणित)) है:

$E(X)=\int _{a}^{b}x{\frac {dx}{b-a}}={\frac {b^{2}-a^{2}}{2(b-a)}}.$

इस वितरण का दूसरा कच्चा क्षण है:

$E(X^{2})=\int _{a}^{b}x^{2}{\frac {dx}{b-a}}={\frac {b^{3}-a^{3}}{3(b-a)}}.$

सामान्य तौर पर, $n$-इस वितरण का कच्चा क्षण है:

$E(X^{n})=\int _{a}^{b}x^{n}{\frac {dx}{b-a}}={\frac {b^{n+1}-a^{n+1}}{(n+1)(b-a)}}.$

इस वितरण का विचरण (दूसरा केंद्रीय क्षण) है:

$V(X)=E\left({\big (}X-E(X){\big )}^{2}\right)=\int _{a}^{b}\left(x-{\frac {a+b}{2}}\right)^{2}{\frac {dx}{b-a}}={\frac {(b-a)^{2}}{12}}.$

आदेश आँकड़े

होने देना $X_{1},...,X_{n}$ एक आई.आई.डी. बनें से नमूना $U(0,1),$ और जाने $X_{(k)}$ हो $k$इस नमूने से -वें क्रम का आँकड़ा।

$X_{(k)}$ मापदंडों के साथ बीटा वितरण है $k$ और $n-k+1.$

अपेक्षित मूल्य है:

$\operatorname {E} (X_{(k)})={k \over n+1}.$

Q-Q प्लॉट बनाते समय यह तथ्य उपयोगी होता है।

भिन्नता है:

$\operatorname {V} (X_{(k)})={k(n-k+1) \over (n+1)^{2}(n+2)}.$

See also: Order statistic § Probability distributions of order statistics

एकरूपता

संभावना है कि एक निरंतर समान रूप से वितरित यादृच्छिक चर निश्चित लंबाई के किसी भी अंतराल के भीतर आता है, अंतराल के स्थान से स्वतंत्र है (लेकिन यह अंतराल के आकार पर निर्भर है) $(\ell )$), जब तक अंतराल वितरण के समर्थन में निहित है।

वास्तव में, यदि $X\sim U(a,b)$ और अगर $[x,x+\ell ]$ का एक उपअंतराल है $[a,b]$ निश्चित के साथ $\ell >0,$ तब:

$P{\big (}X\in [x,x+\ell ]{\big )}=\int _{x}^{x+\ell }{\frac {dy}{b-a}}={\frac {\ell }{b-a}},$

जो स्वतंत्र है $x.$ यह तथ्य वितरण के नाम को प्रेरित करता है।

बोरेल सेट का सामान्यीकरण

इस वितरण को अंतरालों की तुलना में अधिक जटिल सेटों के लिए सामान्यीकृत किया जा सकता है। होने देना $S$ सकारात्मक, परिमित लेब्सेग माप का एक बोरेल सेट बनें $\lambda (S),$ अर्थात। $0<\lambda (S)<+\infty .$ गणवेश वितरण चालू $S$ संभाव्यता घनत्व फ़ंक्शन को शून्य के बाहर परिभाषित करके निर्दिष्ट किया जा सकता है $S$ और लगातार बराबर ${\tfrac {1}{\lambda (S)}}$ पर $S.$

संबंधित वितरण

• यदि X का मानक समान वितरण है, तो व्युत्क्रम परिवर्तन नमूनाकरण विधि द्वारा, Y = - λ⁻¹ ln(X) का (दर) पैरामीटर λ के साथ एक घातीय वितरण है।
• यदि X का मानक समान वितरण है, तो Y = Xⁿ में पैरामीटर (1/n,1) के साथ बीटा वितरण है। जैसे की,
• मानक समान वितरण बीटा वितरण का एक विशेष मामला है, पैरामीटर (1,1) के साथ।
• इरविन-हॉल वितरण n i.i.d. का योग है। यू(0,1) वितरण।
• दो स्वतंत्र, समान रूप से वितरित, समान वितरण का योग एक सममित त्रिकोणीय वितरण उत्पन्न करता है।
• दो आई.आई.डी. के बीच की दूरी समान यादृच्छिक चर का भी त्रिकोणीय वितरण होता है, हालांकि सममित नहीं।

सांख्यिकीय अनुमान

मापदंडों का अनुमान

अधिकतम का अनुमान

न्यूनतम-विचरण निष्पक्ष अनुमानक

Main article: German tank problem

पर एक समान वितरण दिया गया $[0,b]$ अज्ञात के साथ $b,$ अधिकतम के लिए UMVU|न्यूनतम-विचरण निष्पक्ष अनुमानक (UMVUE) है:

${\hat {b}}_{\text{UMVU}}={\frac {k+1}{k}}m=m+{\frac {m}{k}},$

कहाँ $m$ नमूना अधिकतम है और $k$ नमूना आकार है, प्रतिस्थापन के बिना नमूनाकरण (हालांकि यह अंतर लगभग निश्चित रूप से निरंतर वितरण के लिए कोई फर्क नहीं पड़ता है)। यह समान कारणों से समान वितरण (असतत)#अधिकतम का अनुमान का अनुसरण करता है, और इसे अधिकतम अंतर अनुमान के एक बहुत ही सरल मामले के रूप में देखा जा सकता है। द्वितीय विश्व युद्ध के दौरान जर्मन टैंक उत्पादन के अनुमानों के लिए अधिकतम अनुमान लागू करने के कारण, इस समस्या को आमतौर पर जर्मन टैंक समस्या के रूप में जाना जाता है।

अधिकतम संभावना अनुमानक

अधिकतम संभावना अनुमानक है:

${\hat {b}}_{ML}=m,$

कहाँ $m$ नमूना अधिकतम है, इसे भी दर्शाया गया है $m=X_{(n)},$ नमूने का अधिकतम ऑर्डर आँकड़ा।

क्षण अनुमानक की विधि

क्षणों की विधि (सांख्यिकी) अनुमानक है:

${\hat {b}}_{MM}=2{\bar {X}},$

कहाँ ${\bar {X}}$ नमूना माध्य है.

मध्यबिंदु का अनुमान

वितरण का मध्यबिंदु, ${\tfrac {a+b}{2}},$ समान वितरण का माध्य और मध्यिका दोनों है। यद्यपि नमूना माध्य और नमूना माध्यिका दोनों ही मध्यबिंदु के निष्पक्ष अनुमानक हैं, इनमें से कोई भी नमूना मध्य-सीमा के समान दक्षता (सांख्यिकी) नहीं है, यानी नमूना अधिकतम और नमूना न्यूनतम का अंकगणितीय माध्य, जो कि यूएमवीयू अनुमानक है मध्यबिंदु (और अधिकतम संभावना अनुमान भी)।

आत्मविश्वास अंतराल

अधिकतम के लिए

होने देना $X_{1},X_{2},X_{3},...,X_{n}$ से एक नमूना हो $U_{[0,L]},$ कहाँ $L$ जनसंख्या में अधिकतम मान है। तब $X_{(n)}=\max(X_{1},X_{2},X_{3},...,X_{n})$ लेब्सग्यू-बोरेल-घनत्व है $f={\frac {d\Pr _{X_{(n)}}}{d\lambda }}:$

$f(t)=n{\frac {1}{L}}\left({\frac {t}{L}}\right)^{n-1}\!=n{\frac {t^{n-1}}{L^{n}}}1\!\!1_{[0,L]}(t),$ कहाँ $1\!\!1_{[0,L]}$ का सूचक कार्य है $[0,L].$

पहले दिया गया आत्मविश्वास अंतराल गणितीय रूप से गलत है

$\Pr {\big (}[{\hat {\theta }},{\hat {\theta }}+\varepsilon ]\ni \theta {\big )}\geq 1-\alpha$

के लिए हल नहीं किया जा सकता $\varepsilon$ बिना जानकारी के $\theta$. हालाँकि, कोई भी हल कर सकता है

$\Pr {\big (}[{\hat {\theta }},{\hat {\theta }}(1+\varepsilon )]\ni \theta {\big )}\geq 1-\alpha$ के लिए $\varepsilon \geq (1-\alpha )^{-1/n}-1$ किसी भी अज्ञात लेकिन वैध के लिए $\theta ;$

फिर कोई सबसे छोटा चुनता है $\varepsilon$ उपरोक्त शर्त को पूरा करना संभव है। ध्यान दें कि अंतराल की लंबाई यादृच्छिक चर पर निर्भर करती है ${\hat {\theta }}.$

घटना और अनुप्रयोग

फ़ंक्शन रूप की सरलता के कारण समान वितरण फ़ंक्शन की संभावनाओं की गणना करना आसान है।इसलिए, ऐसे कई अनुप्रयोग हैं जिनके लिए इस वितरण का उपयोग किया जा सकता है जैसा कि नीचे दिखाया गया है: परिकल्पना परीक्षण स्थितियां, यादृच्छिक नमूना मामले, वित्त, आदि। इसके अलावा, आम तौर पर, भौतिक उत्पत्ति के प्रयोग एक समान वितरण का पालन करते हैं (उदाहरण के लिए रेडियोधर्मी रेडियोधर्मी क्षय का उत्सर्जन)।हालाँकि, यह ध्यान रखना महत्वपूर्ण है कि किसी भी अनुप्रयोग में, यह अपरिवर्तनीय धारणा है कि निश्चित लंबाई के अंतराल में गिरने की संभावना स्थिर है।

समान वितरण के लिए अर्थशास्त्र उदाहरण

अर्थशास्त्र के क्षेत्र में, आमतौर पर मांग और विकट:विशेष:खोज/पुनःपूर्ति अपेक्षित सामान्य वितरण का पालन नहीं कर सकती है। परिणामस्वरूप, अन्य वितरण मॉडल का उपयोग संभावनाओं और रुझानों की बेहतर भविष्यवाणी करने के लिए किया जाता है जैसे कि बर्नौली प्रक्रिया। लेकिन वान्के (2008) के अनुसार, जीवन-चक्र मूल्यांकन की शुरुआत में इन्वेंट्री प्रबंधन के लिए समय सीमा | लीड-टाइम की जांच के विशेष मामले में, जब एक पूरी तरह से नए उत्पाद का विश्लेषण किया जा रहा है, तो समान वितरण अधिक उपयोगी साबित होता है।इस स्थिति में, अन्य वितरण व्यवहार्य नहीं हो सकता है क्योंकि नए उत्पाद पर कोई मौजूदा डेटा नहीं है या मांग इतिहास अनुपलब्ध है इसलिए वास्तव में कोई उचित या ज्ञात वितरण नहीं है।इस स्थिति में समान वितरण आदर्श होगा क्योंकि नए उत्पाद के लिए लीड-टाइम (मांग से संबंधित) का यादृच्छिक चर अज्ञात है, लेकिन परिणाम दो मानों की एक प्रशंसनीय सीमा के बीच होने की संभावना है।लीड टाइम|लीड-टाइम इस प्रकार यादृच्छिक चर का प्रतिनिधित्व करेगा। समान वितरण मॉडल से, लीड टाइम|लीड-टाइम से संबंधित अन्य कारकों की गणना की जा सकी जैसे कि चक्र सेवा स्तर और प्रति चक्र कमी। यह भी ध्यान दिया गया कि गणना की सरलता के कारण समान वितरण का भी उपयोग किया गया था।

एक मनमाना वितरण से नमूनाकरण

Main article: Inverse transform sampling

एकसमान वितरण मनमाने वितरण से नमूना लेने के लिए उपयोगी है। एक सामान्य विधि व्युत्क्रम परिवर्तन नमूनाकरण विधि है, जो लक्ष्य यादृच्छिक चर के संचयी वितरण फ़ंक्शन (सीडीएफ) का उपयोग करती है। यह विधि सैद्धान्तिक कार्यों में बहुत उपयोगी है। चूंकि इस पद्धति का उपयोग करने वाले सिमुलेशन के लिए लक्ष्य चर के सीडीएफ को उलटने की आवश्यकता होती है, ऐसे मामलों के लिए वैकल्पिक तरीके तैयार किए गए हैं जहां सीडीएफ बंद रूप में ज्ञात नहीं है। ऐसी ही एक विधि अस्वीकृति नमूनाकरण है।

सामान्य वितरण एक महत्वपूर्ण उदाहरण है जहां व्युत्क्रम परिवर्तन विधि कुशल नहीं है। हालाँकि, एक सटीक विधि है, बॉक्स-मुलर परिवर्तन, जो दो स्वतंत्र समान यादृच्छिक चर को दो स्वतंत्र सामान्य वितरण यादृच्छिक चर में परिवर्तित करने के लिए व्युत्क्रम परिवर्तन का उपयोग करता है।

परिमाणीकरण त्रुटि

Main article: Quantization error

एनालॉग-टू-डिजिटल रूपांतरण में, एक परिमाणीकरण त्रुटि उत्पन्न होती है। यह त्रुटि या तो पूर्णांकन या काट-छांट के कारण है। जब मूल सिग्नल एक कम से कम महत्वपूर्ण बिट | कम से कम महत्वपूर्ण बिट (एलएसबी) से बहुत बड़ा होता है, तो परिमाणीकरण त्रुटि सिग्नल के साथ महत्वपूर्ण रूप से सहसंबद्ध नहीं होती है, और लगभग समान वितरण होता है। इसलिए आरएमएस त्रुटि इस वितरण के भिन्नता से उत्पन्न होती है।

यादृच्छिक भिन्न पीढ़ी

ऐसे कई एप्लिकेशन हैं जिनमें सिमुलेशन प्रयोग चलाना उपयोगी है। कई प्रोग्रामिंग भाषाएं छद्म यादृच्छिक संख्या अनुक्रम उत्पन्न करने के लिए कार्यान्वयन के साथ आती हैं | छद्म यादृच्छिक संख्याएं जो मानक समान वितरण के अनुसार प्रभावी ढंग से वितरित की जाती हैं।

दूसरी ओर, समान रूप से वितरित संख्याओं को अक्सर गैर-समान यादृच्छिक विविधता पीढ़ी के आधार के रूप में उपयोग किया जाता है।

अगर $u$ मानक समान वितरण से नमूना लिया गया मान है, फिर मान $a+(b-a)u$ द्वारा मानकीकृत समान वितरण का अनुसरण करता है $a$ और $b,$ जैसा ऊपर वर्णित है।

इतिहास

जबकि समान वितरण की अवधारणा में ऐतिहासिक उत्पत्ति अनिर्णीत है, यह अनुमान लगाया गया है कि वर्दी शब्द पासा खेल में समसंभाव्यता की अवधारणा से उत्पन्न हुआ है (ध्यान दें कि पासा खेल में असतत समान वितरण होगा और निरंतर समान नमूना स्थान नहीं होगा)। इक्विप्रोबेबिलिटी का उल्लेख जेरोम कार्डानो के लिबर डी लूडो एले में किया गया था, जो 16वीं शताब्दी में लिखा गया एक मैनुअल था और पासे के संबंध में उन्नत संभाव्यता कलन पर विस्तृत था।

यह भी देखें

• पृथक समान वितरण
• बीटा वितरण
• बॉक्स-मुलर परिवर्तन
• संभाव्यता कथानक (बहुविकल्पी)
• क्यू-क्यू प्लॉट
• आयताकार कार्य
• इरविन-हॉल वितरण - पतित मामले में जहां n=1, इरविन-हॉल वितरण 0 और 1 के बीच एक समान वितरण उत्पन्न करता है।
• बेट्स वितरण - इरविन-हॉल वितरण के समान, लेकिन n के लिए पुनर्स्केल किया गया। इरविन-हॉल वितरण की तरह, पतित मामले में जहां n=1, बेट्स वितरण 0 और 1 के बीच एक समान वितरण उत्पन्न करता है।

अग्रिम पठन

• Casella, George; Roger L. Berger (2001), Statistical Inference (2nd ed.), ISBN 978-0-534-24312-8, LCCN 2001025794

बाहरी संबंध

• Online calculator of Uniform distribution (continuous)