एल्गोरिथम अनुमान

एल्गोरिथम अनुमान किसी भी डेटा विश्लेषक के लिए व्यापक रूप से उपलब्ध शक्तिशाली कंप्यूटिंग उपकरणों द्वारा संभव बनाए गए सांख्यिकीय अनुमान तरीकों में नए विकास को इकट्ठा करता है। इस क्षेत्र में आधारशिला कम्प्यूटेशनल शिक्षण सिद्धांत, दानेदार कंप्यूटिंग, जैव सूचना विज्ञान, और, बहुत पहले, संरचनात्मक संभाव्यता हैं (Fraser 1966). मुख्य फोकस एल्गोरिदम पर है जो एक यादृच्छिक घटना के अध्ययन को आधार बनाने वाले आंकड़ों की गणना करता है, साथ ही विश्वसनीय परिणाम देने के लिए उन्हें डेटा की मात्रा भी देनी होती है। यह गणितज्ञों की रुचि को संभाव्यता वितरण के अध्ययन से आंकड़ों के कार्यात्मक गुणों में स्थानांतरित कर देता है, और कंप्यूटर वैज्ञानिकों की रुचि डेटा को संसाधित करने के लिए एल्गोरिदम से उनके द्वारा संसाधित की जाने वाली जानकारी की ओर स्थानांतरित कर देता है।

फिशर पैरामीट्रिक अनुमान समस्या

वितरण कानून के मापदंडों की पहचान के संबंध में, परिपक्व पाठक 20वीं शताब्दी के मध्य में प्रत्ययी वितरण के संदर्भ में उनकी परिवर्तनशीलता की व्याख्या के बारे में लंबे विवादों को याद कर सकते हैं। (Fisher 1956), संरचनात्मक संभावनाएँ (Fraser 1966), पूर्व/पश्च (Ramsey 1925), और इसी तरह। ज्ञानमीमांसीय दृष्टिकोण से, इसमें संभाव्यता की प्रकृति के संबंध में एक साथी विवाद शामिल है: क्या यह घटना की एक भौतिक विशेषता है जिसे यादृच्छिक चर के माध्यम से वर्णित किया जाना है या किसी घटना के बारे में डेटा को संश्लेषित करने का एक तरीका है? बाद वाले को चुनते हुए, फिशर किसी दिए गए यादृच्छिक चर के मापदंडों के एक प्रत्ययी वितरण कानून को परिभाषित करता है जिसे वह इसके विनिर्देशों के नमूने से निकालता है। इस कानून के साथ वह गणना करता है, उदाहरण के लिए "संभावना है कि μ (सामान्य वितरण का मतलब - ओमूर नोट) किसी निर्दिष्ट मूल्य से कम है, या संभावना है कि यह किसी निर्दिष्ट मान के बीच स्थित है, या, संक्षेप में, इसकी संभावना वितरण, देखे गए नमूने के आलोक में"।

क्लासिक समाधान

फिशर ने तुलना में पैरामीटर वितरण की अपनी धारणा के अंतर और श्रेष्ठता का बचाव करने के लिए कड़ा संघर्ष किया समान धारणाएँ, जैसे बेयस का पश्च वितरण, फ़्रेज़र की रचनात्मक संभाव्यता और नेमैन का आत्मविश्वास अंतराल। आधी सदी तक, नेमैन के आत्मविश्वास के अंतराल ने सभी व्यावहारिक उद्देश्यों के लिए जीत हासिल की, जिसका श्रेय संभाव्यता की घटनात्मक प्रकृति को दिया गया। इस परिप्रेक्ष्य के साथ, जब आप गाऊसी चर से निपटते हैं, तो इसका माध्य μ आपके द्वारा देखी जा रही घटना की भौतिक विशेषताओं द्वारा तय किया जाता है, जहां अवलोकन यादृच्छिक ऑपरेटर होते हैं, इसलिए देखे गए मान यादृच्छिक नमूने के विनिर्देश होते हैं। उनकी यादृच्छिकता के कारण, आप निश्चित μ वाले नमूना विशिष्ट अंतरालों से एक निश्चित संभावना के साथ गणना कर सकते हैं कि आप आत्मविश्वास को दर्शाते हैं।

उदाहरण

मान लीजिए कि X एक गाऊसी चर है मापदंडों के साथ $\mu$ और $\sigma ^{2}$ और $\{X_{1},\ldots ,X_{m}\}$ इसका एक नमूना निकाला गया। सांख्यिकी के साथ कार्य करना

$S_{\mu }=\sum _{i=1}^{m}X_{i}$

और

$S_{\sigma ^{2}}=\sum _{i=1}^{m}(X_{i}-{\overline {X}})^{2},{\text{ where }}{\overline {X}}={\frac {S_{\mu }}{m}}$

नमूना माध्य है, हम इसे पहचानते हैं

$T={\frac {S_{\mu }-m\mu }{\sqrt {S_{\sigma ^{2}}}}}{\sqrt {\frac {m-1}{m}}}={\frac {{\overline {X}}-\mu }{\sqrt {S_{\sigma ^{2}}/(m(m-1))}}}$

विद्यार्थी के टी वितरण का अनुसरण करता है (Wilks 1962) पैरामीटर (स्वतंत्रता की डिग्री) मी - 1 के साथ, ताकि

$f_{T}(t)={\frac {\Gamma (m/2)}{\Gamma ((m-1)/2)}}{\frac {1}{\sqrt {\pi (m-1)}}}\left(1+{\frac {t^{2}}{m-1}}\right)^{m/2}.$

दो मात्राओं के बीच T का मापन करना और उसकी अभिव्यक्ति को एक फलन के रूप में उलटना $\mu$ आप के लिए विश्वास अंतराल प्राप्त करते हैं $\mu$.

नमूना विशिष्टता के साथ:

$\mathbf {x} =\{7.14,6.3,3.9,6.46,0.2,2.94,4.14,4.69,6.02,1.58\}$

आकार m = 10 होने पर, आप आँकड़ों की गणना करते हैं $s_{\mu }=43.37$ और $s_{\sigma ^{2}}=46.07$, और इसके लिए 0.90 विश्वास अंतराल प्राप्त करें $\mu$ चरम सीमा के साथ (3.03, 5.65)।

कंप्यूटर की सहायता से कार्यों का अनुमान लगाना

मॉडलिंग के नजरिए से पूरा विवाद मुर्गी-अंडे की दुविधा की तरह दिखता है: या तो पहले डेटा द्वारा निश्चित डेटा और परिणाम के रूप में उनके गुणों का संभाव्यता वितरण, या पहले द्वारा निश्चित गुण और परिणाम के रूप में देखे गए डेटा का संभाव्यता वितरण। क्लासिक समाधान में एक लाभ और एक खामी है। पहले की सराहना विशेष रूप से तब की गई जब लोग अभी भी शीट और पेंसिल से गणना करते थे। असल में, निश्चित पैरामीटर θ के लिए नेमैन विश्वास अंतराल की गणना करने का कार्य कठिन है: आप θ नहीं जानते हैं, लेकिन आप इसके चारों ओर एक अंतराल का निपटान करना चाहते हैं जिसमें विफलता की संभवतः बहुत कम संभावना है। बहुत सीमित संख्या में सैद्धांतिक मामलों के लिए विश्लेषणात्मक समाधान की अनुमति है। इसके विपरीत, गाऊसी वितरण के आसपास विश्वास अंतराल के संदर्भ में केंद्रीय सीमा प्रमेय के माध्यम से बड़ी संख्या में उदाहरणों को अनुमानित तरीके से जल्दी से हल किया जा सकता है - यही लाभ है। दोष यह है कि केंद्रीय सीमा प्रमेय तब लागू होता है जब नमूना आकार पर्याप्त रूप से बड़ा होता है। इसलिए, यह आधुनिक अनुमान उदाहरणों में शामिल नमूने के साथ कम और कम लागू होता है। गलती उसकी अपनी ओर से सैंपल साइज में नहीं है. बल्कि, अनुमान समस्या की जटिलता के कारण यह आकार पर्याप्त रूप से बड़ा नहीं है।

बड़ी कंप्यूटिंग सुविधाओं की उपलब्धता के साथ, वैज्ञानिकों ने पृथक मापदंडों के अनुमान से जटिल कार्यों के अनुमान पर फिर से ध्यान केंद्रित किया, यानी कार्यों की पहचान करने वाले अत्यधिक नेस्टेड मापदंडों के सेट। इन मामलों में हम अत्यधिक जानकारीपूर्ण नमूनों के आधार पर कार्यों को सीखने (प्रतिगमन विश्लेषण, न्यूरो फजी | न्यूरो-फ़ज़ी सिस्टम या कम्प्यूटेशनल लर्निंग सिद्धांत के संदर्भ में) के बारे में बात करते हैं। डेटा को जोड़ने वाली एक जटिल संरचना होने का पहला प्रभाव स्वतंत्रता की नमूना डिग्री (सांख्यिकी) की संख्या में कमी है, यानी नमूना बिंदुओं के एक हिस्से का जलना, ताकि केंद्रीय सीमा प्रमेय में प्रभावी नमूना आकार पर विचार किया जा सके। बहुत छोटा। किसी दिए गए आत्मविश्वास स्तर के साथ सीमित सीखने की त्रुटि सुनिश्चित करने वाले नमूना आकार पर ध्यान केंद्रित करने का परिणाम यह होता है कि इस आकार की निचली सीमा जटिलता सूचकांक जैसे कि वीसी आयाम या जटिलता सूचकांक # विवरण के साथ बढ़ती है, जिस फ़ंक्शन को हम सीखना चाहते हैं वह संबंधित है।

उदाहरण

1,000 स्वतंत्र बिट्स का एक नमूना कम से कम 0.99 के विश्वास के साथ अंतर्निहित बर्नौली चर के पैरामीटर पी के अनुमान पर अधिकतम 0.081 की पूर्ण त्रुटि सुनिश्चित करने के लिए पर्याप्त है। समान आकार 0.99 के समान आत्मविश्वास के साथ 0.088 से कम की सीमा की गारंटी नहीं दे सकता है, जब त्रुटि की पहचान इस संभावना के साथ की जाती है कि न्यूयॉर्क में रहने वाला 20 वर्षीय व्यक्ति 1,000 बिग पर देखी गई ऊंचाई, वजन और कमर की सीमा में फिट नहीं बैठता है। सेब निवासी। सटीकता की कमी इसलिए होती है क्योंकि वीसी आयाम और समानांतर चतुर्भुज के वर्ग का विवरण, जिनमें से 1,000 निवासियों की श्रेणियों में से देखा गया है, दोनों 6 के बराबर हैं।

फिशर प्रश्न को हल करने वाली सामान्य व्युत्क्रम समस्या

अपर्याप्त रूप से बड़े नमूनों के साथ, दृष्टिकोण: निश्चित नमूना - यादृच्छिक गुण तीन चरणों में अनुमान प्रक्रियाओं का सुझाव देते हैं:

1.	Sampling mechanism. It consists of a pair $(Z,g_{\boldsymbol {\theta }})$, where the seed Z is a random variable without unknown parameters, while the explaining function $g_{\boldsymbol {\theta }}$ is a function mapping from samples of Z to samples of the random variable X we are interested in. The parameter vector ${\boldsymbol {\theta }}$ is a specification of the random parameter $\mathbf {\Theta }$. Its components are the parameters of the X distribution law. The Integral Transform Theorem ensures the existence of such a mechanism for each (scalar or vector) X when the seed coincides with the random variable U uniformly distributed in $[0,1]$. Example. For X following a Pareto distribution with parameters a and k, i.e. $F_{X}(x)=\left(1-{\frac {k}{x}}^{a}\right)I_{[k,\infty )}(x),$ a sampling mechanism $(U,g_{(a,k)})$ for X with seed U reads: $g_{(a,k)}(u)=k(1-u)^{-{\frac {1}{a}}},$ or, equivalently, $g_{(a,k)}(u)=ku^{-1/a}.$
2.	मास्टर समीकरण. मॉडल और देखे गए डेटा के बीच वास्तविक संबंध को डेटा पर आंकड़ों और अज्ञात मापदंडों के बीच संबंधों के एक सेट के संदर्भ में उछाला जाता है जो नमूना तंत्र के परिणाम के रूप में आते हैं। हम इन संबंधों को मास्टर समीकरण कहते हैं। आँकड़ों के इर्द-गिर्द घूमना $s=h(x_{1},\ldots ,x_{m})=h(g_{\boldsymbol {\theta }}(z_{1}),\ldots ,g_{\boldsymbol {\theta }}(z_{m}))$, मास्टर समीकरण का सामान्य रूप है: $s=\rho ({\boldsymbol {\theta }};z_{1},\ldots ,z_{m})$. इन संबंधों के साथ हम उन मापदंडों के मूल्यों का निरीक्षण कर सकते हैं जो नमूने के बीज का प्रतिनिधित्व करने वाले बीजों की एक विशेष सेटिंग से देखे गए आंकड़ों के साथ एक नमूना उत्पन्न कर सकते थे। इसलिए, नमूना बीजों की जनसंख्या मापदंडों की जनसंख्या से मेल खाती है। इस जनसंख्या के स्वच्छ गुणों को सुनिश्चित करने के लिए, बीज मूल्यों को यादृच्छिक रूप से निकालना और या तो पर्याप्त आँकड़े या, बस, अच्छे व्यवहार वाले आँकड़े शामिल करना पर्याप्त है। मास्टर समीकरणों में पैरामीटर। उदाहरण के लिए, आँकड़े $s_{1}=\sum _{i=1}^{m}\log x_{i}$ और $s_{2}=\min _{i=1,\ldots ,m}\{x_{i}\}$ पेरेटो यादृच्छिक चर $g_{(a,k)}$ हम उन्हें इस प्रकार पढ़ सकते हैं $s_{1}=m\log k+1/a\sum _{i=1}^{m}\log u_{i}$ $s_{2}=\min _{i=1,\ldots ,m}\{ku_{i}^{-{\frac {1}{a}}}\},$ क्रमश।
3.	पैरामीटर जनसंख्या. मास्टर समीकरणों का एक सेट तय करने के बाद, आप नमूना बीजों को या तो बूटस्ट्रैपिंग आबादी के माध्यम से संख्यात्मक रूप से, या ट्विस्टिंग प्रॉपर्टीज # ट्विस्टिंग तर्क के माध्यम से विश्लेषणात्मक रूप से मैप कर सकते हैं। इसलिए बीजों की जनसंख्या से आपको मापदंडों की जनसंख्या प्राप्त होती है। Example. From the above master equation we can draw a pair of parameters, $(a,k)$, compatible with the observed sample by solving the following system of equations: $a={\frac {\sum \log u_{i}-m\log \min\{u_{i}\}}{s_{1}-m\log s_{2}}}.$ $k=\mathrm {e} ^{\frac {as_{1}-\sum \log u_{i}}{ma}}$ where $s_{1}$ and $s_{2}$ are the observed statistics and $u_{1},\ldots ,u_{m}$ a set of uniform seeds. Transferring to the parameters the probability (density) affecting the seeds, you obtain the distribution law of the random parameters A and K compatible with the statistics you have observed. अनुकूलता संगत आबादी के मापदंडों को दर्शाती है, यानी ऐसी आबादी जो देखे गए आँकड़ों को जन्म देते हुए एक नमूना उत्पन्न कर सकती थी। आप इस धारणा को इस प्रकार औपचारिक रूप दे सकते हैं:

परिभाषा

एक यादृच्छिक चर और उससे निकाले गए नमूने के लिए संगत वितरण एक समान एल्गोरिथम अनुमान#नमूना तंत्र वाला वितरण है ${\mathcal {M}}_{X}=(Z,g_{\boldsymbol {\theta }})$ एक मान के साथ X का ${\boldsymbol {\theta }}$ यादृच्छिक पैरामीटर का $\mathbf {\Theta }$ एक अच्छे व्यवहार वाले आँकड़ों पर एक मास्टर समीकरण जड़ों से प्राप्त किया गया।

उदाहरण

मापदंडों का संयुक्त अनुभवजन्य संचयी वितरण कार्य $(A,K)$ पेरेटो यादृच्छिक चर का।

गाऊसी यादृच्छिक चर के माध्य एम का संचयी वितरण फ़ंक्शन

आप पेरेटो पैरामीटर ए और के के वितरण कानून को बूटस्ट्रैपिंग पॉपुलेशन विधि के कार्यान्वयन उदाहरण के रूप में पा सकते हैं जैसा कि बाईं ओर के चित्र में है।

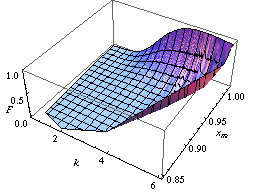
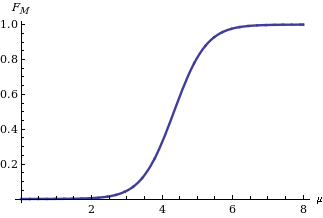
ट्विस्टिंग प्रॉपर्टीज#ट्विस्टिंग तर्क विधि को लागू करने से, आपको वितरण कानून मिलता है $F_{M}(\mu )$आँकड़ों के आधार पर गाऊसी चर X के माध्य M का $s_{M}=\sum _{i=1}^{m}x_{i}$कब $\Sigma ^{2}$के बराबर माना जाता है $\sigma ^{2}$ (Apolloni, Malchiodi & Gaito 2006). इसकी अभिव्यक्ति है:

$F_{M}(\mu )=\Phi \left({\frac {m\mu -s_{M}}{\sigma {\sqrt {m}}}}\right),$

दाहिनी ओर चित्र में दिखाया गया है, कहाँ $\Phi$ मानक सामान्य वितरण का संचयी वितरण फलन है।

एक निश्चित के लिए गॉसियन यादृच्छिक चर के माध्य एम के 90% विश्वास अंतराल के ऊपरी (बैंगनी वक्र) और निचले (नीले वक्र) चरम $\sigma$ और आँकड़ों के विभिन्न मूल्य_m.

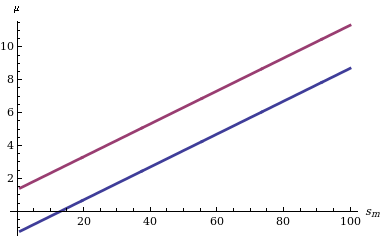
एम के वितरण कार्य को देखते हुए उसके लिए विश्वास अंतराल की गणना करना सीधा है: हमें केवल दो मात्राएँ खोजने की आवश्यकता है (उदाहरण के लिए) $\delta /2$और $1-\delta /2$मात्राएँ (यदि हम पूंछ की संभावनाओं में सममित स्तर के विश्वास अंतराल में रुचि रखते हैं) जैसा कि चित्र में बाईं ओर दर्शाया गया है जो सांख्यिकी के विभिन्न मूल्यों के लिए दो सीमाओं के व्यवहार को दर्शाता है_m.

फिशर के दृष्टिकोण की अकिलीज़ हील एक से अधिक मापदंडों के संयुक्त वितरण में निहित है, जैसे कि गाऊसी वितरण का माध्य और विचरण। इसके विपरीत, अंतिम दृष्टिकोण (और उपर्युक्त तरीकों: बूटस्ट्रैपिंग पॉपुलेशन और ट्विस्टिंग प्रॉपर्टीज#ट्विस्टिंग तर्क) के साथ हम कई मापदंडों का संयुक्त वितरण सीख सकते हैं। उदाहरण के लिए, दो या कई अधिक मापदंडों के वितरण पर ध्यान केंद्रित करते हुए, नीचे दिए गए आंकड़ों में हम दो आत्मविश्वास क्षेत्रों की रिपोर्ट करते हैं जहां सीखा जाने वाला कार्य 90% के आत्मविश्वास के साथ आता है। पूर्व उस संभावना से संबंधित है जिसके साथ एक विस्तारित समर्थन वेक्टर यंत्र एक बाइनरी लेबल 1 को बिंदुओं पर प्रदर्शित करती है $(x,y)$ विमान। दो सतहों को एक विशिष्ट वितरण कानून के अनुसार लेबल किए गए नमूना बिंदुओं के एक सेट के आधार पर तैयार किया जाता है (Apolloni et al. 2008). उत्तरार्द्ध सेंसर किए गए नमूने से गणना की गई स्तन कैंसर की पुनरावृत्ति के खतरे की दर के विश्वास क्षेत्र से संबंधित है (Apolloni, Malchiodi & Gaito 2006).

90% confidence region for the family of support vector machines endowed with hyperbolic tangent profile function

90% confidence region for the hazard function of breast cancer recurrence computed from the censored sample $t=(9,13,>13,18,12,23,31,34,>45,48,>161),\,$ with > t denoting a censored time

संदर्भ

• Fraser, D. A. S. (1966), "Structural probability and generalization", Biometrika, 53 (1/2): 1–9, doi:10.2307/2334048, JSTOR 2334048.
• Fisher, M. A. (1956), Statistical Methods and Scientific Inference, Edinburgh and London: Oliver and Boyd
• Apolloni, B.; Malchiodi, D.; Gaito, S. (2006), Algorithmic Inference in Machine Learning, International Series on Advanced Intelligence, vol. 5 (2nd ed.), Adelaide: Magill, Advanced Knowledge International
• Apolloni, B.; Bassis, S.; Malchiodi, D.; Witold, P. (2008), The Puzzle of Granular Computing, Studies in Computational Intelligence, vol. 138, Berlin: Springer, ISBN 9783540798637
• Ramsey, F. P. (1925), "The Foundations of Mathematics", Proceedings of the London Mathematical Society: 338–384, doi:10.1112/plms/s2-25.1.338.
• Wilks, S.S. (1962), Mathematical Statistics, Wiley Publications in Statistics, New York: John Wiley