इष्टतमता सिद्धांत

From Vigyanwiki
Revision as of 00:11, 19 July 2023 by alpha>Ajays
For other uses, see इष्टतमता सिद्धांत (बहुविकल्पी).
This article contains phonetic transcriptions in the International Phonetic Alphabet (IPA). For an introductory guide on IPA symbols, see Help:IPA. For the distinction between [ ], / / and ⟨ ⟩, see IPA § Brackets and transcription delimiters.

भाषाविज्ञान में, इष्टतमता सिद्धांत (अधिकांशतः संक्षिप्त रूप से ओटी) एक भाषाई मॉडल है जो प्रस्तावित करता है कि भाषा के देखे गए रूप परस्पर विरोधी बाधाओं की इष्टतम संतुष्टि से उत्पन्न होते हैं। ओटी ध्वनिविज्ञान विश्लेषण के अन्य दृष्टिकोणों से भिन्न है, जो सामान्यतः बाधाओं केअतिरिक्तनियमों का उपयोग करते हैं। यद्यपि , प्रतिनिधित्व के ध्वन्यात्मक मॉडल, जैसे कि ऑटोसेगमेंटल ध्वन्यात्मकता, प्रोसोडी (भाषाविज्ञान), और रैखिक ध्वन्यात्मकता (एसपीई), नियम-आधारित और बाधा-आधारित मॉडल के साथ समान रूप से संगत हैं। ओटी व्याकरण को ऐसे प्रणाली के रूप में देखता है जो इनपुट से आउटपुट तक मानचित्रण प्रदान करता है; सामान्यतः, इनपुट को अंतर्निहित प्रतिनिधित्व के रूप में और आउटपुट को उनकी सतही प्राप्ति के रूप में माना जाता है। यह उत्पादक व्याकरण के बड़े ढांचे के अंदर एक दृष्टिकोण है।

भाषाविज्ञान में, इष्टतमता सिद्धांत की उत्पत्ति 1991 में एलन प्रिंस और पॉल स्मोलेंस्की द्वारा दिए गए एक भाषण में हुई है।[1] जिसे पश्चात् में 1993 में उन्हीं लेखकों द्वारा एक पुस्तक पांडुलिपि में विकसित किया गया था।[2]

अवलोकन

सिद्धांत के तीन बुनियादी घटक हैं:

  • जेनरेटर (Gen) एक इनपुट लेता है, और संभावित आउटपुट, या उम्मीदवारों की सूची तैयार करता है,
  • बाधा घटक (Con) उम्मीदवारों के मध्य निर्णय लेने के लिए सख्ती से रैंक की गई उल्लंघन योग्य बाधाओं के रूप में मानदंड प्रदान करता है, और
  • मूल्यांकनकर्ता (Eval) बाधाओं के आधार पर इष्टतम उम्मीदवार का चयन करता है, और यह उम्मीदवार आउटपुट है।

इष्टतमता सिद्धांत मानता है कि यह घटक सार्वभौमिक हैं। व्याकरण में अंतर सार्वभौमिक बाधा समूह की विभिन्न रैंकिंग को दर्शाता है, Con. भाषा अधिग्रहण के हिस्से को इन बाधाओं की रैंकिंग को समायोजित करने की प्रक्रिया के रूप में वर्णित किया जा सकता है।

भाषा पर प्रयुक्त इष्टतमता सिद्धांत मूल रूप से 1991 में भाषाविदों एलन प्रिंस और पॉल स्मोलेंस्की द्वारा प्रस्तावित किया गया था, और पश्चात् में प्रिंस और जॉन मैक्कार्थी (भाषाविद्)|जॉन जे मैक्कार्थी द्वारा इसका विस्तार किया गया। यद्यपि इष्टतमता सिद्धांत में अधिकांश रुचि ध्वनि विज्ञान में इसके उपयोग से जुड़ी हुई है, जिस क्षेत्र में इष्टतमता सिद्धांत को पहली बार प्रयुक्त किया गया था, यह सिद्धांत भाषा विज्ञान के अन्य उपक्षेत्रों (जैसे वाक्यविन्यास और शब्दार्थ) पर भी प्रयुक्त होता है।

इष्टतमता सिद्धांत भाषाई सार्वभौमिकता, भाषाई टाइपोलॉजी और भाषा अधिग्रहण की जांच पर केंद्रित होने के कारण जनरेटिव व्याकरण के अन्य सिद्धांतों की तरह है।

इष्टतमता सिद्धांत की जड़ें तंत्रिका नेटवर्क अनुसंधान में भी हैं। यह आंशिक रूप से हार्मोनिक व्याकरण के कनेक्शनवादी सिद्धांत के विकल्प के रूप में उभरा, जिसे 1990 में गेराल्डिन लीजेंड्रे, योशिहिरो मियाता और पॉल स्मोलेंस्की द्वारा विकसित किया गया था। कनेक्शनवादी-जैसी भारित बाधाओं के साथ इष्टतमता सिद्धांत के वेरिएंट को हाल के काम (पैटर 2009) में अपनाया जाना जारी है।

इनपुट और Gen: उम्मीदवार समूह

इष्टतमता सिद्धांत मानता है कि इनपुट पर कोई भाषा-विशिष्ट प्रतिबंध नहीं हैं। इसे कहते हैं आधार की समृद्धि. प्रत्येक व्याकरण हर संभव इनपुट को संभाल सकता है। उदाहरण के लिए, व्यंजन क्लस्टर के बिना एक भाषा को इनपुट जैसे से निपटने में सक्षम होना चाहिए /flask/. जटिल समूहों के बिना भाषाएँ इस समस्या को कैसे हल करेंगी, इस पर भिन्न हैं; कुछ में एपेन्थेसिस होगा (उदा. [falasak], या [falasaka] यदि सभी कोडा पर प्रतिबंध लगा दिया गया है) और कुछ एलिज़न (उदा.) [fas], [fak], [las], [lak]).

Gen किसी भी संख्या में आउटपुट उम्मीदवार उत्पन्न करने के लिए स्वतंत्र है, यदि वह इनपुट से कितना भी विचलित हों। इसे विश्लेषण की स्वतंत्रता कहते हैं. भाषा का व्याकरण (बाधाओं की रैंकिंग) यह निर्धारित करता है कि उम्मीदवारों में से किसका मूल्यांकन इष्टतम के रूप में किया जाएगा Eval.[3]

Con: बाधा समूह

इष्टतमता सिद्धांत में, प्रत्येक बाधा सार्वभौमिक है। Con हर भाषा में एक समान है। दो बुनियादी प्रकार की बाधाएँ हैं:

  • वफ़ादारी बाधाओं के लिए आवश्यक है कि प्रेक्षित सतह रूप (आउटपुट) किसी विशेष तरीके से अंतर्निहित या शाब्दिक रूप (इनपुट) से मेल खाए; अर्थात्, इन बाधाओं के लिए इनपुट और आउटपुट फॉर्म के मध्य पहचान की आवश्यकता होती है।
  • मार्कडनेस बाधाएं आउटपुट की संरचनात्मक सुगठितता पर आवश्यकताएं लगाती हैं।[4]

प्रत्येक सिद्धांत में एक महत्वपूर्ण भूमिका निभाता है। चिह्नितता की बाधाएं अंतर्निहित रूप से परिवर्तनों को प्रेरित करती हैं, और वफादारी की बाधाएं प्रत्येक इनपुट को कुछ पूरी तरह से अचिह्नित रूप में अनुभूत होने से रोकती हैं (जैसे कि [ba]).

की सार्वभौमिक प्रकृति Con भाषा टाइपोलॉजी के बारे में कुछ तत्काल भविष्यवाणियाँ करता है। यदि व्याकरण भिन्न-भिन्न रैंकिंग के कारण ही भिन्न होते हैं Con, तब संभावित मानव भाषाओं का समूह उपस्तिथ बाधाओं से निर्धारित होता है। इष्टतमता सिद्धांत भविष्यवाणी करता है कि रैंकिंग में जितने क्रमपरिवर्तन हैं, उससे अधिक व्याकरण नहीं हो सकते Con. संभावित रैंकिंग की संख्या बाधाओं की कुल संख्या के कारख़ाने का के सामान्तर है, इस प्रकार फैक्टोरियल टाइपोलॉजी शब्द को जन्म मिलता है। यद्यपि , इन सभी संभावित व्याकरणों को भिन्न करना संभव नहीं हो सकता है, क्योंकि हर बाधा का हर भाषा में अवलोकनीय प्रभाव होने की गारंटी नहीं है। की बाधाओं पर कुल दो आदेश Con इनपुट-आउटपुट मानचित्रण की समान श्रेणी उत्पन्न कर सकता है, किन्तु दो बाधाओं की सापेक्ष रैंकिंग में भिन्नता है जो एक दूसरे के साथ संघर्ष नहीं करते हैं। चूँकि इन दोनों रैंकिंग को भिन्न करने का कोई प्रणाली नहीं है, इसलिए कहा जाता है कि वह एक ही व्याकरण से संबंधित हैं। ओटी में एक व्याकरण एक एंटीमैट्रोइड के सामान्तर है।[5] यदि संबंधों के साथ रैंकिंग की अनुमति दी जाती है, तब संभावनाओं की संख्या एक फैक्टोरियल केअतिरिक्तएक ऑर्डर की गई बेल संख्या है, जो अधिक बड़ी संख्या में संभावनाओं की अनुमति देती है।[6]

वफादारी बाधाएं

मैक्कार्थी और प्रिंस (1995) ने वफादारी की बाधाओं के तीन बुनियादी परिवारों का प्रस्ताव रखा:

  • Max मलोत्सर्ग (अधिकतम से) को रोकता है।
  • Dep एपेंथिसिस (आश्रित से) को प्रतिबंधित करता है।
  • Ident(एफ) फीचर एफ (समान से) के मूल्य में परिवर्तन पर रोक लगाता है।

प्रत्येक बाधा के नाम के साथ -IO या -BR जोड़ा जा सकता है, जो क्रमशः इनपुट/आउटपुट और बेस/रिडुप्लिकेंट के लिए है - जिनमें से उत्तरार्द्ध का उपयोग दोहराव के विश्लेषण में किया जाता है - यदि वांछित हो। एफ इन Ident(एफ) को एक विशिष्ट विशेषता के नाम से प्रतिस्थापित किया जाता है, जैसे कि Ident-IO(आवाज़)।

Max और Dep बदलना Parse और Fillप्रिंस एंड स्मोलेंस्की (1993) द्वारा प्रस्तावित, जिसमें कहा गया था कि अंतर्निहित खंडों को शब्दांश संरचना में पार्स किया जाना चाहिए और शब्दांश पदों को क्रमशः अंतर्निहित खंडों से भरा जाना चाहिए।[7][8] Parse और Fill अनिवार्य रूप से वही कार्य करता है Max और Dep, किन्तु इसमें भिन्नता है कि वह केवल आउटपुट का मूल्यांकन करते हैं, न कि इनपुट और आउटपुट के मध्य संबंध का, जो कि मार्कनेस बाधाओं की विशेषता है।[9] यह प्रिंस और स्मोलेंस्की द्वारा अपनाए गए मॉडल से उपजा है जिसे रोकथाम सिद्धांत के रूप में जाना जाता है, जो मानता है कि आउटपुट द्वारा अप्राप्त इनपुट खंडों को हटाया नहीं जाता है, किंतु एक शब्दांश द्वारा अप्रकाशित छोड़ दिया जाता है।[10] मैककार्थी और प्रिंस (1995, 1999) द्वारा प्रस्तुत मॉडल, जिसे पत्राचार सिद्धांत के रूप में जाना जाता है, ने तब से इसे मानक ढांचे के रूप में प्रतिस्थापित कर दिया है।[8]

मैक्कार्थी और प्रिंस (1995) भी प्रस्ताव करते हैं:

  • I-Contig, उल्लंघन तब होता है जब एक शब्द- या रूपिम-आंतरिक खंड हटा दिया जाता है (इनपुट-कॉन्टिग्युटी से);
  • O-Contig, उल्लंघन तब होता है जब एक खंड को शब्द- या रूपिम-आंतरिक रूप से डाला जाता है (आउटपुट-कॉन्टिगुएटी से);
  • Linearity, जब कुछ खंडों का क्रम बदल जाता है तब इसका उल्लंघन होता है (अर्थात् मेटाथिसिस (भाषाविज्ञान) को प्रतिबंधित करता है);
  • Uniformity, इसका उल्लंघन तब होता है जब दो या दो से अधिक खंडों को एक के रूप में अनुभूत किया जाता है (अर्थात संलयन (भाषाविज्ञान) को प्रतिबंधित करता है); और
  • Integrity, इसका उल्लंघन तब होता है जब एक खंड को अनेक खंडों के रूप में अनुभूत किया जाता है (अर्थात अनपैकिंग (भाषा विज्ञान) या स्वर को तोड़ने पर रोक लगाता है - इसके विपरीत) Uniformity).

चिह्नित बाधाएं

प्रिंस और स्मोलेंस्की (1993) द्वारा प्रारंभ की गई मार्कडनेस बाधाओं में सम्मिलित हैं:

नाम विवरण अन्य नामों
Nuc Syllables must have nuclei.
−Coda Syllables must have no codas. NoCoda
Ons Syllables must have onsets. Onset
HNuc A nuclear segment must be more sonorous than another (from "harmonic nucleus").
*Complex A syllable must be V, CV or VC.
CodaCond Coda consonants cannot have place features that are not shared by an onset consonant. CodaCondition
NonFinality A word-final syllable (or foot) must not bear stress. NonFin
FtBin A foot must be two syllables (or moras). FootBinarity
Pk-Prom Light syllables must not be stressed. PeakProminence
WSP Heavy syllables must be stressed (from "weight-to-stress principle"). Weight-to-Stress

साहित्य में त्रुटिहीन परिभाषाएँ भिन्न-भिन्न होती हैं। कुछ बाधाओं को कभी-कभी कवर बाधा के रूप में उपयोग किया जाता है, जो बाधाओं के एक समूह के लिए खड़े होते हैं जो पूरी तरह से ज्ञात या महत्वपूर्ण नहीं होते हैं।[11]

कुछ चिह्नित बाधाएं संदर्भ-मुक्त हैं और अन्य संदर्भ-संवेदनशील हैं। उदाहरण के लिए, *वीnasal कहा गया है कि स्वरों को किसी भी स्थिति में अनुनासिक नहीं होना चाहिए और इस प्रकार यह संदर्भ-मुक्त है, जबकि *Voralएन का कहना है कि टॉटोसिलेबिक नासिका से पहले स्वर मौखिक नहीं होने चाहिए और इस प्रकार यह संदर्भ-संवेदनशील है।[12]

संरेखण बाधाएं

स्थानीय संयोजन

दो बाधाओं को एक ही बाधा के रूप में जोड़ा जा सकता है, जिसे स्थानीय संयोजन कहा जाता है, जो किसी दिए गए डोमेन, जैसे खंड, शब्दांश या शब्द के अंदर दोनों बाधाओं का उल्लंघन होने पर हर बार केवल एक उल्लंघन देता है। उदाहरण के लिए, [NoCoda & VOP]segment एक कोडा में प्रति ध्वनि अवरोध का एक बार उल्लंघन किया जाता है (वीओपी का अर्थ ध्वनि अवरोध निषेध है), और इसे समान रूप से लिखा जा सकता है *VoicedCoda.[13][14] श्रृंखला बदलाव का विश्लेषण करते समय उत्पन्न होने वाली ध्वनि संबंधी अस्पष्टता की समस्या को दूर करने के तरीके के रूप में स्थानीय संयोजनों का उपयोग किया जाता है।[13]

Eval: इष्टतमता की परिभाषा

मूल प्रस्ताव में, दो उम्मीदवारों, ए और बी को देखते हुए, ए एक बाधा पर बी की तुलना में उत्तम या अधिक हार्मोनिक है, यदि ए बी की तुलना में कम उल्लंघन करता है। यदि ए कम उल्लंघन करता है तब उम्मीदवार ए संपूर्ण बाधा पदानुक्रम पर बी की तुलना में अधिक हार्मोनिक है। ए और बी को भिन्न करने वाली उच्चतम रैंक वाली बाधा का उल्लंघन। ए अपने उम्मीदवार समूह में इष्टतम है यदि यह अन्य सभी उम्मीदवारों की तुलना में बाधा पदानुक्रम पर उत्तम है। यद्यपि , यह परिभाषा Eval नियमित भाषा से अधिक अंतिम संबंध मॉडल करने में सक्षम है।[15] उदाहरण के लिए, बाधाएं सी दी गई हैं1, सी2, और सी3, जहां सी1 C पर हावी है2, जो C पर हावी है3 (सी1 ≫ सी2 ≫ सी3), ए बी को हरा देता है, या बी की तुलना में अधिक हार्मोनिक है, यदि ए के पास उच्चतम रैंकिंग बाधा पर बी की तुलना में कम उल्लंघन हैं जो उन्हें उल्लंघनों की एक भिन्न संख्या प्रदान करता है (ए इष्टतम है यदि ए बी को हराता है और उम्मीदवार समूह में केवल ए और बी सम्मिलित हैं) ). यदि A और B, C पर टाई करते हैं1, किन्तु A, C पर B से उत्तम करता है2, ए इष्टतम है, यदि ए ने सी के और भी अनेक उल्लंघन किए हों3 बी की तुलना में. इस तुलना को अधिकांशतः एक झांकी के साथ चित्रित किया जाता है। सूचकांक (टाइपोग्राफी) इष्टतम उम्मीदवार को चिह्नित करता है, और प्रत्येक कोशिका किसी दिए गए उम्मीदवार और बाधा के प्रत्येक उल्लंघन के लिए एक तारांकन चिह्न प्रदर्शित करती है। एक बार जब कोई उम्मीदवार किसी अन्य उम्मीदवार की तुलना में उन्हें भिन्न करने वाली उच्चतम रैंकिंग बाधा पर खराब प्रदर्शन करता है, तब यह एक घातक उल्लंघन होता है (झांकी में विस्मयादिबोधक चिह्न द्वारा और निचले रैंक की बाधाओं के लिए छायांकित कोशिकाओं द्वारा चिह्नित)। एक बार जब कोई उम्मीदवार घातक उल्लंघन करता है, तब यह इष्टतम नहीं हो सकता है, यदि वह शेष पर अन्य उम्मीदवारों से उत्तम प्रदर्शन करता हो Con.

Tableau
Input Constraint 1 Constraint 2 Constraint 3
a.☞ Candidate A * * ***
b. Candidate B * **!

अन्य सांकेतिक सम्मेलनों में सम्मिलित हैं बिना रैंक वाले या समान रूप से रैंक किए गए बाधाओं के स्तंभों को भिन्न करने वाली बिंदीदार रेखाएं, अस्थायी रूप से रैंक की गई झांकी में एक उंगली के स्थान पर एक चेक मार्क ✔ (हार्मोनिक को दर्शाता है किन्तु निर्णायक रूप से इष्टतम नहीं), और एक गोलाकार तारांकन ⊛ एक विजेता द्वारा उल्लंघन को दर्शाता है; आउटपुट उम्मीदवारों में, कोण कोष्ठक ⟨ ⟩ ध्वन्यात्मक बोध में सम्मिलित खंडों को निरूपित करें, और □ और □́ क्रमशः एक भावात्मक व्यंजन और स्वर को निरूपित करें।[16] चिन्ह ≫ से बहुत बड़ा (कभी-कभी नेस्टेड ⪢) एक बाधा के दूसरे पर प्रभुत्व को दर्शाता है ( C1 ≫ सी2= सी1 C पर हावी है2) जबकि सफल ऑपरेटर ≻ आउटपुट उम्मीदवारों की तुलना में उत्तम सामंजस्य को दर्शाता है (A ≻ B = A, B की तुलना में अधिक हार्मोनिक है)।[17]

बाधाओं को सख्त वर्चस्व के पदानुक्रम में स्थान दिया गया है। सख्त वर्चस्व की कठोरता का कारण है कि एक उम्मीदवार जो केवल उच्च-रैंक वाली बाधा का उल्लंघन करता है, वह पदानुक्रम पर उस उम्मीदवार की तुलना में बुरा प्रदर्शन करता है जो ऐसा नहीं करता है, यदि दूसरे उम्मीदवार ने हर अन्य निचली-रैंक वाली बाधा पर खराब प्रदर्शन किया हो। इसका यह भी अर्थ है कि बाधाओं का उल्लंघन किया जा सकता है; जीतने वाले (अर्थात सबसे सामंजस्यपूर्ण) उम्मीदवार को सभी बाधाओं को पूरा करने की आवश्यकता नहीं है, जब तक कि किसी भी प्रतिद्वंद्वी उम्मीदवार के लिए जो कुछ बाधाओं पर विजेता से उत्तम प्रदर्शन करता है, वहां एक उच्च रैंक की बाधा होती है जिस पर विजेता उस प्रतिद्वंद्वी से उत्तम प्रदर्शन करता है। किसी भाषा के अंदर , एक बाधा को इतना ऊंचा स्थान दिया जा सकता है कि उसका सदैव पालन किया जाए; इसे इतना नीचे स्थान दिया जा सकता है कि इसका कोई देखने योग्य प्रभाव न हो; या, इसकी कुछ मध्यवर्ती रैंकिंग हो सकती है। अचिह्नित का उद्भव शब्द उन स्थितियों का वर्णन करता है जिनमें एक चिह्नित बाधा की एक मध्यवर्ती रैंकिंग होती है, जिससे कि कुछ रूपों में इसका उल्लंघन होता है, किन्तु फिर भी जब उच्च-रैंक वाली बाधाएं अप्रासंगिक होती हैं तब इसका प्रभाव देखने योग्य होता है।

मैक्कार्थी और प्रिंस (1994) द्वारा प्रस्तावित एक प्रारंभिक उदाहरण बाधा है NoCoda, जो अक्षरों को व्यंजन में समाप्त होने से रोकता है। बी एलन हाई में, NoCoda को इतनी ऊंची रैंक नहीं दी गई है कि सदैव उसका पालन किया जा सके, जैसा कि टायनान जैसी जड़ों में देखा गया है (इनपुट के प्रति वफादारी अंतिम को हटाने से रोकती है) /n/). किन्तु , दोहराव रूप मा-तयना-तयन्न में 'बार-बार पीछे छूट जाना', अंतिम /n/ कॉपी नहीं किया गया है. मैक्कार्थी और प्रिंस के विश्लेषण के अनुसार , ऐसा इसलिए है क्योंकि इनपुट के प्रति निष्ठा दोबारा दोहराई गई सामग्री पर प्रयुक्त नहीं होती है, और NoCoda इस प्रकार काल्पनिक मा-तायना-तायना के ऊपर मा-तायना-तायना को प्राथमिकता देने के लिए स्वतंत्र है (जिसमें इसका अतिरिक्त उल्लंघन है) NoCoda).

कुछ इष्टतमता सिद्धांतकार तुलनात्मक झांकियों के उपयोग को पसंद करते हैं, जैसा कि प्रिंस (2002बी) में वर्णित है। तुलनात्मक झांकी क्लासिक या फ्लाईस्पेक झांकी के समान ही जानकारी प्रदर्शित करती है, किन्तु जानकारी इस तरह प्रस्तुत की जाती है कि यह सबसे महत्वपूर्ण जानकारी को उजागर करती है। उदाहरण के लिए, उपरोक्त झांकी को निम्नलिखित तरीके से प्रस्तुत किया जाएगा।

Comparative tableau
Constraint 1 Constraint 2 Constraint 3
A ~ B e W L

तुलनात्मक झांकी में प्रत्येक पंक्ति किसी व्यक्तिगत उम्मीदवार केअतिरिक्तविजेता-हारे हुए जोड़े का प्रतिनिधित्व करती है। उन कोशिकाओं में जहां बाधाएं विजेता-हारने वाले जोड़े का आकलन करती हैं, डब्ल्यू को रखा जाता है यदि उस कॉलम में बाधा विजेता को पसंद करती है, एल यदि बाधा हारने वाले को पसंद करती है, और ई यदि बाधा जोड़ी के मध्य अंतर नहीं करती है। इस तरह से डेटा प्रस्तुत करने से सामान्यीकरण करना आसान हो जाता है। उदाहरण के लिए, लगातार रैंकिंग पाने के लिए कुछ W को सभी L पर हावी होना चाहिए। ब्रासोवेनु और प्रिंस (2005) एक प्रक्रिया का वर्णन करते हैं जिसे फ़्यूज़न के रूप में जाना जाता है और किसी दिए गए तर्क के लिए आवश्यक और पर्याप्त शर्तों को प्राप्त करने के लिए तुलनात्मक झांकी में डेटा प्रस्तुत करने के विभिन्न तरीकों का वर्णन किया गया है।

उदाहरण

एक सरल उदाहरण के रूप में, अंग्रेजी बहुवचन की अभिव्यक्ति पर विचार करें:

  • /dɒɡ/ + /z/ → [dɒɡz] (कुत्ते)
  • /kæt/ + /z/ → [kæts] (बिल्ली की)
  • /dɪʃ/ + /z/ → [dɪʃɪz] (व्यंजन)

वर्चस्व के अवरोही क्रम में निम्नलिखित बाधा समूह पर भी विचार करें:

प्रकार नाम विवरण
Markedness *SS Two successive sibilants are prohibited. One violation for every pair of adjacent sibilants in the output.
Agree(Voice) Output segments agree in specification of [±voice]. One violation for every pair of adjacent obstruents in the output which disagree in voicing.
Faithfulness Max Maximizes all input segments in the output. One violation for each segment in the input that does not appear in the output. This constraint prevents deletion.
Dep Output segments are dependent on having an input correspondent. One violation for each segment in the output that does not appear in the input. This constraint prevents insertion.
Ident(Voice) Maintains the identity of the [±voice] specification. One violation for each segment that differs in voicing between the input and output.
/dɒɡ/ + /z/ → [dɒɡz]
/dɒɡ/ + /z/ *SS Agree Max Dep Ident
a.  ☞ dɒɡz
b. dɒɡs *! *
c. dɒɡɪz *!
d. dɒɡɪs *! *
e. dɒɡ *!
/kæt/ + /z/ → [kæts]
/kæt/ + /z/ *SS Agree Max Dep Ident
a. kætz *!
b.  ☞ kæts *
c. kætɪz *!
d. kætɪs *! *
e. kæt *!
/dɪʃ/ + /z/ → [dɪʃɪz]
/dɪʃ/ + /z/ *SS Agree Max Dep Ident
a. dɪʃz *! *
b. dɪʃs *! *
c.  ☞ dɪʃɪz *
d. dɪʃɪs * *!
e. dɪʃ *!






इससे कोई फर्क नहीं पड़ता कि बाधाओं को कैसे पुनः व्यवस्थित किया जाता है, एलोमोर्फ [ɪs]सदैव हारेंगे [ɪz]. इसे हार्मोनिक बाउंडिंग कहा जाता है। उम्मीदवार द्वारा किए गए उल्लंघन [dɒɡɪz] द्वारा किए गए उल्लंघनों का एक उपसमूह है [dɒɡɪs]; विशेष रूप से, यदि आप किसी स्वर को उपलेखित करते हैं, तब रूपिम की आवाज़ को बदलना बाधाओं का अनावश्यक उल्लंघन है। में /dɒɡ/ + /z/ झांकी, एक उम्मीदवार है [dɒɡz] जिसका कोई भी उल्लंघन नहीं होता है। समस्या के बाधा समूह के अंदर , [dɒɡz] अन्य सभी संभावित उम्मीदवारों को सामंजस्यपूर्ण रूप से बांधता है। इससे पता चलता है कि एक उम्मीदवार को दूसरे उम्मीदवार को सामंजस्यपूर्ण रूप से बांधने के लिए विजेता होने की आवश्यकता नहीं है।

ऊपर की झांकी को तुलनात्मक झांकी प्रारूप का उपयोग करके नीचे दोहराया गया है।

/dɒɡ/ + /z/ → [dɒɡz]
/dɒɡ/ + /z/ *SS Agree Max Dep Ident
dɒɡz ~ dɒɡs e W e e W
dɒɡz ~ dɒɡɪz e e e W e
dɒɡz ~ dɒɡɪs e e e W W
dɒɡz ~ dɒɡ e e W e e
/kæt/ + /z/ → [kæts]
/kæt/ + /z/ *SS Agree Max Dep Ident
kæts ~ kætz e W e e L
kæts ~ kætɪz e e e W L
kæts ~ kætɪs e e e W e
kæts ~ kæt e e W e L
/dɪʃ/ + /z/ → [dɪʃɪz]
/dɪʃ/ + /z/ *SS Agree Max Dep Ident
dɪʃɪz ~ dɪʃz W W e L e
dɪʃɪz ~ dɪʃs W e e L W
dɪʃɪz ~ dɪʃɪs e e e e W
dɪʃɪz ~ dɪʃ e e W L e






के लिए तुलनात्मक झांकी से /dɒɡ/ + /z/, यह देखा जा सकता है कि इन बाधाओं की कोई भी रैंकिंग देखे गए आउटपुट का उत्पादन करेगी [dɒɡz]. क्योंकि हारने वालों को तरजीह देने वाली कोई तुलना नहीं होती, [dɒɡz] इन बाधाओं की किसी भी रैंकिंग के अनुसार जीतता है; इसका कारण यह है कि इस इनपुट के आधार पर कोई रैंकिंग स्थापित नहीं की जा सकती।

के लिए झांकी /kæt/ + /z/ में एक W और एक L वाली पंक्तियाँ हैं। इससे यह पता चलता है Agree, Max, और Dep सभी पर हावी होना चाहिए Ident; यद्यपि , इस इनपुट के आधार पर उन बाधाओं के मध्य कोई रैंकिंग स्थापित नहीं की जा सकती है। इस झांकी के आधार पर, निम्नलिखित रैंकिंग स्थापित की गई है:

Agree, Max, Dep ≫ Ident

के लिए झांकी /dɪʃ/ + /z/ दर्शाता है कि वांछित परिणाम की भविष्यवाणी करने के लिए अनेक और रैंकिंग आवश्यक हैं। तीसरी पंक्ति कुछ नहीं कहती; तीसरी पंक्ति में हारने वालों को पसंद करने वाली कोई तुलना नहीं है। पहली पंक्ति से पता चलता है कि या तब *एसएस या Agree हावी होना चाहिए Dep, के मध्य तुलना के आधार पर [dɪʃɪz] और [dɪʃz]. चौथी पंक्ति यह दर्शाती है Max हावी होना चाहिए Dep. दूसरी पंक्ति दर्शाती है कि या तब *SS या Ident हावी होना चाहिए Dep. से /kæt/ + /z/ झांकी, यह स्थापित किया गया था Dep हावी है Ident; इसका कारण है कि *एसएस को हावी होना चाहिए Dep.

वर्तमान तक, निम्नलिखित रैंकिंग को आवश्यक माना गया है:

*एसएस, Max ≫ Dep ≫ Ident

जबकि ऐसा संभव है Agree हावी हो सकता है Dep, यह आवश्यक नहीं है; ऊपर दी गई रैंकिंग अवलोकन के लिए पर्याप्त है [dɪʃɪz] उभर कर आने के लिए।

जब झांकियों की रैंकिंग को संयोजित किया जाता है, तब निम्नलिखित रैंकिंग सारांश दिया जा सकता है:

*एसएस, Max ≫ Agree, Dep ≫ Ident
या
*एसएस, Max, Agree ≫ Dep ≫ Ident

लगाने के लिए दो संभावित स्थान हैं Agree रैंकिंग को रैखिक रूप से लिखते समय; कोई भी वास्तव में त्रुटिहीन नहीं है। पहला तात्पर्य यह है कि *एसएस और Max हावी होना चाहिए Agree, और दूसरा तात्पर्य यह है Agree हावी होना चाहिए Dep. इनमें से कोई भी सत्य नहीं है, जो इस तरह से एक रैखिक फैशन में रैंकिंग लिखने में विफलता है। इस प्रकार की समस्याएं ही कारण हैं कि अधिकांश भाषाविद् आवश्यक और पर्याप्त रैंकिंग का प्रतिनिधित्व करने के लिए जाली (आदेश) का उपयोग करते हैं, जैसा कि नीचे दिखाया गया है।

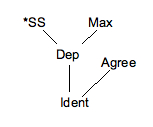आवश्यक और पर्याप्त रैंकिंग का जाली ग्राफ़एक आरेख जो इस शैली में बाधाओं की आवश्यक रैंकिंग का प्रतिनिधित्व करता है वह हस्से आरेख है।

आलोचना

इष्टतमता सिद्धांत ने पर्याप्त मात्रा में आलोचना को आकर्षित किया है, जिनमें से अधिकांश ध्वनिविज्ञान (वाक्यविन्यास या अन्य क्षेत्रों के बजाय) में इसके अनुप्रयोग पर केंद्रित है।[18][19][20][21][22][23]

यह प्रामाणित किया जाता है कि इष्टतमता सिद्धांत ध्वन्यात्मक अस्पष्टता का हिसाब नहीं दे सकता (उदाहरण के लिए, Idsardi 2000 देखें)। व्युत्पन्न ध्वनिविज्ञान में, ऐसे प्रभाव देखे जा सकते हैं जो सतही स्तर पर अस्पष्ट हैं किन्तु अपारदर्शी नियम क्रम के माध्यम से समझाए जा सकते हैं; किन्तु इष्टतमता सिद्धांत में, जिसमें नियमों को संचालित करने के लिए कोई मध्यवर्ती स्तर नहीं है, इन प्रभावों को समझाना समष्टि है।

उदाहरण के लिए, क्यूबेक फ़्रेंच में, उच्च अग्र स्वरों ने एफ़्रिकेशन को ट्रिगर किया /t/, (उदा /tipik/ → [tˢpɪk]), किन्तु उच्च स्वरों की हानि (सतह स्तर पर दिखाई देने वाली) के कारण कोई स्पष्ट स्रोत नहीं रह गया है। व्युत्पन्न ध्वनिविज्ञान इसे यह कहकर समझा सकता है कि स्वर सिंकोप (ध्वनि विज्ञान) (स्वर का हानि) काउंटरबल्ड एफ़्रिकेशन - अर्थात, स्वर सिंकोप होने और रक्तस्राव क्रम (अर्थात रोकने) केअतिरिक्तअफ़्रीकेशन, यह कहता है कि स्वर सिंकोप से पहले अफ़्रीकेशन प्रयुक्त होता है, इसलिए उच्च स्वर को हटा दिया जाता है और उस वातावरण को नष्ट कर दिया जाता है जिससे द्वेष उत्पन्न हुआ था। ऐसे प्रतिघातक नियम आदेशों को इसलिए अपारदर्शी (पारदर्शी के विपरीत) कहा जाता है, क्योंकि उनके प्रभाव सतही स्तर पर दिखाई नहीं देते हैं।

ऐसी घटनाओं की अस्पष्टता को इष्टतमता सिद्धांत में कोई सीधा स्पष्टीकरण नहीं मिलता है, क्योंकि सैद्धांतिक मध्यवर्ती रूप पहुंच योग्य नहीं हैं (बाधाएं केवल सतही रूप और/या अंतर्निहित रूप को संदर्भित करती हैं)। इसे ध्यान में रखते हुए अनेक प्रस्ताव तैयार किए गए हैं, किन्तु अधिकांश प्रस्ताव इष्टतमता सिद्धांत की बुनियादी वास्तुकला को महत्वपूर्ण रूप से बदल देते हैं और इसलिए अत्यधिक विवादास्पद होते हैं। बार-बार, ऐसे परिवर्तन नए प्रकार की बाधाएँ जोड़ते हैं (जो सार्वभौमिक वफ़ादारी या चिह्नितता बाधाएँ नहीं हैं), या गुणों को बदल देते हैं Gen (जैसे कि क्रमिक व्युत्पत्ति की अनुमति देना) या Eval. इनके उदाहरणों में जॉन मैक्कार्थी (भाषाविद्)|जॉन जे. मैक्कार्थी का सहानुभूति सिद्धांत और उम्मीदवार श्रृंखला सिद्धांत, सहित अनेक अन्य सम्मिलित हैं।

एक प्रासंगिक उद्देश्य सर्कुलर चेन शिफ्ट्स का अस्तित्व है, अर्थात ऐसे स्थितियों जहां इनपुट /X/ आउटपुट के लिए मानचित्र [Y], किन्तु इनपुट /Y/ आउटपुट के लिए मानचित्र [X]. इष्टतमता सिद्धांत के अनेक संस्करण इसे असंभव बताते हैं (देखें मोरेटन 2004, प्रिंस 2007)।

इष्टतमता सिद्धांत की भाषण उत्पादन/धारणा के एक असंभव मॉडल के रूप में भी आलोचना की जाती है: संभावित उम्मीदवारों की अनंत संख्या की गणना और तुलना करने में प्रक्रिया में असीम रूप से लंबा समय लगेगा। Idsardi (2006) इस स्थिति पर तर्क देते हैं, चूंकि अन्य भाषाविद् इस दावे का इस आधार पर खंडन करते हैं कि Idsardi बाधा समूह और उम्मीदवारों के बारे में अनुचित धारणाएं बनाता है, और इष्टतमता सिद्धांत के अधिक मध्यम तात्कालिकताएं ऐसी महत्वपूर्ण कम्प्यूटेशनल समस्याएं प्रस्तुत नहीं करती हैं (कोर्नाई (2006 देखें)) और हेंज, कोबेले और रिगल (2009))।[24][25] इष्टतमता सिद्धांत की इस आलोचना का एक और आम खंडन यह है कि रूपरेखा पूरी तरह से प्रतिनिधित्वात्मक है। इस दृष्टिकोण से, इष्टतमता सिद्धांत को भाषाई क्षमता का एक मॉडल माना जाता है और इसलिए इसका उद्देश्य भाषाई प्रदर्शन की विशिष्टताओं को समझाना नहीं है।[26][27]

इष्टतमता सिद्धांत पर एक और आपत्ति यह है कि यह विधि ी रूप से एक सिद्धांत नहीं है, इसमें झूठी भविष्यवाणियां नहीं की जाती हैं। इस मुद्दे का स्रोत शब्दावली में हो सकता है: सिद्धांत शब्द का उपयोग यहां भौतिकी, रसायन विज्ञान और अन्य विज्ञानों की तुलना में भिन्न तरह से किया जाता है। इष्टतमता सिद्धांत की विशिष्ट तात्कालिकताएं झूठी भविष्यवाणियां कर सकती हैं, उसी तरह अन्य भाषाई ढांचे के अंदर विशिष्ट प्रस्ताव भी कर सकते हैं। क्या भविष्यवाणियाँ की जाती हैं, और क्या वह परीक्षण योग्य हैं, यह व्यक्तिगत प्रस्तावों की विशिष्टताओं पर निर्भर करता है (सामान्यतः, यह विश्लेषण में प्रयुक्त बाधाओं की परिभाषा का मामला है)। इस प्रकार, एक रूपरेखा के रूप में इष्टतमता सिद्धांत का सबसे अच्छा वर्णन किया गया है एक वैज्ञानिक प्रतिमान के रूप में।[28]

इष्टतमता सिद्धांत के अंदर सिद्धांत

व्यवहार में, इष्टतमता सिद्धांत के कार्यान्वयन में अधिकांशतः प्रतिनिधित्व के ध्वन्यात्मक सिद्धांतों की अनेक अवधारणाओं का उपयोग किया जाता है, जैसे कि शब्दांश, मोरा (भाषा विज्ञान), या फ़ीचर ज्यामिति। इनसे पूरी तरह से भिन्न, ऐसे उप-सिद्धांत हैं जो पूरी तरह से इष्टतमता सिद्धांत के अंदर प्रस्तावित किए गए हैं, जैसे स्थितिगत वफादारी सिद्धांत, पत्राचार सिद्धांत (ध्वनि विज्ञान) (मैककार्थी और प्रिंस 1995), सहानुभूति सिद्धांत, स्ट्रैटल ओ.टी और सीखने की क्षमता के अनेक सिद्धांत , विशेष रूप से ब्रूस बढ़ई द्वारा। इष्टतमता सिद्धांत के अंदर अन्य सिद्धांत ध्वन्यात्मक डोमेन के अंदर व्युत्पन्न स्तरों की आवश्यकता, बाधाओं के संभावित फॉर्मूलेशन और सख्त वर्चस्व के अतिरिक्त बाधा बातचीत जैसे विवादों से संबंधित हैं।

स्वरविज्ञान के बाहर प्रयोग करें

इष्टतमता सिद्धांत सामान्यतः ध्वनिविज्ञान के क्षेत्र से जुड़ा हुआ है, किन्तु इसे भाषाविज्ञान के अन्य क्षेत्रों में भी प्रयुक्त किया गया है। जेन ग्रिमशॉ, गेराल्डिन लीजेंड्रे और ब्रेस्ना जाओ ने वाक्यविन्यास के अंदर सिद्धांत की तात्कालिकता विकसित की है।[29][30] इष्टतमता सिद्धांत संबंधी दृष्टिकोण आकृति विज्ञान (भाषा विज्ञान) (और विशेष रूप से आकृति विज्ञान-स्वर विज्ञान इंटरफ़ेस) में भी अपेक्षाकृत प्रमुख हैं।[31][32] शब्दार्थ के क्षेत्र में, इष्टतमता सिद्धांत का सामान्यतः कम उपयोग किया जाता है। किन्तु व्याख्या का एक औपचारिक मॉडल प्रदान करने के लिए बाधा-आधारित प्रणालियाँ विकसित की गई हैं।[33] इष्टतमता सिद्धांत का उपयोग व्यावहारिकता के लिए एक रूपरेखा के रूप में भी किया गया है।[34]

शब्दावली के लिए, अन्य बातों के अतिरिक्त, रिचर्ड विसे (भाषाविद्) द्वारा बाधा-आधारित विश्लेषण भी प्रस्तावित किए गए हैं।[35] और सिल्के हामन/इलारिया कोलंबो।[36] बाधाएं ध्वनि और अक्षर के मध्य संबंधों के साथ-साथ वर्तनी की प्राथमिकताओं दोनों को कवर करती हैं।

टिप्पणियाँ

  1. ↑ "Optimality". Proceedings of the talk given at Arizona Phonology Conference, University of Arizona, Tucson, Arizona.
  2. ↑ Prince, Alan, and Smolensky, Paul (1993) "Optimality Theory: Constraint interaction in generative grammar." Technical Report CU-CS-696-93, Department of Computer Science, University of Colorado at Boulder.
  3. ↑ Kager (1999), p. 20.
  4. ↑ Prince, Alan (2004). Optimality theory : constraint interaction in generative grammar. Paul Smolensky. Malden, MA: Blackwell Pub. ISBN 978-0-470-75940-0. OCLC 214281882.
  5. ↑ Merchant, Nazarré; Riggle, Jason (2016-02-01). "OT grammars, beyond partial orders: ERC sets and antimatroids". Natural Language & Linguistic Theory (in English). 34 (1): 241–269. doi:10.1007/s11049-015-9297-5. ISSN 1573-0859. S2CID 254861452.
  6. ↑ Ellison, T. Mark; Klein, Ewan (2001), "Review: The Best of All Possible Words (review of Optimality Theory: An Overview, Archangeli, Diana & Langendoen, D. Terence, eds., Blackwell, 1997)", Journal of Linguistics, 37 (1): 127–143, JSTOR 4176645.
  7. ↑ Prince & Smolensky (1993), p. 94.
  8. ↑ 8.0 8.1 McCarthy (2008), p. 27.
  9. ↑ McCarthy (2008), p. 209.
  10. ↑ Kager (1999), pp. 99–100.
  11. ↑ McCarthy (2008), p. 224.
  12. ↑ Kager (1999), pp. 29–30.
  13. ↑ 13.0 13.1 Kager (1999), pp. 392–400.
  14. ↑ McCarthy (2008), pp. 214–20.
  15. ↑ Frank, Robert; Satta, Giorgio (1998). "इष्टतमता सिद्धांत और बाधा उल्लंघन की उत्पादक जटिलता". Computational Linguistics. 24 (2): 307–315. Retrieved 5 September 2021.
  16. ↑ Tesar & Smolensky (1998), pp. 230–1, 239.
  17. ↑ McCarthy (2001), p. 247.
  18. ↑ Chomsky (1995)
  19. ↑ Dresher (1996)
  20. ↑ Hale & Reiss (2008)
  21. ↑ Halle (1995)
  22. ↑ Idsardi (2000)
  23. ↑ Idsardi (2006)
  24. ↑ Heinz, Jeffrey; Kobele, Gregory M.; Riggle, Jason (April 2009). "इष्टतमता सिद्धांत की जटिलता का मूल्यांकन". Linguistic Inquiry. 40 (2): 277–288. doi:10.1162/ling.2009.40.2.277. ISSN 0024-3892. S2CID 14131378.
  25. ↑ Kornai, András (2006). "Is OT NP-hard?" (PDF).{{cite web}}: CS1 maint: url-status (link)
  26. ↑ Kager, René (1999). Optimality Theory. Section 1.4.4: Fear of infinity, pp. 25–27.
  27. ↑ Prince, Alan and Paul Smolensky. (2004): Optimality Theory: Constraint Interaction in Generative Grammar. Section 10.1.1: Fear of Optimization, pp. 215–217.
  28. ↑ de Lacy (editor). (2007). The Cambridge Handbook of Phonology, p. 1.
  29. ↑ McCarthy, John (2001). A Thematic Guide to Optimality Theory, Chapter 4: Connections of Optimality Theory.
  30. ↑ Legendre, Grimshaw & Vikner (2001)
  31. ↑ Trommer (2001)
  32. ↑ Wolf (2008)
  33. ↑ Hendriks, Petra, and Helen De Hoop. Optimality theoretic semantics. Linguistics and philosophy 24.1 (2001): 1-32.
  34. ↑ Blutner, Reinhard; Bezuidenhout, Anne; Breheny, Richard; Glucksberg, Sam; Happé, Francesca (2003). इष्टतमता सिद्धांत और व्यावहारिकता. Springer. ISBN 978-1-349-50764-1.
  35. ↑ Wiese, Richard (2004). "ऑर्थोग्राफी को कैसे अनुकूलित करें". Written Language and Literacy. 7 (2): 305–331. doi:10.1075/wll.7.2.08wie.
  36. ↑ Hamann, Silke; Colombo, Ilaria (2017). "शब्दावली और धारणा की परस्पर क्रिया का एक औपचारिक विवरण". Natural Language & Linguistic Theory. 35 (3): 683–714. doi:10.1007/s11049-017-9362-3. S2CID 254872721.

संदर्भ

बाहरी संबंध

Retrieved from ‘https://www.vigyanwiki.in/index.php?title=इष्टतमता_सिद्धांत&oldid=221920’