खोज और अनुकूलन में कोई निःशुल्क लंच नहीं

This article is about कंप्यूटिंग का गणितीय विश्लेषण. For संबंधित लोककथाएँ और प्रमेय के व्यापक निहितार्थ, see कोई मुफ़्त लंच प्रमेय नहीं.

समस्या तीव्रता से प्रत्याशी a, b, और c के मध्य समाधान परिक्षण करना है जो किसी भी अन्य के समान उत्तम हो, जहां उत्तम या तो 0 या 1 है। समस्या के आठ उदाहरण (लंच प्लेट) हैं, जहां x, y, और z क्रमशः a, b, और c की उत्तमता को दर्शाते हैं। प्रक्रिया (रेस्तरां) a प्रत्याशी का मूल्यांकन a, b, c क्रम में करता है और b उस क्रम के विपरीत प्रत्याशी का मूल्यांकन करता है, किंतु प्रत्येक 5 स्तिथि में 1 मूल्यांकन, 2 स्तिथि में 2 मूल्यांकन और 1 स्तिथि में 3 मूल्यांकन का शुल्क लेता है।

कम्प्यूटेशनल समिष्टता सिद्धांत और अनुकूलन (गणित) में नो फ्री लंच प्रमेय परिणाम है जो बताता है कि कुछ प्रकार की गणितीय समस्याओं के लिए, समाधान परिक्षण का कम्प्यूटेशनल व्यय, कक्षा में सभी समस्याओं पर औसत, किसी भी समाधान विधि के लिए समान है यह नाम इस कथन की ओर संकेत करता है कि फ्री लंच जैसी कोई चीज़ नहीं होती, अर्थात कोई भी विधि लघु विधि प्रदान नहीं करती। यह इस धारणा के अनुसार है कि शोध स्थान संभाव्यता घनत्व फलन है। यह उस स्तिथि पर प्रारम्भ नहीं होती है जहां शोध स्थान में अंतर्निहित संरचना होती है (उदाहरण के लिए, भिन्न फलन है) जिसे यादृच्छिक परिक्षण की तुलना में अधिक कुशलता से उपयोग किया जा सकता है (उदाहरण के लिए, अनुकूलन में न्यूटन की विधि) या यहां तक ​​कि विवृत-रूप समाधान भी हैं (उदाहरण के लिए, द्विघात बहुपद का शीर्ष) जिसे बिना किसी परिक्षण के निर्धारित किया जा सकता है। ऐसी संभाव्य धारणाओं के लिए, किसी विशेष प्रकार की समस्या को समाधान करने वाली सभी प्रक्रियाओं के आउटपुट सांख्यिकीय रूप से समान होते हैं। ऐसी परिस्थिति का वर्णन करने की रंगीन विधि, परिक्षण की समस्याओं के संबंध में डेविड वोल्पर्ट और विलियम जी. मैकरेडी द्वारा प्रस्तुत किया गयायह कहना है कि कोई फ्री दोपहर का भोजन नहीं है। वोल्पर्ट ने पूर्व मशीन लर्निंग (सांख्यिकीय अनुमान) के लिए कोई निःशुल्क लंच प्रमेय नहीं निकाला था।वोल्पर्ट का लेख प्रकाशित होने से पूर्व, कुलेन शेफ़र ने स्वतंत्र रूप से वोल्पर्ट के प्रमेयों में से प्रतिबंधित संस्करण सिद्ध किया और इसका उपयोग प्रेरण की समस्या पर मशीन लर्निंग अनुसंधान की वर्तमान स्थिति की आलोचना करने के लिए किया।

फ्री लंच नहीं के रूपक में, रेस्तरां (समस्या-समाधान प्रक्रिया) में प्रत्येक लंच प्लेट (समस्या) के मान (समस्या का समाधान करने में प्रक्रिया का प्रदर्शन) के साथ जोड़ने वाला मेनू होता है। रेस्तरां के मेनू स्तिथि को छोड़कर समान हैं- व्यय एक रेस्तरां से दूसरे रेस्तरां में परिवर्तित होती रहती हैं। सर्वाहारी के लिए जो किसी अन्य के जैसे प्रत्येक प्लेट का ऑर्डर देने की संभावना रखता है, दोपहर के भोजन की औसत व्यय रेस्तरां की रूचि पर निर्भर नहीं करती है। किंतु शाकाहारी जो अल्पव्ययता चाहने वाले मांसाहारी के साथ नियमित रूप से दोपहर के भोजन के लिए किया जाता है, उसे दोपहर के भोजन के लिए उच्च औसत व्यय का भुगतान करना पड़ सकता है। औसत व्यय को व्यवस्थित रूप से कम करने के लिए, किसी को पूर्व से ज्ञात होना चाहिए कि (ए) वह क्या ऑर्डर करेगा और (बी) विभिन्न रेस्तरां में ऑर्डर की व्यय क्या होगी। अर्थात्, समस्या-समाधान के प्रदर्शन में सुधार प्रक्रियाओं को समस्याओं से मिलाने के लिए पूर्व सूचना का उपयोग करने पर निर्भर करता है।

औपचारिक शब्दों में, कोई फ्री लंच नहीं होता है जब समस्या के उदाहरणों पर संभाव्यता वितरण ऐसा होता है कि सभी समस्या समाधानकर्ताओं के परिणाम समान रूप से वितरित होते हैं। शोध एल्गोरिदम की स्तिथि में, इस संदर्भ में समस्या उदाहरण विशेष उद्देश्य फलन है, और परिणाम फलन के फलन डोमेन में प्रत्याशी समाधानों के मूल्यांकन में प्राप्त मानों का अनुक्रम है। परिणामों की विशिष्ट व्याख्याओं के लिए, शोध अनुकूलन (गणित) प्रक्रिया है। शोध में कोई निःशुल्क लंच नहीं है यदि केवल प्रत्याशी समाधानों के स्थान के क्रम परिवर्तन के अनुसार वस्तुनिष्ठ कार्यों पर वितरण अपरिवर्तनीय (गणित) है। यह स्थिति व्यवहार में त्रुटिहीन रूप से प्रारम्भ नहीं होती,किंतु (लगभग) कोई निःशुल्क लंच प्रमेय यह विचार नहीं प्रदान करता कि यह लगभग सही है।

अवलोकन

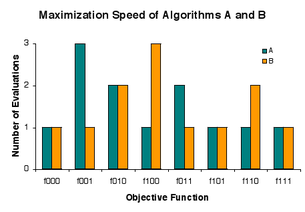
कुछ कम्प्यूटेशनल समस्याओं को प्रत्याशी समाधानों के क्षेत्र में उत्तम समाधानों का शोध करके समाधान किया जाता है। मूल्यांकन के लिए प्रत्याशी समाधानों को बार-बार कैसे चयन किया जाए, इसका विवरण शोध एल्गोरिदम कहलाता है। किसी विशेष समस्या पर, भिन्न-भिन्न शोध एल्गोरिदम भिन्न-भिन्न परिणाम प्राप्त कर सकते हैं, किंतु सभी समस्याओं पर, वे अप्रभेद्य हैं। इसका तात्पर्य यह है कि यदि कोई एल्गोरिदम कुछ समस्याओं पर उत्तम परिणाम प्राप्त करता है, तो उसे अन्य समस्याओं पर हीनता के साथ भुगतान करना होगा। इस अर्थ में शोध में कोई निःशुल्क दोपहर का भोजन नहीं है।वैकल्पिक रूप से, शेफ़र का अनुसरण करते हुए,शोध प्रदर्शन संरक्षण नियम (भौतिकी) है। सामान्यतः शोध की व्याख्या अनुकूलन (गणित) के रूप में की जाती है, और इससे यह निष्कर्ष निकलता है कि अनुकूलन में कोई फ्री लंच नहीं है।

वोलपर्ट और मैकरेडी का 'नो फ्री लंच' प्रमेय, जैसा कि वोलपर्ट और मैकरेडी ने स्पष्ट भाषा में यह कहा है, कि कोई भी दो एल्गोरिदम समतुल्य होते हैं जब उनका प्रदर्शन सभी संभावित समस्याओं के मध्य औसत होता है। निःशुल्क दोपहर के भोजन के न होने के परिणाम दर्शाते हैं कि समस्याओं के लिए एल्गोरिदम का संघ सभी के लिए निश्चित एल्गोरिदम प्रारम्भ करने की तुलना में अधिक औसत प्रदर्शन देता है। इगेल, टूसेंटऔर अंग्रेजी सामान्य नियम स्थापित किया है जिसके अनुसार फ्री दोपहर का भोजन नहीं है। चूँकि यह शारीरिक रूप से संभव है, यह त्रुटिहीन रूप से प्रारम्भ नहीं होता है।ड्रोस्टे, जेन्सन और वेगनर ने प्रमेय में सिद्ध किया है जिसकी व्याख्या वे इस प्रकार करते हैं कि व्यवहार में (लगभग) कोई फ्री दोपहर का भोजन नहीं है।

स्तिथि को अधिक ठोस बनाने के लिए, किसी समस्या का सामना करने वाले अनुकूलन व्यवसायी पर विचार करें। समस्या कैसे उत्पन्न हुई, इसके बारे में कुछ ज्ञान होने पर, अभ्यासकर्ता एल्गोरिदम के चयन में उस ज्ञान का उपयोग करने में सक्षम हो सकता है जो समस्या का समाधान करने में उत्तम प्रदर्शन करेगा। यदि अभ्यासकर्ता यह नहीं समझता है कि ज्ञान का दोहन कैसे किया जाए, या उसके पास कोई ज्ञान नहीं है, तो उसे इस सवाल का सामना करना पड़ता है कि क्या कुछ एल्गोरिदम सामान्यतः वास्तविक संसार की समस्याओं पर दूसरों से उत्तम प्रदर्शन करते हैं। (लगभग) नो फ्री लंच प्रमेय के लेखकों का कहना है कि उत्तर अनिवार्य रूप से नहीं है, किंतु इस बारे में कुछ आपत्तियां स्वीकार करते हैं कि क्या प्रमेय अभ्यास को संबोधित करता है।

प्रमेय

समस्या, अधिक औपचारिक रूप से, उद्देश्यपूर्ण फलन है जो प्रत्याशी समाधानों को उत्तम मानों के साथ जोड़ता है। शोध एल्गोरिदम वस्तुनिष्ठ फलन को इनपुट के रूप में लेता है और प्रत्याशी समाधानों का मूल्यांकन करता है। एल्गोरिथम का आउटपुट प्रेक्षित उत्तम मानों का अनुक्रम है।

वोल्पर्ट और मैकरेडी पूर्व से ही निर्धारित करते हैं कि एल्गोरिदम कभी भी प्रत्याशी समाधान का पुनर्मूल्यांकन नहीं करता है, और एल्गोरिदम का प्रदर्शन आउटपुट पर मापा जाता है। सरलता के लिए, हम एल्गोरिदम में यादृच्छिकता की अनुमति नहीं देते हैं। इन नियमों के अनुसार, जब शोध एल्गोरिदम प्रत्येक संभावित इनपुट पर चलाया जाता है, तो यह प्रत्येक संभावित आउटपुट को उत्पन्न करता है।क्योंकि प्रदर्शन को आउटपुट पर मापा जाता है, एल्गोरिदम इस बात में अप्रभेद्य हैं कि वे कितनी बार प्रदर्शन के विशेष स्तर को प्राप्त करते हैं।

प्रदर्शन के कुछ उपाय दर्शाते हैं कि उद्देश्य फलन के अनुकूलन (गणित) में शोध एल्गोरिदम कितना उत्तम प्रदर्शन करते हैं। वास्तव में, विचाराधीन वर्ग में अनुकूलन समस्याओं के अतिरिक्त शोध एल्गोरिदम का कोई लोकप्रिय अनुप्रयोग नहीं दिखता है। सामान्य प्रदर्शन माप आउटपुट अनुक्रम में सबसे कम मूल्य का सबसे छोटा सूचकांक है। यह वस्तुनिष्ठ फलन को न्यूनतम करने के लिए आवश्यक मूल्यांकनों की संख्या है। कुछ एल्गोरिदम के लिए, न्यूनतम परिक्षण करने के लिए आवश्यक समय मूल्यांकन की संख्या के समानुपाती होता है।

मूल नो फ्री लंच (एनएफएल) प्रमेय मानता है कि सभी वस्तुनिष्ठ फलनों के शोध एल्गोरिदम में इनपुट होने की समान संभावना है।तब से यह स्थापित हो गया है कि एनएफएल तभी है जब, शिथिल रूप से कहें तो, वस्तुनिष्ठ फलनों में परिवर्तन का संभावनाओं पर कोई प्रभाव नहीं पड़ता है।यद्यपि एनएफएल के लिए यह स्थिति भौतिक रूप से संभव है, यह तर्क दिया गया है कि यह निश्चित रूप से त्रुटिहीनता से प्रारम्भ नहीं होती है।

एनएफएल की स्पष्ट व्याख्या फ्री दोपहर का भोजन है, किंतु यह भ्रामक है। एनएफएल डिग्री की स्तिथि है, सब कुछ या कुछ नहीं का प्रस्ताव नहीं है। यदि एनएफएल के लिए नियम लगभग प्रारम्भ होता है, तो सभी एल्गोरिदम सभी उद्देश्य फलनों पर लगभग समान परिणाम देते हैं।एनएफएल का तात्पर्य केवल यह नहीं है कि प्रदर्शन के कुछ मापों के आधार पर एल्गोरिदम समग्र रूप से असमान हैं। रुचि के प्रदर्शन माप के लिए, एल्गोरिदम समतुल्य, या लगभग इतना ही रह सकता है।

कोलमोगोरोव यादृच्छिकता

सभी संभावित फलन के समुच्चय लगभग सभी तत्व (फलन के समुच्चय-सैद्धांतिक अर्थ में) कोलमोगोरोव यादृच्छिकता हैं, और इसलिए एनएफएल प्रमेय फलन के समुच्चय पर प्रारम्भ होते हैं जिनमें से लगभग सभी को लुकअप तालिका की तुलना में अधिक कॉम्पैक्ट रूप से व्यक्त नहीं किया जा सकता है शोध स्थान में प्रत्येक बिंदु के लिए भिन्न (और यादृच्छिक) प्रविष्टि सम्मिलित है। वे फलन जिन्हें अधिक संक्षिप्त रूप से व्यक्त किया जा सकता है (उदाहरण के लिए, उचित आकार की गणितीय अभिव्यक्ति द्वारा) परिभाषा के अनुसार कोलमोगोरोव यादृच्छिक नहीं हैं।

इसके अतिरिक्त, सभी संभावित वस्तुनिष्ठ फलनों के समुच्चय के भीतर, प्रत्याशी समाधानों के मध्य उत्तम के स्तर को समान रूप से दर्शाया जाता है, इसलिए उत्तम समाधान प्रत्याशी के पूर्ण स्थान पर विस्तारित हैं। तदनुसार, शोध एल्गोरिदम अधिक उत्तम समाधान परिक्षण करने से पूर्व संभवतः ही कभी प्रत्याशी के छोटे भाग से अधिक का मूल्यांकन करेगा।

लगभग सभी वस्तुनिष्ठ फलन इतनी उच्च कोलमोगोरोव समिष्टता के हैं कि उन्हें किसी विशेष कंप्यूटर में संग्रहीत नहीं किया जा सकता है।अधिक त्रुटिहीन रूप से, यदि हम किसी दिए गए भौतिक कंप्यूटर को आधुनिक कंप्यूटर की मेमोरी के क्रम में दिए गए आकार की मेमोरी के साथ रजिस्टर मशीन के रूप में मॉडल करते हैं, तो अधिकांश उद्देश्य फलनों को उनकी मेमोरी में संग्रहीत नहीं किया जा सकता है। विशिष्ट वस्तुनिष्ठ फलन या एल्गोरिदम में सेठ लॉयड के अनुमान से अधिक जानकारी है कि अवलोकन योग्य ब्रह्मांड पंजीकरण करने में सक्षम है। उदाहरण के लिए, यदि प्रत्येक प्रत्याशी समाधान को 300 0 और 1 के अनुक्रम के रूप में एन्कोड किया गया है, और उत्तम मान 0 और 1 हैं, तो अधिकांश उद्देश्य फलनों में कोलमोगोरोव समिष्टता कम से कम 2³⁰⁰ बिट्स है, और यह लॉयड की 10⁹⁰ ≈ 2²⁹⁹ बिट्स की सीमा से अधिक है इसका तात्पर्य यह है कि मूल नो फ्री लंच प्रमेय उस चीज़ पर प्रारम्भ नहीं होता है जिसे भौतिक कंप्यूटर में संग्रहीत किया जा सकता है; इसके अतिरिक्त तथाकथित समिष्ट नो फ्री लंच प्रमेय को प्रारम्भ करने की आवश्यकता है। यह भी दिखाया गया है कि एनएफएल परिणाम अतुलनीय कार्यों पर प्रारम्भ होते हैं।

औपचारिक सारांश

$Y^{X}$ सभी वस्तुनिष्ठ फलनों का समुच्चय f:X→Y है, जहाँ $X$ परिमित समाधान समिष्ट है और $Y$ परिमित स्थिति है, X के सभी क्रम परिवर्तनों का समुच्चय J है। यादृच्छिक चर F वितरित किया गया है $Y^{X}$, J में सभी J के लिए, F o j यादृच्छिक चर वितरित किया गया है $Y^{X}$, सभी f के लिए P(F o j = f) = P(F = f o j⁻¹) औए $Y^{X}$ है।

मान लीजिए a(f) इनपुट f पर शोध एल्गोरिदम a के आउटपुट को दर्शाता है। यदि a(F) और b(F) को सभी शोध एल्गोरिदम a और b के लिए समान रूप से वितरित किया जाता है, तो F के पास एनएफएल वितरण है। यह नियम तभी प्रारम्भ होता है जब F और F o j को J में सभी J के लिए समान रूप से वितरित किया जाता है।दूसरे शब्दों में, शोध एल्गोरिदम के लिए कोई फ्री लंच नहीं है यदि केवल समाधान स्थान के क्रम परिवर्तन के अनुसार उद्देश्य फलनो का वितरण अपरिवर्तनीय है। समुच्चय-सैद्धांतिक एनएफएल प्रमेयों को वर्तमान में कार्डिनैलिटी के लिए $X$ और $Y$ में सामान्यीकृत किया गया है।

उत्पत्ति

वोल्पर्ट और मैकरेडी दो प्रमुख एनएफएल प्रमेय देते हैं, प्रथम वस्तुनिष्ठ फलनो के बारे में जो शोध प्रारंभ रहने के समय नहीं परिवर्तित होते हैं, और दूसरा वस्तुनिष्ठ फलनो के बारे में जो परिवर्तित हो सकते हैं।

प्रमेय 1: एल्गोरिदम की जोड़ी के लिए a₁ और a₂

$\sum _{f}P(d_{m}^{y}|f,m,a_{1})=\sum _{f}P(d_{m}^{y}|f,m,a_{2}),$ जहाँ $d_{m}^{y}$ आकार के क्रमबद्ध समुच्चय को दर्शाता है $m$ व्यय मानों का $y\in Y$ इनपुट मानों से संबद्ध $x\in X$, $f:X\rightarrow Y$ क्या फलन को अनुकूलित किया जा रहा है और $P(d_{m}^{y}|f,m,a)$ एल्गोरिथम से व्यय मानों के दिए गए अनुक्रम को प्राप्त करने की सशर्त संभावना है $a$ और $m$ फलन में कई बार $f$ उपस्थित है।

संक्षेप में, यह कहता है कि जब सभी फलन f समान रूप से संभावित होते हैं, तो शोध के समय m मानों के अनुक्रम को देखने की संभावना शोध एल्गोरिदम पर निर्भर नहीं होती है।

दूसरा प्रमेय समय-भिन्न उद्देश्य फलनो के लिए अधिक सूक्ष्म एनएफएल परिणाम स्थापित करता है।

परिणामों की व्याख्या

एनएफएल परिणामों की पारंपरिक, किंतु पूर्ण रूप से त्रुटिहीन नहीं, व्याख्या यह है कि सामान्य-उद्देश्य वाली सार्वभौमिक अनुकूलन रणनीति सैद्धांतिक रूप से असंभव है, और रणनीति दूसरे से उत्तम प्रदर्शन तभी कर सकती है जब वह विचाराधीन विशिष्ट समस्या के लिए विशिष्ट हो। कई टिप्पणियाँ क्रम में हैं:

• सैद्धांतिक रूप से सामान्य-उद्देश्य वाला लगभग-सार्वभौमिक अनुकूलक उपस्तिथ है। प्रत्येक शोध एल्गोरिदम लगभग सभी वस्तुनिष्ठ फलनो पर उत्तम प्रदर्शन करता है।इसलिए यदि कोई शोध एल्गोरिदम के मध्य अपेक्षाकृत छोटे अंतरों से चिंतित नहीं है, उदाहरण के लिए, क्योंकि कंप्यूटर का समय मूल्यहीन है, तो आपको फ्री दोपहर के भोजन के बारे में ध्यान नहीं देना चाहिए।

• एल्गोरिथ्म किसी समस्या पर दूसरे से उत्तम प्रदर्शन कर सकता है जब दोनों में से कोई भी समस्या के लिए विशेषज्ञ न हो। वास्तव में, ऐसा हो सकता है कि दोनों एल्गोरिदम समस्या के लिए सबसे व्यर्थ हों। अधिक सामान्यतः, वोल्पर्ट और मैकरेडी ने एल्गोरिदम और समस्याओं पर वितरण (कठिनता से कहें तो, आंतरिक उत्पाद) के मध्य संरेखण की डिग्री का माप विकसित किया है।यह कहने का तात्पर्य यह नहीं है कि एल्गोरिदम किसी वितरण से दूसरे से उत्तम युग्मित होता है, इसका तात्पर्य यह नहीं है कि उनमें से किसी को निश्चयपूर्वक वितरण के लिए विशेषीकृत किया गया है; किसी एल्गोरिथम में केवल भाग्य से उत्तम संरेखण हो सकता है।

• व्यवहार में, कुछ एल्गोरिदम प्रत्याशी समाधानों का पुनर्मूल्यांकन करते हैं। केवल पूर्व कभी मूल्यांकन न किए गए प्रत्याशी के प्रदर्शन पर विचार करने का कारण यह सुनिश्चित करना है कि एल्गोरिदम की तुलना करते समय एप्पल की तुलना एप्पल से की जा रही है। इसके अतिरिक्त, किसी एल्गोरिदम की श्रेष्ठता जो कभी भी किसी अन्य एल्गोरिदम पर प्रत्याशी का पुनर्मूल्यांकन नहीं करती है जो किसी विशेष समस्या पर करता है, उसका समस्या की विशेषज्ञता से कोई सम्बन्ध नहीं हो सकता है।

• लगभग सभी वस्तुनिष्ठ फलनो के लिए, विशेषज्ञता अनिवार्य रूप से अकारण है। जहाँ तक कोलमोगोरोव यादृच्छिकता को परिभाषित करने के लिए उपयोग की जाने वाली सार्वभौमिक ट्यूरिंग मशीनिंग का संबंध है, असम्पीडित, या कोलमोगोरोव यादृच्छिकता, उद्देश्य फलनो में एल्गोरिथ्म के शोषण के लिए कोई नियमितता नहीं है। तो मान लीजिए कि सार्वभौमिक ट्यूरिंग मशीन का, स्पष्ट रूप से उत्तम विकल्प है। फिर ऑब्जेक्टिव फलन दिया गया है जो उस ट्यूरिंग मशीन के लिए असम्पीडित है, दो एल्गोरिदम के मध्य चयन करने का कोई आधार नहीं है यदि दोनों संपीड़ित हैं, जैसा कि उस ट्यूरिंग मशीन का उपयोग करके मापा जाता है। यदि कोई चयन किया गया एल्गोरिदम अधिकांश से उत्तम प्रदर्शन करता है, तो परिणाम घटित होता है।कोलमोगोरोव यादृच्छिक फलन का लुकअप तालिका से छोटा कोई प्रतिनिधित्व नहीं होता है जिसमें शोध स्थान में प्रत्येक बिंदु के अनुरूप (यादृच्छिक) मान होता है; कोई भी फलन जिसे अधिक संक्षिप्त रूप से व्यक्त किया जा सकता है, परिभाषा के अनुसार, कोलमोगोरोव यादृच्छिक नहीं है।

व्यवहार में, केवल अत्यधिक संपीड़ित (यादृच्छिक से दूर) उद्देश्य फलन कंप्यूटर के भंडारण में फिट होते हैं, और ऐसा नहीं है कि प्रत्येक एल्गोरिदम लगभग सभी संपीड़ित फलनो पर उत्तम प्रदर्शन करता है। एल्गोरिथम में समस्या के पूर्व ज्ञान को सम्मिलित करने में सामान्यतः प्रदर्शन लाभ होता है। जबकि एनएफएल परिणाम, कठिन अर्थ में, अनुकूलन व्यवसायी के लिए पूर्ण रोजगार प्रमेय का गठन करते हैं, बड़े संदर्भ को ध्यान में रखना महत्वपूर्ण है। विचार के लिए, मनुष्यों के पास प्रायः कार्य करने के लिए अधिक कम पूर्व ज्ञान होता है। दूसरे के लिए, पूर्व ज्ञान को सम्मिलित करने से कुछ समस्याओं पर अधिक प्रदर्शन लाभ नहीं मिलता है। अंततः, कंप्यूटर समय की तुलना में मानव का समय अधिक मूल्यवान है। ऐसे कई स्तिथि हैं जिनमें कोई कंपनी मानव-संशोधित प्रोग्राम के अतिरिक्त तीव्रता से अनमॉडिफाइड कंप्यूटर प्रोग्राम के साथ किसी फलन को धीरे-धीरे अनुकूलित करने में रूचि रखती है।

एनएफएल परिणाम यह संकेत नहीं देते हैं कि गैर-विशिष्ट एल्गोरिदम के साथ समस्याओं पर पॉट शॉट लेना व्यर्थ है। किसी ने भी उन व्यावहारिक समस्याओं का भाग निर्धारित नहीं किया है जिनके लिए एल्गोरिदम तीव्रता से उत्तम परिणाम देता है। और वहाँ व्यावहारिक फ्री दोपहर का भोजन है, सिद्धांत के साथ भी विरोधाभास नहीं है। कंप्यूटर पर एल्गोरिदम के कार्यान्वयन को चलाने में मानव समय का व्यय और उत्तम समाधान के लाभ के सापेक्ष अधिक कम व्यय आता है। यदि कोई एल्गोरिदम स्वीकार्य समय में संतोषजनक समाधान परिक्षण करने में सफल होता है, तो छोटे से निवेश से बड़ा लाभ मिलता है। यदि एल्गोरिथम विफल हो जाता है, तो अधिक कम हानि होती है।

सहविकास

वोल्पर्ट और मैकरेडी ने सिद्ध कर दिया है कि सहविकासवादी अनुकूलन में फ्री लंच हैं। उनके विश्लेषण में 'स्वयं-खेल' समस्याओं को सम्मिलित किया गया है। इन समस्याओं में, खिलाड़ियों का समूह चैंपियन तैयार करने के लिए मिलकर कार्य करता है, जो पश्चात के मल्टीप्लेयर गेम में या अधिक विरोधियों को सम्मिलित करता है।अर्थात्, उद्देश्य उत्तम खिलाड़ी प्राप्त करना है, किंतु बिना किसी वस्तुनिष्ठ कार्य के प्रत्येक खिलाड़ी (प्रत्याशीसमाधान) का उत्तम आकलन यह देखकर किया जाता है कि वह दूसरों के विपरीत कितना अच्छा खेलता है। एल्गोरिदम उत्तम खिलाड़ी प्राप्त करने के लिए खिलाड़ियों और उनके खेल की गुणवत्ता का उपयोग करने का प्रयास करता है। एल्गोरिथम द्वारा सबसे उतम समझा जाने वाला खिलाड़ी चैंपियन होता है। वोल्पर्ट और मैकरेडी ने पूर्व में ही प्रदर्शित कर दिया है कि कुछ सह-विकासवादी एल्गोरिदम सामान्यतः प्राप्त चैंपियनों की गुणवत्ता में अन्य एल्गोरिदम से उत्तम होते हैं। स्व-खेल के माध्यम से चैंपियन उत्पन्न करना विकासवादी गणना और गेम सिद्धांत में रुचि रखता है। परिणाम जैविक प्रजातियों के सह-विकास पर प्रारम्भ नहीं होते हैं, जिससे चैंपियन नहीं मिलते हैं।

यह भी देखें

• विकासवादी सूचना विज्ञान
• इंडक्टिव बायस
• ओकम रेजर  
• सिम्प्लिसिटी
• अग्ली डकलिंग प्रमेय

बाहरी संबंध

• http://www.no-free-lunch.org
• Radcliffe and Surry, 1995, "Fundamental Limitations on Search Algorithms: Evolutionary Computing in Perspective" (an early published paper on एनएफएल, appearing soon after Schaffer's ICML paper, which in turn was based on Wolpert's preprint; available in various formats)
• एनएफएल publications by Thomas English
• एनएफएल publications by Christian Igel and Marc Toussaint
• एनएफएल and "free lunch" publications by Darrell Whitley
• Old list of publications by David Wolpert, William Macready, and Mario Koeppen on optimization and search