विस्तार योग्य हैशिंग
एक्सटेंडिबल हैशिंग एक प्रकार का हैश सिस्टम है जो हैश को एक बिट स्ट्रिंग के रूप में मानता है और बकेट लुकअप के लिए ट्राई का उपयोग करता है।।[1] सिस्टम की पदानुक्रमित प्रकृति के कारण, री-हैशिंग एक वृद्धिशील ऑपरेशन है (आवश्यकतानुसार एक समय में एक बाल्टी किया जाता है)। इसका मतलब यह है कि समय-संवेदनशील अनुप्रयोग मानक पूर्ण-टेबल्स रीहैश की तुलना में टेबल्स वृद्धि से कम प्रभावित होते हैं।
एक्सटेंडिबल हैशिंग का वर्णन 1979 में रोनाल्ड फागिन द्वारा किया गया था। व्यावहारिक रूप से सभी आधुनिक फ़ाइल सिस्टम या तो एक्सटेंडिबल हैशिंग या बी-ट्री का उपयोग करते हैं। विशेष रूप से, ग्लोबल फ़ाइल सिस्टम, ZFS और SpadFS फ़ाइल सिस्टम विस्तार योग्य हैशिंग का उपयोग करते हैं[2]
उदाहरण
मान लें कि हैश फ़ंक्शन बिट्स की एक स्ट्रिंग लौटाता है। प्रत्येक स्ट्रिंग के पहले i बिट्स को सूचकांक के रूप में उपयोग किया जाएगा ताकि यह पता लगाया जा सके कि वे निर्देशिका (हैश टेबल्स) में कहां जाएंगे। इसके अतिरिक्त, i सबसे छोटी संख्या है जिससे टेबल्स में प्रत्येक आइटम का सूचकांक अद्वितीय होता है।
उपयोग की जाने वाली कुंजियाँ (कीस):
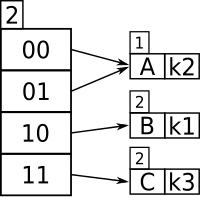
आइए मान लें कि इस विशेष उदाहरण के लिए, बाल्टी का आकार 1 है। डाली जाने वाली पहली दो कुंजियाँ, k1 और k2, को सबसे महत्वपूर्ण बिट द्वारा अलग किया जा सकता है, और टेबल्स में निम्नानुसार डाली जाएगी:

- अब, यदि k3 को टेबल्स में हैश किया जाता है, तो यह सभी तीन कीस को एक बिट से अलग करने के लिए पर्याप्त नहीं होगा (क्योंकि k3 और k1 दोनों में 1 उनके सबसे बाएं बिट के रूप में है)। इसके अतिरिक्त, क्योंकि बाल्टी का आकार एक है, टेबल ओवरफ्लो हो जाएगी। क्योंकि पहले दो सबसे महत्वपूर्ण बिट्स की तुलना करने से प्रत्येक कुंजी (Key) को एक अद्वितीय स्थान मिलेगा, निर्देशिका का आकार निम्नानुसार दोगुना हो गया है:

- और इसलिए अब k1 और k3 इसका एक अद्वितीय स्थान है, जो कि पहले दो सबसे बाईं ओर के बिट्स द्वारा पहचाना जाता है। क्योंकि k2 टेबल्स के शीर्ष भाग में है, 00 और 01 दोनों इसे इंगित करते हैं क्योंकि 0 से प्रारंभ होने वाली कुंजी की तुलना करने के लिए कोई अन्य कुंजी नहीं है।
उपरोक्त उदाहरण से है Fagin et al. (1979).
आगे का विवरण
अब, K4 डालने की आवश्यकता है, और इसमें पहले दो बिट्स 01..(1110) हैं, और निर्देशिका में 2 बिट गहराई का उपयोग करते हुए, यह 01 से बकेट A तक मैप करता है। बकेट A भरा हुआ है (अधिकतम आकार 1), इसलिए यह विभाजित होना चाहिए; क्योंकि बकेट A में एक से अधिक पॉइंटर हैं, इसलिए निर्देशिका का आकार बढ़ाने की कोई आवश्यकता नहीं है।
इसके बारे में जानकारी की आवश्यकता है:
- कुंजी का आकार जो निर्देशिका को मैप करता है (ग्लोबल डेप्थ), और
- कुंजी आकार जिसने पहले बकेट (लोकल डेप्थ) को मैप किया है
दो क्रिया मामलों में अंतर करने के लिए:
- जब एक बाल्टी भर जाती है तो निर्देशिका को दोगुना करना
- एक नई बकेट बनाना, और पुरानी और नई बकेट के बीच प्रविष्टियों को फिर से वितरित करना
एक विस्तार योग्य हैश संरचना के प्रारंभिक मामले की जांच करते हुए, यदि प्रत्येक निर्देशिका प्रविष्टि एक बाल्टी की ओर इंगित करती है, तो लोकल डेप्थ ग्लोबल डेप्थ के बराबर होनी चाहिए।
निर्देशिका प्रविष्टियों की संख्या 2ग्लोबल डेप्थ के बराबर है, और बकेट की प्रारंभिक संख्या 2लोकल डेप्थ के बराबर है।
इस प्रकार यदि ग्लोबल डेप्थ = लोकल डेप्थ = 0, तो 20 = 1, इसलिए एक सूचक से एक बाल्टी तक की प्रारंभिक निर्देशिका है।
दो क्रिया मामलों पर वापस जाएं; यदि बाल्टी भरी है:
- यदि लोकल डेप्थ ग्लोबल डेप्थ के बराबर है, तो बाल्टी में केवल एक सूचक है, और कोई अन्य निर्देशिका सूचक नहीं है जो बाल्टी में मैप कर सके, इसलिए निर्देशिका को दोगुना किया जाना चाहिए।
- यदि लोकल डेप्थ ग्लोबल डेप्थ से कम है, तो निर्देशिका से बकेट तक एक से अधिक पॉइंटर उपस्थित हैं, और बकेट को विभाजित किया जा सकता है।
- कुंजी 01 बकेट A को इंगित करती है, और बकेट A की 1 की लोकल डेप्थ निर्देशिका की 2 की ग्लोबल डेप्थ से कम है, जिसका अर्थ है कि बकेट A में हैश की गई कीस ने केवल 1 बिट उपसर्ग (यानी 0) का उपयोग किया है, और बाल्टी को इसकी आवश्यकता है 1 + 1 = 2 बिट लंबाई वाली कीस का उपयोग करके सामग्री को विभाजित किया गया; सामान्य तौर पर, किसी भी लोकल डेप्थ d के लिए जहां d ग्लोबल डेप्थ D से कम है, तो बाल्टी विभाजन के बाद d को बढ़ाया जाना चाहिए, और नई बकेट की प्रविष्टियों को नई बकेट में पुनर्वितरित करने के लिए प्रत्येक प्रविष्टि कुंजी के बिट्स की संख्या के रूप में नए d का उपयोग किया जाता है।
पुनः प्रयास किया गया है, 2 बिट्स 01 के साथ..., और अब कुंजी 01 एक नई बकेट की ओर संकेत करती है लेकिन अभी भी है इस में ( और 01) से प्रारंभ होता है।
अगर 000110 होता, कुंजी 00 के साथ, कोई समस्या नहीं होती, क्योंकि नई बाल्टी A' में रह जाती और बाल्टी D खाली हो जाती है।
(यह अब तक का सबसे अधिक संभावित मामला होगा जब बाल्टियाँ 1 से अधिक आकार की हों और नई विभाजित बाल्टियों के ओवरफ्लो होने की अत्यधिक संभावना नहीं होगी, जब तक कि सभी प्रविष्टियाँ फिर से एक बाल्टी में न दोहरा दी जाएँ। लेकिन सिर्फ भूमिका पर जोर देने के लिए गहराई से जानकारी, उदाहरण को अंत तक तार्किक रूप से आगे बढ़ाया जाएगा।)
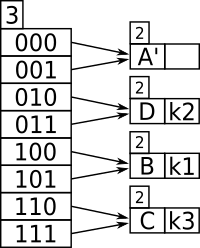
इसलिए बकेट D को विभाजित करने की आवश्यकता है, लेकिन इसकी लोकल डेप्थ की जांच, जो कि 2 है, ग्लोबल डेप्थ के समान है, जो कि 2 है, इसलिए पर्याप्त विवरण की कुंजी रखने के लिए निर्देशिका को फिर से विभाजित किया जाना चाहिए, जैसे 3 बिट्स.
- बाल्टी D भरी होने के कारण उसको विभाजित करने की आवश्यकता है।
- चूंकि D की लोकल डेप्थ = ग्लोबल डेप्थ, कीस का बिट विवरण बढ़ाने के लिए निर्देशिका को दोगुना होना चाहिए।
- निर्देशिका के 3 तक विभाजित होने के बाद ग्लोबल डेप्थ बढ़ गई है।
- नई प्रविष्टि को ग्लोबल डेप्थ 3 बिट्स के साथ पुनः कुंजीबद्ध किया गया है और D में समाप्त होता है जिसकी लोकल डेप्थ 2 है, जिसे अब 3 तक बढ़ाया जा सकता है और D को D' और E में विभाजित किया जा सकता है।
- विभाजित बाल्टी D की सामग्री, , 3 बिट्स के साथ पुनः कुंजीबद्ध किया गया है, और यह D' में समाप्त होता है।
- K4 का पुनः प्रयास किया गया और यह E पर समाप्त हुआ जिसमें एक अतिरिक्त स्लॉट है।

- अब, D में है और 3 बिट्स 011.. के साथ फिर से प्रयास किया गया है, और यह बकेट D की ओर संकेत करता है जिसमें पहले से ही उपस्थित है तो पूर्ण है; D की लोकल डेप्थ 2 है, लेकिन निर्देशिका के दोहरीकरण के बाद अब ग्लोबल डेप्थ 3 है, इसलिए अब D को बकेट के D' और E, D की सामग्री में विभाजित किया जा सकता है। है अपना 3 और के नए ग्लोबल डेप्थ बिटमास्क के साथ पुनः प्रयास किया गया D' में समाप्त होता है, फिर नई प्रविष्टि के साथ पुनः प्रयास किया गया है 3 की नई ग्लोबल डेप्थ बिट गिनती का उपयोग करके बिटमास्क किया गया और यह 011 देता है जो अब एक नई बाल्टी ई को इंगित करता है जो खाली है। इसलिए बकेट ई में जाता है।
उदाहरण कार्यान्वयन
नीचे पायथन (प्रोग्रामिंग लैंग्वेज) में विस्तार योग्य हैशिंग एल्गोरिदम है, जिसमें डिस्क ब्लॉक/मेमोरी पेज एसोसिएशन, कैशिंग और स्थिरता समस्याएं हटा दी गई हैं। ध्यान दें कि यदि गहराई किसी पूर्णांक के बिट आकार से अधिक हो जाती है तो समस्या उपस्थित होती है, क्योंकि तब निर्देशिका को दोगुना करने या बकेट को विभाजित करने से प्रविष्टियों को अलग-अलग बकेट में दोबारा रखने की अनुमति नहीं मिलेगी।
कोड कम से कम महत्वपूर्ण बिट्स का उपयोग करता है, जो टेबल्स का विस्तार करने के लिए इसे और अधिक कुशल बनाता है, क्योंकि संपूर्ण निर्देशिका को एक ब्लॉक के रूप में कॉपी किया जा सकता है (Ramakrishnan & Gehrke (2003)).
पायथन उदाहरण
PAGE_SZ = 10
class Page:
def __init__(self) -> None:
self.map = []
self.local_depth = 0
def full(self) -> bool:
return len(self.map) >= PAGE_SZ
def put(self, k, v) -> None:
for i, (key, value) in enumerate(self.map):
if key == k:
del self.map[i]
break
self.map.append((k, v))
def get(self, k):
for key, value in self.map:
if key == k:
return value
def get_local_high_bit(self):
return 1 << self.local_depth
class ExtendibleHashing:
def __init__(self) -> None:
self.global_depth = 0
self.directory = [Page()]
def get_page(self, k):
h = hash(k)
return self.directory[h & ((1 << self.global_depth) - 1)]
def put(self, k, v) -> None:
p = self.get_page(k)
full = p.full()
p.put(k, v)
if full:
if p.local_depth == self.global_depth:
self.directory *= 2
self.global_depth += 1
p0 = Page()
p1 = Page()
p0.local_depth = p1.local_depth = p.local_depth + 1
high_bit = p.get_local_high_bit()
for k2, v2 in p.map:
h = hash(k2)
new_p = p1 if h & high_bit else p0
new_p.put(k2, v2)
for i in range(hash(k) & (high_bit - 1), len(self.directory), high_bit):
self.directory[i] = p1 if i & high_bit else p0
def get(self, k):
return self.get_page(k).get(k)
if __name__ == "__main__":
eh = ExtendibleHashing()
N = 10088
l = list(range(N))
import random
random.shuffle(l)
for x in l:
eh.put(x, x)
print(l)
for i in range(N):
print(eh.get(i))
टिप्पणियाँ
- ↑ Fagin et al. (1979).
- ↑ Mikuláš Patocka (2006). स्पैड फ़ाइल सिस्टम का डिज़ाइन और कार्यान्वयन (PDF) (Thesis). "Section 4.1.6 Extendible hashing: ZFS and GFS" and "Table 4.1: Directory organization in filesystems"
यह भी देखें
- प्रयास करें
- हैश टेबल्स
- स्थिर हैशिंग
- लगातार हैशिंग
- रैखिक हैशिंग
संदर्भ
- Fagin, R.; Nievergelt, J.; Pippenger, N.; Strong, H. R. (September 1979), "Extendible Hashing - A Fast Access Method for Dynamic Files", ACM Transactions on Database Systems, 4 (3): 315–344, doi:10.1145/320083.320092, S2CID 2723596
- Ramakrishnan, R.; Gehrke, J. (2003), Database Management Systems, 3rd Edition: Chapter 11, Hash-Based Indexing, pp. 373–378
- Silberschatz, Abraham; Korth, Henry; Sudarshan, S., Database System Concepts, Sixth Edition: Chapter 11.7, Dynamic Hashing
बाहरी संबंध
 This article incorporates public domain material from Black, Paul E. "Extendible hashing". Dictionary of Algorithms and Data Structures.
This article incorporates public domain material from Black, Paul E. "Extendible hashing". Dictionary of Algorithms and Data Structures.- Extendible Hashing notes at Arkansas State University
- Extendible hashing notes
- Slides from the database System Concepts book on extendible hashing for hash based dynamic indices