त्रिकोणमिति का उपयोग

अंतर्राष्ट्रीय अंतरिक्ष स्टेशन पर कनाडार्म2 रोबोटिक मैनिपुलेटर इसके जोड़ों के कोणों को नियंत्रित करके संचालित होता है। भुजा के अंत में अंतरिक्ष यात्री की अंतिम स्थिति की गणना के लिए उन कोणों के त्रिकोणमितीय फलनों के पुनः उपयोग की आवश्यकता होती है।

गैर-गणितज्ञों और गैर-वैज्ञानिकों की सामान्य जनता के मध्य, त्रिकोणमिति मुख्य रूप से माप समस्याओं के लिए एवं अपने अनुप्रयोग के लिए जानी जाती है, तत्पश्चात इसका उपयोग अधिकांशतः उन विधियों द्वारा भी किया जाता है जो कहीं अधिक सूक्ष्म होती हैं, जिस प्रकार संगीत सिद्धांत में इसका स्थान है; इसके पश्चात् भी अन्य उपयोग जैसे संख्या सिद्धांत अधिक तकनीकी हैं। फूरियर श्रृंखला और फूरियर रूपांतरण के गणितीय विषय त्रिकोणमितीय फलनों के ज्ञान पर अत्यधिक निर्भर करते हैं और सांख्यिकी सहित कई क्षेत्रों में अनुप्रयोग प्राप्त करते हैं।

थॉमस पेन का कथन

द एज ऑफ रीज़न के अध्याय XI में, अमेरिकी क्रांतिकारी और ज्ञानोदय विचारक थॉमस पेन ने अंकित किया:

मनुष्य किसी ग्रहण अथवा आकाशीय पिंडों की गति से संबंधित किसी अन्य वस्तु का पूर्वज्ञान प्राप्त करने के लिए जिन वैज्ञानिक सिद्धांतों का उपयोग करता है, वे मुख्य रूप से विज्ञान के उस भाग में निहित होते हैं जिसे त्रिकोणमिति, अथवा त्रिकोण के गुण कहा जाता है, जिसे जब स्वर्गीय पिंडों के अध्ययन पर प्रयुक्त किया जाता है, तो इसे खगोल विज्ञान कहा जाता है; जब इसका उपयोग समुद्र में जलयान के मार्ग को निर्देशित करने के लिए किया जाता है, तो इसे नेविगेशन कहा जाता है; जब इसे रूलर और कम्पास द्वारा बनाई गई आकृतियों के निर्माण पर प्रयुक्त किया जाता है, तो इसे ज्यामिति कहा जाता है; जब भवनों की योजनाओं के निर्माण पर प्रयुक्त किया जाता है, तो इसे वास्तुकला कहा जाता है; जब इसे पृथ्वी की सतह के किसी भाग के माप पर प्रयुक्त किया जाता है, तो इसे भूमि-सर्वेक्षण कहा जाता है। वस्तुतः यह विज्ञान की आत्मा है। यह शाश्वत सत्य है: इसमें वह गणितीय प्रदर्शन सम्मिलित है जिसके संबंध में मनुष्य बोलता है, और इसके उपयोग की सीमा अज्ञात है।

इतिहास

महान त्रिकोणमितीय सर्वेक्षण

Main article: महान त्रिकोणमितीय सर्वेक्षण

1802 से 1871 तक, महान त्रिकोणमितीय सर्वेक्षण भारतीय उपमहाद्वीप का उच्च परिशुद्धता के साथ सर्वेक्षण करने की परियोजना थी। तटीय आधार रेखा से प्रारम्भ करके, गणितज्ञों और भूगोलवेत्ताओं ने देश भर में विशाल दूरियों को त्रिकोणित किया। प्रमुख उपलब्धियों में हिमालय पर्वत की ऊंचाई को मापना और यह निर्धारित करना था कि माउंट एवरेस्ट पृथ्वी पर सबसे ऊंचा स्थान है।

गुणन के लिए ऐतिहासिक उपयोग

1614 में लघुगणक के आविष्कार से पूर्व 25 वर्षों तक, गुणनफलों को शीघ्रता से अनुमानित करने की एकमात्र ज्ञात सामान्यतः प्रयुक्त विधि प्रोस्थैफेरेसिस थी। इसने उन कोणों के त्रिकोणमितीय फलनों के गुणनफलों के संदर्भ में कोणों के योग और अंतर के त्रिकोणमितीय फलनों के लिए प्रमाण का उपयोग किया।

कुछ आधुनिक उपयोग

त्रिकोणमिति का उपयोग करने वाले वैज्ञानिक क्षेत्रों में सम्मिलित हैं:

ध्वनिकी, वास्तुकला, खगोल विज्ञान, मानचित्रकला, सिविल अभियांत्रिकी, भूभौतिकी, क्रिस्टलोग्राफी, विद्युतीय अभियांत्रिकी, इलेक्ट्रानिक्स, भूमि सर्वेक्षण और भूगणित, कई भौतिक विज्ञान, यांत्रिक अभियांत्रिकी, मशीनीकरण, मेडिकल इमेजिंग, संख्या सिद्धांत, समुद्र विज्ञान, प्रकाशिकी, फार्माकोलॉजी, प्रायिकता सिद्धांत, भूकंप विज्ञान, सांख्यिकी और दृश्य धारणा

इन क्षेत्रों में त्रिकोणमिति सम्मिलित है इसका अर्थ यह नहीं है कि उनके संबंध में कुछ भी अध्ययन करने के लिए त्रिकोणमिति का ज्ञान आवश्यक है। इसका अर्थ यह है कि इन क्षेत्रों में कुछ वस्तुओं का त्रिकोणमिति के बिना अध्ययन नहीं किया जा सकता है। उदाहरण के लिए, संगीत के प्रोफेसर को संभवतः गणित के संबंध में कुछ ज्ञात नहीं होगा, किन्तु संभवतः उसे यह ज्ञात होगा कि संगीत के गणितीय सिद्धांत में पाइथागोरस सर्वप्रथम ज्ञात योगदानकर्ता था।

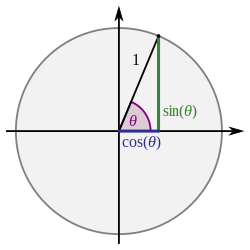
उपरोक्त सारिणी प्रयास के कुछ क्षेत्रों में यह कल्पना करना सरल होता है कि त्रिकोणमिति का उपयोग किस प्रकार किया जा सकता है। उदाहरण के लिए, नेविगेशन और भूमि सर्वेक्षण में, त्रिकोणमिति के उपयोग के अवसर कम से कम कुछ स्थितियों में इतने सरल होते हैं कि उन्हें प्रारंभिक त्रिकोणमिति पाठ्यपुस्तक में वर्णित किया जा सकता है। संगीत सिद्धांत की स्थिति में, त्रिकोणमिति का अनुप्रयोग पाइथागोरस द्वारा प्रारम्भ किए गए कार्य से संबंधित है, जिन्होंने देखा कि भिन्न-भिन्न लंबाई के दो तारों को विभक्त करने से उत्पन्न ध्वनियां व्यंजन हैं यदि दोनों लंबाई सामान्य लंबाई के छोटे पूर्णांक गुणज हैं। कंपायमान तार के आकार और साइन फलन के ग्राफ के मध्य समानता मात्र संयोग नहीं है। समुद्रशास्त्र में कुछ तरंगों के आकार और साइन फलन के ग्राफ के मध्य समानता भी संयोग नहीं है। जलवायु विज्ञान, जीव विज्ञान और अर्थशास्त्र सहित कुछ अन्य क्षेत्रों में ऋतु-संबंधी आवधिकताएँ होती हैं। इनके अध्ययन में अधिकांशतः साइन और कोसाइन फलन की आवधिक प्रकृति सम्मिलित होती है।

फूरियर श्रृंखला

कई क्षेत्र त्रिकोणमिति का उपयोग किसी लेख में की जा सकने वाली तुलना से कहीं अधिक उन्नत विधियों से करते हैं। इनमें अधिकांशतः 18वें और 19वें दशक के फ्रांसीसी गणितज्ञ और भौतिक विज्ञानी जीन बैप्टिस्ट जोसेफ फूरियर के पश्चात् फूरियर श्रृंखला सम्मिलित होती है। फूरियर श्रृंखला के कई वैज्ञानिक क्षेत्रों में विशेष रूप से ऊपर उल्लिखित ऋतु-संबंधी आवधिकों और तरंग गति से संयोजित सभी घटनाओं में, और इसलिए विकिरण के, ध्वनिकी के, भूकंप विज्ञान के, रेडियो मॉड्यूलेशन के, इलेक्ट्रॉनिक्स और विद्युत शक्ति अभियांत्रिकी में तरंगों के अध्ययन में आश्चर्यजनक रूप से विविध प्रकार के अनुप्रयोग हैं।

फूरियर श्रृंखला इस रूप का योग है:

$\square +\underbrace {\square \cos \theta +\square \sin \theta } _{1}+\underbrace {\square \cos(2\theta )+\square \sin(2\theta )} _{2}+\underbrace {\square \cos(3\theta )+\square \sin(3\theta )} _{3}+\cdots \,$

जहां प्रत्येक वर्ग ($\square$) भिन्न संख्या है, और अपरिमित रूप से कई पद जोड़ रहा है। फूरियर ने ऊष्मा प्रवाह और प्रसार का अध्ययन करने के लिए इनका उपयोग किया (प्रसार वह प्रक्रिया है जिसके अंतर्गत, जब आप गैलन पानी में चीनी का अवयव डालते हैं, तो चीनी धीरे-धीरे पानी के माध्यम से घुलती है, अथवा प्रदूषक वायु के माध्यम से प्रसारित होता है, अथवा कोई भी घुला हुआ पदार्थ किसी तरल पदार्थ के माध्यम से प्रसारित होता है)।

फूरियर श्रृंखला उन विषयों पर भी प्रयुक्त होती है जिनका तरंग गति से संबंध स्पष्ट नहीं है। सर्वव्यापी उदाहरण डेटा संपीड़न है जिसके द्वारा छवि संपीड़न, ऑडियो संपीड़न (डेटा) और वीडियो संपीड़न डेटा को अधिक छोटे आकार में संपीड़ित किया जाता है जो टेलीफ़ोन, इंटरनेट और ब्रॉडकास्टिंग कंप्यूटर नेटवर्क पर उनके प्रसारण को संभव बनाता है। अन्य उदाहरण, जिसका ऊपर उल्लेख किया गया है, वह प्रसार है। अन्य में संख्याओं की ज्यामिति, आइसोपरिमेट्री, यादृच्छिक चाल की पुनरावृत्ति, द्विघात पारस्परिकता, केंद्रीय सीमा प्रमेय, हाइजेनबर्ग की असमानता सम्मिलित हैं।

फूरियर रूपांतरण

फूरियर श्रृंखला की तुलना में अधिक अमूर्त अवधारणा फूरियर रूपांतरण का विचार है। फूरियर रूपांतरण में योग के अतिरिक्त समाकल सम्मिलित होते हैं, और वैज्ञानिक क्षेत्रों के समान विविध प्रकार में उपयोग किए जाते हैं। कई प्राकृतिक नियम मात्राओं में परिवर्तन की दरों को मात्राओं से संयोजित करके व्यक्त किए जाते हैं। उदाहरण के लिए: जनसंख्या में परिवर्तन की दर कभी-कभी संयुक्त रूप से (1) वर्तमान जनसंख्या और (2) वह मात्रा जिसके द्वारा वर्तमान जनसंख्या वहन क्षमता से कम हो जाती है, के समानुपाती होती है। इस प्रकार के संबंध को अवकल समीकरण कहा जाता है। यदि, यह जानकारी देते हुए, कोई जनसंख्या को समय के फलन के रूप में व्यक्त करने का प्रयास करता है, तो वह अंतर समीकरण को हल करने का प्रयास कर रहा है। फूरियर ट्रांसफॉर्म का उपयोग कुछ अंतर समीकरणों को बीजगणितीय समीकरणों में परिवर्तित करने के लिए किया जा सकता है, जिसके लिए उन्हें हल करने के तरीके ज्ञात हैं। फूरियर ट्रांसफॉर्म के कई उपयोग हैं। लगभग किसी भी वैज्ञानिक संदर्भ में जिसमें स्पेक्ट्रम, लयबद्ध , या अनुनाद शब्द सामने आते हैं, फूरियर ट्रांसफॉर्म या फूरियर श्रृंखला निकट हैं।

गणितीय मनोविज्ञान सहित सांख्यिकी

बुद्धि लब्धि को कभी-कभी सामान्य वितरण के वक्र के अनुसार वितरित माना जाता है। वक्र के अंतर्गत लगभग 40% क्षेत्र 100 से 120 के अंतराल में है; तदनुसार, लगभग 40% जनसंख्या का आईक्यू परीक्षणों में 100 और 120 के मध्य स्कोर होता है। वक्र के अंतर्गत लगभग 9% क्षेत्र 120 से 140 के अंतराल में है; तदनुसार, लगभग 9% जनसंख्या का आईक्यू परीक्षणों आदि पर 120 और 140 के मध्य स्कोर होता है। इसी प्रकार कई अन्य वस्तुएँ सामान्य वितरण के वक्र के अनुसार वितरित की जाती हैं, जिसमें कई भौतिक मापों में माप त्रुटियां भी सम्मिलित होती हैं। घंटी के आकार के वक्र की सर्वव्यापकता क्यों? इसका सैद्धांतिक कारण है, और इसमें फूरियर रूपांतरण और इसलिए त्रिकोणमितीय फलन सम्मिलित हैं। यह सांख्यिकी में फूरियर रूपांतरण के विभिन्न अनुप्रयोगों में से है।

जब सांख्यिकीविद् ऋतु-संबंधी आवधिकों का अध्ययन करते हैं, तो त्रिकोणमितीय फलन भी प्रयुक्त होते हैं, जिन्हें अधिकांशतः फूरियर श्रृंखला द्वारा दर्शाया जाता है।

संख्या सिद्धांत

त्रिकोणमिति और संख्या सिद्धांत के मध्य संबंध का संकेत मिलता है। शिथिल रूप से कहें तो, कोई यह कह सकता है कि संख्या सिद्धांत संख्याओं के मात्रात्मक गुणों के बजाय गुणात्मक गुणों से संबंधित है।

${\frac {1}{42}},\qquad {\frac {2}{42}},\qquad {\frac {3}{42}},\qquad \dots \dots ,\qquad {\frac {39}{42}},\qquad {\frac {40}{42}},\qquad {\frac {41}{42}}.$

जो निम्नतम शर्तों में नहीं हैं उन्हें त्यागें; केवल वही रखें जो निम्नतम शर्तों में हों:

${\frac {1}{42}},\qquad {\frac {5}{42}},\qquad {\frac {11}{42}},\qquad \dots ,\qquad {\frac {31}{42}},\qquad {\frac {37}{42}},\qquad {\frac {41}{42}}.$

फिर त्रिकोणमिति लाएँ:

$\cos \left(2\pi \cdot {\frac {1}{42}}\right)+\cos \left(2\pi \cdot {\frac {5}{42}}\right)+\cdots +\cos \left(2\pi \cdot {\frac {37}{42}}\right)+\cos \left(2\pi \cdot {\frac {41}{42}}\right)$

योग का मान -1 है, क्योंकि 42 में विषम संख्या में अभाज्य गुणनखंड हैं और उनमें से कोई भी दोहराया नहीं गया है: 42 = 2 × 3 × 7. (यदि गैर-दोहराए गए कारकों की संख्या सम संख्या में होती तो योग होता) 1 रहा है; यदि कोई दोहराया गया अभाज्य गुणनखंड होता (उदाहरण के लिए, 60 = 2 × 2 × 3 × 5) तो योग 0 होता; योग 42 पर मूल्यांकन किया गया मोबियस फलन है।) यह संभावना की ओर संकेत करता है संख्या सिद्धांत पर फूरियर विश्लेषण लागू करना।

गैर-त्रिकोणमितीय समीकरणों को हल करना

त्रिकोणमिति का उपयोग करके विभिन्न प्रकार के समीकरणों को हल किया जा सकता है।

उदाहरण के लिए, स्थिर गुणांक वाले [[रैखिक अंतर समीकरण]] या रैखिक अंतर समीकरण के समाधान इसके विशिष्ट समीकरण के eigenvalues ​​​​के संदर्भ में व्यक्त किए जाते हैं; यदि कुछ eigenvalues ​​​​संमिश्र संख्या हैं, तो जटिल शब्दों को वास्तविक शब्दों के त्रिकोणमितीय कार्यों द्वारा प्रतिस्थापित किया जा सकता है, यह दर्शाता है कि गतिशील चर दोलन प्रदर्शित करता है।

इसी प्रकार, क्यूबिक फलन#त्रिकोणमिति और तीन वास्तविक समाधानों वाले हाइपरबोलिक समाधानों में बीजगणितीय समाधान होता है जो अनुपयोगी होता है क्योंकि इसमें जटिल संख्याओं के घनमूल होते हैं; वास्तविक पदों के त्रिकोणमितीय फलनों के संदर्भ में फिर से वैकल्पिक समाधान मौजूद है।