सांस्थितिक वर्गीकरण

"Dependency resolution" redirects here. For other uses, see Dependency (disambiguation).

कंप्यूटर विज्ञान में, एक निर्देशित ग्राफ का टोपोलॉजिकल सॉर्ट या टोपोलॉजिकल ऑर्डरिंग इसके शीर्ष (ग्राफ सिद्धांत) का कुल क्रम है, जैसे कि प्रत्येक निर्देशित किनारे यूवी के लिए शीर्ष यू से शीर्ष वी तक , u क्रम में v से पहले आता है। उदाहरण के लिए, ग्राफ़ के शीर्ष निष्पादित किए जाने वाले कार्यों का प्रतिनिधित्व कर सकते हैं, और किनारे उन बाधाओं का प्रतिनिधित्व कर सकते हैं कि एक कार्य दूसरे से पहले किया जाना चाहिए; इस एप्लिकेशन में, टोपोलॉजिकल ऑर्डरिंग कार्यों के लिए सिर्फ एक वैध अनुक्रम है। संक्षेप में, एक टोपोलॉजिकल सॉर्ट एक ग्राफ़ ट्रैवर्सल है जिसमें प्रत्येक नोड v पर उसकी सभी निर्भरताओं का दौरा करने के बाद ही दौरा किया जाता है। एक टोपोलॉजिकल ऑर्डरिंग तभी संभव है जब ग्राफ़ में कोई निर्देशित चक्र न हो, अर्थात , यदि यह एक निर्देशित अचक्रीय ग्राफ (डीएजी) है। किसी भी डीएजी में कम से कम एक टोपोलॉजिकल ऑर्डरिंग होती है, और कलन विधि रैखिक समय में किसी भी डीएजी के टोपोलॉजिकल ऑर्डरिंग के निर्माण के लिए जाने जाते हैं। टोपोलॉजिकल सॉर्टिंग के कई अनुप्रयोग हैं, विशेष रूप से फीडबैक आर्क सेट जैसी रैंकिंग समस्याओं में। डीएजी में कनेक्टिविटी (ग्राफ सिद्धांत) होने पर भी टोपोलॉजिकल सॉर्टिंग संभव है।

उदाहरण

टोपोलॉजिकल सॉर्टिंग का विहित अनुप्रयोग जॉब शॉप में उनके निर्भरता ग्राफ के आधार पर नौकरियों या कार्यों के अनुक्रम को शेड्यूल करना है। कार्यों को शीर्षों द्वारा दर्शाया जाता है, और यदि कार्य x को कार्य y शुरू करने से पहले पूरा किया जाना चाहिए तो x से y तक एक बढ़त होती है (उदाहरण के लिए, कपड़े धोते समय, कपड़े को ड्रायर में डालने से पहले वॉशिंग मशीन को समाप्त करना होगा) . फिर, एक टोपोलॉजिकल सॉर्ट एक आदेश देता है जिसमें कार्य करना है। परियोजना प्रबंधन में शेड्यूलिंग के लिए कार्यक्रम मूल्यांकन और समीक्षा तकनीक तकनीक के संदर्भ में टोपोलॉजिकल सॉर्टिंग एल्गोरिदम के निकट संबंधी अनुप्रयोग का पहली बार 1960 के दशक की शुरुआत में अध्ययन किया गया था। इस एप्लिकेशन में, ग्राफ़ के कोने किसी प्रोजेक्ट के मील के पत्थर का प्रतिनिधित्व करते हैं, और किनारे उन कार्यों का प्रतिनिधित्व करते हैं जिन्हें एक मील के पत्थर और दूसरे के बीच निष्पादित किया जाना चाहिए। टोपोलॉजिकल सॉर्टिंग परियोजना के महत्वपूर्ण पथ विधि, मील के पत्थर और कार्यों के अनुक्रम को खोजने के लिए रैखिक-समय एल्गोरिदम का आधार बनाती है जो समग्र परियोजना अनुसूची की लंबाई को नियंत्रित करती है।

कंप्यूटर विज्ञान में, इस प्रकार के अनुप्रयोग अनुदेश शेड्यूलिंग, स्प्रेडशीट्स में फॉर्मूला मानों की पुन: गणना करते समय फॉर्मूला सेल मूल्यांकन का क्रम, तर्क संश्लेषण, मेकफ़ाइल में प्रदर्शन करने के लिए संकलन कार्यों के क्रम का निर्धारण, डेटा क्रमबद्धता, और लिंकर (कंप्यूटिंग) में प्रतीक निर्भरता को हल करने में उत्पन्न होते हैं। ). इसका उपयोग यह तय करने के लिए भी किया जाता है कि डेटाबेस में विदेशी कुंजियों के साथ तालिकाओं को किस क्रम में लोड किया जाए।

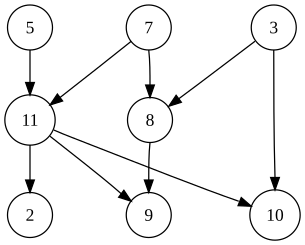
The graph shown to the left has many valid topological sorts, including: 5, 7, 3, 11, 8, 2, 9, 10 (visual top-to-bottom, left-to-right) 3, 5, 7, 8, 11, 2, 9, 10 (smallest-numbered available vertex first) 5, 7, 3, 8, 11, 10, 9, 2 (fewest edges first) 7, 5, 11, 3, 10, 8, 9, 2 (largest-numbered available vertex first) 5, 7, 11, 2, 3, 8, 9, 10 (attempting top-to-bottom, left-to-right) 3, 7, 8, 5, 11, 10, 2, 9 (arbitrary)

एल्गोरिदम

टोपोलॉजिकल सॉर्टिंग के लिए सामान्य एल्गोरिदम में नोड्स की संख्या और किनारों की संख्या में रैखिक समय चलता है, असममित रूप से, $O(\left|{V}\right|+\left|{E}\right|).$

काह्न का एल्गोरिदम

Not to be confused with Kuhn's algorithm.

इनमें से एक एल्गोरिदम, जिसका वर्णन सबसे पहले किया गया था Kahn (1962), अंतिम टोपोलॉजिकल सॉर्ट के समान क्रम में शीर्षों को चुनकर काम करता है। सबसे पहले, प्रारंभ नोड्स की एक सूची ढूंढें जिनमें कोई आने वाला किनारा नहीं है और उन्हें सेट एस में डालें; गैर-रिक्त चक्रीय ग्राफ़ में कम से कम एक ऐसा नोड मौजूद होना चाहिए। तब:

एल ← खाली सूची जिसमें क्रमबद्ध तत्व होंगे
एस ← बिना आने वाले किनारे वाले सभी नोड्स का सेट

'जबकि' S' खाली नहीं है 'करें'
    S से एक नोड n हटाएँ
    L में n जोड़ें
    'प्रत्येक के लिए' नोड एम किनारे ई के साथ एन से एम तक 'करें'
        ग्राफ़ से किनारा e हटाएँ
        'यदि' एम के पास कोई अन्य आने वाला किनारा नहीं है 'तो'
            S में m डालें

'यदि' ग्राफ़ में किनारे हैं 'तो'
    'वापसी' त्रुटि (ग्राफ़ में कम से कम एक चक्र है)
'अन्य'
    'वापसी' एल (एक स्थैतिक रूप से क्रमबद्ध क्रम)

यदि ग्राफ़ एक निर्देशित चक्रीय ग्राफ़ है, तो एक समाधान सूची L में समाहित होगा (समाधान आवश्यक रूप से अद्वितीय नहीं है)। अन्यथा, ग्राफ़ में कम से कम एक चक्र होना चाहिए और इसलिए टोपोलॉजिकल सॉर्ट असंभव है।

परिणामी प्रकार की गैर-विशिष्टता को दर्शाते हुए, संरचना एस केवल एक सेट या कतार या स्टैक हो सकती है। सेट एस से नोड्स एन को हटाए जाने के क्रम के आधार पर, एक अलग समाधान बनाया जाता है। काह्न के एल्गोरिदम का एक रूपांतर जो शब्दकोषीय क्रम के संबंधों को तोड़ता है, समानांतर शेड्यूलिंग और स्तरित ग्राफ़ ड्राइंग के लिए कॉफ़मैन-ग्राहम एल्गोरिदम का एक प्रमुख घटक बनाता है।

गहराई-पहली खोज

टोपोलॉजिकल सॉर्टिंग के लिए एक वैकल्पिक एल्गोरिदम गहराई-पहली खोज पर आधारित है। एल्गोरिदम ग्राफ़ के प्रत्येक नोड के माध्यम से एक मनमाना क्रम में लूप करता है, एक गहराई-पहली खोज शुरू करता है जो तब समाप्त होता है जब यह किसी भी नोड से टकराता है जो टोपोलॉजिकल सॉर्ट की शुरुआत के बाद से पहले ही देखा जा चुका है या नोड में कोई आउटगोइंग किनारा नहीं है (यानी ए) लसीका नोड):

एल ← खाली सूची जिसमें क्रमबद्ध नोड्स होंगे
'जबकि' एक स्थायी चिह्न 'डू' के बिना नोड्स मौजूद है
    एक अचिह्नित नोड का चयन करें n
    यात्रा(एन)

'फ़ंक्शन' विज़िट (नोड एन)
    'यदि' n का स्थायी चिह्न 'तब' है
        'वापस करना'
    'यदि' n में अस्थायी चिह्न 'तो' है
        'स्टॉप' (ग्राफ़ में कम से कम एक चक्र है)

    अस्थायी चिह्न से n अंकित करें

    'प्रत्येक' नोड m के लिए n से m तक के किनारे के साथ 'करें'
        यात्रा(एम)

    n से अस्थायी चिह्न हटाएँ
    n को स्थायी चिह्न से चिह्नित करें
    L के शीर्ष में n जोड़ें

प्रत्येक नोड n को अन्य सभी नोड्स पर विचार करने के बाद ही आउटपुट सूची L में जोड़ा जाता है जो n (ग्राफ़ में n के सभी वंशज) पर निर्भर होते हैं। विशेष रूप से, जब एल्गोरिदम नोड एन जोड़ता है, तो हमें गारंटी दी जाती है कि सभी नोड्स जो एन पर निर्भर हैं वे पहले से ही आउटपुट सूची एल में हैं: उन्हें एल में पुनरावर्ती कॉल द्वारा विज़िट() में जोड़ा गया था जो एन पर जाने के लिए कॉल से पहले समाप्त हो गया था, या विज़िट() के लिए कॉल द्वारा जो n पर विज़िट करने के लिए कॉल से पहले ही शुरू हो गया था। चूँकि प्रत्येक किनारे और नोड का एक बार दौरा किया जाता है, एल्गोरिथ्म रैखिक समय में चलता है। यह गहराई-प्रथम-खोज-आधारित एल्गोरिदम द्वारा वर्णित है Cormen et al. (2001); ऐसा लगता है कि इसका वर्णन पहली बार 1976 में टार्जन द्वारा मुद्रित रूप में किया गया था।

समानांतर एल्गोरिदम

एक समानांतर रैंडम-एक्सेस मशीन पर, O((लॉग एन) में एक टोपोलॉजिकल ऑर्डरिंग का निर्माण किया जा सकता है²) प्रोसेसर की बहुपद संख्या का उपयोग करते हुए, समस्या को जटिलता वर्ग एनसी (जटिलता) में डालें². ऐसा करने का एक तरीका यह है कि दिए गए ग्राफ़ के आसन्न मैट्रिक्स को बार-बार लघुगणकीय रूप से कई बार वर्गाकार किया जाए, जिसमें न्यूनतमकरण के स्थान पर अधिकतमीकरण के साथ न्यूनतम-प्लस मैट्रिक्स गुणन का उपयोग किया जाए। परिणामी मैट्रिक्स ग्राफ़ में सबसे लंबी पथ समस्या दूरी का वर्णन करता है। शीर्षों को उनके सबसे लंबे आने वाले पथों की लंबाई के आधार पर क्रमबद्ध करने से एक टोपोलॉजिकल ऑर्डरिंग उत्पन्न होती है।

वितरित मेमोरी मशीनों पर समानांतर टोपोलॉजिकल सॉर्टिंग के लिए एक एल्गोरिदम एक निर्देशित एसाइक्लिक ग्राफ के लिए काह्न के एल्गोरिदम को समानांतर करता है $G=(V,E)$. उच्च स्तर पर, काह्न का एल्गोरिदम बार-बार इंडिग्री 0 के शीर्षों को हटाता है और उन्हें उसी क्रम में टोपोलॉजिकल सॉर्टिंग में जोड़ता है जिसमें उन्हें हटाया गया था। चूंकि हटाए गए शीर्षों के आउटगोइंग किनारों को भी हटा दिया गया है, डिग्री 0 के शीर्षों का एक नया सेट होगा, जहां प्रक्रिया तब तक दोहराई जाती है जब तक कि कोई शीर्ष न बचे। यह एल्गोरिथम कार्य करता है $D+1$ पुनरावृत्तियाँ, कहाँ D सबसे लंबा रास्ता है G. प्रत्येक पुनरावृत्ति को समानांतर किया जा सकता है, जो निम्नलिखित एल्गोरिदम का विचार है।

निम्नलिखित में यह माना गया है कि ग्राफ़ विभाजन पर संग्रहीत है p प्रसंस्करण तत्व (पीई) जिन्हें लेबल किया गया है $0,\dots ,p-1$. प्रत्येक पीई i स्थानीय शीर्षों के एक सेट को प्रारंभ करता है $Q_{i}^{1}$ डिग्री 0 के साथ, जहां ऊपरी सूचकांक वर्तमान पुनरावृत्ति का प्रतिनिधित्व करता है। चूँकि सभी शीर्ष स्थानीय सेट में हैं $Q_{0}^{1},\dots ,Q_{p-1}^{1}$ डिग्री 0 है, यानी वे आसन्न नहीं हैं, उन्हें वैध टोपोलॉजिकल सॉर्टिंग के लिए मनमाने ढंग से क्रम में दिया जा सकता है। प्रत्येक शीर्ष पर एक वैश्विक सूचकांक निर्दिष्ट करने के लिए, एक उपसर्ग योग की गणना आकारों पर की जाती है $Q_{0}^{1},\dots ,Q_{p-1}^{1}$. तो हर कदम पर हैं ${\textstyle \sum _{i=0}^{p-1}|Q_{i}|}$ टोपोलॉजिकल सॉर्टिंग में शीर्ष जोड़े गए।

दो प्रसंस्करण तत्वों के साथ डीएजी पर समानांतर टोपोलॉजिकल सॉर्टिंग एल्गोरिदम का निष्पादन।

पहले चरण में पी.ई j सूचकांक निर्दिष्ट करता है ${\textstyle \sum _{i=0}^{j-1}|Q_{i}^{1}|,\dots ,\left(\sum _{i=0}^{j}|Q_{i}^{1}|\right)-1}$ में स्थानीय शिखर तक $Q_{j}^{1}$. इन शिखरों में $Q_{j}^{1}$ उनके संगत आउटगोइंग किनारों सहित हटा दिए जाते हैं। प्रत्येक आउटगोइंग किनारे के लिए $(u,v)$ समापन बिंदु के साथ v दूसरे पीई में $l,j\neq l$, संदेश $(u,v)$ पीई में पोस्ट किया गया है l. आख़िरकार शिखर में $Q_{j}^{1}$ हटा दिए जाते हैं, पोस्ट किए गए संदेश उनके संबंधित पीई को भेज दिए जाते हैं। प्रत्येक संदेश $(u,v)$ स्थानीय वर्टेक्स की डिग्री के अपडेट प्राप्त हुए v. यदि डिग्री शून्य हो जाती है, v जोड़ा गया है $Q_{j}^{2}$. फिर अगली पुनरावृत्ति शुरू होती है.

चरण में k, पर j सूचकांक निर्दिष्ट करता है ${\textstyle a_{k-1}+\sum _{i=0}^{j-1}|Q_{i}^{k}|,\dots ,a_{k-1}+\left(\sum _{i=0}^{j}|Q_{i}^{k}|\right)-1}$, कहाँ $a_{k-1}$चरण दर चरण संसाधित शीर्षों की कुल मात्रा है $k-1$. यह प्रक्रिया तब तक दोहराई जाती है जब तक कि प्रक्रिया के लिए कोई शीर्ष शेष न रह जाए ${\textstyle \sum _{i=0}^{p-1}|Q_{i}^{D+1}|=0}$. नीचे इस एल्गोरिथम का एक उच्च स्तरीय, एसपीएमडी|एकल प्रोग्राम, एकाधिक डेटा छद्म कोड अवलोकन है।

ध्यान दें कि स्थानीय ऑफसेट के लिए उपसर्ग योग#समानांतर एल्गोरिदम ${\textstyle a_{k-1}+\sum _{i=0}^{j-1}|Q_{i}^{k}|,\dots ,a_{k-1}+\left(\sum _{i=0}^{j}|Q_{i}^{k}|\right)-1}$ समानांतर रूप से कुशलतापूर्वक गणना की जा सकती है।

0 से पी-1 तक की आईडी वाले पी प्रोसेसिंग तत्व
इनपुट: जी = (वी, ई) डीएजी, पीई को वितरित, पीई इंडेक्स जे = 0, ..., पी - 1
आउटपुट: जी की टोपोलॉजिकल सॉर्टिंग

फ़ंक्शन ट्रैवर्सडीएजीवितरित
    δ स्थानीय शीर्षों की आने वाली डिग्री V     

Q = {v ∈ V | δ[v] = 0} // इंडिग्री 0 वाले सभी शीर्ष

    nrOfVerticesProcessed = 0

    करना
        Q के आकार पर वैश्विक बिल्ड उपसर्ग योग // इस चरण में ऑफसेट और शीर्षों की कुल मात्रा प्राप्त करें
        ऑफसेट = nrOfVerticesProcessed + sum(Qi, i = 0 से j - 1) // j प्रोसेसर इंडेक्स है
        'foreach' u 'in' Q
            लोकलऑर्डर[यू] = इंडेक्स++;
            'foreach' (u,v) in E 'do' post message (u, v) to PE owning vertex v
        nrOfVerticesProcessed += sum(|Qi|, i = 0 से p - 1)
        Q में शीर्षों के पड़ोसियों को सभी संदेश भेजें
        स्थानीय शीर्ष V के लिए संदेश प्राप्त करें
        Q में सभी शीर्ष हटाएँ
        foreach संदेश (यू, वी) प्राप्त हुआ:
            यदि --δ[v] = 0
                Q में v जोड़ें
    जबकि Q का वैश्विक आकार > 0 है

    स्थानीय ऑर्डर वापस करें

संचार लागत दिए गए ग्राफ़ विभाजन पर काफी हद तक निर्भर करती है। रनटाइम के लिए, CRCW PRAM|CRCW-PRAM मॉडल पर जो निरंतर समय में फ़ेच-एंड-डिक्रीमेंट की अनुमति देता है, यह एल्गोरिदम चलता है ${\textstyle {\mathcal {O}}\left({\frac {m+n}{p}}+D(\Delta +\log n)\right)}$, कहाँ D फिर से सबसे लंबा रास्ता है G और Δ अधिकतम डिग्री.

सबसे छोटा पथ खोजने के लिए आवेदन

टोपोलॉजिकल ऑर्डरिंग का उपयोग भारित ग्राफ निर्देशित एसाइक्लिक ग्राफ के माध्यम से सबसे छोटी पथ समस्या की त्वरित गणना करने के लिए भी किया जा सकता है। होने देना V ऐसे ग्राफ़ में शीर्षों की सूची टोपोलॉजिकल क्रम में हो। फिर निम्नलिखित एल्गोरिदम कुछ स्रोत शीर्ष से सबसे छोटे पथ की गणना करता है s अन्य सभी शीर्षों के लिए:

• होने देना d समान लंबाई की एक सरणी बनें V; यह सबसे कम पथ की दूरी बनाए रखेगा s. तय करना d[s] = 0, अन्य सभी d[u] = ∞.
• होने देना p समान लंबाई की एक सरणी बनें V, सभी तत्वों को आरंभीकृत करते हुए nil. प्रत्येक p[u] का पूर्ववर्ती धारण करेगा u से सबसे छोटे रास्ते में s को u.
• शीर्षों पर लूप करें u जैसा आदेश दिया गया है V, से शुरू s:
  • प्रत्येक शीर्ष के लिए v सीधे अनुसरण कर रहा हूँ u (यानी, वहां से एक किनारा मौजूद है u को v):
    • होने देना w से किनारे का वजन हो u को v.
    • किनारे को आराम दें: यदि d[v] > d[u] + w, तय करना
      • d[v] ← d[u] + w,
      • p[v] ← u.

समान रूप से:

• होने देना d समान लंबाई की एक सरणी बनें V; यह सबसे कम पथ की दूरी बनाए रखेगा s. तय करना d[s] = 0, अन्य सभी d[u] = ∞.
• होने देना p समान लंबाई की एक सरणी बनें V, सभी तत्वों को आरंभीकृत करते हुए nil. प्रत्येक p[u] का पूर्ववर्ती धारण करेगा u से सबसे छोटे रास्ते में s को u.
• शीर्षों पर लूप करें u जैसा आदेश दिया गया है V, से शुरू s:
  • प्रत्येक शीर्ष के लिए v में u (यानी, वहां से एक किनारा मौजूद है v को u):
    • होने देना w से किनारे का वजन हो v को u.
    • किनारे को आराम दें: यदि d[u] > d[v] + w, तय करना
      • d[u] ← d[v] + w,
      • p[u] ← v.

के ग्राफ पर n शीर्ष और mकिनारे, यह एल्गोरिदम लेता है Θ(n + m), यानी, रैखिक समय, समय।

अद्वितीयता

यदि टोपोलॉजिकल सॉर्ट में यह गुण है कि क्रमबद्ध क्रम में लगातार शीर्षों के सभी जोड़े किनारों से जुड़े हुए हैं, तो ये किनारे निर्देशित एसाइक्लिक ग्राफ में एक निर्देशित हैमिल्टनियन पथ बनाते हैं। यदि हैमिल्टनियन पथ मौजूद है, तो टोपोलॉजिकल सॉर्ट क्रम अद्वितीय है; कोई अन्य आदेश पथ के किनारों का सम्मान नहीं करता। इसके विपरीत, यदि कोई टोपोलॉजिकल सॉर्ट हैमिल्टनियन पथ नहीं बनाता है, तो डीएजी के पास दो या अधिक वैध टोपोलॉजिकल ऑर्डर होंगे, इस मामले में दो लगातार शीर्षों को स्वैप करके दूसरा वैध ऑर्डर बनाना हमेशा संभव होता है जो एक किनारे से जुड़े नहीं होते हैं एक दूसरे से। इसलिए, रैखिक समय में परीक्षण करना संभव है कि क्या एक अद्वितीय क्रम मौजूद है, और क्या हैमिल्टनियन पथ मौजूद है, अधिक सामान्य निर्देशित ग्राफ़ (यानी चक्रीय निर्देशित ग्राफ़) के लिए हैमिल्टनियन पथ समस्या की एनपी-कठोरता के बावजूद।

आंशिक आदेशों से संबंध

टोपोलॉजिकल ऑर्डरिंग का गणित में आंशिक ऑर्डर के रैखिक विस्तार की अवधारणा से भी गहरा संबंध है। आंशिक रूप से ऑर्डर किया गया सेट ≤ असमानता संबंध की परिभाषा के साथ वस्तुओं का एक सेट है, जो रिफ्लेक्सिविटी (x ≤ x), एंटीसिममेट्री (यदि x ≤ y और y ≤ x है तो x = y) और सकर्मक संबंध ( यदि x ≤ y और y ≤ z, तो x ≤ z)। कुल क्रम एक आंशिक क्रम है, जिसमें सेट में प्रत्येक दो वस्तुओं x और y के लिए, या तो x ≤ y या y ≤ x होता है। कुल ऑर्डर कंप्यूटर विज्ञान में परिचित हैं क्योंकि तुलना ऑपरेटरों को तुलना सॉर्टिंग एल्गोरिदम निष्पादित करने की आवश्यकता होती है। परिमित सेटों के लिए, कुल आदेशों को वस्तुओं के रैखिक अनुक्रमों से पहचाना जा सकता है, जहां ≤ संबंध सत्य होता है जब भी पहली वस्तु क्रम में दूसरी वस्तु से पहले आती है; इस तरह कुल ऑर्डर को अनुक्रम में बदलने के लिए एक तुलनात्मक सॉर्टिंग एल्गोरिदम का उपयोग किया जा सकता है। आंशिक क्रम का एक रैखिक विस्तार एक कुल क्रम है जो इसके साथ संगत है, इस अर्थ में कि, यदि आंशिक क्रम में x ≤ y है, तो कुल क्रम में x ≤ y भी है।

कोई भी किसी भी DAG से आंशिक क्रम को परिभाषित कर सकता है, वस्तुओं के सेट को DAG का शीर्ष मान सकता है, और किसी भी दो शीर्ष x और y के लिए x ≤ y को सत्य के रूप में परिभाषित कर सकता है, जब भी x से y तक कोई निर्देशित पथ मौजूद होता है; यानी, जब भी y, x से पहुंच योग्य हो। इन परिभाषाओं के साथ, डीएजी का टोपोलॉजिकल ऑर्डरिंग इस आंशिक ऑर्डर के रैखिक विस्तार के समान है। इसके विपरीत, किसी भी आंशिक आदेश को डीएजी में पहुंच योग्यता संबंध के रूप में परिभाषित किया जा सकता है। ऐसा करने का एक तरीका एक डीएजी को परिभाषित करना है जिसमें आंशिक रूप से ऑर्डर किए गए सेट में प्रत्येक ऑब्जेक्ट के लिए एक शीर्ष होता है, और वस्तुओं की प्रत्येक जोड़ी के लिए एक किनारा xy होता है जिसके लिए x ≤ y होता है। ऐसा करने का एक वैकल्पिक तरीका आंशिक क्रम की सकर्मक कमी का उपयोग करना है; सामान्य तौर पर, यह कम किनारों वाले डीएजी उत्पन्न करता है, लेकिन इन डीएजी में पहुंच योग्यता संबंध अभी भी वही आंशिक क्रम है। इन निर्माणों का उपयोग करके, कोई आंशिक आदेशों के रैखिक विस्तार को खोजने के लिए टोपोलॉजिकल ऑर्डरिंग एल्गोरिदम का उपयोग कर सकता है।

शेड्यूलिंग अनुकूलन से संबंध

परिभाषा के अनुसार, एक शेड्यूलिंग समस्या का समाधान जिसमें एक प्राथमिकता ग्राफ शामिल है, टोपोलॉजिकल सॉर्ट (मशीनों की संख्या की परवाह किए बिना) के लिए एक वैध समाधान है, हालांकि, टोपोलॉजिकल सॉर्ट अपने आप में एक शेड्यूलिंग अनुकूलन समस्या को बेहतर ढंग से हल करने के लिए पर्याप्त नहीं है। हू का एल्गोरिदम एक लोकप्रिय तरीका है जिसका उपयोग शेड्यूलिंग समस्याओं को हल करने के लिए किया जाता है जिसके लिए प्राथमिकता ग्राफ की आवश्यकता होती है और इसमें प्रसंस्करण समय शामिल होता है (जहां लक्ष्य सभी नौकरियों के बीच सबसे बड़े समापन समय को कम करना है)। टोपोलॉजिकल सॉर्ट की तरह, हू का एल्गोरिदम अद्वितीय नहीं है और इसे डीएफएस का उपयोग करके हल किया जा सकता है (सबसे बड़ी पथ लंबाई ढूंढकर और फिर नौकरियां निर्दिष्ट करके)।

यह भी देखें

• tsort, टोपोलॉजिकल सॉर्टिंग के लिए एक यूनिक्स प्रोग्राम
• फीडबैक आर्क सेट, किनारों का एक सेट जिसे हटाने से शेष सबग्राफ को टोपोलॉजिकल रूप से क्रमबद्ध किया जा सकता है
• टार्जन का दृढ़ता से जुड़े घटकों का एल्गोरिदम, एक एल्गोरिदम जो एक ग्राफ़ में दृढ़ता से जुड़े घटकों की टोपोलॉजिकल रूप से क्रमबद्ध सूची देता है
• प्री-टोपोलॉजिकल ऑर्डर

अग्रिम पठन

• D. E. Knuth, The Art of Computer Programming, Volume 1, section 2.2.3, which gives an algorithm for topological sorting of a partial ordering, and a brief history.

बाहरी संबंध

• NIST Dictionary of Algorithms and Data Structures: topological sort
• Weisstein, Eric W., "Topological Sort", MathWorld